Рабочая программа тип: общеобразовательная вид: адаптированная по Математике в 7-9 классах (базовый уровень)
| Вид материала | Рабочая программа |
- Рабочая программа тип: общеобразовательная вид: адаптированная по Математике в 10-11, 447.87kb.
- Приказ № от 20 г. Программа среднего (полного) общего образования по математике (базовый, 161.31kb.
- Рабочая программа по географии, для 10-11 класса основного общего образования (базовый, 1109.3kb.
- Рабочая программа педагога шашаевой татьяны георгиевны, II квалификационная категория, 379.29kb.
- Рабочая программа педагога шашаевой татьяны георгиевны, II квалификационная категория, 400.13kb.
- Кунаревой Арины Вячеславовны по учебному курсу «Алгебра и начала анализа» 10-11 класс, 408.51kb.
- Рабочая учебная программа по русскому языку 5-9 классы базовый уровень, 1943.89kb.
- Рабочая программа учебного курса «Информатика и икт. Базовый уровень» для 7-9 классов, 676.52kb.
- Рабочая учебная программа по литературе 10-11 классы базовый уровень, 652.87kb.
- Приказ № от 2010 г рабочая учебная программа по геометрии для 10 класса на 2010-2011, 355.59kb.
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №4
| СОГЛАСОВАНО Руководитель МО _____________Юшманова Н.М. Протокол № ___ от «____»____________2011 г. | СОГЛАСОВАНО Заместитель директора школы по УР МОУ СОШ №4 _____________ Бровко Н.Н. «____»____________2011 г. |
|
РАБОЧАЯ ПРОГРАММА
тип: общеобразовательная
вид: адаптированная
по Математике в 7-9 классах (базовый уровень)
Учитель:Перункова Г.А.
УМК: Мордкович А.Г.Алгебра. Части 1 и 2 для 7, 8, 9 классов.М:Мнемозина,2007г.
Учебник: Атанасян Л.С.и др.Геометрия 7-9.М:Просвещение,2007г.
Учебная нагрузка: 5часов в неделю (всего 340 часов)
Рассмотрено на заседании
педагогического совета школы
протокол № ____от «__»_______2011 г.
2011 - 2012 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Структура документа
Рабочая программа по математике включает разделы: пояснительную записку (цели изучения математики), требования к уровню подготовки выпускников, основное содержание с примерным распределением учебных часов по разделам курса, календарно-тематическое планирование, учебно-методическое обеспечение.
Рабочая программа по математике разработаны в соответствии с Примерной программой основного общего образования по математике, с учетом требований федерального компонента государственного стандарта общего образования 2004 г. и на основе авторских программ: Алгебра.7-9 классы. Авт.-сост. И.И. Зубарева, А.Г. Мордкович. – М.Мнемозина, 2007; Геометрия 7-9 классы. Авт-сост. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. М. Просвещение, 2008.
Нормативные документы:
Дорофеев Г. В. и др. Оценка качества подготовки выпускников средней (полной) школы по математике. М., «Дрофа», 2002.
- Концепция модернизации российского образования на период до 2010// «Вестник образования» -2002- № 6 - с.11-40.
- Концепция математического образования (проект)//Математика в школе.- 2000. – № 2. – с.13-18.
- Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразовательных школ, гимназий, лицеев. Математика 5 – 11 классы. М., «Дрофа», 2002.
5. Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //«Вестник образования» -2004 - № 14 - с.107-119
Изучение математики в основной школе направлено на овладение умениями общеучебного характера, разнообразными способами деятельности, приобретение опыта:
- планирования и осуществления алгоритмической деятельности, выполнения заданий конструирования новых алгоритмов;
- решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска путей и способов решения;
- исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
- ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
- проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Место предмета в базисном учебном плане
На изучение математики в 7-9 классах отводится 510 часов из расчета 5 часов в неделю.
Алгебра-324 часа
Геометрия-186 часов.
Программа разработана для общеобразовательного класса средней общеобразовательной школы.
Контроль и оценивание знаний осуществляется путем проведения самостоятельных работ, проверочных работ, тестов, практических работ, математических диктантов, теоретических зачетов, контрольных работ.
Тематическое распределение часов
| №№ | Тематические блоки | Количество часов | |
| | | государственная примерная программа (5-9 класс) | адаптированная программа (5-6 класс) |
| 1 | Арифметика | 250 | 214 |
| 2 | Алгебра | 270 | 38 |
| 3 | Геометрия | 220 | 37 |
| 4 | Элементы логики, комбинаторики, статистики и теории вероятностей | 45 | 20 |
| 5 | Повторение | 90 | 31 |
| | Итого | 875 | 340 |
СОДЕРЖАНИЕ ОБУЧЕНИЯ по разделу: Элементы логики, комбинаторики, статистики и теории вероятностей.
| | Алгебра | Геометрия |
| 7 класс | 6 часов: Размах. Мода. Медиана. Примеры решения комбинаторных задач: перебор вариантов, правило умножения. Перестановки. | 2 часа. Доказательство. Определения, доказательства, аксмомы и теоремы. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы. |
| 8 класс | 4 часа. Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки. | |
| 9 класс | 12 часов. Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Частота события. Несовместные события. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность. Множество. Элемент множества, подмножества. Объединение и пересечение множеств. Диаграммы Эйлера. | 1 час. Беседа об аксиомах геометрии. Пятый постулат Евклида и его история. Понятие об аксиоматике и аксиоматическом построении геометрии. |
СОДЕРЖАНИЕ ОБУЧЕНИЯ
АЛГЕБРА
7 класс
МАТЕМАТИЧЕСКИЙ ЯЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ (14 ч).
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной.
Недопустимое значение переменной. Первые представления о математическом языке и о
математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней
ЛИНЕЙНАЯ ФУНКЦИЯ (12 ч).
Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки M (a;b) в прямоугольной системе координат.
Линейное уравнение с двумя переменными. Решение уравнения ax + by + c = 0.
График уравнения. Алгоритм построения графика уравнения ax+by+c=0. Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График
линейной функции. Наибольшее и наименьшее значения линейной функции на заданном
промежутке. Возрастание и убывание линейной функции. Линейная функция y=kx и ее график. Взаимное расположение графиков линейных функций.
СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ (13 ч).
Система уравнений. Решение системы уравнений. Графический метод решения системы
уравнений. Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ (7 ч).
Степень. Основание степени. Показатель степени. Свойства степени с натуральным
показателем. Умножение и деление степеней с одинаковыми основаниями. Степень с нулевым показателем.
ОДНОЧЛЕНЫ. ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ (9 ч).
Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлена.
Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИК ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ (21 ч).
Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена. Сложение и вычитание многочлена. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов.
Деление многочлена на одночлен.
РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ (20 ч).
Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на
множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата. Понятие алгебраической дроби. Сокращение алгебраической дроби.
Тождество. Тождественно равные выражения. Тождественные преобразования.
ФУНКЦИЯ Y = X2 (9 ч).
Функция y = x2, ее свойства и график. Функция y =-x2, ее свойства и график.
Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции.
Первое представление о непрерывных функциях. Точка разрыва. Разъяснение записи у=f(x). Функциональная символика.
ЭЛЕМЕНТЫ ЛОГИГИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ (6 ч).
Размах. Мода. Медиана. Примеры решения комбинаторных задач: перебор вариантов, правило умножения. Перестановки.
8 класс.
АЛГЕБРАИЧЕСКИЕ ДРОБИ (21 ч).
Понятие алгебраической дроби. Основные свойства алгебраической дроби.Сокращение
алгебраических дробей. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений
(первые представления). Степень с отрицательным целым показателем.
ФУНКЦИЯ Y = √X. СВОЙСТВА КВАДРАТНОГО КОРНЯ (18 ч).
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция y = √x, ее свойства и график. Выпуклость функции. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения
квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль
действительного числа График функции y=|x|. Формула √x2 = |x|.
КВАДРАТИЧНАЯ ФУНКЦИЯ. ФУНКЦИЯ Y=K/X (18 x)
Функция y=k/x, ее график, свойства. Функция y=k/x, ее свойства, график. Гипербола. Асимптота.
Построение графиков функций y=f(x+а), y=f((x)+m, y=f(x+а)+m, y=-f(x) по известному графику функции y =f(x). Квадратный трехчлен. Квадратичная функция, ее свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций y=C, y=kx+m, y=k/x, y =ax2+bx+c, y=√x, y=| x|.
Графическое решение квадратных уравнений.
КВАДРАТНЫЕ УРАВНЕНИЯ (21ч).
Квадратное уравнение. Приведенное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата. Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные представления).
Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной. Рациональные уравнения как математические модели реальных ситуаций. Частные случаи формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Иррациональное уравнение. Метод возведения в квадрат
НЕРАВЕНСТВА (15 ч)
Свойства числовых неравенств. Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильные неравенства. Равносильное преобразование неравенства. Квадратное неравенство. Алгоритм решения квадратного неравенства. Возрастающая функция. Убывающая функция. Исследование функций на монотонность (с использованием свойств числовых неравенств).
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку к избытку. Стандартный вид числа.
ЭЛЕМЕНТЫ ЛОГИГИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ
ВЕРОЯТНОСТЕЙ (4 ч).
Статистические данные. Представление данных в виде таблиц, диаграмм, графиков. Средние результатов измерений. Понятие о статистическом выводе на основе выборки.
9 класс.
РАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА И ИХ СИСТЕМЫ (13 ч).
Линейные и квадратные неравенства (повторение). Рациональное неравенство. Метод интервалов. Система неравенств. Решение системы неравенств.
СИСТЕМЫ УРАВНЕНИЙ (19 ч).
Рациональные уравнения с двумя переменными. Решение уравнения p(x; y)=0. Равносильные уравнения с двумя переменными. Формула расстояния между двумя точками координатной плоскости. График уравнения (x-a)2+(y–b)2=r2. Система уравнений с двумя переменными. Решение системы уравнений. Неравенства и системы неравенств с двумя переменными. Методы решения систем уравнений (метод подстановки, алгебраического сложения, введения новых переменных). Равносильность систем уравнений. Системы уравнений как математические модели реальных ситуаций.
ЧИСЛОВЫЕ ФУНКЦИИ (25 ч).
Функция. Независимая переменная. Зависимая переменная. Область определения функции. Естественная область определения функции. Область значений функции.
Способы задания функции (аналитический, графический, табличный, словесный).
Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность).
Исследование функций: y=C, y=kx+m, y=kx2, y=k/x, y=√x, y= x|, y =ax2+bx+c.
Четные и нечетные функции. Алгоритм исследования функции на четность. Графики четной и нечетной функции.
Степенная функция с натуральным показателем, ее свойства и график. Степенная функция
отрицательным целым показателем, ее свойства и график. Функция y=3√x, ее свойства и график.
ПРОГРЕССИИ (15 ч).
Числовая последовательность. Способы задания числовых последовательностей
(аналитический, словесный, рекуррентный). Свойства числовых последовательностей.
Арифметическая прогрессия. Формула n-члена. Формула суммы членов конечной
арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. Формула n-го члена. Формула суммы членов конечной геометрической прогрессии. Характеристическое свойство. Прогрессии и банковские расчеты.
ЭЛЕМЕНТЫ ЛОГИГИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ
ВЕРОЯТНОСТЕЙ (12 ч).
Вероятность. Событие (случайное, достоверное, невозможное). Классическая вероятностная схема. Противоположные события. Частота события. Несовместные события. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности. Вероятность суммы двух событий. Вероятность противоположного события. Статистическая устойчивость. Статистическая вероятность.
Множество. Элемент множества, подмножества. Объединение и пересечение множеств.
Диаграммы Эйлера.
ГЕОМЕТРИЯ
7 класс
НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ (7 ч)
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.
ТРЕУГОЛЬНИКИ (14 ч).
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы,
биссектрисы и высота треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ (9ч).
Признаки параллельности прямых. Аксиома параллельности прямых. Свойства параллельных прямых.
СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА (16ч).
Сумма углов треугольника. Соотношение между сторонами и углами треугольника.
Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.
ЭЛЕМЕНТЫ ЛОГИГИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ
ВЕРОЯТНОСТЕЙ (2 ч).
Доказательство. Определения, доказательства, аксмомы и теоремы. Необходимые и достаточные условия. Контрпример. Доказательство от противного. Прямая и обратная теоремы.
8 класс
ЧЕТЫРЕХУГОЛЬНИКИ (14ч).
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Основная и центральная симметрия.
ПЛОЩАДЬ (14 ч).
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ ( 19 ч).
Подобные треугольники. Признаки подобия треугольников. Применение подобия к
доказательству теорем и решение задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
ОКРУЖНОСТЬ (17 ч).
Взаимное расположение прямой и окружности. Касательная к окружности, ее свойства и
признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
9 класс
ВЕКТОРЫ. МЕТОД КООРДИНАТ (18 ч).
Понятие вектора. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Уравнение окружности и прямой. Применение векторов и координат при решении задач.
СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ ВЕКТОРОВ (10 ч).
Синус, косинус и тангенс угла. Теоремы синусов и косинусов. Решение треугольников.
Скалярное произведение векторов и его применение в геометрических задачах.
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА (12 ч).
Правильные многоугольники. Окружности, описанная около правильного многоугольника и вписанная в него. Построение правильных многоугольников. Длина окружности. Площадь круга.
ДВИЖЕНИЕ (8 ч).
Отображение плоскости на себя. Понятие движения. Осевая и центральная симметрия.
Параллельный перенос. Поворот. Наложения и движения.
ЭЛЕМЕНТЫ ЛОГИГИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ
ВЕРОЯТНОСТЕЙ (1 ч).
Беседа об аксиомах геометрии. Пятый постулат Евклида и его история. Понятие об аксиоматике и аксиоматическом построении геометрии.
НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ (8 ч).
Предмет стереометрии. Геометрические тела и поверхности. Многогранники призма,
параллелепипед, пирамида, формулы для вычисления их объемов. Тела и поверхности вращения: цилиндр, конус, сфера, шар, формулы для вычисления их площадей поверхностей и объемов.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики ученик должен
знать/понимать
• существо понятия математического доказательства; приводить примеры доказательств;
• существо понятия алгоритма; приводить примеры алгоритмов;
• как используются математические формулы, уравнения и неравенства; примеры их
применения для решения математических и практических задач;
• как математически определенные функции могут описывать реальные зависимости;
приводить примеры такого описания;
• как потребности практики привели математическую науку к необходимости расширения понятия числа;
• вероятностный характер многих закономерностей окружающего мира; примеры
статистических закономерностей и выводов;
• каким образом геометрия возникла из практических задач землемерия; примеры
геометрических объектов и утверждений о них, важных для практики;
• смысл идеализации, позволяющей решать задачи реальной действительности
математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
уметь
• выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
• переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь – в виде процентов; записывать большие и малые числа с
использованием целых степеней десятки;
• выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
• округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
• пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
• решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
• устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
• интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
• составлять буквенные выражения и формулы по условиям задач; осуществлять в
выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
• выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
• применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
• решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
• решать линейные и квадратные неравенства с одной переменной и их системы,
• решать текстовые задачи алгебраическим методом, интерпретировать полученный
результат, проводить отбор решений, исходя из формулировки задачи;
• изображать числа точками на координатной прямой;
• определять координаты точки плоскости, строить точки с заданными координатами;
изображать множество решений линейного неравенства;
• распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
• находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
• определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
• описывать свойства изученных функций, строить их графики;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
• моделирования практических ситуаций и исследовании построенных моделей с
использованием аппарата алгебры;
• описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;
• интерпретации графиков реальных зависимостей между величинами.
Геометрия
уметь
• пользоваться геометрическим языком для описания предметов окружающего мира;
• распознавать геометрические фигуры, различать их взаимное расположение;
• изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
• распознавать на чертежах, моделях и в окружающей обстановке основные
пространственные тела, изображать их;
• в простейших случаях строить сечения и развертки пространственных тел;
• проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
• вычислять значения геометрических величин (длин, углов, площадей, объемов); в том числе: для углов от 0 до 180°, определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
• проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
• решать простейшие планиметрические задачи в пространстве;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• описания реальных ситуаций на языке геометрии;
• расчетов, включающих простейшие тригонометрические формулы;
• решения геометрических задач с использованием тригонометрии
• решения практических задач, связанных с нахождением геометрических величин
(используя при необходимости справочники и технические средства);
• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Элементы логики, комбинаторики,
статистики и теории вероятностей
уметь
• проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений,
использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
• извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
• решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
• вычислять средние значения результатов измерений;
• находить частоту события, используя собственные наблюдения и готовые статистические данные;
• находить вероятности случайных событий в простейших случаях;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: выстраивания аргументации при доказательстве и в диалоге;
• распознавания логически некорректных рассуждений;
• записи математических утверждений, доказательств;
• анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
• решения практических задач в повседневной и профессиональной деятельности с
использованием действий с числами, процентов, длин, площадей, объемов, времени,
скорости;
• решения учебных и практических задач, требующих систематического перебора вариантов;
• сравнения шансов наступления случайных событий, для оценки вероятности случайного
события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
| ТЕМАТИЧЕСКОЕ ПЛАНАРОВАНИЕ по АЛГЕБРЕ 8 класс | |||
| Тема (общая и подтемы) | Кол час сроки | Формы организ уч. деятельн. | Виды контроля |
| Повторение курса 7 класса | 3часа | | С/р 1.1,1.2 |
| Тема 1. Алгебраические дроби. Алгебраические операции над ними. | 21 час | | |
| Основные понятия. | 1 | Комбинирован. | |
| Основное свойство алгебраической дроби. | 2 | Комбинирован. Частично поиск | Фронт.опрос |
| Сложение и вычитание алг. дробей с одинаковыми знаменат | 2 | Комбинирован. Практикум | С/р2.1 |
| Сложение и вычитание алг. дробей с разными знаменат. | 4 | Комбинирован. Частично поиск | Взаимопров. С/р 2.2 |
| Контрольная работа №1 | 1 | Контроль | |
| Умножение и деление алг. др. Возведение дроби в степень. | 2 | Частично поиск Комбинирован. | С/р 2.3 |
| Преобразование рациональных выражений. | 3 | Проблемн.излож Комбинирован. | Фронт.опрос С/р2.4 |
| Первые представления о решении рациональных уравнен. | 2 | Комбинирован. Практикум | Тест 1 «Рац дроби» |
| Степеньс отрицательным целым показателем. | 3 | Комбинирован Проблемн.излож | Фронт.опрос С/р |
| Контрольная работа №2 | 1 | Кор.знан.,контр. | |
| Тема №2. Функция у= 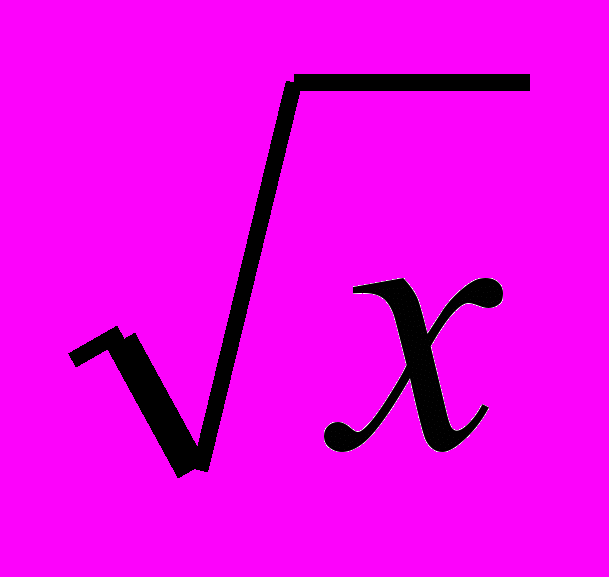 . Свойства квадратного корня. . Свойства квадратного корня. | 18 час | | |
| Рациональные числа. | 1 | Проблемн.излож | |
| Понятие квадратного корня из неотрицательного числа. | 2 | Комбинирован | Индив.опрос |
| Иррациональные числа. | 2 | Проблемн.излож | Фронт.опрос |
| Множество действит. чисел. | 1 | Частично поиск | С/р |
| Функция у= 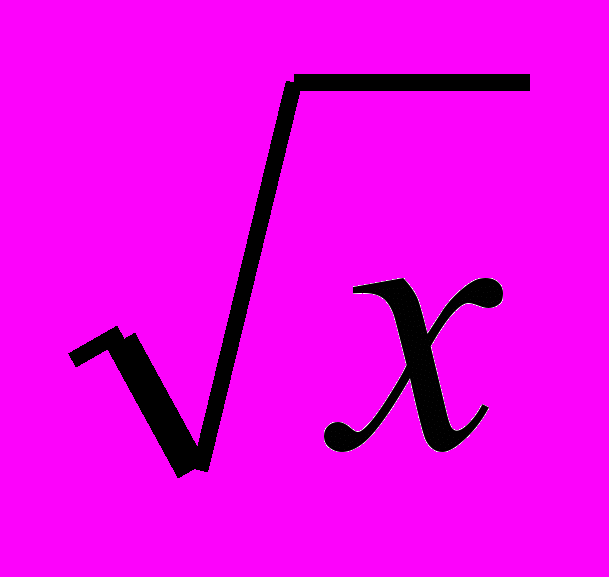 , ее свойства и график. , ее свойства и график. | 2 | Проблемн.излож | Взаимопров С/р 3.2 |
| Свойства квадратных корней. | 2 | Комбинирован. Частично поиск | Фронт.опрос С/р 3.3 |
| Преобразование выражений, содержащих операцию извлечения корня. | 4 | Комбинирован. Частично поиск Проблемн.излож | Фронт.опрос Индив.опрос Тест 2 |
| Контрольная работа №3 | 1 | Контроль | |
| Модуль действительного числа, графики функций, содержащих модуль. | 3 | Лекция Практикум | С/р |
| Тема №3. Квадратичная функция. Функция у=к/х. | 18 час | | |
| Функция у=кх  | 1 | Комбинирован. | Фронт.опрос |
| Свойства и графики функции у=кх  при к>0 и к<0 при к>0 и к<0 | 2 | Частично поиск | Матем.дикт. |
| Функция у=к/х, ее свойства и график. | 2 | Комбинирован. Практикум | Индив.опрос С/р |
| Алгоритм построения графика функции у=f(x+n) | 2 | Комбинирован. | Взаимопров |
| Алгоритм построения графика функции у=f(x)+m. | 2 | Комбинирован. | Взаимопров |
| Контрольная работа №4 | 1 | Коррекция знан. Контроль | |
| Алгоритм построения графика функции у=f(x+n)+m. | 2 | Практикумы | |
| Функция у=ах  +вх+с, ее свойства и график. +вх+с, ее свойства и график. | 1 | Комбинирован. | Фронт.опрос |
| Построение графиков квадратичной ф-ции, описание свойств. | 3 | Практикумы | С/р |
| Графическое решение квадратных уравнений | 1 | Комбинирован | Взаимопров |
| Контрольная работа №5 | 1 | Коррекция знан. Контроль | |
| Тема 4. Квадратные уравнения. | 21 час | | |
| Основные понятия. | 1 | Лекция | Фронт.опрос |
| Формулы корней квадратного уравнения. | 3 | Комбинирован. Частично поиск | Индив.опрос С/р 4.1 |
| Рациональные уравнения. | 3 | Практикумы | Взаимопров |
| Контрольная работа №6. | 1 | Контроль знан. | |
| Рацион. ур-ния как математ. модели реальных ситуаций. | 4 | Комбинирован Ур.реш-я задач | Самопровер. С/р 4.3 |
| Частные случаи формулы корней квадратного уравнения. | 3 | Частично-поиск Комбинирован | |
| Теорема Виета. Разложение кв. трехчлена на множители. | 3 | Комбинирован Практикум | Индив.опрос Тест 3 |
| Контрольная работа №7 | 1 | Контроль | |
| Иррациональные уравнения. | 2 | Лекция | |
| Тема №5. Неравенства. | 15 час | | |
| Свойства числовых неравенств. | 3 | Комбинирован | Индив.опрос |
| Исследование функций на монотонность. | 3 | Комбинирован. Проблемн.излож | С/р 5.2 |
| Решение линейных неравенств. | 2 | Комбин,практик | Фронт.опрос |
| Решение квадратных неравенств | 3 | Комбин,практик | Индив.опрос Тест 4 |
| Контрольная работа №8 | 1 | Контроль | |
| Приближен. значения действит. чисел, погрешность приближен, приближен. по недос-ку и изб. | 1 | Лекция Комбинирован | Взаимопров |
| Стандартный вид числа. | 2 | Комбинирован | |
| Элементы статистики. | 4 часа. | | |
| Представление статистических данных в виде графиков, таблиц, диаграмм. | 2 | | |
| Средние результатов статистических измерений. | 2 | | |
| Итоговое повторение. Резерв. | 2 час | | |
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ по ГЕОМЕТРИИ 8класс
| Тема (общая и подтемы) | Кол. Час. | Формы организ учебн. деят-ти | Виды контроля |
| Уроки вводного повторения | 2 | Фронтальная уст.работа, с/р по уровням. | |
| Тема 1. Четырехугольники | 14 ч | | |
| Многоугольники | 2 | Беседа, работа в малых группах | Опрос у , С/р 1.1. |
| Параллелограмм и трапеция | 6 | Комбинирован. | Уст.опрос |
| Прямоугольник и трапеция | 2 | Комбинирован. | Уст. опрос |
| Решение задач. Подготовка к контр. работе. | 3 | Практикум Обобщение знан | С/р 1.2 |
| Контрольная работа №1. | 1 | Контроль | |
| Тема 2. Площадь | 14 ч. | | |
| Площадь многоугольника. | 2 | Лекция Комбинарован. | |
| Площадь параллелограмма, треугольника и трапеции. | 6 | Комбинирован. Решение задач | Фронт.опрос С/р 2.1 |
| Теорема Пифагора. | 2 | Лекция | |
| Решение задач. | 3 | Практикумы Обобщение знан | Взаимопровер. С/р 2.2 |
| Контрольная работа №2. | 1 | Контроль | |
| Тема 3. Подобные многоугольники. | 19 ч. | | |
| Определение подобных треугольников. | 2 | Комбинирован Закрепление | Уст.опрос |
| Признаки подобия треугольников. | 5 | Лекция. Решение задач | Фронт. опрос С\р3.1 |
| Контрольная работа №3 | 1 | Контроль | |
| Применение подобия треугольников к решению задач и доказательству теорем. | 6 | Практич. работа. | Самопроверка С/р 3.2 |
| Соотношения между сторонами и углами прямоугольн. треугольника. | 3 | | Индивид. опрос С/р 3.3 |
| Подготовка к к/р. | 1 | Обобщение знан | |
| Контрольная работа №4. | 1 | Контроль | |
| Тема 4. Окружность. | 17 ч. | | |
| Касательная к окружности. | 3 | Комбинирован. | Фронт. опрос |
| Центральные и вписанные углы. | 4 | Комбинирован. Решение задач | Индивид. опрос С/р 4.1 |
| Замечательные точки треугольника. | 3 | Лекция Комбинирован. | С/р 4.2 |
| Вписанные и описанные окружности. | 4 | Лекция Практикум. | Взаимопровер. С/р4.3 |
| Решение задач | 2 | Обобщение знан | Самопроверка |
| Контрольная работа №5. | 1 | Контроль | |
| Повторение. Решение задач. | 2 | | |
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ:
А.Г Мордкович. Алгебра 7, 8, 9 Часть 1.Учебник. Мнемозина, 2007.
А.Г. Мордкович,Т.А. Минустина, Е.Е. Тульчинская, П.А. Александрова.
Алгебра 7,8 ,9. Часть 2. Задачник. Мнемозина, 2007.
П.А. Александрова. Алгебра. Контрольные работы. Мнемозина, 2008.
А.Г.Мордкович, Е.Е Тульчинская. Алгебра. Тесты. Мнемозина, 2006.
П.А. Александрова. Алгебра. Самостоятельные работы. Мнемозина, 2007.
А.Г.Мордкович, П.В. Семенов. События. Вероятности. Статистическая обработка данных. 7-9
кл. Мнемозина, 2008.
Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 кл. Л.В. Кузнецова и др.
М. Просвещение, 2007.
Геометрия. 7-9 кл. общеобразовательных учреждений. П.С. Атанасян, В.Ф. Бутузов,С.Б.
Кадомцев и др. М, «Просвещение», 2002.
Уроки геометрии в 7-9 кл., методические рекомендации для учителя к учебнику П.С
Атанасяна. В.И. Жохов, Г.Д. Карташева, П.Б. Крайнова. Вербум-м, М, 2003.
Геометрия. 7-9 кл. общеобразовательных учреждений. П.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др. М, «Просвещение», 2004.
Геометрия. Рабочая тетрадь для 7 кл., П.С. Атанасян, В.Ф. Бутузов, И.И. Юдина. М.
«Просвещение», 2008.
Геометрия. Рабочая тетрадь для 8 кл., П.С. Атанасян, В.Ф. Бутузов, И.И. Юдина. М.
«Просвещение», 2008.
Геометрия. Рабочая тетрадь для 9 кл., П.С. Атанасян, В.Ф. Бутузов, И.И. Юдина. М.
«Просвещение», 2008.
Геометрия: Дидактические материалы для 7 кл. Б.Г. Зив, В.М. Мейлер. М. «Просвещение.»
Уроки геометрии в 7-9 кл., методические рекомендации для учителя к учебнику П.С
Атанасяна. В.И. Жохов, Г.Д. Карташева, П.Б. Крайнова. Вербум-м, М, 2003.
Изучение геометрии в 7, 8, 9 классах: метод. Рекомендации: кн.для учителя.Л.С. Атанасян В.Ф.,
Бутузов Ю.А., Глазков. М. Просвещение, 2003-2008.
Интерактивная математика. ООО “Деома». Электронное пособие к учебнику А.Г Мордковича.
