Лабораторная работа №4

Вид материала

Лабораторная работа

Содержание Введение в работу Порядок проведения работы

Подобный материал:

• Методические указания к лабораторным работам Лабораторная работа, 357.24kb.
• Лабораторная работа №3 кпк лабораторная работа №3 Тема: карманный персональный компьютер, 173.34kb.
• Методические возможности стенда Особенности работы на стендах уилс-1 Ознакомительное, 1487.3kb.
• Лабораторная работа по курсу «Физические основы микроэлектроники», 136.21kb.
• Лабораторная работа, 166.92kb.
• Самостоятельная работа по учебным пособиям, 471.48kb.
• Конспект урока в 9 классе по теме: «Магний», 84.54kb.
• Лабораторная работа №1 Введение в Windows. Работа с окнами и приложениями в Windows, 67.41kb.
• Знакомство c Excel, 1212.51kb.
• Лабораторная работа, 105.21kb.

Санкт-Петербургский государственный морской технический университет

КАФЕДРА СУДОВОЙ АВТОМАТИКИ И ИЗМЕРЕНИЙ

Лаборатория моделирования динамических систем

ДИСЦИПЛИНА : "Теория автоматического управления"


Лабораторная работа № 4


Моделирование и исследование системы автоматического регулирования

( машина - двигатель, управляемая регулятором Ф. Дженкина ).

Условие устойчивости Д. К. Максвелла.


ЦЕЛЬ РАБОТЫ : получить практические навыки в исследовании устойчивости состояний

равновесия простейших астатических систем автоматического

регулирования.


ВВЕДЕНИЕ В РАБОТУ


Систему автоматического регулирования условно можно представить в виде объекта регулирования ( машина-двигатель ) и регулятора, замкнутых в единый контур с внешним возмущением ( изменением нагрузки ), воздействующим на этот контур извне.





Математической моделью машины-двигателя, управляемой астатическим регулятором является система дифференциальных уравнений следующего вида :

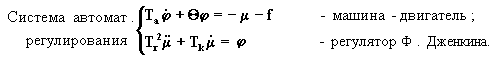(1)

где f(t) внешнее возмущающее воздействие ;

t) регулируемая величина ( входной сигнал регулятора ) ;

(t) регулирующее воздействие ( выходной сигнал регулятора ).


ПРИМЕЧАНИЕ : (t) для системы уже не является внешним воздействием ( как это было

при рассмотрении машины-двигателя ), а является присущей системе

переменной вместе со своими производными 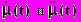, определяющей

состояние системы.


Представленную систему дифференциальных уравнений можно записать в виде одного уравнения :

а) относительно переменной t) 

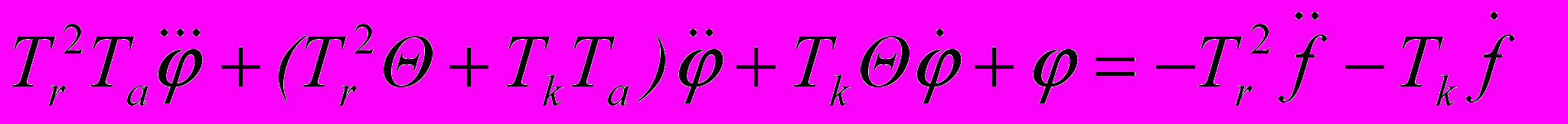(2)

б) относительно переменной (t)

(3)


Внешний вид левой части уравнений (2) и (3) при смене переменных t),(t) не изменяется, характеристическое уравнение системы определяется выражением :



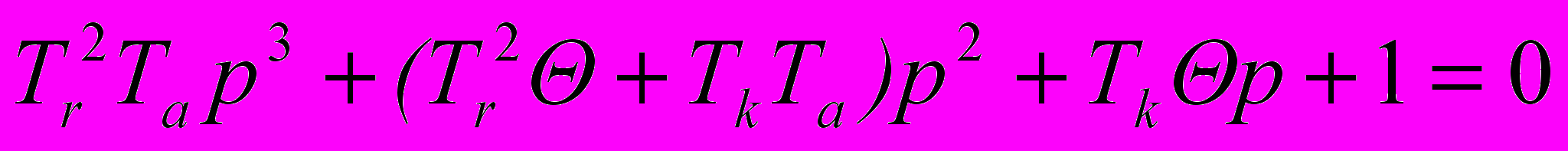
где  корни этого характеристического уравнения.


Состояние равновесия системы определяются как


Свободное движение системы ( движение, возникающее при f = 0 и ненулевых значениях начальных условий ) может быть представлено в пространстве состояния системы ( фазовом пространстве )



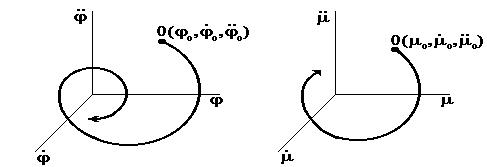
Состояние равновесия считается устойчивым, если свободное движение системы с течением времени приближается к нему и наоборот  неустойчивым, если удаляется от него.

Состояние равновесия данной системы будет устойчивым, если удовлетворяется условие :

( Условие Максвелла ).

Структурная математическая модель системы имеет следующий вид :



Обратите внимание на минус в главном контуре ( контуре регулирования ) отмеченный значком .


Запомните основное правило регулирования  сигнал, обходя контур регулирования, должен поменять знак.




ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ :


1. Используя ранее заданные параметры объектов получите графики переходных процессов

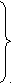(t)

 (t) на одном поле.

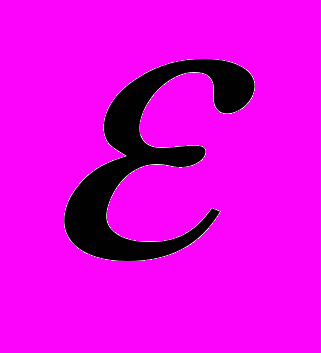(t)


2. Постройте фазовые портреты  () и ()


3. Определите основное свойство системы – устойчива, неустойчива.


4. Используя условие Максвелла изменяя параметры регулятора переведите систему в другое качественное состояние.


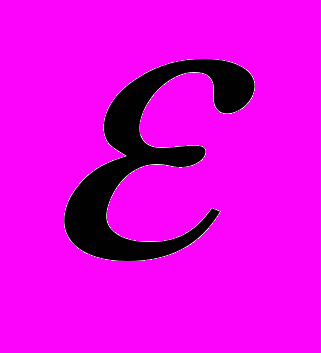5. Получите графики: (t),  (t), (t), (), ().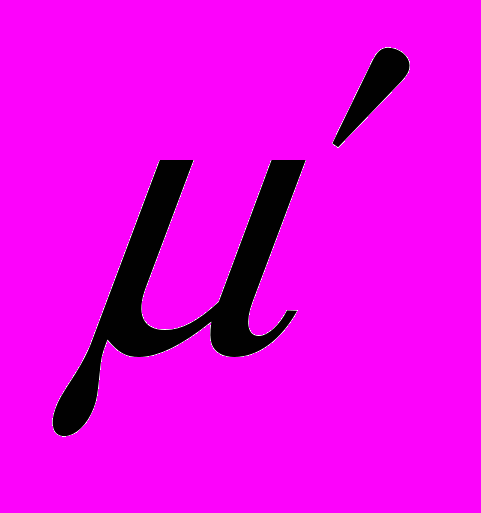


6. Сделайте необходимые выводы.