Рабочая программа учебной дисциплины «математическое моделирование» очная

Вид материала

Рабочая программа

Содержание «математическое моделирование» Общее количество часов Практические занятия, час Курсовое проектирование, час Экзамены, кол. Всего аудиторных занятий, час Северск - 2005 Цели и задачи учебной дисциплины Содержание теоретического раздела дисциплины Получение моделей из фундаментальных законов природы. Модели из вариационных принципов, иерархии моделей. Исследование математических моделей. Содержание практического раздела дисциплины Самостоятельная работа студентов Текущий и итоговый контроль результатов изучения дисциплины Учебно-методическое обеспечение дисциплины Календарный план

Подобный материал:

• Рабочая программа учебной дисциплины ен. Р. 02 Математическое моделирование процессов, 353.5kb.
• Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 85.92kb.
• Рабочая программа дисциплины «Математическое моделирование» од. А. 08; цикл од., 124.08kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Магистерская программа: Энергетика теплотехнологии (кафедра эвт); Форма обучения: очная, 55.97kb.
• Учебно-методический комплекс учебной дисциплины «численные методы и математическое, 428.92kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Рабочая программа учебной дисциплины методы математического моделирования Наименование, 122.11kb.
• Рабочая программа дисциплины математическое моделирование (Математические методы оптимизации), 521.88kb.
• Программа дисциплины «Математическое моделирование в менеджменте», 242.16kb.

Министерство Российской Федерации по атомной энергии

Северская государственная технологическая академия


УТВЕРЖДАЮ

П
д.т.н., профессор
роректор по УР


В.В. Гузеев

_____________

(
05
подпись)

__________20 г.

(дата)



655400 «Энерго- и ресурсосберегающие процессы в

химической технологии, нефтехимии и биотехнологии»

170500 «Машины и аппараты химических производств»




Направление


Специальность


Рабочая программа

учебной дисциплины


«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»


очная

Форма обучения - ______________

(очная, очно-заочная)

О
Кафедра высшей математики
беспечивающая кафедра ____________________________________________

	Семестр
	4	Всего
Общее количество часов	85	85
Теоретические занятия, час	17	17
Практические занятия, час	-	-
Лабораторные работы, час	17	17
Курсовое проектирование, час	-	-
Контрольные работы, кол.	1	1
Экзамены, кол.	-	-
Зачеты, кол.	1	1
Всего аудиторных занятий, час	34	34
Самостоятельная работа, час	51	51

Северск - 2005


Предисловие


1
№220 тех\дс по направлению 655400 «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии»


Рабочая программа составлена на основе:

- ГОС ВПО

27.03.2000 г.

утвержденного _________________;


2.102-04 по специальности 170500 «Машины и аппараты химических производств»





- ОС СГТИ


утвержденного _________________;


-
Высшей математики

16.04.2004 г.

5
РАССМОТРЕНА и ОДОБРЕНА на заседании обеспечивающей кафедры

_____________________________ ____________ протокол № _____.


2
доцент

ВМ

В.Н. Брендаков
Разработчик(и)

_________________ __________ ___________

(должность) (кафедра) (подпись)


ВМ

Н.И. Федосов

3 Зав. обеспечивающей кафедрой ___________ _____________

(кафедра) (подпись)


4 Рабочая программа СОГЛАСОВАНА с выпускающей кафедрой специальности.

МАХП

В.П. Пищулин

Зав. выпускающей кафедрой ________________ __________

(кафедра) (подпись)





АННОТАЦИЯ

Рабочая программа учебной дисциплины «Математическое моделирование» предназначена для подготовки инженеров по специальности 170500 «Машины и аппараты химических производств».

Данная рабочая программа соответствует современному состоянию и перспективам развития науки и практики в области программного обеспечения и информационных технологий, обеспечивает междисциплинарные связи данной учебной дисциплины с другими, соответствует ГОС ВПО и ОС СГТИ по специальности 170500 «Машины и аппараты химических производств».

Рабочая программа составлена доцентом кафедры высшей математики СГТИ Брендаковым Владимиром Николаевичем.

1. ЦЕЛИ И ЗАДАЧИ УЧЕБНОЙ ДИСЦИПЛИНЫ
   

Целью курса является формирование у студентов высокого уровня знаний в области методологических подходов, позволяющих строить адекватные математические модели изучаемых объектов.

Курс дает возможность уяснить основные методы и приемы построения и анализа математических моделей для различных задач механики, физики, экономики на основе использования фундаментальных законов физики, вариационных принципов, иерархических цепочек, методов аналогий.

В результате изучения дисциплины студент должен:

знать:

• основные принципы, понятия и этапы математического моделирования;
  
• классификацию математических моделей и используемых математических методов;
  
• динамическое и статистическое моделирование;
  
• дифференциальные уравнения как средство описания математических моделей;
  
• численное интегрирование: метод прямоугольников, трапеции, Симпсона;
  
• методы Эйлера, Рунге-Кутта решения системы дифференциальных уравнений;
  
• метод прогонки для решения уравнения теплопроводности;
  
• начальные и граничные условия, их смысл;
  

уметь:

• составлять математическое описание создаваемой модели;
  
• записывать алгоритм решения поставленной задачи;
  
• использовать компьютерную технику в режиме пользователя для решения инженерных задач;
  

владеть:

• навыками работы в операционной системе Windows; способностью решать инженерные задачи на персональных компьютерах.
  

2. СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
   
   Тематика теоретического раздела дисциплины – 17 часа
   
3. Основные понятия математического моделирования.
   

Элементарные математические модели. О нелинейности математических моделей. Общая схема принципа Гамильтона. Универсальность математического моделирования. Некоторые модели простейших нелинейных объектов.

4. Получение моделей из фундаментальных законов природы.
   

Сохранение массы вещества. Некоторые свойства уравнения Буссинеска. Сохранение энергии. Вывод закона Фурье. Уравнение баланса тепла. Совместное применение нескольких фундаментальных законов. Уравнения движения газа. Особенности моделей газовой динамики.

5. Модели из вариационных принципов, иерархии моделей.
   

Уравнения движения механической системы в форме Ньютона. Уравнения движения в форме Лагранжа. Законы сохранения и свойства пространства-времени. Уравнение Больцмана и производные от него. Распределение Максвелла. Цепочка гидродинамических моделей газа.

6. Исследование математических моделей.
   

Применение методов подобия. Принцип максимума и теоремы сравнения. Метод осреднения. Дискретные модели. Численное моделирование. Системы линейных уравнений. Интерполяция. Решение нелинейных уравнений. Обыкновенные дифференциальные уравнения. Понятия теории разностных схем.

7. СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ
   
   Перечень лабораторных работ – 17 часов
   

3.1 Создание и анализ простейших математических моделей.

3.2 Задача о кольцах Сатурна. Движение системы «шарик-пружина».

3.3 Колебания маятника в поле силы тяжести. Учет силы трения.

3.4 Нелинейные модели системы «шарик-пружина».

3.5 Контрольная работа.

3.6 Примеры численного интегрирования.

3.7 Задача Коши.

3.8 Уравнение теплопроводности.

8. САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ
   

Самостоятельная работа студентов организуется в двух формах:

• аудиторной - на лабораторных работах при решении поставленных индивидуальных задач;
  
• внеаудиторной - проработка лекций, изучение рекомендованной литературы, подготовка рефератов и докладов, самостоятельное изучение теоретических разделов дисциплины, подготовка к выполнению лабораторных работ, оформление отчетов – 51 часов (3 часа в неделю).
  

9. ТЕКУЩИЙ И ИТОГОВЫЙ КОНТРОЛЬ РЕЗУЛЬТАТОВ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ
   

Текущий контроль изучения дисциплины состоит из следующих видов:

• контроль за своевременным и правильным выполнением лабораторных работ и сдачей отчетов;
  
• контроль усвоения теоретического материала – проведение тестов и контрольных работ;
  

По результатам текущего контроля в 4-м семестре формируется допуск студента к итоговому контролю – зачету по дисциплине.

Варианты текущего и итогового контроля приведены в приложениях А, Б, В.

10. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
    
11. Перечень рекомендуемой литературы
    

Основная литература

1. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств: Учеб. пособие для вузов. – М.: Высшая школа, 1991.– 400 с.
   
2. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – 2-е изд., испр. – М.: Физматлит, 2002. – 320 с.
   
3. Рябенький В.С. Введение в вычислительную математику: Учеб. пособие. - 2-е изд., испр. - М.: Физматлит, 2000. – 296 с.
   

Дополнительная литература

1. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ. – М.: Мир, 1998. – 575 с.
   
2. Федоренко Р.П. Введение в вычислительную физику: Учеб. пособие для вузов. – М.: Изд-во Моск. физ.-техн. ин-та, 1994. – 528 с.
   
3. Самарский А.А. Введение в теорию разностных схем. - М.: Наука, 1971. – 552 с.
   
4. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. – М.: Едиториал УРСС, 2003. – 784 с.
   
5. Дьяконов В.П. Компьютерная математика. Теория и практика. – М.: Нолидж, 2001. – 1296 с.
   
6. Джонс Ж., Харроу К. Решение задач в системе Турбо-Паскаль. - М.: Финансы и статистика, 1991. - 720 с.
   
7. Фаронов В.В. Паскаль и Windows. - М.: Учебно-инженерный центр «МВГУ-Фесто Дидактик», 1995. - 539 с.
   
1. Средства обучения и контроля
   

При изучении курса используются персональные ЭВМ типа Pentium -133, 166, операционная система WINDOWS 2000, пакет программ Microsoft Office 2000, программная оболочка Far, интегрированная среда программирования Turbo Pascal 7.0. Работа осуществляется в локальной сети института под управлением сетевой операционной системы Novell NetWare 4.


Приложение А

Примерный список контрольных вопросов для зачета за 4-й семестр

1. Схема математического моделирования реального объекта.
   
2. Фундаментальные законы природы.
   
3. Вариационные принципы.
   
4. Применение аналогий при построении моделей.
   
5. Иерархический подход к получению моделей.
   
6. Нелинейность математических моделей.
   
7. Замыкание закона сохранения масс.
   
8. Вывод уравнения Буссинеска.
   
9. Закон Фурье для потока тепла.
   
10. Уравнение баланса тепла.
    
11. Постановка краевых условий для уравнения теплопроводности.
    
12. Уравнение неразрывности для сжимаемого газа.
    
13. Уравнение энергии.
    
14. Краевые условия для уравнений газовой динамики.
    
15. Вариационный принцип Гамильтона.
    
16. Различные формы уравнения движения механической системы.
    
17. Модель непотенциального движения.
    
18. Описание совокупности частиц с помощью функции распределения.
    
19. Н-теорема Больцмана.
    
20. Автомодельные процессы.
    
21. Различные способы осреднения.
    
22. Понятие численного моделирования.
    
23. Теория разностных схем.
    
24. Интегро-интерполяционный метод построения разностного аналога.
    

Приложение Б

Пример варианта контрольной работы


Вариант №1


1 Построить модель и найти решение задачи о всплытии подводной лодки, которая в момент времени t=0 находится на глубине Н и имеет постоянную горизонтальную скорость V. Сопротивлением воды пренебрегаем.


2 Проанализировать математическую модель системы «шарик-пружина» с учетом силы трения, взятой по формуле Стокса.




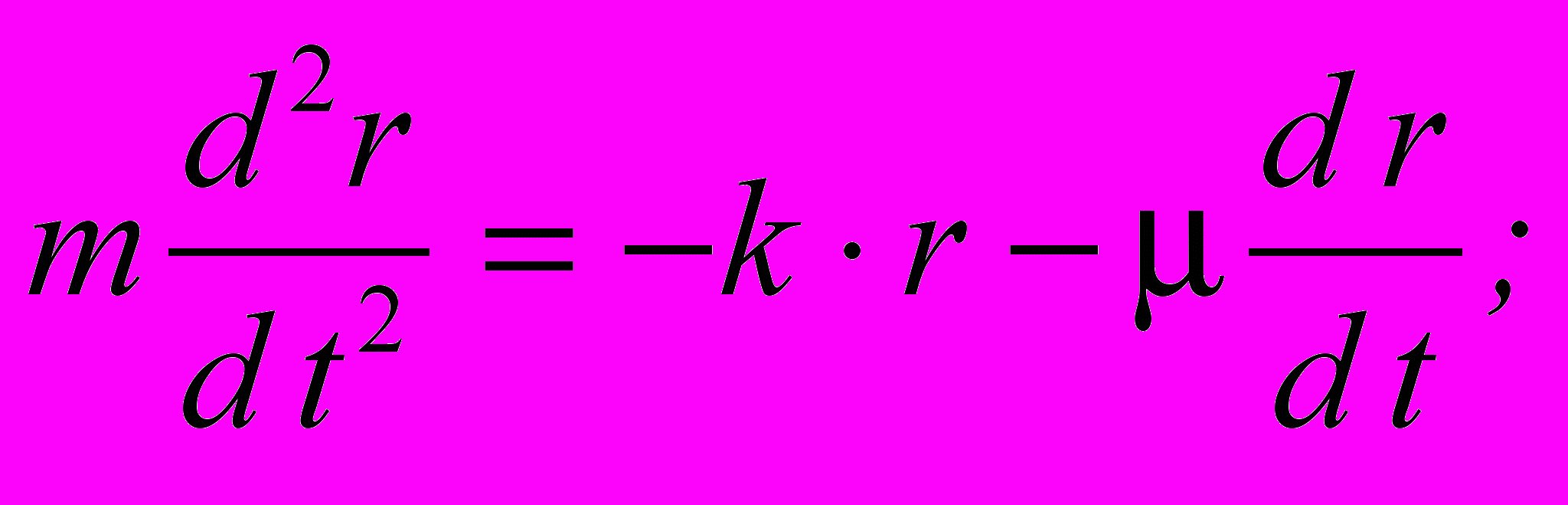
Приложение В

Примерный список задач по теме "Уравнение теплопроводности"

1. 
   Решить уравнение теплопроводности и построить график изменения температуры вдоль стержня во времени.
   
   
   
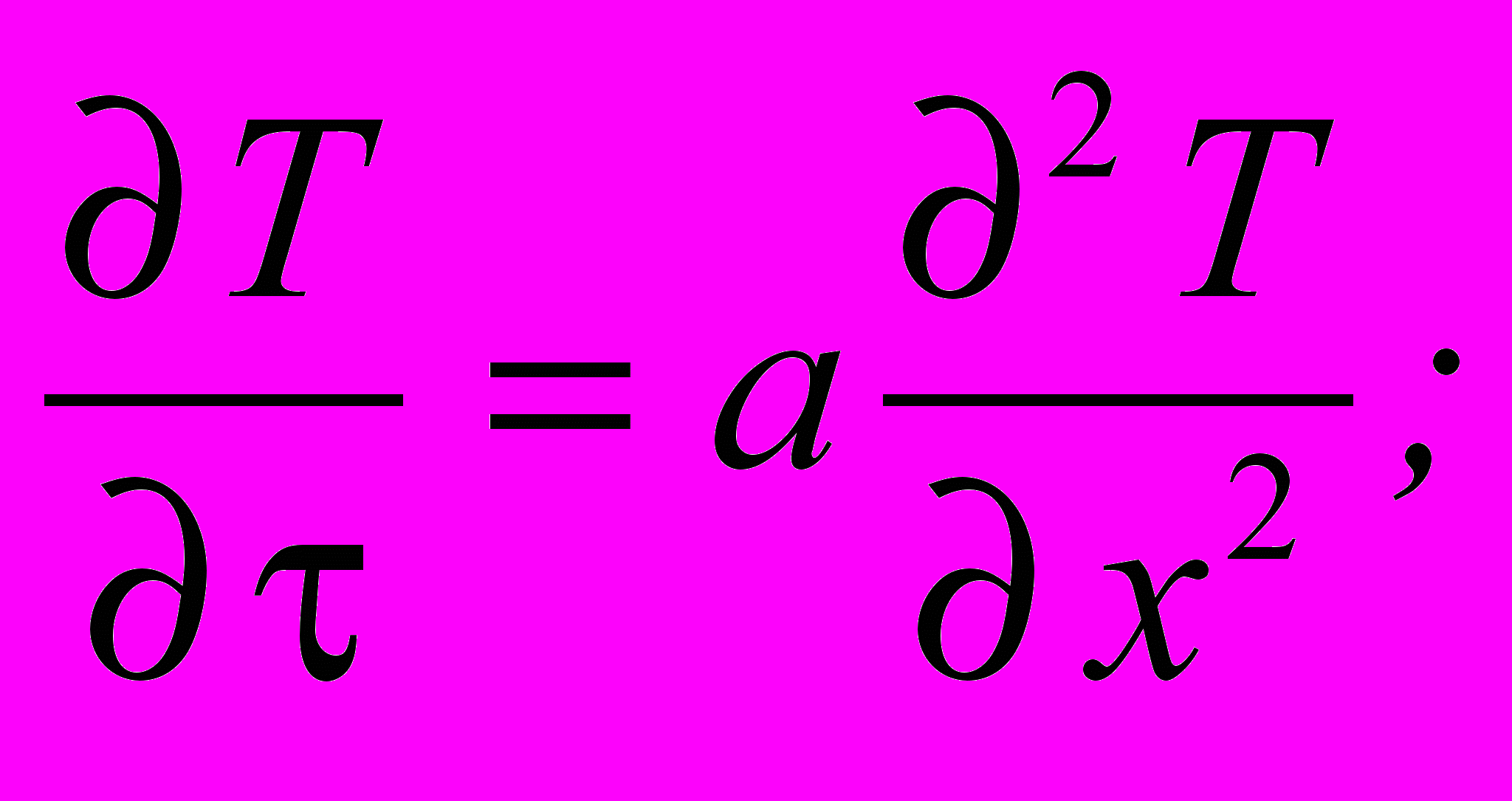
   Длина стержня L=5, на левой границе T_w=100⁰C, в начальный момент времени стержень имеет температуры T₀=15⁰C, коэффициент температуропроводности a=0,01.
   
   
   
2. Решить первую краевую задачу для одномерного процесса теплопроводности.
   
   
   
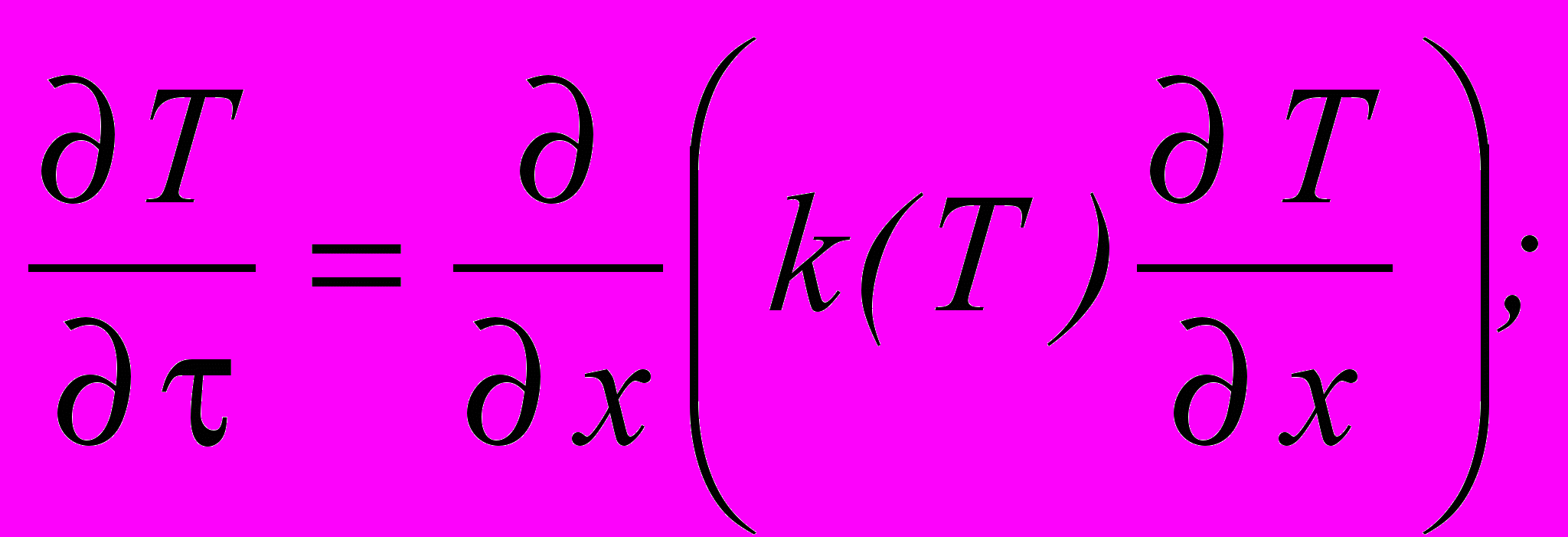
   Выбираем T₁=10⁰C, T₂=110⁰C, k(T)=0,1T ^½.
   
   
   
3. Решить двухмерную краевую задачу стационарной теплопроводности.
   
   
   
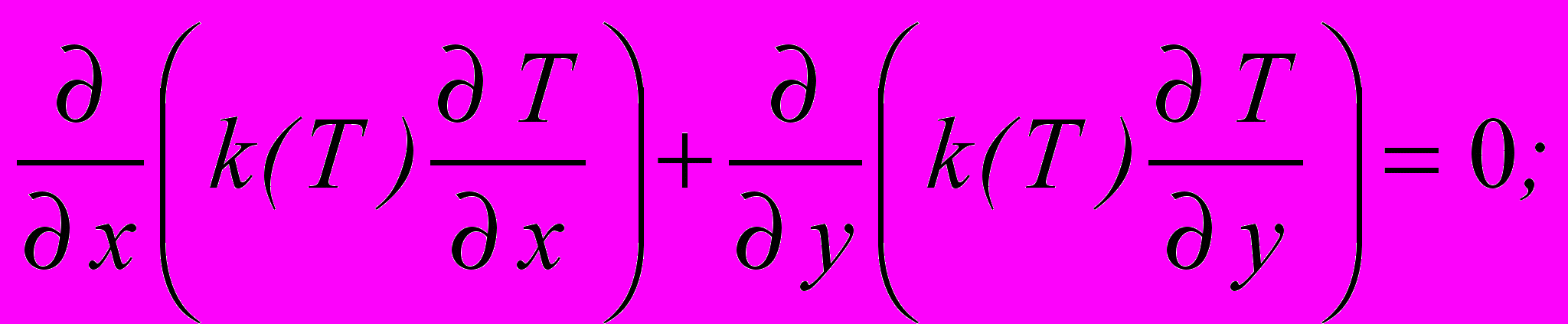
   где k=0,1T ^5/2 и граничные условия в виде: T(0,y)=0⁰C, T(1,y)=100⁰C, T(x,0)=T(x,1)=50⁰C.
   
   
   

Приложение Г

КАЛЕНДАРНЫЙ ПЛАН

дисциплины «Математическое моделирование» для студентов специальности 170500 «Машины и аппараты химических производств»

очной формы на 4-й семестр

№ учебной недели	Теоретический раздел дисциплины		Практический раздел дисциплины						Самостоятельная работа
	Содержание	Кол-во часов	Лабораторные работы		Практические занятия		Курсовое проектирование		Содержание	Кол-во часов
			Содержание	Кол-во часов	Содержание	Кол-во часов	Содержание	Кол-во часов
1	2.1	2	3.1	2					2.1; 3.1	3
2									2.1; 3.2	3
3	2.1	2	3.2	2					2.1; 3.2	3
4									2.1; 3.3	3
5	2.2	2	3.3	2					2.2; 3.3	3
6									2.2; 3.4	3
7	2.2	2	3.4	2					2.2; 3.4	3
8									2.2; 3.5	3
9	2.3	2	3.5	2					2.3; 3.5	3
10									2.3; 3.6	3
11	2.3	2	3.6	2					2.3; 3.6	3
12									2.3; 3.7	3
13	2.4	2	3.7	2					2.4; 3.7	3
14									2.4; 3.8	3
15	2.4	2	3.8	2					2.4; 3.8	3
16									2.4; 3.8	3
17	Резервная	1	3.8	1					2.4; 3.8	3