Geum.ru

Тема: «Интеграл» (заключительный урок) 11 кл

Вид материалаУрок

Содержание


Ход урока
Подобный материал:

Фалькова Л.А.

МОУ:СОШ п.Горноправдинск



Тема: «Интеграл» (заключительный урок) 11 кл.


Цель: Дополнить знания учащихся по теме. Способствовать достижению более высокого уровня умственного развития учащихся. Развивать интерес к предмету. Апробировать современные подходы в обучении. Способствовать выработке у учащихся инженерного подхода к решению задач, ознакомить их с реализацией численных методов с помощью ЭВМ. Повышать общую математическую культуру.


«Величие человека – в его способности мыслить»

(Б.Паскаль)

Ход урока:
  1. Целевая установка.

Сегодня у нас заключительный урок по теме «Интеграл». На предыдущих занятиях мы изучили понятие первообразная, элементарные правила и формулы вычисления первообразных, научились находить площадь криволинейной трапеции, узнали, что такое интеграл, что великими учеными Ньютоном и Лейбницем была выведена формула, которая носит их имя, с ее помощью можно вычислять интеграл, решать задачи прикладного характера в физике, геометрии. Прослушали доклады, историческую справку, где узнали, что метод суммирования использовал еще в глубокой древности знаменитый Архимед, а в средние века описал метод объема винных бочек Кеплер и ряд ученых продолжили изучение этого вопроса: Эйлер – работавший более 3- лет в Петербургской академии, не надо забывать имена русских ученых 19 века Остроградского, Буняковского, Чебышева. В частности П.Л.Чебышев доказал, что существуют интегралы, не выразимые через элементарные функции.

Сегодня мы посмотрим как можно с помощью ЭВМ, если ей задать программу, вычислять интегралы.

Как-то в шутливой форме Пафнутий Львович Чебышев высказал мысль: «В своем развитии математика прошла три периода:

-в первом – задачи ставили боги (задачи удвоения куба по древнегреческому преданию приписывались оракулу),

-во втором – полубоги (т.е.математики, такие как Ферма),

- в третьем периоде задачи ставит жизнь.»

Открытия в физике, астрономии привели к открытию интегрального и дифференциального исчисления. Того математического инструмента, существовавшего ранее, было не достаточно.
  1. Устно
  1. Среди трех данных функций укажите такую, что две другие являются соответственно производной и первообразной для нее:

f (x)=3x+2 cos x

g (x)=3-2 sin x

h (x)=1,5x2+2sinx
  1. Найдите общий вид первообразных:


f(x)=cos 5x

g(x)=


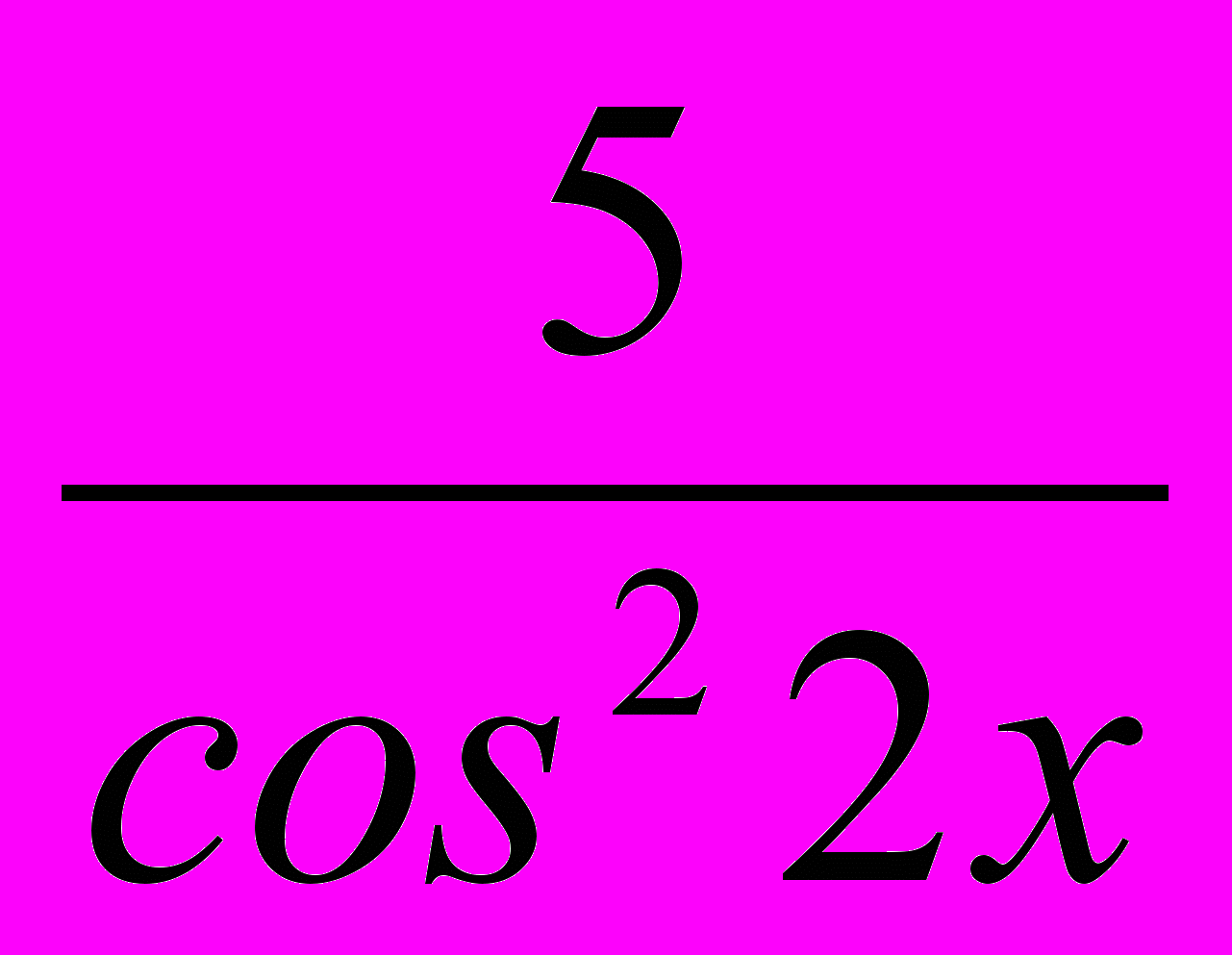
F(x)=

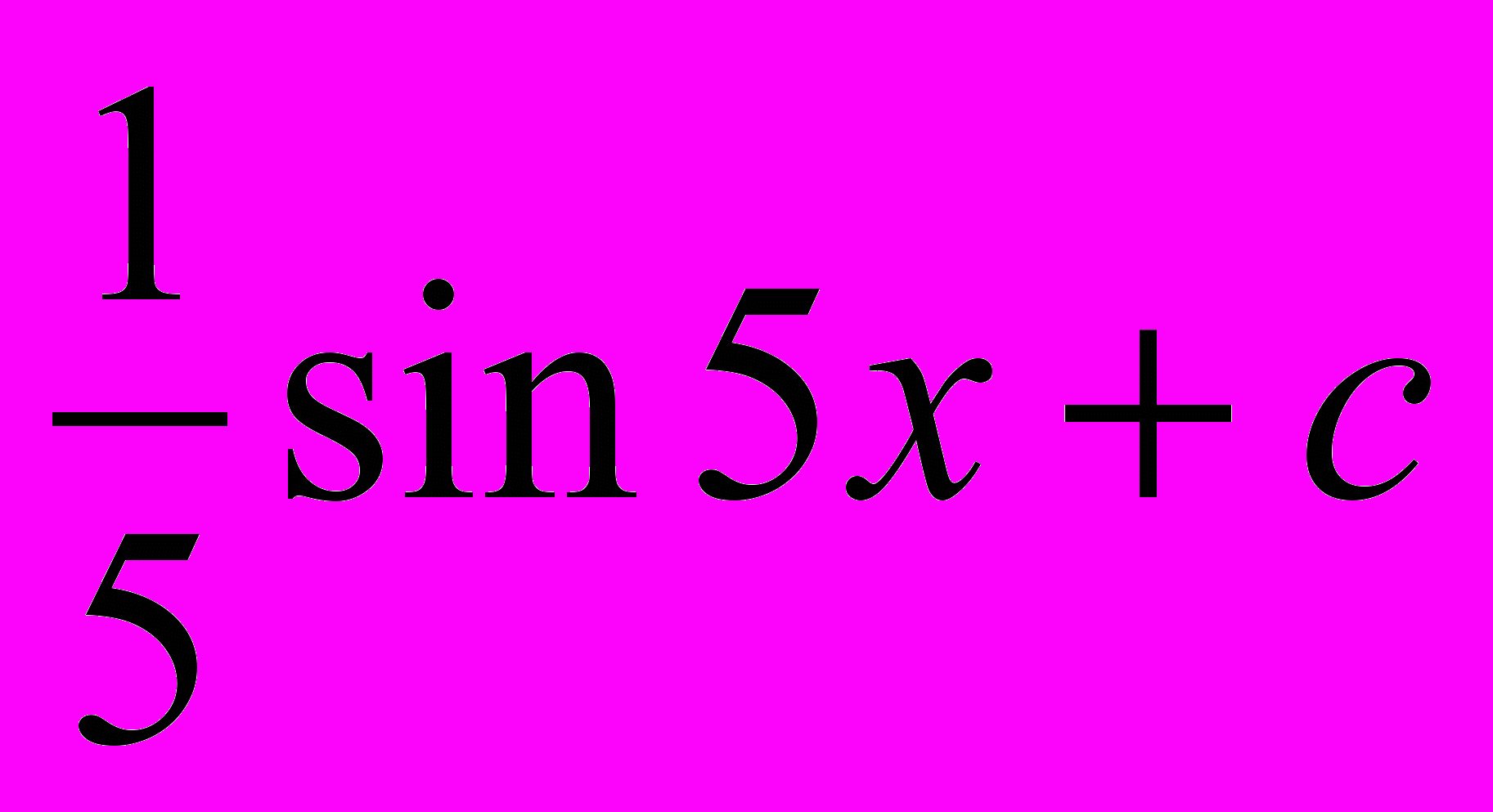
F(x)=


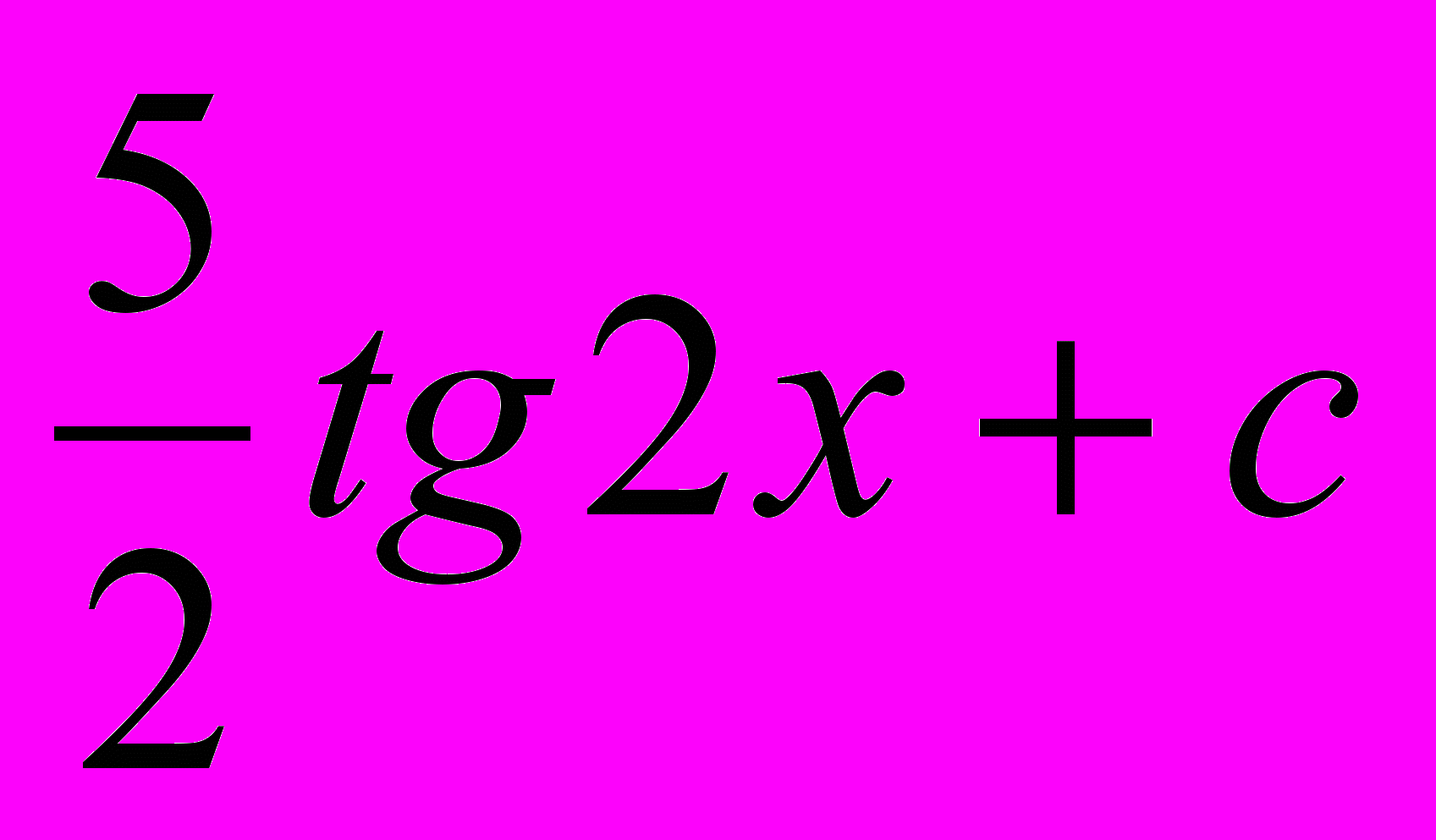
Графики всех первообразных представляют семейство кривых, зависящих от параметра С, получающихся одна из другой путем параллельного сдвига вдоль оси ОУ.
  1. Вычислите интегралы








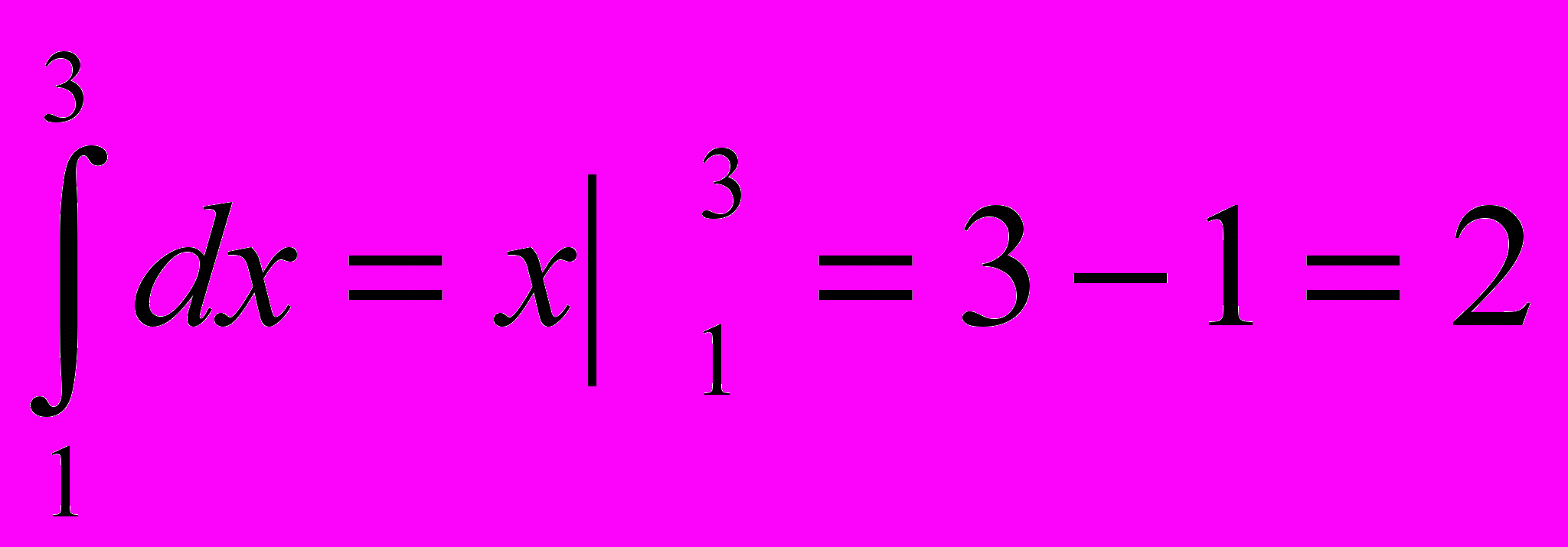
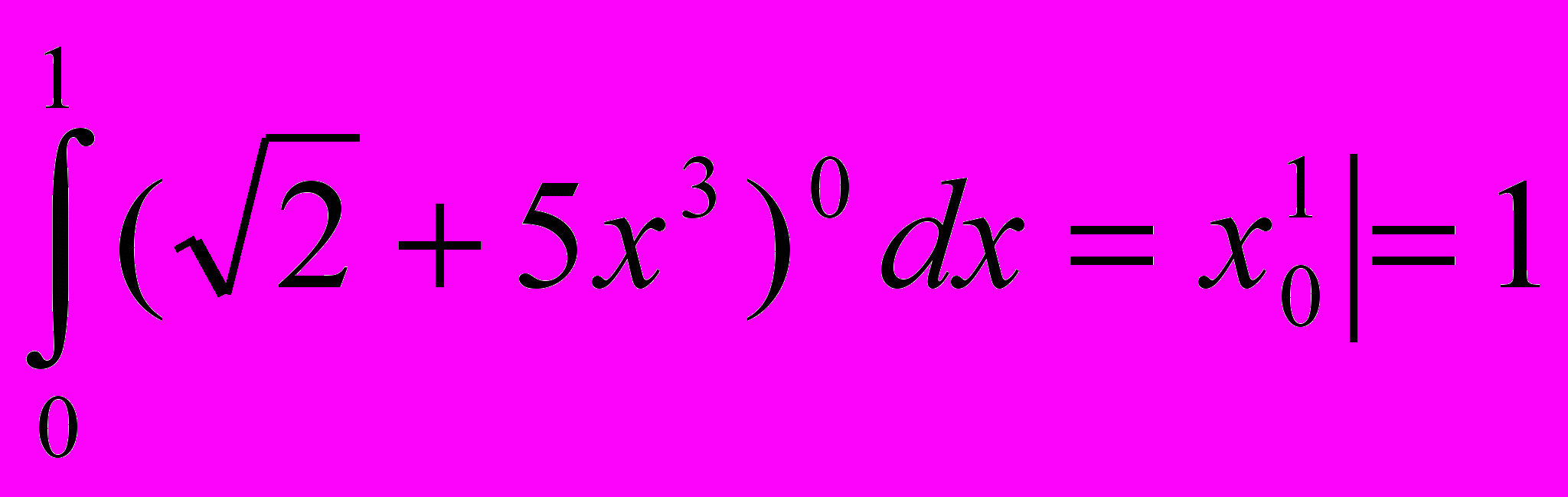
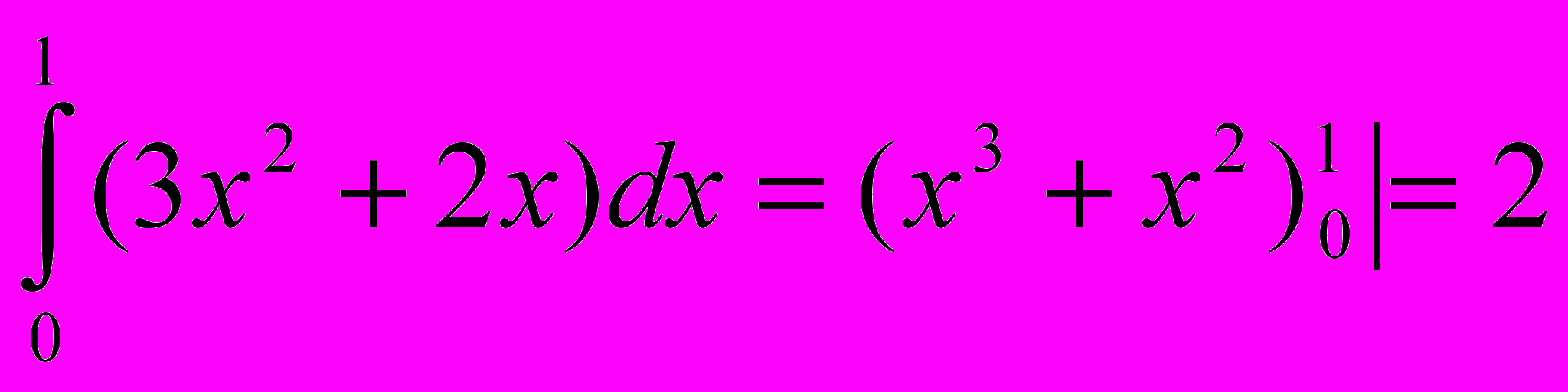
  1. Рассмотрение задач
  1. Найдите площадь фигуры, ограниченной кривой у=3х2+2х и осью абсцисс. Вычислите самостоятельно.

S=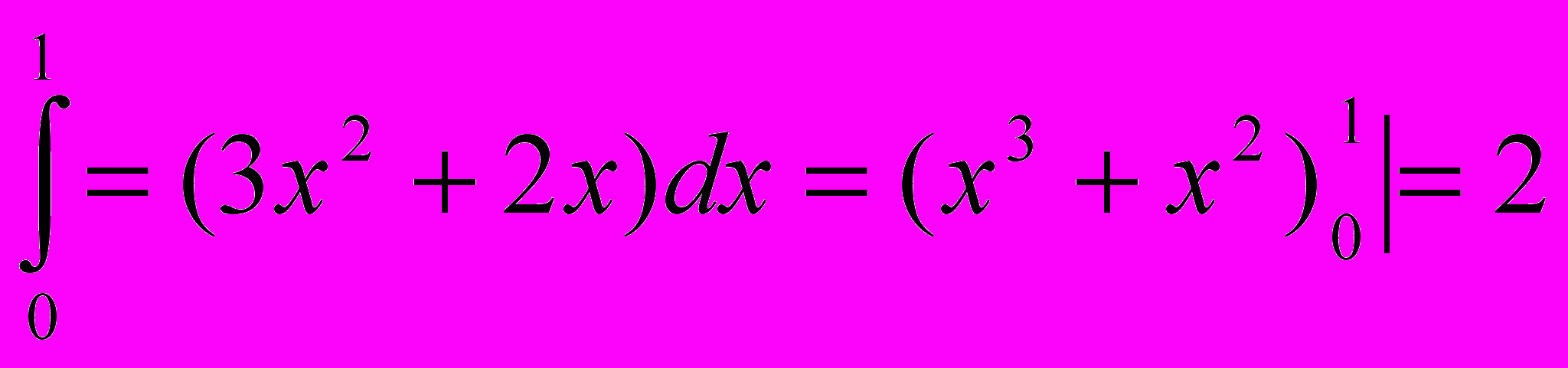(ед2)





На уроках мы рассматривали физические задачи при изучении производной. Только что решили задачу на вычисление площади криволинейной трапеции. Вот еще две задачи с одной и той же математической моделью:

а)Тело движется прямолинейно со скоростью 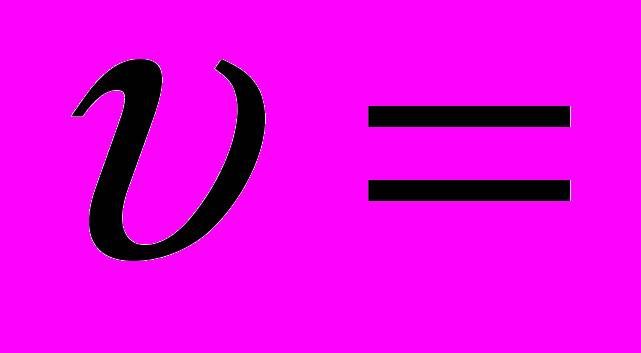3х2+2х. Найдите длину пути, пройденного телом за первую секунду от начала движения.

S=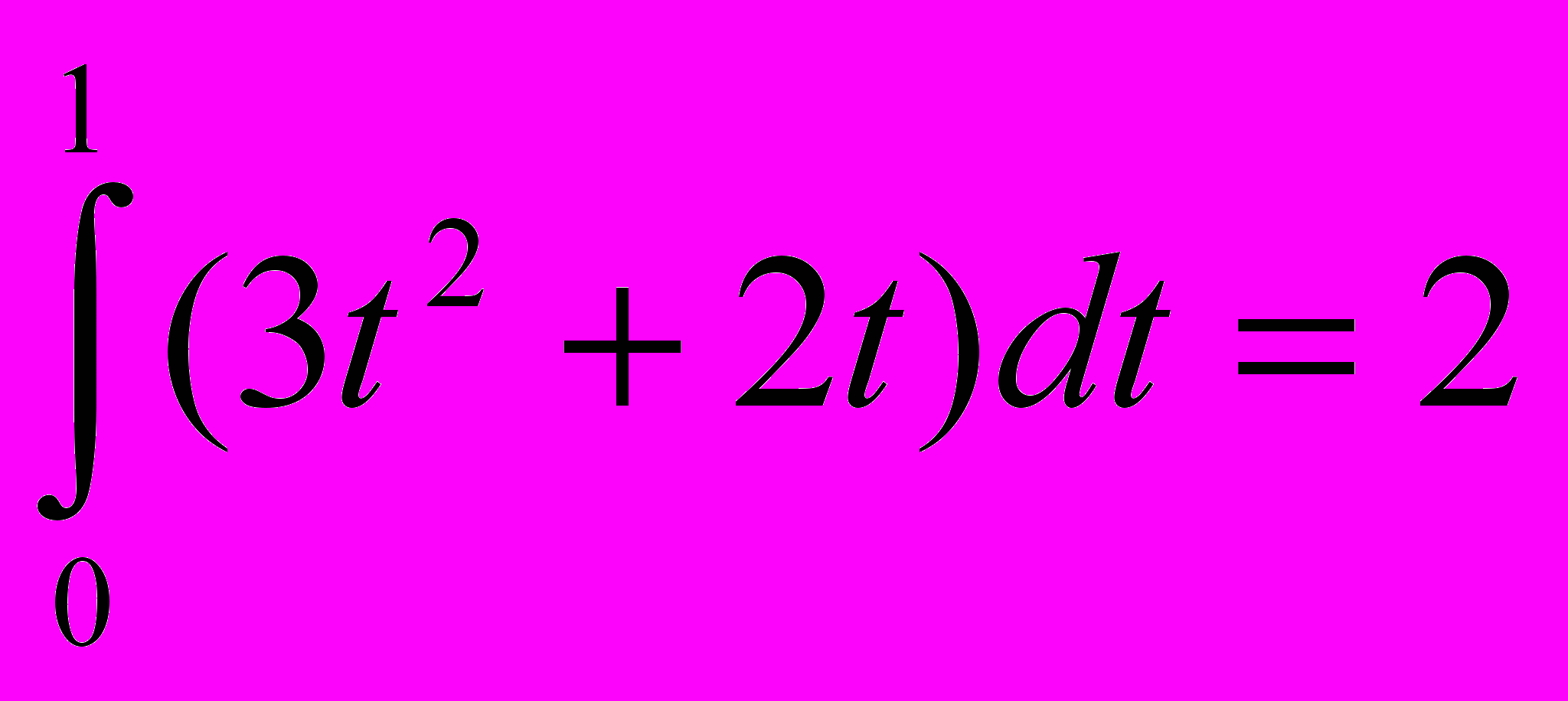(м)

б) По цепи идет переменный ток. У=3х2+2х. Найдите величину заряда, прошедшего по цепи за первую секунду.

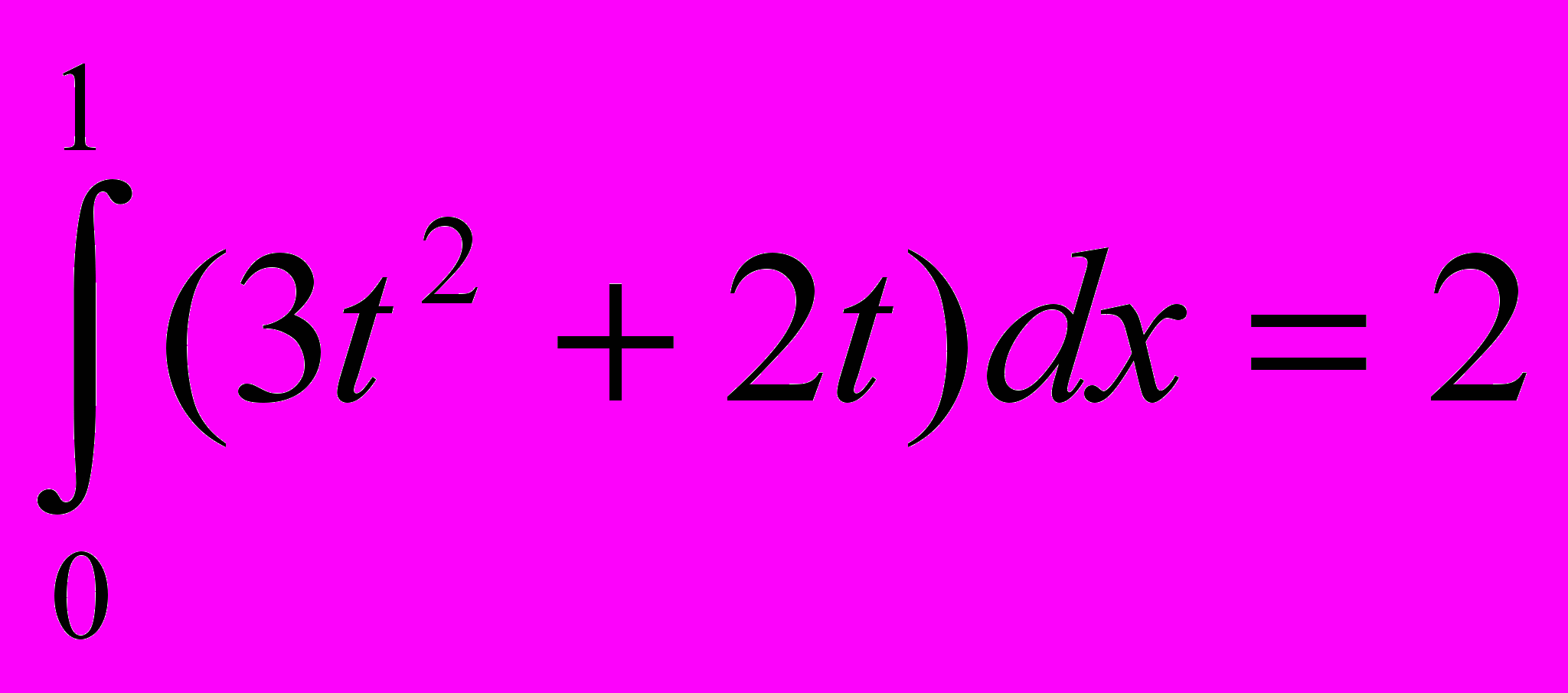G = (кл)

Использование физического материала расширяет навыки в применении математического аппарата, помогает сформировать представление о роли математики в изучении окружающего мира, формирует дополнительный интерес и мотивацию к учению.

  1. Беседа по выбору метола решения следующих упражнений.

2) Вычислите площадь фигуры, ограниченной линиями:

f(x)= 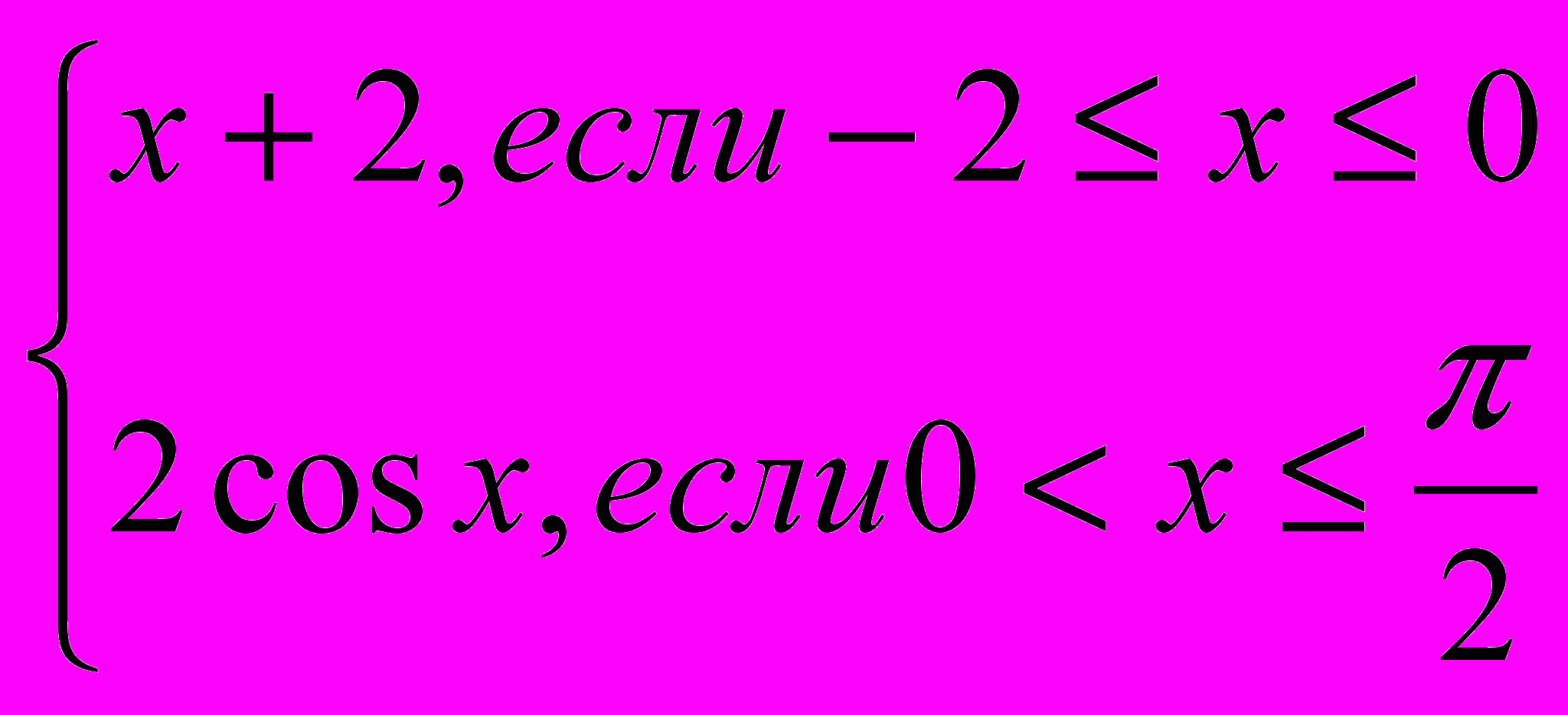и у=0

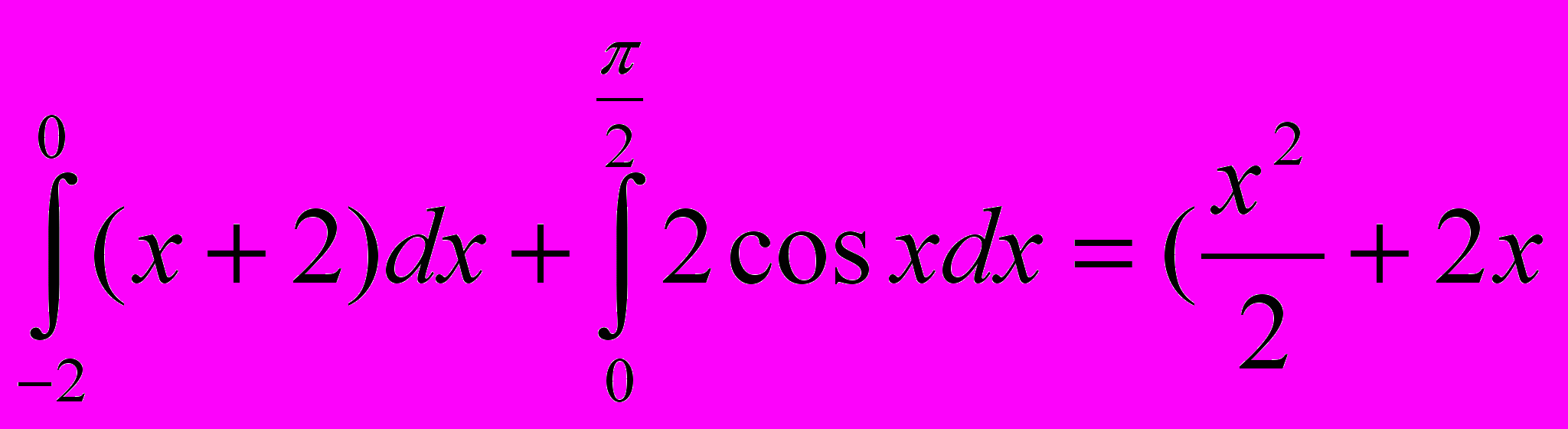
S= 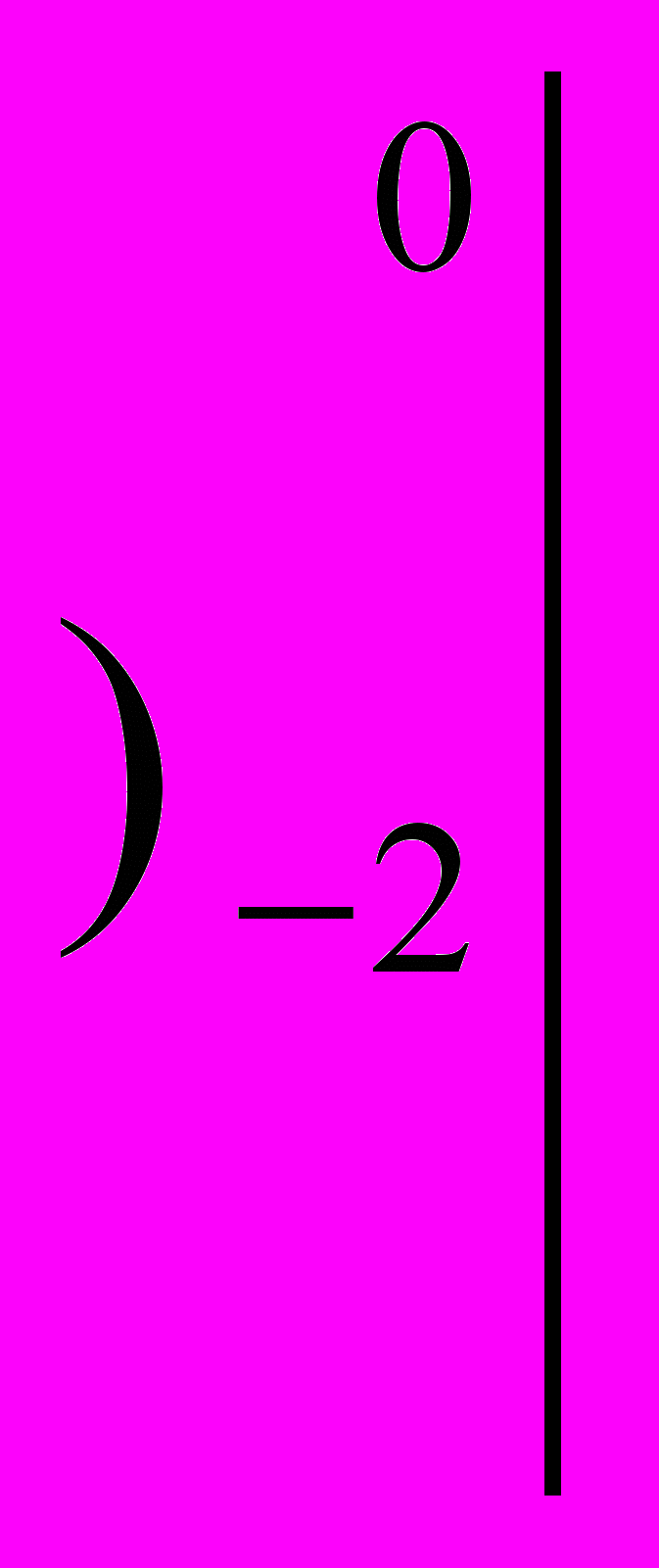+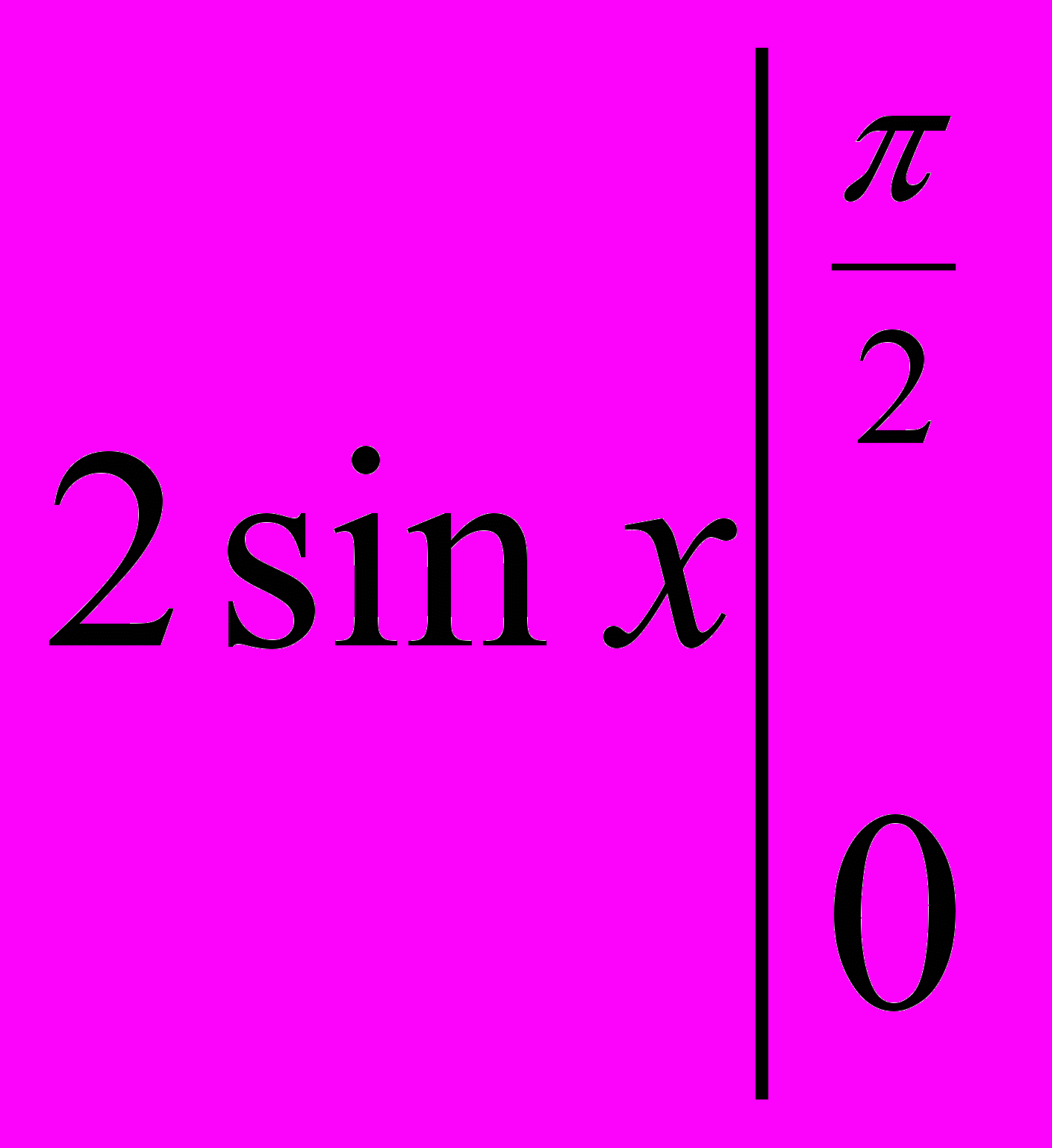=0-2+4+2sin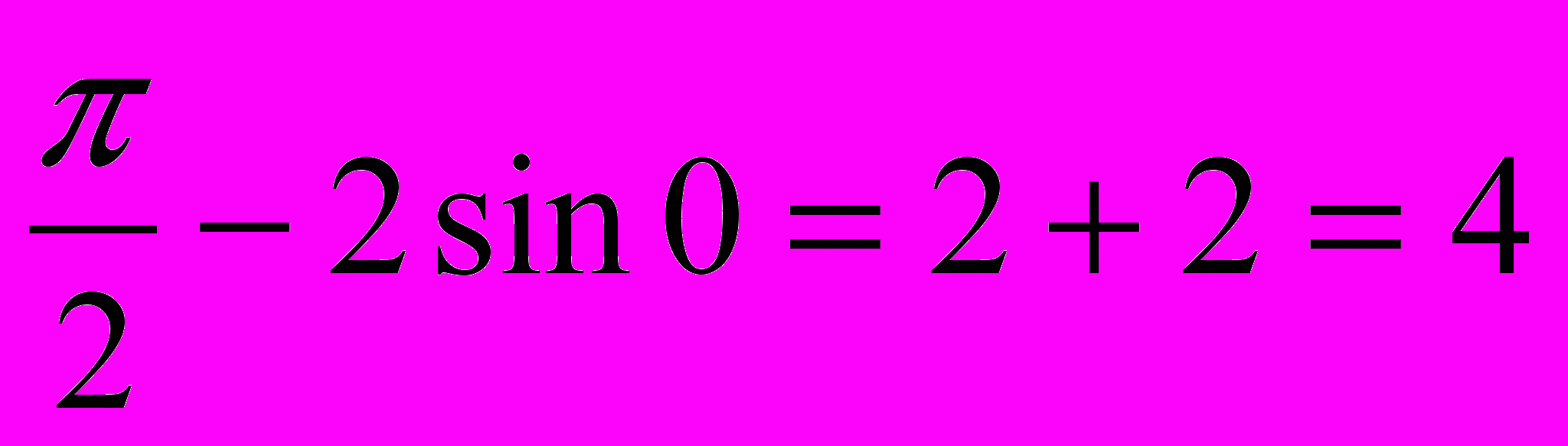








3) Изобразите на координатной плоскости линию заданную уравнением:

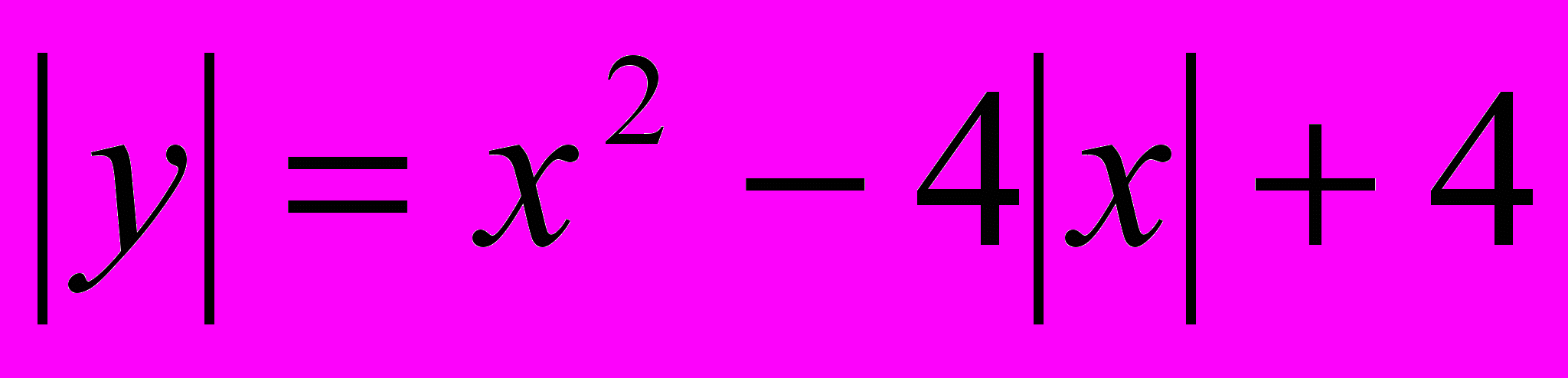, и найдите площадь фигуры, ограниченной этой линией.

х>0, у>0 у=х2-4х+4


S=








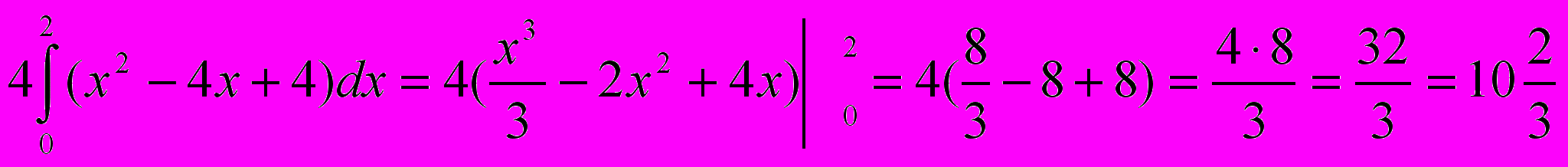
4)Вычислите площадь фигуры задаваемой на координатной плоскости неравенством:






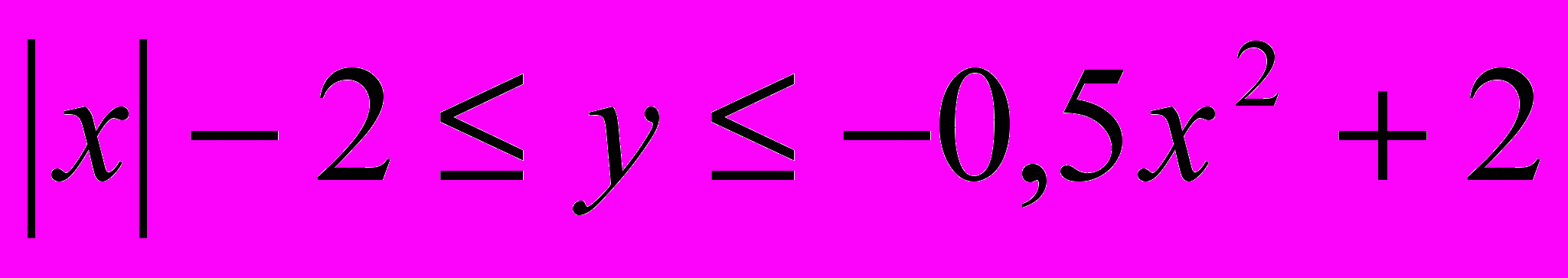
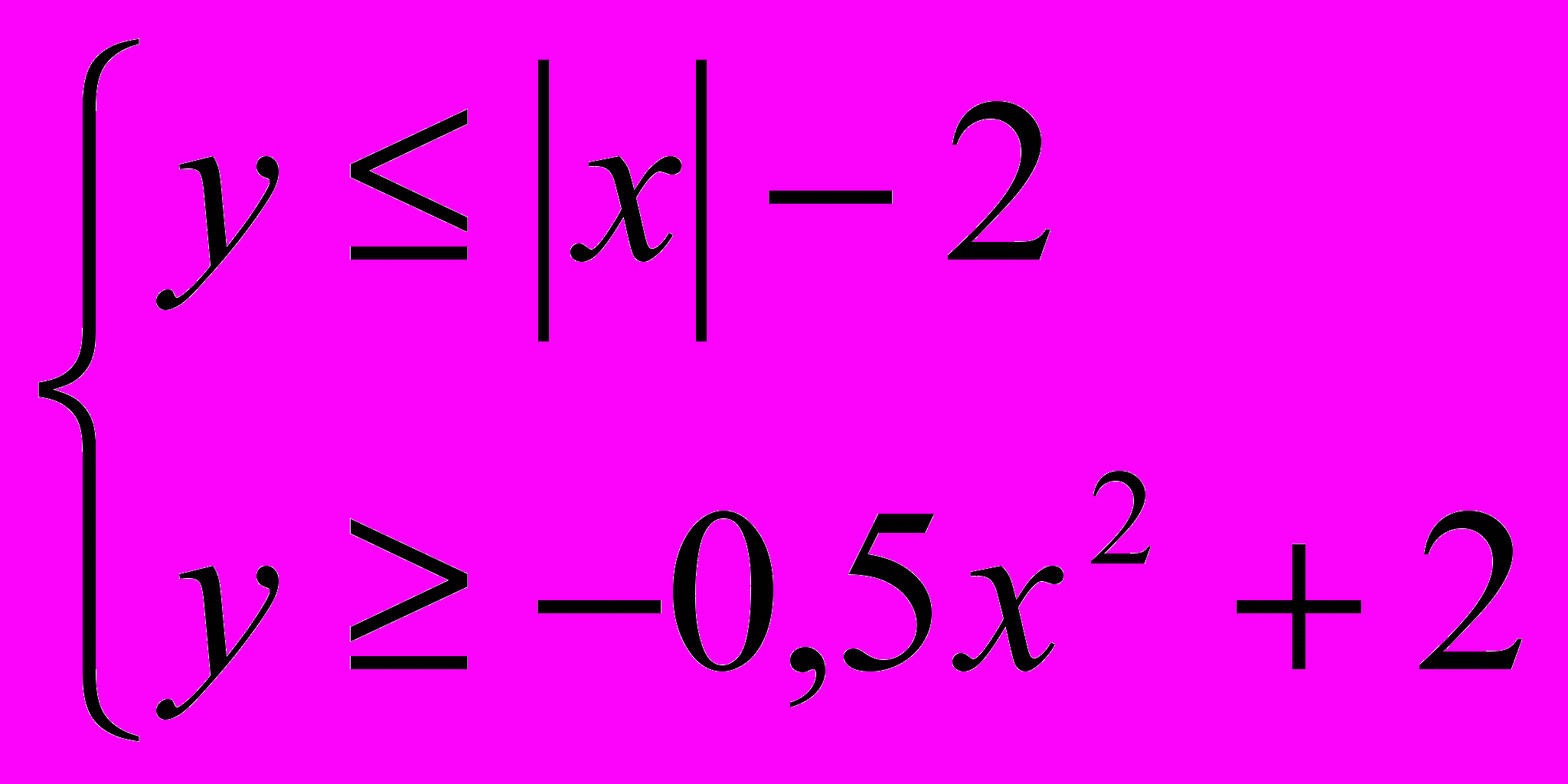
S=2







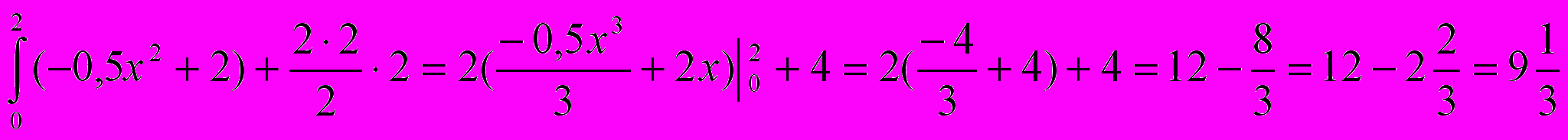
Вычисление площадей криволинейных трапеций рассмотрим на факультативе (подготовка к ЕГЭ).


  1. Повторение.

Большинство инженерных расчетов оперирует с величинами, измеряемыми с определенной степенью точности. Иногда аналитическое решение затруднено или невозможно. Например, при проектировании гидроэлектростанции нужно знать площадь поперечного сечения реки или при решении задачи на нахождение пути по заданной скорости.

S=


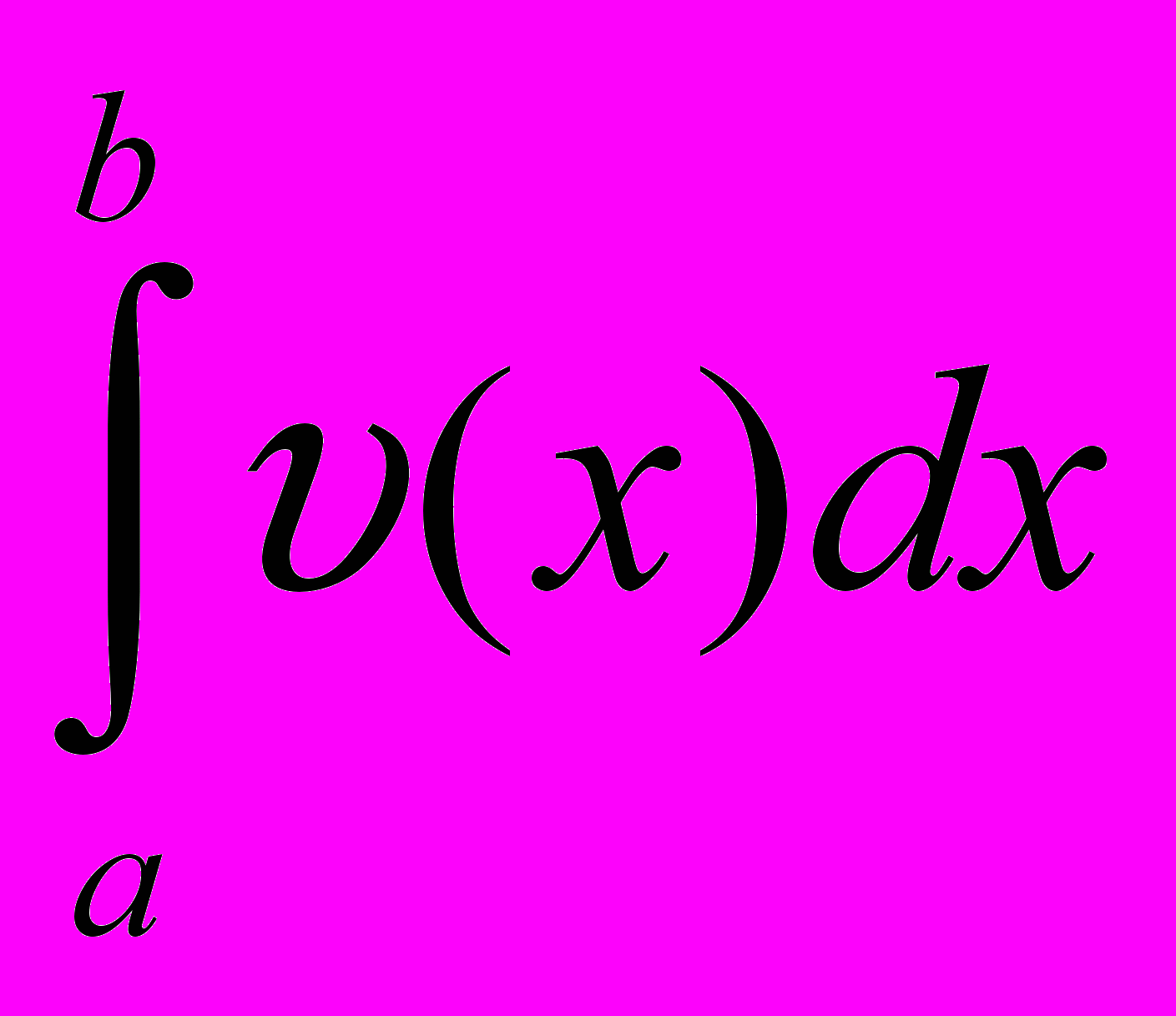
Функция может оказаться очень сложной и тогда можно прибегнуть к методу, который мы рассматривали на уроках: метод трапеции.

Пусть необходимо вычислить S=

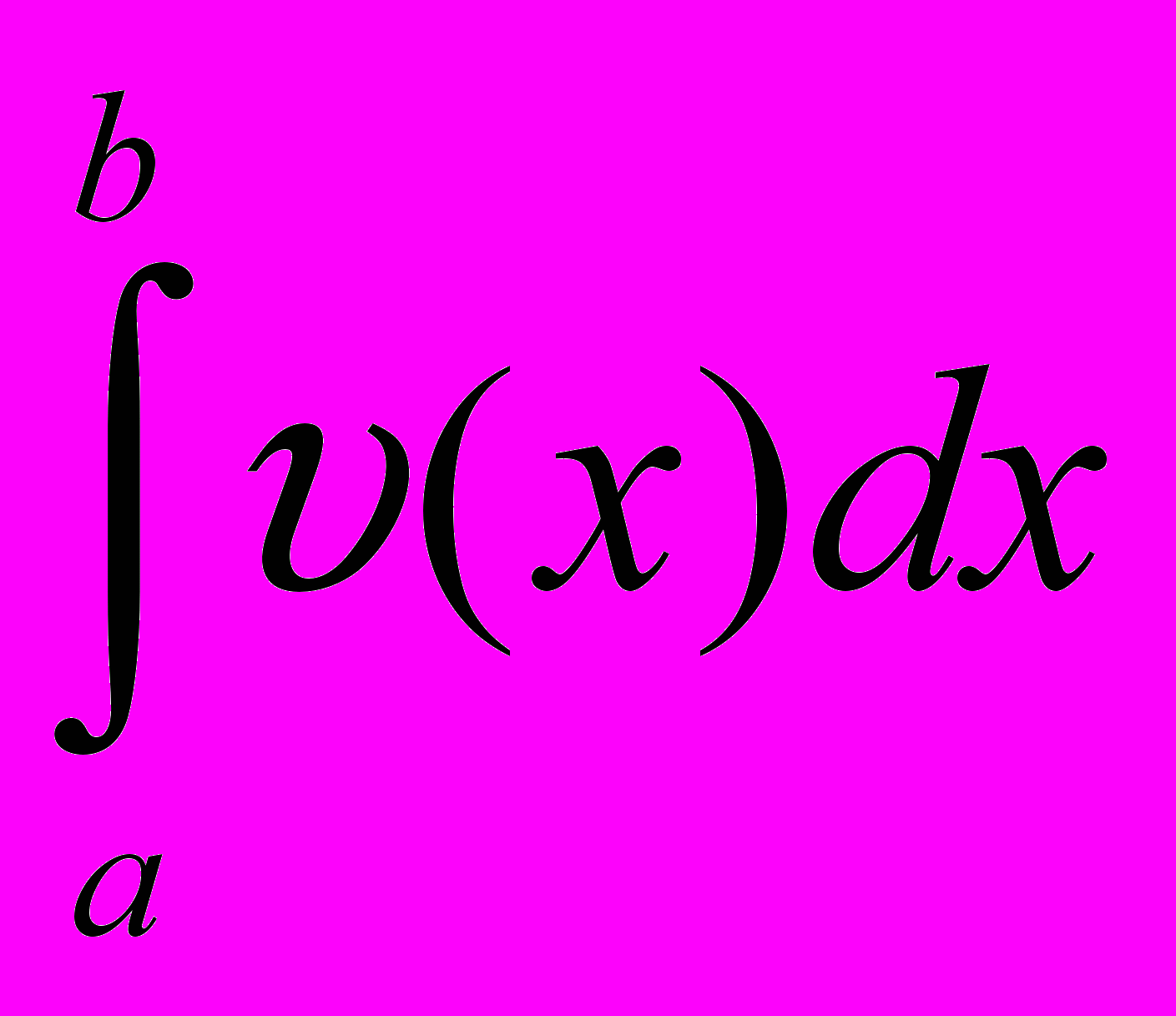
Известно, что значение площади фигуры АВСД, ограниченной кривой у=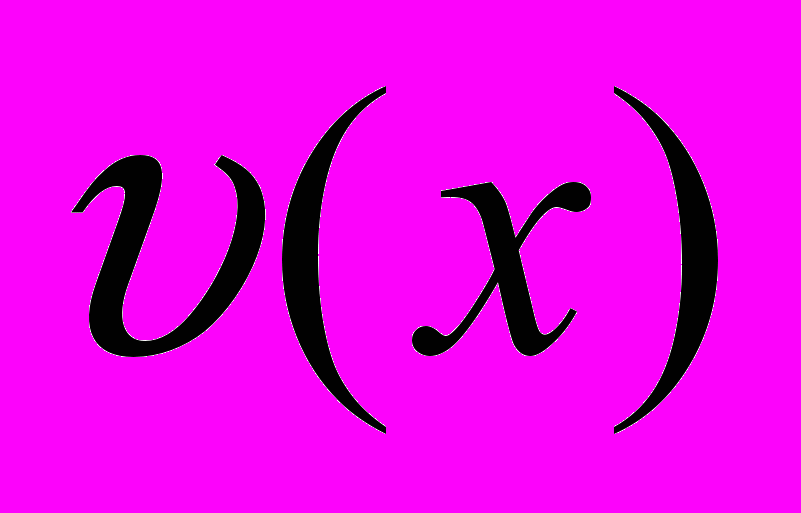и прямыми х=а, х=в, у=0 (см. рисунок). Разделим отрезок АВ на n равных частей точками х1, х2, …, хn-1. Через эти точки проведем прямые, параллельные оси ОY до пересечения графиком функции 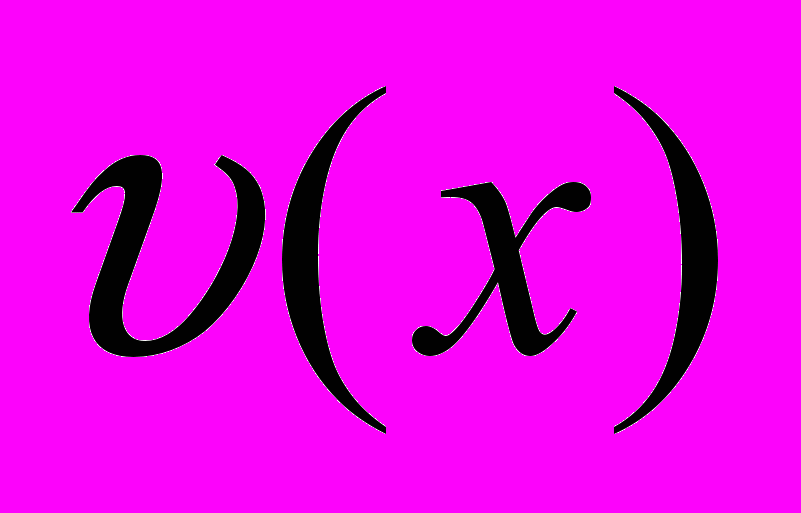в точках у1, у2, …, уn-1. При этом у1=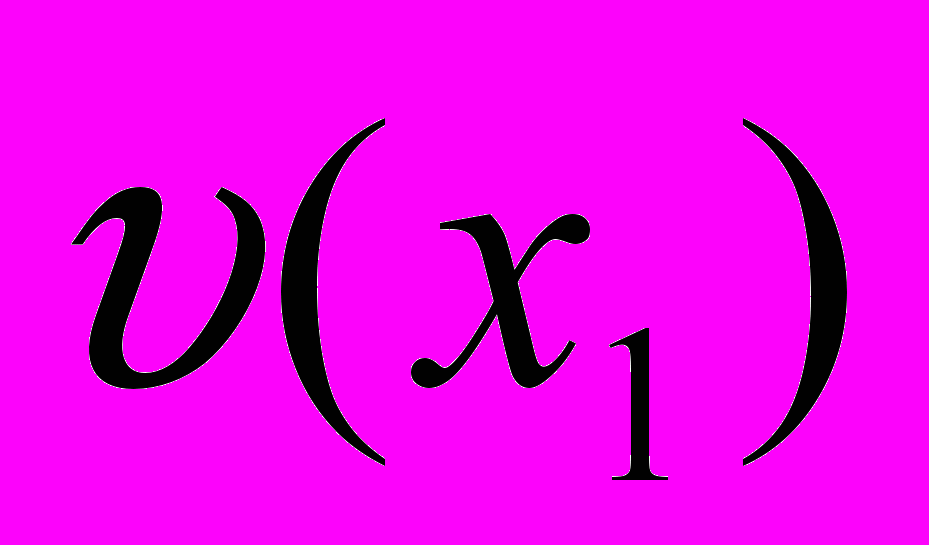. Последовательно соединим точки у1отрезками прямой. Таким образом, кривую 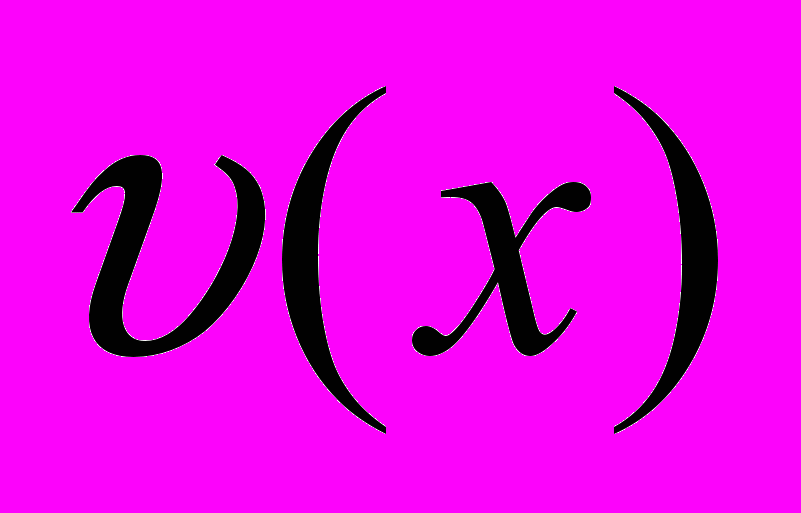заменили ломаной линией и получили n трапеций. Площадь каждой из них вычисляется по формуле.

Si=


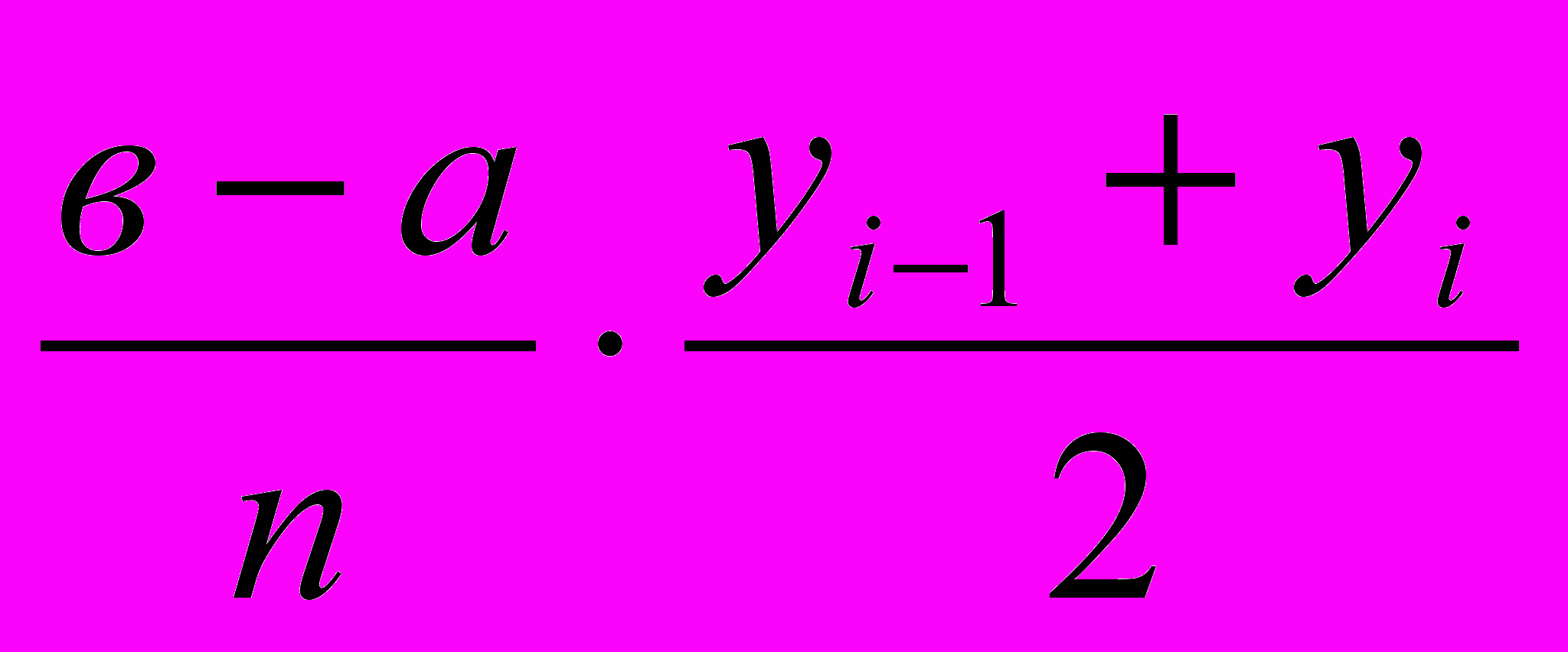
S= 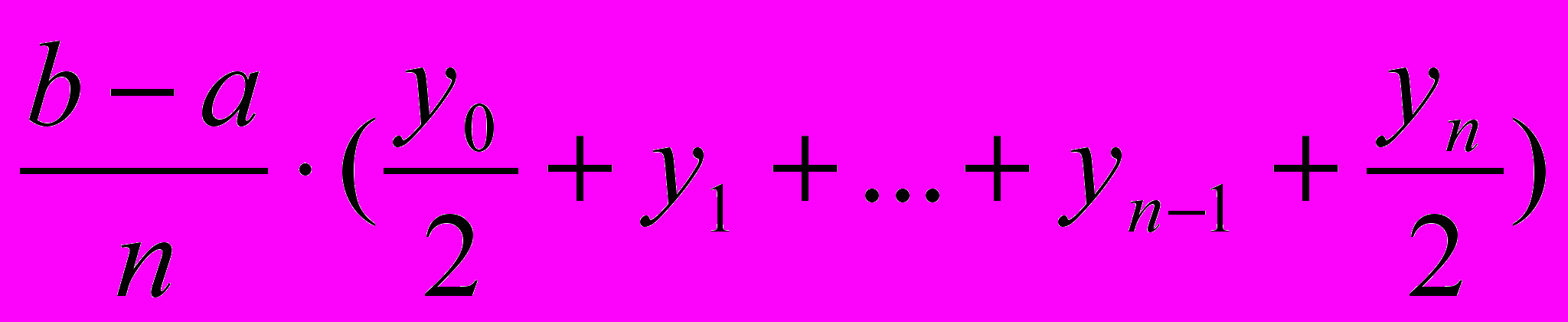или

S=

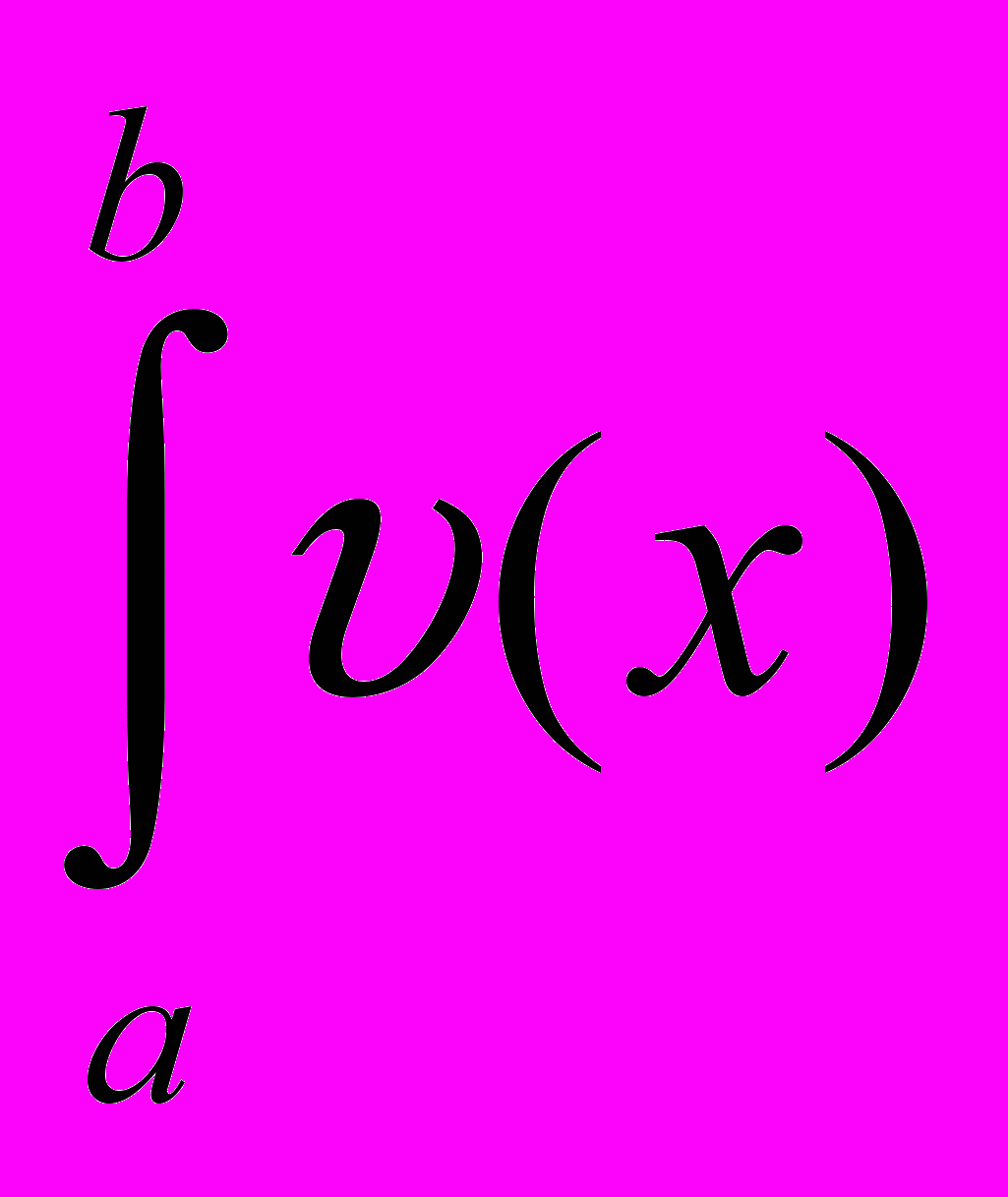
Чем больше n, тем точнее расчет, т.к. ломаная стремится к кривой.








  1. Составление программы вычисления площади методом трапеции функции у=3х2+2х и работа на ЭВМ. Сравнение результатов с аналитическим исчислением. Определить значение n, при котором ответы совпадают.
  2. Сообщение учащихся «Из истории интегрального исчисления» (учебник «Алгебра и начала анализа» стр.194-198)
  3. Домашнее задание. Составить программу вычисления площади методом трапеции для f(х)=х2-6х(по желанию).
  4. Заключительное слово учителя: слова П.Л.Чебышева:

«Сближение теории с практикой дает самые благотворные результаты, и не только практика от этого выигрывает».