Лекция по физике с высшей математикой на тему: основы термодинамики

Вид материала

Лекция

Содержание Вычисление изменения энтропии. Упорядоченность структуры К открытым системам относятся все живые организмы. 1) Изменение за счёт процессов Общее изменение энтропии открытой системы равно Продукция энтропии и поток энтропии. Стационарные состояния. Теорема Пригожина. Процессы с преодолением потенциального баоьера A служит формула Больцмана Описание лабораторной работы Ход выполнения работы Второе начало термодинамики

Подобный материал:

• Программа курса лекций (3 курс, 6 сем, 24 ч лекций + 8 ч семинаров, экзамен), 52.52kb.
• Молекулярная физика и основы термодинамики электронный учебник по физике кгту-кхти., 493.33kb.
• К. Э. Циолковский о втором начале термодинамики опарин Е. Г. Известно множество формулировок, 315.41kb.
• Решение задач по тоэ, отц, Высшей математике, Физике, Программированию, 184.85kb.
• Аннотация дисциплины «Магнетизм конденсированного состояния», 11.15kb.
• «Физические основы бестопливной энергетики. Ограниченность второго начала термодинамики», 124.14kb.
• Программа курса лекций, 38.47kb.
• Лекция Активные мультимедийные развивающие среды по физике. Ресурсы Интернета по школьной, 196.29kb.
• Темы лекций по медицинской и биологической физике, 17.25kb.
• «Физические модели и реальность. Проблема согласования термодинамики и меха­ники», 1712.23kb.

ЛЕКЦИЯ

по физике с высшей математикой на тему:


ОСНОВЫ ТЕРМОДИНАМИКИ

( 2 )

для курсантов 1 курсов ФПВ, ФПГВ

и отделения ППВ V факультета


Санкт-Петербург

2002


Понятие энтропии. Вычисление изменения энтропии.


Первое начало термодинамики даёт основу для расчёта энергетики всех процессов. Однако, оно ничего не говорит о направлении этих процессов. С точки зрения первого начала прямой и обратный процессы (например, синтез АТФ и её расщепление) одинаково возможны. На самом деле, в каких-то конкретных условиях процесс всегда идёт в одном направлении (например, в митохондриях происходит синтез АТФ, а во всех остальных участках клеток – расщепление). Правило, позволяющее определить, в каком именно направлении будет идти процесс при заданных условиях, называется вторым началом термодинамики. Однако, прежде, чем сформулировать это правило, надо познакомиться с важной физической величиной, которая называется энтропия.

В прошлой лекции мы познакомились с понятием связанной энергии, то есть той части внутренней энергии, которую нельзя использовать для совершения работы. По ряду причин оказалось удобнее вместо связанной энергии ввести другую величину, которая называется энтропия и выражается формулой:


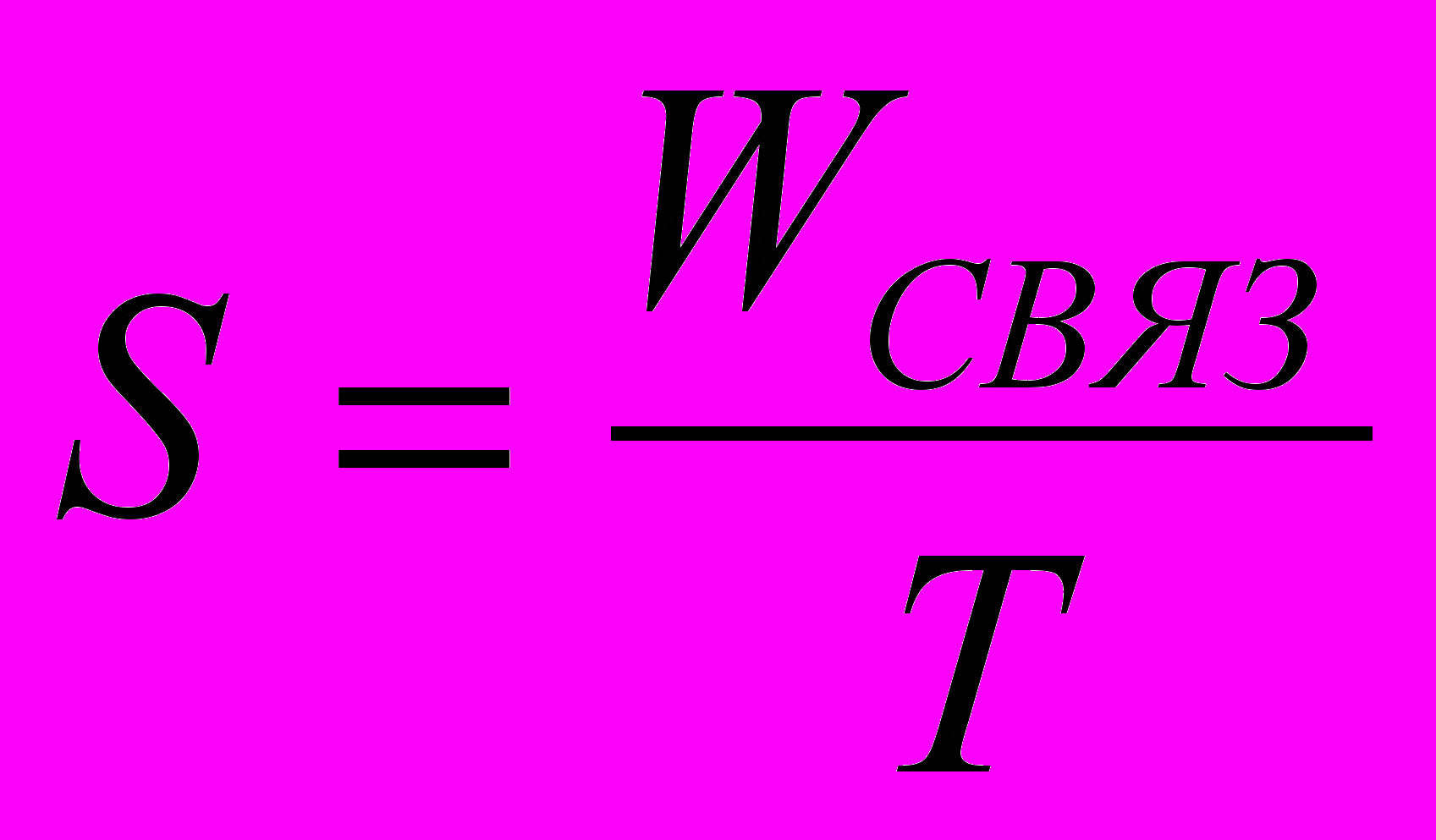(1)


то есть энтропия S – это величина связанной энергии на единицу температуры (по шкале Кельвина). Размерность энтропии – Дж.К ^–1. Очевидно, что W_СВЯЗ = T.S, и

U = G + W_СВЯЗ = G + T·S,

откуда получаем связь между свободной энергией и энтропией:

G = U – T· S (2)

Почти всегда при изучении конкретных процессов нас интересует не столько сама энергия, сколько её изменение. В биологической термодинамике мы чаще всего имеем дело с изотермическими процессами (температура тела постоянна). В этом случае :

ΔG = ΔU – T·ΔS (3)

Однако, надо учесть, что в некоторых случаях может меняться объём участвующих в процессе тел. Это особенно существенно, когда возникают или поглощаются газы (например, при окислении глюкозы возникает СО₂). В этом случае внутренняя энергия будет меняться также за счёт работы расширения или сжатия газа, равной р·ΔV. Тогда ΔG = ΔU + p·ΔV -T·ΔS

Величина H = U + p.V называется энтальпия . Используя это обозначение можно написать:

ΔG = ΔH – T·ΔS (3-а)

Вычисление изменения энтропии.


Рассмотрим сначала изотермические процессы, наиболее характерные для организма. Если изменение энтропии при переходе из состояния 1 в состояние 2 обозначить ΔS_1→2 ,то


, (4)

где Q_1→2 - это количество тепла, полученного системой в ходе обратимого перехода из первого состояния во второе.

Например, при плавлении 1 кг льда при 0⁰С в условиях, когда нет потерь тепла (и, значит, можно процесс считать обратимым), надо сообщить льду 335 кДж (эта величина называется удельной теплотой плавления). Поэтому в данном процессе изменение энтропии льда равно 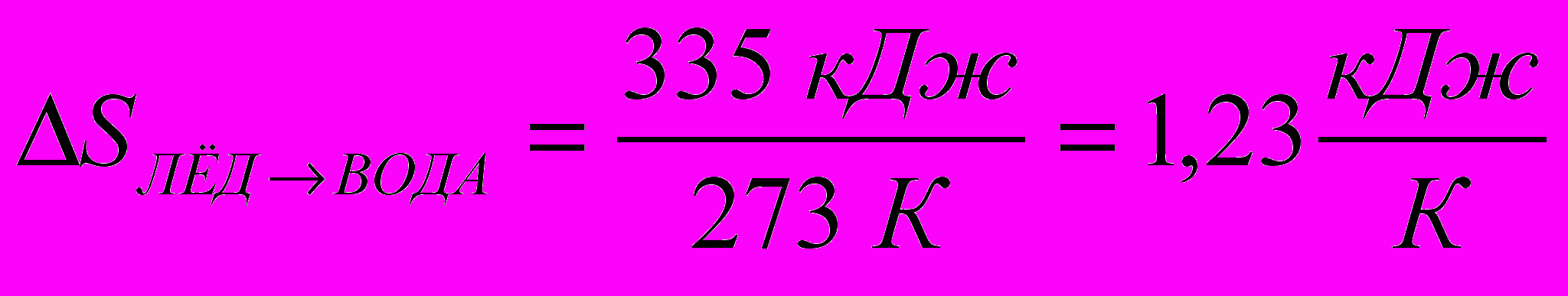, то есть при 0⁰С (273 К) энтропия 1 кг воды на 1,23 кДж/К больше, чем энтропия льда.

Если температура в ходе процесса изменяется, то изменение энтропии находится по более сложной формуле :

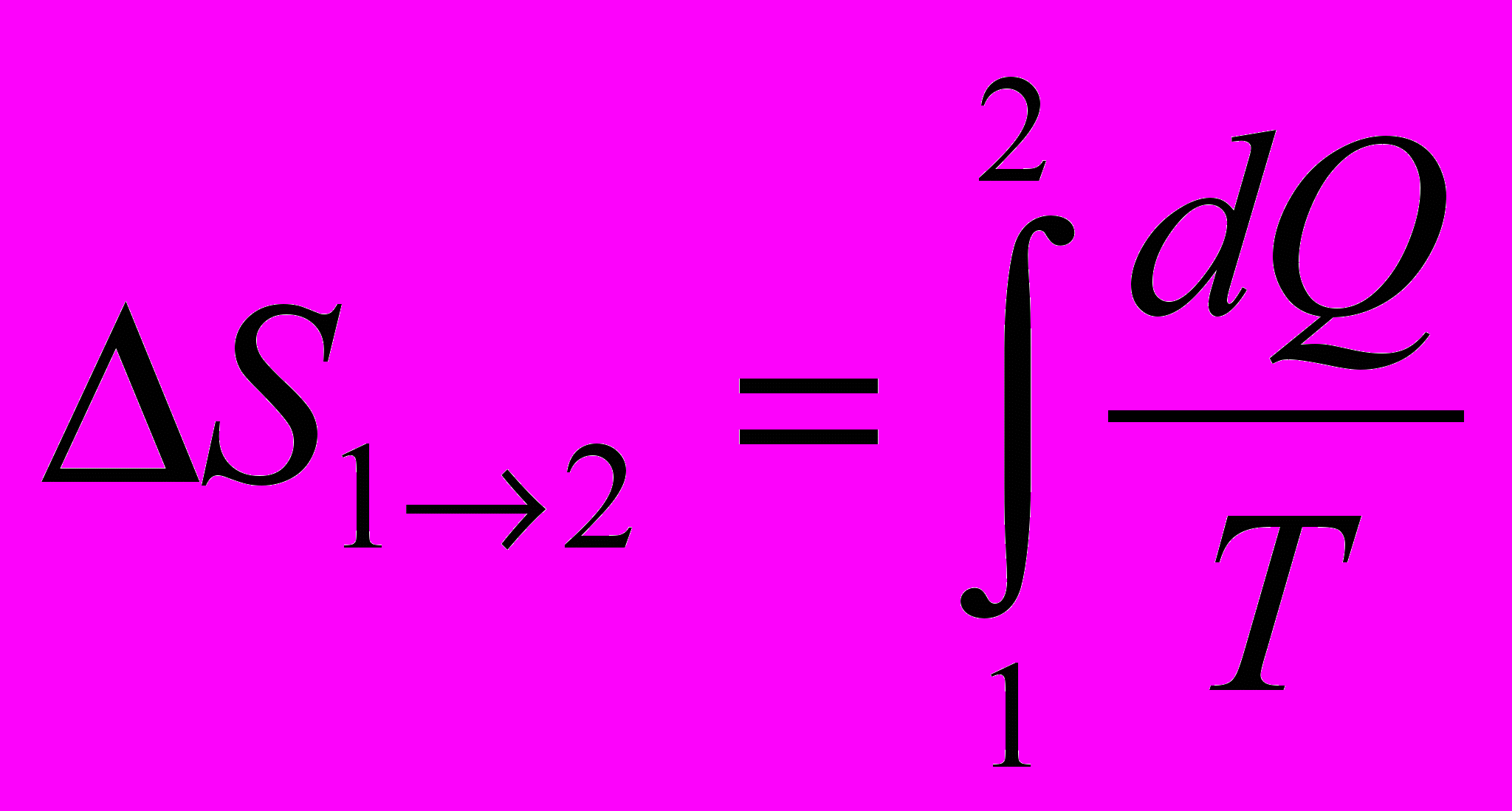(5)

(цифры 1 и 2 обозначают величины, характеризующие начальное и конечное состояния).

Найдём, например, изменение энтропии 1 кг воды при нагревании от 0⁰С до 100⁰С. В этом случае dQ = c·m·dT , где с – удельная теплоёмкость воды (4 180 Дж.К^-1.кг^-1). Подставляя в (5), получаем:




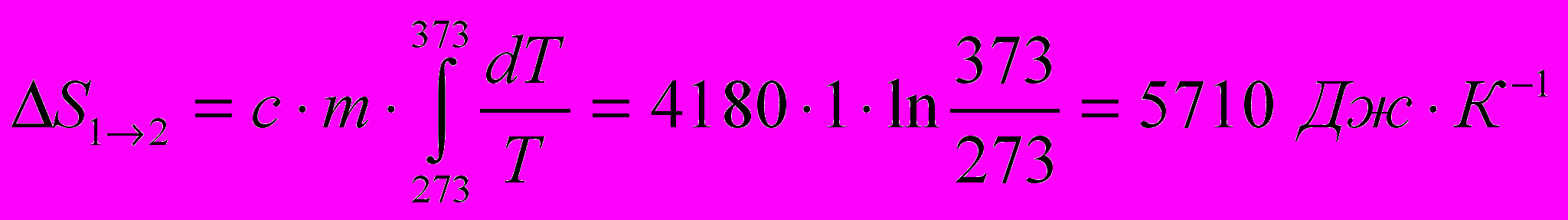
Второе начало термодинамики для изолированных систем.


Изолированными называют системы, которые не обмениваются с окружающей средой ни веществом, ни энергией. Абсолютно изолированных систем не бывает, но во многих случаях (например, для вещества в хорошем термосе) можно практически считать систему изолированной.

В изолированной системе общее изменение энтропии всегда положительно (то есть общая энтропия изолированной системы всегда возрастает).

Здесь важно не опустить слово „общая“. В какой-то части системы энтропия может уменьшиться, но это обязательно должно быть скомпенсировано увеличением энтропии в других частях системы.

Из формулы (3): ΔG = ΔU – T·ΔS видно, что если энтропия возрастает (ΔS > 0), то свободная энергия системы уменьшается (ΔG < 0). Поэтому второе начало можно сформулировать и по другому:

В изолированной системе общее изменение свободной энергии всегда отрицательно (то есть свободная энергия изолированной системы всегда уменьшается).

Эта формулировка более наглядна. Мы знаем, что во всех реальных процессах происходит диссипация свободной энергии, то есть часть свободной энергии превращается в связанную (преимущественно в тепловую). Если система изолированная, то извне свободная энергия не поступает, поэтому общий запас свободной энергии системы должен уменьшаться.

Второе начало термодинамики в приведенной формулировке имеет очень большое практическое значение, потому что оно позволяет точно установить, в каком направлении будет происходить тот или иной процесс. Например, если мы установим при расчёте, что при некотором процессе общая свободная энергия изолированной системы должна увеличиваться, можно категорически утверждать, что такой процесс невозможен.

Ещё чаще встречается такая ситуация: мы хотим провести некоторый физический или химический процесс в нужном нам направлении, и надо определить, при каких условиях это можно осуществить. В большинстве случаев применение второго начала термодинамики позволяет найти чёткий ответ на этот вопрос. Можно привести такой пример из техники. Для многих отраслей промышленности необходимо иметь в большом количестве алмазный инструмент. Природные алмазы слишком дороги, поэтому ещё в XIX веке пытались получить искусственные алмазы. Было потрачено много сил и средств, но эти попытки ни к чему не приводили, пока киевский физик Верещагин не провёл термодинамический расчёт и не определил условия, при которых графит может превращаться в алмаз. Условия оказались очень непростыми (температура не ниже 1000⁰С и давление не менее 150 тысяч атмосфер), но когда необходимые условия были чётко сформулированы, довольно быстро удалось наладить промышленное производство искусственных алмазов. Таких примеров можно привести много (в том числе из химических производств, технологии изготовления электронных приборов, ракетно-космической техники и т.п.).


Вероятностный смысл второго начала. Флюктуации.

Упорядоченность структуры в свете 2 начала термодинамики.


Данное ранее определение энтропии носит несколько формальный характер. Остаётся неясным, почему именно изменение энтропии указывает направление процессов. Первым понял суть дела гениальный физик Людвиг Больцман. Он обратил внимание на то, что разные состояния тела, соответствующие различному расположению молекул (атомов, ионов) и разным значениям их скоростей, осуществляются с очень разной вероятностью. Поясним этот сложный вопрос на относительно простых примерах.

Начнём с простейшего случая, когда в каком-то объёме находятся всего две одинаковые молекулы „а“ и „б“ Разделим мысленно объём на две половины. Очевидно, что возможны четыре варианта расположения молекул:

№	слева	справа
1	а, б	---
2	а	б
3	б	а
4	---	а, б

Вероятность каждого варианта равна 0,25. Но варианты 2 и 3 практически неотличимы, так как молекулы одинаковы. Поэтому их надо считать за одно состояние, вероятность которого равна 0,5. Таким образом, состояние с равномерным распределением будет

встречаться вдвое чаще, чем те состояния, когда обе молекулы слева или обе справа, хотя такие случаи тоже будут наблюдаться. По законам теории вероятностей с ростом числа молекул состояния с равномерным распределением будут иметь всё большую вероятность по сравнению с другими. Скажем, можно ли ожидать, что 40% молекул воздуха сами по себе в результате хаотического теплового движения соберутся в одной половине колбы, а 60% - в другой ? В принципе такой случай возможен, но вероятность подобного события исчезающе мала.

Один физик придумал такой пример. Он подсчитал вероятность того, что в одной половине стакана с воздухом случайно окажется на 1% больше молекул, чем в другой. Оказывается, что эта вероятность того же порядка, как если бы мы посадили тысячу обезьян за пишущие машинки с вставленными листами бумаги, дали бы им колотить по клавишам, потом собрали и сложили все листы, и получился бы роман „Война и мир“. В принципе это не противоречит законам природы, но практически такое событие никогда не произойдёт. Точно так же практически невероятно, чтобы без воздействия внешней силы заметно больше молекул в теле двигалось в одну сторону, чем в противоположную (имеется в виду тепловое движение).

В результате глубокого анализа Л.Больцман установил связь между вероятностью состояния и энтропией системы частиц. Эта связь выражается формулой Больцмана:

S = k · ln P_ТД (6)


Здесь k – постоянная Больцмана (k = 1,37.10 ^–23 Дж.К ^–1), а Р_ТД – термодинамическая вероятность данного состояния системы.

Понятие термодинамической вероятности весьма сложное (об этом будет сказано далее). В простейших случаях (например, для идеального газа) можно дать такое определение:

Термодинамическая вероятность – это число вариантов расположения молекул и распределения их скоростей, соответствующая данному состоянию системы.

В простейшем виде понятие термодинамической вероятности можно пояснить на таком примере. Пусть «состояние» группы курсантов определено таким образом: «Взвод (30 человек) находится в аудитории № 10». Курсанты могут разместиться в аудитории как попало. Математика показывает, что число вариантов расположения „n“ объектов равно n! (n! –– „n-факториал“– это произведение всех чисел подряд от 1 до n). В данном примере это число вариантов и есть термодинамическая вероятность системы „взвод курсантов“.

Р_ТД = n! = 30! = 2,6.10 ³²

Если будет дана команда сесть по отделениям (в каждом отделении по 15 человек), то число вариантов будет n₁ ! · n₂ ! =

= 15!· 15! = 1,7.10 ²⁴, то есть термодинамическая вероятность в этом случае меньше в 1,5.10 ⁸ раз.

По самому смыслу понятия вероятности любая система, предоставленная сама себе (то есть изолированная), будет переходить из состояния с меньшей вероятностью в состояние, вероятность которого больше. Обратный переход в принципе возможен, но практически невероятен. Учитывая формулу Больцмана, мы сразу приходим к формулировке второго начала термодинамики: все реальные процессы в изолированной системе происходят в сторону состояний с большей вероятностью, то есть с увеличением энтропии. Таким образом, второе начало является вероятностным законом.

Работы Больцмана имели большое значение не только для термодинамики; они существенно повлияли на развитие науки в целом. До этого все процессы в природе считались строго детерминированными, то есть полагали, что зная точно состояние какой-то системы в данный момент времени, можно однозначно предсказать, что будет с этой системой в будущем. Конечно, было понятно, что для сложных систем может потребоваться практически невыполнимый объём вычислений, но это считалось вопросом техники. Больцман первым показал, что физические законы могут иметь принципиально вероятностный характер. Развитие науки в ХХ веке показало, что большинство законов природы являются вероятностными, хотя есть и абсолютно строгие законы (например, закон сохранения заряда).

Это достаточно хорошо известно и на практике – недаром одним из основных предметов в подготовке офицера-артиллериста является теория вероятностей. Методы теории вероятностей широко используются в любой науке (в том числе – биологии и медицине), и не только потому, что наши измерения являются не абсолютно точными. Современная физика показала, что основные физические процессы, в конечном счёте определяющие все свойства вещества, являются в принципе вероятностными. Принципиально невозможно, например, предсказать, какие именно атомы радиоактивного изотопа распадутся именно в данную секунду – мы можем говорить только о вероятности данного процесса. Мы не будем здесь подробно рассматривать этот сложный вопрос, но в настоящее время не вызывает сомнений, что абсолютно точный прогноз принципиально невозможен не только при предсказании погоды, но и при расчёте полёта снаряда или космического корабля, и при исследовании поведения элементарных частиц, и в очень многих других случаях. При этом зачастую речь идёт не о каких-то незначительных ошибках, а о вполне заметных и даже больших непредсказуемых отклонениях, имеющих нередко принципиальный характер. Приведём простейший, но вполне серьёзный пример. Предположим, Вы обладаете большой ловкостью, и Вам удалось поставить карандаш на острый конец. Ясно, что долго он так не простоит, но никакие вычисления на самых мощных компьютерах не помогут Вам предсказать, в какой момент и в какую сторону он упадёт.

Разумеется, всё сказанное относится и к живым организмам, и даже в большей степени, чем к неживым системам. Врач в своей деятельности обязательно должен учитывать вероятностный характер тех закономерностей, которые он использует в своих рассуждениях. Прямолинейное мышление по типу: „если мы имеем то-то и то-то, то обязательно будет именно так, а не иначе“ – самая частая причина врачебных ошибок.


Флюктуации.


Когда мы имеем дело с телами относительно большой массы, содержащими огромное количество молекул, отступления от второго начала практически никогда не наблюдаются. Однако, если мы переходим к малым (микроскопическим) масштабам, отступления от строгих законов теории вероятностей становятся всё более заметными. Например, если в стакане воздуха самопроизвольное отклонение в плотности газа на 1% абсолютно невероятно (вспомните пример с обезьянами), то в объёме газа диаметром меньше 1 микрометра (1 мкм = 10 ^–6 м) подобные колебания плотности воздуха на самом деле всё время происходят. Точно так же вследствие хаотичности движения молекул в микроскопических масштабах колеблются давление, энергия, концентрация ионов и многие другие величины. Подобные самопроизвольные колебания физических характеристик, происходящие в микроскопических масштабах, называются флюктуациями.

Флюктуации являются наглядным примером вероятностного характера физических процессов. Абсолютно невозможно точно предсказать, где, когда и в какую сторону изменится, например, плотность в данном объёме газа. Однако, вполне возможно(по крайне мере, в не очень сложных случаях) рассчитать вероятность той или иной флюктуации; такие расчёты многократно проводились в хорошим согласии с опытом.

Интересно, что флюктуации плотности воздуха в атмосфере мы видим в буквальном смысле слова. Дело в том, что из-за флюктуаций воздух в микроскопических масштабах оказывается неоднородным по плотности. Размеры неоднородностей сравнимы с длиной световой волны, поэтому на этих неоднородностях происходит рассеяние солнечного света. Лучи с короткой длиной волны (то есть синие) рассеиваются сильнее, и именно этим объясняется синий цвет неба.

Несмотря на малость масштабов, флюктуации во многих случаях имеют существенное практическое значение. Например, флюктуации скоростей электронов в электронной аппаратуре вызывают хаотические колебания силы тока в цепи (тепловой шум), что заметно мешает работе приборов. Особенно большое значение это имеет в современных микросхемах, где размеры отдельных элементов составляют микрометры и доли микрометра.

Флюктуации бывают и в живых организмах. Например, вследствие флюктуаций молекул мембраны каналы, через которые идёт перенос ионов через мембрану, случайным образом то открываются, то закрываются (это можно наблюдать в опыте). Флюктуации в рецепторных клетках заметно влияют на восприятие слабых сигналов (света, звука и др.), которые теряются на фоне флюктуационного „шума“, то есть хаотических колебаний разности потенциалов на мембране, возникающих в результате флюктуаций. Для борьбы с этим явлением живые организмы выработали в ходе эволюции сложные приспособления, о которых не место говорить в данной лекции. Сейчас большое внимание уделяется исследованию флюктуаций в центральной нервной системе; по-видимому, они играют существенную роль во многих нервных процессах.

Особенно интересно, что, как показал Н.В.Тимофеев-Рессовский, возникающее в результате флюктуаций точечное кратковременное возрастание энергии около молекулы ДНК может вызвать мутацию. По мнению Тимофеева-Рессовского, большинство мутаций в обычных условиях возникают именно таким образом, а не за счёт внешних причин (ионизирующее излучение, мутагенные химические вещества и т.п.).

Упорядоченность структуры

в свете второго начала термодинамики

Надо сказать, что понятие термодинамической вероятности является более сложным, чем сформулировано на стр. 8. Слишком упрощенное использование этого понятия неоднократно приводило к заблуждениям и грубым ошибкам. Например, можно часто встретить такое рассуждение. Математика показывает, что наиболее вероятным является равномерное распределение частиц, когда в равных объёмах число частиц одинаково. Значит, любая система будет переходить в бесструктурное состояние с равномерным распределением частиц, которому соответствует максимальная вероятность (такое состояние часто называют хаотическим). На самом деле это справедливо только для идеального газа в отсутствие внешних сил; во всех прочих случаях равномерное распределение вовсе не является наиболее вероятным.

Например, в атмосфере молекулы воздуха распределены вовсе не равномерно: внизу их гораздо больше, чем наверху. Причина очевидна: при наличии силы тяжести нахождение молекулы внизу гораздо более вероятно, чем наверху. В этом случае для расчёта вероятности надо использовать более сложную формулу, учитывающую действие силы тяжести. Другой пример: в мембранах клеток молекулы фосфолипидов, образующие мембрану, расположены совсем не хаотически, а почти строго параллельно. При наличии больших сил молекулярного взаимодействия такое расположение оказывается наиболее вероятным. Таких примеров очень много, но они говорят не о нарушении второго начала термодинамики, а о том, что к определению вероятности состояния (то есть термодинамической вероятности) надо подходить очень внимательно, с учётом всех внешних и внутренних сил, действующих в данном конкретном случае.

Пожалуй, наиболее наглядно можно показать неправильность представлений о „стремлении всего к хаосу“ на примере кристаллов. Высокая упорядоченность структуры кристаллов очевидна, но она вовсе не противоречит 2 началу. Дело в том, что между атомами или ионами в кристаллической решётке существуют большие силы взаимодействия (при малых расстояниях преобладает отталкивание, при больших – притяжение). В этих условиях нельзя пользоваться простой формулой Р_ТД = n!, но можно показать, что наиболее вероятным является такое состояние, когда атомы (или ионы) находятся в узлах кристаллической решётки, где притяжение и отталкивание уравновешиваются. Это легко понять и без расчёта – очевидно, что такое состояние, когда сумма сил равна нулю, соответствует минимуму свободной энергии, и оно будет наиболее вероятным. При низкой температуре тепловое движение вызывает колебания атомов около узлов, но не может заметно нарушить структуру кристалла. При нагревании тепловое движение усиливается. При определённой температуре (точке плавления) энергия теплового движения превышает энергию сил взаимодействия, неупорядоченное состояние оказывается более вероятным – кристалл плавится. Но для этого надо извне подвести к кристаллу тепло, при этом энтропия кристалла возрастает, что соответствует второму началу. При понижении температуры происходит обратный переход – кристаллизация. В ходе кристаллизации кристалл обязательно должен отдать тепло в окружающую среду, при этом энтропия кристалла уменьшается. На первый взгляд это противоречит 2 началу, но на самом деле это не так. Кристалл не является изолированной системой; за изолированную систему надо принять систему «кристалл + окружающая среда». Среда получает тепло, которое теряет кристалл. Общее изменение энтропии при этом равно

,

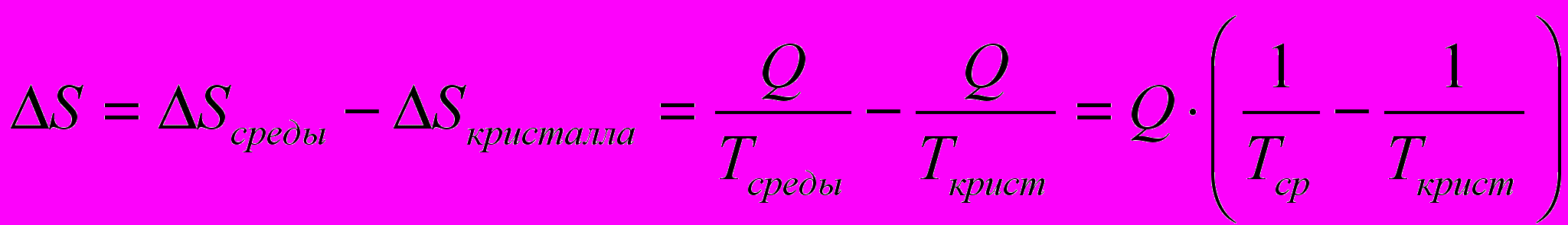(см. формулу «4»). Но температура среды обязательно должна быть ниже, чем температура кристалла – иначе кристаллизация невозможна, то есть Т_среды < T_крист , но тогда 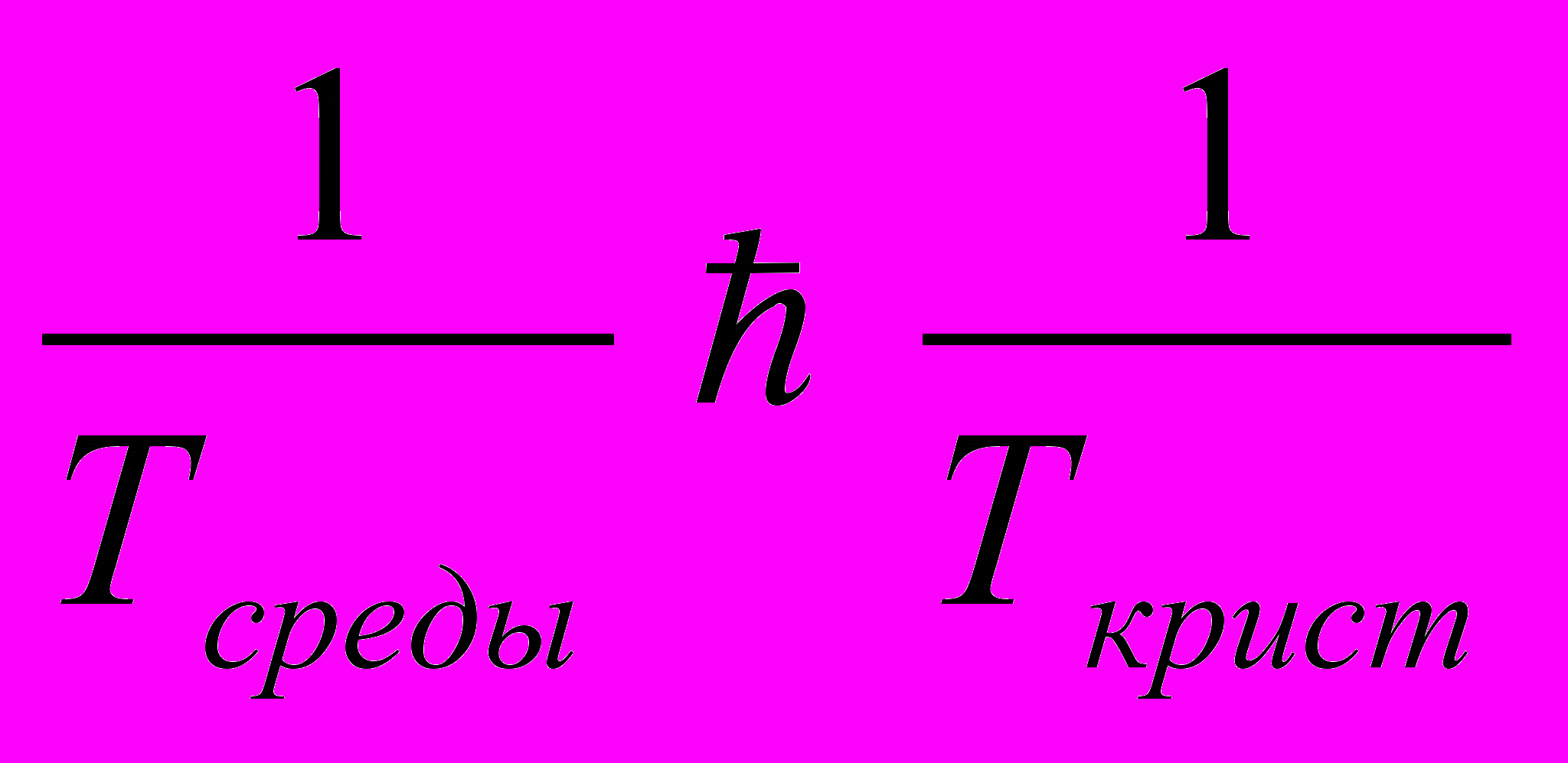, и выражение в скобке положительно, значит, ΔS > 0. Таким образом, общее изменение энтропии положительно в полном соответствии со вторым началом термодинамики.

В общем случае можно показать, что всегда при повышении упорядоченности в каком-то объекте его энтропия понижается, а при уменьшении упорядоченности энтропия объекта возрастает. При этом общая энтропия системы „объект + среда“ всегда увеличивается.

В конце ХХ века возникла новая научная дисциплина, получившая название синергетика, которая изучает процессы самоорганизации, то есть возникновение структуры (упорядоченности) в самых различных объектах. Несмотря на свою молодость, синергетика дала уже много важных результатов при изучении разнообразных процессов в природе, технике и в нашем организме, но эти вопросы выходят за рамки программы нашего курса.


Формулировка второго начала термодинамики

для открытых систем.


Открытыми называются такие системы, которые обмениваются веществом и энергией с окружающей средой. К открытым системам относятся все живые организмы. Очевидно, что запас свободной энергии открытой системы (в том числе и человека) может как расти, так и убывать – всё зависит от того, что будет преобладать: приток свободной энергии из окружающей среды или убыль свободной энергии в результате совершения работы и процессов диссипации энергии. В частности, свободная энергия организма может и не изменяться, если названные процессы сбалансированы. Это обстоятельство долгое время смущало учёных; многие даже утверждали, что 2 начало нельзя применять к живым организмам. Надо прямо сказать, что ни один физический закон не породил столько нелепостей и ошибок, сколько было высказано по поводу второго начала термодинамики и понятия энтропии. В частности, широко распространённой была точка зрения, согласно которой живые организмы „борются“ с возрастанием энтропии мира, и в этом, якобы, и состоит космическая роль жизни. (сторонниками таких взглядов были, например, академик В.И.Вернадский и известный учёный и писатель-фантаст И.Ефремов).

Все эти недоразумения были окончательно выяснены только во второй половине ХХ века, когда проблема была рассмотрена выдающимся биофизиком, лауреатом Нобелевской премии И.Р.Пригожиным. Подход Пригожина сводится к следующему. Для открытых систем надо различать два вида процессов:

1) процессы внутри системы и

2) процессы обмена с окружающей средой

Поэтому изменение любой величины, характеризующей систему, надо представлять, как сумму двух частей:

1) Изменение за счёт процессов внутри системы и

2) Изменение за счёт процессов обмена с окружающей средой

Например, для свободной энергии:


ΔG = ΔG_I +ΔG_E (7)

где ΔG – общее изменение свободной энергии, ΔG_I - изменение за счёт процессов внутри системы, ΔG_E - изменение за счёт обмена веществом и энергией с окружающей средой (индекс I обозначает слово interna – внутреннее, а индекс E – externa, внешнее). Все процессы внутри системы идут с диссипацией свободной энергии, поэтому изменение свободной энергии за счёт процессов внутри системы всегда отрицательно (ΔG_I < 0). Что же касается члена ΔG_E, то он может иметь любой знак. Часто система получает извне поток свободной энергии, то есть ΔG_E > 0, но вполне возможны и случаи, кода система отдаёт свободную энергию другим телам; тогда ΔG_Е < 0. Поэтому общее изменение свободной энергии открытой системы может иметь любой знак (или равняться нулю); это никак не противоречит второму началу термодинамики.

Аналогичные рассуждения можно провести и для энтропии. Общее изменение энтропии открытой системы равно:


ΔS = ΔS_I + ΔS_E (8)

где индексы имеют тот же смысл.

Исходя из этих положений, Пригожин предложил такую формулировку второго начала термодинамики для открытых систем (в том числе, для живых организмов):

в открытой системе изменение внутренней энергии за счёт процессов внутри системы всегда отрицательно, а изменение энтропии за счёт процессов внутри системы всегда положительно.

ΔG_I < 0 ; ΔS_I > 0 (9)


Подход Пригожина позволил разрешить все противоречия и спорные вопросы, которые накопились за столетие. Формулировка Пригожина сейчас принята всеми; не известно ни одного случая нарушения установленных им закономерностей.


Продукция энтропии и поток энтропии.


Во многих случаях представляет интерес скорость изменения энтропии, которая выражается производной энтропии по времени. Дифференцируя формулу (8), получим:


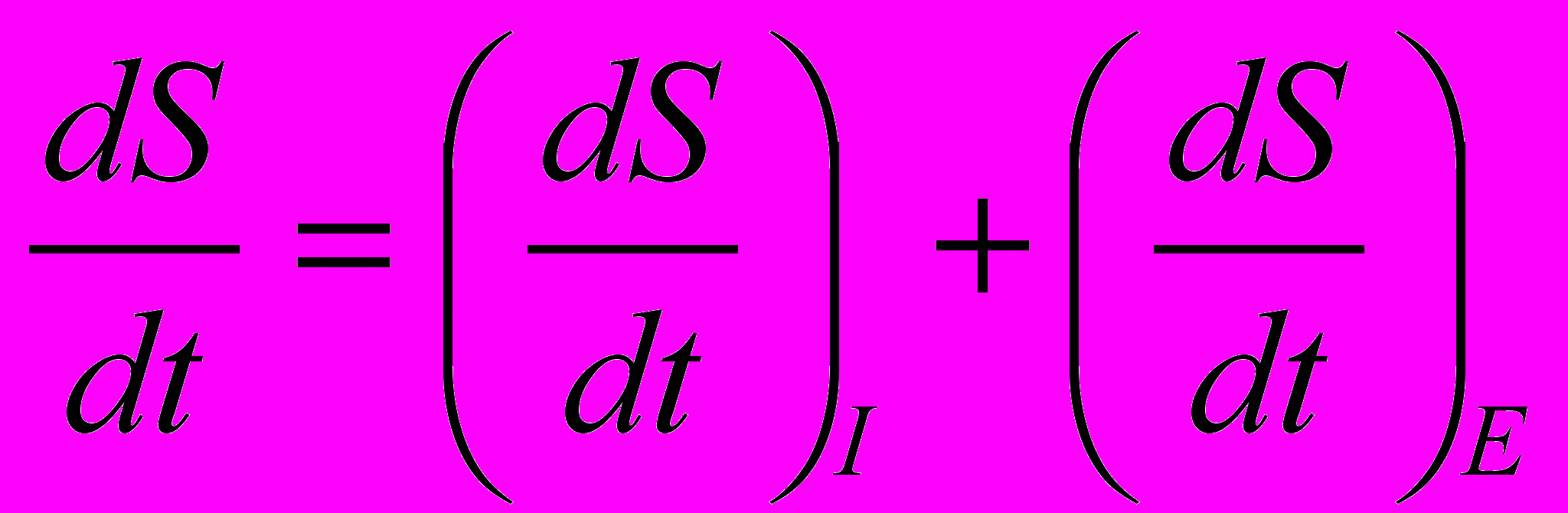(10)

Первый член справа называют продукцией энтропии, а второй член – потоком энтропии. Очевидно, что

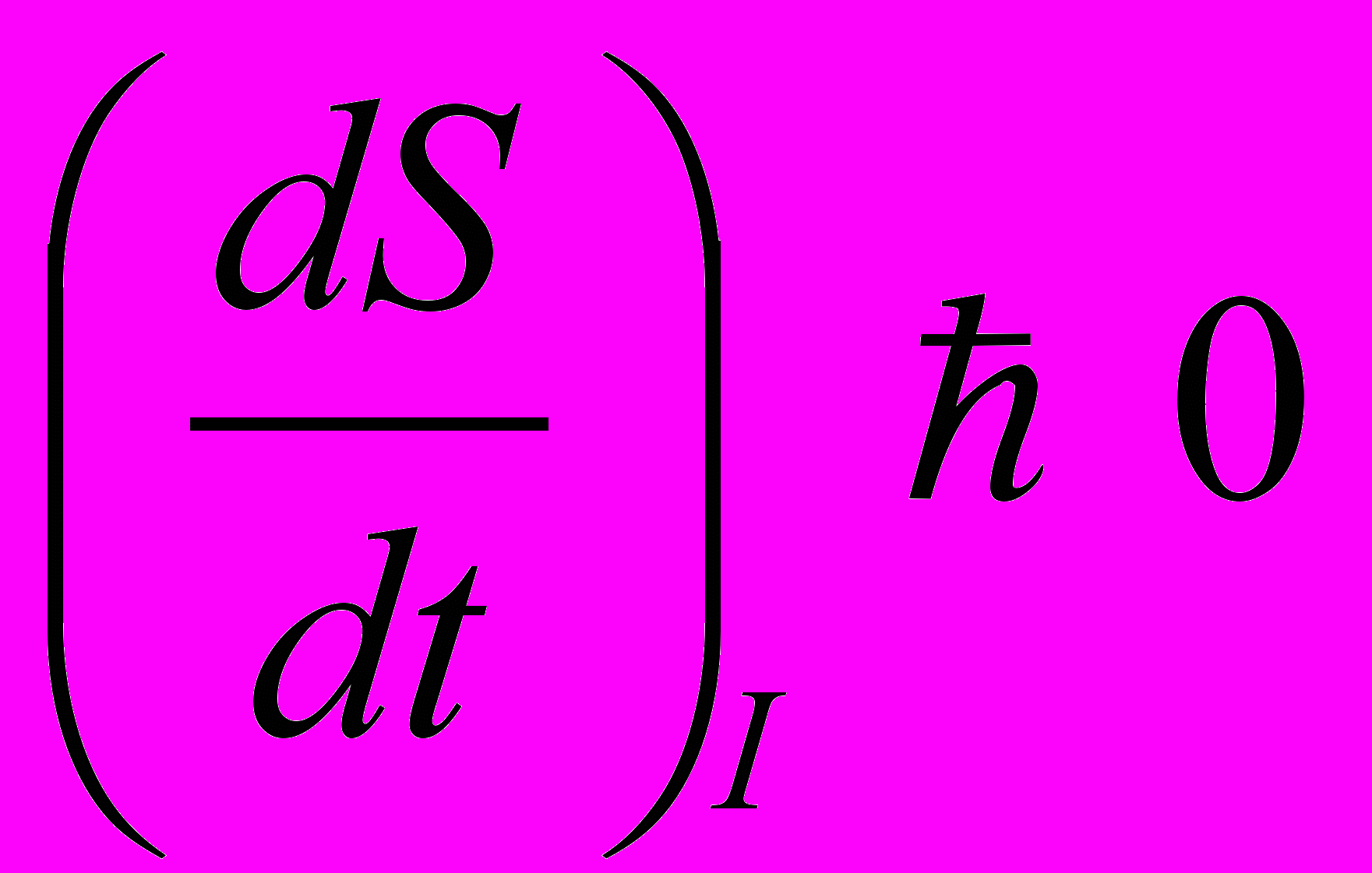(11)

Эту формулу тоже можно считать выражением 2 начала термодинамики для открытых систем.


Стационарные состояния. Теорема Пригожина.


Стационарным состоянием системы называют состояние, в котором процессы в системе так сбалансированы, что основные величины, характеризующие систему, остаются постоянными.

Живые организмы большую часть времени проводят именно в стационарном состоянии (точнее – переходя время от времени из одного стационарного состояния в другое, например – из состояния сна в состояние бодрствования и наоборот). Это свойство живых существ называют гомеостазом. Поддержание стационарного состояния (гомеостаз) имеет большое значение для нормальной жизнедеятельности. В организме всё время идут длинные цепи сопряжённых физических процессов и химических реакций. Эти процессы очень по разному зависят от температуры, рН и многих других параметров. Поэтому, если эти параметры меняются, нарушается согласование важных жизненных процессов. Чтобы такое не происходило, в организме существуют сложные системы регулирования, достаточно точно поддерживающие стационарное состояние. Наоборот, болезни в большинстве случаев сопровождаются нарушением гомеостаза.

Пригожин доказал положение, которое называется теоремой Пригожина: в стационарном состоянии продукция энтропии минимальна 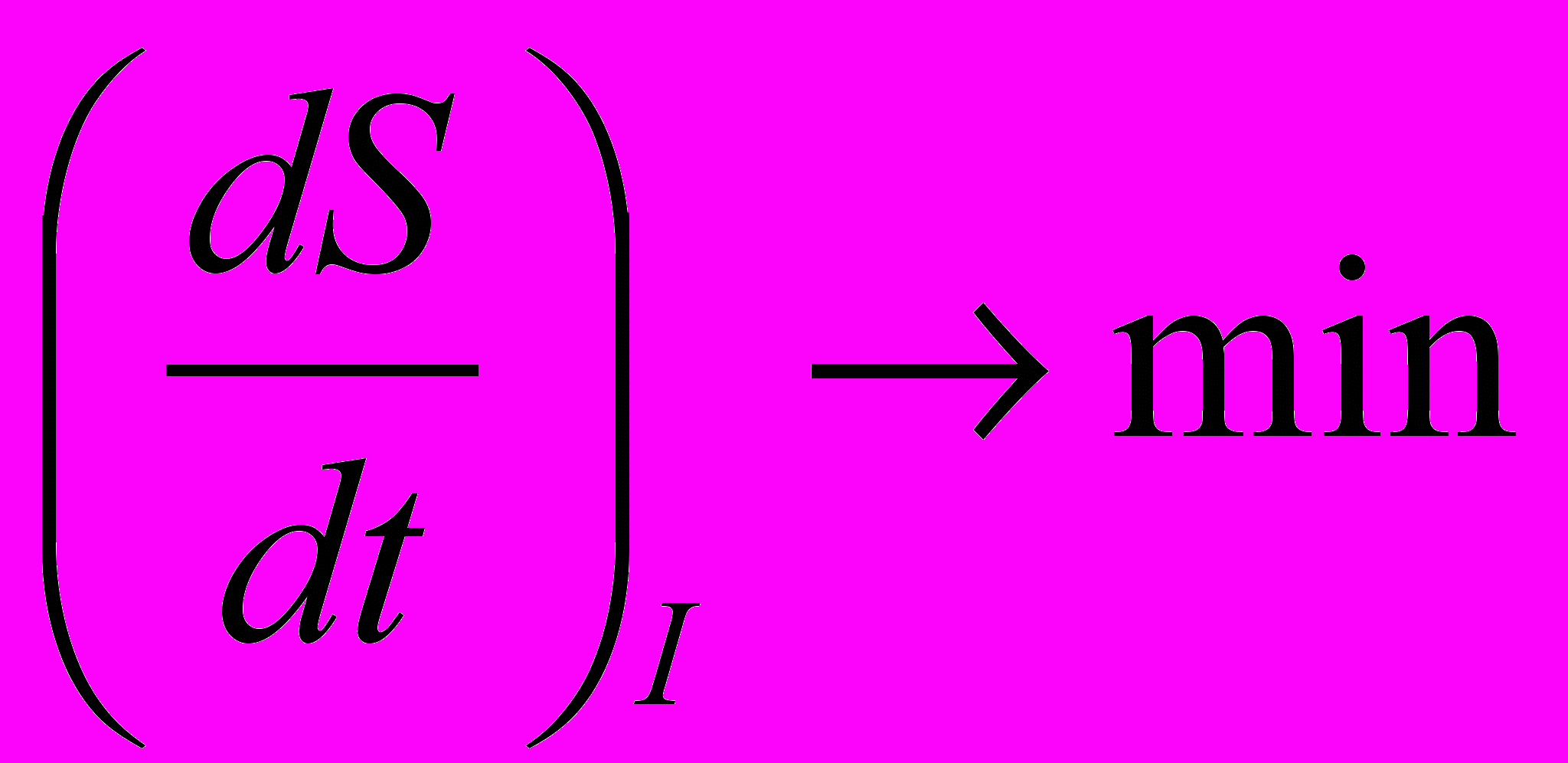(в стационарном состоянии) (12)

Нетрудно понять, что минимальная продукция энтропии соответствует минимальной диссипации свободной энергии (минимальным потерям энергии), то есть максимальному КПД. Поэтому можно сказать, что в стационарном состоянии КПД системы наибольший. Это тоже важное свойство стационарных состояний.


Процессы с преодолением потенциального баоьера


В очень многих случаях процессы в системе идут таким образом, что переход из начального состояния (1) в конечное состояние (2) происходит через промежуточное состояние (3) с более высокой энергией:


Хотя с точки зрения закона сохранения энергии переход из (1) в (2) вполне возможен, на самом деле, чтобы он произошел, надо сначала сообщить системе дополнительную энергию U _АКТ (энергию активации), тогда система перейдёт в состояние (3), а оттуда, уже с выделением энергии – в состояние (2). В таких случаях говорят, что процесс идёт с преодолением потенциального барьера. Например, в воде все молекулы связаны водородными связями. Чтобы молекула могла перейти из жидкой фазы в пар, она должна разорвать водородные связи, то есть преодолеть довольно высокий потенциальный барьер (U _А около 40 кДж на моль). Другой пример – переход электрона из одного полупроводника в другой. На границе двух полупроводников всегда возникает разность потенциалов. Если эта разность потенциалов направлена так, что она препятствует прохождению электронов, на границе создаётся потенциальный барьер; в этом случае U _A = F.U Дж/моль (F – число Фарадея). С преодолением потенциального барьера идут очень многие химические реакции.

Энергия активации может быть сообщена извне (например, к полупроводникам можно приложить дополнительную разность потенциалов), но наибольший интерес представляют те случаи, когда преодоление потенциального барьера происходит за счёт теплового движения молекул. Из-за хаотического характера теплового движения какая-то часть молекул (или других частиц – ионов, электронов и др.) будет иметь энергию, превышающую энергию активации U_A (часто говорят, что их энергия больше высоты потенциального барьера). Такие частицы принято называть активными частицами, Очевидно, что процесс в данном случае будет идти только за счёт активных частиц, а скорость процесса будет пропорциональна числу активных частиц.

Для расчёта числа активных частиц n _A служит формула Больцмана:

(13)

Из этой формулы можно вывести выражение для отношения скоростей процессов при двух разных температурах Т ₁ и Т₂ . Если при температуре Т₁ скорость процесса υ₁, а при температуре Т₁ – соответственно υ₂ , то

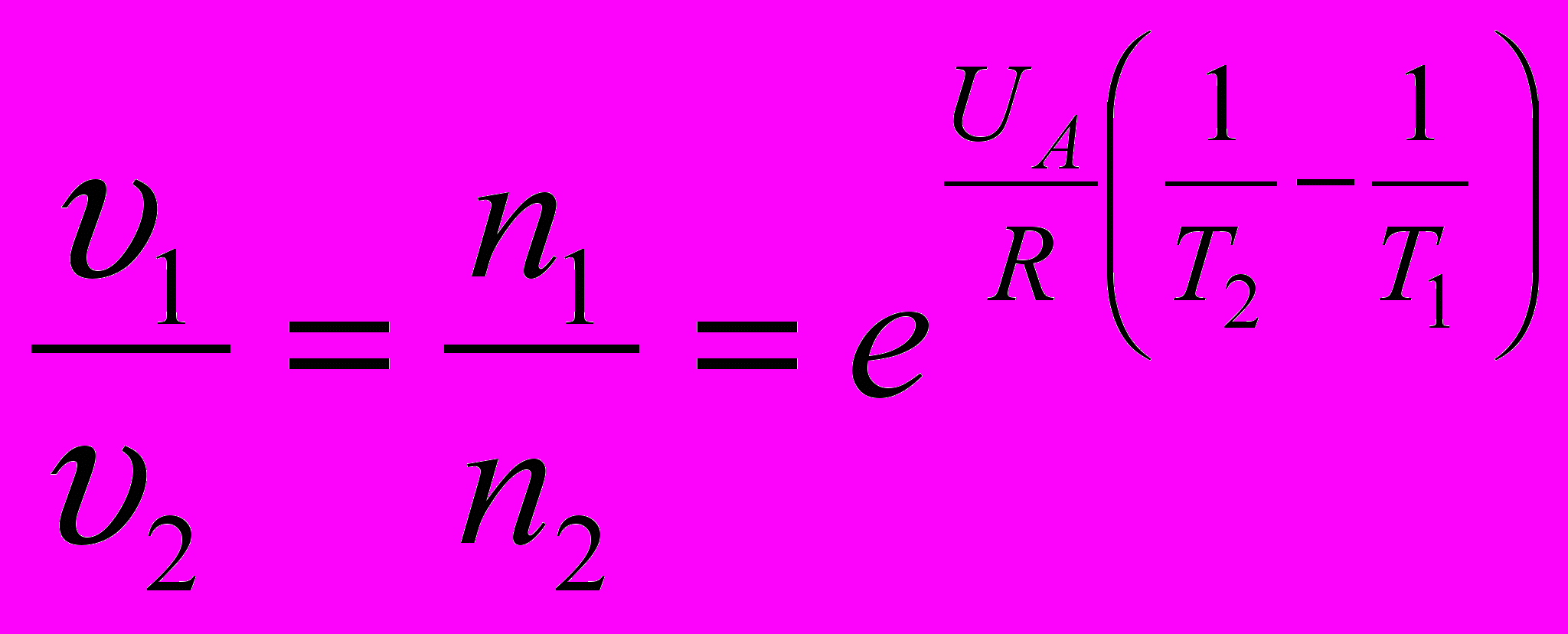(14)

Эту формулу называют формулой Аррениуса.

Иногда в литературе энергию активации приводят в расчёте не на моль, а на одну частицу.В этом случае в формулах вместо R надо брать постоянную Больцмана k = 1,37.10 ^{– 23} Дж.К ^{– 1} .

Очень важным примером процессов с преодолением потенциального барьера является ускорение химических реакций катализаторами, в том числе – биологическими катализаторами (ферментами). При всём разнообразии механизмов действия ферментов, в основе этого действия почти всегда лежит снижение потенциального барьера. Из-за экспоненциальной зависимости в формулах (13) и (14) даже небольшое уменьшение активации значительно ускоряет процесс. Например, АТФ-аза при температуре 37^оС увеличивает скорость расщепления АТФ в 1,3.10¹⁰ раз! нетрудно подсчитать, что для расщепления того количества АТФ, которое АТФ-аза разлагает за одну минуту, без фермента потребовалось бы 25 000 лет.


Коэффициент Вант-Гоффа Q₁₀


Этот коэффициент является наглядной характеристикой зависимости скорости процесса от температуры. Он равен:



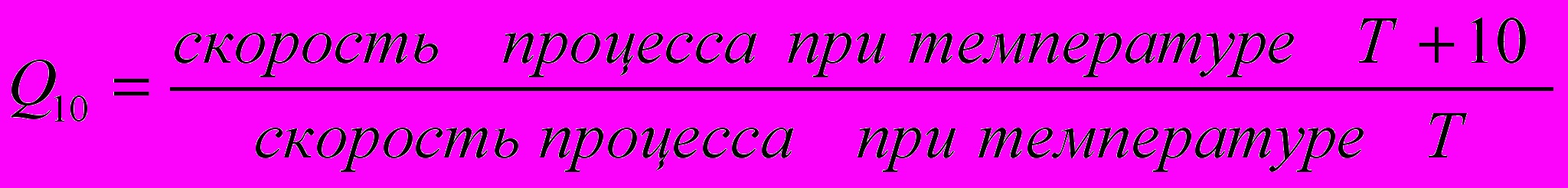
Из формулы Аррениуса легко получить, что

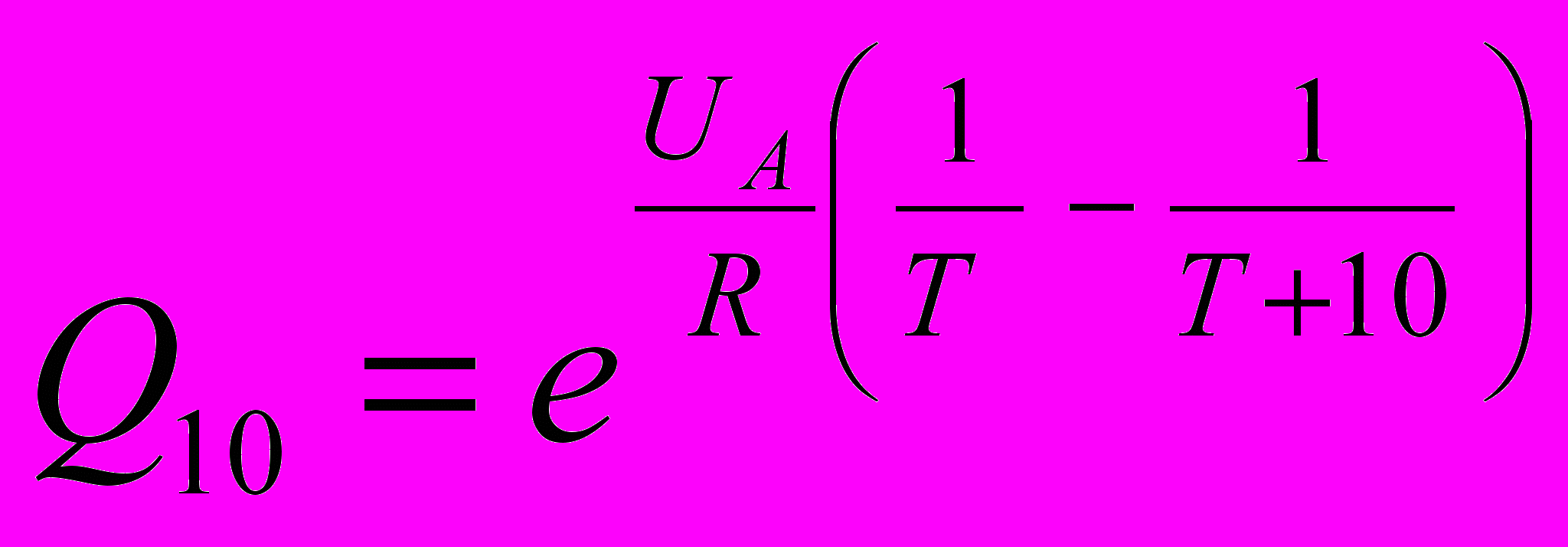(15)

Определив Q₁₀ (что легко сделать на практике), можно рассчитать энергию активации. Если же Q ₁₀ близко к единице, это показывает, что потенциального барьера нет, или он очень низкий и не имеет существенного значения.


Заключение


Из материала лекции Вы усвоили, что законы термодинамики имеют большое значение для понимания самых разных сторон жизнедеятельности организма. Методы термодинамики успешно используются при исследовании самых разнообразных процессов, связанных с превращениями энергии в организме (питание, мышечное сокращение, обмен веществ, возникновение и проведение нервных импульсов, работа органов чувств и многое другое). Поэтому знание основных положений биологической термодинамики будет необходимо Вам при изучении большинства дисциплин. В то же время, становится всё яснее, что хотя законы термодинамики в живых организмах не нарушаются, но в целом направление развития организмов и всей биосферы как в онтогенезе, так и в филогенезе определяется не законами термодинамики (в частности, принципом возрастания энтропии), а чисто биологическими закономерностями . При этом основное значение имеют не процессы разрушения структур организма (хотя они всё время происходят), а процессы самоорганизации, строящие и поддерживающие эти структуры.


ПРИЛОЖЕНИЕ


ОПИСАНИЕ ЛАБОРАТОРНОЙ РАБОТЫ

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ПОВЕРХНОСТНО АКТИВНЫХ ВЕЩЕСТВ НА ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТИ


Цель работы: 1) познакомиться с одним из способов изметения коэффициента поверхностного натяжения

2) исследовать влияние поверхностно активного вещества на свободную энергию поверхности жидкости.


Введение


Более подробно о поверхностном натяжении сказано в лекции по свойствам жидкостей и в учебнике А.Н.Ремизова (гл. 7, § 7 и 8.).


Силы, действующие на молекулы жидкости, находящиеся в тонком поверхностном слое, отличаются от сил, действующих внутри. Молекула, находящаяся внутри, равномерно окружена со всех сторон другими молекулами, поэтому равнодействующая сил притяжения равна нулю. Если же молекула лежит близко к поверхности, то другие молекулы окружают её преимущественно с одной стороны. Возникает равнодействующая сила, направленная внутрь жидкости. Эта сила стремится втянуть молекулу вглубь жидкости, то есть уменьшить площадь поверхности жидкости. Такую силу называют силой поверхностного натяжения.

Если условия таковы, что уменьшение площади поверхности возможно, то сила поверхностного натяжения совершает какую-то работу. Отсюда следует, что поверхностный слой жидкости обладает дополнительной свободной энергией G_ПН (работа совершается за счёт именно свободной энергии). Мерой этой свободной энергии является коэффициент поверхностного натяжения σ , равный дополнительной свободной энергии поверхностного слоя на единицу площади:

(1)

Размерность σ есть Дж.м ^{– 2} .

Многие вещества ослабляют силы межмолекулярного взаимодействия и тем самым снижают величину коэффициента поверхностного натяжения σ . Такие вещества называются поверхностно активными веществами ( сокращённо ПАВ; подробнее о ПАВ сказано в лекции по свойствам жидкостей). В данной работе предлагается экспериментально исследовать это явление.

Теория метода


В работе используется метод измерения σ по отрыву пузырька. Если в жидкости находится небольшой пузырёк газа, силы поверхностного натяжения стремятся уменьшить его поверхность, то есть сжать пузырёк. Поэтому в пузырьке создаётся добавочное давление Δр, равное :

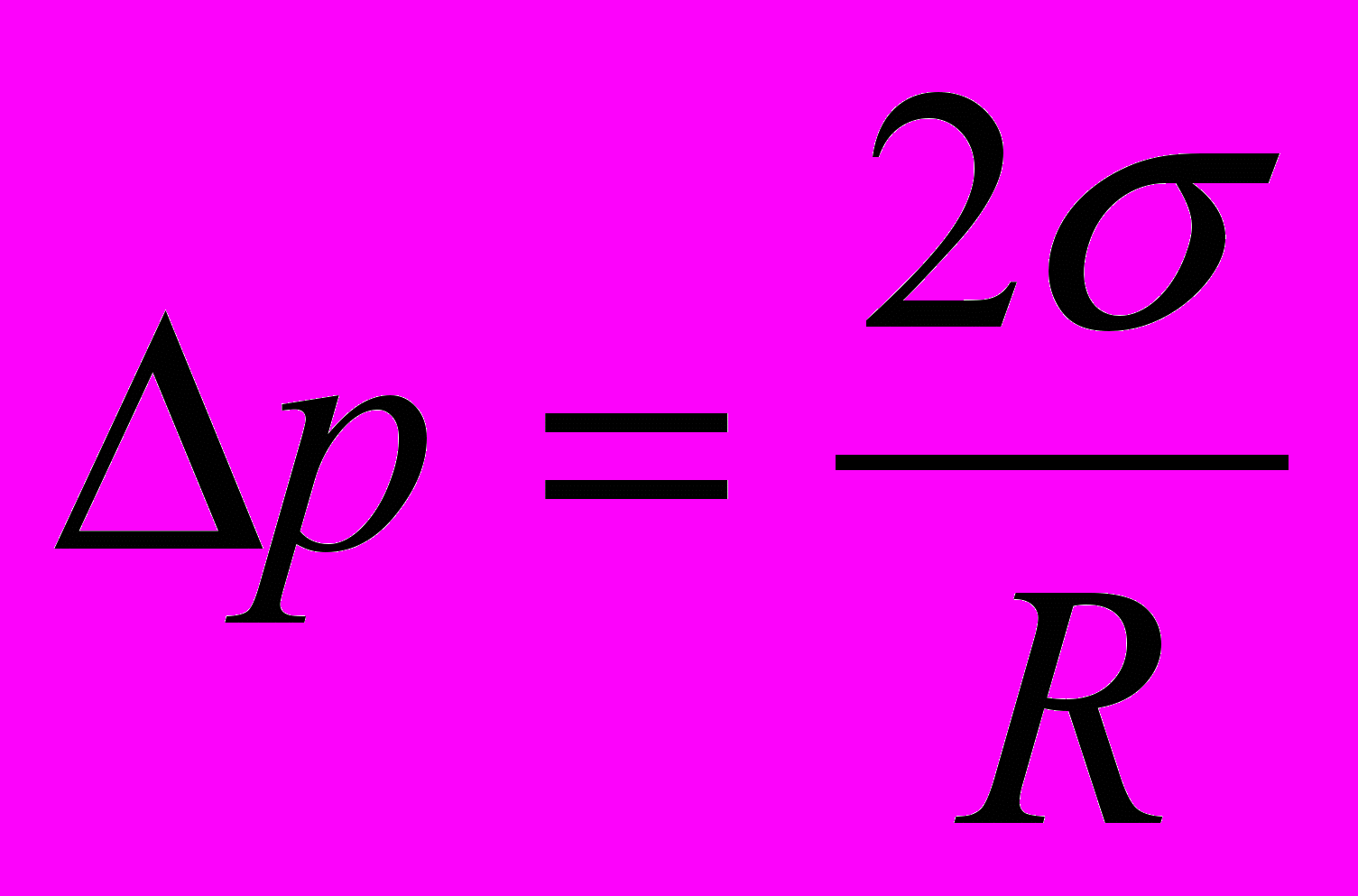, (2)

где R - радиус пузырька.

Если в жидкость погружён капилляр, в котором создано добавочное (по сравнению с атмосферным) давление, то пузырёк воздуха выйдет из кончика капилляра тогда, когда давоение воздуха станет равным Δ р, определённому по формуле (2). Поэтому, измерив давление в капилляре, можно найти σ.


Установка состоит из капилляра 1, который можно опускать в стаканчик с исследуемой жидкостью 2. Капилляр через тройник 3 соединён с колбой, 4 в которую по каплям капает вода из банки 5. Скорость подачи воды можно регулировать зажимом 6. Давление в капилляре измеряется жидкостным U-образным манометром 7 . Добавочное давление Δ р прямо пропорционально разности уровней h₂ – h₁ :

Δ р = k ( h₂ – h₁ ) ,

откуда с учётом формулы (2)

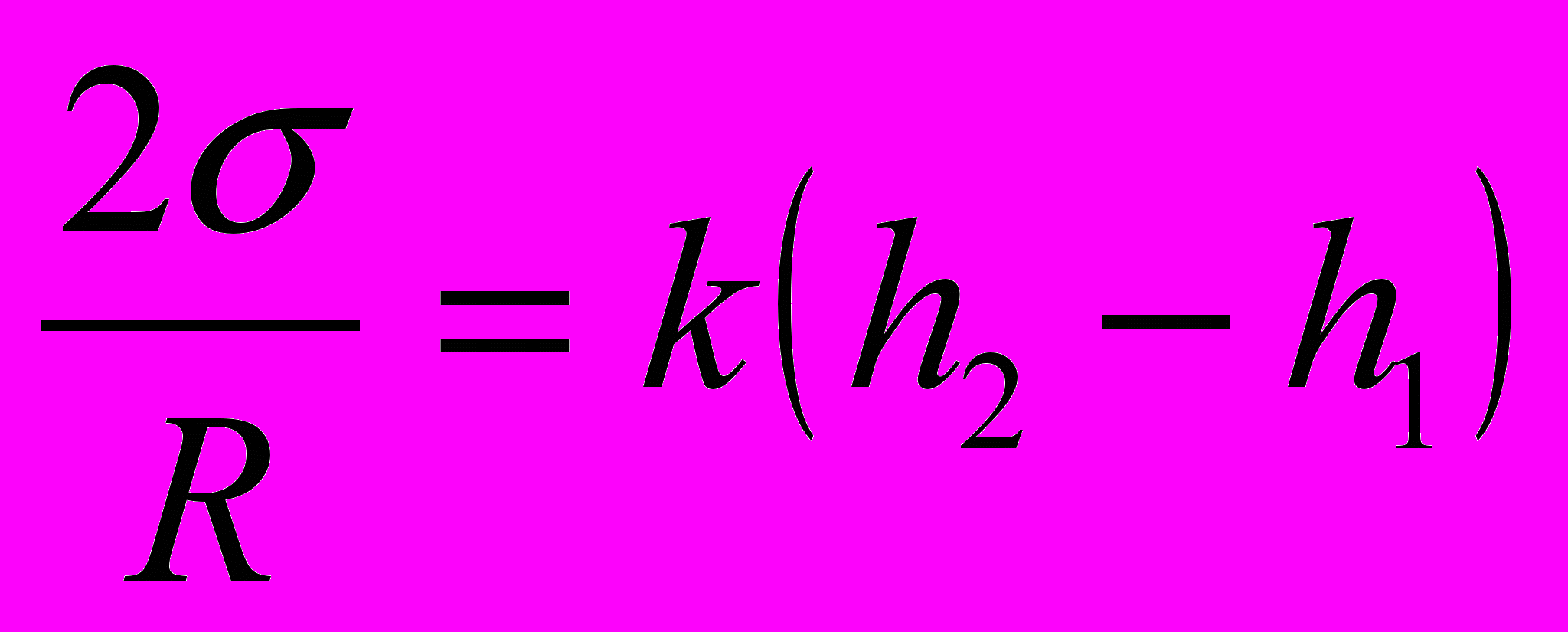(3)


Так как измерить радиус пузырька затруднительно, опыт проводят два раза: один раз с жидкостью, коэффициент поверхностного натяжения которой хорошо известен (например, с дистиллированной водой), а другой раз – с исследуемой жидкостью.

Тогда можно формулу (3) написать два раза:






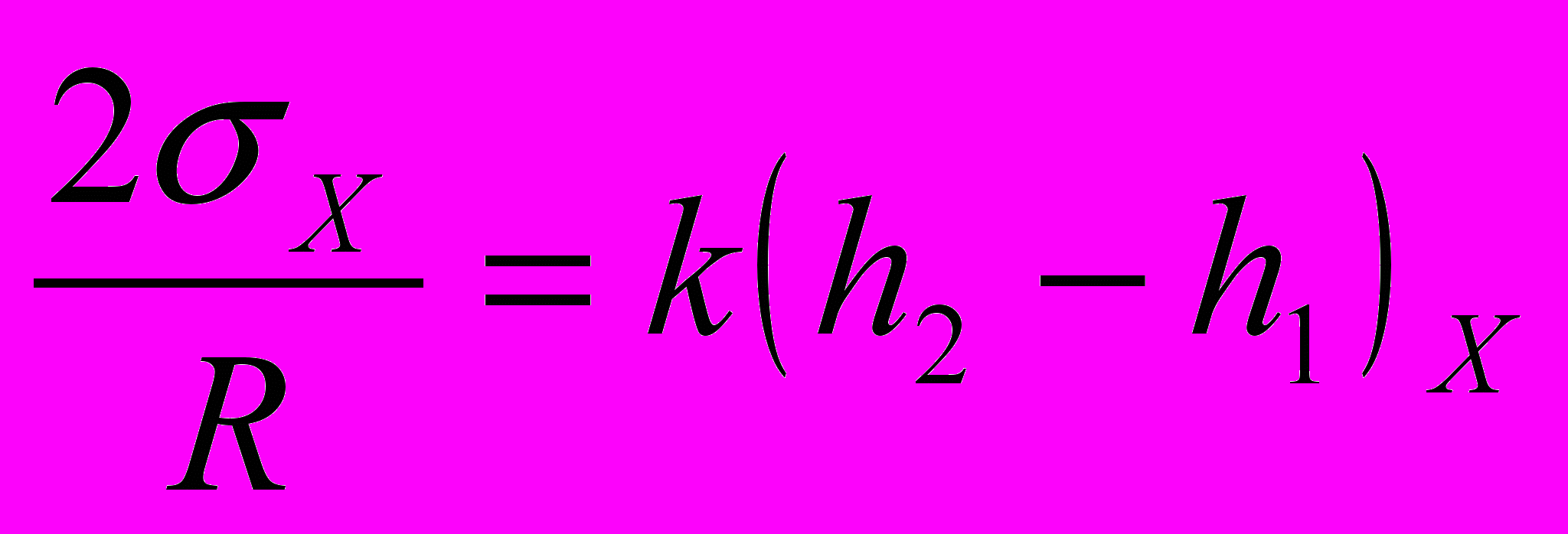
(индекс „х“ относится к исследуемой жидкости, индекс „в“ к воде).

Деля первое равенство на второе получаем формулу для нахождения коэффициента поверхностного натяжения исследуемой жидкости:

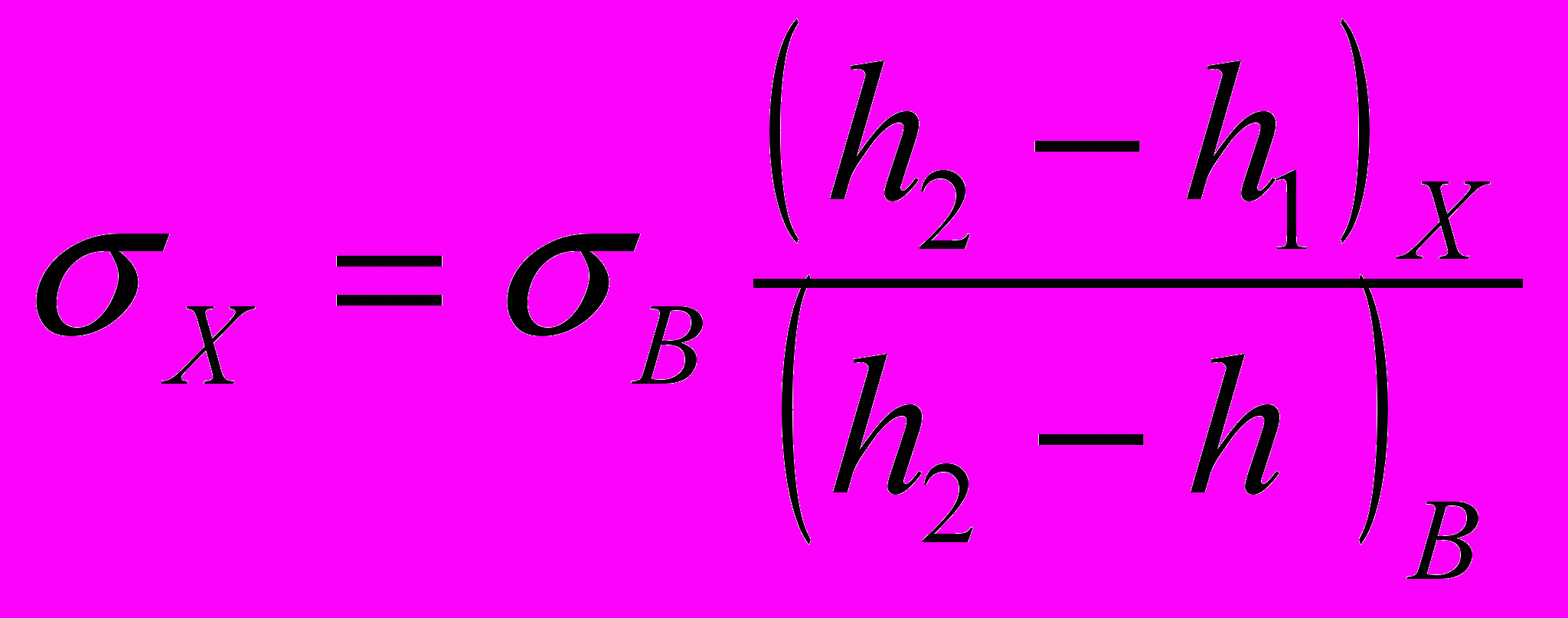(4)

Для исследования влияния ПАВ на поверхностное натяжение жидкости предлагается определить σ_х для шести растворов с разной концентрацией ПАВ.


Ход выполнения работы


1. Ознакомиться с установкой. Налить в стаканчик для воды дистиллированную воду. Перед началом измерений обязательно промыть кончик капилляра. Для этого опустить капилляр в воду и, открывая зажим 6, дать воде капать из колбы, пока из капилляра не выйдет несколько пузырьков. Не закрывая зажима, поднять капилляр с помощью рукоятки кремальеры, снова опустить его в воду и опять выпустить несколько пузырьков. После этого поднять капилляр и аккуратно опустить его так, чтобы кончик капилляра только-только касался поверхности жидкости. После этого отрегулировать зажим так, чтобы пузырьки выходили через каждые 5 – 10 секунд. Добившись этого, приступить к измерению уровней в коленах манометра в момент отрыва пузырька. По мере повышения давления в колбе уровень жидкости в одном колене манометра постепенно растёт, а в другом – понижается. В момент отрыва пузырька происходит резкий скачёк уровней жидкости. Надо заметить и записать в таблицу предельные значения уровней h₁ и h₂ , непосредственно предшествующие скачку. (Так как Вы будете делать работу вдвоём, удобно одному смотреть на левый уровень, а другому на правый и каждому записывать свои показания).

Для повышения точности надо сделать 3 – 4 измерения, а потом найти среднее значение.

2. В другой стаканчик налить раствор ПАВ с наименьшей концентрацией (величину концентрации записать в таблицу). Промыть капилляр этим раствором, как это Вы делали в первом опыте и провести измерения уровней.

3. Повторить измерения последовательно со всеми растворами. При каждой смене раствора не забывайте промывать кончик капилляра. Нарушение этого правила – основной источник ошибок в данной работе. После окончания измерений погрузите капилляр в воду.

4. По записанным в таблице результатам вычислите значения коэффициента поверхностного натяжения σ для всех растворов.

По этим данным постройте график зависимости σ от концентрации раствора, включив и результат для воды. Подумайте, почему при малых концентрациях коэффициент поверхностного натяжения быстро падает, а при больших – становится почти постоянным. Ваше мнение по этому поводу отразите в отчёте (учтите при этом, что ПАВ оказывают воздействие на силы межмолекулярного взаимодействия только в тонком поверхностном слое; молекулы ПАВ, ушедшие вглубь жидкости на силы между молекулами жидкости не влияют).


Вопросы к занятию по теме:

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ


1. Энтропия. Вычисление изменений энтропии. Гл. 2, § 1 (стр.32-34)

2. Вероятностный смысл энтропии. Формула Больцмана. Гл. 2, § 2 (стр. 35-36).

3. Второе начало термодинамики для изолированных систем Гл. 2, § 3 (стр. 37-38).

4. Упорядоченность структуры и энтропия. Гл. 2, §6 (стр. 43-46)

5. 2 начало термодинамики для открытых систем. Продукция энтропии, поток энтропии. Гл. 2, , § 9 (стр. 50-53).

6. 6. Стационарные состояния. ГЛ. 2, § 10 (до мелкого шрифта). Теорема Пригожина § 11 (до мелкого шрифта (стр.56)

7. Процессы с преодолением потенциального барьера. Расчёт числа активных частиц; связь этого числа со скоростью процесса, Формулы Больцмана и Аррениуса. Коэффициент Вант-Гоффа Q₁₀. Гл.3, § 4 (стр. 65-67 до мелкого шрифта и 68).

8. Лабораторная работа „Исследование влияния поверхностно активных веществ на поверхностное натяжение жидкости“

По этому вопросу надо прочитать Приложение к лекции (описание лабораторной работы) До начала занятий в тетрадях для лабораторных работ необходимо написать название и цель работы и подготовить таблицу для записи результатов (в конце описания).


ЛИТЕРАТУРА


«Медицинская биофизика» под ред. проф. Самойлова, изд. ВМА


Основы термодинамики(2), лекция. Издание кафедры. Это пособие надо получить на кафедре накануне дня практического занятия с 15 до 17 часов