Свойства бесконечно больших последовательностей

Вид материала

Документы

Подобный материал:

• График занятий по курсу «высшая математика часть, 136.64kb.
• Вопрос №1. "Понятие системы. Примеры системы. Свойства сложных систем", 1038.39kb.
• Лекция Бесконечно малые функции, 80.71kb.
• Аннотации базовой части дисциплин циклов фгос, 550.23kb.
• Стремлением к саморазвитию, повышению своей квалификации и мастерства (ок-9), 360.86kb.
• Закон больших чисел и центральная предельная теорема и их роль в природе, технике, 35.67kb.
• Тонкие миры Альберта-Виктора Вейника, 682.64kb.
• Попытка создать единую научную религию, очевидно берёт начало с философии розенкрейцеров, 2238.8kb.
• Николаева Мария Андреевна, доктор технических наук, профессор, заведующий кафедрой, 367.89kb.
• Урок химии в 9 классе. Тема: «Оксиды азота», 68.76kb.

Свойства бесконечно больших последовательностей

1) Если 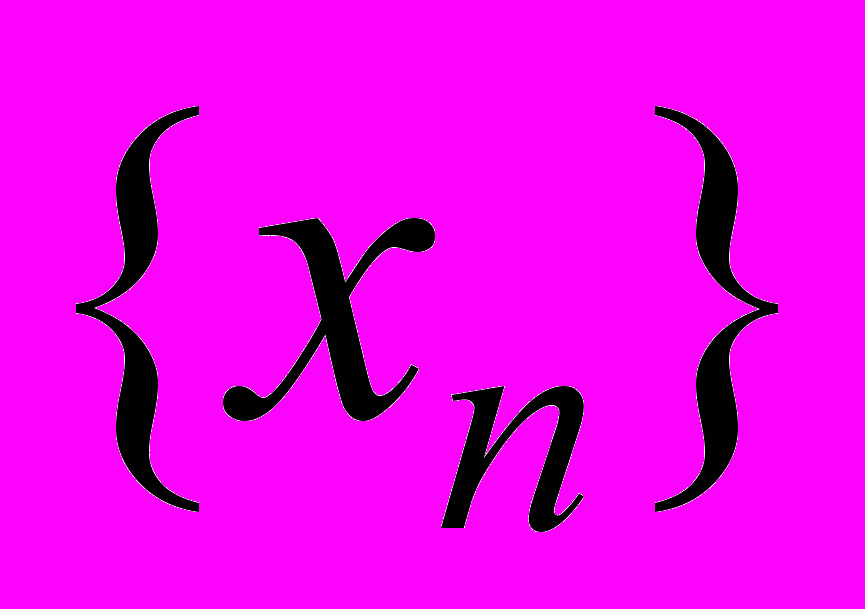– бесконечно большая, то последовательность 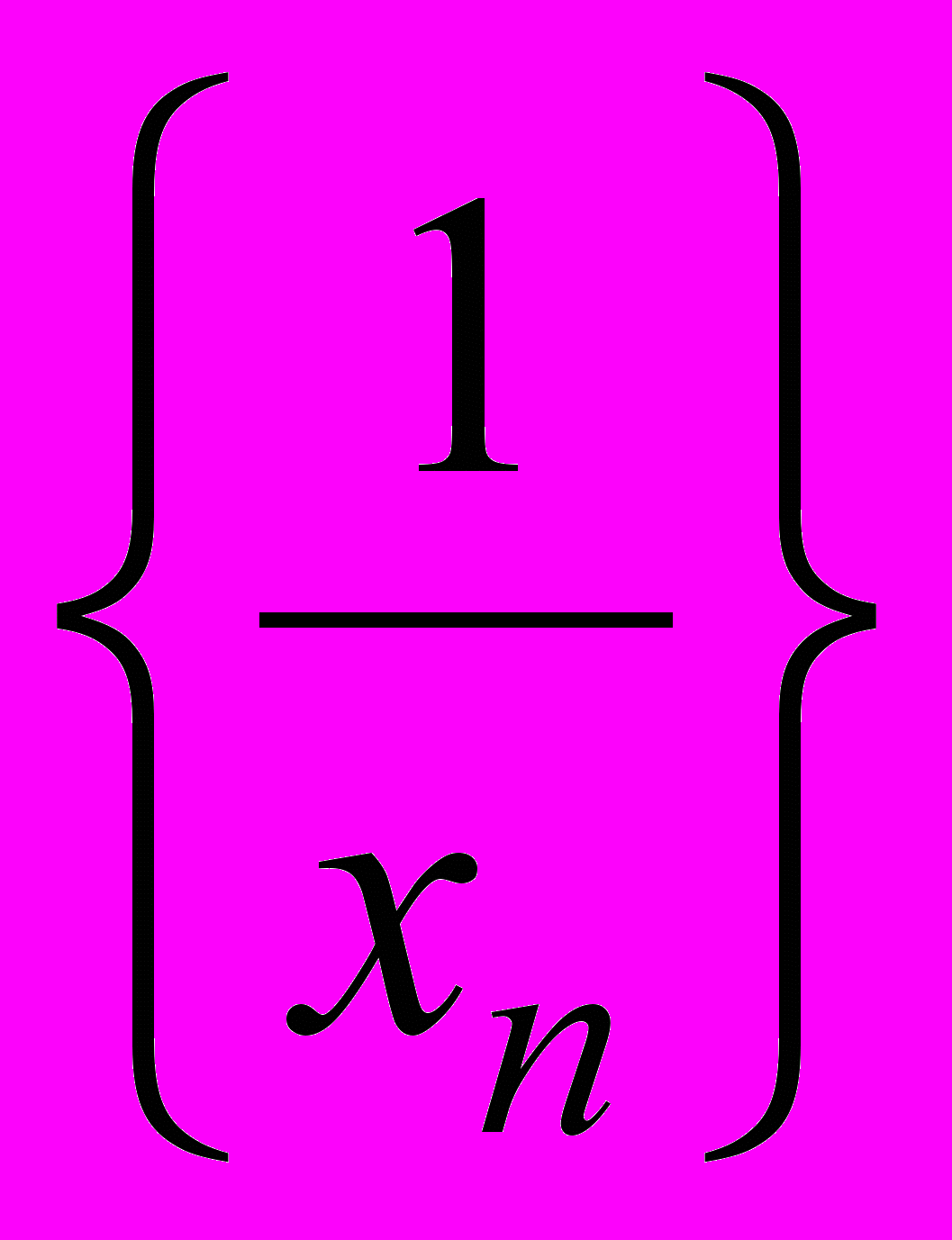– бесконечно малая. Если последовательность – бесконечно малая, то последовательность 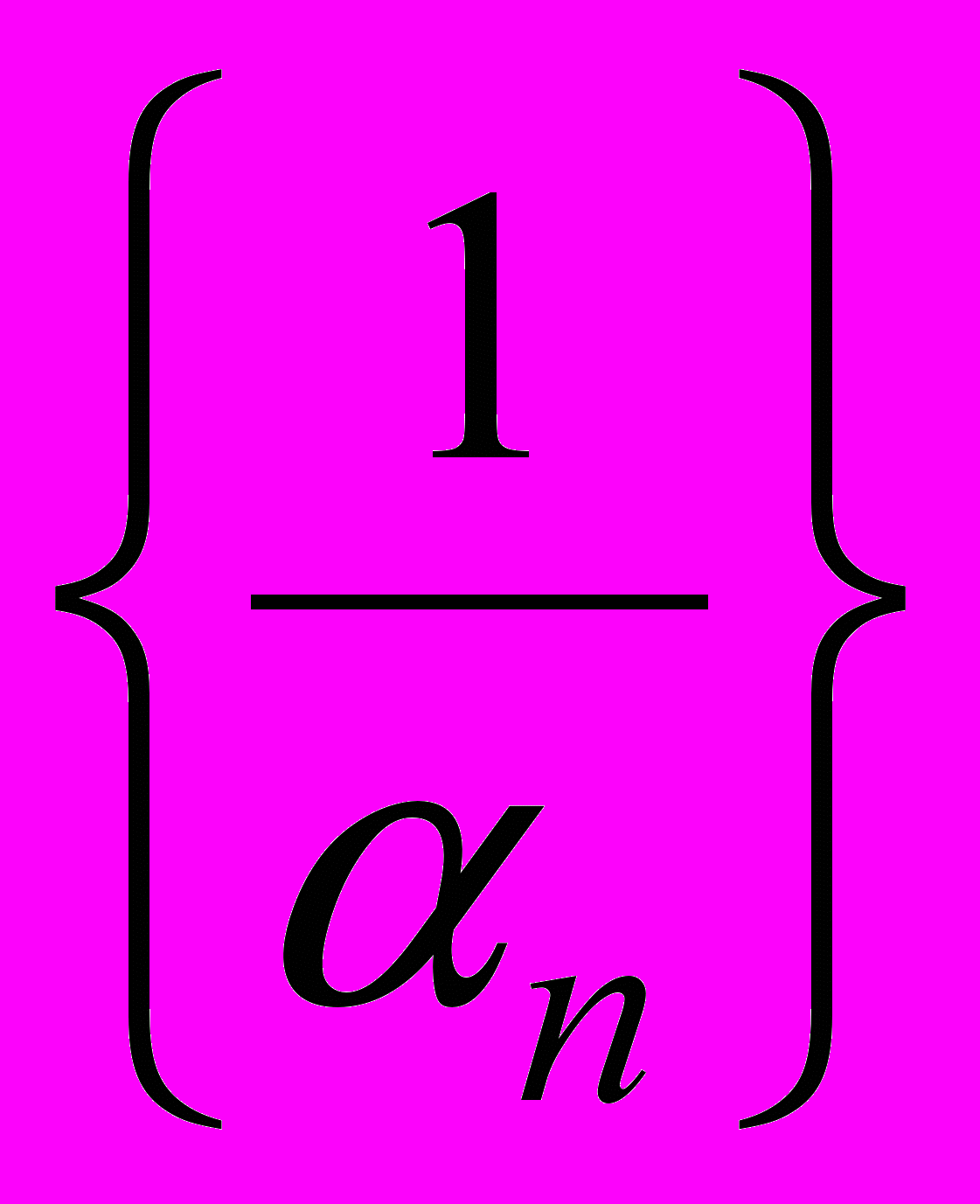– бесконечно большая.

ДОКАЗАТЕЛЬСТВО (дано на лекции)


2) Если последовательности 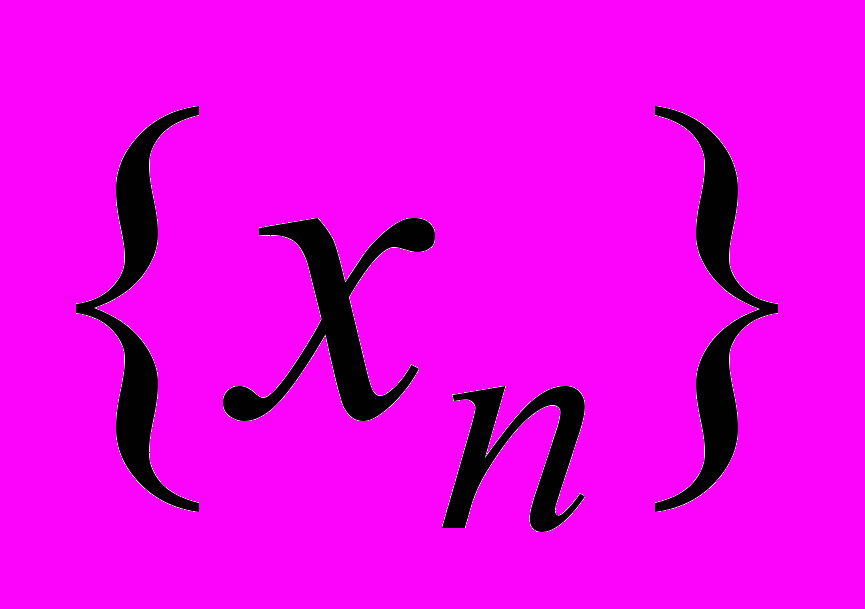и – бесконечно большие одного знака, то их сумма 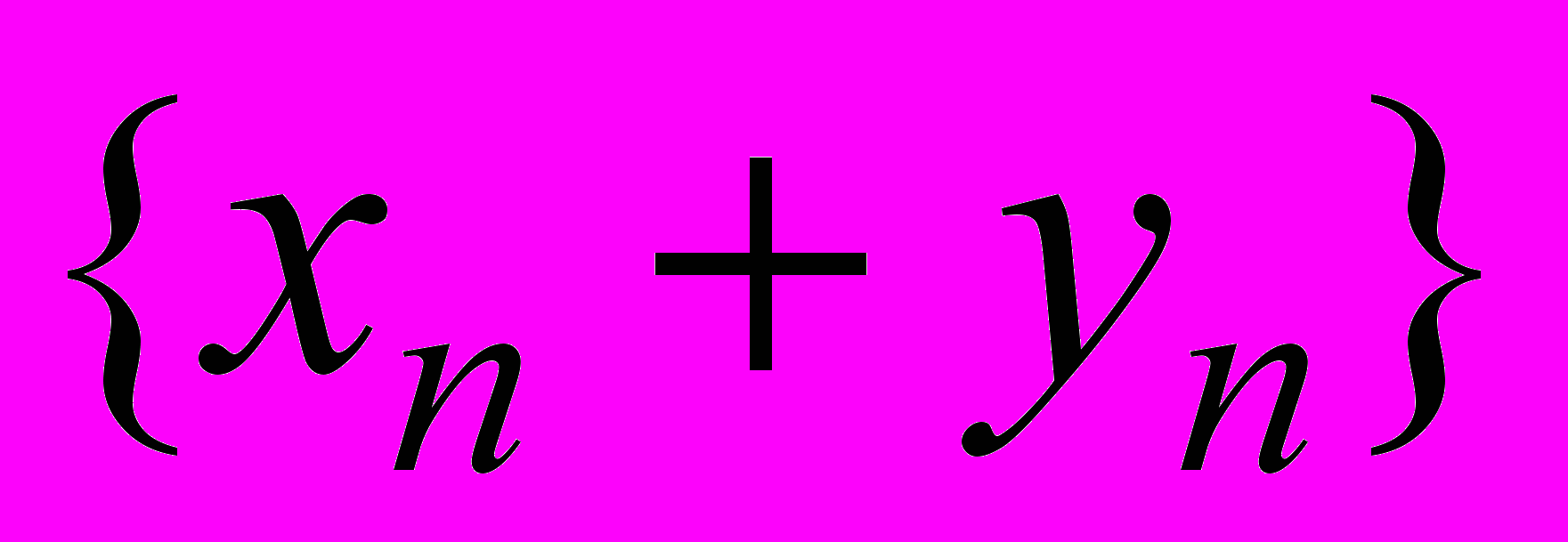– бесконечно большая того же знака.

ДОКАЗАТЕЛЬСТВО самостоятельно


3) Если последовательности 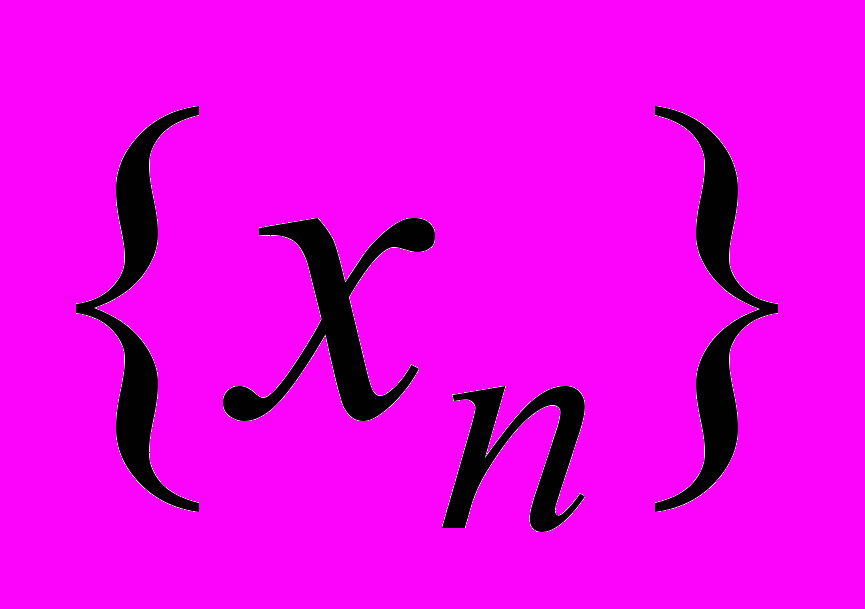– бесконечно большая, а последовательность – ограниченна, то их сумма 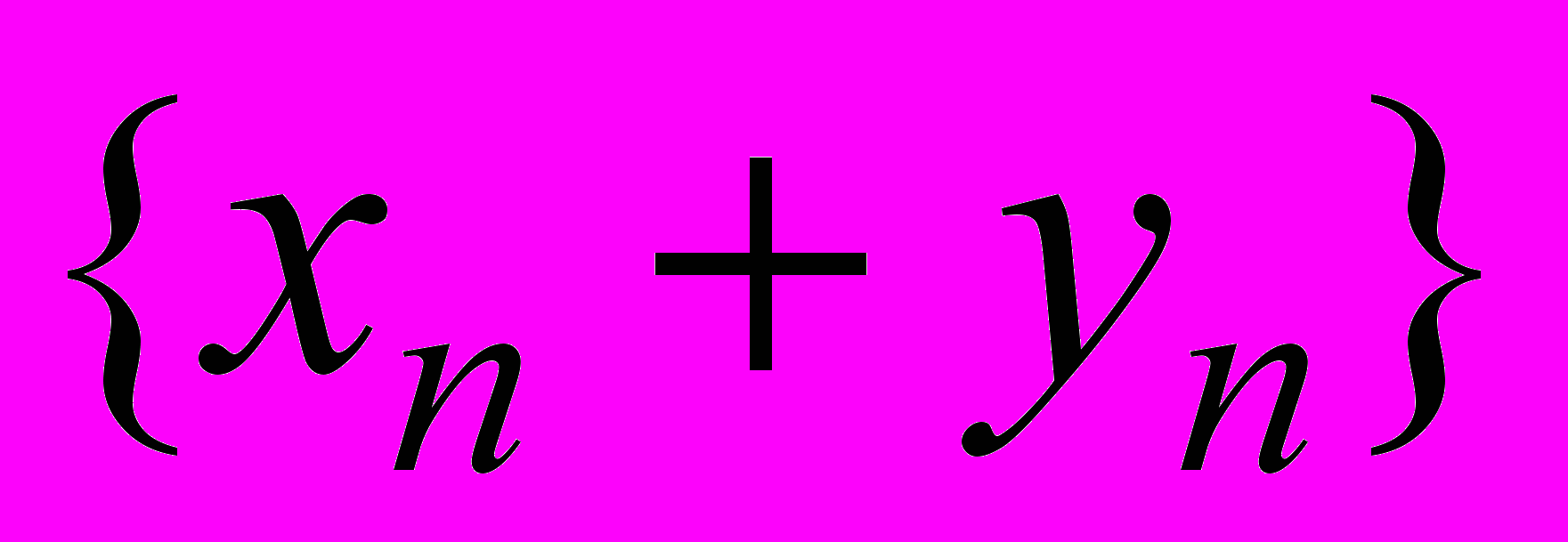– бесконечно большая последовательность.

ДОКАЗАТЕЛЬСТВО самостоятельно


4) Если последовательности 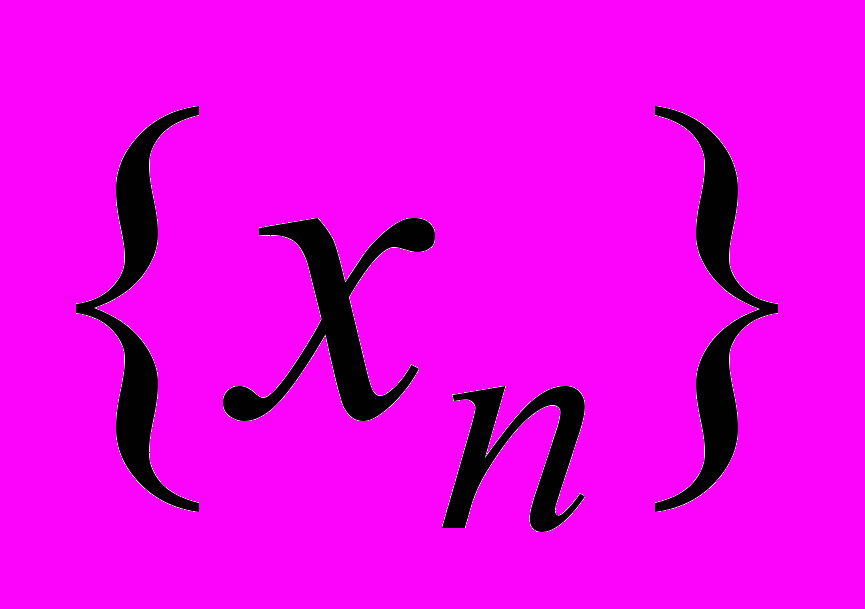и – бесконечно большие, то их произведение – бесконечно большая последовательность.

ДОКАЗАТЕЛЬСТВО самостоятельно


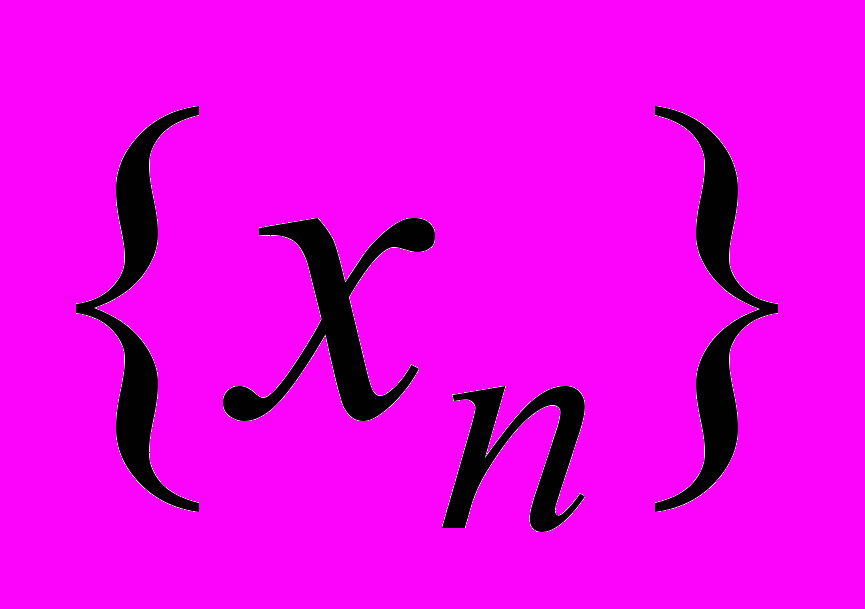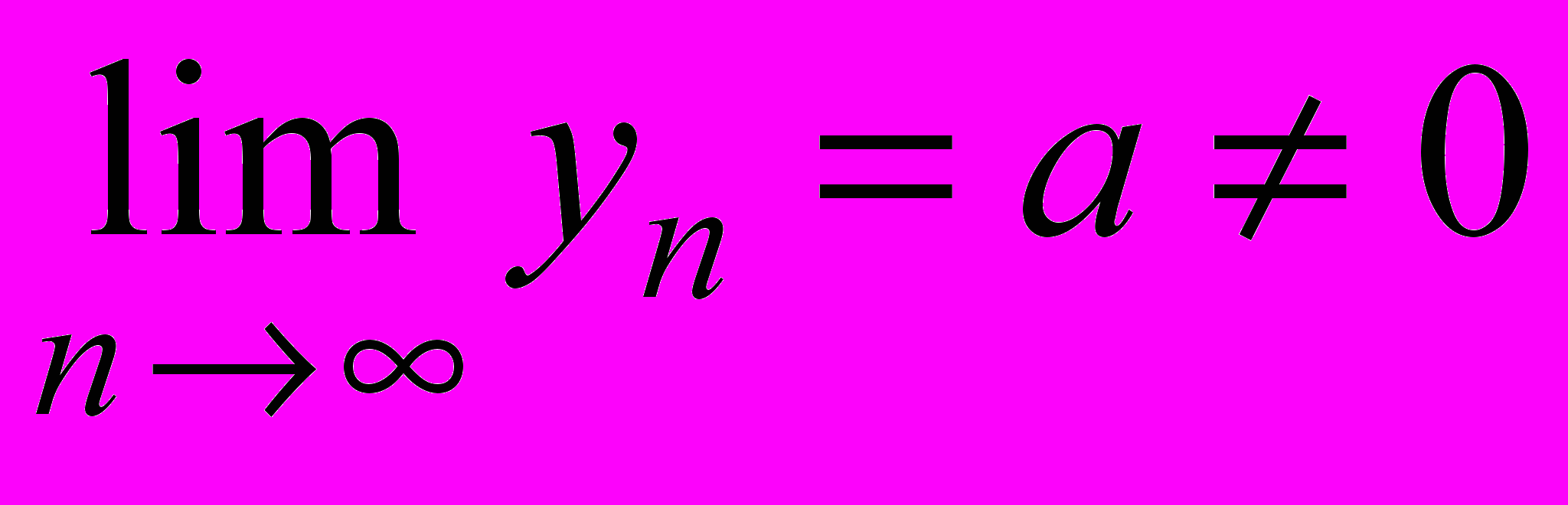5) Если последовательность – бесконечно большая, а последовательность – сходящаяся, причем , то их произведение – бесконечно большая последовательность.


ОПРЕДЕЛЕНИЕ. Последовательность 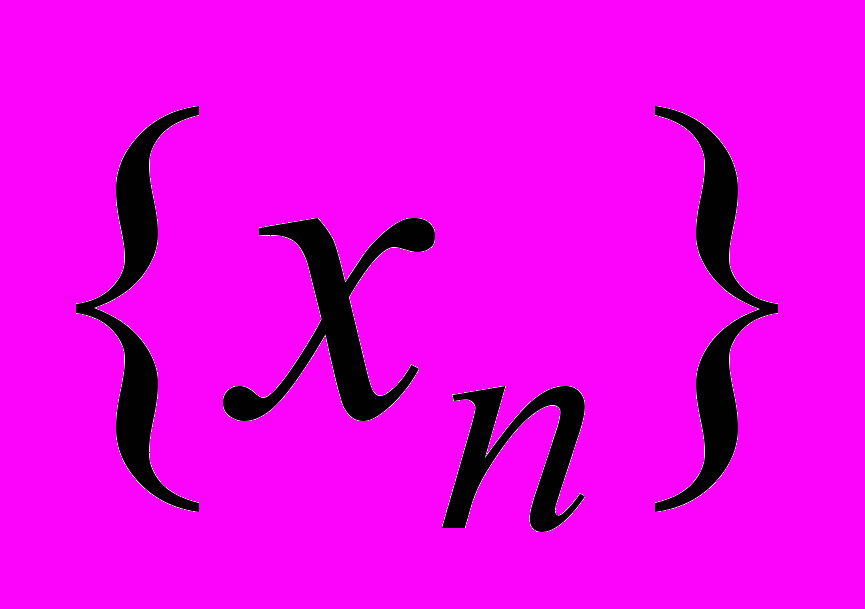называют отделимой от нуля, если существуют число 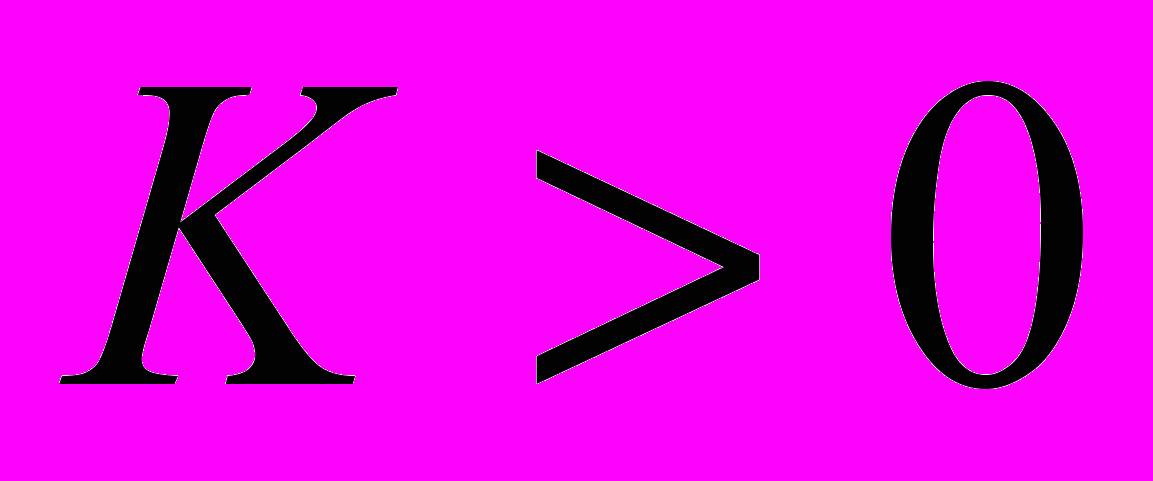и номер 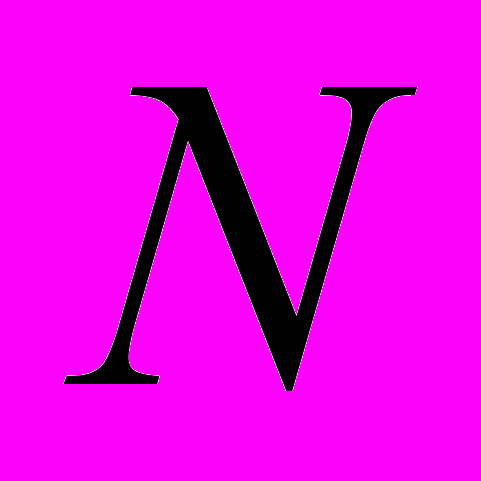такие, что , .


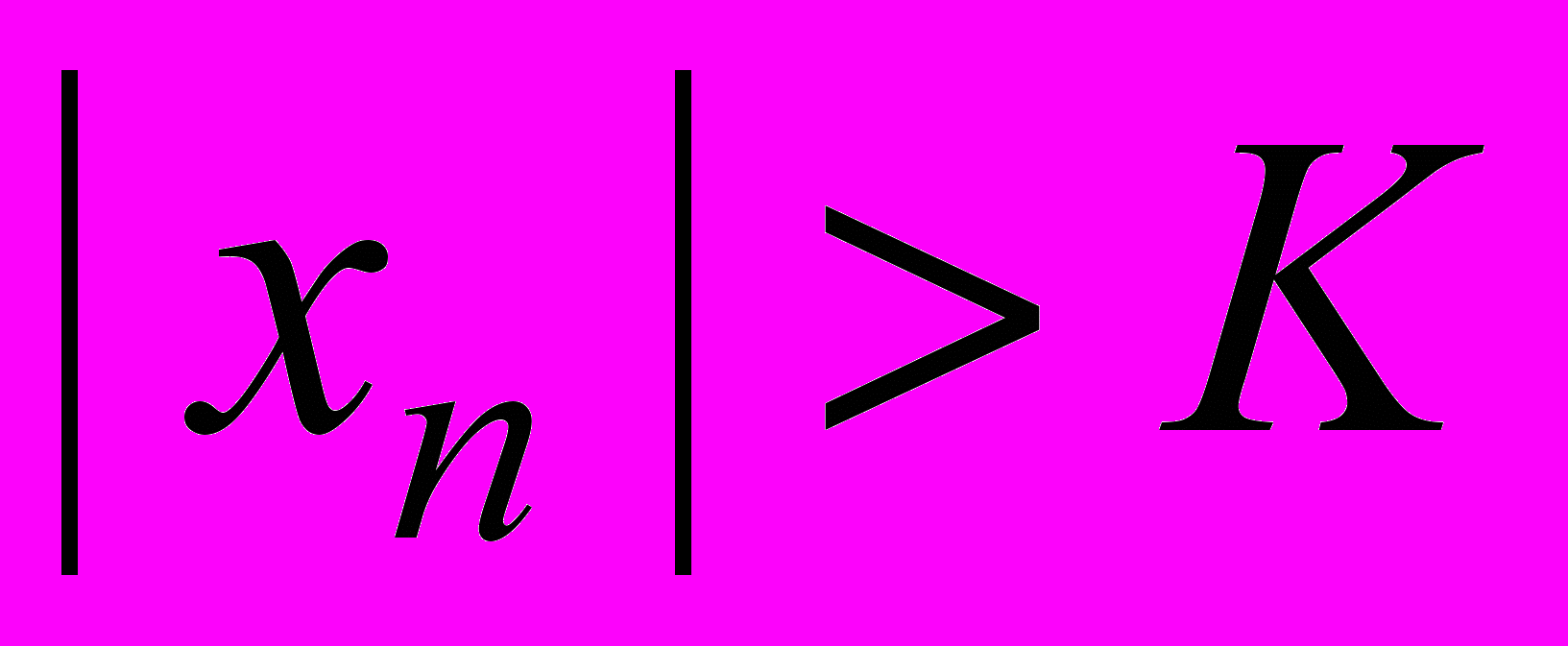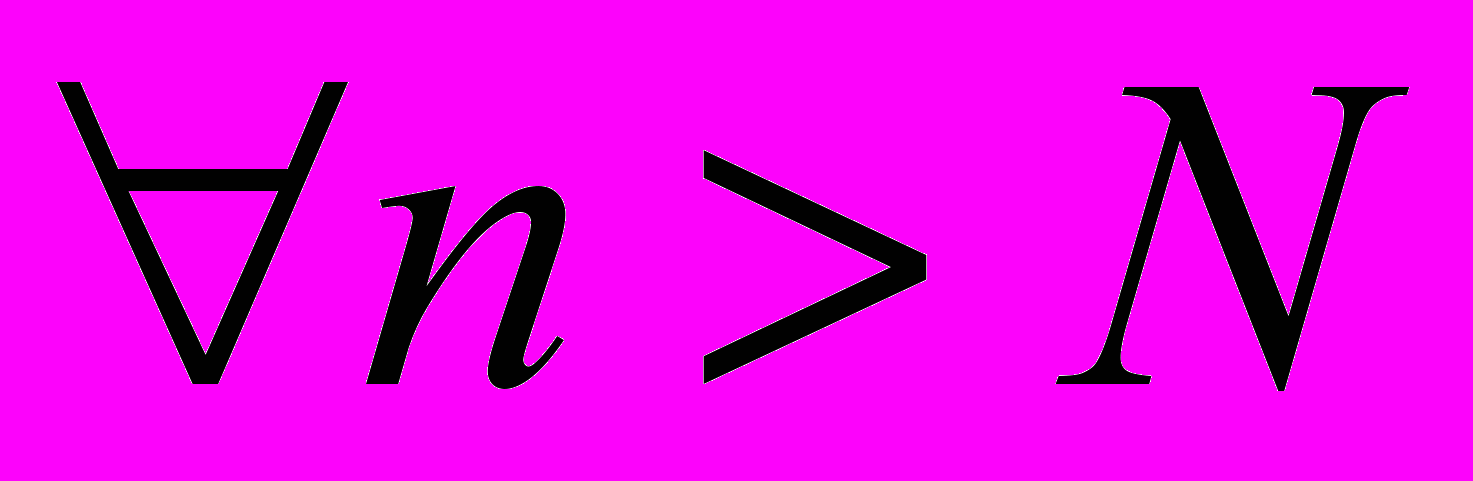6) Если последовательность 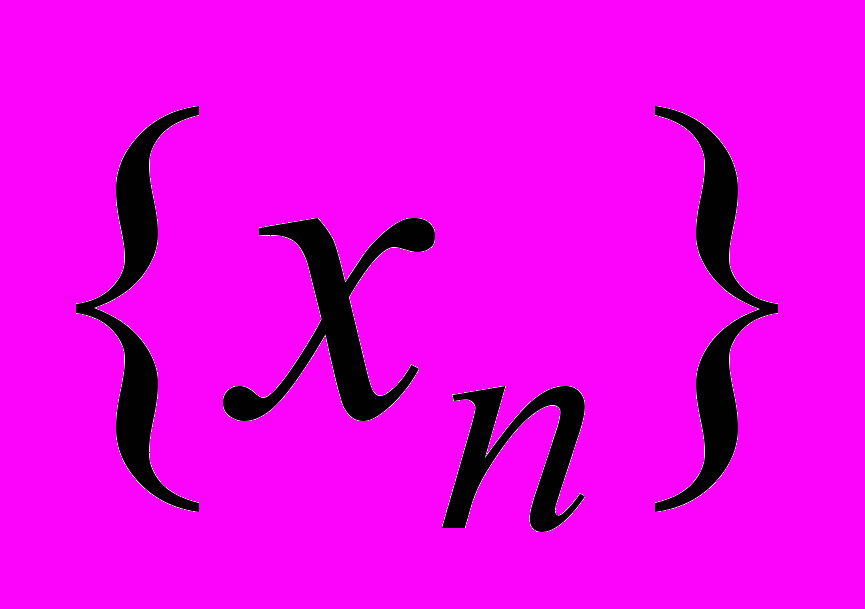– ограниченная и отделимая от нуля, а – бесконечно большая, то их произведение – бесконечно большая последовательность.

ДОКАЗАТЕЛЬСТВО самостоятельно


7) Если последовательность 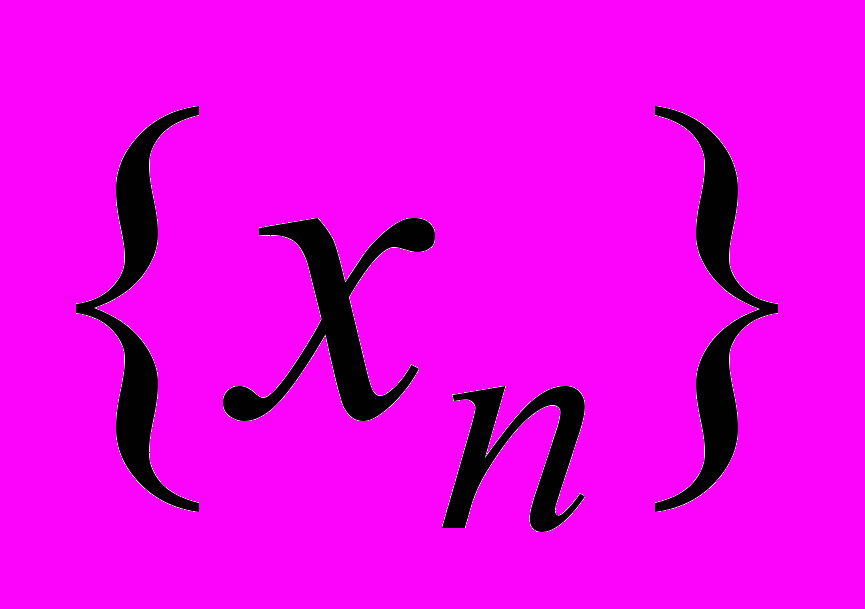– бесконечно большая и для любого ℕ имеет место неравенство (), то последовательность тоже является бесконечно большой.

ДОКАЗАТЕЛЬСТВО самостоятельно