Материалы микроэлектроники

Вид материала

Документы

Содержание Модификация многокомпонентных материалов при ионной бомбардировке Рентгенодифракционные методы исследования атомной структуры вещества X равна отношению амплитуд дифрагированной и проходящей рентгеновских волн,  – длина волны, F K от температуры нагрева DT Cвойства ионно-синтезированных аморфно-кристаллических слоев кремния Ю.А. Менделева, Д.И. Тетельбаум ННГУ им. Н.И. Лобачевского, Н. Новгород ЭЛЕКТРОФИЗИЧЕСКИЕ СВОЙСТВА ПЛЕНОК Ni Моделирование динамической дифракции Ферритов-гранатов с точкой компенсации магнитного момента Зарождение кристаллической фазы в амс. Упаковоки икосаэдров и пентагондодекаэдров и их применение для описания кристаллических структур Методика расчета огранки кристалла по его атомной структуре Полупроводниковые преобразователи больших уровней свч - мощности Угловые зависимости ширины линии мод Рентгенографические исследования эволюции структуры микрокристаллических сплавов Расчет зависимости ширины линий мод Групп симметрии кристаллов Влияние пластической деформации на магнитные свойства парамагнитных сплавов Исследование распада пересыщенного твердого раствора в хромовой бронзе ... Полное содержание

Подобный материал:

• Семинар \"Новые магнитные материалы микроэлектроники\" (нммм 19). 28 июня 2 июля 2004,, 23.32kb.
• «Материалы и компоненты микроэлектроники», 359kb.
• Xxi международная конференция, 74.63kb.
• Республики Беларусь «24», 3587.94kb.
• Программа спецкурса " Электронно-зондовая диагностика материалов и приборов микроэлектроники", 13.07kb.
• Введение в специальность, 2241.27kb.
• Физика полупроводниковых приборов, 1091.64kb.
• Твердые растворы на основе карбида кремния: технология и свойства, 66.85kb.
• Физика полупроводников и твердотельная электроника введение, 56.3kb.
• Физика твердого тела и твердотельная электроника введение, 40.45kb.

Материалы

микроэлектроники

ПЕРСПЕКТИВЫ ИСПОЛЬЗОВАНИЯ ШИРОКОЗОННЫХ

ПОЛУПРОВОДНИКОВЫХ МАТЕРИАЛОВ

В СОВРЕМЕННОЙ ЭЛЕКТРОНИКЕ


Чибиркин В.В., Гейфман Е.М., Арискин Н.А., Гарцев Н.А.

ОАО "Электровыпрямитель", г. Саранск


Современная полупроводниковая электроника базируется пока на кремнии (Si) и арсениде галлия (GaAs). В то же время параметры кремниевых и арсенидгаллиевых приборов уже подошли к своему физическому пределу, устанавливаемому фундаментальными характеристиками этих материалов. Поэтому в настоящее время для создания приборов электроники нового поколения все более актуальным становится освоение новых полупроводниковых материалов с большей шириной запрещенной зоны, которые способны дать новый импульс научно-техническому прогрессу.

К наиболее перспективным широкозонным полупроводниковым материалам следующего поколения относится карбид кремния (SiC) и нитрид галлия (GaN), обладающие уникальными физическими и электронными свойствами. К этим свойствам относятся: широкая запрещенная зона (в три раза больше, чем у кремния), высокое критическое поле лавинного пробоя (приблизительно в 10 раз больше, чем у кремния), высокая насыщенная скорость дрейфа электронов (в 2,5 раза больше, чем в кремнии и арсениде галлия) и др..

Карбид кремния существует в различных кристаллических модификациях (например, кубической, гексагональной, ромбоэдрической). Из всех существующих модификаций для изготовления полупроводниковых приборов лучшим является только гексагональный политип 4H SiC, так как он имеет самую высокую подвижность электронов, а его получение настолько успешно, что в настоящее время на его основе начался процесс серийного производства полупроводниковых приборов.

4H SiC – это полупроводниковый материал с широкой запрещенной зоной, которой при высоких температурах не плавится, а сублимирует и является очень твердым. В таблице 1 приведены наиболее важные для электроники его физические параметры при температуре 300 K.

Большой интерес для конструирования полупроводниковых приборов представляет максимально допустимая концентрация легирующей примеси, необходимая для обеспечения заданного значения блокируемого напряжения (U_BR). Если допустить, что полупроводниковый материал однородно легирован и прибор сконструирован без смыкания базы, то получается, что для того чтобы достичь заданное значение U_BR, SiC по сравнению с кремнием может быть легирован значительно сильнее (см.
таблицу 1). Таким образом, при блокировании заданного напряжения в SiC область пространстве нного заряда может быть приблизительно в 10 раз меньше, чем в Si, а легирование SiC может быть приблизительно в 100 раз выше. Учитывая более низкую подвижность электронов в SiC, получается, что дрейфовое сопротивление в SiC силовых приборах может быть в 700 раз меньше, чем в кремниевых силовых приборах, при их равной площади.


Таблица 1

Физические параметры кремния и SiC.

(V_B – блокирующее напряжение)

Параметр		SiC	4H SiC
Ширина запрещенной зоны, Eg	эВ	1,12	3,26
Собственная концентрация носителей заряда, ni	см-3	1,4·1010	5·10-9
Подвижность электронов, μn	см2/В·с	1400	1000
Критическое электрическое поле Ec (VB=1200 В)	МВ/см	0,24	2,64
Концентрация легирующей примеси (VB=1200 В)	см-3	1,57·1014	1,56·1016
Относительная диэлектрическая проницаемость, εr		11,8	9,7
Теплопроводность, λ	Вт/см·К	1,5	3,5

Эти свойства SiC делают его очень привлекательным материалом для большинства монополярных приборов, таких как диоды Шоттки, полевые транзисторы с управляющим p-n-переходом (JFET), MESFET и др.

С другой стороны p-n-переход SiC, легированный до 10¹⁴ см^-3, может блокировать напряжение до 50 кВ при ширине области пространственного заряда 730 мкм, в то время как p-n-переход, созданный в также легированном кремнии можно блокировать напряжение 1,7 кВ. Таким образом биполярные полупроводниковые приборы на SiC значительно могут превосходить биполярные полупроводниковые приборы на Si по величине блокируемого напряжения и быстродействию.

Кроме того способность SiC приборов работать при экстремально высоких температурах до 600 - 700°С (для сравнения: кремниевые приборы работоспособны только до 150-200°С) позволяет резко увеличить удельную мощность, коммутируемую этими приборами.

На рис. 1 приведена структура SiC диода Шоттки SDTO4S60 фирмы Infineon Technoloqies. Эти диоды в основном предназначаются для работы в качестве бустерных диодов в импульсных источниках вторичного электропитания (параметры бустерных диодов влияют на коммутационные потери в таких источниках). В SiC диодах обратный ток переключения очень мал; нет влияния температуры на динамические характеристики переключения; практически отсутствуют токи утечки (см. рис. 2).




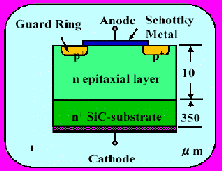
а) б)

Рис. 1. Cтруктура SiC диода Шоттки SDTO4S60 фирмы Infineon Technoloqies (a – вертикальное сечение SiC диода Шоттки; б – кристалл SiC диода Шоттки).




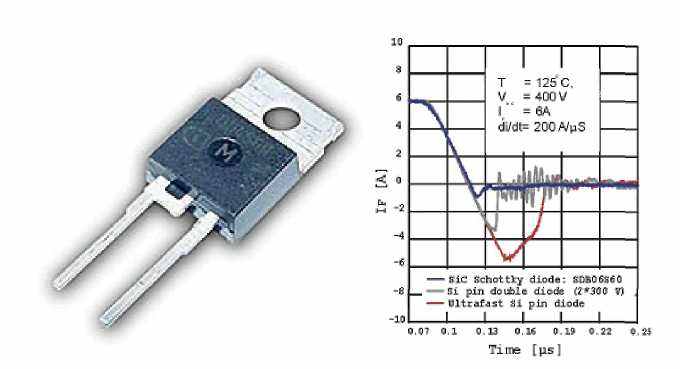
Рис. 2. SiC диоды Шоттки SDB06S60 фирмы Infineon Technoloqies и их характеристики выключения по сравнению с аналогичными характеристиками кремниевых pin-диодов.


На рис. 3 представлена структура прибора JFET, который разработан рядом фирм и в ближайшее время может быть запущен в производство. В нем в открытом состоянии поток электронов течет от источника тока через боковой канал, ширина которого определяется двумя p-n-переходами и через щель между двумя скрытыми затворами вертикально к стоку.



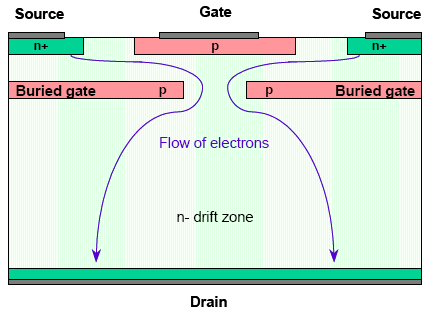
Рис. 3. Схематическое изображение поперечного сечения JFET


В настоящее время JFET с размером чипа 2,7 мм × 2,3 мм (с площадью активной области 4,1 мм²) имеет сопротивление в отрытом состоянии 0,24 Ом при комнатной температуре и могут блокировать напряжения
1200 В.

Его недостатком является то, что он является «нормально открытым» прибором. Для устранения этого недостатка JFET соединяется в SiC\Si каскодную схему с MOSFET, как показано на рис. 4.



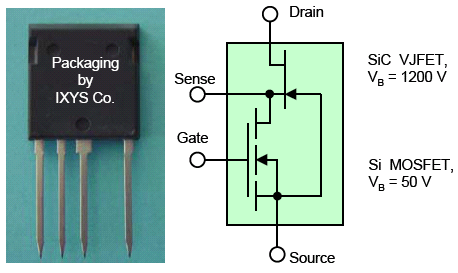
Рис. 4. SiC\Si гибридная каскодная схема.


Производство биполярных приборов в ближайшие несколько лет вряд ли начнется. Это в основном определяется недостаточно высоким качеством и высокой ценой коммерчески доступного SiC. Тем не менее имеются сообщения о создании силовых тиристоров на блокируемое напряжение
10 кВ и ток 100 А на кристалле площадью 1 см². На Si тиристор аналогичной площади имеет блокирующее напряжение 1500 В и ток 10 А.

В настоящее время наибольшая часть производимого в мире монокристаллического SiC (70 - 80%) используется в качестве подложечного материала для производства светодиодов видимого диапазона на основе нитридов галлия, индия и алюминия (InGaN, AlGaN/GaN) (это производство в последние годы развивается очень быстрыми темпами, см. рис. 5).

По сравнению с традиционными подложками из лейкосапфира (Al₂O₃), SiC обладает рядом преимуществ для создания приборов на основе нитридов галлия - меньшим рассогласованием параметров кристаллической решетки (3,5% против 16%), большей теплопроводностью, высокой электропроводностью (это позволяет использовать вертикальную топологию приборов и увеличить степень их интеграции на пластине).

Другим перспективным полупроводниковым материалом является нитрид галлия. На его основе уже разработан ряд приборов: яркие светодиоды, излучающие в зелено-голубой и ультрафиолетовой частях спектра (в настоящее время в мире осуществляется их массовое производство), лазерные диоды, СВЧ транзисторы с высокой подвижностью электронов (HEMT) и др.





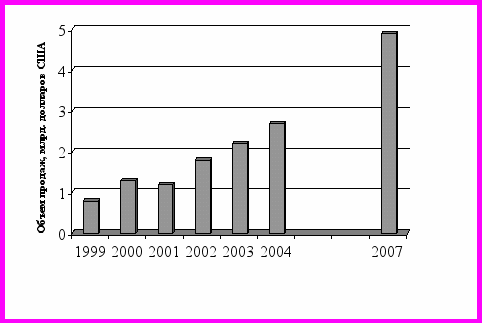
Промышленное применение широкозонных полупроводников (SiC) сейчас только начинается. Тем не менее в 2004 году объем продаж изделий из монокристаллического SiC составил  400 млн. долларов США и за последние годы растет на 35% ежегодно.

Объем продаж полупроводниковых приборов на основе GaN (в основном яркие светодиоды) составил в 2004 году 2,5 млр. долларов США. Можно ожидать, что к 2007-2008 годам он достигнет 5 млрд. долларов США.

Вместе с тем вполне вероятным представляется, что к 2010 - 2015 гг. большая часть военной электроники США и стран НАТО будет изготавливаться на основе карбида кремния и нитридных соединений. Поэтому, если не принять экстренные меры по разработке аналогичной отечественной электроники, это сделает Российские военные системы управления неконкурентоспособными и малоэффективными.

В течение последних 10 - 12 лет из-за прекращения государственного финансирования исследований и отсутствия внутреннего платежеспособного рынка высоких технологий произошло существенное отставание исследований и разработок в области SiC и GaN в России от мирового уровня. Несмотря на то, что до этого времени она занимала лидирующие позиции в мире. В то же время в России имеется большой научно-технический задел по этим работам. Поэтому при выделении необходимого финансирования и объедини потенциалов соответствующих научных школ и изготовителей возможно создании в России новой ультрасовременной отрасли полупроводниковой промышленности. Это позволит снять зависимость потенциальных российских потребителей SiC и GaN приборов от импортных поставок, а с другой стороны принести ощутимую коммерческую выгоду.


[1] Dietrich S. Prospects of SiC Power Devices From the State of the Art to Future Trends // PSIM 2002: Power Electronics Conference. May 14 - 16, 2002, Nürnberg, Germany.


Модификация многокомпонентных материалов при ионной бомбардировке


Л.Б.Беграмбеков

МИФИ, г. Москва


Аннотация

Ионное и плазменное облучение может привести к изменению рельефа, а также структуры и состава поверхностных слоёв твёрдых тел. Характер таких изменений зависит от природы и структуры облучаемых материалов, параметров облучающих потоков (тип облучающих частиц, энергия и плотность потока, угол облучения и т.п.), условий облучения (температура поверхности, состав окружающего газа).

В лекции демонстрируются и анализируются результаты корпускулярного воздействия на металлы, сплавы, графиты, карбиды, окислы, гидриды, нитриды. На основании приведённых примеров выявляются и анализируются характерные типы изменений, происходящих в поверхностных слоях твёрдых тел при ионном и плазменном облучении, обсуждаются механизмы таких изменений, суммируются общие закономерности и специфические особенности модификации твёрдых тел различных типов под действием ионного и плазменного воздействия. Обсуждаются условия облучения, стимулирующие развитие определённых типов поверхностных модификаций


РЕНТГЕНОДИФРАКЦИОННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ АТОМНОЙ СТРУКТУРЫ ВЕЩЕСТВА


Чупрунов Е.В.

Нижегородский государственный университет им. Н.И.Лобачевского


Стремительное движение современной физики к исследованию и использованию нанообъектов выводит на новый уровень актуальности вопросы исследования атомной структуры вещества. Как известно, одним из самых мощных методов определения атомной структуры и исследования электронной плотности в твердых телах является рентгеноструктурный анализ.

Рентгеноструктурный анализ представляет собой совокупность дифракционных методов исследования с использованием рентгеновского излучения с длиной волны порядка ангстрема. Начало рентгеноструктурно анализа связано с открытием 8 ноября 1895 г В.К.Рентгеном лучей, которые носят его имя, и М.Лауэ совместно с ассистентом Зоммерфельда Вальтером Фридрихом аспирантом Паулем Книппингом дифракции этих лучей на кристаллических решетках.

Дифракция рентгеновского излучения дает важную информацию о твердых телах – их атомной структуре, а также о жидкостях, аморфных телах и больших молекулах. Дифракционный метод применяется также для точного (с погрешностью менее 10^–5) определения межатомных расстояний, выявления напряжений и дефектов и для определения ориентации монокристаллов. По дифракционной картине можно идентифицировать неизвестные материалы, а также обнаружить присутствие в образце примесей и определить качественный и количественный состав.

Дифракция рентгеновских лучей на кристаллической решетке представляет собой фраунгоферову дифракцию. При этом геометрия дифракционной картины и интенсивность дифракционных максимумов определяется атомным строением дифрагирующего образца, степенью его совершенства, наличием примесей и т.д.

Дифракция рентгеновских лучей происходит благодаря взаимодействию падающего рентгеновского излучения с электронами в кристалле. Вследствие того, что длина волны рентгеновского излучения того же порядка, что и размеры атома, длина волны рассеянного рентгеновского излучения та же, что и падающего. Этот процесс является результатом вынужденных колебаний электронов под действием падающего рентгеновского излучения. Электроны во всех направлениях одновременно рассеивают падающее и испускают собственное рентгеновское излучение той же длины волны, хотя и разной интенсивности. Интенсивность рассеянного излучения связана с атомным номером элемента, т.к. атомный номер равен числу электронов, которые участвуют в рассеянии.

Расшифровка атомной структуры кристалла включает: установление размеров и формы его элементарной ячейки; определение принадлежности кристалла к одной из 230 федоровских групп симметрии; построение распределения функции электронной плотности и получение координат базисных атомов структуры. Кроме того, с помощью РСА определяются характер и величина тепловых колебаний атомов, коэффициенты заполнения атомами (в частности примесью) различных позиций в кристаллическом пространстве и многое другое.

Первую и частично вторую задачи можно решить методами Лауэ и качания или вращения кристалла, т.е. анализируя лишь геометрические особенности рентгеновских дифракционных картин. Построение функции электронной плотности и определение координат атомов сложных структур возможно только с помощью сложного анализа и трудоёмкой математической обработки значений интенсивностей всех дифракционных отражений от данного кристалла.

Трехмерная периодичность атомной структуры кристаллов позволяет записать их функции электронной плотности 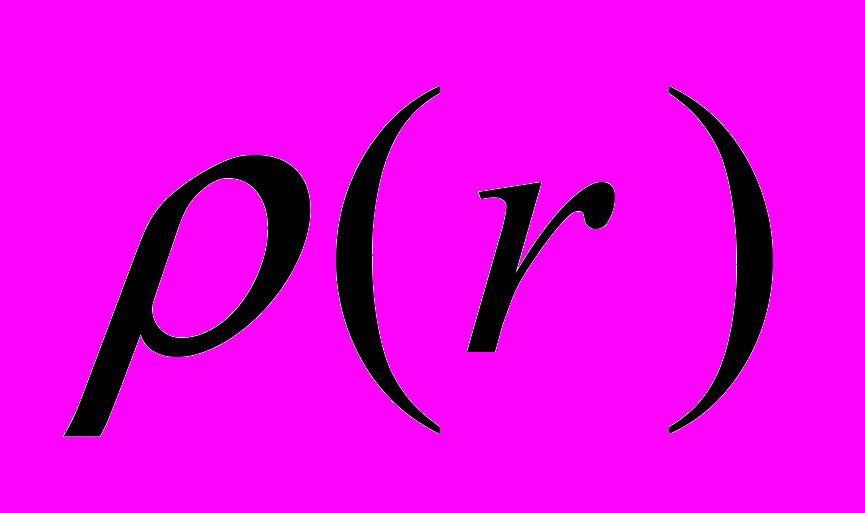в в виде разложения в ряд Фурье:

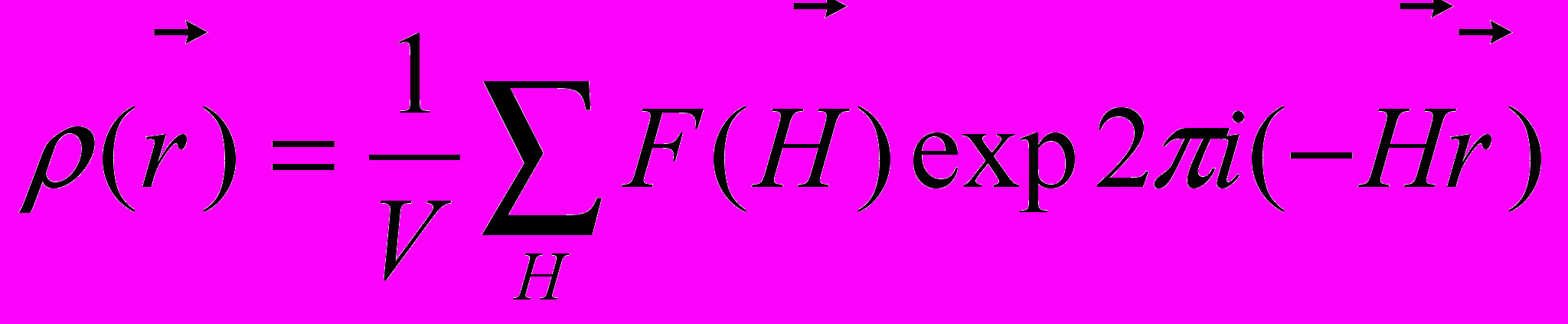(1)

Здесь V- объем элементарной ячейки кристалла, 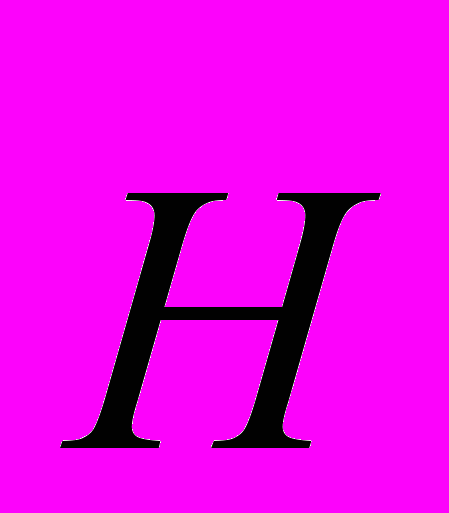- тройка индексов (hkl) узлов обратной решетки, 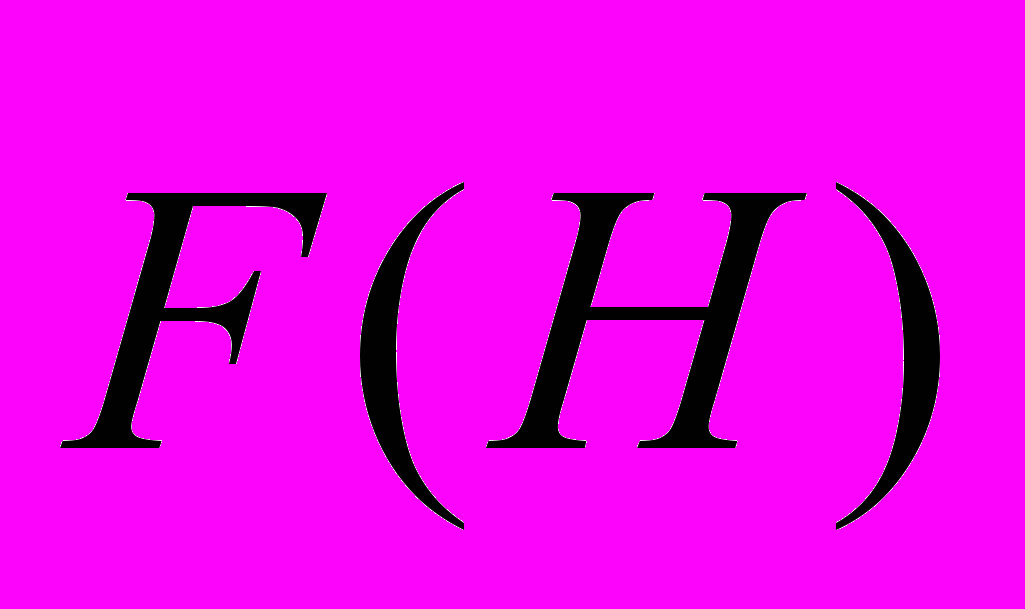-структурные амплитуды, которые являются коэффициентами разложения Фурье и представляют собой комплексные числа, определяющиеся распределением электронной плотности (координатами атомов) конкретного кристалла.

Каждая структурная амплитуда характеризуется тремя целыми числами hkl и связана с дифракционным максимумом с индексами hkl. Измеряя интенсивность всех экспериментально наблюдаемых рентгеновских дифракционных максимумов (обычно из несколько тысяч или десятков тысяч), можно рассчитать квадраты модулей структурных амплитуд (коэффициентов разложения электронной плотности в ряд Фурье).

Если бы было возможно экспериментально измерить не только модули, но и фазы структурных амплитуд, то задача структурного анализа решалась бы достаточно просто. Для получения полной информации об атомной структуре кристалла (построения функции электронной плотности) достаточно было бы просто «свернуть» ряд Фурье в заранее выбранных точках элементарной ячейки кристалла, используя экспериментально полученные коэффициенты 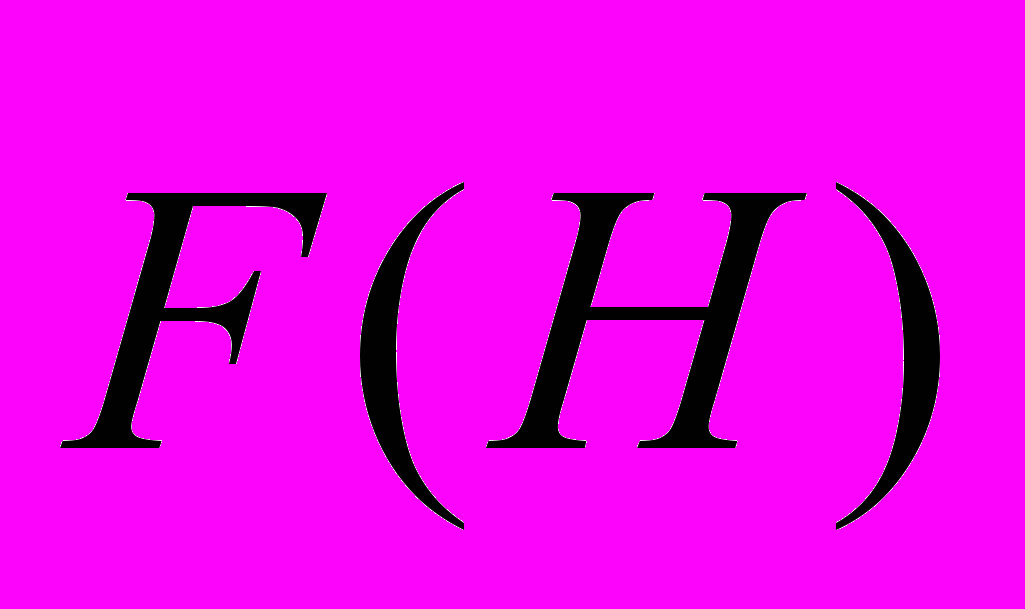. Однако, это можно будет сделать лишь при наличии источников когерентного рентгеновского излучения (рентгеновских лазеров). Таким образом, в настоящее время экспериментально можно получить лишь половину необходимой для рентгеноструктурного анализа информации. В этом существо т.н. фазовой проблемы в РСА.

Однако, анализ показывает, что и экспериментально определяемые модули коэффициентов Фурье содержат достаточно информации, чтобы успешно решать структурные задачи. Структурная амплитуда может быть рассчитана по известной структуре с помощью обычных выражений для коэффициентов Фурье трехмерно-периодических функций

. (2)

Здесь 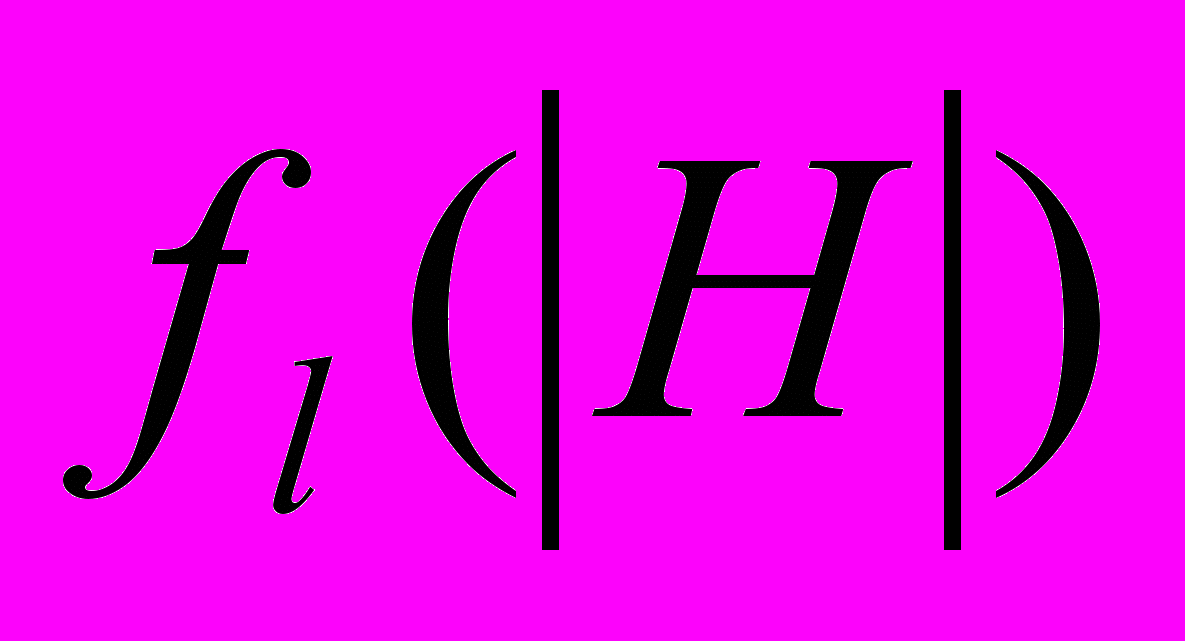- функция, задающая интенсивность рассеяния рентгеновкого излучения l-м атомом, и суммирование ведется по всем атомам в элементарной ячейке кристалла. Можно составить систему уравнений для модуля каждой структурной амплитуды. Этих уравнений будет ровно столько, сколько экспериментально исследовали дифракционных максимумов. При этом это число уравнений оказывается на порядок больше, чем число неизвестных (координат атомов) структуры, т.е. в принципе из этой системы можно получить всю структурную информацию о кристалле.

На практике решение фазовой проблемы проводится двумя способами. Рассмотрим ряд Фурье, в котором в качестве коэффициентов используются квадраты модулей структурных амплитуд

(3)

Функция 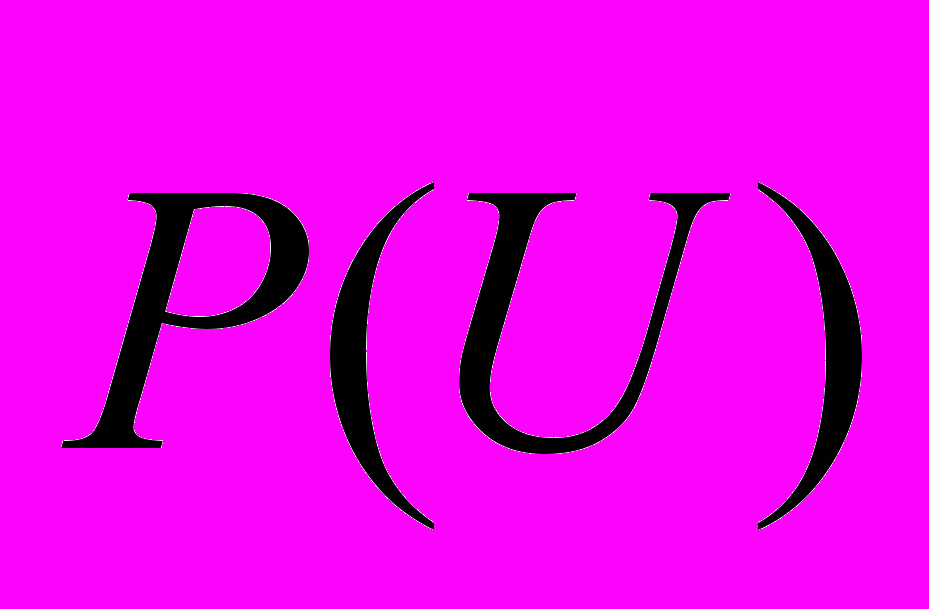представляет собой самосвертку функции электронной плотности

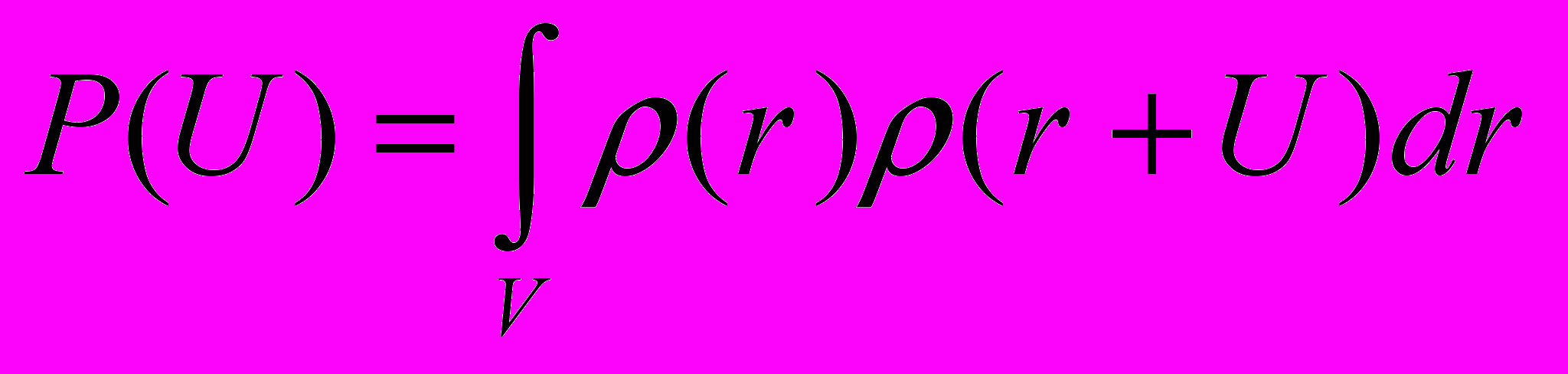(4)

Эта функция принимает максимальные значения на концах межатомных векторов и называется межатомной функцией или функцией Патерсона. Существует целый ряд методов получения функции электронной плотности из функции Паттерсона.

Другими способами решения фазовой проблемы являются так называемые прямые методы определения фаз структурных амплитуд. Учитывая тот факт, что значение функции электронной плотности в кристалле всегда отрицательно (или равно нулю), можно получить большое число неравенств, которым подчиняются коэффициенты Фурье (структурные амплитуды). Для более сложных структур применяются методы, основанные на вероятностном подходе к проблеме: структурные амплитуды и их фазы рассматриваются как случайные величины; из физических представлений выводятся функции распределения этих случайных величин, которые дают возможность оценить с учётом экспериментальных значений модулей структурных амплитуд наиболее вероятные значения фаз. Эти методы реализованы на ЭВМ и позволяют расшифровать структуры, содержащие 100-200 и более атомов в элементарной ячейке кристалла.

В настоящее время число расшифрованных атомных структур кристаллов исчисляется сотнями тысяч. Вершиной достижений рентгеноструктурного анализа является расшифровка трёхмерной структуры белков, нуклеиновых кислот и других макромолекул. Белки в естественных условиях, как правило, кристаллов не образуют. Чтобы добиться регулярного расположения белковых молекул, белки кристаллизуют и затем исследуют их структуру. Для решения этой проблемы необходимо получить и исследовать кристаллы самого белка, а также его производных с включением тяжёлых атомов. Первую рентгенограмму кристаллов пепсина получили в 1934 г. англичане Джон Бернал и Дороти Хочкин. Наличие четкой дифракционной картины (системы рентгеновских пятен, или рефлексов) показало, что все молекулы белка имеют упорядоченную структуру. Однако расшифровать строение белка на основании дифракционной картины в то время не смогли вследствие больших трудностей решения фазовой проблемы. Эту задачу решил М.Перутц с сотрудниками в 1954 г., используя рентгенограммы производных кристаллов, содержащих атомы тяжелых металлов. С помощью такого метода изоморфного замещения Дж.Кендрью с сотрудниками в 1958г. получили пространственную конфигурацию миоглобина с разрешением 6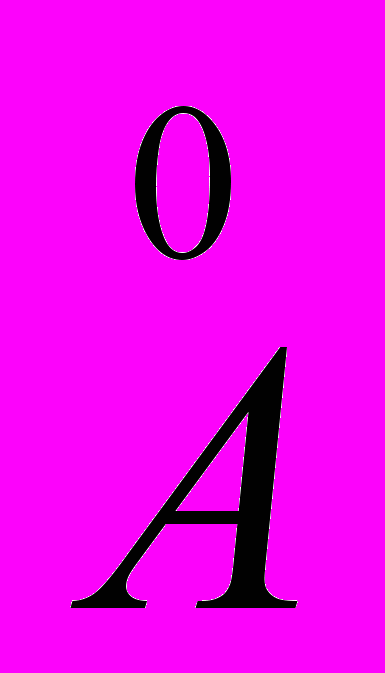, а еще через два года - с разрешением 2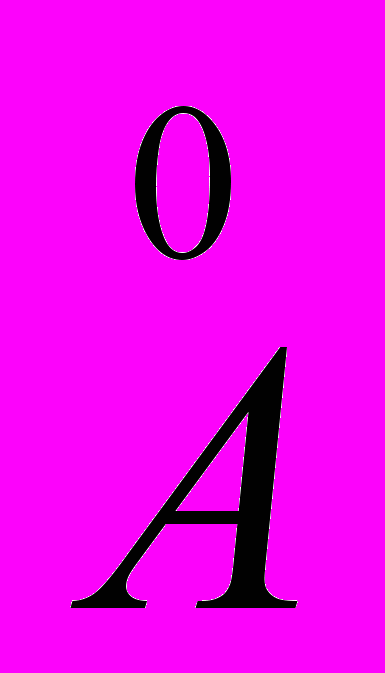. Одновременно Перутц с сотрудниками установили строение гемоглобина с разрешением 5.5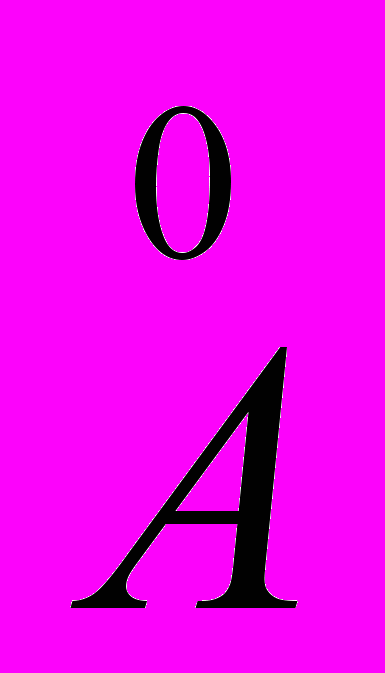. В нашей стране изучение структуры белков методами рентгеновской кристаллографии и электронной микроскопии было начато Б.К.Вайнштейном с сотрудниками в 1959-1960гг. в лаборатории структуры белка, созданной в Институте кристаллографии АН СССР. В 1975-1978 гг. расшифровали структуру растительного аналога гемоглобина, леггемоглобина, сначала с разрешением 5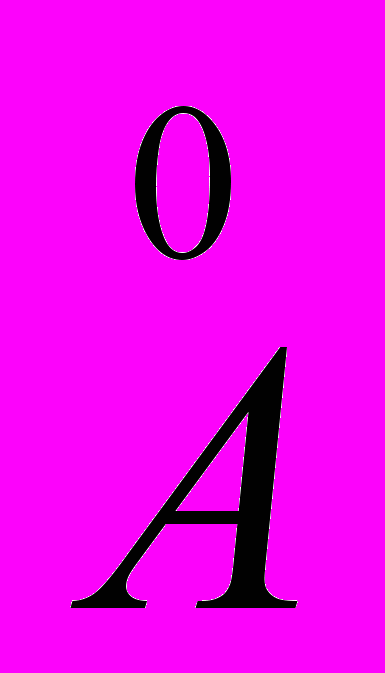, а затем 2.8.

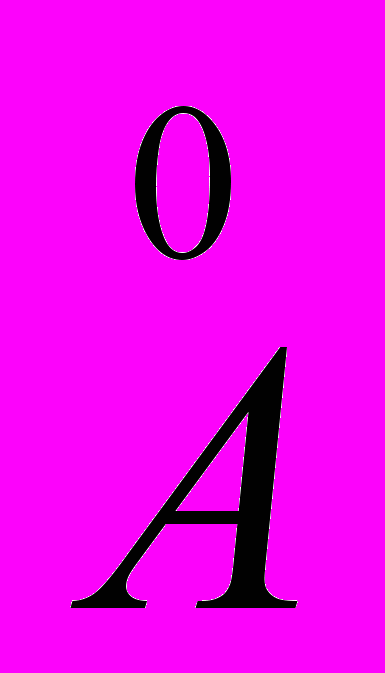В последние годы возможности рентгеновских дифракционных экспериментов по исследованию кристаллических структур значительно возросли благодаря применению источников синхротронного излучения. По мощности они превосходят рентгеновские трубки в сотни и даже тысячи раз.

Синхротронное (магнитотормозное) излучение - это излучение электромагнитных волн заряженными частицами, движущимися с релятивистскими скоростями в однородном магнитном поле. Синхротронное излучение обусловлено ускорением, связанным с искривлением траекторий частиц в магнитном поле. В рентгеновской трубке электроны при соударении с анодом теряют свою энергию. При этом небольшая ее часть переходит в энергию рентгеновских квантов, а большая часть – в тепло. В синхротроне энергия электрона практически полностью переходит в электромагнитное излучение. Большая интенсивность и малая расходимость пучка синхротронного излучения весьма полезны при структурных исследованиях очень мелких кристаллов с размерами 5-50 мкм. Именно таким путем была получена четкая дифракционная картина от монокристалла флюорита с ребром около 0,006 мм. С помощью достаточно мощной (3 кВт) рентгеновской трубки аналогичную картину удалось получить от кристалла флюорита с объемом, почти в 1000 раз большим.


1. Современная кристаллография. Под ред. Б.К.Вайнштейна. т.1- М.: Наука, 1979. 383с.

2. Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А. Основы кристаллографии.-М.: Физматлит, 20043.-500с.

3. Пущаровский Д.Ю. Рентгенография минералов. - М.: ЗАО «Геоинформмарк», 2000. – 292 с.

4. Куранова И.П. // Кристаллография. 2001. Т.46. №4. С.667-686.

5. Владимиров Ю.А..//Природа, 2003№11,


Динамическая дифракция рентгеновских лучей в неоднородных кристаллах


М. А. Фаддеев

Нижегородский государственный университет имени Н. И. Лобачевского, Н. Новгород


Рентгеновская дифракция рентгеновского излучения является основой экспериментальных методов, которые относятся к самым информативным и надежным способам исследования микроструктуры твердых тел. Динамическая теория дифракции рентгеновских лучей, базирующаяся решении на фундаментальных уравнениях Максвелла, глубоко разработана для идеальных кристаллов и демонстрирует хорошее согласие с экспериментальными данными [1, 2]. Но реальные, даже высоко совершенные кристаллические образцы содержат некоторое количество дефектов различных типов. Следует заметить, что экспериментальные исследования отклонений наноструктуры кристалла от идеальной являются одним из самых важных направлений современной физики.

Динамическая теория дифракции рентгеновских лучей на реальных кристаллах в настоящее время далека от завершения из-за разнообразия типов дефектов и сложного вида поля рентгеновского излучения в искаженной кристаллической структуре. Для решения прикладных задач микро-, нано и оптоэлектроники целесообразно разрабатывать частные теории динамической дифракции на кристаллах с определенным классом дефектов. Специализированные модели позволяют интерпретировать наблюдаемые рентгенооптические эффекты [3, 4].

Многие кристаллические образцы, выращенные из водных растворов демонстрируют эффект обратимого изменения интенсивности рентгеновского дифракционного максимума (РДМ) рефлекса при маломощном воздействии на дифрагирующий кристалл [5 – 7]. Количественной характеристикой эффекта является безразмерный коэффициент

K = (I  I₀)/ I₀ (1)


где I₀. – интенсивность РДМ до воздействия, I – установившаяся интенсивность того же РДМ при воздействии на кристалл. Воздействие может быть механическим, тепловым, оптическим и т.д. Например, эффект отчетливо наблюдается при падении на дифрагирующий кристалл лазерного луча мощностью порядка 20 мВт и выше. Для некоторых кристаллических образцов коэффициент K достигал 300 % [7, 8].

В работах [4, 7, 8] показано, что эффект обратимого изменения интенсивности РДМ успешно объясняется динамической дифракцией рентгеновских лучей на зонарных кристаллах, обладающих слоистой микроструктурой. Однако, эксперименты продемонстрировали, что данный эффект наблюдается и на кристаллах с другими типами отклонения микроструктуры от идеальной.

В частности, иногда выращенные монокристаллы обладают явно выраженной блочной структурой. Такие кристаллы состоят из отдельных монокристаллических блоков, слабо разориентированных относительно друг друга. Если углы разориентации имеют порядок угловых секунд, а средние размеры блоков составляют десятки микрон, то такие кристаллы относятся к совершенным, так как дают картины рентгеновской дифракции с резкими рефлексами. Покажем, что воздействие маломощного лазерного пучка на блочный кристалл вызывает обратимое увеличение интенсивности РДМ.

Пучки первичных рентгеновских лучей в экспериментальных установках обычно обладают расходимостью с углом ₀ порядка десятка угловых минут и более. Пятно первичного рентгеновского излучения на облучаемой грани кристалла имеет размер около 1 мм.

Пусть исследуемый кристаллический образец находится в отражающем положении, причем регистрация дифрагированного излучения проводится в геометрии Брэгга. Предположим сначала, что все блоки в мозаичном кристалле практически не разориентированы. Отражающие плоскости всех блоков параллельны относительно друг друга. Тогда дифракция будет происходить лишь на одном из идеальных блоков, для которого угол между отражающей плоскостью (для определенного рефлекса hkl) и волновым вектором отдельного пучка является углом Брэгга _b. На остальные блоки отдельные пучки первичных рентгеновских лучей будут падать под углом, отличающимся от брэгговского.




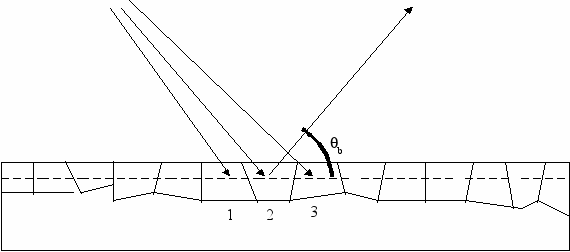
Рис.1. Схема дифракции рентгеновских лучей на блочном кристалле в симметричной геометрии Брэгга.

Все блоки имеют одинаковую ориентацию. Штриховая линия – след отражающей плоскости с определенными индексами (hkl).


Рассеяние рентгеновских лучей на отдельном блоке описывается динамической теорией дифракции. В случае геометрии Брэгга угловое распределение коэффициента отражения рентгеновского рефлекса имеет характерный вид «столика Дарвина».

При любом неоднородном воздействии на такой кристалл его блоки получают случайную разориентацию. Тогда у некоторых блоков угол между отражающей плоскостью и одним из отдельных пучков может стать равным углу Брэгга. Эти микрокристаллы окажутся в отражающем положении, и дифракция на этих блоках увеличит вклад в поток регистрируемого рефлекса. Разориентация блоков задается изменением угла  между отражающей плоскостью и облучаемой поверхностью кристалла на случайную величину . Углы разориентации могут описываться распределением Гаусса с плотностью


p(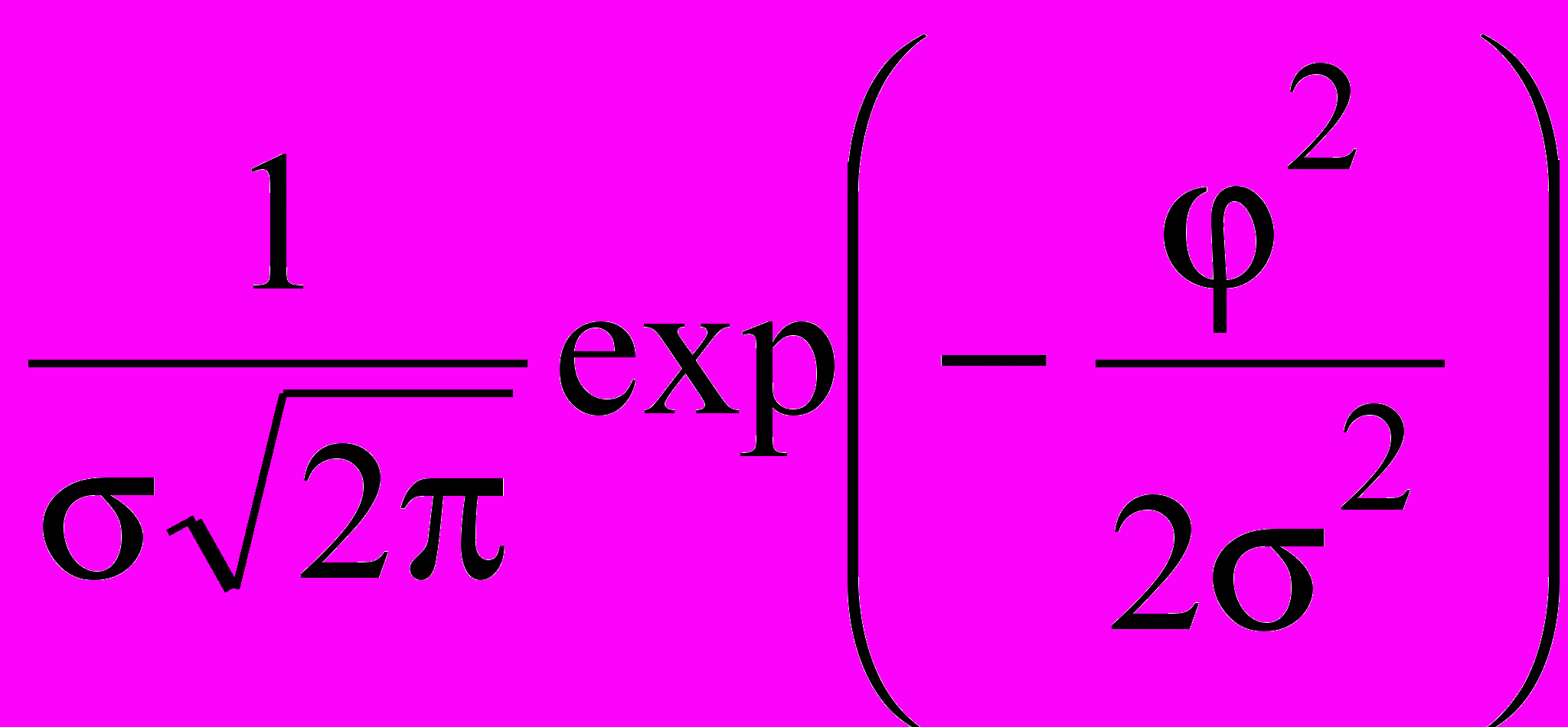) = , (2)


где   средний угол разориентации блоков.

Моделирование разориентации блоков проводилось методом Монте-Карло, а интенсивность РДМ рассчитывалась по динамической теории дифракции. Расчеты показали, что с ростом величины  угловая ширина рентгеновского рефлекса увеличивается, и коэффициент K значительно возрастает.

Р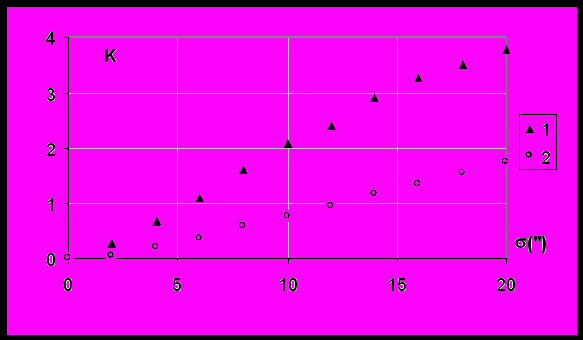ис.2. Зависимость коэффициента K от среднего угла  разоринтации блоков. Кристалл KDP. Рефлекс (400). Размер блока 50 мкм. Расходимость первичного пучка ₀ =10. 1 –  = 0,71 Å, 2 –  = 1,54 Å.


Так как угол разориентации блоков растет с температурой кристалла, то полученные результаты согласуются с экспериментальными данными. Кроме того, типичный пример на рис.2 демонстрирует резкую зависимость коэффициента K от длины волны  рентгеновского излучения, которая наблюдается в экспериментах.

Зависимости коэффициента K от размера блока S_b при определенном угле расходимости первичного пучка ₀ имеют немонотонный вид (см.рис.3). Максимум этих зависимостей лежит в области 20 – 50 мкм, что согласуются с результатами экспериментов.




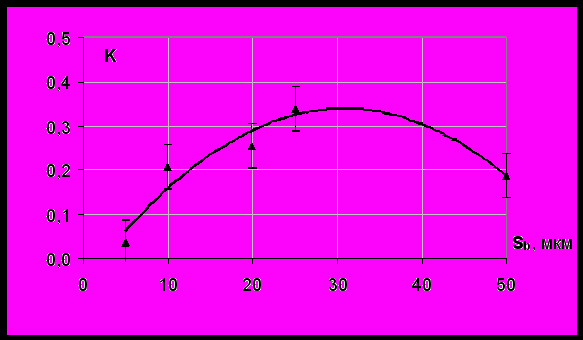
Рис.3. Зависимость коэффициента K от размера блока S_b при расходимости первичного пучка ₀ =1΄.

Кристалл алюмокалиевых квасцов.  = 0,71 Å. Рефлекс (600).


Более серьезной проблемой является распространение динамическую теорию дифракции рентгеновских лучей на неоднородно деформированные кристаллы. Неоднородные деформации описываются полем векторов смещения u(r), где функция точки u(r), вообще говоря, может иметь произвольный вид. Решение уравнений Максвелла для рентгеновских лучей в неоднородно деформированных кристаллах общего вида приводит к принципиальным трудностям, поэтому динамическая теория дифракции строится для разумных приближений. Для практических потребностей особенно важен случай малых деформаций, определяемых неравенством | ¶u_i / ¶x_j | << 1, где индексы i, j пробегают значения 1, 2, 3.

Для слабодеформированных кристаллов вводится понятие локальной обратной решётки – вектор обратной решетки H становится функцией точки. Тогда связь волновых векторов проходящей k₀ и дифрагированной k_g волн с вектором обратной решетки записывается в обычном виде


k_g= k₀ + H (3)


Локальный вектор обратной решетки H в окрестности точки r₀ представляется следующим образом:


H = H – grad[H u(r₀)] (4)


где H – соответствующий вектор обратной решетки в идеальном кристалле. Подстановка выражения (4) в уравнения динамической теории дифракции рентгеновских лучей для идеальных кристаллов дает очень громоздкую систему уравнений Такаги, которая несколько упрощается отбрасыванием членов высшего порядка малости [9].

Ограничимся случаем плоской падающей рентгеновской волны и одномерной деформацией кристалла, когда вектор смещения u зависит только от координаты z, перпендикулярной облучаемой поверхности исследуемого образца. Это приближение удовлетворительно описывает условия экспериментов по измерению интенсивности РДМ при облучении идеального кристалла маломощным лазером.

Трудности решения системы дифференциальных уравнений Такаги для граничных условий, реализованных в условиях экспериментов, преодолеваются при переходе к уравнению Топена [10].


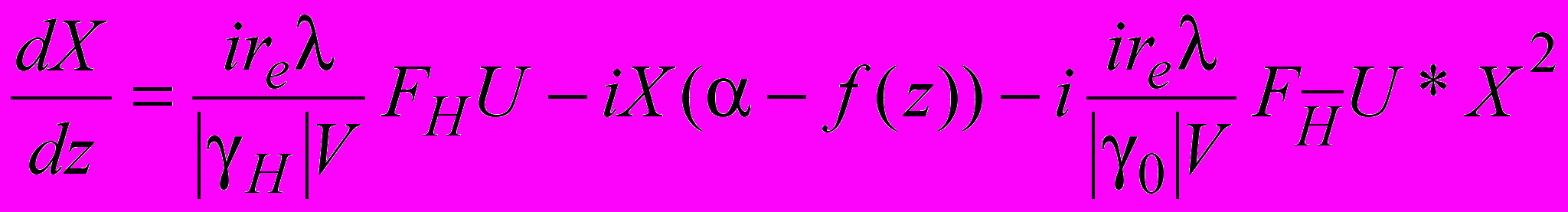(5)


где функция X равна отношению амплитуд дифрагированной и проходящей рентгеновских волн,  – длина волны, F_H – структурная амплитуда, V – объем элементарной ячейки, ₀ и _H – косинусы углов падения и отражения соответственно, r_e –классический радиус электрона.


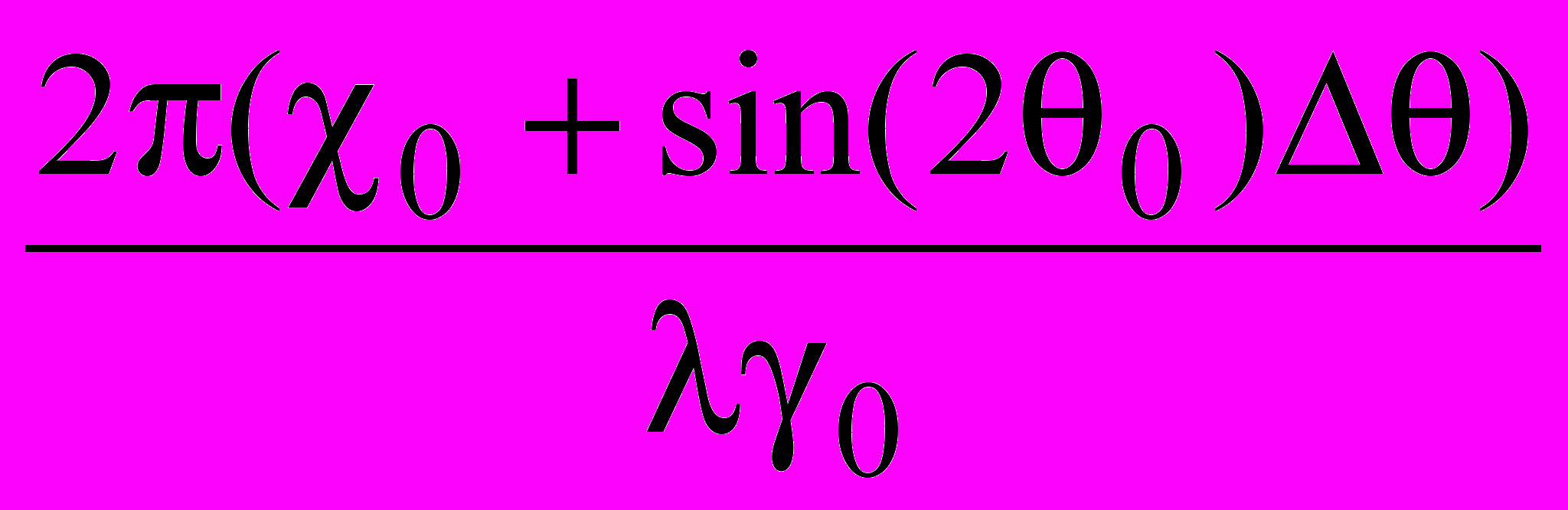= (6)


где  – локальное отклонение угла рассеяния от кинематического угла Брэгга ₀ .

Функция f(z) выражается через изменение межплоскостного расстояния d(z), вызванного неоднородной деформацией приповерхностного слоя кристаллического образца


f(z) = 2d(z) / d ² (7)


где d – расстояние между отражающими кристаллическими плоскостями с кристаллографическими индексами (hkl). При этом величина U задается следующим интегралом

U(z) = exp(–i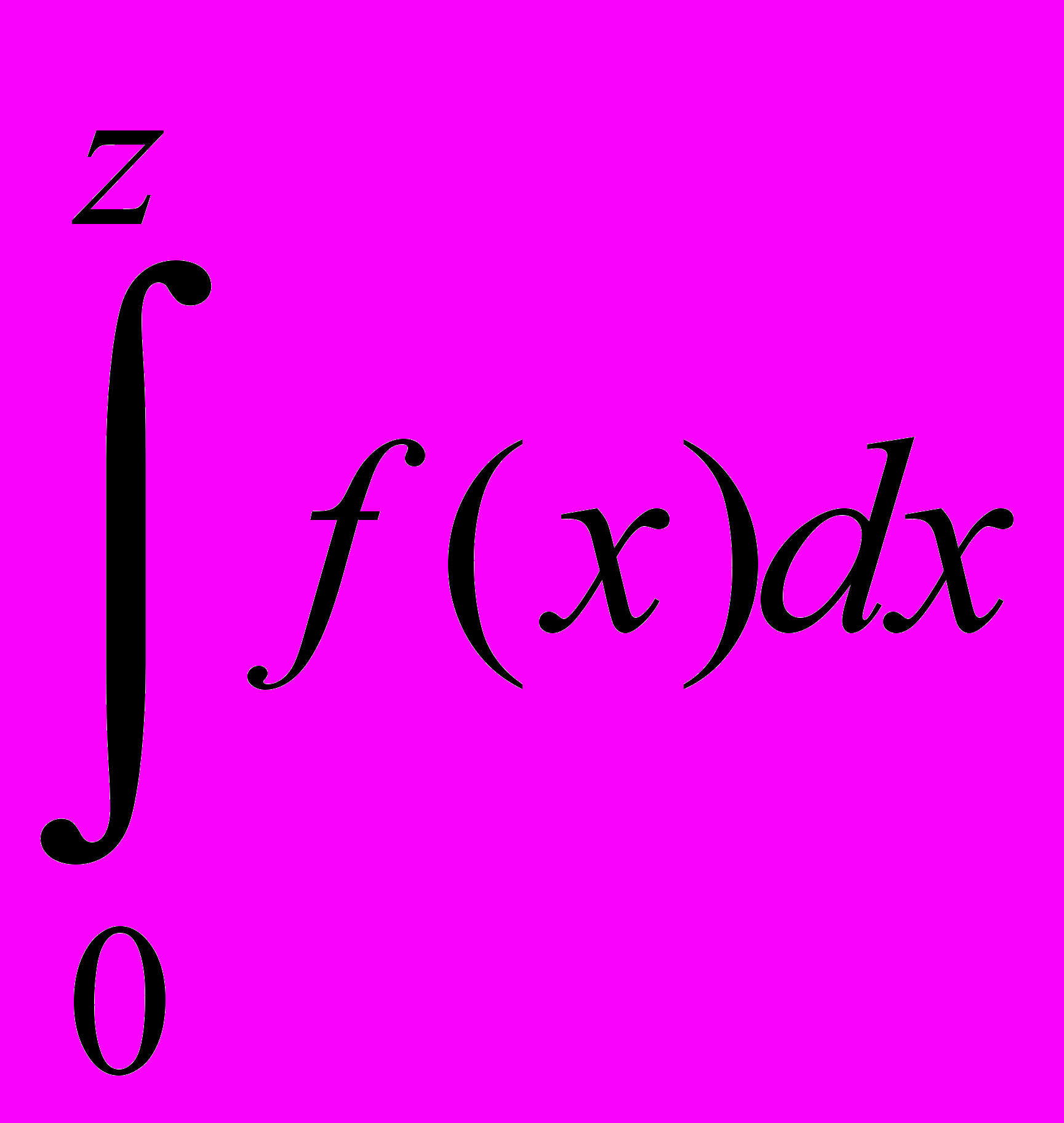) (8)


Так как функция X комплексная, то уравнение (5) преобразуется к двум – для действительной и мнимой частей.

Граничные условия формулируются для идеального кристалла, в приповерхностном слое которого образовано поле неоднородной деформации. Так как деформация создается из-за нагрева лазерным лучом, то распределение температуры внутри кристалла может быть найдено путем решения стационарного уравнения теплопроводности. В результате было получено, что функция d(z) успешно аппроксимируется экспоненциальной зависимостью вида


d = d _T T exp(-z/L) (9)


где _T – коэффициент температурного расширения, T – разность между температурой облучаемой поверхности кристалла T и комнатной температурой T₀ . Параметр L определяет характерную толщину деформированного слоя.

Для устойчивости решения полученной системы уравнений Топена и приемлемой точности результатов был применен метод Рунге-Кутта с переменным шагом. Разработанный алгоритм позволил рассчитывать угловое распределение рентгеновского рефлекса для неоднородно нагретого кристалла, установленного в отражающее положение при регистрации в геометрии Брэгга. На рис.4 приведен характерный пример, который демонстрирует увеличение интегральной интенсивности РДМ с ростом температуры облучаемой поверхности кристалла T₀ + T. При этом возрастает асимметрия формы рефлекса и увеличивается динамический сдвиг центра рефлекса в область меньших углов. Результаты расчетов, полученные для ряда водорастворимых кристаллов (KDP, ADP, алюмокалиевые квасцы) согласуются с экспериментальными данными. Численное интегрирование угловой зависимости R() дает интегральный коэффициент отражения R_i . Нормировка величины R_i на интегральный коэффициент для идеального кристалла R_i0 дает коэффициент обратимого изменения интенсивности РДМ (1)


K = (R_i  R_i0)/R_i0 (10)





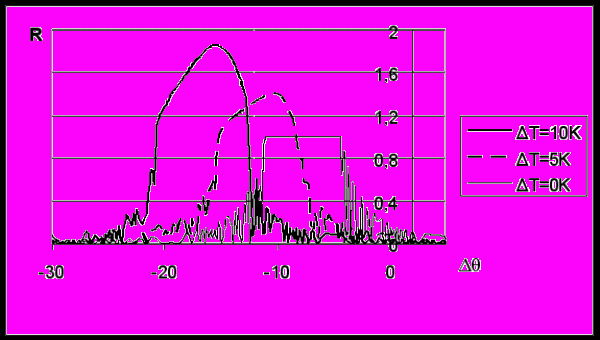
Рис.4. Угловое распределение рентгеновского рефлекса. Кристалл KDP. Рефлекс (200). l = 1,54 Å. Толщина деформированного слоя 25 мкм.


Пример зависимостей коэффициента K от температуры дополнительного нагрева облучаемой поверхности T для двух различных длин волн l рентгеновских лучей представлен на рис.5.





Рис. 5. Зависимость коэффициента K от температуры нагрева DT. Кристалл KDP. hkl = (400). Толщина деформированного слоя 50 мкм.


Расчеты показали, что для любых длин волн  функция K(T) является монотонно возрастающей, а при фиксированной температуре нагрева DT коэффициента K уменьшается с ростом длины волны, что согласуется с результатами экспериментов [4, 7].

Таким образом, обратимое изменение интенсивности РДМ, происходящее при внешнем воздействии на дифрагирующий кристалл может вызываться различными физическими процессами. Согласно изложенному выше, помимо динамической дифракции в слоях зонарного кристалла, возрастание коэффициента K возможно в мозаичных структурах при определенных параметрах блоков. Наконец показано, что даже в изначально идеальных кристаллах неоднородный нагрев приводит к эффекту обратимого изменения интенсивности рентгеновских рефлексов, из-за особенностей динамической дифракции в упругих термодеформациях кристаллической структуры.

1. Пинскер З.Г. Рентгеновская кристаллооптика. М.: Наука. 1982. 392с.
   
2. Зайцева Е.В., Фаддеев М.А., Чупрунов Е.В. Динамическая теория рассеяния рентгеновских лучей в кристаллах. Н.Новгород. Изд-во ННГУ. 1999. 132с.
   
3. Чупрунов Е.В. и др. // Поверхность. 1999. № 1. С.98.
   
4. Фаддеев М.А., Чупрунов Е.В., Зайцева Е.В. // Поверхность. 2002. № 9. С.84.
   
5. Трушин В.Н. и др. // Кристаллография. 1993. Т.38. № 4. С.213.
   
6. Гораздов В.Е. и др. // Кристаллография. 1997. Т.42. № 1. С.43.
   
7. Зайцева Е.В. и др. // Кристаллография. 1997. Т.42. № 6. С.969.
   
8. Зайцева Е.В. и др. // Вестник ННГУ, сер.ФТТ, вып.2, 1998. С.91.
   
9. Takagi S.A. Acta Cryst., 15, 1311, 1962.
   
10. Taupin D., Burgeat J. // Acta Cryst. A. 1968. V.24. P.99.
    

CВОЙСТВА ИОННО-СИНТЕЗИРОВАННЫХ АМОРФНО-КРИСТАЛЛИЧЕСКИХ СЛОЕВ КРЕМНИЯ