Материалы микроэлектроники

Вид материала

Документы

Содержание Ферритов-гранатов с точкой компенсации магнитного момента Зарождение кристаллической фазы в амс. Упаковоки икосаэдров и пентагондодекаэдров и их применение для описания кристаллических структур Методика расчета огранки кристалла по его атомной структуре

Подобный материал:

• Семинар \"Новые магнитные материалы микроэлектроники\" (нммм 19). 28 июня 2 июля 2004,, 23.32kb.
• «Материалы и компоненты микроэлектроники», 359kb.
• Xxi международная конференция, 74.63kb.
• Республики Беларусь «24», 3587.94kb.
• Программа спецкурса " Электронно-зондовая диагностика материалов и приборов микроэлектроники", 13.07kb.
• Введение в специальность, 2241.27kb.
• Физика полупроводниковых приборов, 1091.64kb.
• Твердые растворы на основе карбида кремния: технология и свойства, 66.85kb.
• Физика полупроводников и твердотельная электроника введение, 56.3kb.
• Физика твердого тела и твердотельная электроника введение, 40.45kb.

Теория базируется на решении уравнения Топена для отношения комплексных амплитуд проходящей и дифрагированной рентгеновских волн [1]. Рассматривается идеальный кристалл, в приповерхностном слое которого создана неоднородная деформация путем нагрева облучаемой поверхности. Граничные условия записываются для геометрии Брэгга и деформации, которая зависит только от координаты z, перпендикулярной внешней грани дифрагирующего кристалла. Зависимость изменения межплоскостного расстояния от координаты z при поверхностном нагреве кристалла аппроксимировалась экспоненциальной функцией. Исходное уравнение Топена преобразовано в систему удобную для численного интегрирования. Для повышения устойчивости и точности решения использовался метод Рунге-Кутта с переменным шагом.

В результате компьютерного моделирования динамической дифракции были получены угловые распределения рентгеновских рефлексов для ряда водорастворимых центросимметричных кристаллов. Интегрирование угловых распределений позволило вычислить коэффициент K, равный величине относительного изменения интенсивности рентгеновского рефлекса при неоднородной деформации монокристалла. Получено, что зависимости K(T), где T – разность температуры поверхности кристалла и комнатной, являются монотонно возрастающими в исследуемом диапазоне (0  T  25К). Обнаружено, что коэффициент K возрастает при увеличении температурного градиента, который возникает из-за повышения температуры на поверхности образца. Наблюдается уменьшение коэффициента K с ростом длины волны рентгеновских лучей при разных профилях деформации. Результаты расчетов согласуются с данными экспериментов.

1. Taupin D. // Bull. Soc. Franc. Mineral. Cryst. 1964. Vol. 87. P. 469-511.
   

ФЕРРИТОВ-ГРАНАТОВ С ТОЧКОЙ КОМПЕНСАЦИИ МАГНИТНОГО МОМЕНТА


М.А.Бакулин, А.М.Зюзин

Мордовский государственный университет им. Н.П. Огарева.


Исследования температурные зависимости спектров спин-волнового резонанса в пленках с точкой компенсации магнитного момента.

Д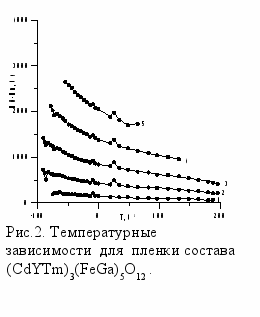ля проведения эксперимента были использованы двухслойные пленки выращенные на подложках гадолиний-галиевого граната с ориентацией (111). Первый слой, обладающий большим параметром затухания α_d=0.2, имел состав (SmEr)₃Fe₅O₁₂, толщину h=1.2 мкм. Второй слой (CdYTm)₃(FeGa)₅O₁₂ имел толщину на разных образцах от 0.3 до 1.5 мкм.

На рис.1 показаны зависимости разности резонансных полей нулевой и n-ой мод. Уменьшение числа мод при приближении к точке Кюри объясняется сближением полей однородного резонанса в слоях возбуждения и закрепления.

Уменьшение числа мод при приближении к точке компенсации магнитного момента связано с уменьшением степени закрепления из-за уменьшения намагниченности.

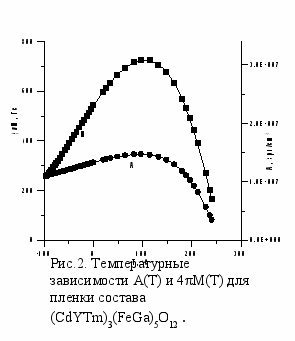
На рис.2 показаны температурные зависимости A и 4πM в пленках состава (CdYTm)₃(FeGa)₅O₁₂ , обладающих точкой компенсации магнитного момента. Температура Кюри для них составляла 238 ^оС. При приближении к точке компенсации со стороны высоких температур происходит уменьшение 4πM. В тоже время зависимость A(T) для пленок обладающих точкой компенсации магнитного момента, имеет характер, отличный от зависимости A(T) для пленок ЖИГ.


1. А.Г.Гуревич, Магнитный резонанс в ферритах и антиферромагнетиках, М.: Наука, 1973.

2. А.М.Зюзин, В.Н.Ваньков, В.В.Радайкин, Письма в ЖТФ 17(23), 65 (1991).

3. А.М.Зюзин, А.Г.Бажанов, Письма в ЖТФ 63, 7 (1996

Учет влияния нагрева кристалла на дифракцию рентгеновских лучей с помощью эффективных узлов обратной решетки


А.В. Марков, М.А. Фаддеев

Нижегородский государственный университет имени Н. И. Лобачевского,

Нижний Новгород


Экспериментальные исследования показывают, что нагрев кристалла вызывает изменение параметров рентгеновских дифракционных максимумов (РДМ). Учет нагрева с помощью фактора Дебая-Валлера для монокристаллов с размерами более 100 мкм нельзя признать удовлетворительным [1].

Дифракция рентгеновских лучей на крупных монокристаллах описывается динамической теорией рассеяния. Каждый РДМ характеризуется вектором обратной решетки H с определенными индексами (hkl).

Влияние нагрева кристалла на дифракционную картину в нашей модели интерпретируются заменой точечных узлов обратной решетки некоторыми эффективными объемами со сферической симметрией. Радиус эффективного узла принимается пропорциональным температуре. Моделирование дифракции проводилось нами в рамках двухволнового приближения [2]. Угловые распределения РДМ формируются интерференцией рентгеновских волн D₁ и D₂. Начальные точки соответствующих волновых векторов k₁ и k₂ находятся в центрах распространения на нормали к облучаемой поверхности кристалла. Концы векторов k₁ и k₂ располагаются в случайных точках внутри эффективного узла обратной решетки. Положение случайных точек определялось методом Монте-Карло. Распределение конечных точек волновых векторов задавалось функцией Гаусса, что позволило ввести величину эффективного радиуса узла обратной решётки σ. Характеристики РДМ вычислялись усреднением по конечному множеству случайных точек.

Расчеты показали, что как в геометрии Лауэ, так и в геометрии Брэгга нагревание кристалла приводит к характерному сглаживанию отдельных максимумов углового распределения РДМ (см.рис.1).

В случае геометрии Брэгга нагревание кристалла всегда приводит к ослаблению интенсивности РДМ. В геометрии Лауэ возможно как уменьшение, так и возрастание интенсивности РДМ, что определяется видом центрального максимума рефлекса.




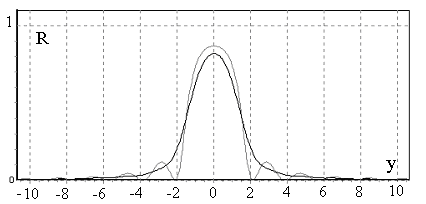
Рис 1. Угловая зависимость коэффициента отражения в геометрии Брэгга для кристалла ADP hkl:(400). λ =1.54 Å. Ширина рефлекса 2”, величина σ = 3.8·10^-8 Ǻ^-1, толщина пластины 100 mkm. Черная кривая – с учётом нагрева, серая кривая – без учёта нагрева.


Изменение интегральной интенсивности характеризуется коэффициентом K = (I₀ – I)/I₀, где I₀ и I – интегральные коэффициенты отражения без учёта нагрева и с учётом нагрева (см. рис.2).




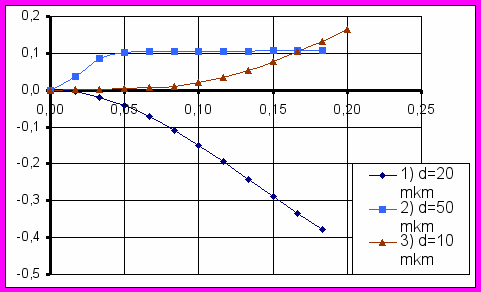
Рис. 2. Зависимость относительного изменения интегральной интенсивности РДМ от эффективного радиуса σ для кристалла KDP. hkl : (200). Ширина рефлекса 30”. d – толщина кристалла. λ =1,54 Ǻ. Кривые 1) и 2) для геометрии Лауэ, кривая 3) для геометрии Брэгга.


1. Иверонова В. И., Ревкевич Г. П. Теория рассеяния рентгеновских лучей. – М.: МГУ, 1972.

2. Зайцева Е. В., Фаддеев М. А., Чупрунов Е. В. Динамическая дифракция рентгеновских лучей в кристаллах, Часть 1. – ННГУ, 1999.


ЗАРОЖДЕНИЕ КРИСТАЛЛИЧЕСКОЙ ФАЗЫ В АМС.


Кириндясов Е.М., Кяшкин В.М.

Мордовский государственный университет им. Н.П. Огарева, г. Саранск


Свойства аморфных металлических сплавов (АМС) во многом определяются их структурой, которая является метастабильной и с течением времени релаксирует в более стабильное (кристаллическое) состояние.

Нами был исследован аморфный сплав Fe₅Co₇₀Si₁₅B₁₀ после длительной выдержки при комнатной температуре. На рентгенограммах полученных от обеих сторон образца в Mo K_α-излучении в диапазоне углов от 4.5º до 16º, видны слабые дифракционные рефлексы, которые свидетельствуют о наличии небольших включений кристаллической фазы. По картотеке ASTM дифракционные рефлексы от контактной поверхности (5.7º и 11.4º) могут соответствовать рефлексам (001) и (002) фазы Fe₃Si₂O₅(OH)₄ или Co₃(OH)₄Si₂O₅. Узкий дифракционный максимум, полученный от свободной поверхности (13º) не соответствует рефлексам указанных фаз, что, возможно, указывает на зарождение нескольких различных кристаллических соединений. Это различие может быть связано либо с разным составом поверхностей [1], либо с различными механизмами, способствующими этому зарождению. В работе [2] указывается, что кристаллизация АМС начинается с поверхности образца и затем распространяется в его объем, это можно предположить и в нашем случае. Образование сложных фаз, скорее всего, вызвано взаимодействием поверхностей образца с атмосферой при его изготовлении [3] и дальнейшем пребывании на воздухе (окисление).

Методом наклонной съемки [4] было также обнаружено, что с изменением наклона образца интенсивности рефлексов уменьшаются для обеих его поверхностей, при этом линии фона остаются неизменными. Такое изменение интенсивности указывает на то, что зарождение кристаллов является ориентированным относительно нормали к поверхности образца. По нашему мнению, этому способствуют напряжения, возникающие из-за действия градиента температуры при изготовлении образца.

1. Шабанова И.Н.// Известия АН СССР, серия физическая, 1985, Т.49, №8, С.1541-1544.
   
2. Зайцев А.К., Калошкин С.Д., Кандыба Г.И., Томилин И.А.// ФММ, 1986, Т.61, №5, С.1019-1022.
   
3. Канунникова О.М., Гильмутдинов Ф.З.// Неорганические материалы, 1996, Т.32, №1, С.120-123.
   
4. Еркин В.М., Кяшкин В.М., Смирнов В.В., Миркин Л.И.// Межвузовский сборник научных трудов, Саранск, Мордовский университет, 1986, С.151-154.
   

Физико-механические свойства плёнок TiN и опыт их применения в кабельном производстве


¹Панькин Н.А., ¹Смоланов Н.А., ²Бузлаев А.В.

¹Мордовский государственный университет им. Н.П.Огарёва, г. Саранск

²ОАО «Сарансккабель», г. Саранск


Покрытия нитридов переходных металлов IVB группы нашли широкое распространение для создания упрочняющих, защитных, декоративных плёнок и в качестве барьерных покрытий в микроэлектронике [1]. Эксплуатационные же характеристики плёнок зависят во многом от метода и режима их осаждения [1-3].

В настоящей работе проводилось исследование зависимости свойств и структуры ионно-плазменных плёнок TiN от размещения образцов в вакуумной камере. Кроме этого были проведены испытания на износостойкость в лабораторных и заводских условиях (ОАО «Сарансккабель»).

В исследуемых покрытиях обнаружено присутствие капельной фазы (макрочастиц). Изменение расстояния до катода от 22 до 72 см приводит к уменьшению среднего диаметра макрочастиц из от 2.5 до 0.9 мкм при одновременном увеличении их числа.

Фазовый состав плёнок состоит из δ-фазы TiN и не зависит от местоположения образца в вакуумной камере. Отмечена смена преимущественной ориентации в покрытии от (111) к (200) при удалении образца от катода – следствие изменения механизма роста. Плёнки характеризуются большими значениями микродеформаций ε~10^-3, которые обусловлены неравновесным содержанием Ti, N, различных примесей и наличием макрочастиц.

Остаточные напряжения σ_ост в тонких плёнках нитрида титана носят сжимающий характер и изменяются в интервале от 1.5 до 5.6 ГПа, основной вклад, в которые, вносят ростовые напряжения.

Зависимости размера блоков, ε и σ_ост в покрытии TiN от расстояния до катода объясняются изменениями толщины плёнки, размера частиц капельной фазы, их числа и преимущественной ориентации покрытия.

Заводские испытания покрытий на вальцах при волочении медной катанки показали увеличение износостойкости и срока службы (до появления признаков канавки) в два с лишним раза.

1. Ивановский Г.Ф., Петров В.И. Ионно-плазменная обработка материалов. – М.: Радио и связь, 1986. 232 с.
   
2. Смоланов Н.А., Панькин Н.А. // Вестник СамГТУ. Сер. физико-математические науки, 2004, № 27. с. 175-178.
   
3. Панькин Н.А., Смоланов Н.А. // Взаимодействие ионов с поверхностью: материалы XVII международной конференции (Звенигород, 25-29 августа 2005 г.) Т. 2. – М.: МАИ, 2005, с. 395-398.
   

УПАКОВОКИ ИКОСАЭДРОВ И ПЕНТАГОНДОДЕКАЭДРОВ И ИХ ПРИМЕНЕНИЕ ДЛЯ ОПИСАНИЯ КРИСТАЛЛИЧЕСКИХ СТРУКТУР


Смирнов Д.А.

Нижегородский государственный университет им. Н.И.Лобачевского, Нижний Новгород.


В настоящий момент известно достаточно большое количество веществ, состоящих из элементов с некристаллической симметрией (фуллерены, фуллериды, фуллериты, и т.д.), структур с некристаллическим упорядочением (квазикристаллы) а также модулированных и частично упорядоченных систем [1]. Основную структурную единицу бора, например, можно представить в виде икосаэдра, в вершинах которого находятся атомы. Исследование общих геометрических свойств таких структур возможно на модели упаковок платоновых тел с икосаэдрической симметрией в пространстве.

Целью настоящей работы является разработка алгоритмов построения трансляционно упорядоченных упаковок из платоновых тел с икосаэдрической симметрией в пространстве и исследование свойств таких упаковок. В работе рассматриваются упаковки икосаэдров и додекаэдров с максимальным количеством общих граней (совпадающих).

Предложена следующая классификация упаковок. Каждой упаковке ставится в соответствие матрица, характеризующая касания многогранников принадлежащих одной элементарной ячейки. Количество строк в ней равно числу многогранников приходящихся на элементарную ячейку, а количество столбцов соответствует количеству граней в многограннике. Эта матрица однозначно задает упаковку. Однако одну и туже упаковку могут задавать разные матрицы.

В работе разработан алгоритм поиска упаковок такого типа. С помощью него было проведено исследование упаковок с двумя, тремя и четырьмя многогранниками на элементарную ячейку (один многогранник на элементарную ячейку невозможен). Для пентагондодекаэдров обнаружено две трехмерных упаковки с четырьмя многогранниками на ячейку. Их группы симметри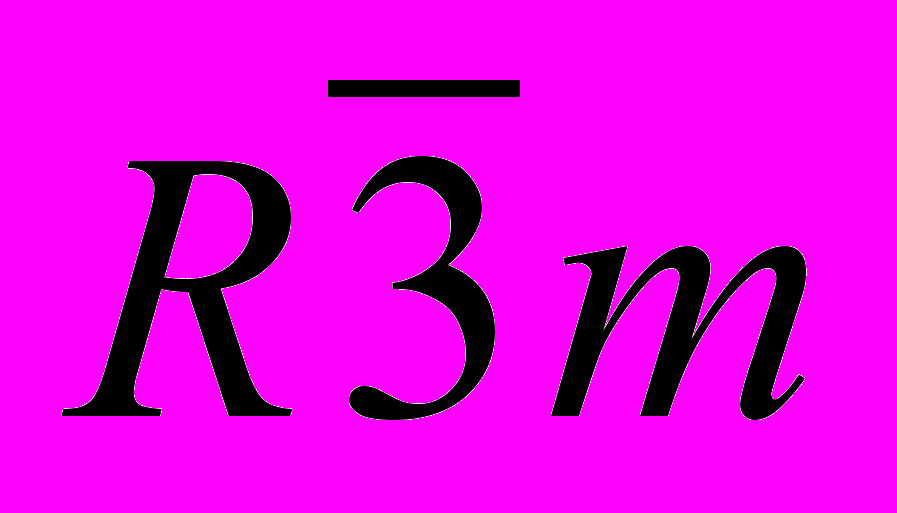и и 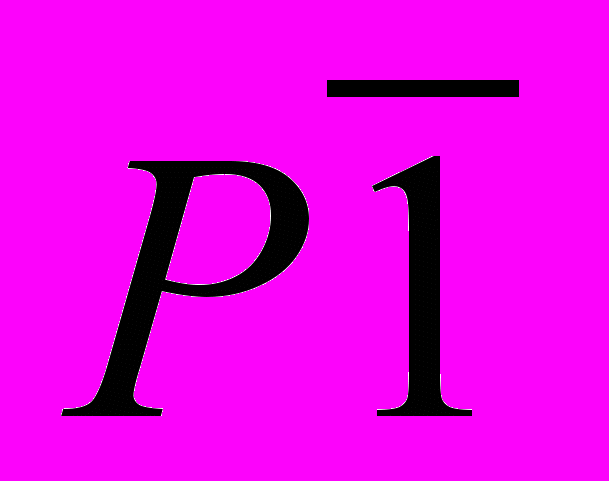. Для икосаэдров было найдено четыре с четырьмя многогранниками трехмерных упаковки. Одна упаковка здесь имеет группу симметрии 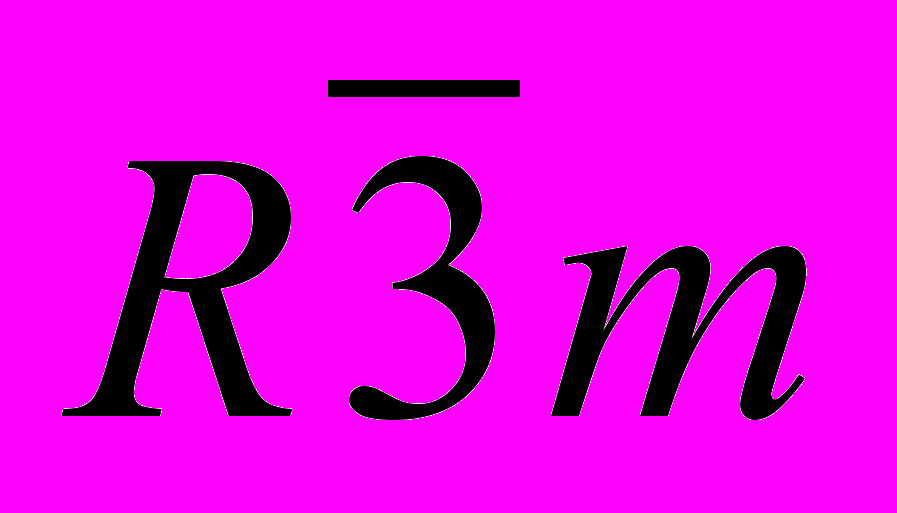, а три другие .


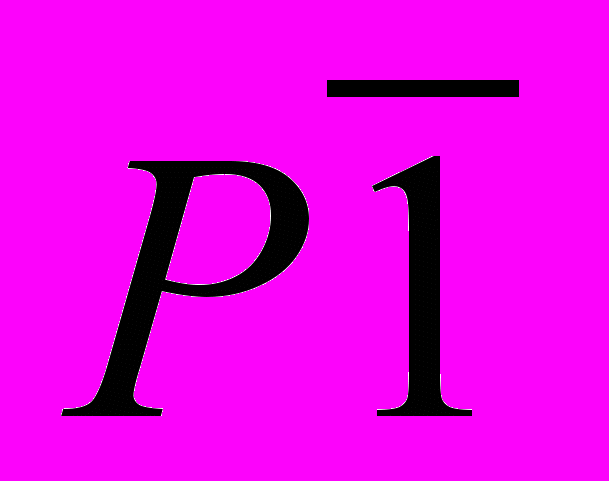1. Чупрунов Е.В., Хохлов А.Ф., Фаддеев М.А.. Кристаллография. М. 2000


НАВЕДЕНИЕ МАГНИТНОЙ АНИЗОТРОПИИ В ПЛЕНКАХ Co/Cu/Co С СИЛЬНОЙ КОСВЕННОЙ ОБМЕННОЙ СВЯЗЬЮ.


Иванов¹ Ю.П., Огнев^1.2 А.В., Чеботкевич^1,2 Л.А.

¹Дальневосточный государственный университет

²Институт автоматики и процессов управления ДВО РАН г. Владивосток


Одним из ключевых факторов, определяющих практическое использование наноструктурных многослойных пленок, является контроль магнитной структуры посредством магнитной анизотропии.

В настоящей работе исследуется поведение магнитной анизотропии и ориентации оси легкого намагничивания пленок Co/Cu/Co с антиферромагнитной (АФМ) косвенной обменной связью между слоями Со при низкотемпературном отжиге в магнитном поле.

Пленки получали магнетронным методом в атмосфере инертного газа Ar. Отжиг проводился в вакууме 10^-4 Торр при температуре 240 ^оС в течение 2 часов с шагом 30 мин. Ориентация осей легкого намагничивания (о.л.н.) определялась по полярным диаграммам относительной намагниченности M/Ms = f() (М – намагниченность в поле, Мs - намагниченность насыщения) при вращении пленки вокруг нормали к ее плоскости с шагом 10^о.

В 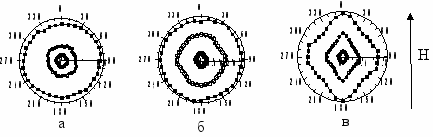полях (Н = 100 и 150 Э), полярные диаграммы осажденной пленки с АФМ связью между слоями Со (d_Cо = 2,1 нм) изотропны. Однако в поле 50 Э на диаграмме присутствует четыре максимума, что свидетельствует о наличии в пленке двухосной анизотропии, рис. 1а. Отжиг в поле Н_отж=800Э меньше поля насыщения Н_S=1450Э не изменяет отношение M/M_s в двух взаимно перпендикулярных направлениях, рис. 1б. Двухосная анизотропия


Рис.1


хорошо проявляется уже в поле 100 Э, так как в результате отжига произошло сглаживание рельефа поверхности пленки, что привело к увеличению АФМ связи между слоями Со. Отжиг пленки в поле Н_отж=3000Э, рис. 1в, показал, что отношение M/M_s в направлении поля стало больше, чем в перпендикулярном направлении, что свидетельствует о наведении о.л.н. в направлении приложенного поля. В результате отжига в поле Н_отж> H_S поле одноосной анизотропии 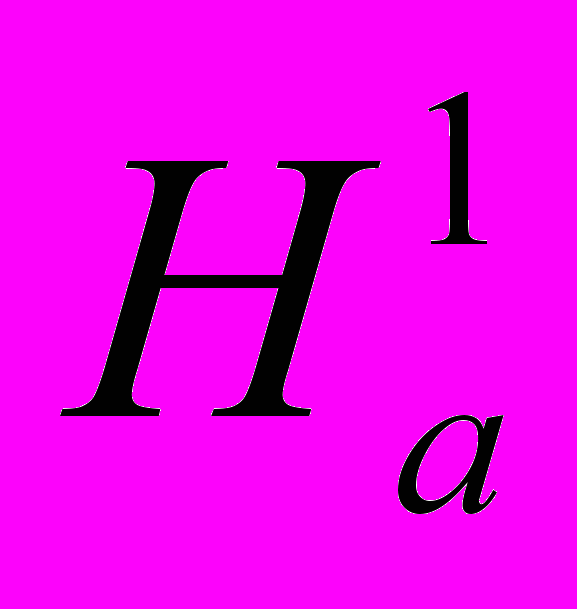увеличилось в два раза, а поле двухосной анизотропии 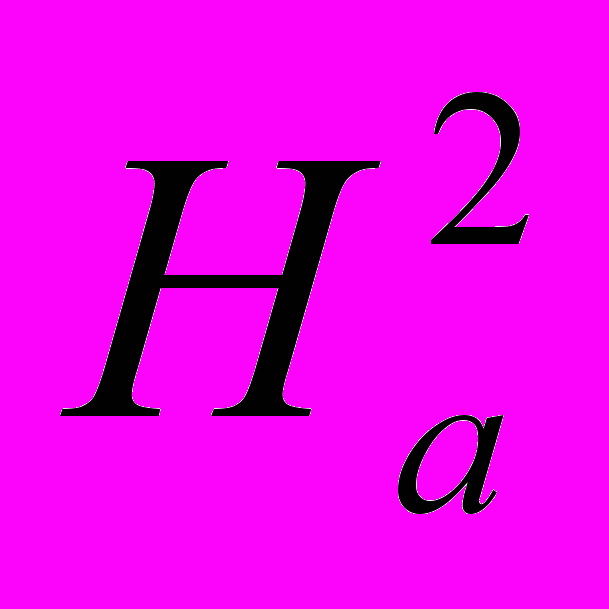уменьшилось в 1,6 раза по сравнению с 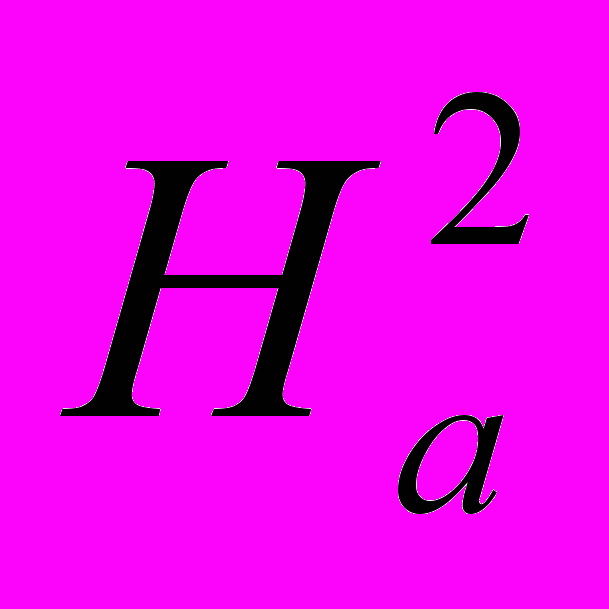пленки, отожженной без поля.


МЕТОДИКА РАСЧЕТА ОГРАНКИ КРИСТАЛЛА ПО ЕГО АТОМНОЙ СТРУКТУРЕ


С. С. Гуськов, М. А. Фаддеев

Нижегородский государственный университет имени Н. И. Лобачевского, Н. Новгород


Для определения огранки кристалла существует несколько подходов. Широко известна эмпирическая методика Бравэ [1], базирующаяся на геометрии кристаллической решетки: кристаллический образец ограничивается плоскостями с максимальной ретикулярной плотностью R_hkl. Последняя определяется как число узлов кристаллической решетки, приходящееся на единицу площади грани (hkl). В этом случае кристаллы разных структур с одинаковым типом решетки Бравэ должны иметь одинаковую форму, что противоречит экспериментальным фактам.

Нами предложена методика расчета вероятной огранки кристалла, в которой используется более детальная характеристика грани кристалла, учитывающая его атомную структуру. Идея заключается в том, что для кристаллических структур с ненаправленными химическими связями грани с большей плотностью упаковки атомов обладают меньшей удельной поверхностной энергией. Следовательно, появление плотноупакованных граней в процессе роста наиболее вероятно. Для оценки плотности упаковки атомов данной грани используется коэффициент заполнения Q_hkl [2].

В ходе работы для 70-ти кристаллических структур проведены расчеты огранки и сравнение результатов расчета с наблюдавшейся [3] огранкой природных и синтетических кристаллов. Исследовались кристаллы, отличающиеся симметрией, типом связи и сложностью формульных единиц. Проведенные вычисления показывают, что предлагаемая методика (Q-метод) обеспечивает значительно более высокую степень совпадения экспериментальных и расчетных данных по сравнению с методикой Бравэ (R-методом). Нами установлено, что R-метод показывает примерно одинаковые результаты для веществ с любым типом связи. Q-метод обеспечивает надежные результаты для кристаллов с ненаправленными химическими связями.

1. Современная кристаллография. Т. 3. / Ред. Чернов А. А. и др. – М.: Наука, 1980, 360 с.
   
2. Гуськов С. С., Фаддеев М. А. О связи равновесной формы и структуры кристалла // Известия вузов. Поволжский регион. Естественные науки. № 5 (14) 2004 – Пенза, ПГУ, 2004, с 130 – 139.
   
3. Бетехтин А. Г. Курс минералогии. М.: Государственное научно-техническое издательство литературы по геологии, 1956. 559 с.