Geum.ru

Методические указания для студентов 1 курса факультета математики, механики и компьютерных наук

Вид материалаМетодические указания

Содержание


2.3Сравнение списков и массивов
2.4Двусвязные линейные списки
Подобный материал:
1   2   3   4   5   6   7   8

2.3Сравнение списков и массивов


Сравним производительность различных операций для списков с массивами. Основное преимущество массивов – возможность обратиться к произвольному элементу по его индексу. Для списка подобная операция потребует просмотра всех предшествующих элементов. Однако добавление в начало и середину массива, а также удаление из начала и середины требует сдвига всех элементов массива, расположенных после вставляемого (удаляемого). Для списка же производительность операций добавления и удаления не зависит ни от длины списка, ни от места вставки. Сортировка вставками в списке имеет такую же производительность, что и простые виды сортировок для массивов (например, пузырьковая сортировка или сортировка выбором).

Таким образом, если в задаче требуется структура с частыми операциями вставки и удаления в середине, следует предпочесть список, если же важнее быстрый доступ по индексу – следует выбрать массив. При выборе структуры следует также учитывать, что для организации односвязного списка на каждый элемент требуется одно поле связи, занимающее 4 байта (для массива подобные накладные расходы отсутствуют). С другой стороны, список может динамически расширяться во время работы программы, в то время как под массив отводится фиксированное количество элементов, которое необходимо указать на этапе компиляции.

2.4Двусвязные линейные списки


Двусвязный линейный список состоит из элементов, каждый из которых хранит адреса следующего и предыдущего. Для удобства работы со списком поддерживаются указатели first и last на первый и последний элемент соответственно:



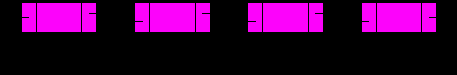
В структуру Node добавляется указатель prev на предыдующий элемент списка:

type
  PNode=Node;
  Node=record
    data: integer;
    prev,next: PNode;
  end;

Вспомогательная функция NewNode при этом изменяется очевидным образом:

function NewNode(data: integer; prev, next: PNode): PNode;
begin
  New(Result);
  Result.data:=data;
  Result.next:=next;
  Result.prev:=prev;
end;

Рассмотрим основные операции с двусвязным списком, реализация которых отличается от односвязного. После выполнения каждой операции first и last должны по-прежнему оставаться указателями на начало и конец списка, а если список пуст, то получать нулевое значение.

1. Инициализация.

При инициализации список пуст:

first:=nil;
last:=nil;

2. Добавление элемента со значением x в начало.

Осуществляется аналогично добавлению в односвязный список. Если список был пустым, то last также должен указывать на добавленный элемент.

first:=NewNode(x,nil,first);

if last=nil then last:=first;

3. Добавление элемента со значением x в конец.

Симметрично добавлению в начало:

last:=NewNode(x,last,nil);

if first=nil then first:=last;

4. Вставка элемента со значением x перед текущим.

Пусть указатель p хранит адрес текущего элемента.



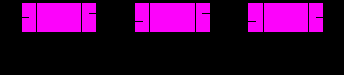
Создадим новый элемент, поле next которого указывает на текущий, поле prev – на предыдущий. При этом поле prev текущего элемента и поле next предыдущего должны указывать на вставляемый. Если же предыдущего элемента нет, то осуществляется вставка в начало, и требуется скорректировать указатель на первый элемент:

t:=NewNode(x,p.prev,p);
p.prev:=t;
if p.prev<>nil then
  p.prev.next:=t
else first:=t;



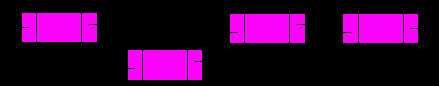
Аналогично производится вставка после текущего элемента.


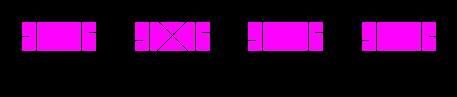
5. Удаление текущего элемента.

Пусть указатель p хранит адрес текущего элемента.

 

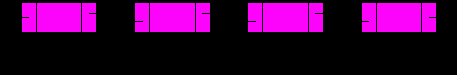
Перед освобождением памяти под текущий элемент следует перенаправить указатель next у предыдущего элемента на следующий, а у следующего указатель prev –на предыдущий. Если же следующего элемента нет, то необходимо удалить последний элемент и скорректировать переменную last. Аналогично если предыдущего элемента нет, то удаляется первый, и необходимо скорректировать first.

if p.prev<>nil then
   p.prev.next:=p.next
else first:=p.next;
if p.next<>nil then
  p.next.prev:=p.prev
else last:=p.prev;
Dispose(p);



Заметим, что если удаляется единственный элемент, то указатели first и last получают значение nil, т.е. список становится пустым.

В заключение приведем пример, иллюстрирующий высокую эффективность списков в некоторых задачах.

Пример. Объединение списков.

Имеется два списка, заданные указателями на начало и конец.





Требуется добавить содержимое второго списка в конец первого, очистив при этом второй список.



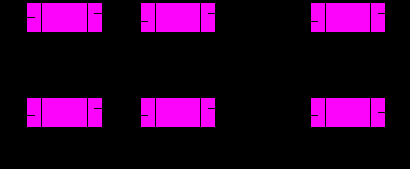
Для решения указанной задачи достаточно выполнить всего пять операторов присваивания:

last1.next:=first2;
first2.prev:=last1;

last1:=last2;

first2:=nil;

last2:=nil;

Заметим, что решение аналогичной задачи для массива требует использования цикла с числом итераций, равным размеру добавляемого массива.