Geum.ru

Методические указания для студентов 1 курса факультета математики, механики и компьютерных наук

Вид материалаМетодические указания

Содержание


2Динамические структуры данных 2.1Общие сведения
2.2Односвязные линейные списки
Подобный материал:
1   2   3   4   5   6   7   8

2Динамические структуры данных

2.1Общие сведения


Данные могут объединяться в структуры. Примерами структур являются массивы и записи. Но эти структуры во время выполнения программы имеют постоянный размер, то есть являются статическими. Если же размер структуры меняется в процессе работы программы, то такая структура данных называется динамической. Один из способов создать динамическую структуру данных – составить ее из однотипных элементов-записей, каждая из которых, помимо полей данных, имеет поля связи, указывающие на другие элементы. В простейшем случае имеется одно поле связи, которое хранит адрес следующего элемента или nil, если следующий элемент отсутствует.

Попытаемся описать тип элемента такой структуры:

type
  Node=record
    data: integer;
    next: Node; // ошибка!
  end;

Данное определение в Delphi Pascal ошибочно. Проблема состоит в том, что тип Node частично определяется через самого себя (рекурсия по данным) и к моменту определения поля next: Node тип Node еще не определен полностью. Проблема решается следующим образом: определяется тип PNode=TNode, после чего определяется тип Node, в котором поле next имеет тип PNode:

type
  PNode=Node;
  Node=record
    data: integer;
    next: PNode;
  end;

Здесь действует следующее правило Паскаля: в секции type можно описывать указатель на еще не определенный тип при условии, что данный тип будет определен позднее в этой же секции.

Как уже было сказано, элементы типа Node можно завязать в цепочку. Для этого полю next каждого элемента необходимо присвоить указатель на следующий, поле next последнего элемента следует присвоить значение nil (конец цепочки):



Структура, изображённая на рисунке, называется линейным односвязным списком, а ее элементы часто называются узлами списка. Доступ к элементам такого списка – последовательный: нельзя обратиться к какому-то элементу, не перебрав предыдущие.

Если поле next последнего элемента списка указывает на первый элемент, то такая структура называется кольцевым односвязным списком:



В отличие от линейного списка кольцевой не имеет явного начала и конца.

Если у каждого элемента, помимо указателя на следующий, имеется указатель на предыдущий элемент prev: PNode, то такая структура называется линейным двусвязным списком:



Двусвязные списки используются, если требуется двигаться по списку не только в прямом, но и в обратном направлении.

Если в двусвязном списке первый и последний элементы указывают друг на друга, то он называется кольцевым двусвязным списком:


2.2Односвязные линейные списки


Для удобства определим вспомогательную функцию NewNode, создающую в динамической памяти узел линейного односвязного списка, заполняющую его поля значениями data и next и возвращающую указатель на него:

function NewNode(data: integer; next: PNode): PNode;
begin
  New(Result);
  Result.data:=data;
  Result.next:=next;
end;

Основными действиями с линейным односвязным списком являются вставка, удаление, поиск элементов, проход по списку и сортировка. Будем считать, что во всех приводимых операциях указатель p типа PNode хранит адрес текущего элемента списка.

Если поле данных data элемента списка содержит значение x, то для простоты будем говорить, что элемент или узел имеет значение x.

1. Вставка элемента со значением x в начало списка.

Пусть первый элемент является текущим (указатель p хранит адрес первого элемента):



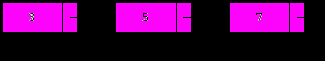
Создадим новый элемент со значением x, поле next которого указывает на первый элемент, после чего сделаем этот элемент первым, присвоив его адрес указателю p:

p:=NewNode(x,p);



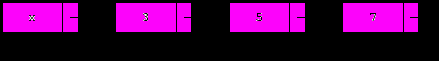
Отметим, что данная операция производит добавление также и в пустой список (p=nil). При многократном ее выполнении происходит заполнение списка, причем, элементы в списке будут располагаться в порядке, обратном порядку их включения.


2. Удаление элемента из начала непустого списка.



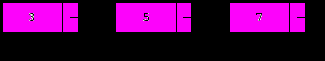
Запомним адрес первого элемента в переменной t, после чего переместим указатель на первый элемент вперед и освободим элемент, контролируемый указателем t:

t:=p;
p:=t.next;
Dispose(t);



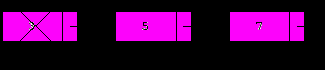
3. Вставка элемента со значением x после текущего.



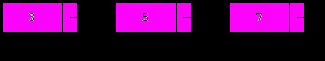
Данная операция аналогична вставке в начало, но вместо p используется p.next:

p.next:=NewNode(x,p.next);




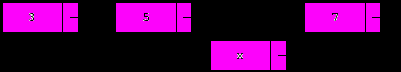
4. Удаление элемента, следующего за текущим.



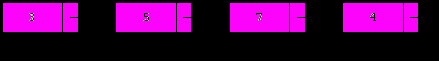
Данная операция аналогична удалению из начала, но вместо p используется p.next; если p.next=nil, то никаких действий не производится:

t:=p.next;
if t<>nil then
begin
  p.next:=t.next;
  Dispose(t);
end;



5. Вставка элемента со значением x перед текущим.



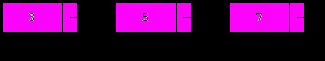
Вставим после текущего элемента его копию, затем присвоим полю данных текущего элемента значение x и передвинем текущий элемент вперед:

p.next:=NewNode(p.data,p.next);
p.data:=x;
p:=p.next;



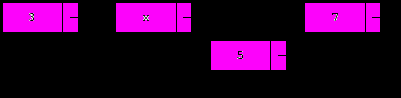
6. Удаление текущего элемента.



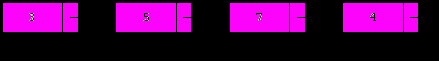
Для быстрого выполнения этого действия требуется, чтобы существовал элемент, следующий за текущим. Скопируем поле данных и поле next из следующего элемента в текущий, после чего освободим следующий:

t:=p.next;
p.data:=t.data;
p.next:=t.next;
Dispose(t);



7. Проход по списку.



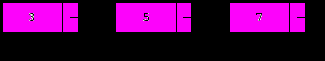
Пусть над всеми элементами списка необходимо выполнить некоторую операцию Oper, заданную процедурой с одним ссылочным параметром, например:

procedure Oper(var i: integer);
begin
  i:=i*2;
end;

Установим указатель на его первый элемент и, пока значение указателя не равно nil, будем выполнять операцию Oper и передвигаться на следующий элемент:

while p<>nil do
begin
  Oper(p.data);
  p:=p.next;
end;

Очевидно, во время прохода по списку можно не только менять элементы, но и выводить их или производить вычисления: например, подсчитывать сумму или количество элементов, удовлетворяющих некоторому условию.

8. Поиск элемента со значением x.



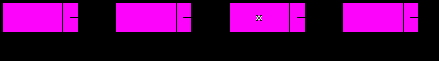
Проход по списку здесь надо совершать либо до конца списка, либо до момента, когда текущий элемент будет иметь значение x. Если после цикла текущий элемент не нулевой, то он содержит первое найденное значение x.

while (p<>nil) and (p.data<>x) do

  p:=p.next;

found:=p<>nil;

Следует обратить внимание на то, что порядок следования операндов в операции and важен и для корректной работы последнего алгоритма в Delphi должен быть установлен ключ компиляции сокращенного вычисления логических выражений {$B-}.

9. Разрушение списка.



При разрушении мы удаляем элементы из начала списка до тех пор, пока список не станет пустым:

while p<>nil do

begin

  t:=p;

  p:=p.next;

  Dispose(t);

end;

10. Вставка элемента в упорядоченный список с сохранением упорядоченности.

Пусть список не пуст и его элементы упорядочены по возрастанию. Чтобы вставить элемент со значением x с сохранением упорядоченности, найдем первый элемент с большим значением и произведем вставку перед ним. Для вставки перед элементом будем «заглядывать» на один элемент вперед, используя вместо переменной p выражение p.next. Оформим данную операцию в виде процедуры:


procedure SortedListAdd(p: PNode; x: integer);

begin

while (p<>nil) and (p.next.data<=x) do
  p:=p.next;
p.next:=NewNode(x,p.next);

end;



Отметим, что наш алгоритм осуществляет добавление после элемента, на который указывает p, поэтому он не может добавить в начало списка. Для решения указанной проблемы поместим в начало списка барьерный элемент, поле данных которого содержит самое маленькое число (-MaxInt). Список при этом сохранит свою упорядоченность, и теперь любой элемент будет добавляться после барьерного. Например, вот как выглядит заполнение упорядоченного списка n случайными числами с последующим его выводом:

readln(n);

p:=NewNode(-MaxInt,nil); // барьер

for i:=1 to n do

SortedListAdd(p,Random(1000));

t:=p;

while t<>nil do

begin

write(t.data);

t:=t.next;

end;

По существу, приведенный код реализует алгоритм сортировки вставками. Поскольку при вставке одного элемента в список длины n может потребоваться n операций (в случае прохода по всему списку), то для вставки n элементов требуемое количество операций пропорционально .
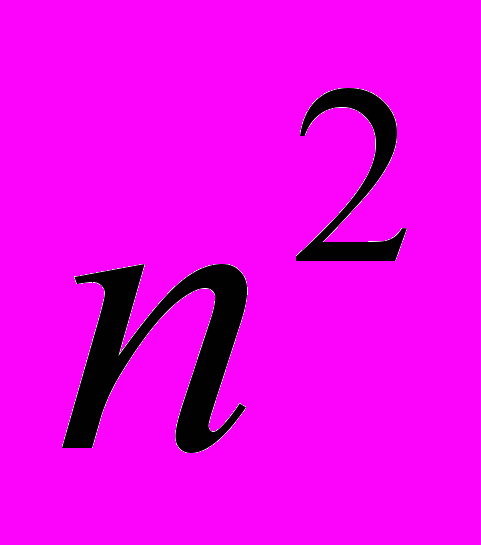