Програма фахових вступних випробувань для прийому на навчання за освітньо-професійною програмою підготовки окр «спеціаліст», «магістр»

Вид материала

Документы

Содержание III.«Експертні системи в медицині»

Подобный материал:

• Програма фахових вступних випробувань для прийому на навчання за освітньо-професійною, 209.47kb.
• Програма фахових випробувань для прийому на навчання за освітньо-кваліфікаційним рівнем, 390.11kb.
• Програма фахових випробувань для прийому на навчання за освітньо-кваліфікаційним рівнем, 520.72kb.
• Програма фахових вступних випробувань для бакалаврів, які бажають продовжувати навчання, 138.89kb.
• Програма вступних випробувань з географії для вступників на навчання за освітньо-професійною, 749.45kb.
• Програма вступних випробувань з біології для вступників на навчання за освітньо-професійною, 471.04kb.
• Програма фахового вступного випробування на навчання за освітньо-професійними програмами, 442.16kb.
• Програма фахового випробування для прийому на навчання за освітньо-кваліфікаційними, 204.17kb.
• Програма вступних випробувань з хімії для вступників на навчання за освітньо-професійною, 336.23kb.
• Програма фахового вступного випробування на навчання за освітньо-професійною програмою, 416.72kb.

^

III.«Експертні системи в медицині»

Контрольні запитання

1. Нечіткі множини та способи їх зображення. Основні характеристики нечітких множин. Основні операції, які виконуються над нечіткими множинами.
   
2. Нечіткі відношення та способи їх зображення. Основні характеристики нечітких відношень. Основні операції, які виконуються над нечіткими відношеннями.
   
3. Основні властивості бінарних нечітких відношень, визначених на одному універсумі.
   
4. Нечітке відношення еквівалентності, приклади.
   
5. Нечітка та лінгвістична змінні.
   
6. Нечіткі величини, числа й інтервали. Приклади арифметичних операцій над ними.
   

Практичні завдання

1. Нехай задана множина Х={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Розглянемо відношення R(Х, X)={| x,уХ: “x і у мають один і той же самий залишок при діленні на 3”}. Назвіть його основні властивості, обґрунтуйте їх.

2. Описати процедуру визначення нечіткого відношенння С як результату (max-min) - композиції двох бінарних нечітких відношень С=АB, де А – бінарне нечітке відношення, побудоване на двох базисних множинах: Х={х₁, х₂} і Y={y₁, y₂}, а В - на двох базисних множинах: Y і Z={z₁, z₂, z₃}. Матриці цих нечітких відношень мають наступний вигляд:

;

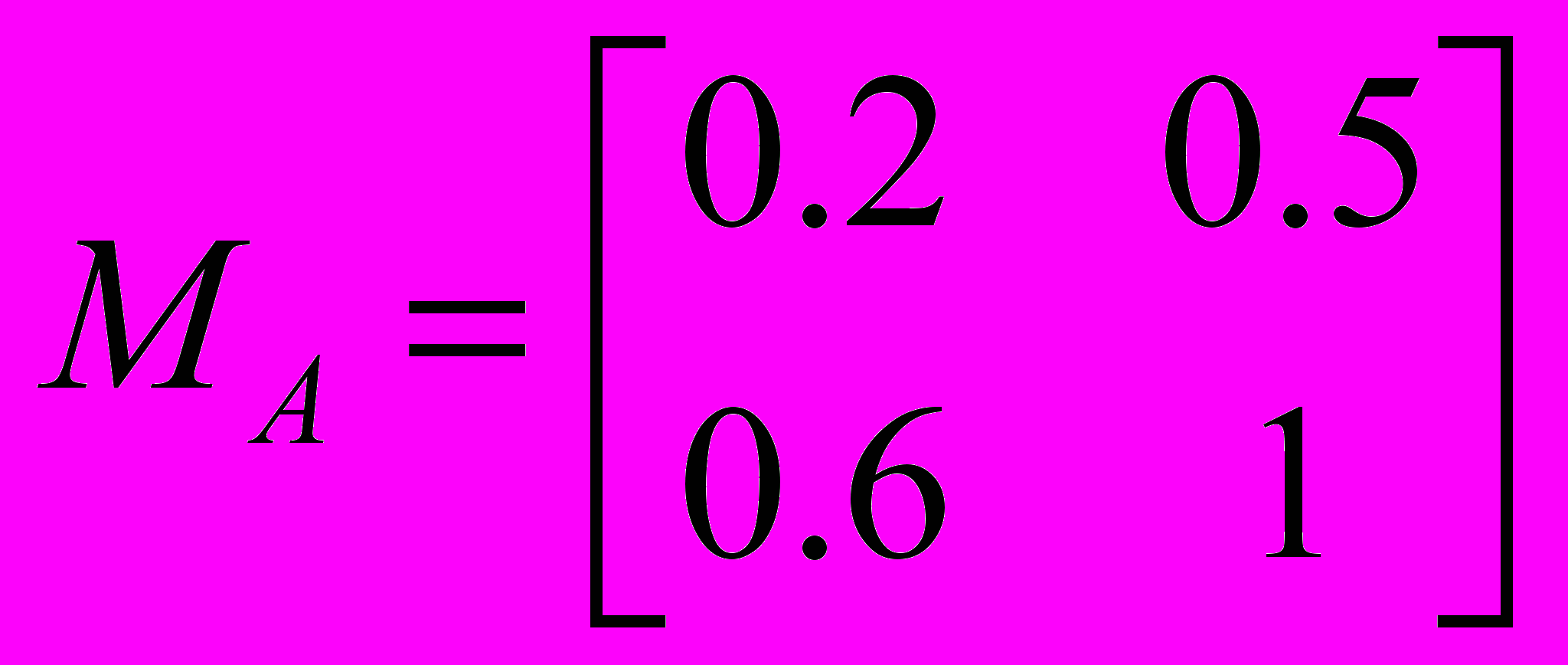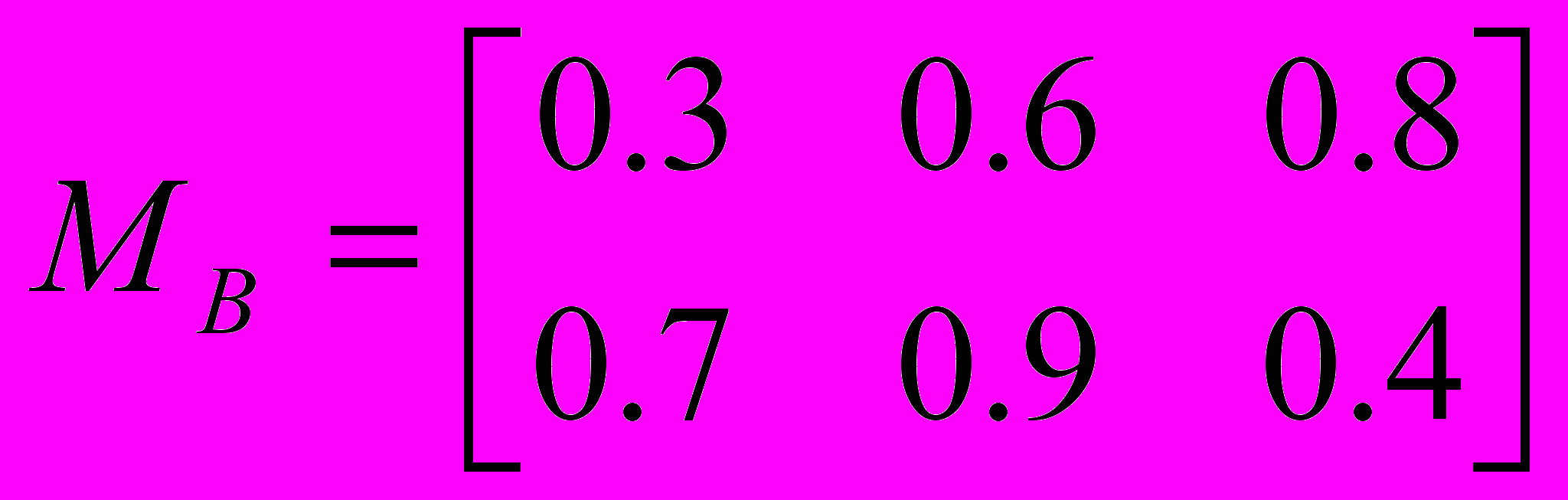
3. Нехай задана множина Х={Іван, Петро, Миколай, Тетяна}. Розглянемо відношення R(X,X)=«бути родичем». Назвіть його основні властивості, обґрунтуйте їх.

4. Описати процедуру визначення нечіткого відношенння С як результату (max-prod) - композиції двох бінарних нечітких відношень С=АB, де А – бінарне нечітке відношення, побудоване на двох базисних множинах: Х={х₁, х₂} і Y={y₁, y₂}, а В - на двох базисних множинах: Y і Z={z₁, z₂, z₃}. Матриці цих нечітких відношень мають наступний вигляд:

;

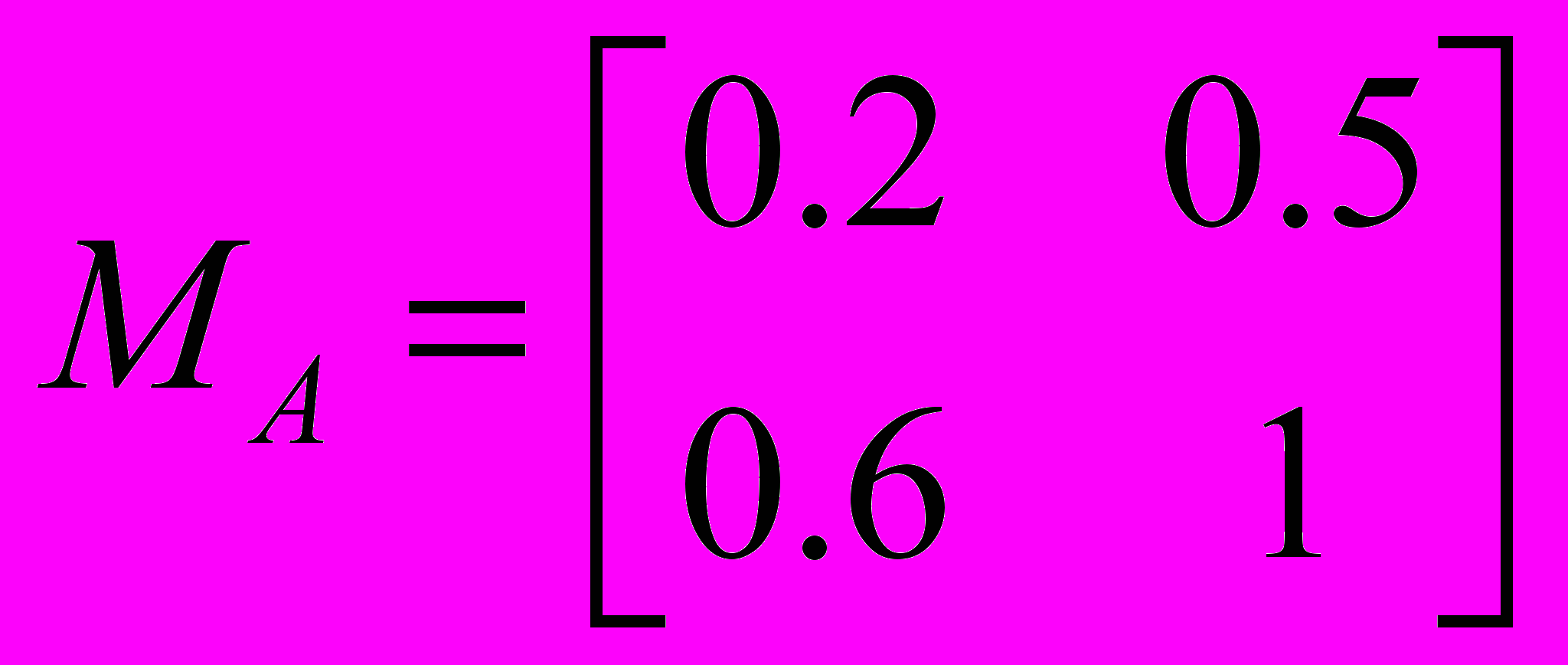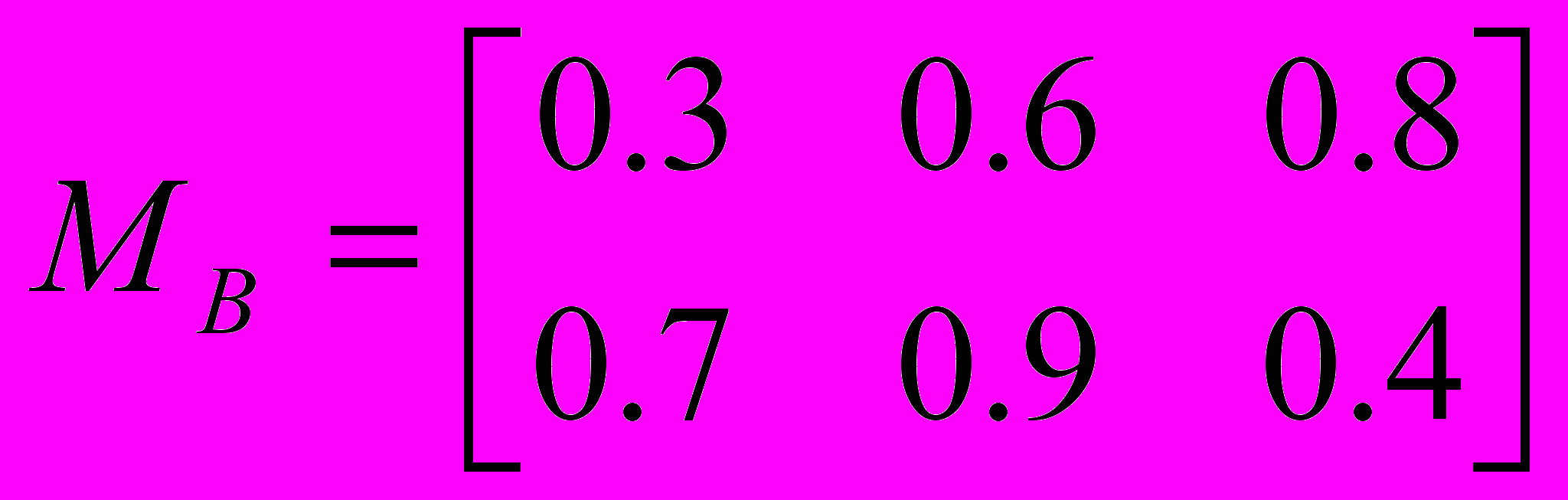
5. Нехай задана множина Х={Іван, Петро, Миколай, Тетяна}. Розглянемо відношення R(X,X)=«мати однаковий зріст». Назвіть його основні властивості, обґрунтуйте їх.

6. Описати процедуру визначення нечіткого відношенння С як результату (max-max) - композиції двох бінарних нечітких відношень С=АB, де А – бінарне нечітке відношення, побудоване на двох базисних множинах: Х={х₁, х₂} і Y={y₁, y₂}, а В - на двох базисних множинах: Y і Z={z₁, z₂, z₃}. Матриці цих нечітких відношень мають наступний вигляд:

;

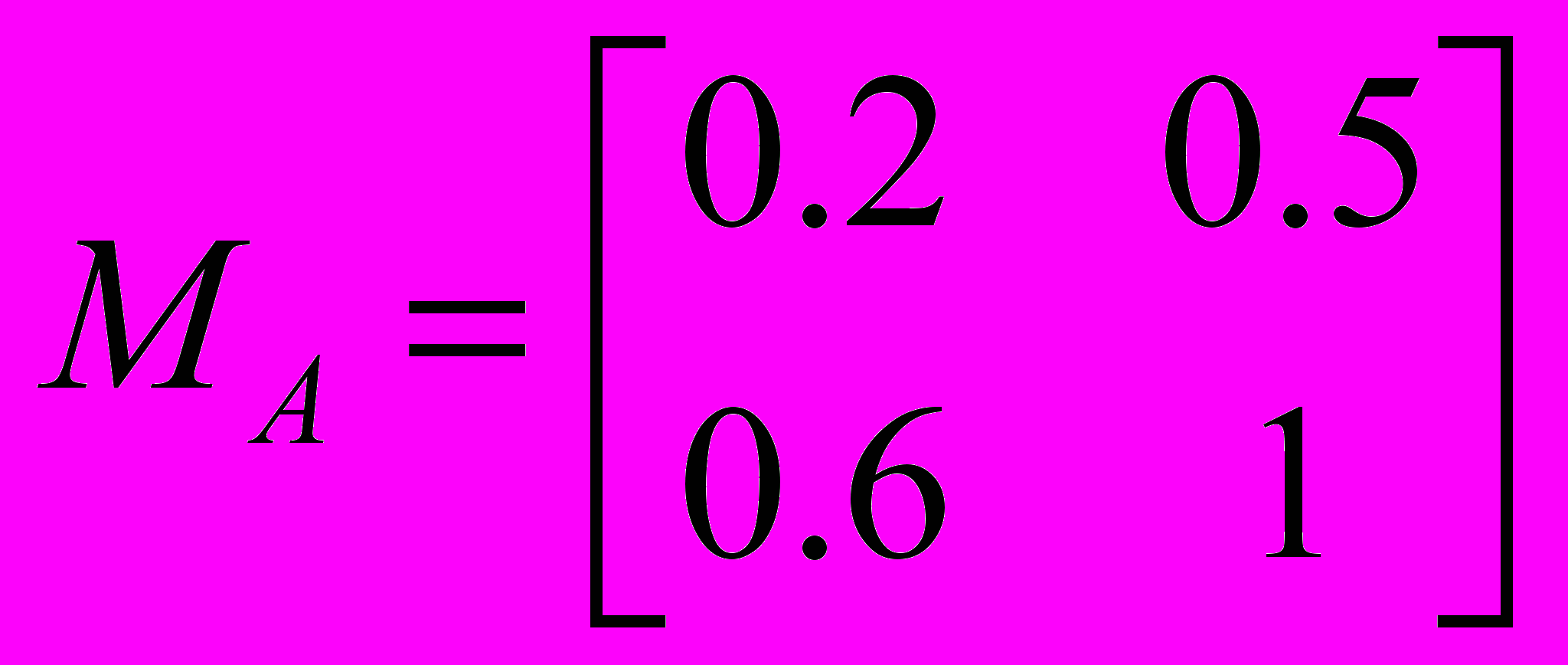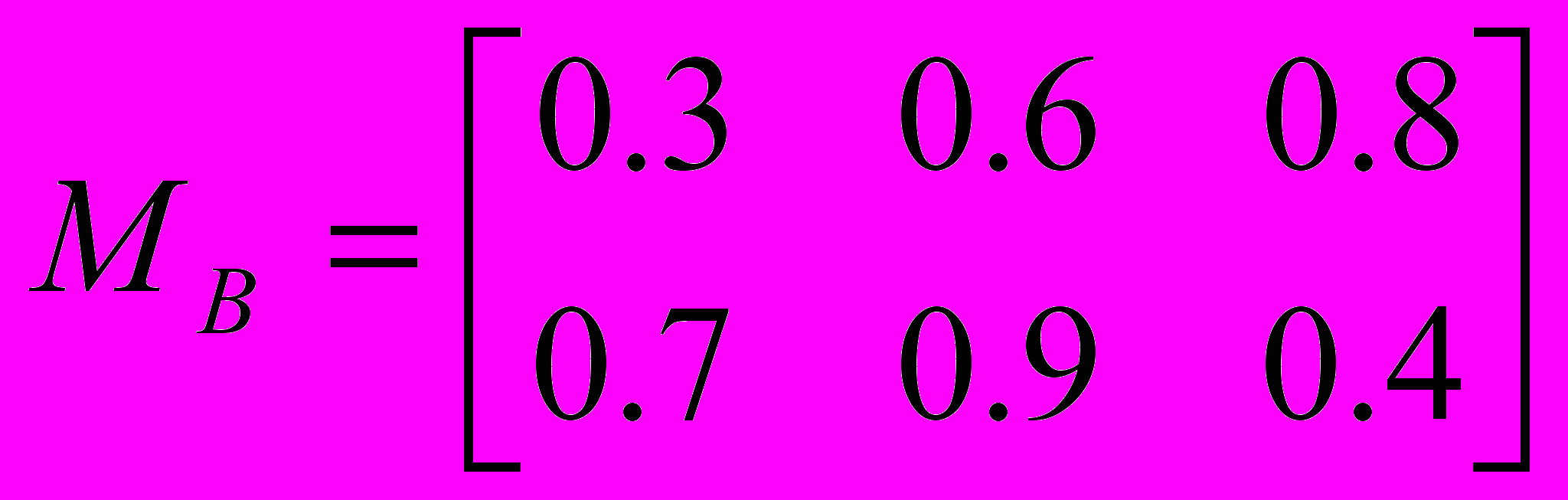
7. Нехай задана множина Х={гумка, олівець, зошит}. Розглянемо відношення R(X,X)=«мати однакову ціну». Назвіть його основні властивості, обґрунтуйте їх.

8. Описати процедуру визначення нечіткого відношенння С як результату (min-max) - композиції двох бінарних нечітких відношень С=АB, де А – бінарне нечітке відношення, побудоване на двох базисних множинах: Х={х₁, х₂} і Y={y₁, y₂}, а В - на двох базисних множинах: Y і Z={z₁, z₂, z₃}. Матриці цих нечітких відношень мають наступний вигляд:

;

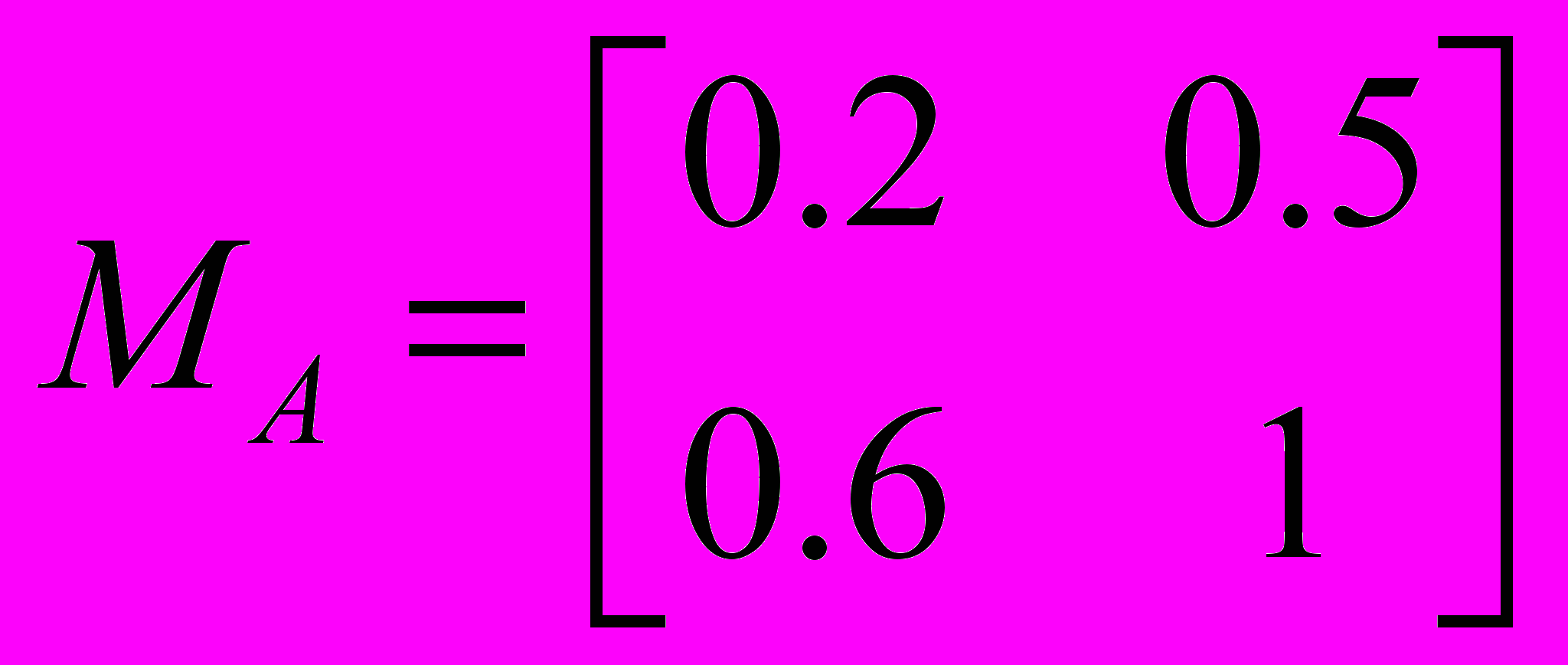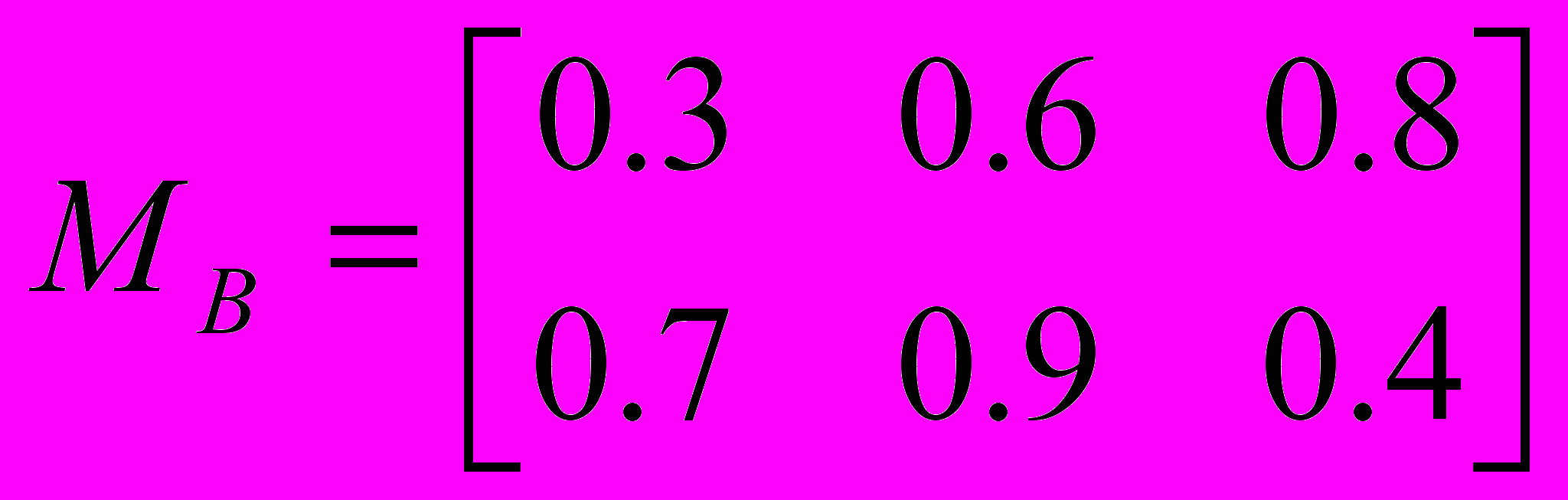
9. Нехай задана множина Х у вигляді скінченої множина різних предметів. Розглянемо відношення R(Х,X)={| x, уХ: “y набагато більше за x”}. Назвіть його основні властивості, обґрунтуйте їх.

10. Описати процедуру визначення нечіткого відношенння С як результату (min-min)-композиції двох бінарних нечітких відношень С=АB, де А – бінарне нечітке відношення, побудоване на двох базисних множинах: Х={х₁, х₂} і Y={y₁, y₂}, а В - на двох базисних множинах: Y і Z={z₁, z₂, z₃}. Матриці цих нечітких відношень мають наступний вигляд:

;

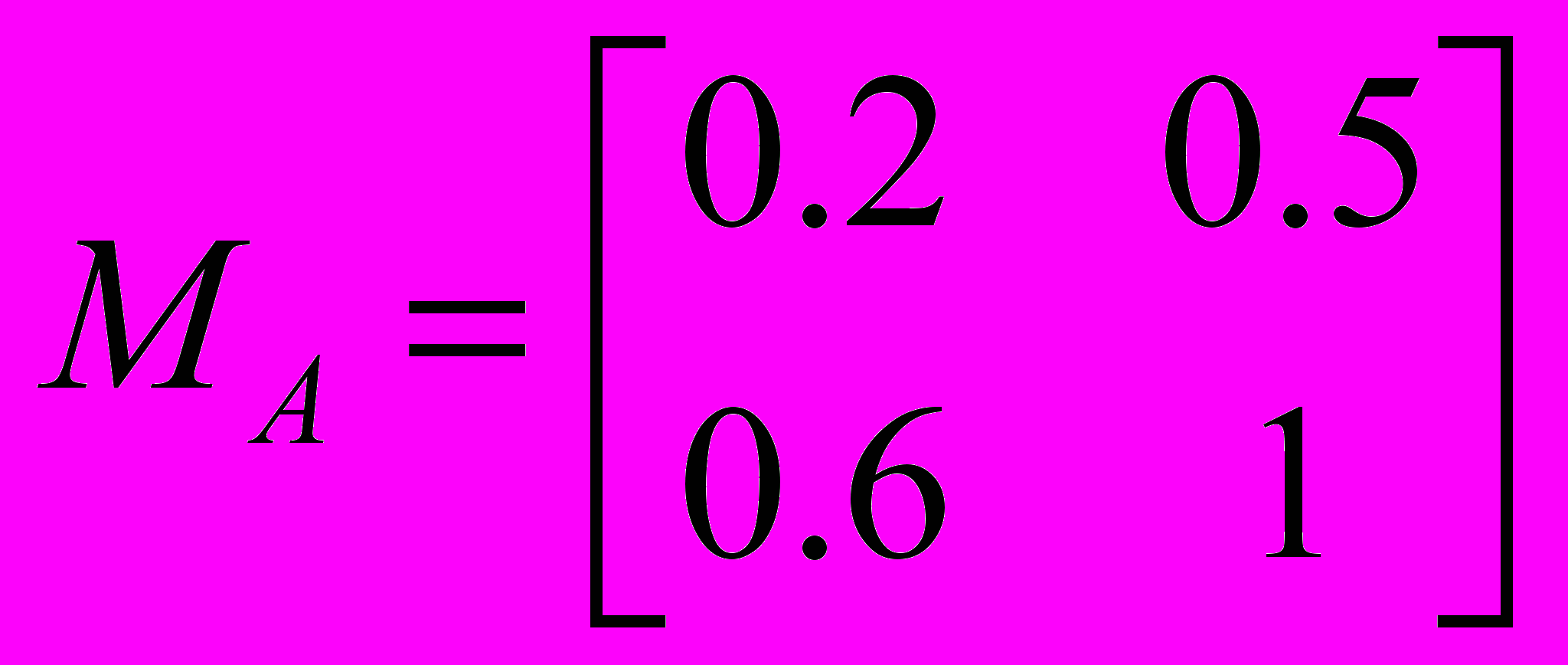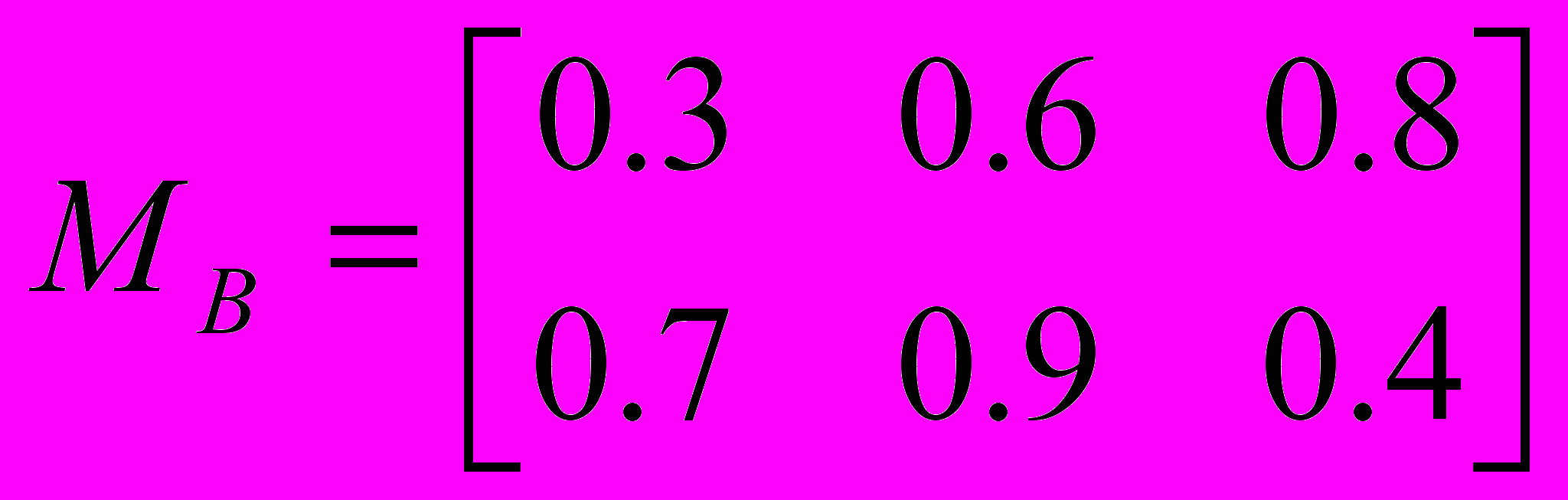
11. Нехай задано нечітке число – «нечітка одиниця», яка описується нечіткою множиною 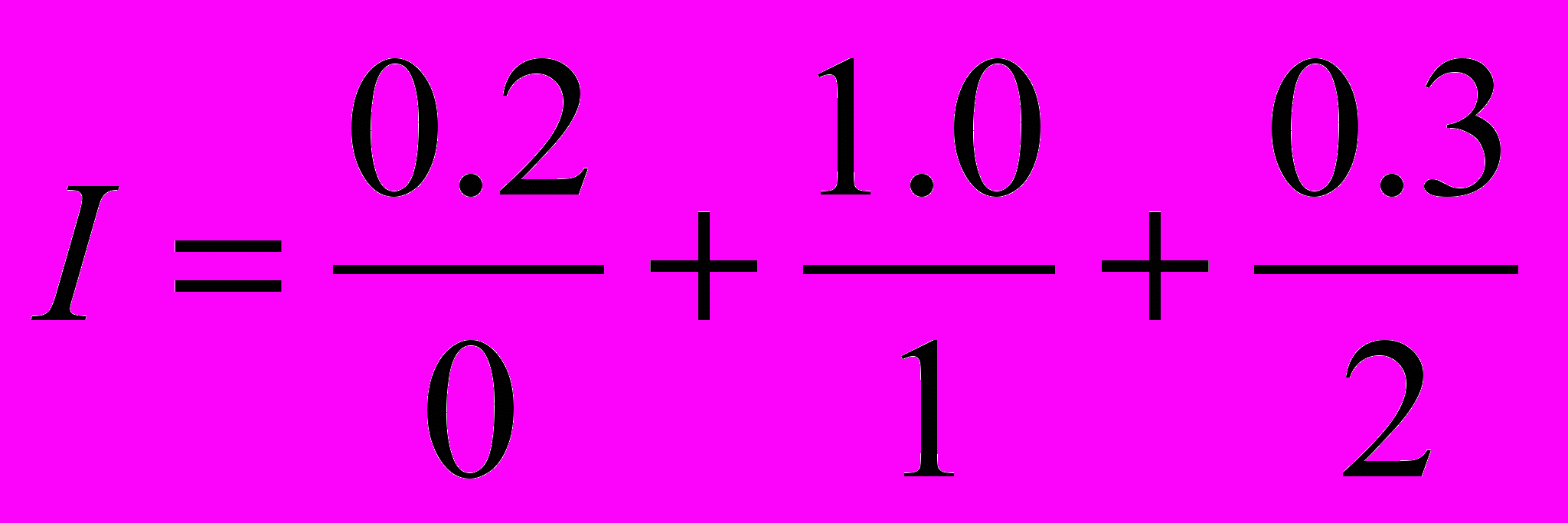. Описати процедуру визначення нечіткого числа «нечіткий нуль», який описується нечіткою множиною В, враховуючи той факт, що B=(I - I) .

12. Нехай задано нечітке число – «нечітка одиниця», яка описується нечіткою множиною 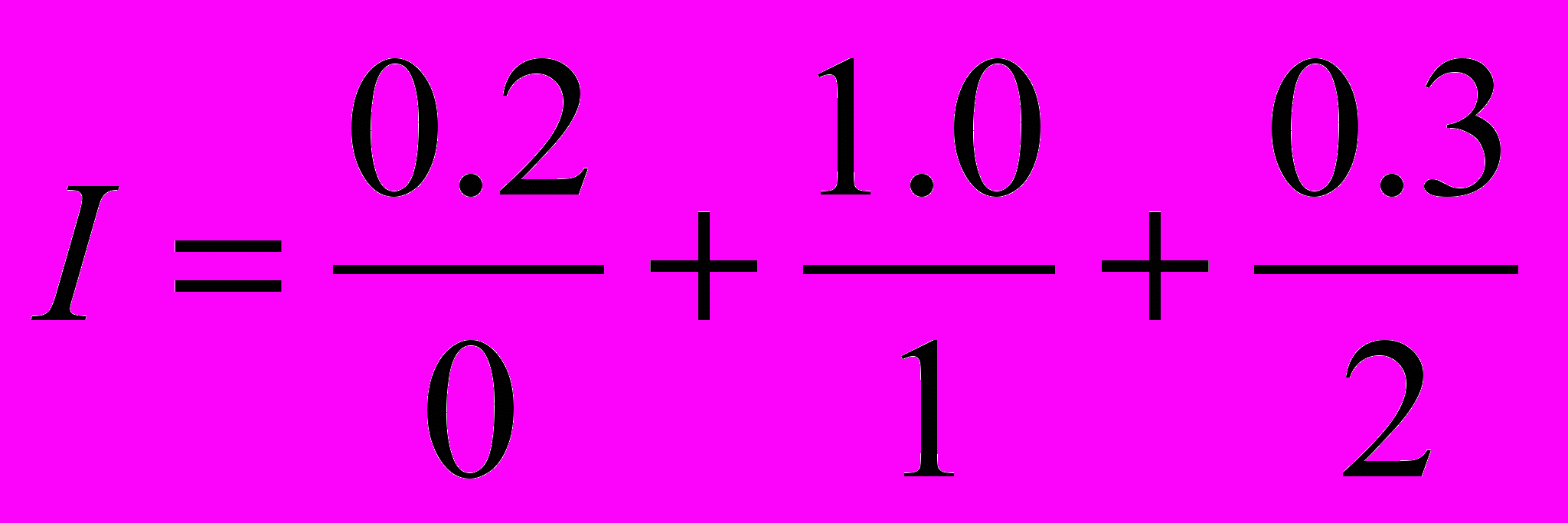. Описати процедуру визначення нечіткого числа «нечітка двійка», яка описується нечіткою множиною В, враховуючи той факт, що B=(I + I) .

13. Нехай задано нечітке число – «нечітка двійка», яка описується нечіткою множиною 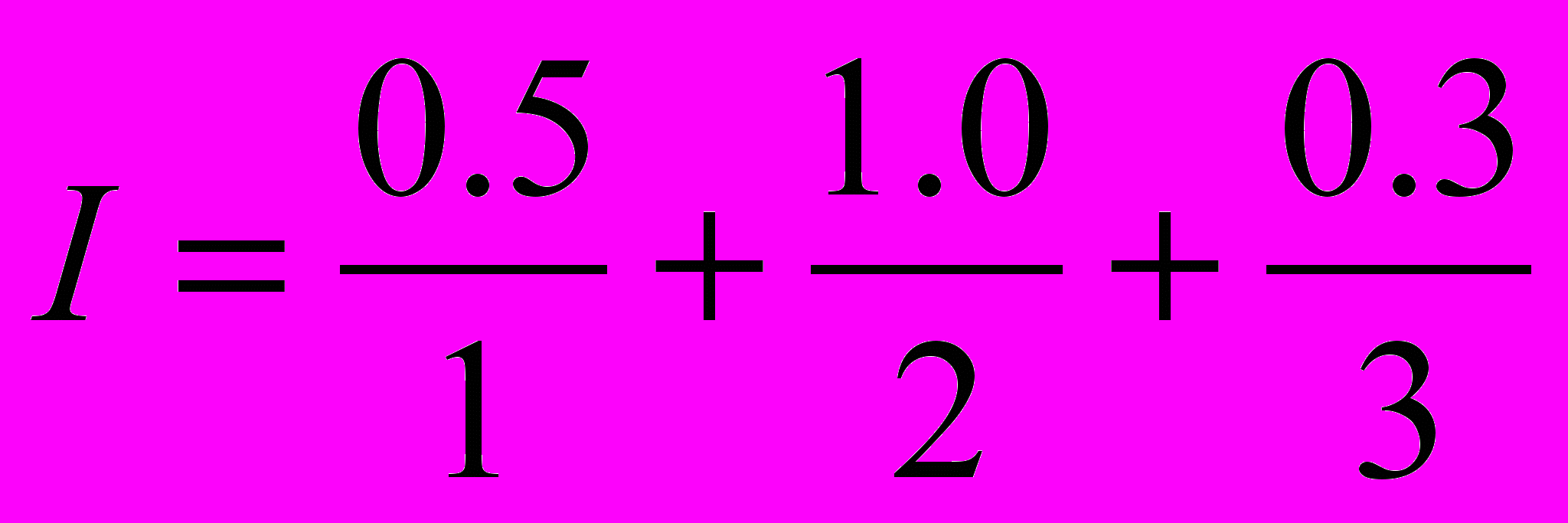. Описати процедуру визначення нечіткого числа «нечітка четвірка», яка описується нечіткою множиною В, враховуючи той факт, що B=(I * I) .

14. Визначте нечітку множину - «понижена температура тіла», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

15. Визначте нечітку множину - «нормальна температура тіла», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

16. Визначте нечітку множину - «підвищена температура тіла», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

17. Визначте нечітку множину - «висока температура тіла», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

18. Визначте нечітку множину - «людина похилого віку», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

19. Визначте нечітку множину - «людина середнього віку», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

20. Визначте нечітку множину - «молода за віком людина», побудуйте графік її функції належності, опишіть математично наведену функцію належності.

21. Наведіть приклади (не менше трьох) нечітких множин, які мають графік функції належності трикутного вигляду, визначте ці множини і їх функції належності математично.

22. Наведіть приклади (не менше трьох) нечітких множин, які мають графік функції належності у вигляді трапеції, визначте ці множини і їх функції належності математично.

23. Наведіть приклади (не менше трьох) нечітких множин, які мають S-подібний графік функції належності, визначте ці множини і їх функції належності математично.

24. Маємо два нечітких числа: перше - «нечітка трійка», яка описується нечіткою множиною 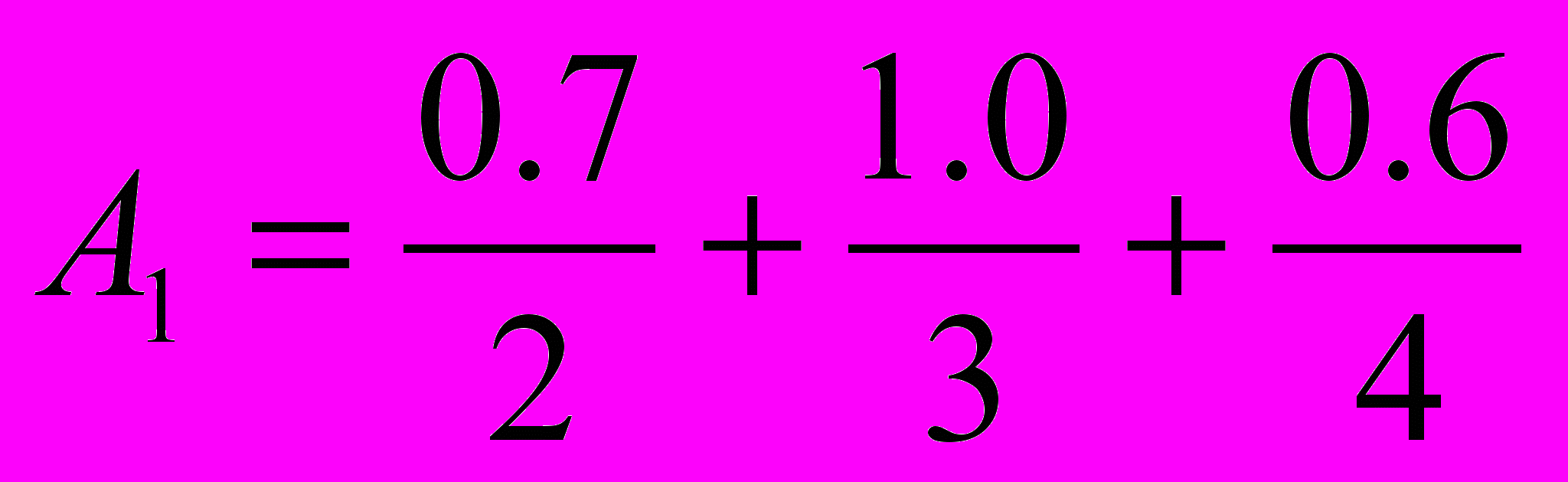, і друге - «нечітка четвірка», яка описується нечіткою множиною 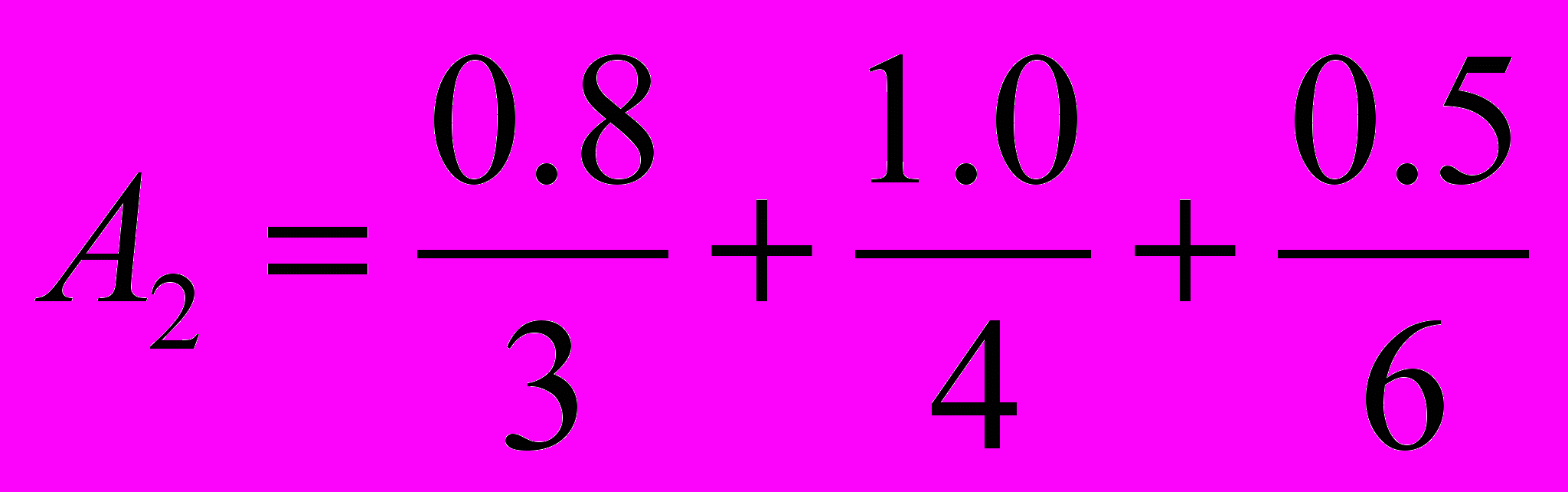. Визначте нечітке число В - «нечітка сімка», враховуючи той факт, що B=(A₁ + А₂) .

25. Маємо два нечітких числа: перше - «нечітка трійка», яка описується нечіткою множиною 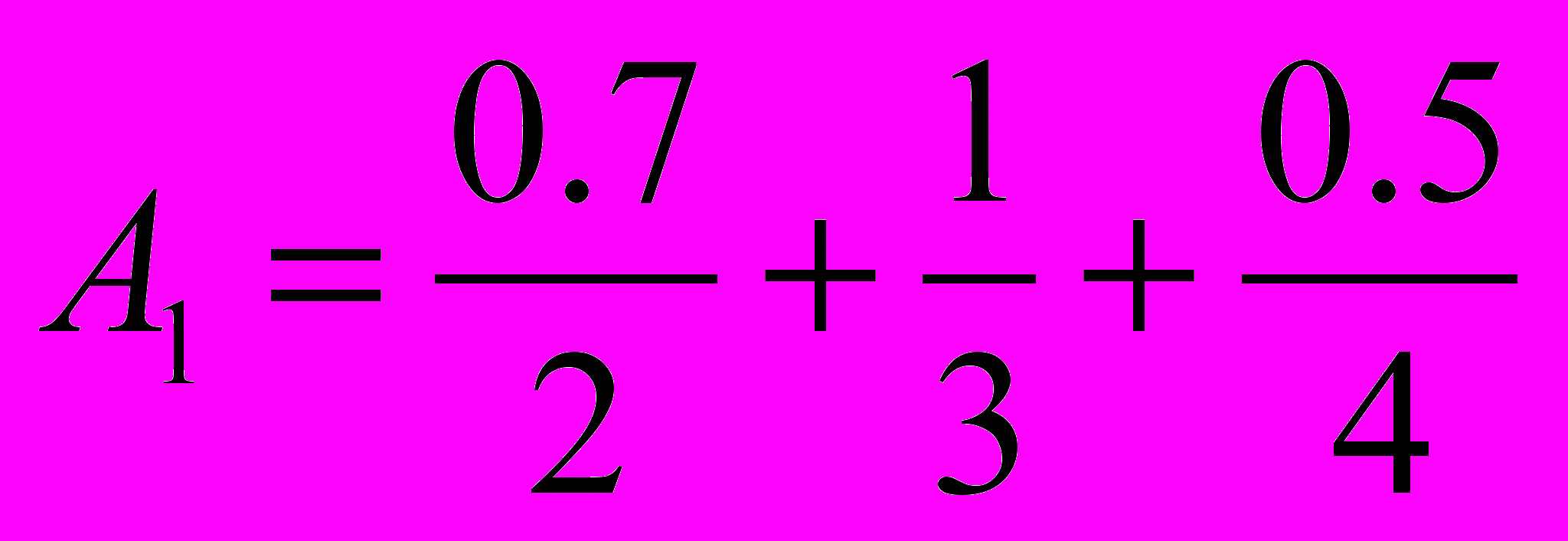, і друге - «нечітка четвірка», яка описується нечіткою множиною 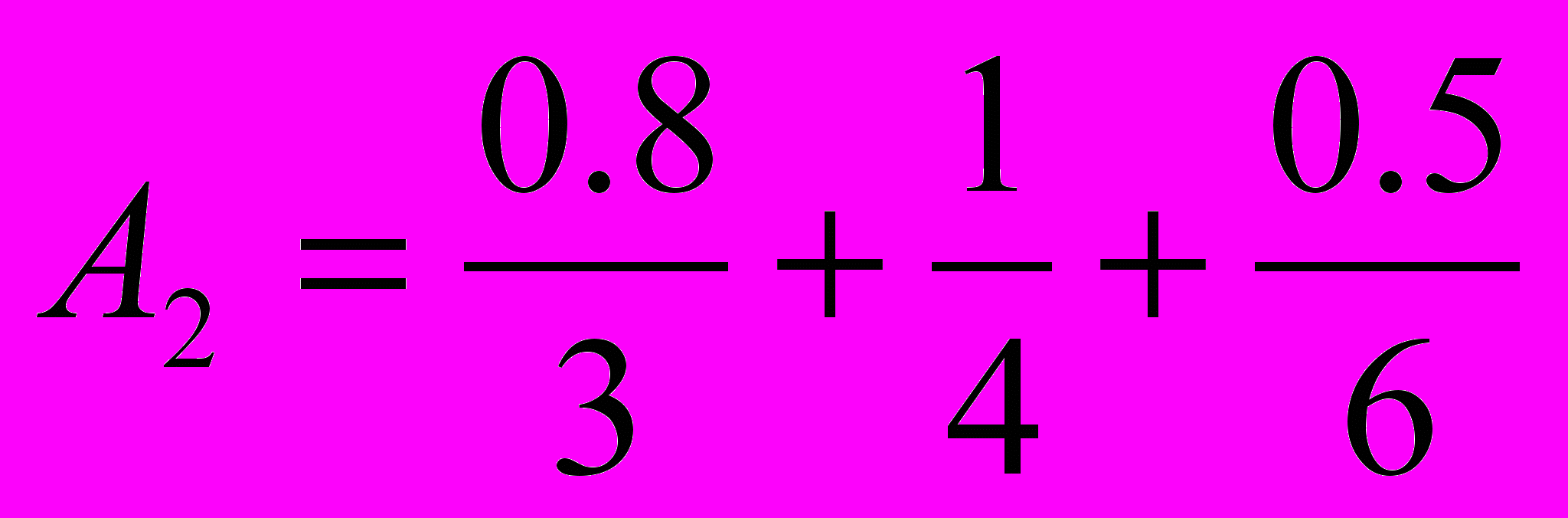. Визначте нечітке число В - «нечітка 12-тка», враховуючи той факт, що B=(A₁ * А₂) .

26. Маємо два нечітких числа: перше - «нечітка трійка», яка описується нечіткою множиною 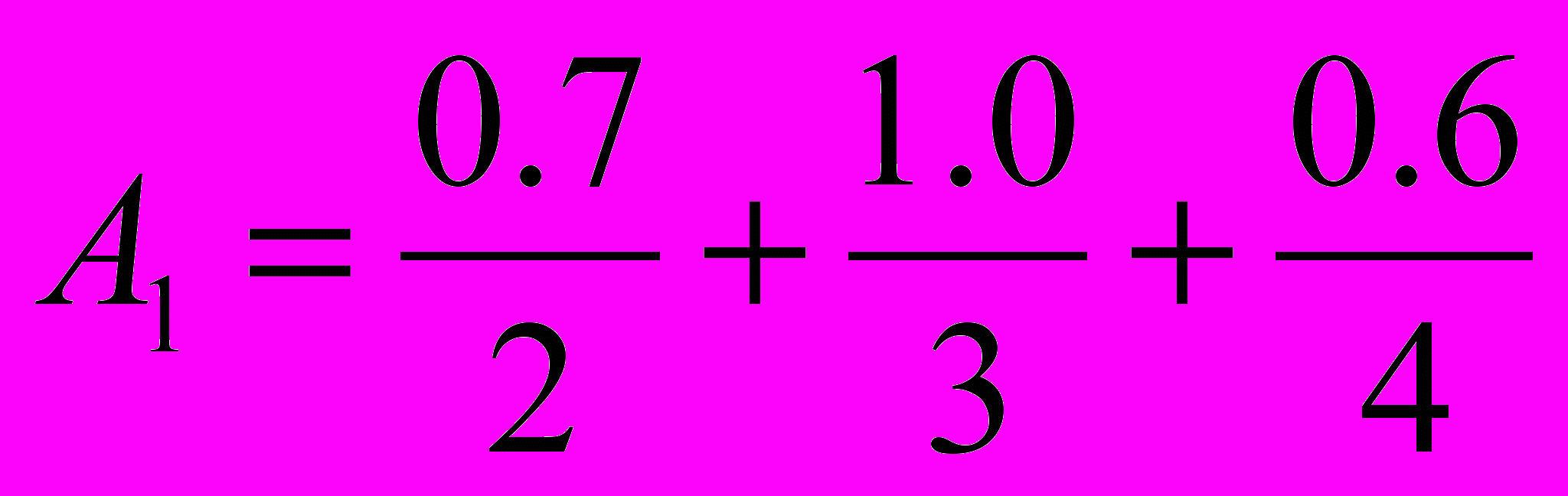, і друге - «нечітка четвірка», яка описується нечіткою множиною 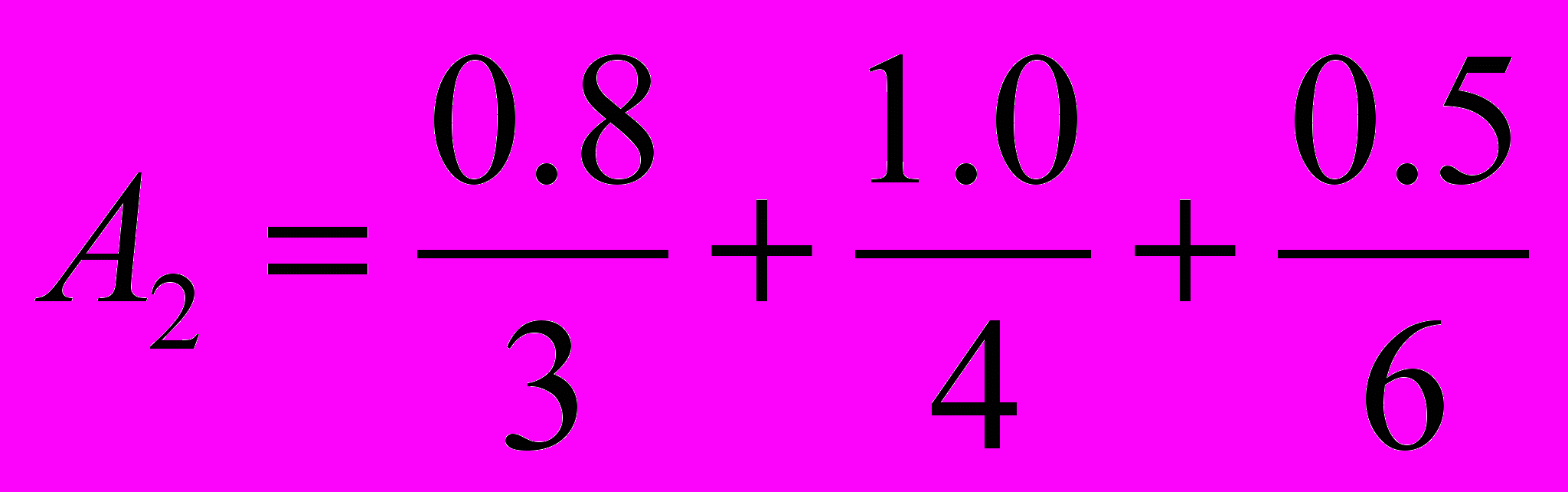. Визначте нечітке число В - «нечітка одиниця», враховуючи той факт, що B=(A₂ - А₁).

27. Нехай задана множина Х у вигляді скінченої множини назв різних міст. Розглянемо відношення R(Х,X)={| x, уХ: “y дуже далеко від x”}. Назвіть його основні властивості, обґрунтуйте їх.

28. Нехай задана множина Х у вигляді скінченої множини назв різних міст. Розглянемо відношення R(Х,X)={| x, уХ: “y дуже близько від x”}. Назвіть його основні властивості, обґрунтуйте їх.

29. Наведіть приклади лінгвістичних змінних, опишіть їх.

30. Наведіть приклади нечітких змінних, опишіть їх.