Информационные технологии консультирования и обучения

Вид материала

Содержание

Задачи оптимизации со многими неизвестными
Задача оптимизации туристических групп
1. Изучение функций ЕСЛИ, СЧЕТЕСЛИ. 2. Изучение фильтров.
Второй вариант
ABC-анализ с использованием фильтров

Подобный материал:

Информационные технологии консультирования и обучения

направление «Менеджмент»

магистратура «Управленческое консультирование в АПК»

Темы семинарских занятий

Групповая работа над документом Word. Рецензирование документа. Создание структурированного документа.
Разработка шаблона презентации для доклада (лекции), представления компании и нового бренда и т.д.
Excel. Задачи оптимизации. Задача оптимизации туристических групп. Выборочная обработка данных. Анализ данных с помощью фильтров.
Работа с поисковыми системами Интернет. Создание классификатора информационных ресурсов Интернет по видам информации, по различным критериям.
По материалам Интернета: поиск, обзор и классификация консалтинговых компаний России.
По материалам Интернета: поиск и обзор направлений управленческого консультирования.
По материалам Интернета: поиск и обзор подходов и мероприятий по антикризисному управлению.
По материалам Интернета: поиск и обзор систем моделирования и оптимизации бизнес-процессов предприятия.
По материалам Интернет: поиск и обзор методики управления предприятием с помощью Системы Сбалансированных Показателей (BSC).
По материалам Интернета: корпоративные системы, поиск, обзор, классификация. Основные функции и возможности.
Поиск, обзор и классификация систем электронной торговли, систем денежных расчетов, сиcтем Интернет-телефонии.
Поиск, обзор и классификация систем электронного документооборота.
По материалам Интернета: обзор подходов и стандартов управления проектами.
Подготовка иерархической структуры работ по проекту. Подготовка в MS Project перечня работ, назначение ресурсов, составление расписания.

Образец семинарского занятия №3. Excel. Задачи оптимизации

Задачи оптимизации со многими неизвестными

Для численного решения уравнений со многими неизвестными и ограничениями в Excel включен инструмент Поиск решения.

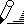По умолчанию инструмент не установлен и его следует установить: вставьте дистрибутивный CD-диск и выберите в списке надстроек СервисНадстройки… соответствующий флажок.

Если целевая функция и ограничения линейны, то решение состоит в нахождении множества чисел (х₁, х₂, … х_n), минимизирующих (максимизирующих) линейную целевую функцию f(х₁, х₂, … х_n)= c₁х₁+c₂х₂+… +c_nх_n при mi₁х₁+а_i₂х₂+… +а_inх_n(где i=1,2, … m) и n линейных ограничениях-неравенствах х_k>=0 (где k=1, 2, … n). Инструмент Поиск решения обеспечивает максимум 200 изменяемых ячеек х_i при поиске решения (n_мах=200).

В качестве первого содержательного примера рассмотрим задачу о комбинезонах:

Ателье шьет комбинезоны трех типов К1, К2, К3 и использует ткани четырех типов Т1, Т2, Т3, Т4. Нормы расхода ткани каждого типа на каждый комбинезон и объем дневных затрат приведены на рис. ниже. Стоимость пошива

комбинезона типа К1 равна 100 руб., К2 – 120 руб., К3 – 110 руб. Дневной запас тканей в ателье следующий: ткани Т1 – 50м, ткани Т2 – 80м, ткани Т3 – 25м, ткани Т4 – 60м. Сколько комбинезонов каждого типа надо производить в день, чтобы получить максимальную стоимость производства? При этом использовать все типы тканей.

Переложим условие задачи на язык формул, т.е. опишем математическую оптимизируемую модель. В процессе решения надо найти дневной выпуск х₁, х₂ и х₃ каждого комбинезона, такой, чтобы получить максимум целевой функции 100х₁+120х₂+110х₃ при ограничениях

х₁+ 2х₂+ х₃<= 50

2х₁+ 1.5х₂+ 3х₃<= 80

0.5х₁+ х₂+ 0.5х₃<= 25

3х₁+ х₂+ 0.5х₃<= 60

Кроме того, количество комбинезонов не может быть дробным и отрицательным, поэтому добавляются ограничения: (х₁, х₂, х₃) >= 0 и (х₁, х₂, х₃) – целые числа.

Теперь введем условие задачи в Excel, как показано ниже:

Как видно в ячейку Н3 введена формула =$B$9*B3+$C$9*C3+$D$9*D3, которая размножена на Н4:Н6. В ячейку F9 введена формула целевой функции =100*B9+120*C9+110*D9. В ячейках В9:D9 будет производиться подбор значения – здесь введены начальные значения х_i.

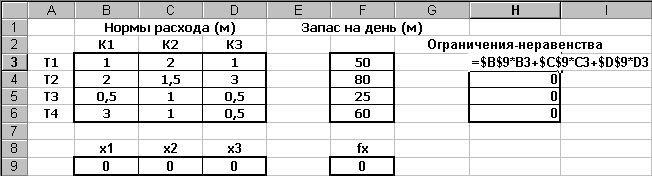
Далее вызываем инструмент СервисПоиск решения…, вводим адреса подготовленных ячеек и ограничения (как на рис. 2.39) и нажимаем кнопку Выполнить.

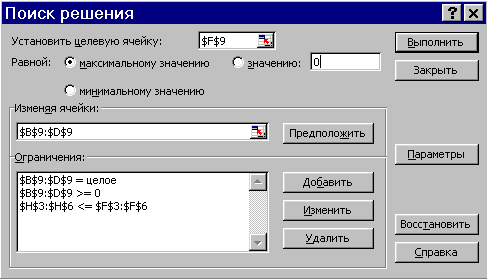
Рис. 2.39

Заполнение окна Поиск решения не вызывает трудностей. Ограничения добавляются кнопкой Добавить; при этом появляется окно ввода ограничения:

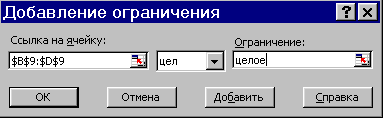
Результат вычислений показан на рис. 2.40:

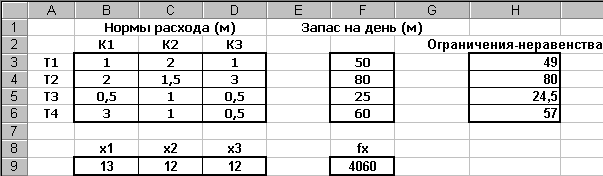
Рис. 2.40

Как видно, оптимальный дневной выпуск комбинезонов равен 13, 12 и 12. При этом в колонке Н видно, что часть тканей остается неизрасходованной.

Поэкспериментируйте: попробуйте вручную изменить подобранные значения (например, х1=14), оцените значения целевой функции и ячеек Н3:Н6. Повторно вызовите инструмент Поиск решения, удалите условие ($B$9:$D$9 = целое) и выполните подбор.

Обобщим проделанную работу и выделим этапы решения задачи оптимизации со многими неизвестными в Excel с помощью инструмента Поиск решения:

анализ задачи, выделение свойств, параметров, ограничений;
математическое описание оптимизируемой модели – введение обозначений, ограничений и создание целевой функции;
грамотное размещение модели и поиск решения в Excel.

Задача оптимизации туристических групп

В качестве второго содержательного примера рассмотрим задачу формирования экскурсионных пакетов. Российская туристическая фирма ежедневно отправляет в три отеля Анталии, Кемера и Мармариса (Турция) соответственно 30, 20 и 16 человек. Экскурсионная программа каждой группы состоит из рафтинга (спуск по горной реке на плоту), яхт-тура вдоль побережья и путешествия джип-сафари в турецкую глубинку. Стоимость экскурсий с трансфером на человека для отелей разных городов следующая:

	Рафтинг	Яхт-тур	Джип-сафари
Анталия	55	20	35
Кемер	65	35	20
Мармарис	60	25	25

При этом существуют ограничения на количество человек в экскурсии: рафтинг – 25 чел., яхт-тур – 20 чел., джип-сафари – 30 чел. От каждого отеля на каждую экскурсию должно быть послано не менее 5 чел.

Необходимо определить оптимальное количество туристов для участия в каждой экскурсии при заданных ограничениях. Под оптимальностью понимать минимизацию суммарных расходов турфирмы.

Приступим к ее решению. Постановка задачи выполнена достаточно четко, поэтому можно сразу приступить к описанию математической модели. Введем обозначения подбираемых значений неизвестных х_i – число туристов каждого отеля на каждый вид экскурсии:

	Рафтинг	Яхт-тур	Джип-сафари
Анталия	х₁	х₂	х₃
Кемер	х₄	х₅	х₆
Мармарис	х₇	х₈	х₉

Целевая функция (стоимость), которую следует минимизировать, запишется так:

55х₁ + 20х₂ + 35х₃ + 65х₄ + 35х₅ + 20х₆ + 60х₇ + 25х₈ + 25х₉

Ограничения на ежедневное количество человек в экскурсиях:

х₁ + х₂ + х₃ = 30 х₄ + х₅ + х₆ = 20 х₇ + х₈ + х₉ = 16

Ограничения на ежедневное количество мест в экскурсиях:

х₁ + х₄ + х₇ <= 25 х₂ + х₅ + х₈ <=20 х₃ + х₆ + х₉ <=30

Другие ограничения – количество туристов от каждого отеля на экскурсию неделимо и больше 5: (х₁, х₂, … х₉) >= 5 и (х₁, х₂, … х₉) – целые числа

Следующим шагом разместим оптимизируемую модель в Excel, как показано ниже:

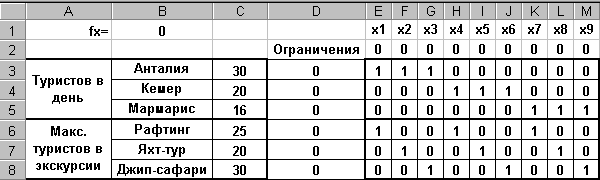
Здесь, в ячейках Е2:М2 размещены начальные значения неизвестных (х₁, х₂, … х₉)=0. Для единообразной записи ограничений использована таблица коэффициентов Е3:М8. В ячейку D3 записана формула =E$2*E3+F$2*F3+G$2*G3+H$2*H3+I$2*I3+J$2*J3+K$2*K3+L$2*L3+M$2*M3, которая размножена на диапазон D4:D8. В ячейках С3:С8 записаны граничные значения числа туристов от отелей и в экскурсиях. Целевая функция записана в ячейке В1: =55*E2+20*F2+35*G2+65*H2+35*I2+20*J2+60*K2+25*L2+25*M2.

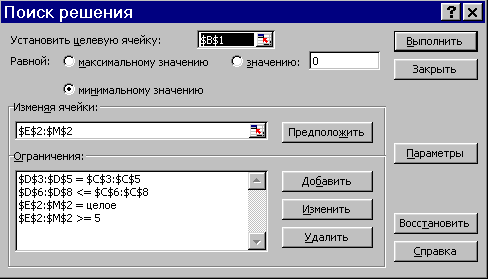
Нам осталось запустить поиск решения и ввести адреса ячеек и ограничения, как на рисунке ниже:

Результат поиска решения показан ниже:

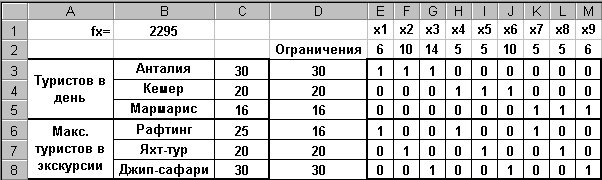
Здесь в ячейках Е2:М2 подобрано оптимальное количество туристов, дающее минимальную стоимость расходов, равную 2295$. Проанализируйте полученное решение и поэкспериментируйте.

1. Изучение функций ЕСЛИ, СЧЕТЕСЛИ. 2. Изучение фильтров.

Функция ЕСЛИ, в зависимости от Условия, принимает Значение1 (если Условие верно) или Значение2 (если Условие не верно) и имеет следующий формат:

ЕСЛИ ( Условие ; Значение1_если_истина ; Значение2_если_ложь )

Выборочная обработка данных

Задачи получения обобщенных данных, выборочной обработки данных по некоторым критериям могут решаться в Excel различными способами. Рассмотрим задачу получения обобщенных данных из таблицы (рис. 2.29) прибылей фирмы за три года по месяцам. По каждому году требуется определить количество убыточных месяцев, сумму убытков, максимальную прибыль за месяц и среднемесячную прибыль.

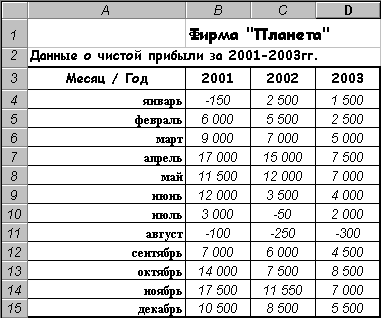
Рис. 2.29

Первый, самый простой вариант решения может выглядеть так:

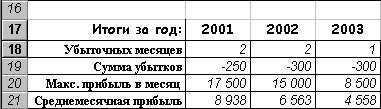
Воссоздайте это решение - в ячейках B18:B21 записаны следующие формулы:

в В18 – =СЧЁТЕСЛИ(B4:B15;"<0"). Функция СЧЁТЕСЛИ из группы Статистические подсчитывает число ячеек в заданном диапазоне, удовлетворяющие указанному условию;
в В19 – =СУММЕСЛИ(B4:B15;"<0"). Функция СУММЕСЛИ из группы Математические суммирует ячейки из заданного диапазона, удовлетворяющие указанному условию;
в В20 и В21 – =МАКС(B4:B15) и =СРЗНАЧ(B4:B15).

В настоящем примере для удобства копирования формул в колонки С18:С21 и D18:D21 удобнее использовать абсолютные ссылки.

Второй вариант решения основан на возможности вложения функций ЕСЛИ друг в друга и показан ниже – итоговые данные выводятся в одной, общей колонке и изменение года в ячейке G3 приводит к пересчету итогов:

Вложенность функций ЕСЛИ означает, что вместо любого аргумента Значение может стоять другая функция ЕСЛИ, всего до 7 вложений. В нашем случае, для одного года, например 2001, функция ЕСЛИ запишется так:

=ЕСЛИ(G3=2001;СЧЁТЕСЛИ(B4:B15;"<0");"Нет данных")

Вместо значения «Нет данных» можно записать функцию ЕСЛИ для 2002 года и т.д. С учетом сказанного в ячейках G4:G7 соответственно записаны формулы:

=ЕСЛИ(G3=2001;СЧЁТЕСЛИ(B4:B15;"<0");ЕСЛИ(G3=2002;СЧЁТЕСЛИ(C4:C15;"<0");ЕСЛИ(G3=2003;

СЧЁТЕСЛИ(D4:D15;"<0");"Нет данных")))

=ЕСЛИ(G3=2001;СУММЕСЛИ(B4:B15;"<0");ЕСЛИ(G3=2002;СУММЕСЛИ(C4:C15;"<0");ЕСЛИ(G3=2003;

СУММЕСЛИ(D4:D15;"<0");"Нет данных")))

=ЕСЛИ(G3=2001;МАКС(B4:B15);ЕСЛИ(G3=2002;МАКС(C4:C15);ЕСЛИ(G3=2003;МАКС(D4:D15);"Нет данных")))

=ЕСЛИ(G3=2001;СРЗНАЧ(B4:B15);ЕСЛИ(G3=2002;СРЗНАЧ(C4:C15);ЕСЛИ(G3=2003;СРЗНАЧ(D4:D15);"Нет данных")))

Как видно, в зависимости от года (G3) выбираются нужные значения. Если введен неверный год, то печатается текст «Нет данных».

ABC-анализ с использованием фильтров

Рассмотрим использование фильтров Excel для оперативного получения оценочных данных на примере задачи ABC-анализа. Суть ABC-анализа состоит в разбиении всех товаров (клиентов) по важности на три группы (A, B и C) по некоторому показателю – объему продаж, прибыли и т.д.

ABC-анализ строится на законе Парето, который гласит, что, как правило, 80% от всего объема продаж (прибыли) фирмы достигается за счет не более, чем 20% товаров (клиентов), и, наоборот, 80% всех товаров (клиентов) дают не более 20% оборота.

В связи с этим все товары (клиентов) можно разбить на 3 группы:

A – товары (клиенты), дающие 80% прибыли. В группу А попадают те, которые в основном определяют обороты фирмы;
C – 80% товаров (клиентов) с наименьшей важностью, доля участия которых в обороте фирмы невелика;
В – все остальные товары (клиенты), занимающие промежуточное положение между группами A и С, если группы А и С не пересекаются.

Пусть имеются данные по отгрузке некоторых товаров за месяц, приведенные на рис. 2.30. Необходимо определить суммы (и %) отгрузки, которые дают 80% товаров с наименьшей важностью (группа С) и 20% товаров с наибольшей важностью.

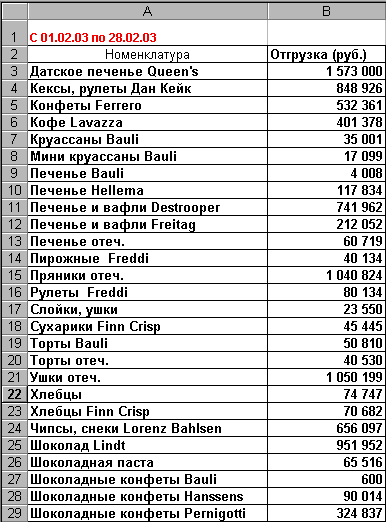Рис. 2.30

Определим сумму отгрузки, которую дают 80% товаров с наименьшей важностью (группа С). Для этого проделайте следующие действия:

В ячейку В31 запишите формулу =СУММ(B3:B29) – общая сумма отгрузки равна 9150411.
Установите фильтр на данные, т.е. выделите диапазон ячеек А2:В29 и выберите ДанныеФильтрАвтофильтр. В строке 2 появятся кнопки списков (как на рис. 2.31).
В списке Отгрузка выберите пункт (Первые 10…) как на рис. 2.31. В появившемся окне установите наше условие:

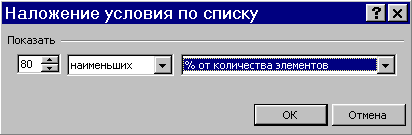
После нажатия ОК Вы получите 80% списка товаров, дающих минимальные объемы – рис. 2.31. Выделите отфильтрованный диапазон А5:А29. После выделения в строке состояния (внизу) Вы увидите Сумму в выделенной области – рис. 2.31.

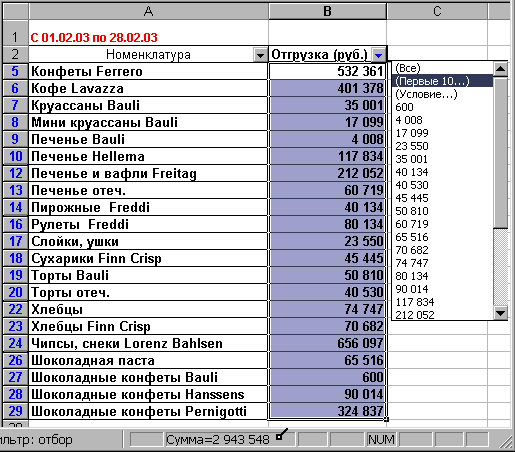
Рис. 2.31

Как видно, 80% товаров наименьшей важности дает отгрузку 2943548 руб., что составляет около 32% от общего объема продаж.

Аналогично оцените объем продаж 20% наибольшей важности, применив следующее условие:

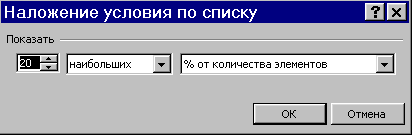
Вы должны получить сумму 5464901 руб., что составляет почти 60% от объема продаж.

Снимите фильтр, еще раз выбрав пункт ДанныеФильтрАвтофильтр.

Отобранные с помощью фильтра строки (ячейки) можно удалять, изменять формат отображения (цвет, шрифт и пр.) – при этом остальные, не отобранные строки (ячейки) остаются без изменения. Это удобно для выборочного изменения, удаления строк (ячеек) по условию.

Blog

Информационные технологии консультирования и обучения

Содержание

Задачи оптимизации со многими неизвестными

Задача оптимизации туристических групп