Владимир Каплунов Новая философия

• Христова Николай Антонович Половодов 8-9062732980 новая религия входе своего развития, 80.16kb.
• «И. Лакатос», 261.06kb.
• Никита Юрьевич Белых лидер партии "Союз правых сил", 95.51kb.
• Владимир Николаевич Лавриненко Философия Философия: учебник, 6688.53kb.
• Ю. М. Бохенский современная европейская философия, 3328.46kb.
• Тесты для самопроверки знаний раздел I. Что такое философия? Тема Философия в системе, 1997.45kb.
• Т. А. Сулейменов Курс лекции по философии Шымкент-2010 г. 1-лекция, 1988.6kb.
• А. Л. Доброхотов Введение в философию, 478.73kb.
• С. В. Булярский Принято на зас каф философии и политологии 4 апреля 2000 г., протокол, 128.66kb.
• Программа «Московская семья компетентные родители» новая философия взаимодействия детского, 87.78kb.

Вероятность реализации событий Энтропия и негэнтропия в своих понятиях и в формуле Шеннона содержат величину «вероятности событий». Поскольку энтропия и негэнтропия диалектически противоположные понятия, то и определения «вероятностей событий» должны пониматься по-разному, в соответствии со смыслами, которые «информационный подход» вкладывает в понятия энтропии и негэнтропии. Для наглядности математическая «фикция» формулы К. Шеннона может быть представлена в виде графика (см. рис. 1). На графике изображены кривые изменения величин, входящих в формулу информационной энтропии-негэнтропии. График, помещенный в этом тексте, подлежит различной интерпретации в зависимости от того, что с помощью него рассматривается — энтропия или негэнтропия. На оси x графика отложены значения величин от нуля до единицы вероятностей (i-тых) из всего множества (n) социальных событий. При этом в энтропии вероятность социального события понимается как «субъективная вероятность» или «возможность» отнесения события к некоторому «образу» или к информационному полю Добра-Зла, а в негэнтропии эта величина означает вероятность реализации модели. На оси y отложены: 1 -- условная величина множителя log pi, понимаемого в «информационном подходе» как «показатель эмоциональности», «показатель возбуждения» или «временной показатель»; 2 -- условная величина сомножителя pi log pi, понимаемая в «информационном подходе» как «событие» или «воля» (или единство «логика-чувство»); 3 -- условная величина социальной энтропии H или социальной негэнтропии I в их комплексном выражении, где n -- число «событий» вида pi log pi, которые в энтропии являются внешними по отношению к субъекту, а в негэнтропии внутренними, направленными во внешнюю среду. Вероятность или возможность? Сначала надо обратиться к различным источникам, в которых даются определения понятия вероятности. В «Философском энциклопедическом словаре» (М. «ИНФРА-М». 2003): «В математике вероятностью называется отношение числа случаев, благоприятствующих данному событию к числу всех равновозможных случаев». В «Кратком словаре по философии» (М. «ИПЛ» 1982): «Степень развития возможности – показатель ее близости к действительности – выражается понятием «вероятность». «Максимум вероятности» обозначает точку качественного превращения возможности в действительность». В статистике, имеющей отношение к психологии и социологии у Грегори Кимбла («Как правильно пользоваться статистикой» -- М. «Финансы и статистика». 1982 г. С. 103): «Вероятность осуществления любого конкретного случайного события равна отношению числа всех возможных реализаций этого события к общему числу всех возможных исходов». А вот более пространное определение понятия вероятности данное Ричардом Фейнманом: «Мы можем говорить о вероятности исхода только тех наблюдений, которые собираемся проделать в будущем. Под вероятностью данного частного результата наблюдения понимается ожидаемая нами наиболее правдоподобная доля исходов с данным результатом при некотором числе повторений наблюдения». … «под вероятностью P(A) результата A мы понимаем отношение Н 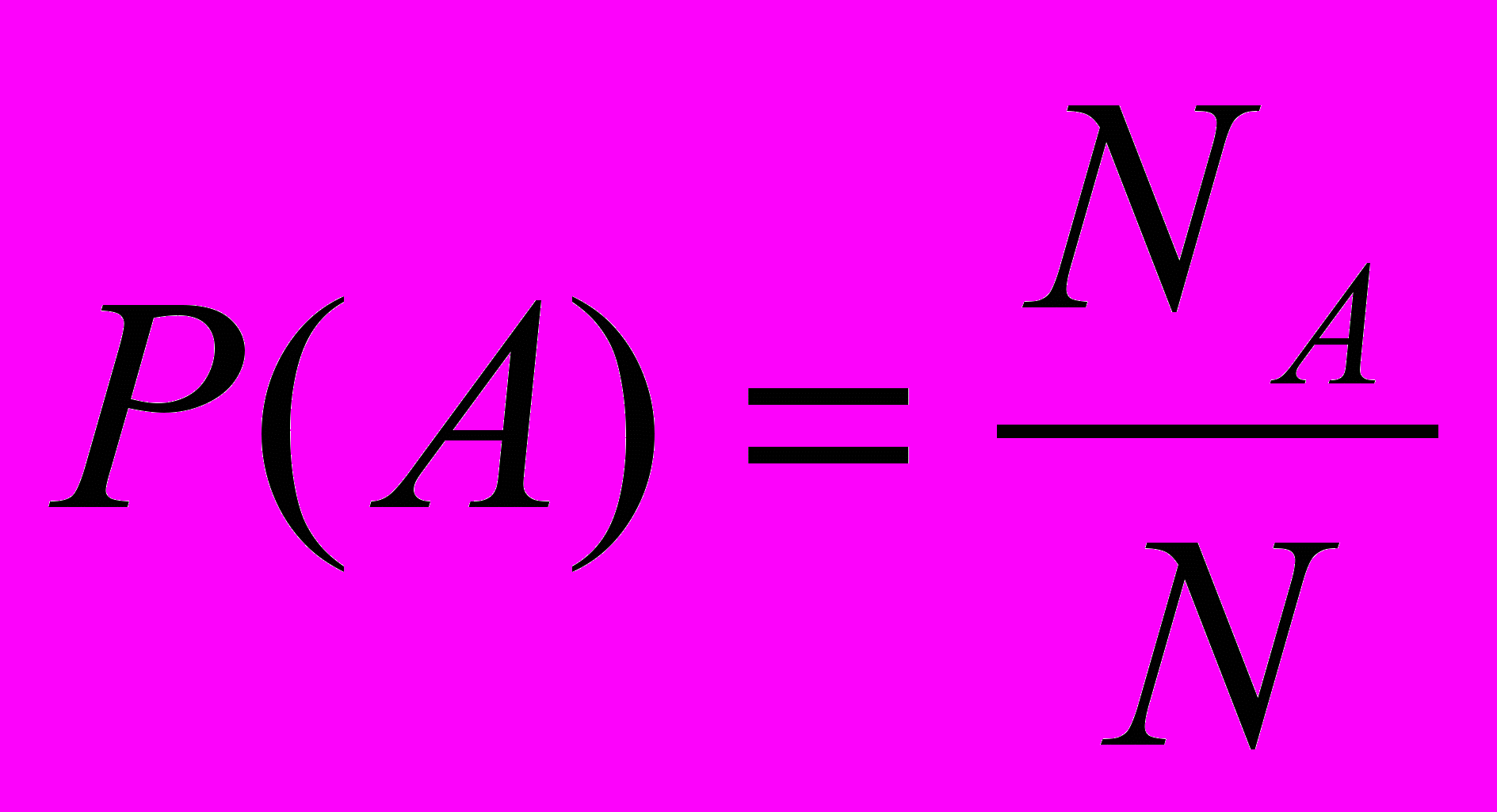аше определение требует некоторых комментариев. Прежде всего мы говорим о вероятности какого-то события только в том случае, если оно представляет собой возможный результат испытания, которое можно повторить. Но отнюдь не ясно, имеет ли смысл такой вопрос: какова вероятность того, что в этом доме поселилось привидение. Вы, конечно, можете возразить, что никакая ситуация не может повториться в точности. Это верно. Каждое новое наблюдение должно происходить по крайней мере в другое время или в другом месте. По этому поводу я могу сказать только одно: необходимо, чтобы каждое «повторное» наблюдение казалось нам эквивалентным. Мы должны предполагать по крайней мере, что каждый новый результат наблюдения возник из равноценных начальных условий и из одного и того же уровня начальных знаний. Последнее особенно важно. (Если вы заглянули в карты противника, то, конечно, ваши прогнозы о шансах на выигрыш будут совсем другими, чем если бы вы играли честно!). Хочу отметить, что я не собираюсь рассматривать величины N и NA в (6. 1) только как результат каких-то действительных наблюдений. Число NA – это просто наилучшая оценка того, что могло бы произойти при воображаемых наблюдениях. Поэтому вероятность зависит от наших знаний и способностей быть пророком, в сущности от нашего здравого смысла! К счастью, здравый смысл не столь уж субъективен, как это кажется на первый взгляд. Здравым смыслом обладают многие люди, и их суждения о степени правдоподобия того или иного события в большинстве случаев совпадают. Однако вероятность все же не является «абсолютным» числом. Поскольку в каком-то смысле она зависит от степени нашего невежества, постольку с изменением наших знаний она может меняться» [69]. Из этих определений видно, что, во всех определениях вероятности, как математического отношения, есть допущение в качестве основания определения понятие «возможность» (у Фейнмана еще и – «правдоподобие»). Понятие же возможность – философская категория (экзистенциал). «Как таковая возможность постижима лишь в понятиях, которые уже содержат понятия возможности» (Ф. Э. С.). Такая органическая тавтология, не устраняемая логическими рассуждениями в поисках дефектной логики, означает фундаментальность понятия. С точки зрения «информационного подхода» энтропия и понимается как фундаментальное определение пространства-времени возможности. Но, информационная энтропия у Шеннона получила и свое математическое выражение в виде формулы энтропии, содержащей в себе математический показатель «вероятность события». Тогда возникает вопрос: следует ли пользоваться математическим определением вероятности в энтропии также как в негэнтропии или необходимо использовать нестрогое определение вероятности, а, в некоторых случаях вообще отказаться от термина «вероятность» в пользу термина «возможность» в энтропии, и пользоваться термином «вероятность» только в негэнтропии? Бертран Рассел, посвятивший исследованию проблемы вероятности целый раздел в своей книге «Человеческое познание: его сфера и границы», различает два вида понятия вероятности. Он пишет: «Первое из них является математической вероятностью, которая поддается числовому измерению и удовлетворяет требованиям аксиом вычисления вероятности; это — тот вид вероятности, который предполагается при использовании статистики, будь то в физике, в биологии или в общественных науках ... Этот вид вероятности всегда имеет дело с классами, а не с отдельными случаями, за исключением того обстоятельства, когда они могут рассматриваться только как образцы. Но существует и другой вид, который я называю «степенью правдоподобия». Этот вид применим к отдельным предложениям и всегда связан с учетом всех относящихся к делу обстоятельств. Он применим даже в некоторых таких случаях, в которых нет никакого известного свидетельства». [70]. Чуть раньше в своем тексте Б. Рассел называет этот второй вид вероятности «руководителем жизни». «Вероятность, являющаяся руководителем жизни не относится к математическому виду вероятности не только потому, что она относится не к произвольным данным, а ко всем данным, которые с самого начала имеют отношение к вопросу, но также и потому, что она должна учитывать нечто целиком лежащее вне сферы математической вероятности, что можно назвать «внутренне присущей сомнительностью» [71]. «Учитывать нечто целиком лежащее вне сферы математической вероятности» -- означает учитывать энтропию как возможность. Вероятность в энтропии это возможность Фейнмановское и другие математические определения вероятности можно отнести к вероятности социального события в негэнтропии, но об этом чуть позже. Вероятность же в социальной энтропии полнее. В социальной энтропии «вероятность того, что в доме поселилось привидение» не может быть отвергнута на том основании, что она не имеет смысла (см. выше). В энтропии главным «действующим лицом» является не смысл как логическая конструкция, а значение как чувство, выделяющее данное событие из ряда равновозможных. Это обстоятельство хорошо прослеживается на графике энтропии расположением кривой «возбуждения» (log pi), которая, начиная с вероятности 0, 5 и меньше, выходит за пределы кривой энтропии и растет экспоненциально. Тот факт, что кто-то хочет продать дом потому, что ему надоели привидения, а другой хочет купить такой дом потому, что в нем есть привидения, которые можно показывать туристам, есть социальное событие. Реальность такого события базируется на значении факта, вероятность которого определяется не повторными наблюдениями в «сходных начальных условиях», а мнениями тех людей, кто говорит о том, что в доме «поселилось привидение». Таким образом, вероятность социального события в энтропии хотя и может быть оценена как отношение числа людей наблюдавших какой-то факт с неизвестной поляризацией по признакам Добра или Зла, к числу людей, которые данный факт не наблюдали, тем не менее, тяготеет к оценке как «возможность» или по Расселу — к «внутренне присущей сомнительности». Дальше. Если внимательно отнестись к свидетельствам людей, которые говорят о каком-то редком (единичном) событии, свидетелями которых им, как они утверждают, довелось быть, то обнаружится «поляризация» такого социального факта по признакам Добра или Зла с возможностью взаимопревращения этих признаков в свою противоположность. Поэтому в энтропии множество социальных событий с вероятностью, определяемой отношением числа свидетелей редкого или единичного факта (числа мнений) к числу людей, не наблюдавших этот факт, предстает как континуум возможности, «нечетко» поляризованный по признакам Добра-Зла. Едва ли у Колумба были более достоверные сведения о том, что существует более короткий путь в Индию, чем сведения о том, что «в доме поселилось привидение». Но эти сведения имели значение возможности Добра. И эти сведения приобрели смысл после открытия Америки. А это уже негэнтропия, т. е. действительность, возникшая из «точки качественного перехода возможности в действительность» -- действительность Добра для европейцев и Зла для американских индейцев. Не следует думать, что множество «субъективных вероятностей» образуют континуум возможности только в обыденном сознании, наполненном мнениями различных людей по редким или единичным событиям. Наука, там, где она начинается с неизвестной причинности (физика микромира) и заканчивается в неизвестности будущего мира (астрофизика) также вынуждена использовать и «субъективную вероятность» и энтропийную математику в виде «математики непрерывности», «нечеткой алгебры», и др. Вот как, например, рассматривает И.С. Шкловский формулу N = n P1 P2 P3 P4 t1:T [формула Дрэйка, оценивающая вероятность существования разумной цивилизации в нашей галактике] «Прежде всего стоит подчеркнуть, что в нашем случае термин «вероятность» не имеет обычного математического смысла. Ведь обычные приложения теории вероятностей всегда подразумевают существование статистического ансамбля. В нашем же случае все величины, о которых идет речь в формуле Дрэйка, известны только в одном экземпляре… «Вероятности» Pi фигурирующие в формуле Дрэйка, носят характер более или менее субъективных оценок достаточно компетентных специалистов. Отсюда и термин для такого рода вероятностных оценок – «субъективная вероятность», который особенно часто звучал на Советско-американском симпозиуме по внеземным цивилизациям, состоявшемся в Бюраканской обсерватории в сентябре 1971г.» [72]. Поэтому в социальной энтропии и «здравый смысл», оправданный мнением Р. Фейнмана, и «научный прогноз» оценивают возможность социального события в виде «субъективных вероятностей», представляющих в своей множественности континуум. И этот континуум имеет поляризации по признакам Добра-Зла («свой-чужой», «этот-не- этот») – «сколько людей – столько и мнений» относительно вреда или пользы какого-то редкого события или относится ли данное событие к тому или иному «образу», «схеме» или явлению. Социальная энтропия является всеобщей, охватывающей всё, а не только земное пространство. Эта энтропия состоит из множества различных мнений по самым разным вопросам (в том числе и по вопросам мироустройства) и из множества научных знаний. Всеобщая энтропия дробится на множество локальных энтропий – есть энтропии личности, семьи, энтропии группы, энтропии социального слоя, энтропии класса, но все они, с той или иной степенью определенности, охватываются общим энтропийным полем социума – множеством «оценочных мнений», в основе которых обнаруживается поляризация информационного поля по признакам Добра-Зла («свой-чужой», «этот-не этот»). Локальная энтропия, той или другой размерности по пространству и времени восприятия, предстает перед индивидуальным сознанием со снятой неопределенностью в отношении всеобщего информационного поля Добра и Зла. Например, семья окружает заботой малыша, который вне семейной опеки (или вне человеческой опеки) оказывается абсолютно незащищенным перед всеобщей Энтропией Природы (если не считать «маугли» чем-то закономерным). В локальной энтропии, когда снята угроза уничтожения в пространстве общей Энтропии Природы, индивид оказывается перед поляризацией локальной энтропии, условно говоря, тоже по признакам Добра и Зла, которая не несет остроту уничтожения организма, но несет различную поляризацию по степеням реализации свободы желаний и поведения. В этом состоянии внутренняя энтропия желаний и поведения индивида вступает в противоречивые отношения с локальной энтропией семьи, группы, слоя, класса. И оказывается, что эта внешняя локальная энтропия поляризована по признакам определенности видов желаний и форм поведения таким образом, что некоторые виды желания и некоторые формы поведения оказываются запрещенными. Тогда запретные желания и запретные формы поведения поляризуют внешнее поле по признакам Зла, а разрешенные – формируют информационное поле Добра. Неизвестные, но возможные, виды желаний и форм поведения представляют собой энтропию неизвестного состояния возможного будущего. Таким образом, внешняя локальная энтропия, выступающая для ребенка как «мир взрослых», представляет собой «энтропию источника u с двумя состояниями u1 и u2», которые понимаются как состояние Добра и состояние Зла. Локальная энтропия социального слоя поляризована по признакам «свой-чужой», когда какой-то индивид признается по каким-то очень субъективным признакам своим или чужим. Энтропийная выделенность какой-то личности — как «образ» -- среди множества людей определяется как «этот» или «не этот» (другой из множества одного класса). Итак, вероятность pi на графике социальной энтропии понимается как возможность Добра или Зла в социальной среде; как возможная принадлежность какого-то индивида к какой-то нации, к некоему социальному слою; как возможно знакомый образ, выделенный из множества других. А вот, определенность видов желаний и форм поведения уже относится к информационной социальной негэнтропии, которая структурирует поле социальной энтропии и синтетически в нее входит. Соответственно от возможности всякого поведения индивида по отношению к социуму и от возможности всякого поведения социума по отношению к индивиду, следует переходить к вероятности реализации определенного социального события той или другой полярности. Определенность принадлежности к той или другой социальной группе достигается различными средствами, например, формой одежды, документально и др. Тогда обладание пенсионным удостоверением означает математическую вероятность того, что обладатель пенсионного удостоверения — пенсионер. Что касается определения «образа» знакомой (или не знакомой) личности, то оно достигается множеством информационных актов общения в соответствии со «структурой поведенческого акта» (Судаков), в процессе которого достигается определенность полной характеристики этой личности.