Теория сигналов и систем
| Вид материала | Документы |
- Теория сигналов и систем, 145.8kb.
- Теория сигналов и систем, 143.44kb.
- Тема пространство и метрология сигналов физическая величина более точно определяется, 595.48kb.
- Программа учебной дисциплины «Теория сигналов» Специальности 071500, 013900 (СД. 05), 82.24kb.
- Программа-минимум кандидатского экзамена по специальности 05. 12. 14 «Радиолокация, 134.92kb.
- Программа-минимум кандидатского экзамена по специальности 05. 12. 14 «Радиолокация, 236.33kb.
- Н. Г. Чернышевского кафедра радиофизики и нелинейной динамики рабочая программа, 145.34kb.
- Цифровая обработка сигналов, 25.15kb.
- Программа-минимум кандидатского экзамена по специальности 05. 12. 13 «Системы, сети, 151.82kb.
- Программа-минимум кандидатского экзамена по специальности 05. 12. 13 «Системы, сети, 121.7kb.
Теория сигналов и систем
A MODIFIED METHOD OF MINIMUM DISPERSION IN THE FSK SIGNAL PARAMETERS ESTIMATION TASK
Khmelev S., Loginov A., Morozov O., Soldatov E.
Physical-Technical Research Institute of N.I. Lobachevsky State Univerity of Nizhni Novgorod
The task of digital filtration is encountered in many fields of applied physics and engineering. Particularly digital filtration can be applied for changing the representation of the signal with the purpose of making following analysis easier. One of traditional approaches is converting FSK signal from harmonic representation to that one, in which each of the possible frequencies
 ,
,  corresponds to some fixed output level.
corresponds to some fixed output level.In this paper an algorithm of optimal linear filtration of FSK-signals, based on the modified Capon minimum dispersion approach, is proposed. The Capon approach implies building a linear filter, which passes a harmonic signal of a specified frequency, by minimizing an output’s dispersion. A modification of this method for processing FSK signals follows building a linear filter with minimum output’s dispersion with specified transmission coefficients
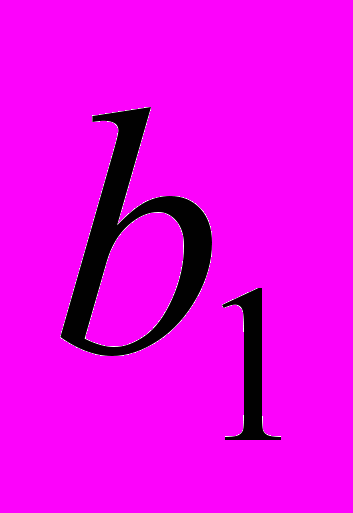 ,
,  on frequencies
on frequencies  ,
,  , that can be written as follows:
, that can be written as follows:  (1),
(1),where
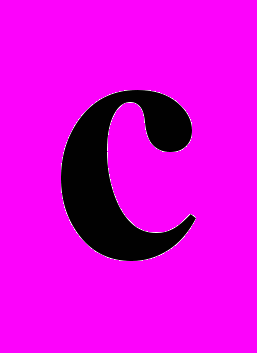 – a vector of filter coefficients,
– a vector of filter coefficients,  – a vector of complex exponents of respected frequencies,
– a vector of complex exponents of respected frequencies,  – an autocorrelation matrix of a signal, which consists of two sinusoidal functions with harmonics
– an autocorrelation matrix of a signal, which consists of two sinusoidal functions with harmonics  ,
,  . This task can be analytically solved on the base of Lagrange’s method of undetermined multipliers and it’s solution corresponds to the Capon minimum dispersion solution under certain conditions.
. This task can be analytically solved on the base of Lagrange’s method of undetermined multipliers and it’s solution corresponds to the Capon minimum dispersion solution under certain conditions.As in the classical approach it is assumed that autocorrelation matrix is nonsingular and the number of filter coefficients depends on model order of a signal. When the number of coefficients is rising an autocorrelation matrix becomes singular that leads to infinite number of solutions. In this case a usual approach is to replace the inverse matrix with Moore-Penrose pseudo-inverse matrix that leads to least-squares solution.
At the same time, an existence of infinite number of solutions makes possible to choose the one, which corresponds to some criteria, which in agreement with general mathematical approach should be chosen as a functional, which optimum corresponds to a solution with desired properties. Particularly, the use of Berg entropy functional can be proved in tasks with lack of information. A filter amplitude-frequency response which is limited and nonnegative can be chosen as an argument of Berg’s functional with the respect of building a filter with low-energy side-lobes.
An output of such filter can be used for solving different FSK parameters estimation tasks. Another way is to use a dispersion of an output. This way implies a computation of an autocorrelation matrix by the short sequence. This makes such approach more complicated but also more stable in the presence of noise and frequency shifts.
A number of different FSK parameters estimation tasks, such as demodulation, delay estimation in case of multipath propagation, detection and other can be solved on the base of the proposed algorithm in the presence of noise. Compared to traditional the main advantage of the proposed algorithm is the ability of working in a case of inexact knowledge of central frequency with no complicated schemes of frequency shift compensation or automatic frequency control. An efficiency of proposed algorithm is shown in tasks of demodulation and delay estimation by computer simulation.
Применение дискриминирующей функции в задачах оценивания порядка марковской цепи и контекстной функции марковской цепи переменного порядка
Авдашов С.А.1, Коньков Е.А.2
1Нижегородский государственный университет им. Н.И. Лобачевского
2Научно-исследовательский физико-технический институт
Нижегородского государственного университета им. Н. И. Лобачевского
Математическими моделями различных радиотехнических устройств, процессов, сигналов в системах связи являются простые (односвязные) марковские цепи, в ряде случаев применяется обобщение этих моделей — многосвязные марковские цепи и марковские цепи переменного порядка [1, 2].
Введем обозначение для последовательности отсчетов случайного процесса
 .
.Многосвязной однородной по времени марковской цепью называется стохастическая модель у которой переходные вероятности выражаются следующим образом
 , (1)
, (1)где t — моменты дискретного времени, xt — отсчеты случайного процесса, принимающие значения из конечного множества A={ai: i=0..M-1}, k — порядок марковской цепи [1]. В данной работе M=2, отсчеты случайного процесса можно считать битами. Важным параметром данной модели является ее порядок k, который необходимо эмпирически оценить исходя из имеющейся выборки длины n.
Следует отметить, что количество параметров данной модели растет экспоненциально как (M−1)Mk. Для преодоления трудностей, связанных с ограниченным объемом выборки при оценке параметров модели (1) был предложен способ уменьшения количества параметров модели за счет ее усложнения [2]. Марковская цепь переменного порядка — это многосвязная марковская цепь, порядок которой зависит в каждый момент времени t от предыдущих отсчетов случайного процесса, переходные вероятности этой модели выражаются следующим образом
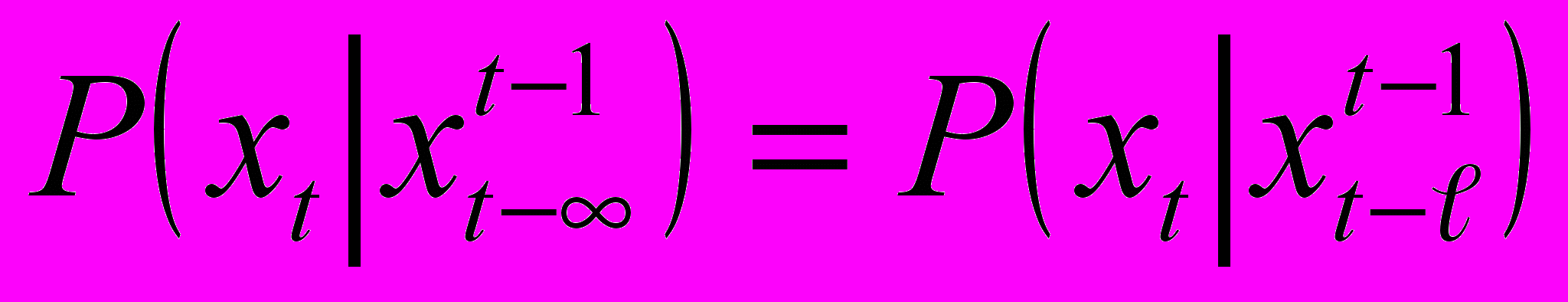 , (2), где переменный марковский порядок определяется как
, (2), где переменный марковский порядок определяется как  . (3).
. (3).Контекстной функцией c в данном случае будет отображение
 , а результат действия этой функции
, а результат действия этой функции 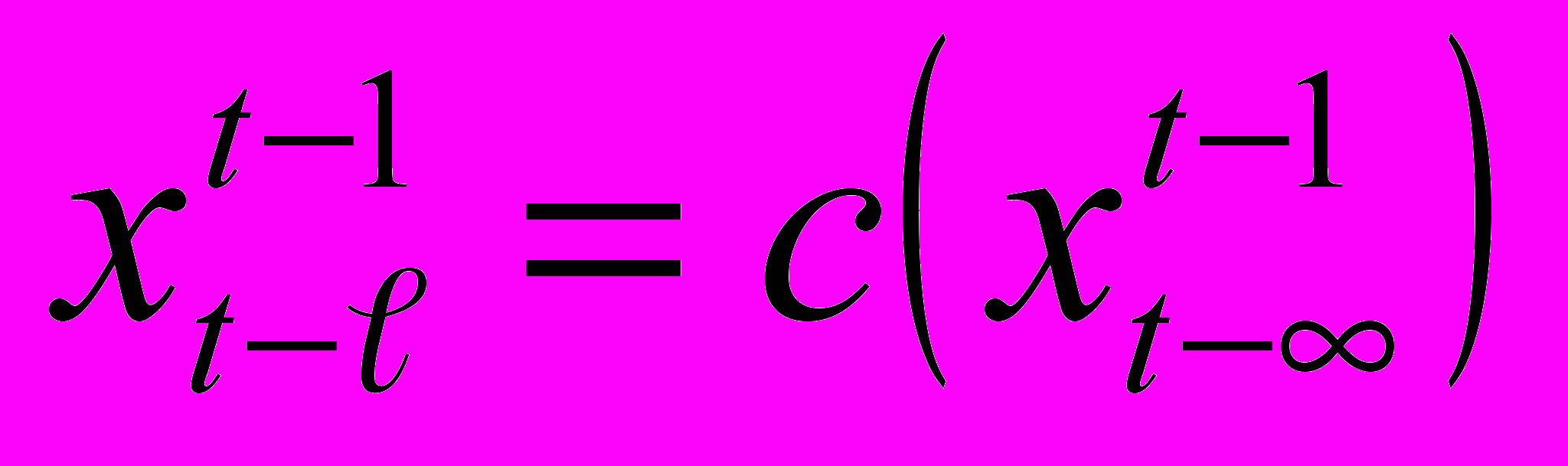 — последовательность отсчетов переменной длины, которая определяет распределение последующего отсчета в (2). Задача оценивания параметров данной модели сводится к отысканию вида контекстной функции c или, что аналогично, оцениванию зависимости (3). Следует отметить, что марковская цепь переменного порядка является марковской цепью некоторого порядка 0≤k≤∞, такого, что
— последовательность отсчетов переменной длины, которая определяет распределение последующего отсчета в (2). Задача оценивания параметров данной модели сводится к отысканию вида контекстной функции c или, что аналогично, оцениванию зависимости (3). Следует отметить, что марковская цепь переменного порядка является марковской цепью некоторого порядка 0≤k≤∞, такого, что  .
.Основное отличие от традиционной многосвязной цепи конечного порядка состоит в том, что некоторые переходные вероятности многосвязной марковской цепи, эквивалентной марковской цепи переменного порядка, будут совпадать.
В работе предложены методы оценивания порядка многосвязной двоичной марковской цепи и оценивания контекстной функции марковской цепи переменного порядка на основе дискриминирующей функции для биномиального распределения [3].
Дискриминирующая функция представляет собой некоторую меру, показывающую, насколько близки между собой две переходные вероятности, оцененные по конечной выборке, и выражается следующим образом
 , (4), где
, (4), где  ,
,  ,
,  ,
,  ,
,  , где функция
, где функция  представляет собой число повторений в анализируемой выборке соответствующей комбинации бит.
представляет собой число повторений в анализируемой выборке соответствующей комбинации бит.Алгоритм оценивания порядка марковской цепи состоит в следующем. Рассчитывается k+1 значение дискриминирующей функции (4) между соответствующими переходными вероятностями марковских моделей порядка k и k+1, отличающихся только одним отсчетом, максимально удаленным от текущего. В качестве критерия используется среднее значение дискриминирующей функции.
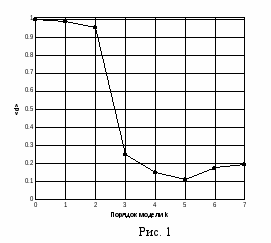
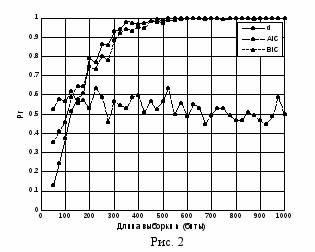
На рис. 1 приведен пример зависимости среднего значения дискриминирующей функции от порядка модели k, причем для генерации исследуемой выборки использовался порядок модели, равный 3. Там же показан порог Δ=0.5 по которому производится оценивание порядка марковской цепи. В качестве оценки поряд-ка марковской цепи принимается минимальное значение k при котором среднее значение дискриминирующей функции будет меньше порога Δ. На рис. 2 приведены зависимости вероятности правильной оценки порядка марковской цепи в зависимости от длины выборки. Представленные зависимости — для предложенного метода (кривая d), метода на основе информационного критерия Акаике (кривая AIC) и метода на основе информационного критерия Байеса (кривая BIC). Зависимости получены усреднением по 200 выборкам и для одного распределения второго порядка.
Анализ зависимостей на рис. 2 показывает, что предложенный метод при длине выборки более 200 бит ведет себя не хуже, чем метод на основе информационного критерия Байеса и лучше, чем метод на основе информационного критерия Акаике. При этом вычисление дискриминирующей функции не связано с операцией логарифмирования, что исключает вычислительные трудности, возникающие при стремлении аргумента логарифма к нулю.
Алгоритм оценивания контекстной функции основан на непосредственном сравнении оценок для каждой пары соответствующих переходных вероятностей и заключается в следующем.
На первом шаге строится граф (полное контекстное дерево) корневой узел которого соответствует приближению случайного процесса с одинаково и независимо распределенными отсчетами. Вначале контекстное дерево состоит только из корневого узла.
На следующих шагах к имеющемуся дереву добавляются дочерние узлы, соответствующие переходным вероятностям марковского процесса всё увеличивающегося порядка. Процесс построения полного кон-текстного дерева продолжается до тех пор пока встречается не менее двух комбинаций бит, соответствующих предыстории (контексту) в переходных вероятностях.
На следующем шаге производится обрезание узлов дерева, в качестве критерия используется значение дискриминирующей функции (4). Если значение дискриминирующей функции, рассчитанное между листом дерева и его предком, меньше некоторого порога Δ, данный лист дерева отбрасывается. Отбрасывание узлов из контекстного дерева продолжается до тех пор, пока есть возможность это делать. По полученному в конце контекстному дереву можно установить вид контекстной функции
 и зависимость переменного порядка марковской цепи
и зависимость переменного порядка марковской цепи  .
.Порог принятия решения Δ является параметром алгоритма и его оптимальное значение может быть определено численным моделированием и анализом зависимости логарифма правдоподобия или по бутстреп методу, предложенному в [2].
Предложенный метод был применен к оцениванию параметров марковской цепи переменного порядка для двоичных сверточно кодированных сигналов. Использовались два сверточных кодера в следующем полиномиальном представлении [7 5] и [7 7 5]. В таблице приведены характеристики моделей, параметры которых были оценены предложенным методом и методом на основе меры Кульбака-Лейблера [2], где оптимальное значение порога определялось по минимуму отрицательного нормированного логарифма правдоподобия.
Таблица
| Кодер | Предложенный метод | Метод [2] | ||||||
| AIC | D | k | D/2k | AIC | D | k | D/2k | |
| [7 5] | 1063 | 60 | 11 | 0.029 | 982 | 50 | 11 | 0.024 |
| [7 7 5] | 695 | 85 | 11 | 0.042 | 662 | 97 | 13 | 0.012 |
В таблице приведены следующие значения AIC — информационный критерий Акаике, D — количество свободных параметров модели, k — порядок эквивалентной марковской цепи, отношение D/2k — показывает превосходство марковской модели переменного порядка над многосвязной марковской цепью по количеству параметров.
Анализируя результаты приведенные в таблице, можно сказать, что в некоторых случаях модели пара-метры, которых оценены предложенным методом получаются переоцененными. На это указывает тот факт, что значение информационного критерия Акаике для них получается большим, чем для моделей оцененных методом [2], но количество параметров у этих моделей различается слабо.
Таким образом показано, что предложенный алгоритм на основе дискриминирующей функции не хуже, чем алгоритм на основе меры Кульбака-Лейблера и избавлен от вычислительных трудностей, связанных со стремлением аргумента логарифма к нулю.
Литература
- Яншин В. В. Многосвязные цепи Маркова и их свойства // Радиотехника и электроника.— 1993.— Т. 38, № 6.— С. 1081–1091.
- Buhlmann P., Wyner A. J. Variable length Markov chains // The Annals of Statistics.— 1999.— V. 27, No. 2.— P. 480–513.
- Бурланков Д.Е., Коньков Е.А. Дискриминирующая функция для сравнения статистических свойств двоичных сигналов // Труды РНТОРЭС им. А. С. Попова № IX-2.— 2007.—28–30 марта 2007 г., Москва, Институт проблем управления РАН.— С. 439–442.
Application of discrimination function in markov chain order estimation and estimation of context function for variable length markov chain
Avdashov S.1, Konkov E.2
1Nizhny Novgorod State University
2Physical-Technical Research Institute of Nizhny Novgorod State University
Simple Markov chains are used as mathematical models of wide range of devices, processes, signals in digital communication systems. In some cases high-order and variable length Markov chains are used [1, 2].
To overcome difficulties related to limited sample size in high-order Markov chain parameters estimation method of reduction of parameters number was proposed [2]. Variable length Markov chain is high-order Markov chain which order is depends on previous samples of process. The main difference between variable length Markov chain and high-order Markov chain is than some probabilities of equivalent high-order Markov chain is equal to each other.
In this paper we propose two methods based on discrimination function for binomial distribution [3]. The first method is method of order estimation of high-order binary Markov chain and the second method of parameters estimation of variable length Markov chain.
High-order Markov chain order estimation method consists in comparison of transition probability distributions belongs to Markov chains of order k and k+1 by discrimination function, criterion is average value of discrimination function. High-order Markov chain order estimator is defined as minimum value of k on condition that average value of discrimination function is less than threshold Δ. Computer simulation results analysis shows that proposed method is better than method based on Akaike information criterion and not worse than method based on Bayes information criterion on condition that sample length is greater than 200 bits. In proposed methods calculation of discrimination function doesn’t involve logarithm operation, which eliminates computational difficulties arisen in the case when argument of logarithm tends to zero.
Algorithm of estimation of parameters of variable length Markov chain is based on direct comparison of estimation for every pair of corresponding transition probabilities. Proposed method was applied in model parameters estimation of binary convolution coded signals. Analysis of results shows than in some cases models, which estimated by proposed method is slightly overestimated than models estimated by method based on Kullback-Leibler measure [2].
References
- Яншин В. В. Многосвязные цепи Маркова и их свойства // Радиотехника и электроника.— 1993.— Т. 38, № 6.— С. 1081–1091.
- Buhlmann P., Wyner A. J. Variable length Markov chains // The Annals of Statistics. — 1999.— V. 27, No. 2.— P. 480–513.
- Burlankov D., Konkov E. Discrimination function for comparison of statistic properties of binary signals // Proceedings of the 9-th International Conference Digital signal processing and its applications — 28–30 March, 2007, Moscow, Russia. — P. 439–442.
Применение комбинированных цепей Маркова для анализа двухуровневой синхронизации системы передачи OFDM
Чвало В.А., Чесноков Е.А.
Ярославский Государственный Университет им. П.Г. Демидова
Развитие современных систем передачи информации порождают потребность в универсальных и более эффективных методах анализа. Для удовлетворения такой потребности хорошо подходит метод анализа на основе Марковских цепей. Как известно, большинство систем синхронизации можно представить в виде цепей Маркова [1]. Аппарат Марковских цепей позволяет получить широкий спектр статистических характеристик системы, тем самым произвести полный и эффективный анализ работы исследуемой системы синхронизации.
Известные методы анализа цикловой синхронизации данных в OFDM системах основываются на усредненных оценках ошибок работы системы символьной синхронизации, осуществляющей поиск начала символа на основе циклического префикса [2]. Подобный подход не учитывает статистические особенности возмущающих воздействий на систему цикловой синхронизации данных. Интерес представляет исследование влияния реальных помех на точность синхронизации обеих систем в целом. Для этого необходимо две парциальные системы синхронизации объединить в одну комбинированную. Сложность состоит в существовании двух временных шкал (по числу уровней синхронизации) и, соответственно, в переводе систем более низкого уровня синхронизации во временное измерение систем высокого уровня.
В работе предложен метод для исследования комбинированной системы символьной синхронизации OFDM и цикловой синхронизации данных в условиях воздействия аддитивной помехи. Большинство алгоритмов символьной синхронизации OFDM, как показано на рис.1а, состоят из двух основных операций [3]: грубой символьной (кадровой) синхронизации, т.е. приблизительной оценки позиции старта OFDM кадра и точной символьной синхронизации, ориентированной на компенсацию частотных сдвигов.


а) б)
Рис.1. Цепь синхронизации (а) и схема OFDM демодулятора (б).
Будем предполагать, что в исследуемой системе отсутствует частотный сдвиг. Тогда для осуществления цикловой синхронизации достаточно грубой символьной синхронизации, для которой используется обычный коррелятор (рис.2а). Для него можно определить следующий алгоритм [3]:
 . (1),
. (1),  (2),
(2),где NG – длина циклического префикса OFDM символа в преамбуле, NI – длина OFDM символа в преамбуле, le – пороговое значение, xcoarse – грубая оценка начала OFDM кадра, r – сигнал на входе OFDM демодулятора.
На выходе OFDM демодулятора данные детектируются, и для того, чтобы выделить из потока данных полезную информацию, применяется цикловая синхронизация. Структурная схема циклового синхронизатора показана на рис.2б. Для него можно определить следующее выражение [3]:
 . (3)
. (3) , (4), где m – оценка расположения синхрослова, le – пороговое значение, s – синхропоследовательнось, ρ – принятый сегмент, K – длина синхрослова.
, (4), где m – оценка расположения синхрослова, le – пороговое значение, s – синхропоследовательнось, ρ – принятый сегмент, K – длина синхрослова.
а)

б)
Рис.2. Система грубой синхронизации OFDM символов (а) и цикловой синхронизации данных (б).
Анализ случайных процессов, описывающих потерю и восстановление синхронизации, может быть выполнен с помощью математической модели в форме комбинированной цепи Маркова (рис. 3), которая состоит из двух графов разных уровней синхронизации.
На нижнем уровне рис.3 приведен граф системы символьной синхронизации OFDM, где p – вероятность правильного распознавания начала кадра, учитывающая аддитивную помеху и связана с реализацией алгоритма. Вероятность p определяется следующим выражением:
 (5)
(5)
Рис.3. Математическая модель двухуровневой системы синхронизации в виде графа комбинированной цепи Маркова.
Из графа видно, что из состояния правильной синхронизации A0 устройство синхронизации символов мо-жет перейти в состояние B0 только после α последовательно ошибочно определенных «тренировочных» символов в преамбуле. В состоянии B0 устройство синхронизации символов находится в процессе поиска и, как только оно находит начало кадра, переключается в состояние правильной синхронизации символов C0. Из этого состояния устройство синхронизации символов переходит в состояние A0 только после δ+1 последовательно безошибочно принятых «тренировочных» символов. После определения первого же ложного начала кадра устройство возвращается обратно в состояние B0, и процесс поиска начинается снова.
На верхнем уровне рис.3 приведен граф системы цикловой синхронизации данных после детектора, где p’ – вероятность правильного распознавания начала кадра данных, учитывающая аддитивную помеху и работу системы символьной синхронизации OFDM через вероятность p, связана с реализацией алгоритма поиска через вероятность распознавания кадра при нулевой битовой ошибке p’0:
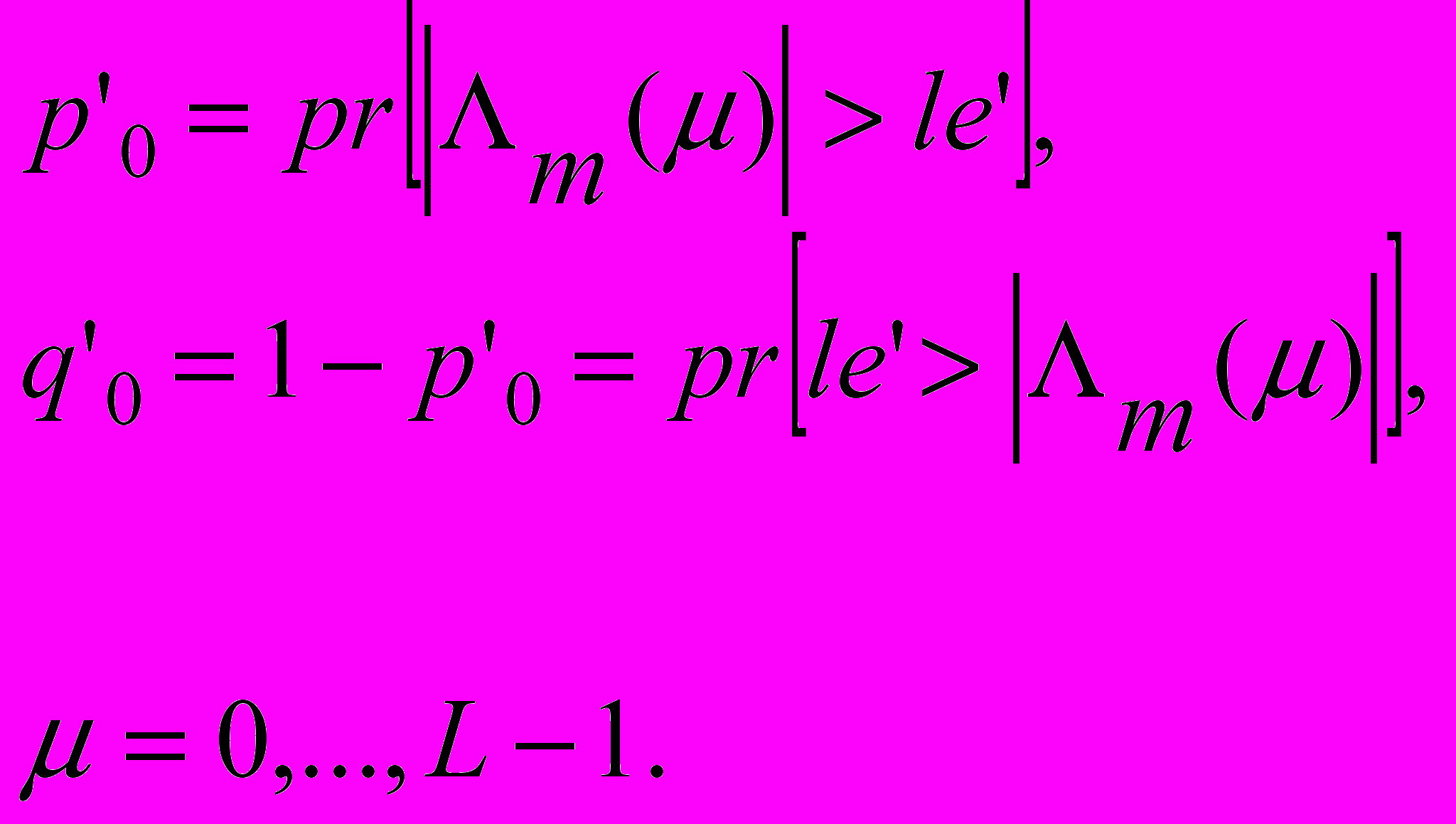 (6), где L - длина цикла.
(6), где L - длина цикла.Структура графа аналогична структуре для системы синхронизации OFDM кадра.
Матрица состояния комбинированной цепи [4,5]:
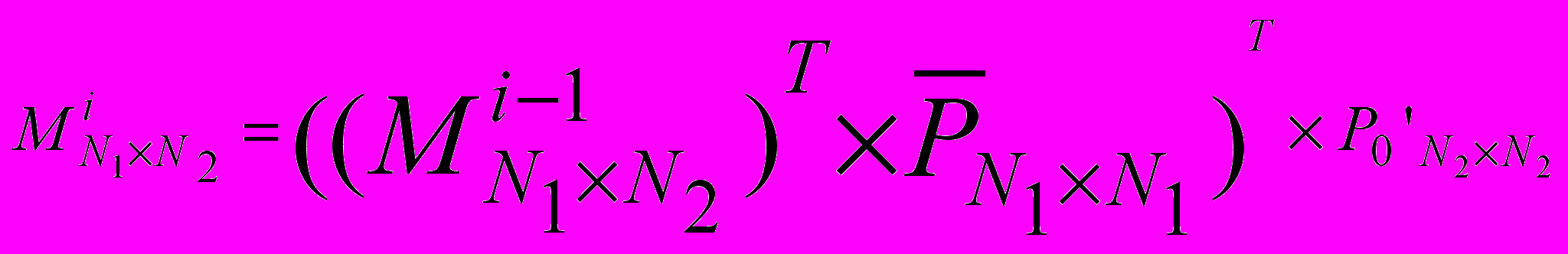 , (7), где
, (7), где 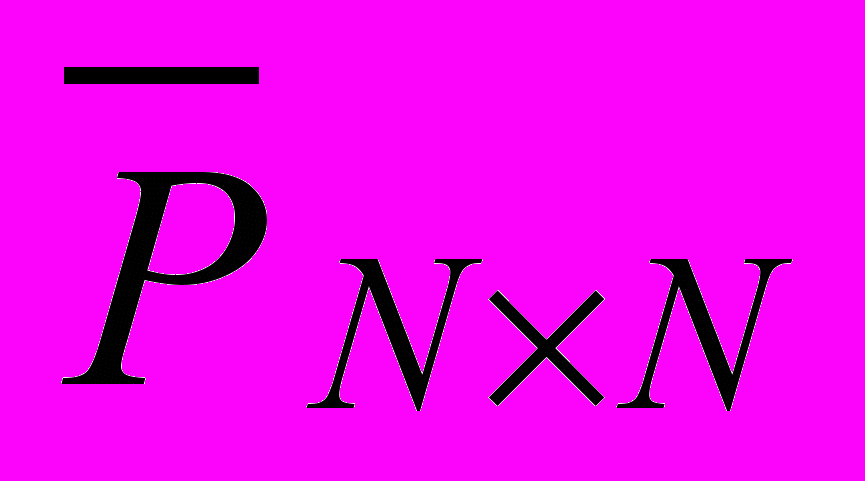 – приведенная матрица, характеризующая работу системы символьной синхронизации OFDM (8); N1, N2 – количество состояний системы синхронизации нижнего и верхнего уровня рис.3 соответственно.
– приведенная матрица, характеризующая работу системы символьной синхронизации OFDM (8); N1, N2 – количество состояний системы синхронизации нижнего и верхнего уровня рис.3 соответственно.  . (8)
. (8)Выражение (7) можно представить в следующем виде [4,5]:
 , (9)
, (9)где
 – матрица, характеризующая работу комбинированной цепи.
– матрица, характеризующая работу комбинированной цепи.Состояние комбинированной цепи определяется двумя состояниями (i, j) и определяется матрицей состояния
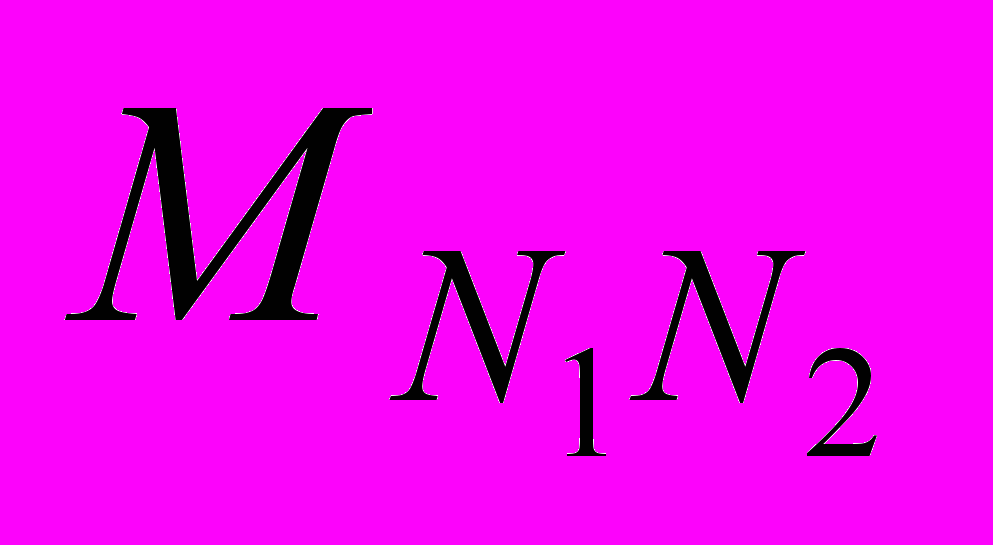 (9). Рабочее время системы равно одному циклу данных. Всего возможных состояний системы – N1 N2.
(9). Рабочее время системы равно одному циклу данных. Всего возможных состояний системы – N1 N2.Выражения (7) и (9) позволяют рассчитать достаточно широкий набор статистических характеристик, описывающих качество работы системы, таких как среднее время вхождения в синхронизм, среднее время до срыва слежения, средняя ошибка синхронизации.
На основе построенной модели и полученных выражений для матрицы вероятностей перехода были проведены исследования статистических характеристик описанной модули цикловой синхронизации. Некоторые результаты для случая комбинированного воздействия аддитивной и фазовой помех представлены на рис. 4. Здесь q1 – отношение сигнал / аддитивный шум на входе OFDM демодулятора, N g – длина циклического префикса, L – длина цикла данных, K – длина синхрослова.

Рис. 4. СКО ошибки синхронизации для NI=128, α=3, δ=3, L=128, K=16, α’=3, δ’=3.
На рис. 4 показана зависимость СКО ошибки синхронизации системы цикловой синхронизации данных от q1 для разных длин циклического префикса. Интересным результатом здесь является уменьшение СКО ошибки при увеличении Ng. Данный результат можно объяснить тем, что, чем длиннее циклический префикс, тем меньшее СКО ошибки синхронизма за счет лучшего усреднения аддитивного шума при вычислении корреляционных моментов, что приводит к более стабильной работе системы символьной синхронизации OFDM.
Литература
1. Тихонов В.И., Миронов М.А. Марковские процессы. М.: "Советское радио", 1977. 488 с.
2. Брени С. Синхронизация цифровых сетей связи. М.: Мир, 2003. 456 с.
3. Mody, "Time and frequency synchronization in multi-input, multi-output (MIMO) systems " U.S. Patent 7,088,782,B2 filed Apr. 24 2002 issued Aug. 8 2006.
4. Чвало В.А., Волченков А.В. Применение комбинированных цепей Маркова для анализа систем тактовой и цикловой синхронизации // труды конференции Цифровая обработка сигнала и ее применение, выпуск IX-1, Москва,2007.
5. Чвало В.А., Волченков А.В Применение комбинированных цепей Маркова для анализа систем тактовой и цикловой синхронизации. // труды научно-технического семинара "Системы синхронизации, формирования и обработки сигналов для связи и вещания", Одесса, 2007.
APPLICATION OF COMBINED CIRCUITS МАРКОВА FOR THE ANALYSIS OF TWO-LEVEL SYNCHRONIZATION OF TRANSFER OFDM SYSTEM
Chvalo V., Chesnokov E.
Yaroslavl State University
Development of modern data-transmission system generate need for universal and more effective methods of the analysis. For satisfaction of such need the method of the analysis on the basis of Markov chain well approaches. As is known, the majority of synchronization systems can be presented in the form of Markov chains [1]. It is obvious, that device of Markov chains allows to receive a wide spectrum of statistical characteristics of system [1]. Thus, it is possible to make the full and effective analysis of work of investigated synchronization system.
In the majority of methods of the analysis of data cyclic synchronization system the account of work of OFDM symbolical synchronization system is carried out due to values of its average mistake. Interest represents research of influence of real handicapes on both systems as a whole. For this purpose it is necessary to present two simple synchronization systems as one combined. Complexity consists in translation of lower level synchronization systems in time measurement of a high level systems.
The analysis of the casual processes describing loss and restoration of synchronization, can be executed by means of mathematical model of combined Markov chain [3,4] which consists of two graphs different levels of synchronization.
The equation of combined Markov chain [3,4]:
 , (1), where
, (1), where  – matrix, describing work of the combined chain, N1, N2 – quantity of conditions of synchronization system bottom and top level.
– matrix, describing work of the combined chain, N1, N2 – quantity of conditions of synchronization system bottom and top level.The condition of the combined circuit is defined by two conditions (i, j) and defined by a matrix of a condition
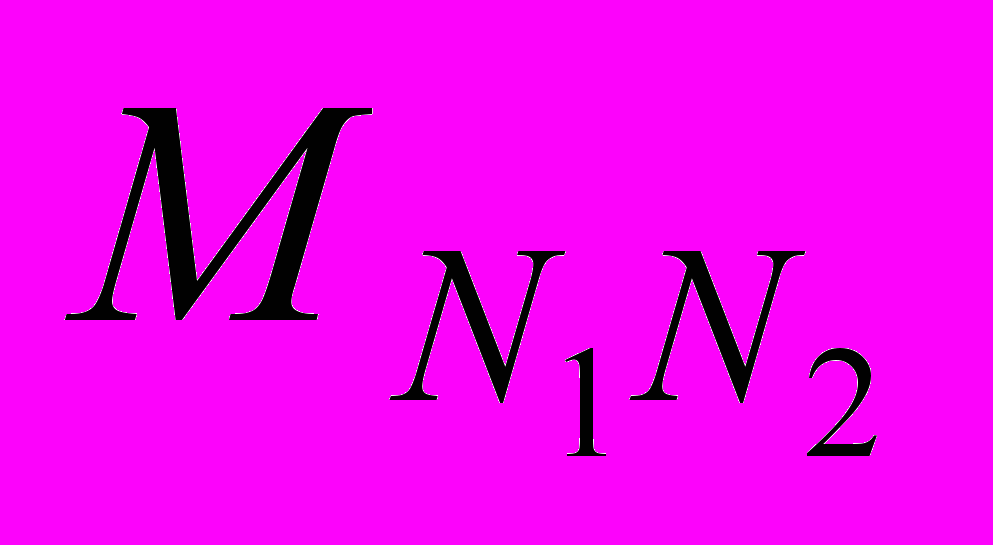 (1). Working hours of system to equally one cycle of data. In total possible conditions of system – N1 N2.
(1). Working hours of system to equally one cycle of data. In total possible conditions of system – N1 N2.Expression (1) allows to calculate wide enough set of the statistical characteristics describing quality of work of system, such as average time of ocurrence in synchronism, average time before failure of tracking, an average mistake of synchronization.
Bibliography
1. Тихонов В.И., Миронов М.А. Марковские процессы. М.: "Советское радио", 1977. 488 с.
2. Mody, "Time and frequency synchronization in multi-input, multi-output (MIMO) systems " U.S. Patent 7,088,782,B2 filed Apr. 24 2002 issued Aug. 8 2006.
3. Чвало В.А., Волченков А.В. Применение комбинированных цепей Маркова для анализа систем тактовой и цикловой синхронизации // труды конференции Цифровая обработка сигнала и ее применение, выпуск IX-1, Москва,2007.
4. Чвало В.А., Волченков А.В Применение комбинированных цепей Маркова для анализа систем тактовой и цикловой синхронизации. // труды научно-технического семинара "Системы синхронизации, формирования и обработки сигналов для связи и вещания", Одесса, 2007.
система компенсации фазы несущей сигнала OFDM на основе частотно-фазовой автоподстройки
Шабанов А.В., Марков К.А.
Ярославский государственный университет имени П.Г. Демидова, alexsh@uniyar.ac.ru
Аннотация
В работе предложена комбинированная система компенсации частоты и фазы несущей сигнала OFDM с учетом нескольких спектральных компонент фазового шума. Показана зависимость эффективности работы системы от количества оцениваемых компонент для фазового шума c умеренными корреляционными свойствами.
Рассмотрим передачу сигнала с ортогональным частотным разделением на N поднесущих при наличии нескомпенсированного фазового шума в канале. В случаи идеальной временной синхронизации OFDM-сигнал может быть представлен следующим образом:
 , (1), где p(k) представляет собой результат свертки последовательности отсчетов OFDM-сигнала и импульсной характеристики канала, w(k) - АБГШ и
, (1), где p(k) представляет собой результат свертки последовательности отсчетов OFDM-сигнала и импульсной характеристики канала, w(k) - АБГШ и 
 -мультипликативная помеха, обусловленная фазовым шумом генератора и частотной ошибкой в гетеродине.
-мультипликативная помеха, обусловленная фазовым шумом генератора и частотной ошибкой в гетеродине. В приемнике после удаления циклического префикса и применения БПФ принятый сигнал
 m-ого OFDM-символа, l-ой (l=0,1,…N-1) поднесущей представляется следующим образом [1]:
m-ого OFDM-символа, l-ой (l=0,1,…N-1) поднесущей представляется следующим образом [1]: , (2), где
, (2), где  . (3)
. (3)Первый член в (2) обуславливает одинаковое вращение полезной компоненты
 всех поднесущих; I(0) называется групповой фазовой ошибкой (CPE). Второй член обуславливает интерференцию между поднесущими из-за потери их ортогональности. Большинство известных алгоритмов компенсации фазы несущей сигнала OFDM учитывает только CPE компоненту, причем оценка производится в спектральной области (после БПФ). Тем не менее, в некоторых ситуациях требуется дополнительная компенсация, например, в случае широкополосного фазового шума или при наличии частотной ошибки.
всех поднесущих; I(0) называется групповой фазовой ошибкой (CPE). Второй член обуславливает интерференцию между поднесущими из-за потери их ортогональности. Большинство известных алгоритмов компенсации фазы несущей сигнала OFDM учитывает только CPE компоненту, причем оценка производится в спектральной области (после БПФ). Тем не менее, в некоторых ситуациях требуется дополнительная компенсация, например, в случае широкополосного фазового шума или при наличии частотной ошибки.Рассмотрим влияние некомпенсированного частотного сдвига на OFDM сигнал. В случае,
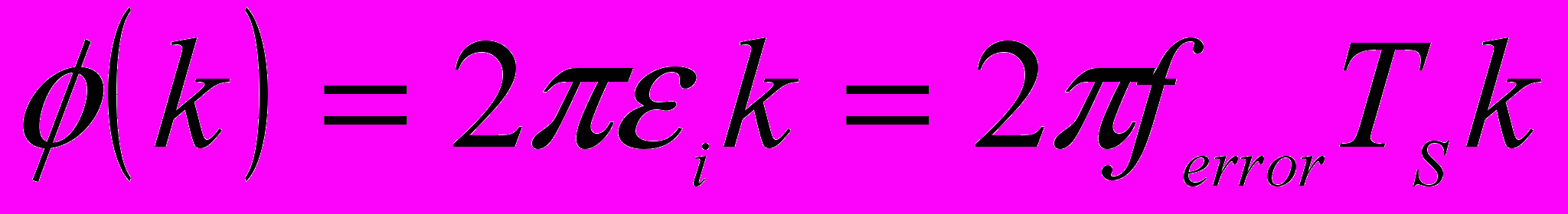 , где
, где  - частотная ошибка, а
- частотная ошибка, а  - период символа OFDM. Результирующее отношение сигнал/шум с учетом влияния частотной ошибки имеет следующий вид [2]:
- период символа OFDM. Результирующее отношение сигнал/шум с учетом влияния частотной ошибки имеет следующий вид [2]: , (4), где
, (4), где  - средняя энергия, приходящаяся на отдельную несущую в полученном сигнале, а N/2 - спектральная плотность мощности АБГШ.
- средняя энергия, приходящаяся на отдельную несущую в полученном сигнале, а N/2 - спектральная плотность мощности АБГШ.Несмотря на то, что при большом числе поднесущих действие межканальной интерференции эквивалентно воздействию АБГШ на каждую несущую, рассматривая одновременно несколько несущих и используя последовательную оценку, мы можем скомпенсировать воздействие фазового шума.
Поскольку для решения системы из K неизвестных необходимо K уравнений, при наличии N несущих мы имеем возможность получить [N/K] оценок для каждой искомой компоненты фазового шума, что позволяет, применив усреднение по ансамблю, снизить влияние АБГШ на оценку. Отсюда следует, что при увеличении количества оцениваемых компонент эффективность алгоритма компенсации в условиях присутствия аддитивной помехи будет неизбежно падать.
Следует заметить, что при отсутствии частотной расстройки мощность нулевой составляющей межканальной интерференции I(0) на порядок превышает мощность любой другой компоненты. При наличии частотной ошибки основная мощность шума приходится на старшие спектральные компоненты в разложении (2). Как сказано выше, поскольку с увеличением количества оцениваемых компонент вероятность ошибочной оценки возрастает, оценка частотной ошибки в спектральной области нецелесообразна. Следовательно, для оценки частотной ошибки необходим алгоритм, работающий во временной области. В этом случае целесообразно применить трехступенчатую схему компенсации:
- Компенсация постоянной на периоде символа составляющей частотной ошибки во временной области.
- С использования любого известного алгоритма производится оценка CPE компоненты. При этом к точности компенсации CPE компоненты предъявляются строгие требования: мощность остаточной CPE компоненты после компенсации должна быть как минимум на порядок меньше мощности старших спектральных составляющих.
- После оценки CPE компоненты необходимо приступить к оценке старших спектральных компонент в (3).
В соответствии с данными выводами была разработана комбинированная система компенсации фазы несущей, использующая для своей работы информационные каналы и содержащая работающую во временной области оптимальную систему ЧАП, систему компенсации CPE с многоканальным фазовым дискриминатором и систему компенсации высокочастотных составляющих фазового шума. Блоки компенсации CPE и высокочастотных составляющих фазового шума функционируют в частотной области – после БПФ в приемнике.
Система ЧАП синтезирована при помощи квазилинейного гауссовского метода синтеза следящих систем при помощи теории оптимального фильтра Калмана. В качестве основы частотного дискриминатора использован априори введенный оптимальный по критерию максимума правдоподобия частотный оцениватель, использующий корреляционные свойства сигнала OFDM [2].
Система оценки CPE, работающая в частотной области, также является оптимальным фильтром Калмана [4]. Блок компенсации высокочастотных спектральных компонент фазового шума предложен автором в работе [6].

Рис. 1. Эквивалентная схема комбинированной системы частотно-фазовой автоподстройки
На рис. 1. представлена эквивалентная схема комбинированной системы компенсации частоты и фазы, не учитывающая блок компенсации высокочастотных составляющих. Результаты исследования разбиты на две группы: зависимости дисперсии фазовой ошибки и вероятности ошибки на бит от параметров системы и канала (рис. 2 и зависимости дисперсии фазовой ошибки от количества оцениваемых спектральных компонент фазового шума (рис. 3).
Как видно из рис. 2, предлагаемая система обеспечивает достаточный (до 0.001) уровень ошибки в условиях переменной частотной ошибки и широкополосного фазового шума.

Рис. 2.Зависимость вероятности ошибки (а) и дисперсии фазовой ошибки от ОСШ для разных коэффициентов в кольце ЧАП при коэффициенте в кольце ФАП К2=0.7
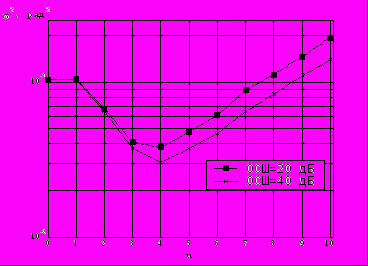
Рис. 3. Зависимость дисперсии фазовой ошибки от порядка аппроксимации для случая воздействия синтезаторной модели фазового шума
На рис. 3 можно видеть зависимость точности компенсации непосредственно от количества оцениваемых компонент. Как можно видеть, для случая фазового шума средней степени корреляции (с характеристикой спектральной плотности мощности, характерной для синтезаторов частоты на основе колец ФАП) с параметрами, выбранными исходя из области выигрыша данного алгоритма для данного типа шума, эффективность компенсации резко возрастает при переходе от компенсации одной компоненты к учету первых двух и трех компонент (вероятность ошибки падает с 0.1 до 0.06 при учете двух и до 0.04 при учете трех спектральных компонент). При дальнейшем увеличении выигрыш от увеличения количества компонент снижается, а с увеличением их до 5 начинает наблюдаться увеличение вероятности ошибки, объясняющееся уменьшением точности оценки в условиях наличия АБГШ за счет снижения статистического массива для усреднения. Таким образом, увеличение порядка аппроксимации, особенно с учетом вычислительной сложности алгоритма, выше 3-4 нецелесообразно.
Литература
- Petrovic, W. Rave, and G. Fettweis. Intercarrier Interference due to Phase Noise in OFDM – Estimation and Suppression. // In Proceedings of the 60th IEEE Vehicular Technology Conference (VTC'04 Fall) California. - 2004.
- J.-J van de Beek et al. ML Estimation of Timing and Frequency Offset in Multicarrier Systems // IEEE Trans. on Signal Processing, Vol. 45, Issue 7, 1997 – pp. 1800 - 1805.
- Александров А.С, Шабанов А.В. Carrier Frequnency Recovery with Maximum Likelihood Frequency Detector in OFDM Systems // IEEE International Conference: Сборник докладов 2-й международной конференции 30 июня – 2 июля 2004 г. – М., 2004., 4c
- Казаков Л.Н., Кукушкин Д.С., Шабанов А.В. Система коррекции фазы в канале OFDM на основе многомерного фильтра Калмана // Сборник трудов 61 научной сессии, посвященной дню радио, 14–15 мая 2006 г. – М., 2006. - С. 123-125.
- V.S Abhayawardhana, I.J. Wassel Common Phase Error Correction with Feedback for OFDM in Wireless Communication,
- Шабанов А.В., Карпов С.В. Сравнительный анализ эффективности различных алгоритмов компенсации фазовой ошибки в OFDM-системах // Электросвязь.-2006.-№10.-С.18-21.
- Шабанов А.В., Карпов С.Б., Марков К.А. Компенсация низкочастотных составляющих фазового шума в OFDM системах // Цифровая обработка сигналов и ее применение: Сборник докладов 9–ой международной конференции 28-30 марта 2007 г. – М., 2007. – C. 187-190.
OFDM signal`s carrier phase compensation system on the basis of combined frequency-phase tracking
Shabanov A., Markov K.
Yaroslavl state university, alexsh@uniyar.ac.ru
In the work the OFDM signal`s carrier phase compensation system on the basis of combined frequency-phase tracking considering several spectral components of phase noise is offered. In work the three-stage algorithm of indemnification is applied:
1. Compensation of a constant on the period of a symbol frequency error, implemented in time domain, to be made.
2. Utilizing any known algorithm estimation of common phase error (CPE) component to be applied. Here there are strict demands made to accuracy of compensation CPE: the power of residual CPE component after compensation should be much less then the high-frequency spectral components` one.
3. After estimation CPE component it is necessary to start an estimation of high-frequency ones.
According to the given conclusions the combined frequency-phase tracking system, utilizing information channels and containing optimum frequency-tracking system, implemented in time domain, CPE compensation system with the multichannel phase discriminator and high-frequency phase noise components estimation system has been developed. CPE compensation and high-frequency phase noise components estimation blocks function in frequency domain after FFT in receiver. Frequency-tracking system is synthesized by means of quasilinear gaussian method of tracking systems synthesis applying the optimum Kalman filtering theory. As a basis of the frequency discriminator it is used a priori entered optimum by criterion of a maximum likelihood frequency estimator, using correlation properties of OFDM signal [2]. The CPE estimation system works in frequency domain and is a kind of optimum Kalman filter too[4]. The high-frequency phase noise spectral components estimation is proposed by the author in [6]. The offered system provides sufficient (up to 0.001) bit error rate in conditions of a variable frequency error and broadband phase noise. In case of average-correlated phase noise, efficiency of compensation sharply increases at transition from consideration of one component to the first two and three components (the probability of a mistake falls with 0.1 till 0.06 at the account of two and till 0.04 at the account of three spectral components). With the further increase of considered components number a gain decreases, and with their increase up to 5 the increase in BER is observed. It can be explained by reduction of accuracy of an estimation in conditions of AWGN presence due to statistical array decreasing. Thus, the increase in the order of approximation, especially in view of computing complexity of algorithm, above 3-4 is inexpedient.
Bibliography
- Petrovic, W. Rave, and G. Fettweis. Intercarrier Interference due to Phase Noise in OFDM – Estimation and Suppression. // In Proceedings of the 60th IEEE Vehicular Technology Conference (VTC'04 Fall) California. - 2004.
- J.-J van de Beek et al. ML Estimation of Timing and Frequency Offset in Multicarrier Systems // IEEE Trans. on Signal Processing, Vol. 45, Issue 7, 1997 – pp. 1800 - 1805.
- Александров А.С, Шабанов А.В. Carrier Frequnency Recovery with Maximum Likelihood Frequency Detector in OFDM Systems // IEEE International Conference: Сборник докладов 2-й международной конференции 30 июня – 2 июля 2004 г. – М., 2004., 4c
- Казаков Л.Н., Кукушкин Д.С., Шабанов А.В. Система коррекции фазы в канале OFDM на основе многомерного фильтра Калмана // Сборник трудов 61 научной сессии, посвященной дню радио, 14–15 мая 2006 г. – М., 2006. - С. 123-125.
- V.S Abhayawardhana, I.J. Wassel Common Phase Error Correction with Feedback for OFDM in Wireless Communication,
- Шабанов А.В., Карпов С. В. Сравнительный анализ эффективности различных алгоритмов компенсации фазовой ошибки в OFDM-системах // Электросвязь.-2006.-№10.-С.18-21.
Цифровая обработка сигналов и ее применение
Digital signal processing and its applications
