Теория сигналов и систем

Вид материала

Документы

Содержание Характеристики алгоритмов приема ансамблей сигналов с небольшим информационным объемом Performances of decoding algorithms for signals with constrained information volume Эффективность многопороговых декодеров при использовании многопозиционных фм и кам N, жесткий модем На рис. 1 кривыми 4 1 еще раз показаны характеристики МПД самоортогонального кода с кодовой скоростью R The performance of multithreshold decoders at using multipositional modulation

Подобный материал:

• Теория сигналов и систем, 143.44kb.
• Тема пространство и метрология сигналов физическая величина более точно определяется, 595.48kb.
• Программа учебной дисциплины «Теория сигналов» Специальности 071500, 013900 (СД. 05), 82.24kb.
• Программа-минимум кандидатского экзамена по специальности 05. 12. 14 «Радиолокация, 134.92kb.
• Программа-минимум кандидатского экзамена по специальности 05. 12. 14 «Радиолокация, 236.33kb.
• Н. Г. Чернышевского кафедра радиофизики и нелинейной динамики рабочая программа, 145.34kb.
• Цифровая обработка сигналов, 25.15kb.
• Программа-минимум кандидатского экзамена по специальности 05. 12. 13 «Системы, сети, 151.82kb.
• Программа-минимум кандидатского экзамена по специальности 05. 12. 13 «Системы, сети, 121.7kb.
• Программа вступительного экзамена по специальности 05. 13. 06 " автоматизация и управление, 128.46kb.

THE ERROR-PERFORMANCE INVESTIGATIONS FOR TURBO-CODES BASED ON BLOCK CODES


Nazarov L., Golovkin I.

Institute of Radioengineering and Electronics RAS, Fryazino


There are the results of investigations for error-performances for class of turbo-codes based on block codes. The base of analytical technique for error-performance 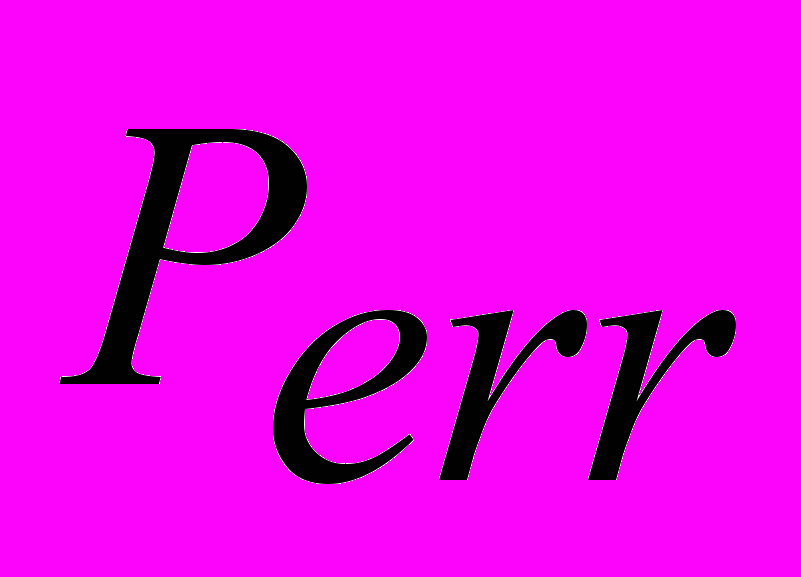evaluation is multiplicative upper bound 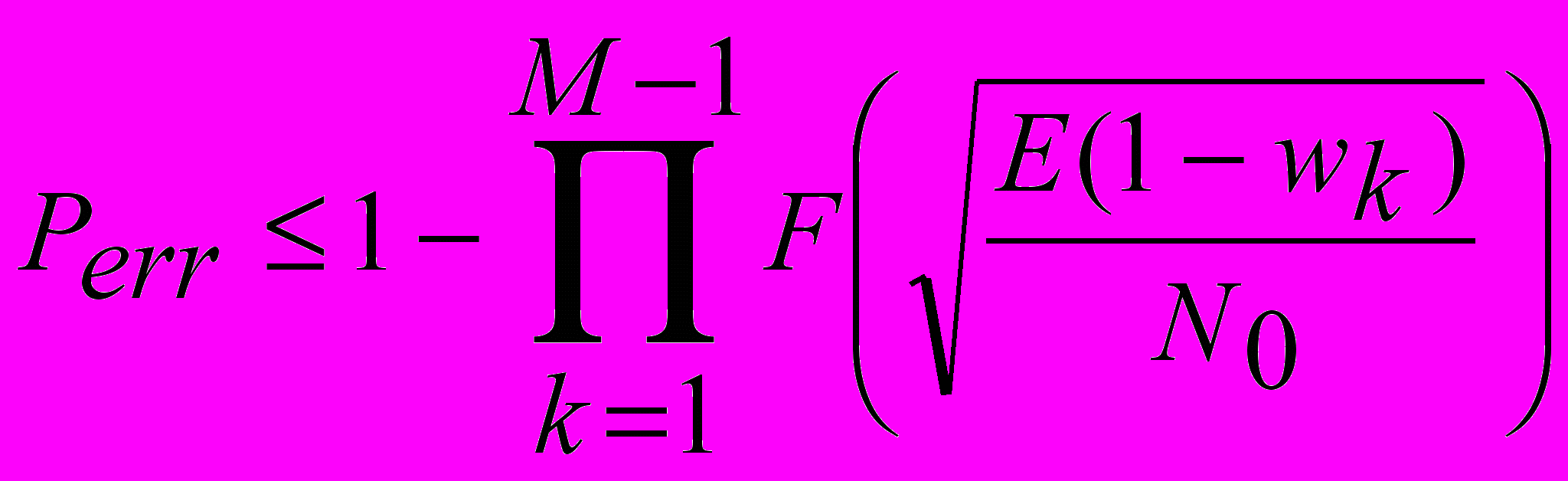. This bound employs full weight enumerating function 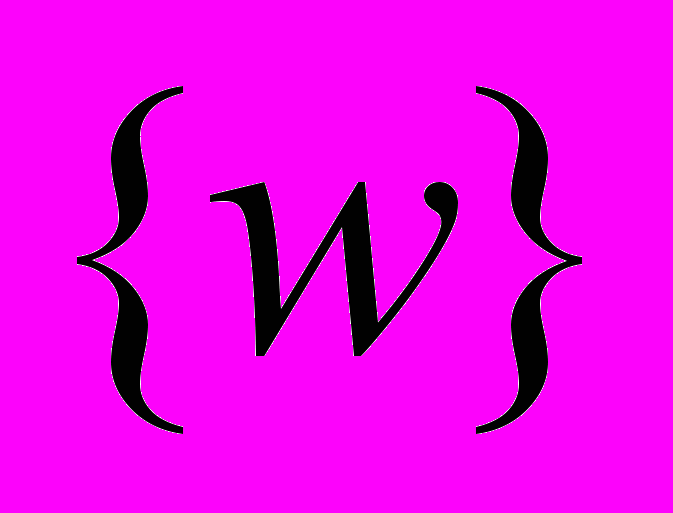and it is more effective than known upper additive bound. Here - volume of signal set, - signal energy.

To simplify the problem of determination set 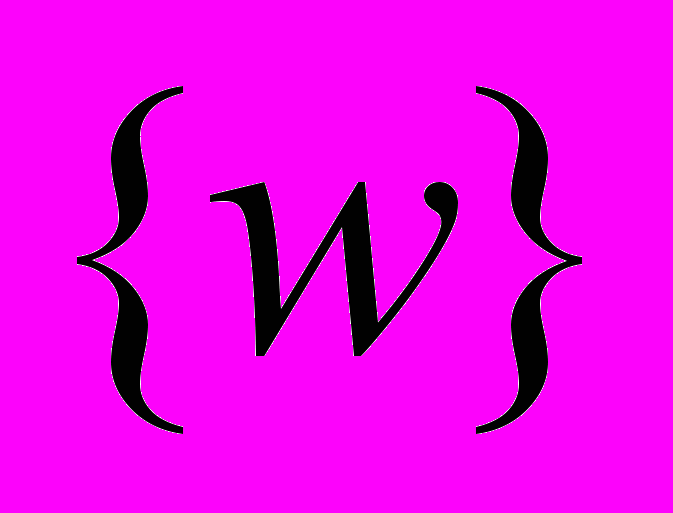one can utilize the theory of uniform interleaver and evaluate the conditional weight enumerating function averaged on class of interleavers.

The results of this technique utilization for class of turbo-codes and analysis of comparing those with simulation iterative decoding results are presented in the report.




^ ХАРАКТЕРИСТИКИ АЛГОРИТМОВ ПРИЕМА АНСАМБЛЕЙ СИГНАЛОВ С НЕБОЛЬШИМ ИНФОРМАЦИОННЫМ ОБЪЕМОМ

Назаров Л.Е., Головкин И.В.

Институт радиотехники и электроники РАН, Фрязино


В настоящее время ансамбли сигналов под общим названием турбо-коды, а также ансамбли сигналов на основе блоковых низкоплотностных кодов рассматриваются как одни из наиболее перспективных для использования в системах передачи дискретных сообщений с информационным объемом, превышающим несколько десятков тысяч битов [1,2]. Применение данных ансамблей сигналов обеспечивает достижение вероятностных характеристик, близких к предельным характеристикам Шенноновской пропускной способности каналов передачи.

Для систем передачи дискретных сообщений с информационным объемом до несколько десятков – сотен битов проблема выбора ансамблей сигналов и алгоритмов их приема остается открытой. В докладе приведены результаты анализа вероятностных характеристик для ряда ансамблей сигналов и сложности алгоритмов их приема, перспективных для решения данной проблемы.

Одно из направлений, связанное с решением рассматриваемой проблемы, основано на использовании алгоритма приема Витерби, реализующего критерий максимального правдоподобия и минимизирующего вероятность ошибочного приема дискретных сообщений. Применение алгоритма Витерби предполагает представление сигналов в виде решетчатой структуры [3]. Общее число состояний решетки или общее число ребер решетки определяют сложность реализации алгоритма приема Витерби.

Теория конструирования ансамблей сигналов со свойством решетчатой структуры является достаточно разработанной. К основным методам конструирования можно отнести следующие: формирование на основе сверточных кодов с конечной длительностью кодовых слов, применяя частичную или полную нейтрализацию “хвостов” (tail biting); формирование квадратичных конструкций (решетки Forney [4]); формирование ансамблей сигналов со свойством прямых сумм, задающие оптимальные решетки Wolf-Forney [5]. В класс ансамблей сигналов, формируемых на основе последней методики, входят сигналы, соответствующие ряду блоковых циклических кодов, а также сигналы на основе совокупности блоковых кодов, что является обобщением квадратичной конструкции Forney.

Реализация алгоритма Витерби для приема рассматриваемых ансамблей сигналов не требует оценки энергетического параметра и нелинейных операций. Это является его полезным свойством. Типичные значения отношений сигнал/помеха, требуемые для передачи с вероятностью ошибки 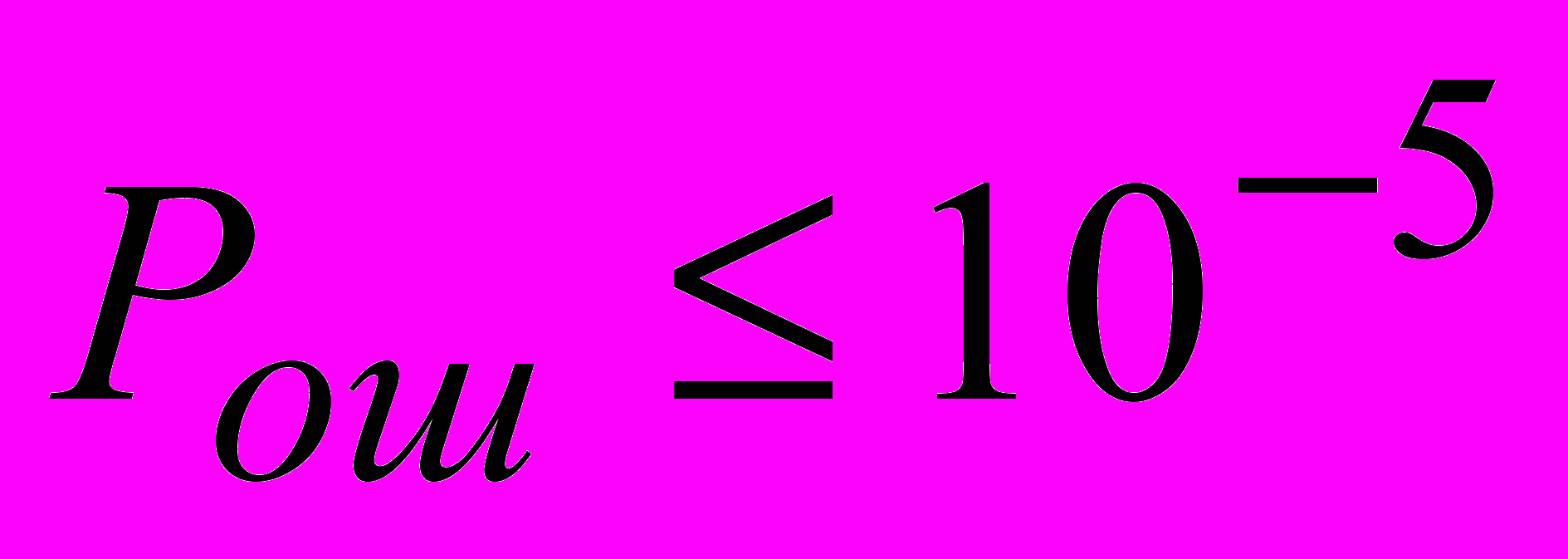, не меньше 4.5 – 5.0 дБ. Для рассматриваемых ансамблей сигналов с информационным объемом до 50 битов число состояний решетки достигает значений 9 – 12 и более [5]. Например, для ансамбля сигналов на основе блокового кода (63,45) число состояний решетки равно 11, оценка требуемых вычислительных операций на информационный бит равна 21000.

Второе направление основано на использовании правила посимвольного приема, минимизирующего вероятность ошибки на информационный бит 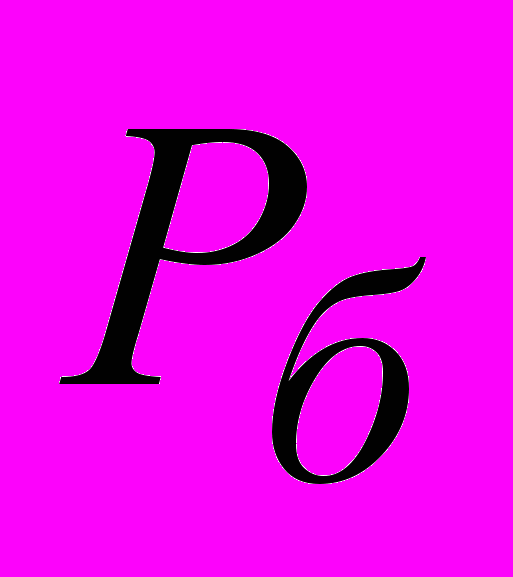. Авторами исследованы два класса данных алгоритмов: алгоритм Хартмана-Рудольфа [6] и алгоритмы АРР [2].

Алгоритм Хартмана-Рудольфа применяется при приеме ансамблей сигналов, соответствующих блоковым кодам, и использует множество кодовых слов дуального кода. Это определяет эффективность его применения для блоковых кодов с низкой избыточностью. Возможна реализация данного алгоритма с использованием быстрого спектрального преобразования в базисе Уолша-Адамара, размерность базиса определяется размерностью дуального кода. Для линейных блоковых кодов со свойством прямой суммы для дуальных кодов размерность базиса Уолша-Адамара может быть уменьшена. Например, для ансамбля сигналов на основе блокового кода (63,48) со свойством прямой суммы для дуального кода исходная размерность базиса Уолша-Адамара равна 18, размерность базиса для модифицированного алгоритма посимвольного приема равна 3. На рис.1 (кривая 1) приведена вероятность ошибки 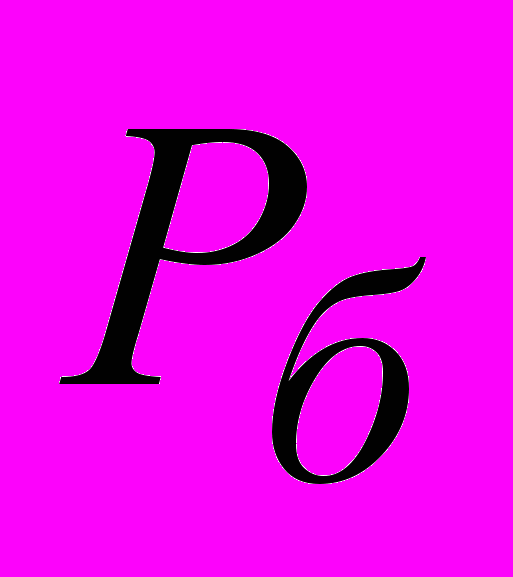для данного ансамбля сигналов, оценка объема требуемых вычислительных операций на информационный бит равна 1000. Видно, что вероятность ошибки 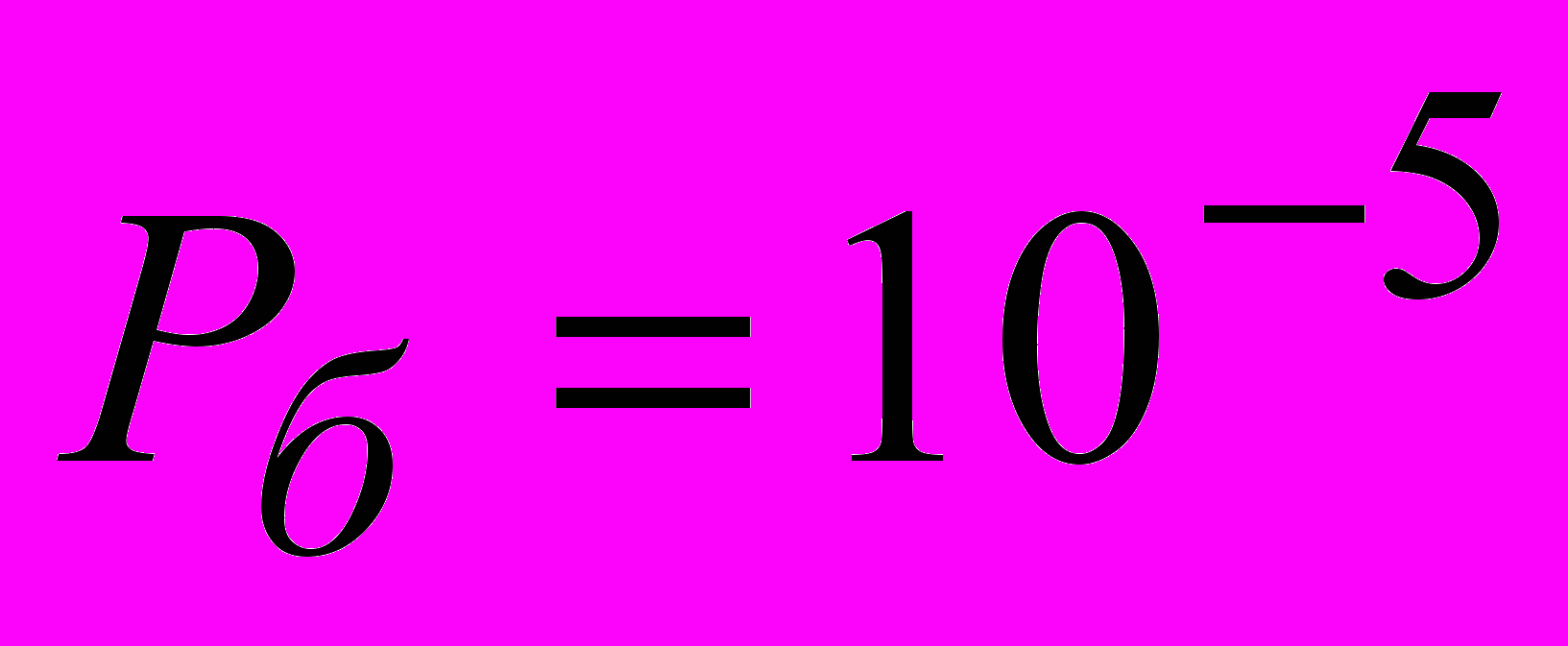достигается при отношении сигнал/помеха 5 дБ.

Алгоритмы АРР (APP - a’posteriori probability, BP – belief propagation) применяются при приеме ансамблей сигналов, соответствующих классу низкоплотностных кодов [2]. При их реализации используются подмножества кодовых слов дуального кода. Авторами исследован алгоритм итеративного посимвольного приема АРР для ансамблей сигналов, соответствующих низкоплотностным кодам на основе конечных геометрий (евклидово-геометрические и проективно-геометрические коды). В этом случае разработанный алгоритм итеративного приема характеризуется большей эффективностью и более низкой сложностью технической реализации, чем известный алгоритм ВР. На рис.1 (кривая 2) приведены значения 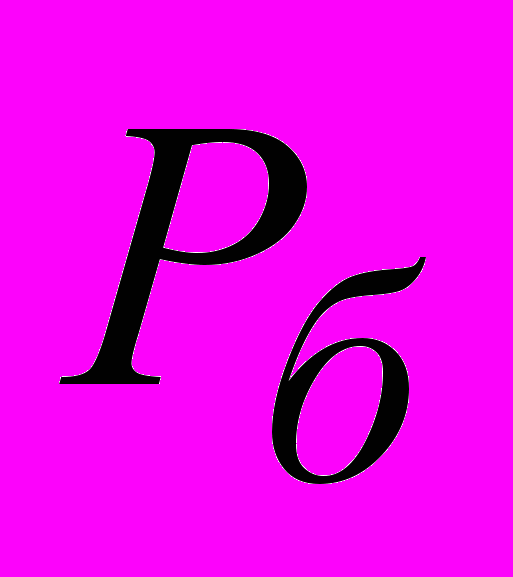для ансамбля сигналов, соответствующего евклидово-геометрическому коду (63,37), оценка объема требуемых вычислительных операций на информационный бит при выполнении одной итерации равна ≈100. Видно, что вероятность ошибки 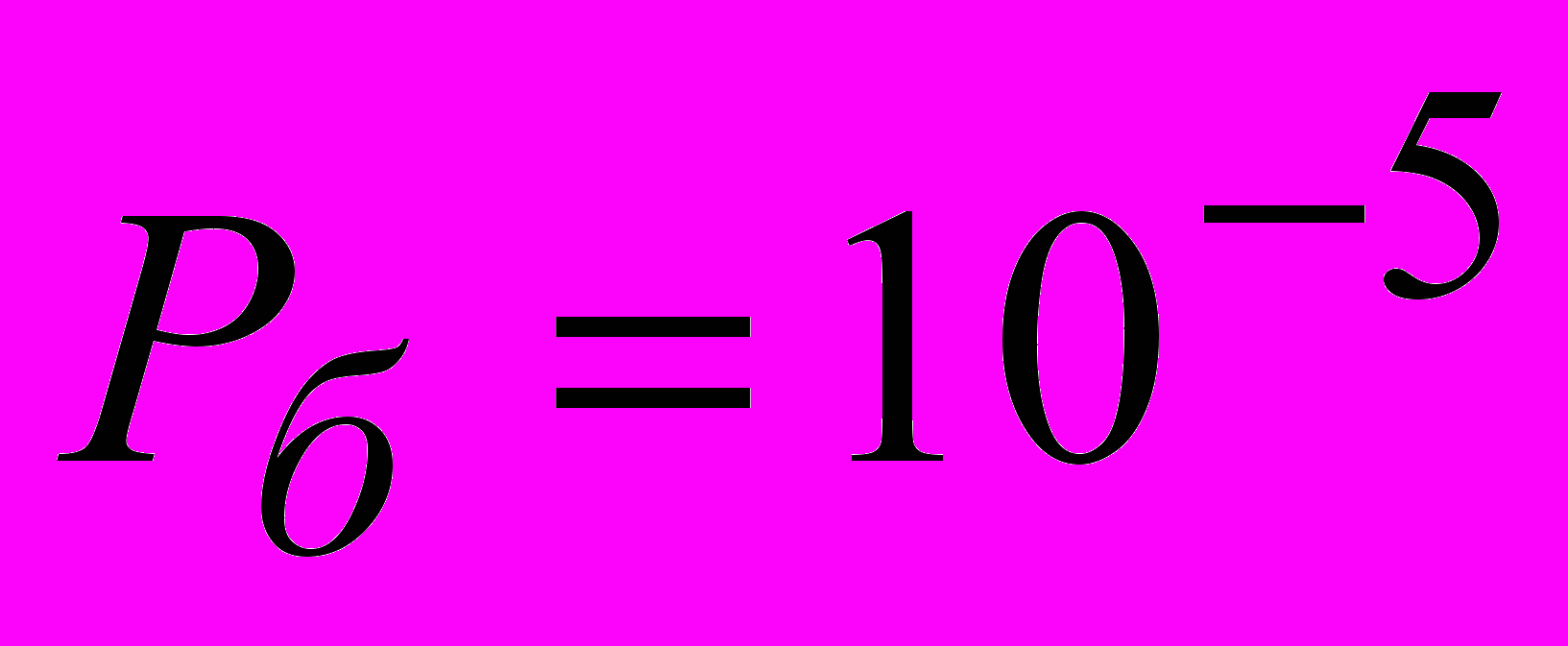достигается при отношении сигнал/помеха 4.5 дБ (8 итераций).

Недостатками данных алгоритмов являются: необходимость оценки энергетического параметра, а также необходимость использования нелинейных функций 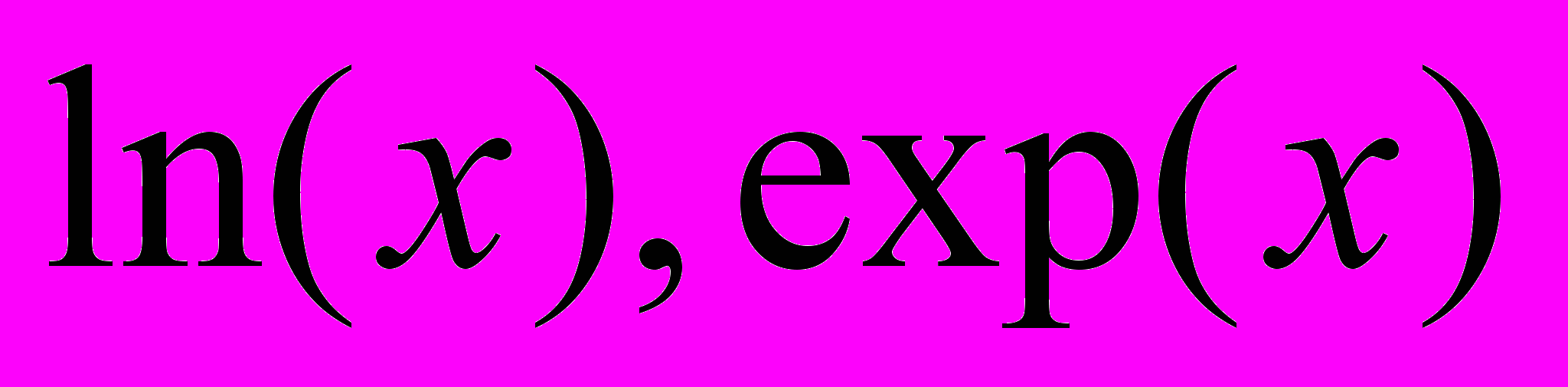. В докладе приведена модификации алгоритма итеративного приема АРР, при ее реализации требуются лишь линейные арифметические операции и не требуется оценка энергетического параметра. Энергетические потери при использовании модифицированного алгоритма итеративного приема по отношению к исходному алгоритму не превышают 0.25 дБ.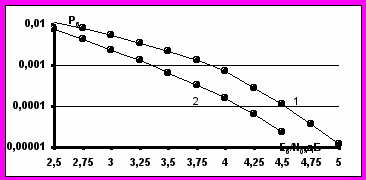



Рис.1. Вероятности ошибки 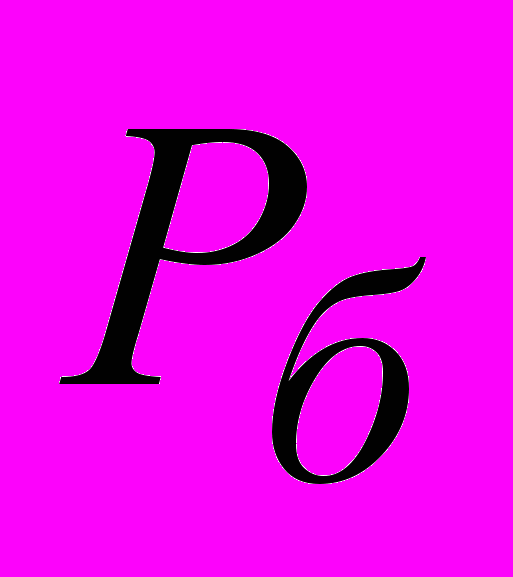для ансамбля сигналов, соответствующего блоковому коду (63,48) (кривая 1) и евклидово-геометрическому блоковому коду (63,37) (кривая 2).

Литература

1.Berrou C., Glavieux A., Thitimajshima P. IEEE Int. Conf. Communications. 1993. P. 1064.

2. MacKay D.J.C. Good error-correcting codes based on very sparse matrices. //IEEE Trans. 1999. V.IT-45. №3. P.399-432.

3. Wolf J.K. Efficient maximum likelihood decoding of linear block codes using a trellis. //IEEE Trans. 1978. V.IT-24. №1. P.76-80.

4. Forney G.D. Coset codes – partII: binary lattices and related codes. //IEEE Trans. 1988. V.IT-34. №5. P.1152-1187.

5. Vardy A., Be’ery Y. Maximum-likelihood soft decision decoding of BCH codes. //IEEE Trans. 1994. V.IT-40. №2. P.546-554.

6. Hartmann C.R.P., Rudolph L.D. An optimum symbol-by-symbol decoding rule for linear codes. //IEEE Trans. 1976. V.IT-22. №9. P.514-517.




^ PERFORMANCES OF DECODING ALGORITHMS FOR SIGNALS WITH CONSTRAINED INFORMATION VOLUME

Nazarov L., Golovkin I.

Institute of Radioengineering and Electronics RAS, Fryazino


There are the results of investigations for error-performances end complexities of decoding algorithms for signal sets with information volume less than several hundred bits in the report. The two classes of decoding algorithms are investigated:

- the maximum-likelihood decoding algorithms using a code trellis (convolutional codes, Forney’s trellis as iterated squaring constructions, trellis structures based on direct-sum and zero-concurring codewords);

- the symbol-by-symbol decoding algorithms which minimize the probability of symbol error (Hartmann-Rudolph decoding algorithm, APP decoding algorithm).

The examples of these decoding algorithm simulations for codes (tail biting convolutional codes, circular block codes, one-step majority logic decodable LDPC codes ) are presented in the report.




^ ЭФФЕКТИВНОСТЬ МНОГОПОРОГОВЫХ ДЕКОДЕРОВ ПРИ ИСПОЛЬЗОВАНИИ МНОГОПОЗИЦИОННЫХ ФМ И КАМ^*


Золотарев В.В.¹, Овечкин Г.В.², Овечкин П.В.<sup>2


1</sup>Институт космических исследований РАН, Москва

²Рязанский государственный радиотехнический университет, Рязань


Огромное значение для развития информатики и телекоммуникаций имеют методы обеспечения высокодостоверного обмена цифровыми данными, среди которых важное место занимают методы помехоустойчивого кодирования. Обзор наиболее перспективных методов кодирования по критерию «эффективность-производительность» был сделан в [1], где указывалось, что наибольшее предпочтение в высокоскоростных каналах спутниковой связи заслуживают многопороговые декодеры (МПД) [2]. Данные методы характеризуются очень малой сложностью практической реализации как при программном, так и при аппаратном исполнении. Принцип работы данного метода заключается в применении нескольких итераций декодирования информационных символов, каждая из которых является небольшой модификацией простейшего порогового декодера Месси. При этом МПД обладают важнейшим строго доказанным свойством – сходимостью к решению оптимального декодера при сохранении линейной от длины кода сложности реализации.

В большинстве последних публикаций по МПД представлены результаты его исследования в каналах передачи данных с двоичной фазовой модуляцией (ФМ2). В таких условиях при сопоставимой эффективности МПД оказывается существенно проще для реализации, чем другие методы коррекции ошибок [3]. Вместе с тем в современных телекоммуникационных системах на каналы передачи данных часто накладываются значительные ограничения по занимаемой полос частот и с каждым годом эти ограничения становятся все жестче. Одним из способов уменьшения занимаемой полосы частот является использование многопозиционных сигналов, для формирования которых обычно применяется многопозиционная фазовая (ФМN) или квадратурная амплитудная модуляция (КАМN). В таких условиях для улучшения энергетики канала также необходимо применять помехоустойчивые коды.

При переходе к многомерным сигналам типа КАМN и ФМN все подходы к применению МПД совместно с такими сигнальными конструкциями остаются аналогичными двумерному случаю, что позволяет одновременно получить значительный энергетический выигрыш кодирования и существенно сэкономить полосу частот передаваемого сигнала [4].

Представим результаты моделирования МПД и других методов коррекции ошибок в канале с многопозиционными системами сигналов. При моделировании использовалась модель канала, задаваемая выражением r = s + w, где 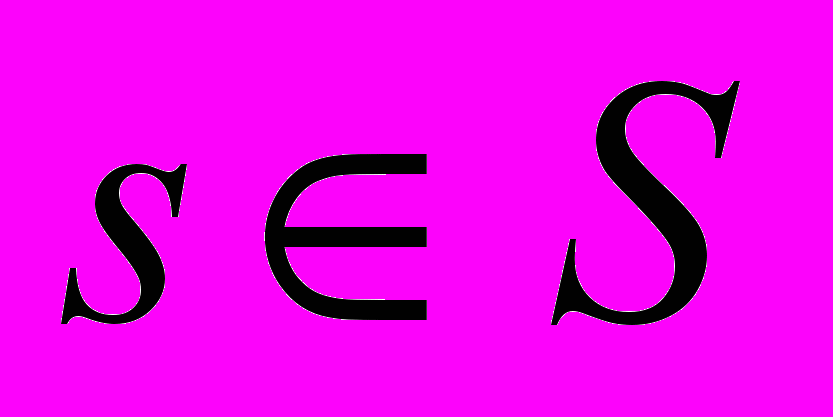 – передаваемый комплексный сигнал; S  – множество возможных сигналов, определяемое выбранным типом модуляции; r – принятый комплексный сигнал; w – комплексный аддитивный белый гауссовский шум со спектральной плотностью мощности N₀/2 в каждой размерности.

Представленные далее результаты получены для случая использования как жесткого (когда демодулятор не формирует оценок надежности своих решений для принятых битов), так и мягкого (когда демодулятор формирует оценки надежности своих решений) модемов.

Для получения жестких решений использовался демодулятор по максимуму правдоподобия, выполняющий оценку переданного символа по формуле .

Мягкие решения относительно принятых битов формировались в соответствии со следующим выражением:

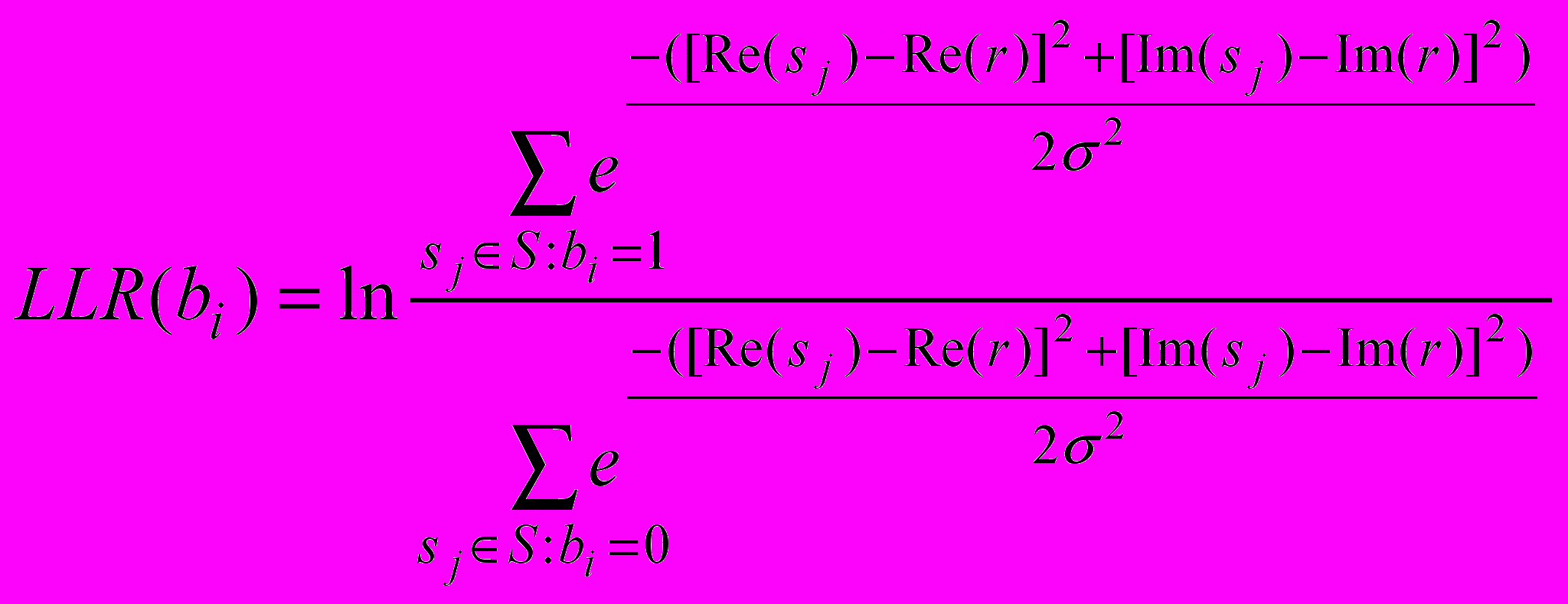(1).

Здесь r – принятый символ; Re(s) – действительная часть s; Im(s) – мнимая часть s; 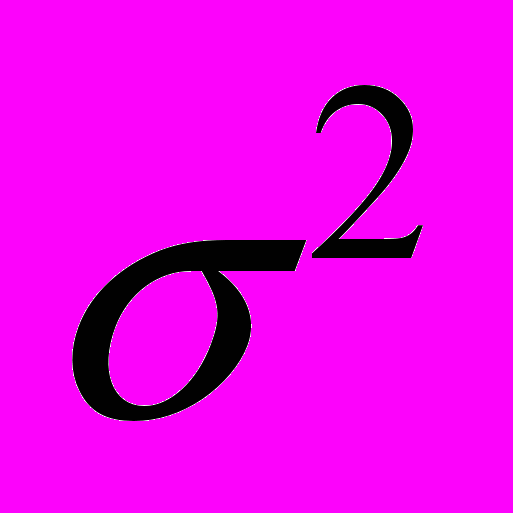– дисперсия гауссовского шума; 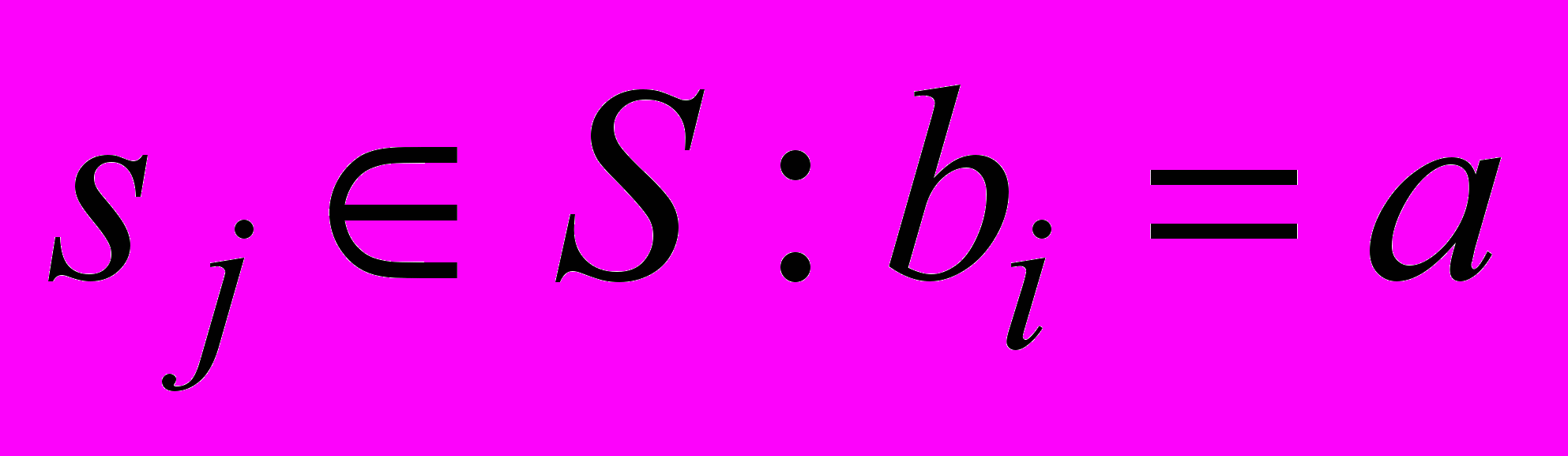– все символы сигнального созвездия, для которых i-й бит равен a.

На рис. 1 кривыми 1 – 3 представлены экспериментальные графики зависимости вероятности ошибки на бит P_b(e) на выходе многопорогового декодера от отношения сигнал-шум E_b/N₀ в канале связи с аддитивным белым гауссовским шумом (АБГШ) и КАМ при использовании 16, 32 и 64 символьных созвездий для случая использования жестких решений демодулятора. При декодировании выполнялось от 10 до 20 итераций декодирования сверточного самоортогонального кода с кодовой скоростью R = 1/2, кодовым расстоянием d = 11 и длиной n порядка 10000. Заметим, что при этом использовался так называемый код с параллельным каскадированием [5, 6], в котором в исходном самоортогональном коде выделяются несколько составляющих кодов, по очереди включаемых в процесс декодирования.



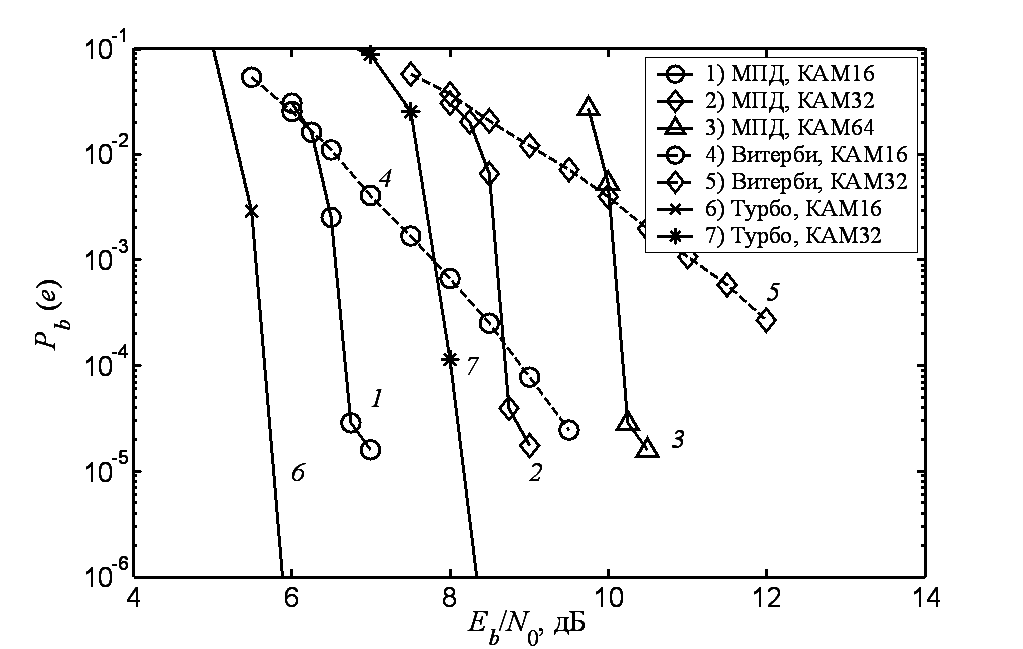
Рис. 1. Эффективность МПД в каналах с КАМ^ N, жесткий модем

На рис. 1 кривыми 4 и 5 также представлены характеристики классического декодера Витерби [7] для кода с длиной регистра K = 7 при использовании КАМ16 и КАМ32 соответственно. Как видно, декодер Витерби в данных условиях при P_b(e) = 10^–4 проигрывает МПД примерно 2 и 3 дБ. Кривыми 6 и 7 на рис. 1 также показаны характеристики очень мощного турбо кода [8] с кодовой скоростью R = 1/2, который образован путем параллельного каскадирования двух рекурсивных систематических сверточных кодов с конструктивной длиной K = 4. В данном турбо коде применялся перемежитель типа S-random длиной L = 5000 (общая длина такого турбо кода составляет n = 10000). При декодировании турбо кода выполнялось 8 итераций, на каждой из которых для декодирования составляющих кодов применялся субоптимальный Max-Log-MAP алгоритм. Из сравнения характеристик турбо кода и МПД видно, что эффективность последнего оказывается хуже примерно на 1 дБ, но МПД при этом почти на два порядка проще для практической реализации, чем данный турбо код [3].

Результаты моделирования, полученные для случая использования многопозиционной фазовой модуляции ФМN в канале с АБГШ и жесткими решениями демодулятора показывают, что соотношения между характеристиками многопорогового декодера, декодера Витерби и турбо кода сохраняются и в этом случае.

На рис. 2 соответствующими кривыми представлены характеристики тех же методов коррекции ошибок, что и на рис. 1, но при использовании мягких решений демодулятора, формируемый в соответствии с выражением (1). Из данных рисунков следует, что в этих условиях характеристики МПД оказываются примерно на 1 дБ лучше характеристик декодера Витерби при P_b = 10^–4. Кроме того, видно, что МПД проигрывает по эффективности турбо коду порядка 1,5 дБ. Такая же ситуация наблюдается и при использовании модуляции типа ФМN.



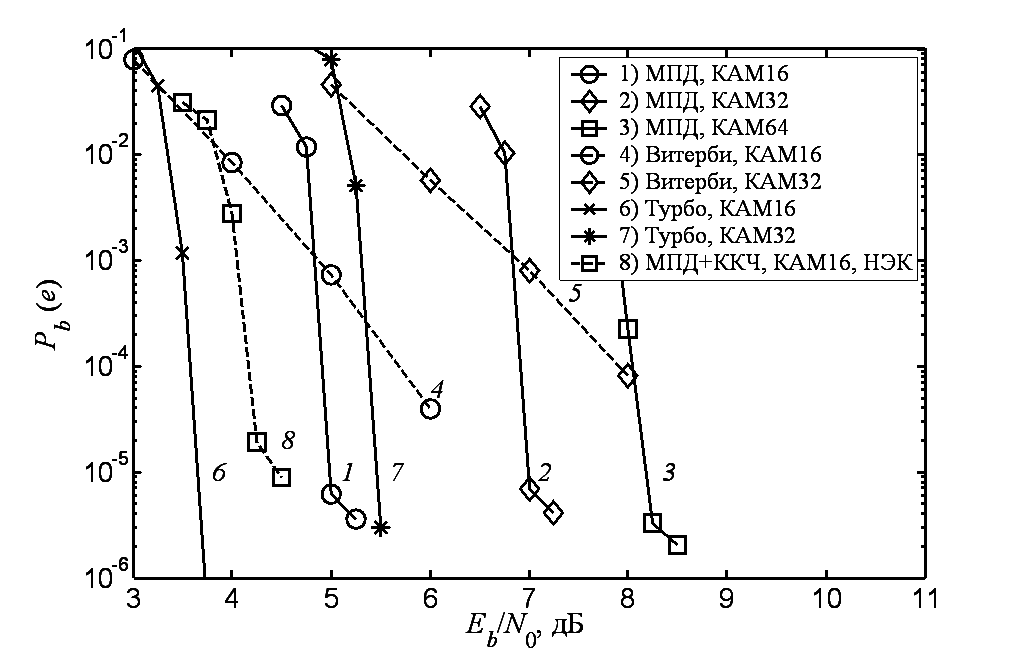
Рис. 2. Эффективность МПД в каналах с КАМN, мягкий модем

Одним из возможных способов приближения области эффективной работы МПД к пропускной способности канала является его использования в каналах с неравномерной энергетикой [9], когда при передаче информационные символы передаются сигналами с большей энергией, а проверочные – с меньшей. При этом общая энергия, требуемая для передачи данных, остается постоянной. В публикациях по многопороговым методам декодирования показано, что в таких каналах граница эффективного применения МПД смещается в область бóльших уровней шума в канале, но при этом несколько понижается достоверность его решений.

Известно, что в каналах с многопозиционными системами сигналов отдельные биты сигнального созвездия защищены по-разному. Например, для системы КАМ16 первый и третий биты защищены больше, а второй и четвертый – меньше. При этом оказывается, что вероятность ошибки в первом и третьем битах в два раза меньше вероятности ошибки во втором и четвертом битах. Похожая ситуация наблюдается и при использовании других многопозиционных систем сигналов. Таким образом, канал с многопозиционными системами сигналов можно рассматривать в качестве канала с неравномерной энергетикой. В результате для приближения области эффективной работы МПД к пропускной способности канала можно информационные символы сообщения располагать в более надежных битах созвездия, а проверочные – в менее надежных.

На рис. 3 кривой ^ 1 еще раз показаны характеристики МПД самоортогонального кода с кодовой скоростью R = 1/2, кодовым расстоянием d = 11 и длиной n порядка 10000 в канале с АБГШ при использовании КАМ16 и демодулятора, формирующего жесткие решения. Кривая 2 соответствует случаю расположения информационных битов в более надежных позициях символа, а проверочных – в менее надежных. Заметим, что область эффективной работы МПД приблизилась к пропускной способности канала примерно на 0,5 дБ, но при этом область насыщения вероятности ошибки оказалась несколько выше. Вместе с тем для уменьшения вероятности ошибки в области эффективной работы, как показано в [6], возможно использование совместно с МПД простейшего кода с контролем четности (ККЧ). Применение ККЧ позволяет снизить вероятность ошибки декодирования на 1..2 порядка практически без увеличения сложности результирующей схемы [6]. Характеристики каскадной схемы, состоящей из МПД и ККЧ длины 50, в случае расположения информационных битов в более надежных позициях символа для тех же условий показаны на рис. 3 кривой 3. Из рисунка видно, что применение предложенного подхода позволило приблизить эффективность МПД к пропускной способности канала примерно на 0,5 дБ. В результате преимущество гораздо более сложного ранее рассмотренного турбо кода (кривая 5) перед МПД при вероятности ошибки порядка 10^–4 оказалось даже меньшим, чем 0,5 дБ.

Результаты моделирования рассмотренной каскадной схемы при расположении информационных битов в более надежных позициях символа для случая использования мягких решений демодулятора показаны на рис. 2 кривой 8. В данном случае улучшение характеристик МПД оказалось равным 0,7 дБ. Заметим, что похожего результата можно добиться и при использовании других многопозиционных систем сигналов.



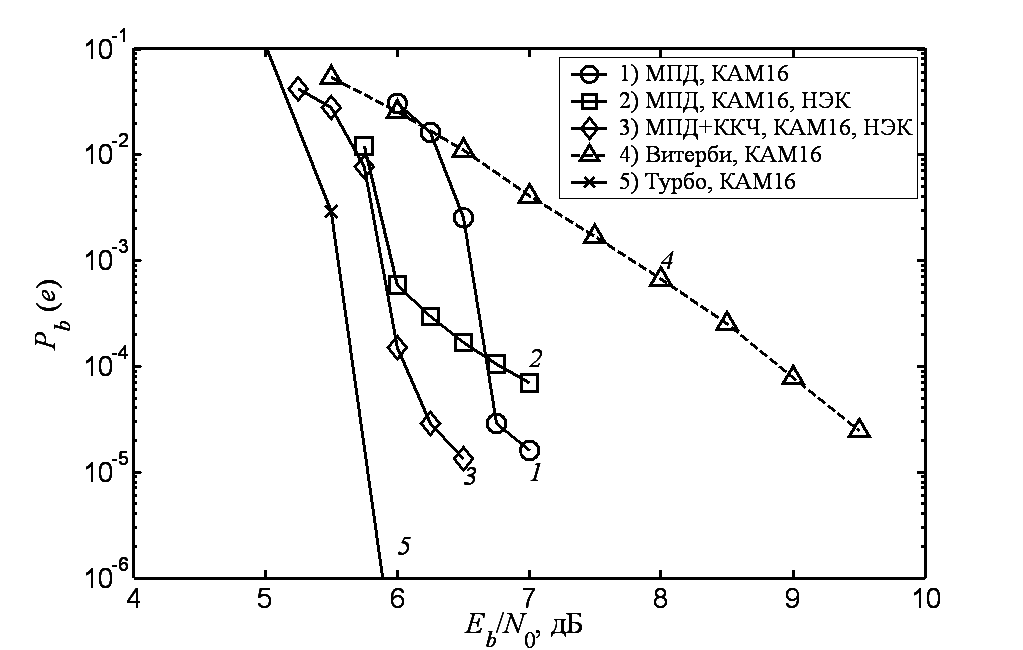
Рис. 3. Эффективность МПД в каналах с КАМ16, жесткий модем

Таким образом, в докладе рассмотрены вопросы применения многопороговых методов декодирования в каналах с многопозиционными системами модуляции, таких как КАМ и ФМN. Показано, что в данных условиях при использовании как жестких, так и мягких решений демодулятора, МПД является на 1..3 дБ более эффективным, чем классический декодер Витерби, и уступает декодеру турбо кода около 1..1,5 дБ. При этом сложность практической реализации МПД оказывается на два или даже более порядков меньше сложности декодера турбо кода и других методов коррекции ошибок с сопоставимой эффективностью. Также рассмотрена методика улучшения эффективности МПД за счет оптимизации расположения информационных и проверочных битов в символах сигнального множества. Показано, что применение данной методики позволяет приблизить область эффективной работы МПД к пропускной способности канала более чем на 0,5 дБ. Все это допускает применение многопороговых декодеров в высокоскоростных системах передачи данных, в которых наряду с высокими требованиями к энергетике канала накладываются жесткие ограничения на расширение полосы частот.

Дополнительную информацию о МПД можно найти на веб-сайте www.mtdbest.iki.rssi.ru.

*Работа выполнена при поддержке РФФИ (грант №05-07-90024в)

Литература

1. Золотарев В.В., Овечкин Г.В. Эффективные алгоритмы помехоустойчивого кодирования для цифровых систем связи // Электросвязь. 2003. №9. С. 34–37.

2. Золотарев В.В., Овечкин Г.В. Помехоустойчивое кодирование. Методы и алгоритмы. Справочник. М.: Горячая линия – Телеком, 2004. 126 с.

3. Золотарев В.В., Овечкин Г.В. Сложность реализации эффективных методов декодирования помехоустойчивых кодов // 6-я межд. конф. и выст. «Цифровая обработка сигналов и ее применение». М.: 2004. Том 1. С. 220–221.

4. Банкет В.Л., Золотарев В.В. Эффективность многопозиционных систем модуляции и многопорогового декодирования // В сб.: ЕС Всесоюзная школа-семинар по вычислительным сетям». М.-Пушкино, 1984. Ч. 3.2.

5. Золотарев В.В. Параллельное кодирование в каналах СПД //В сб.: «Вопросы кибернетики». ВК-120. – М.: 1986.

6. Золотарев В.В., Овечкин Г.В. Использование многопорогового декодера в каскадных схемах // Вестник РГРТА, 2003, вып.11, С. 112-115.

7. Витерби А. Границы ошибок для сверточных кодов и асимптотически оптимальный алгоритм декодирования // Некоторые вопросы теории кодирования. М.: Мир, 1970. С. 142–165.

8. Berrou C., Glavieux A., Thitimajshima P. Near Shannon Limit Error-Correcting Coding and Decoding: Turbo Codes // Proc. of the Intern. Conf. on Commun. (Geneva, Switzerland). 1993. May. P. 1064–1070.




^ THE PERFORMANCE OF MULTITHRESHOLD DECODERS AT USING MULTIPOSITIONAL MODULATION MPSK AND QASK

Zolotarev V.¹, Ovechkin G.², Ovechkin P.<sup>2

1</sup>Space Research Institute of Russian Science Academy, Moscow

²The Ryazan State Radio Engineering University, Ryazan

One of the major problems at creation of high-speed digital communication is the correct choice of methods for error-correction codes decoding. For today in the coding theory many classes of error-correction codes are known. These codes distinguished from each other by structure, functional purpose, power efficiency, algorithms of decoding and many other parameters. The review [1] of most perspective decoding methods by criterion «efficiency-

productivity» has shown, that the greatest preference in high-speed channels of a satellite communication multithreshold decoders [2] deserve. The given decoders, based on ordinary threshold decoder, allow decoding even very long codes with linear implementation complexity.

In the most of publications on multithreshold decoders efficiency of its application over an AWGN channel with binary phase shift keying (BPSK) are submitted. In such conditions at comparable efficiency multithreshold decoders appear essentially (on two or even three order) easier for implementation, than other error-correcting codes [3]. At the same time in modern telecommunication systems on channel significant restrictions on occupied bandwidth are frequently imposed and every year these restrictions become more rigid. One of ways for reduction of an occupied bandwidth is use of multipositional modulation system such as multipositional phase shift keying (NPSK) or quadrature amplitude shift keying (QАSK). In such conditions also it is necessary to apply error-correcting codes to improvement of a channel capacity using.

In the report questions of application of multithreshold decoders over AWGN channels with multipositional modulation (QAM and NPSK) are considered. It is shown, that in these given conditions at use both hard- and soft-decision demodulators, multithreshold decoders are on 1..3 dB more effective than classical Viterbi decoder and on about 1..1,5 dB less effective than very complex turbo code decoder.

Also the technique of multithreshold decoders efficiency improvement is considered. The technique is based on follow. In multipositional modulation system the bits of signal constellation are unequal protected. Thus such channel may be considered as channel with non-equal energy. It’s knows in non-equal energy channel multithreshold decoders work nearer to channel capacity at some BER degradation. This BER degradation may be compensated by using of simple concatenated code (parity check code for example). It the report questions of using technique for non-equal energy channel with multithreshold decoders to channels with multipositional modulation are considered.

It is shown, that application of the given technique allows to approach area of effective work of multithreshold decoders to the channel capacity more than on 0,7 dB. In results very complex turbo codes outperforms multithreshold decoders only on about 0,5 dB. All this supposes application of multithreshold decoders in high-speed communication systems in which alongside with high requirements to using of channel capacity the rigid restrictions on bandwidth expansion are imposed.

Great volume of the additional scientific and school-methodical information on algorithms of class multithreshold decoders can be found on a website [4].

^*The work has been supported by Russian Foundation for Basic Research (grant №05-07-90024).

References

1. Zolotarev V.V., Ovechkin G.V. Effective algorithms of error-correcting coding for digital systems of communication // Telecommunication, 2003. №9. P. 34–37.
   
2. Zolotarev V.V., Ovechkin G.V. Error-correcting coding. Methods and algorithms. The quick reference. M.: Hot line - Telecom, 2004. 126 p.
   
3. Zolotarev V.V., Ovechkin G.V. The complexity of high performance methods of error-correcting codes decoding // Proc. 6th Intern. Conf. «Digital signals processing and its application». Moscow 2004. Vol. 1, P. 220-222.
   
4. www.mtdbest.iki.rssi.ru.
   

