26. Дерево достижимости

Вид материала

Документы

Содержание Алгоритм построения дерева достижимости. Очередной шаг Теорема. Построение дерева достижимости всегда завершается за конечное число шагов. 27. Применение дерева достижимости Проверка безопасности Проверка, что сеть сохраняющая Задача покрываемости 27. Матричные уравнения Теорема. Сеть Петри уровня активности 1 является сохраняющей тогда и только тогда, когда система линейных уравнений Dw = 0

Подобный материал:

• Деревья неориентированное дерево, 380.81kb.
• Викторина «В мире интересного» Самое высокое дерево на земле? (Эвкалипт), 26.14kb.
• Абоненты Beeline отправили более 5 000 смс в поддержку проекта «смс-дерево», 115.95kb.
• Александр белых фудзивара тэйка1, 93.36kb.
• Ополовников А. В., Ополовникова Е. А. Дерево и гармония, 91.93kb.
• Комплекс упражнений при миопии введение "Баньяновое дерево живет пять тысяч лет,, 175.77kb.
• Іiі етапу Всеукраїнської олімпіади з російської мови І літератури, 20.9kb.
• После проведённых мероприятий необходимо узнать эмоци­ональное настроение детей, получили, 408.62kb.
• Областная научно-практическая конференция учащихся, 265.39kb.
• Сказка. Москва 1956. Перевод с урду В. Быковой, 775.73kb.

26. Дерево достижимости.


Пусть имеется сеть Петри с начальной разметкой. Достаточно очевидна идея графа достижимости для этой сети. Начиная с взятой вершины ₀ мы строим граф, считая вершинами все возможные элементы R(₀) и изображая ребрами (с соответствующими пометками) переходы, срабатывание которых меняет одну маркировку на другую. Понятно, что подобный граф бесконечен, если множество достижимости R(₀) бесконечно. Оказывается, что этот граф всегда можно в некотором смысле “сжать” в конечный (практически в конечное дерево), который, однако, сохранит много полезной информации о графе достижимости. Этот сжатый граф называется деревом достижимости сети Петри.

Алгоритм построения дерева достижимости. Для начала введем символ , который будет наряду с фишками использоваться в маркировках дерева. Как нетрудно догадаться,  будет означать конечное, но как угодно большое количество фишек. Мы считаем, что для всех натуральных n имеет место: n<, n+ = +n = ,  - n = , и, естественно, =  и . Если при маркировке какого-то места в сети используется , то никаких фишек туда уже не ставится. В результате пространство маркировок становится множеством всевозможных n-мерных векторов из (N {})ⁿ. Исходя из этого для сети, маркированной обычными фишками и этим символом , определяется понятие разрешенного или неразрешенного перехода, а так же результат срабатывания разрешенного перехода, т.е. функция

 : (N{})ⁿT (N {})ⁿ.

Итак, требуемое дерево будет графом, вершины которого помечены маркировками указанного вида, а ребра помечены символами переходов. Сразу заметим, что в отличие от графа достижимости здесь могут быть разные вершины, соответствующие одним и тем же маркировкам. Обычно это концевые вершины, метки которых совпадают с метками вершин на пути от этих концов к корню дерева.

Дерево строится по шагам.

Логической основой построения является тот простой факт, что если переход t разрешен для маркировки  и , то t разрешен для маркировки . При этом, если переход от  к  случился серией переходов t₁,…,t_n, то стартуя с , переходы t₁,…,t_n снова все разрешены и после их срабатывания получим маркировку +2(- ). Так можно повторять сколь угодно раз, получая маркировки вида +k(- ).

На первом шаге в дерево заносится одна вершина и помечается как ₀ (стартовая разметка сети). Это вершина считается граничной. На каждом шаге мы имеем конечное дерево, концевые вершины (листья) которого бывают одного из трех видов: граничные, терминальные, дублирующие. Все прочие вершины – внутренние (т.е. не концевые). Построение продолжается до тех пор, пока имеются граничные вершины.

Очередной шаг. Пусть x - граничная вершина построенного к данному шагу дерева. Пусть  - разметка, помечающая x.

1) Допустим, что при маркировке  нет разрешенных переходов. Тогда вершина x переводится в класс терминальных. Конец шага.

Пусть, далее,  = _k…₁₀ – маркировки на маршруте от вершины x к корню дерева (сам x в маршрут не входит).

2) В последовательности  есть вершина с меткой , для которой  = .. Тогда  переводится в класс дублирующих. Конец шага.

3) Для каждого перехода t, разрешенного для маркировки , делаем следующее:

1. Вычисляем = (, t). Если в последовательности  есть символ , для которого  <, то для всех i=1,…,n, для которых (p_i)<(p_i), заменяем в  i-е значение на , т.е. делаем присваивание  (p_i) := .
   
2. Добавляем к дереву новую вершину z и помечаем ее маркировкой . Из x в z проводим ребро и помечаем его символом t.
   
3. Вершину z относим к граничным.
   

4) Вершину x относим к внутренним. Конец шага.

Конец алгоритма.


Следующий рисунок иллюстрирует этап 3.a.



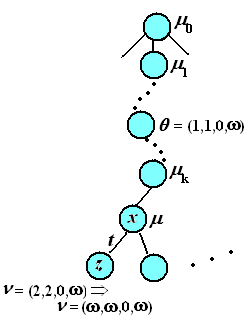
Теорема. Построение дерева достижимости всегда завершается за конечное число шагов.

Доказательство. Допустим, что процесс построения дерева никогда не завершается и в результате получается бесконечный граф. Тогда, стартуя с корневой вершины, нетрудно построить бесконечную цепочку связанных вершин. Она строится по индукции с выполнением условия: “Под каждой очередной вершиной цепочки лежит бесконечное поддерево”.

В построенной цепочке не будет ни одной пары вершин метки  и , которые удовлетворяли бы условию  =. Действительно, иначе, согласно п.2 алгоритма нижняя из этих вершин перешла бы в семейство дублирующих и от нее никаких ребер построено бы не было.

Теперь прореживаем найденную цепочку, т.е. ищем ее подпоследовательность добиваясь, чтобы метки вершин строго возрастали.

Сначала рассматриваем первые компоненты меток. Если среди них бесконечно много одинаковых, то соответствующие вершины и берем в качестве подпоследовательности. Если любое значение первой компоненты встречается лишь конечное число раз, то очевидно, что есть подпоследовательность вершин, где эти значения строго возрастают.

Теперь рассматириваем вторые компоненты меток и аналогично прореживаем полученую перед этим подпоследовательность. Проделав это n раз (количество мест в сети) получим то, что требовалось.

Мы получим окончательное противоречие, если заметим, что спускаясь в исходном дереве от корня вниз по какой-нибудь бесконечной последовательности ребер мы вообще никогда не можем столкнуться с ситуацией, когда для пары вершин этого маршрута - для их верхней  и нижней  меток имеет место  <, причем для некоторых i=1,…,n, для которых (p_i)<(p_i), величина (p_i) есть число, а не . Такая картина невозможна потому, что согласно алгоритму (п.3a) величина (p_i) должна стать равной .


Пример построения дерева достижимости. Дана сеть






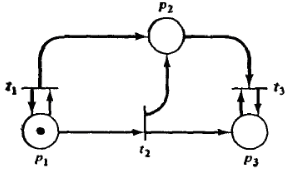
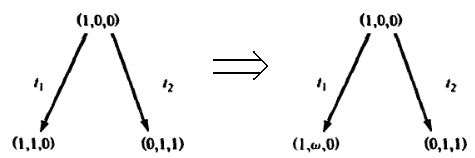
Первый шаг




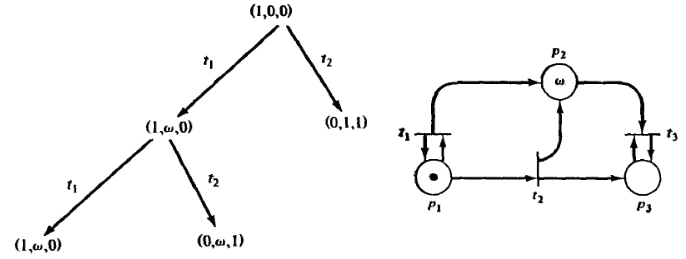
Второй шаг




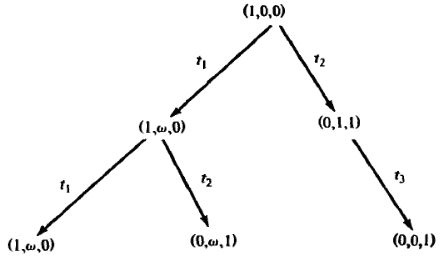
Третий шаг




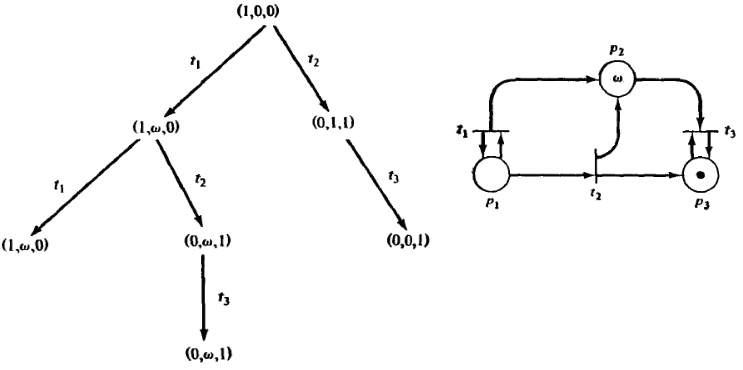
Результат


Роль символов  объясняется следующей леммой.

Теорема. Если в дереве достижимости сети Петри имеется вершина с меткой =(₁, ₂,…, _n), причем _i1=_i2=…= _ik=, а остальные компоненты – числа, то в этой сети достижимыми являются макировки =(₁, ₂,…, _n), у которых компоненты _i1, _i2,…, _ik могут быть сколь угодно большими, а все прочие компоненты такие же, как у .


Доказательство. Рассмотрим последовательность переходов , которыми помечены ребра из корневой вершины дерева достижимости к вершине с меткой . Утверждение теоремы докажем индукцией по длине .

Если эта длина равна нулю, то речь идет о корневой вершине со стартовой разметкой. В этой разметке нет символов  и поэтому доказывать нечего.

Рассмотрим вершину x с разметкой =(₁, ₂,…, _n) и маршрутом . Для вершин, находящихся ближе к корню, утверждение считаем верным.

Пусть y – вершина, находящаяся непосредственно над x и t – переход между ними.

Случай 1. В метке  вершины x и метке ’ вершины y величины  всречаются в одинаковых количествах и стоят на одинаковых местах. Тогда по индукционному допущению в сети достижима маркировка ’=(₁, ₂,…, _n), у которой компоненты _i1, _i2,…, _ik могут быть сколь угодно большими, а все прочие компоненты такие же, как у ’ . Выполним из ’переход t и получим, очевидно, , которая требуется в лемме.

Случай 2. В метке  вершины x по сравнению с меткой ’ вершины y есть новые символы . Этот случай иллюстрирует рисунок.



В ’ был только один , в  появилось еще два (ясно, что исчезать эти символы не могут). Новые  появились согласно шагу 3a) алгоритма из-за существования выше в цепочке маркровки , которая меньше, чем (t, ’) = (4,0,1,,1,2,7). Строгие неравенства в местах, где появляются новые . Согдасно индукционному допущению в сети достижимы маркировки, совпадающие с , но у которых вместо  стоят как угодно большие числа (т.е., в примере, вида (4,0,1,*,1,1,5)). Из такой маркировки цепочкой переходов от  к ’получим (1,3,0,*,1,2,2) и далее, посредством t - маркировки вида (4,0,1,*,1,2,7). Значит имеем цепочку переходов от (4,0,1,*,1,1,5) к (4,0,1,*,1,2,7). Применяя ее многократно можно сделать как угодно большими две последние цифры. На позиции * число может, конечно, уменьшиться, но, если в начале сделать его достаточно большим, оно все равно останоется как угодно большим. Это доказывает теорему для .


27. Применение дерева достижимости


1) Проверка ограниченности. Сеть ограничена тогда и только тогда, когда символ  отсутствует в ее дереве достижимости.

При этом положение символов  в векторе маркировки указывает, какие позиции, могут иметь сколь угодно большое число фишек.

2) Проверка безопасности. Если сеть неограничена, то она, конечно, не является безопасной. В противном случае мы имеет конечное дерево достижимости без символов . Безопасность, очевидно, означает, что все маркировки этого дерева по всех позициях имеют значение не превосходящие 1.

3) Проверка, что сеть сохраняющая. Пусть выбран какой-то способ приписать неотрицательный вес каждой позиции.

Пусть сеть неограничена. Тогда, понятно, что она не сохраняющая, если какое-то место в дереве достижимости имеет маркировку с символом  и соответствующей позиции приписан ненулевой вес.

Для всех остальных случаях при заданной системе весов проверка сохранения делается очень просто: надо только для каждой вершины дерева вычислить весовую сумму и проверить их совпадение.

Если веса не заданы, то сеть, напомним, сохраняющая, если она является таковой при некоторых строго положительных весовых коэффициентах. Неограниченная сеть при таком условии не может быть сохраняющей. Однако, если сильно хочется, неограниченную сеть можно назвать сохраняющей, если она сохраняющая при некоторых весовых коэффициентах, строго положительных только для ограниченных позиций. Дерево достижимости в любом случае позволяет решить вопрос о существовании такой системы весов. Вопрос сводится к решению системы линейных уравнений вида

w₁₁+ w₂₂+…+ w_n_n = s

по всем =(₁, ₂,…, _n) из дерева. На неизвестные (w₁, w₂,…, w_n,s) накладываются ограничения w_i>0. Если сеть неограничена, то в уравнениях следует рассматривать только те слагаемые, у которых _i< для всех маркировок .

Эта система решается одним из алгебраических методов или методами линейного программирования. При этом устанавливается и возможная неразрешимость задачи.

4) Задача покрываемости. Дана сеть Петри с начальной маркировкой ₀. Требуется алгоритм, который по любой маркировке  определит, существует ли такая R(₀), что . Если такая  существует, требуется найти соответствующую последовательность переходов.

Данная задача решается просмотром всех маркировок в дереве достижимости. Если в этом дереве нет таких , то их нет и вообще. Если в дереве есть такая маркировка *, что *, то из * можно построить , заменяя символы  достаточно большими числами. Их конкретные значения можно получить, выполнив достаточное число раз переходы, помечающие ребра маршрута к *.


Задачи активности и достижимости не решаются в общем случае с помощью дерева достижимости.


27. Матричные уравнения


Сеть Петри представляет собой конечный объект, но когда мы пытаемся моделировать ее работу с целью анализа результатов, то появляется опасность “сорваться” в бесконечность, каковой может быть граф переходов.

Замена этого графа деревом достижимости позволяет решить некоторые вопросы, но это дерево не несет всей информации о сети и поэтому некоторые задачи с его помощью принципиально не решаются.

Другой подход к анализу – работа с самим графом. Это не приводит к потере информации, но возникает естественное затруднение – а как собственно работать? Ниже излагается одна из таких возможностей, суть которой в том, что граф можно задать матрицей. Оказывается, что действие перехода при этом моделируется известной матричной операцией. А это открывает возможность использовать для решения задач на сети Петри хорошо изученные методы линейной алгебры.

Итак, пусть P={p₁, p₂,…,p_n} – множество позиций, T={t₁, t₂,…,t_m} – множество переходов. Сеть определяется:

1) Ребрами из элементов T в элементы P. Для t_i  T, p_j  P обозначим их количество из t_i в p_j через d⁺[i,j]. Вместе они образуют целочисленную матрицу D⁺, в которой m строчек, соответствующих переходам t₁, t₂,…,t_m, и n столбиков, соответствущих позициям p₁, p₂,…, p_n. Значок “+” у этой матрицы символизирует тот факт, что стрелки, выходящие из переходов увеличивают количество фишек в соответствующих позициях.

2) Аналогично с помощью матрицы D^–, запишаем информацию о ребрах, идущих из позиций в переходы. На этот раз d^–[i,j] есть число ребер, которые из позиции p_j P идут в переход t_i T. Матрица по-прежнему состоит из m строк и n столбцов. У этой матрицы значок “-” указывает, что стрелки, выходящие из позиции уменьшают количество фишек в этой позиции.


Допустим теперь, что =(₁, ₂,…, _n) – некоторая маркировка и t_i – переход, разрешенный в данной ситуации. Согласно определению при срабатывании перехода t_i в позиции p_j число фишек _j изменится и станет равно

_j = _j + d⁺[i,j] - d^–[i,j]

Пусть E_i = (0,…,0,1,0,…,0) – строка длины n, в которой единица стоит на i-той позиции. Тогда указанное равенство можно переписать в матричной форме

 =  + E_i (D⁺- D^–)

Пусть D = D⁺- D^–. Это так называемая матрица изменений. Тогда  =  + E_i D. Теперь, если имеется последовательность переходов t_i1 t_i2,…, t_ik , которые могут сработать, стартуя с маркировки , то результирующая маркировка  выражается как

 =  + (E_ik+E_ik-1+…+E_i2+E_i1)D

Сумма (E_ik+E_ik-1+…+E_i2+E_i1) представляет собой целочисленный вектор x = (x₁,x₂,…,x_m). А все равенство превращается в систему линейных уравнений

xD = - (1)

Таким образом задача достижимости маркировки  из маркировки  приводит к задаче – решить указанную систему в целых неотрицательных числах. Нельзя сказать, что одна задача сводится к другой. К сожалению, если найти решение системы (1), это не даст полной информации о цепочке переходов. Не гарантрует даже, что такая цепочка существует. Однако если получится неразрешимость системы (1), то это докажет, что   .

Какая, однако, информация относительно последовательности запусков t_i1, t_i2,…, t_ik имеется в решении x = (x₁,x₂,…,x_m) системы (1)? Очевидно, что x_i – число запусков перехода t_i. По этой причине вектор x называется вектором запусков последовательности t_i1, t_i2,…, t_ik. Таким образом, если  может быть получена из , то мы, решив систему, получим информации о том, какой переход и сколько раз должен быть для этого запущен. Для конкретного решения системы x = (x₁,x₂,…,x_m) таких комбинаций конечное число и переборным алгоритмом их все можно найти. К сожалению система (1) может иметь бесконечно много решений и подобный анализ их всех за конечное число шагов становится невозможным.

Таким образом матричный подход способен помочь в решении задачи недостижимости, но не решает ее полностью.


Задача определения, является ли сеть сохраняющей, имеет решение с помощью матричного подхода.

Теорема. Сеть Петри уровня активности 1 является сохраняющей тогда и только тогда, когда система линейных уравнений

Dw = 0

относительно вектор-столбца неизвестных w = {w_i}_i=1,…,n имеет решение с условием w_i >0 (i=1,…,n).

Доказательство. Допустим, что сеть с некоторой начальной маркировкой ₀ является сохраняющей. Тогда существуют числа w_i>0 (i=1,…,n), что скалярные произведения ₀w и w для всех R(₀) совпадают. Для вектора x=(x₁,x₂,…,x_m) запусков, которые переводят ₀ в  имеем:

₀w = w = (₀+ xD)w

Значит xDw =0 для любого вектора запусков x. По условию теоремы любой переход сети срабатывает при какой-то последовательности запусков. Возьмем произвольный индекс j от 1 до m и найдем кратчайшую последовательность переходов , в которой t_j срабатывает. Естественно, что в этой последовательности t_j встречается один раз и стоит на последнем месте. Имеем и соответствующий вектор запусков x=(x₁,x₂,…,x_m), в котором на j-том месте стоит 1. Если длина  равна единице, то для kj x_k=0 и из xDw=0 получим, что j-тый элемент столбика Dw равен нулю. Теперь индукцией по длине  доказываем, что в любом случае j-тый элемент Dw равен нулю. Для этого рассмотрим в  любой предшествующий t_j переход t_r. Кратчайшая допустимая цепочка к нему конечно короче, чем . Значит r-тый эдемент Dw равен нулю. Значит в xDw останется только 1 (Dw)_j. Значит и j-тый эдемент Dw равен нулю. Итак, Dw =0.

Обратно, если Dw =0, то из w = (₀+ xD)w немедленно получаем, что w = ₀w. Теорема доказана.

Теорема говорит о том, что проверка, является сеть сохраняющей или нет, эквивалентна поиску положительных решений системы линейных уравнений Dw = 0. Это можно сделать методами линейной алгебры привлекая при необходимости линейное программирование. При этом получается и весовой вектор w.