Федеральное агентство по образованию

Вид материала

Документы

Содержание ЧИСЛОВЫЕ РЯДЫ. ПРИЗНАК КУММЕРА Л.Н. Валимухаметова, Л.Г. Карыев Признак Куммера

Подобный материал:

• Федеральная целевая программа "Развитие электронной компонентной базы и радиоэлектроники", 3538.74kb.
• Сверху вниз//Рособразование Федеральное агентство по образованию, 866.01kb.
• Российской Федерации Федеральное агентство по образованию обнинский государственный, 90.77kb.
• Российской Федерации Федеральное агентство по образованию обнинский государственный, 77.01kb.
• Российской Федерации Федеральное агентство по образованию обнинский государственный, 84.76kb.
• Российской Федерации Федеральное агентство по образованию обнинский государственный, 130.31kb.
• Российской Федерации Федеральное агентство по образованию обнинский государственный, 81.87kb.
• Федеральное агентство по науке и инновациям федеральное агентство по образованию, 214.87kb.
• Федеральное агентство по образованию государственное образовательное учреждение высшего, 427.38kb.
• Федеральное агентство, 77.37kb.

^

ЧИСЛОВЫЕ РЯДЫ. ПРИЗНАК КУММЕРА

Л.Н. Валимухаметова, Л.Г. Карыев

Пусть дана числовая последовательность a₁, a₂, a₃, … , a_n, … Выражение вида

a₁ + a₂ + a₃ + … + a_n + …=

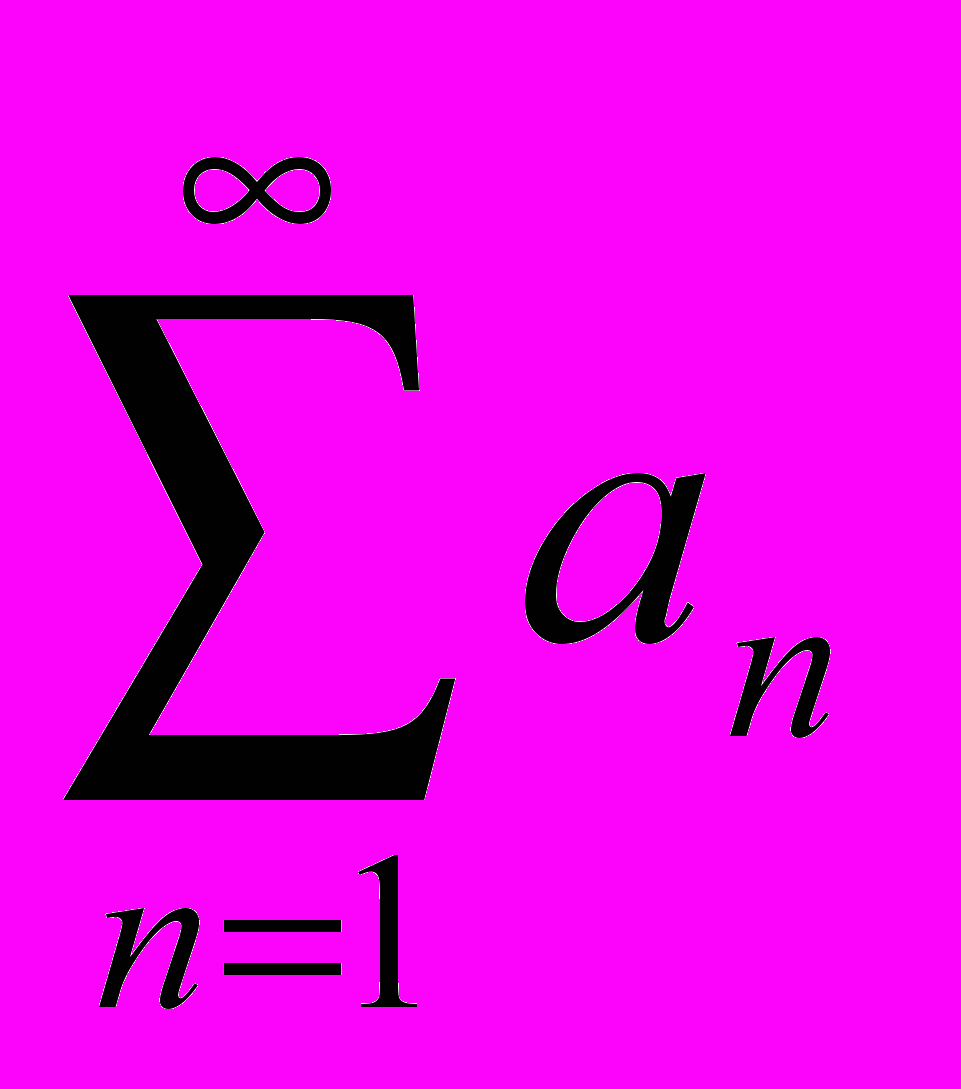
называется числовым рядом или просто рядом. Числа a₁, a₂, a₃, … , a_n, … называются членами ряда, член a_n – общим членом ряда.

Введем общий признак, принадлежащий Куммеру; его скорее можно рассматривать как общую схему для получения конкретных признаков.

^ Признак Куммера. Пусть

c₁, с₂, …, с_n, …

будет произвольная последовательность положительных чисел, такая, что ряд



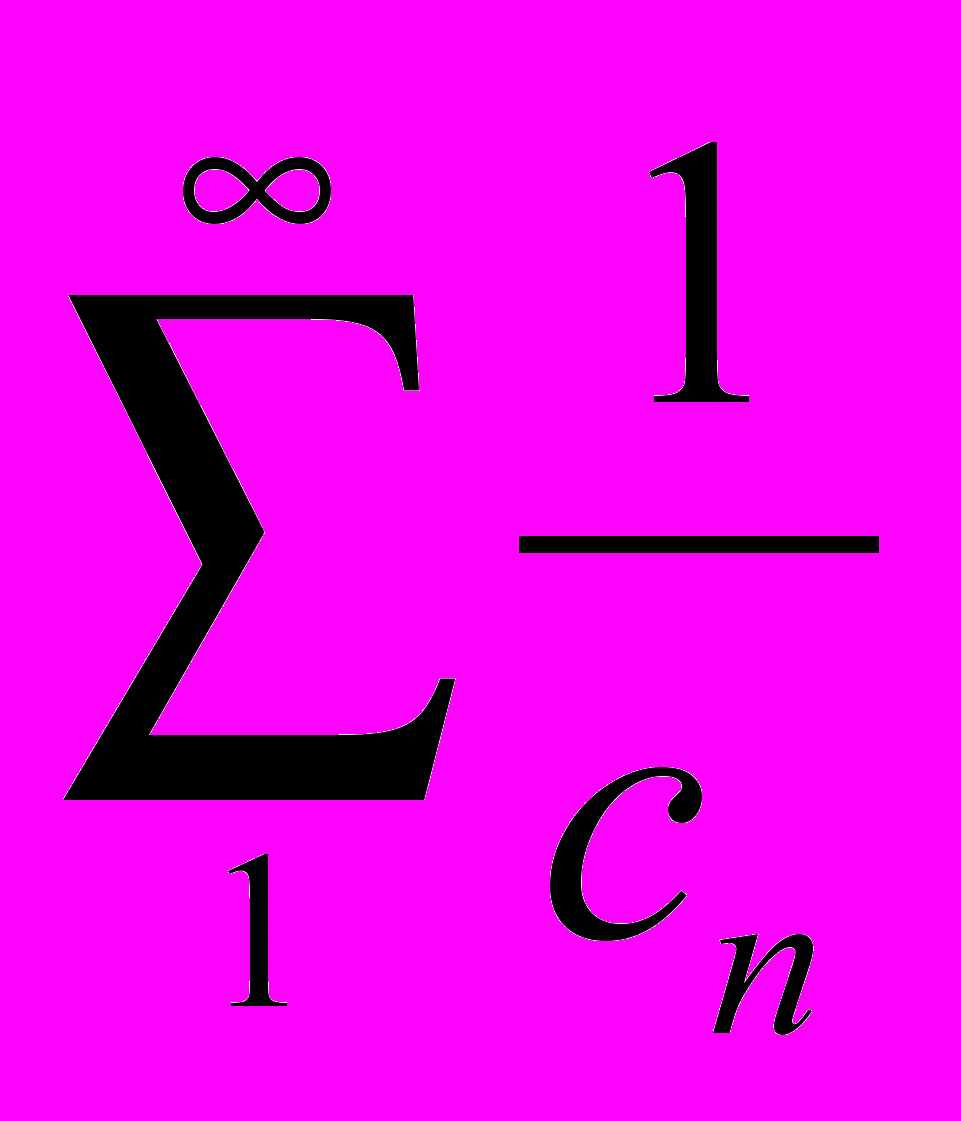
расходится (признак сходимости не нуждается при выводе предположения). Составим для испытуемого ряда (А) варианту

К_n = с_n ∙ 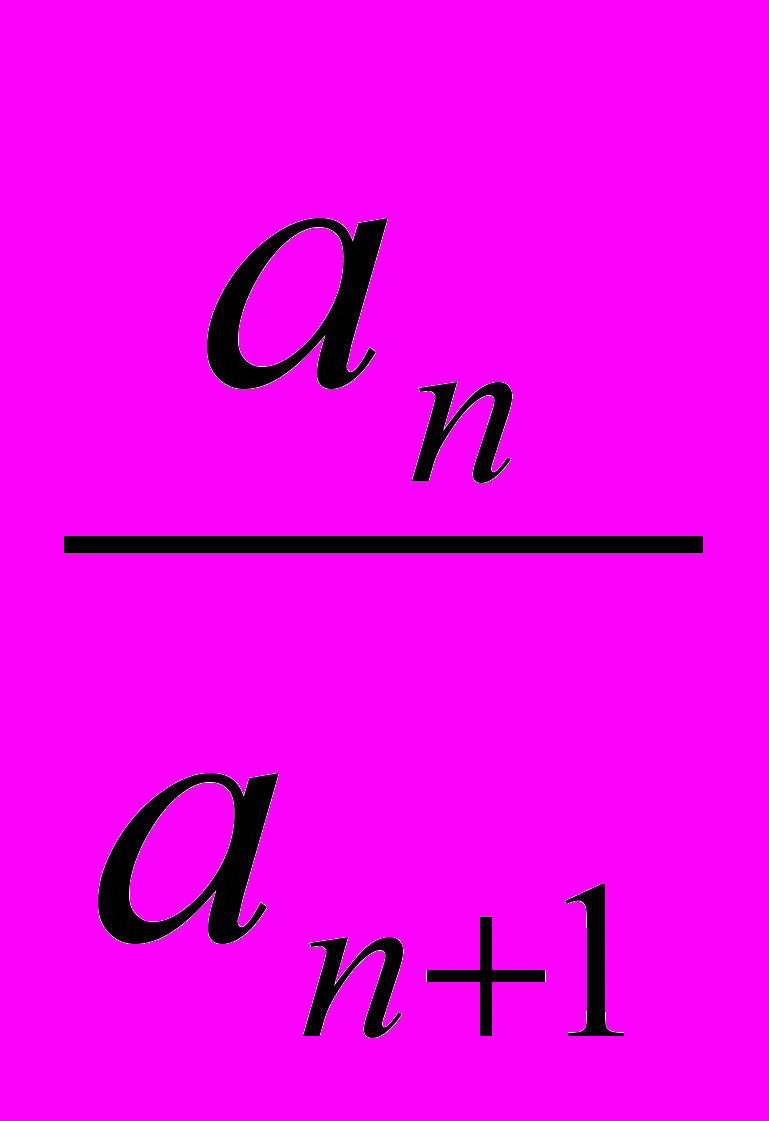- c_n+1

Если (для n>N) выполняется неравенство

К_n ≥δ

где δ – постоянное положительное число, то ряд сходится. Если же (для n>N)

К_n ≤0,

то ряд расходится.

Доказательство. Пусть

К_n = с_n ∙ 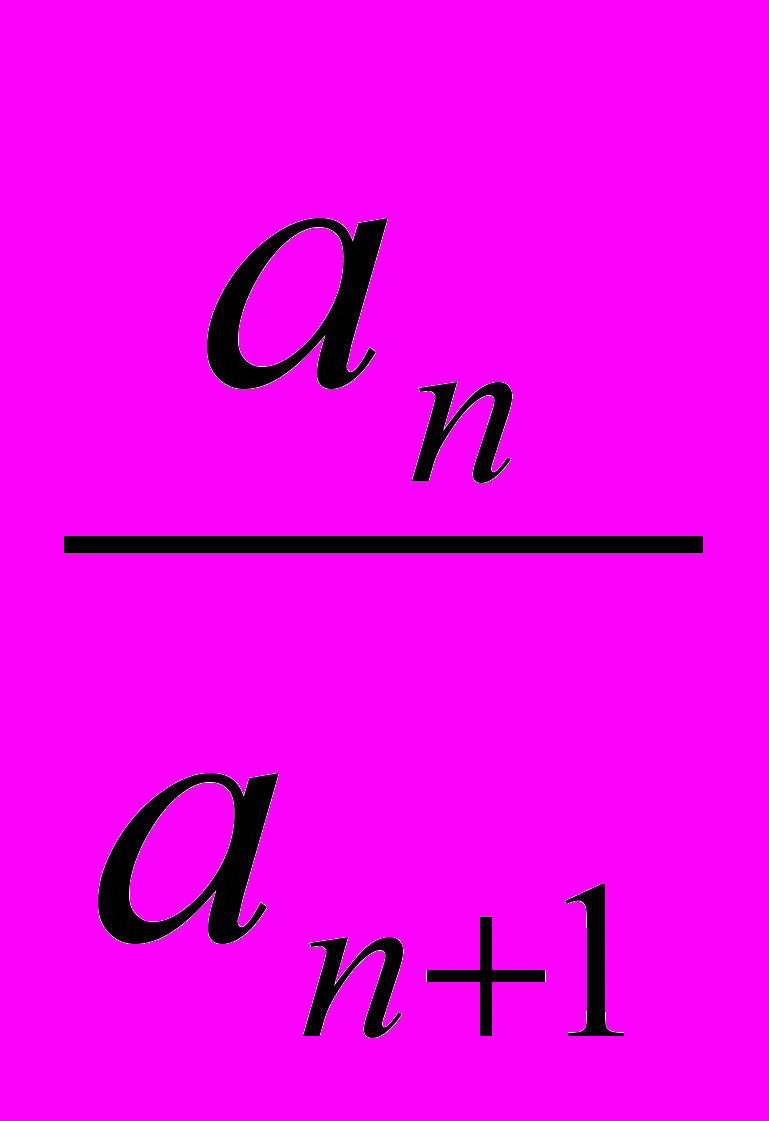- c_n+1 ≥ δ > 0


(неравенство это, очевидно, можно считать выполненным при всех n).

Умножив обе части этого неравенства на a_n+1, получим:

c_na_n – c_n+1a_n+1 ≥ δ ∙ a_n+1

значит,

c_na_n – c_n+1a_n+1 > 0 или c_na_n > c_n+1a_n+1

Отсюда следует, что переменная c_na_n монотонно убывает и, следовательно, стремится к конечному пределу (так как она ограничена снизу нулем).

Итак, ряд

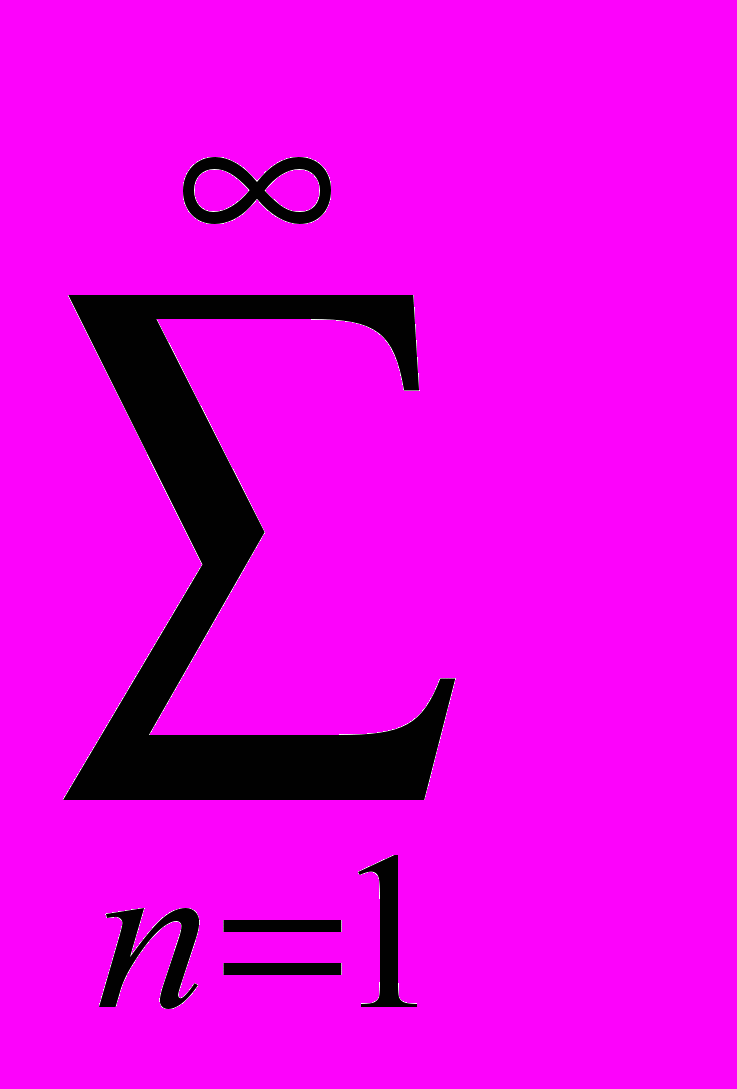(c_na_n – c_n+1a_n+1 )

сходится, ибо сумма его n первых членов:

c₁ a₁ − c_n+1a_n+1

имеет конечный предел. Тогда следует, что ряд 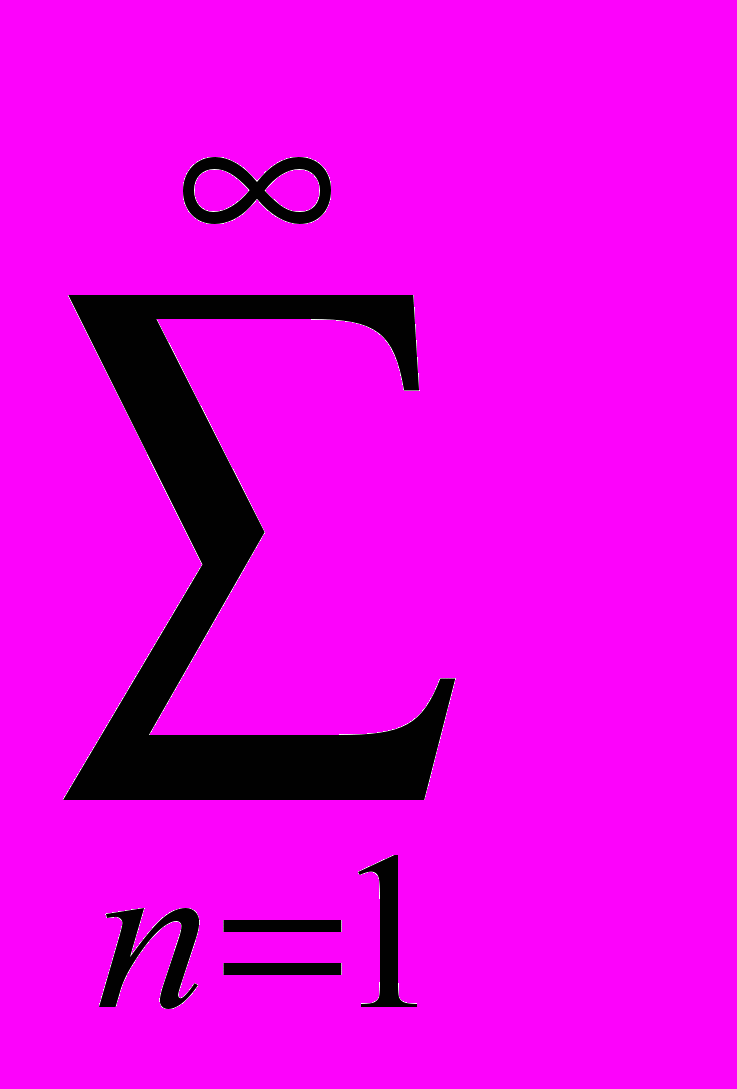δa_n+1 сходится.

Если же, для n>N,

К_n = с_n ∙ 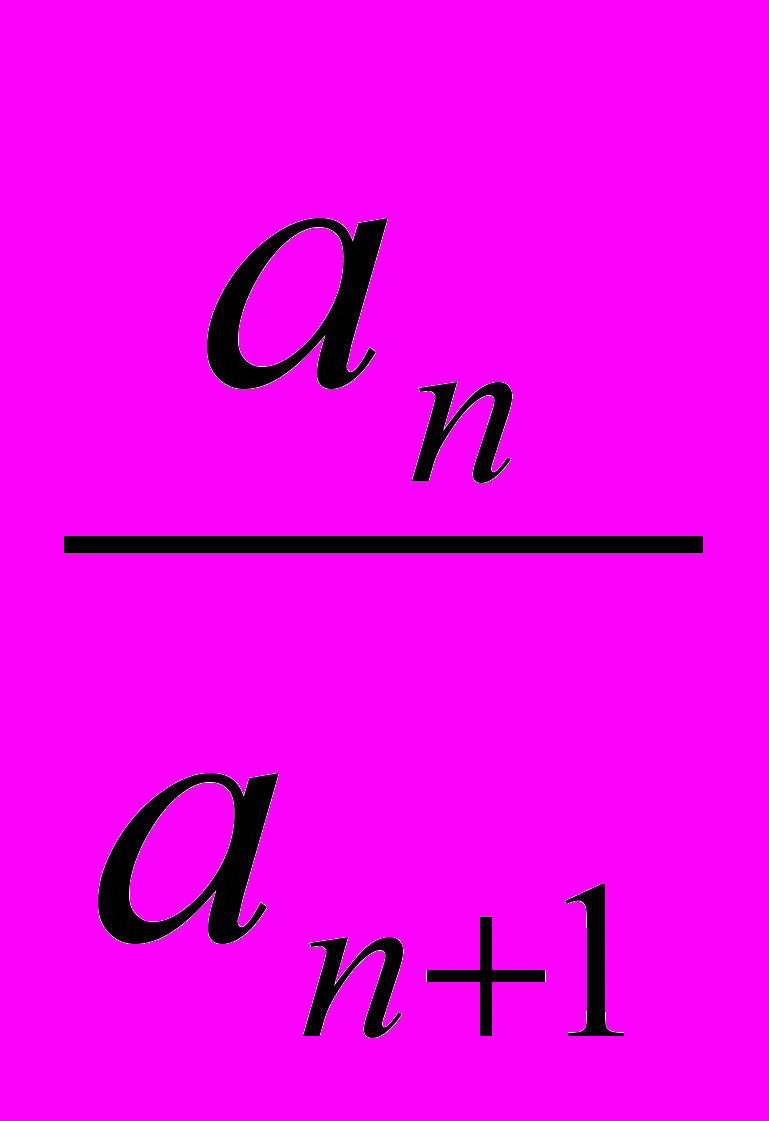- c_n+1 ≤ 0,

то имеем,



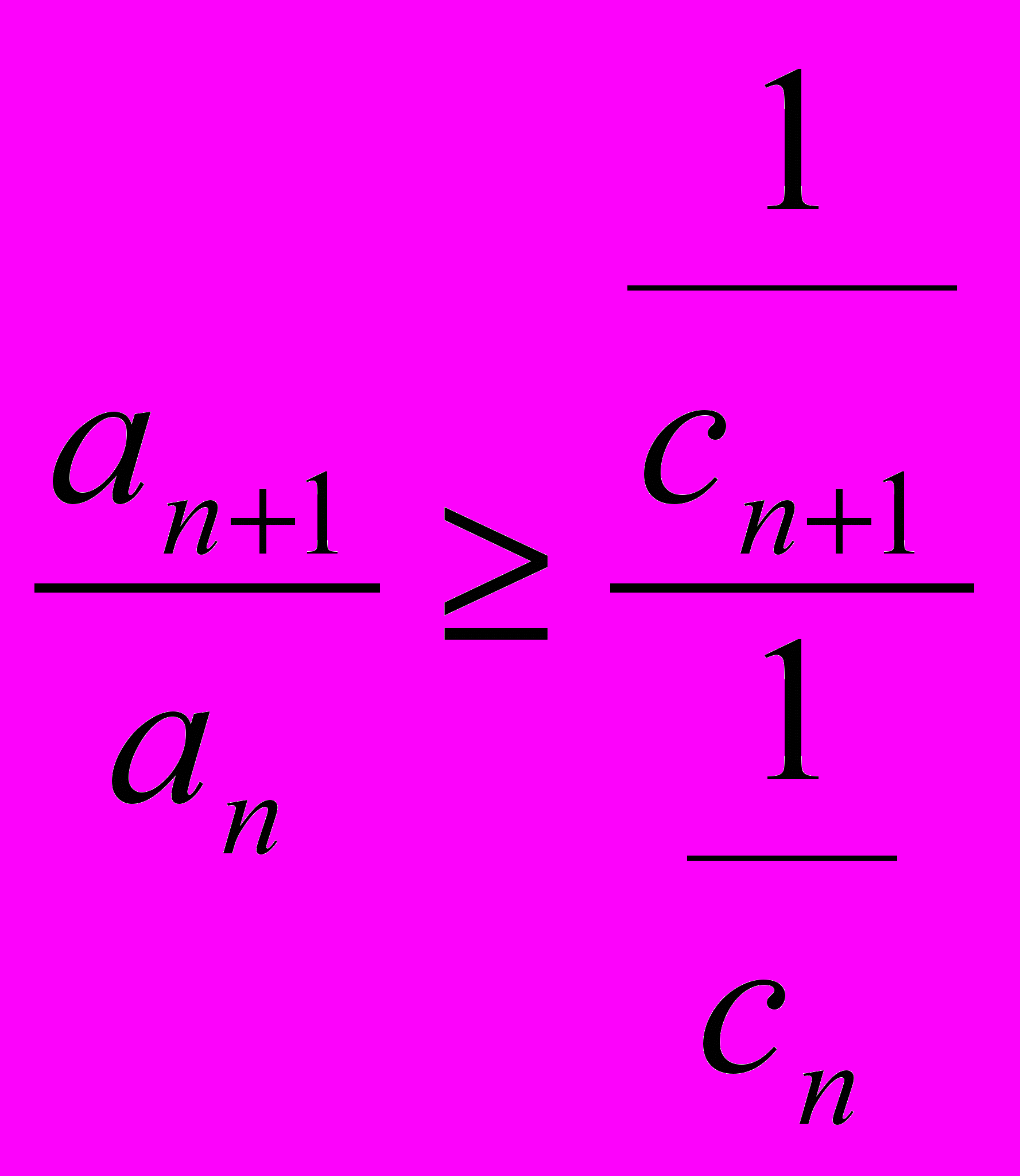
Так как ряд 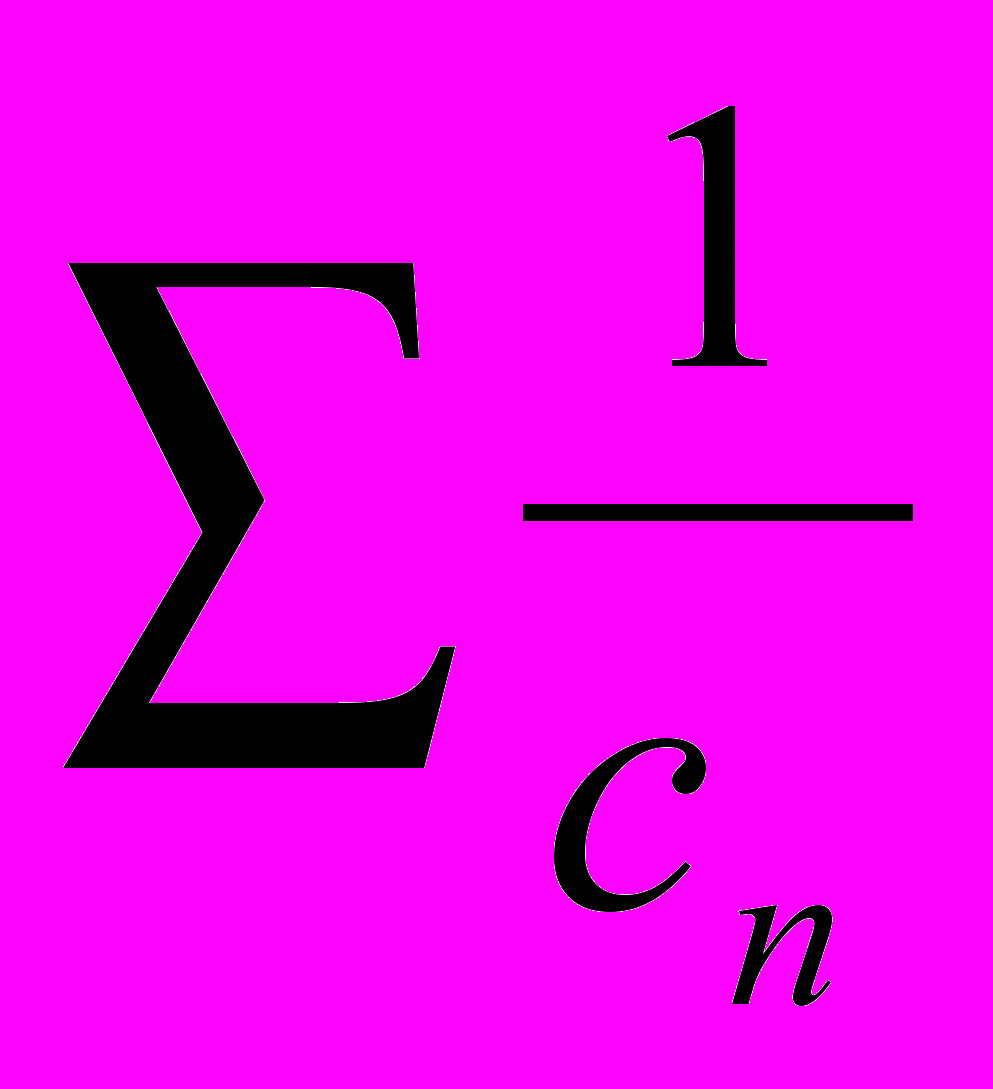предположен расходящимся, то расходится и испытуемый ряд.

В предельной форме признак Куммера выглядит так:

Допустим, что варианта имеет предел (конечный или нет): limК_n = К

Тогда при К >0 ряд сходится, а при К <0 - расходится.

Покажем теперь, как при помощи признака Куммера можно получить некоторые важные признаки сходимости как частные случаи его.

а) Положим, например, c_n=1; условие, чтобы ряд расходился, соблюдено. Имеем:

К_n =

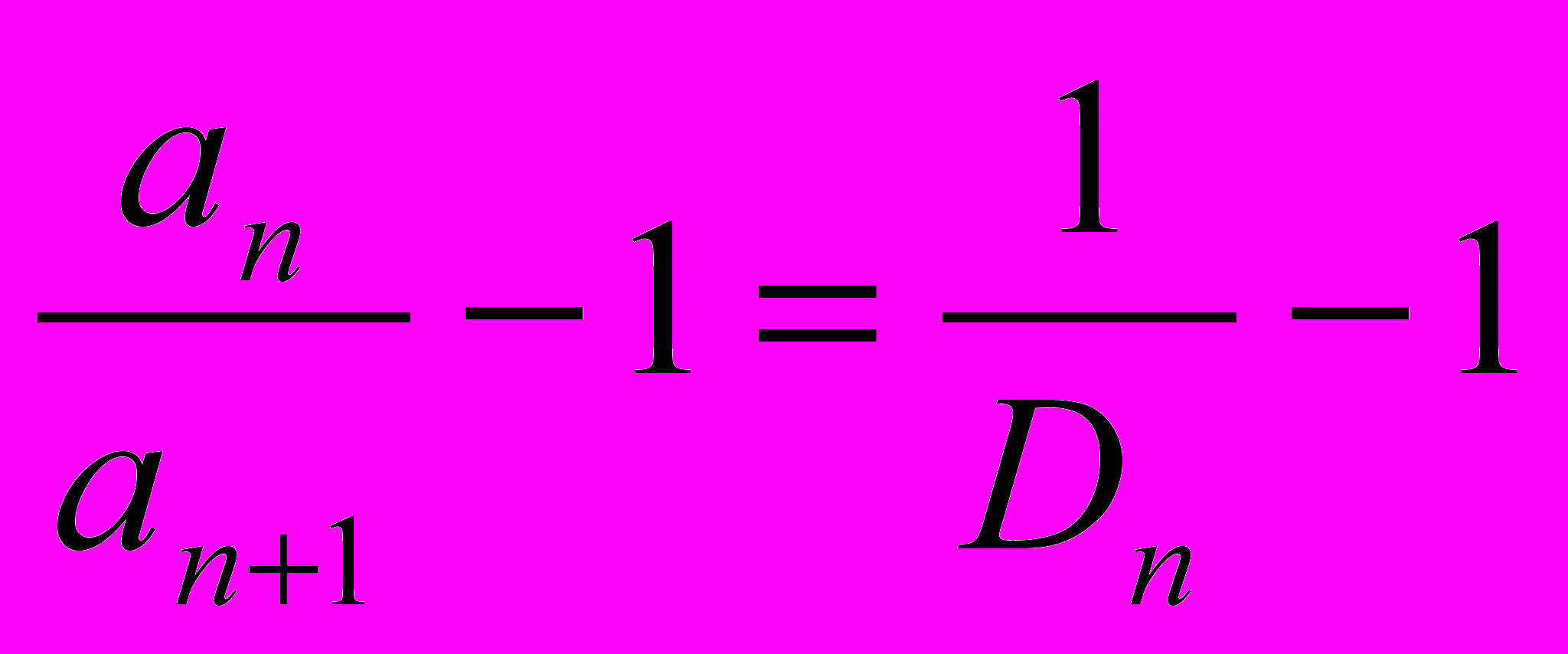
Если варианта D_n стремится к пределу D, то К_n стремится к пределу

К = К 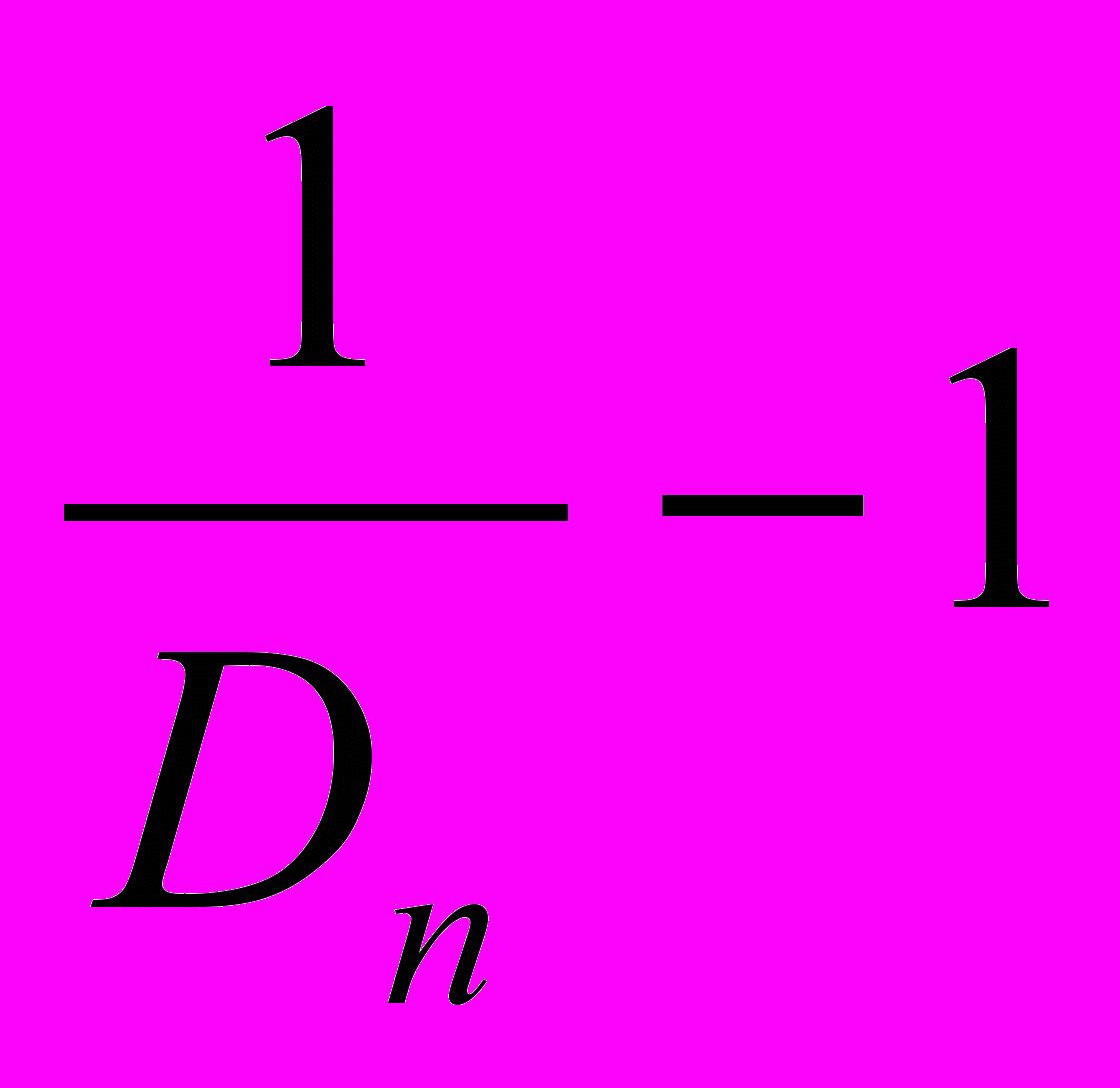(К = +∞, если D = 0, К = -1, если D = +∞). При D>1, очевидно,

К <0, и по признаку Куммера ряд расходится; если же D<1, то К > 0, и ряд сходится. Таким образом, мы пришли вновь к признаку Даламбера.

б) Положим, далее, c_n=n и отметим, что ряд 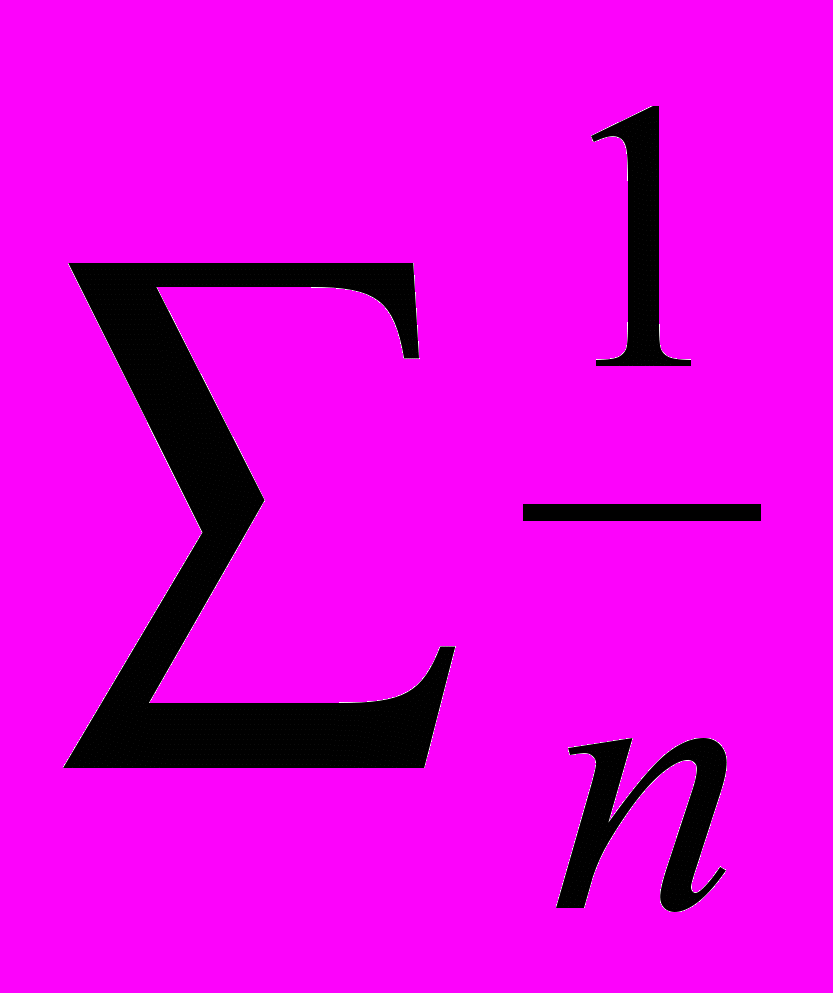расходится. Выражение К_n получит вид:

К_n = 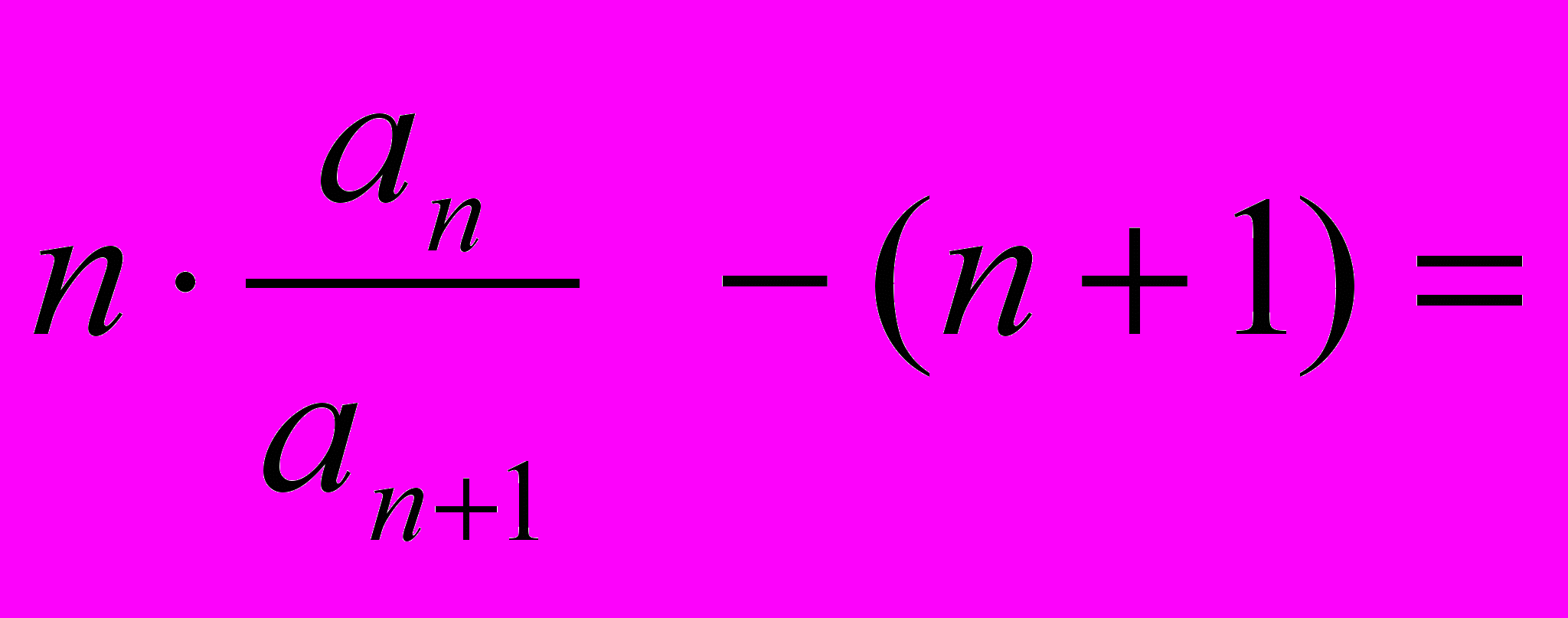R_n – 1 .

Если варианта R_n стремится к пределу R, то К_n стремится к пределу К=R – 1

(К = ±∞, если R = ±∞). При R >1 имеем К > 0, и по признаку Куммера ряд сходится; если же R < 1, то К <0, так что ряд расходится. Мы вновь получили признак Раaбе.

Литература:

1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. – М.: «Наука» - 1970.