Динамика и синтез широкополосных сейсмических приборов 01. 02. 06 Динамика, прочность машин, приборов и аппаратуры, 05. 13. 01 Системный анализ, управление и обработка информации (промышленность, технические системы)

Вид материала

Автореферат

Содержание Динамика скважинного прибора Динамика сейсмических источников Третья глава В четвертой главе Пятая глава. Шестая глава.

Подобный материал:

• Динамика управляемого движения мобильного ползающего робота с изменяемой формой корпуса, 219.75kb.
• Оценка и повышение живучести несущих конструкций технологического оборудования металлургического, 294.38kb.
• Разработка расчетных методов оценки живучести рабочих и опорных прокатных валков 01., 250.79kb.
• Программа-минимум кандидатского экзамена по специальности 01. 02. 06 «Динамика, прочность, 76.1kb.
• Беспружинная пневмогидроарматура с уплотнительными затворами различной физической природы, 1044.02kb.
• Высокоточное нейросетевое распознавание в системах технического зрения, 248.39kb.
• Касьянов Константин Геннадьевич оценка несущей способности и ресурса конструкционных, 452kb.
• Краткосрочное прогнозирование на основе технологии нейросетевого пространственно-параметрического, 194.81kb.
• Эволюционный метод синтеза непрерывно дискретных систем управления, 288.26kb.
• Системный анализ параметров сердечно-сосудистой системы учащихся югры 05. 13. 01 системный, 641.8kb.

Динамика скважинного прибора

В работе предложена математическая модель для аналитического исследования влияния различных факторов на динамику прибора.

Предварительно задача решается в статике.

На рис. 2 приведена схема исследуемой модели прибора в динамике. Как правило, скважинные приборы имеют значительную, по сравнению с поперечными размерами, длину, поэтому в модели прибор представлен двумя жестко соединенными друг с другом сосредоточенными массами m₁ и m₂ .




D – диаметр скважины; c₁ – жесткость нижнего контакта прибора со скважиной;

c₂ – жесткость верхнего контакта прибора со скважиной; c₃ – жесткость прижимающего элемента; c₄ – жесткость корпуса прибора между массами; f₁, f₂ – возмущающие воздействия (вибрация стенки скважины в точках контакта)

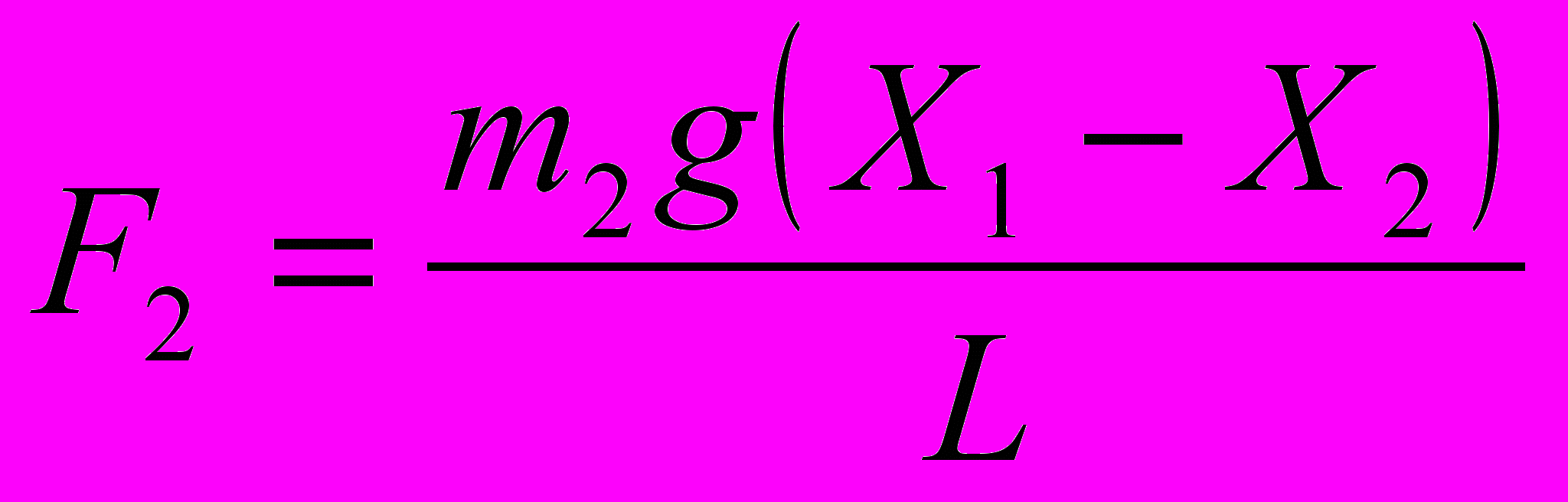. (6)

На рис. 2 не обозначены длина прибора L, длина прижимающего упругого элемента l, коэффициенты демпфирования d₁ и d_2.


С учетом принятых обозначений в общем случае для описания динамики

прибора получаем следующую систему уравнений




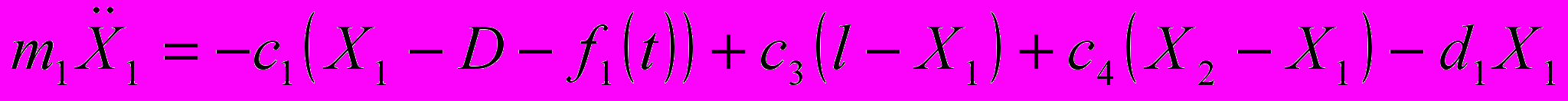
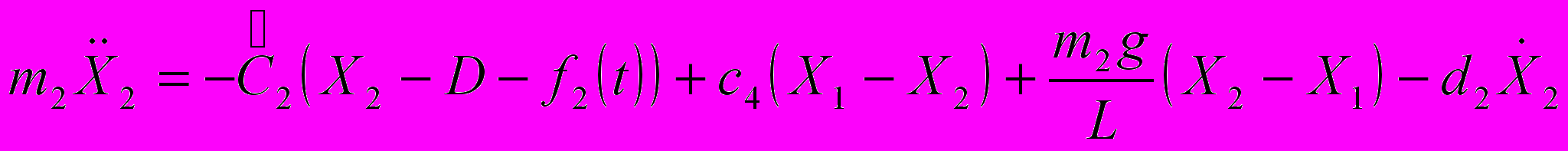, (7)

где X_i ─ координаты m_i ,

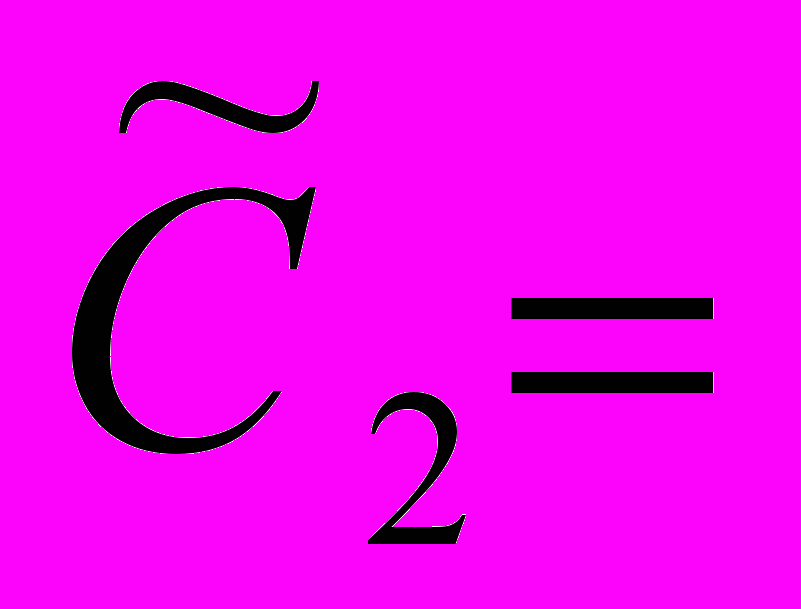
c₂, если X₂ -f₂

0 , если X₂≥ -f₂

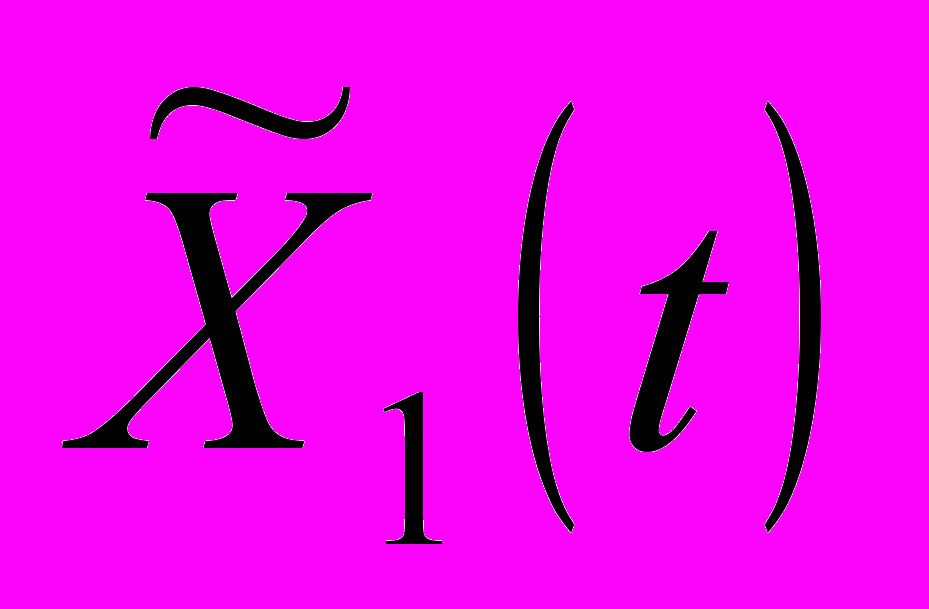и 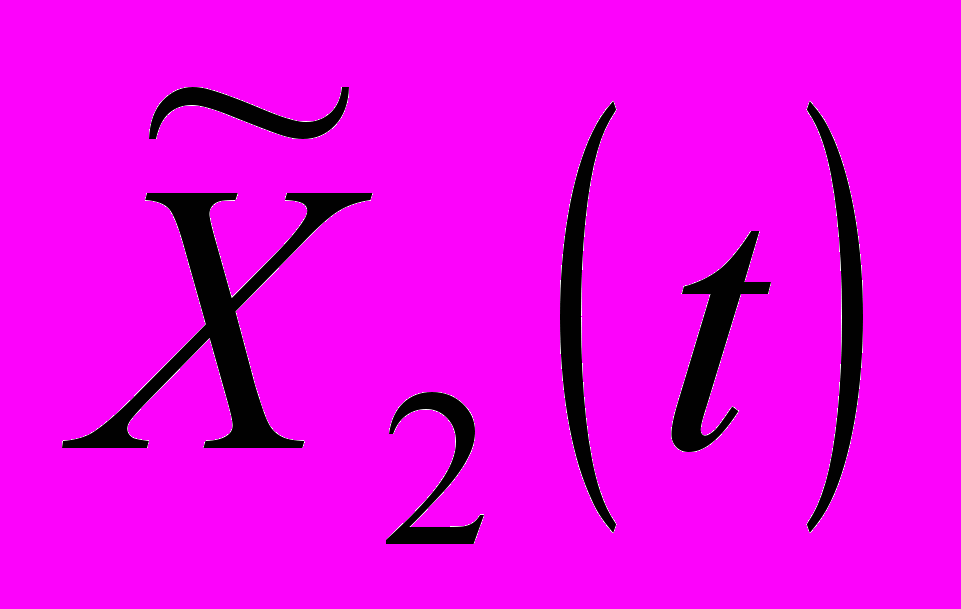– общие решения соответствующей однородной системы 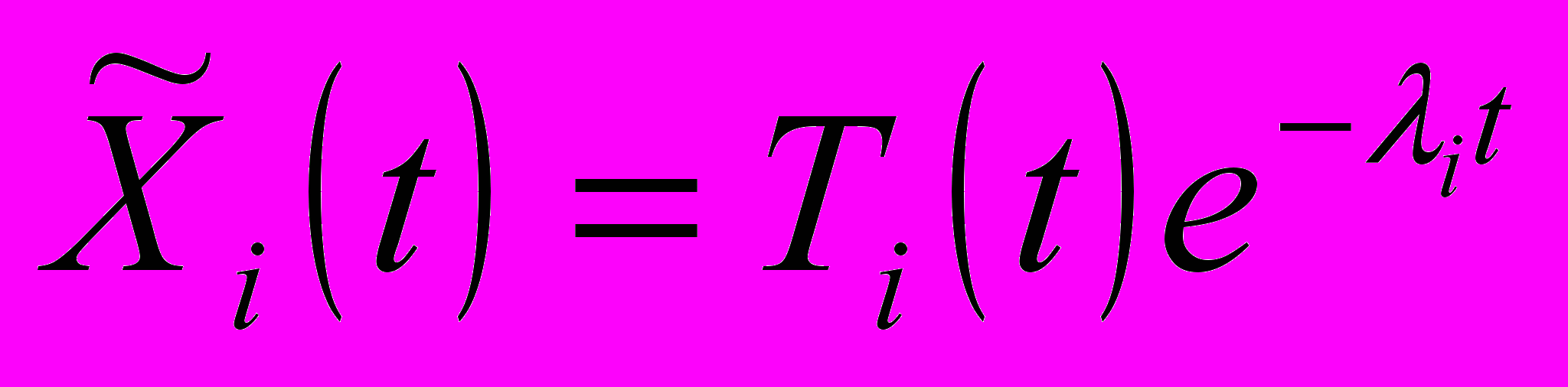, где λ_i>0, T_i(t) – тригонометрический полином.

X₁⁰(t), X₂⁰(t) – частные решения неоднородной системы.



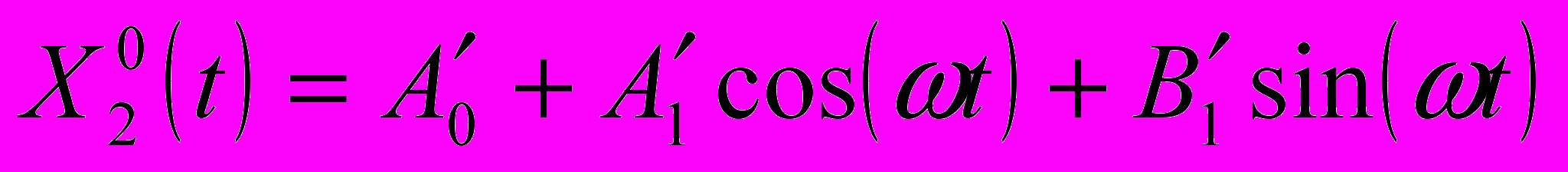
Система уравнений для определения коэффициентов A₀, A₁, B₁, A₀’, A₁’, B₁’.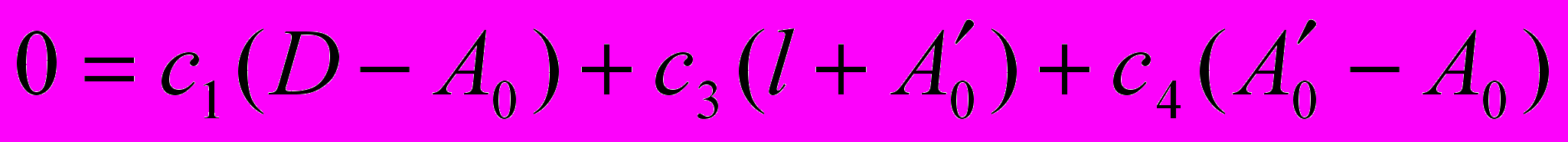







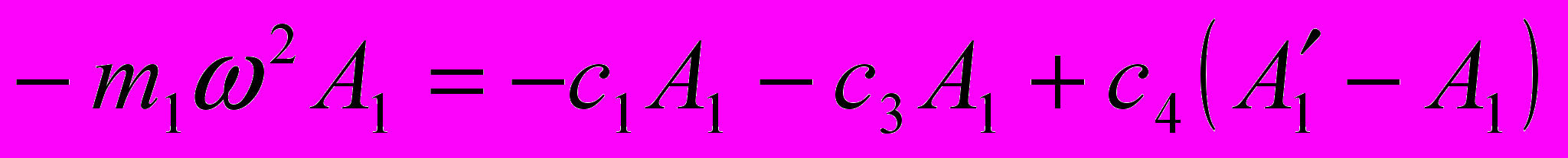
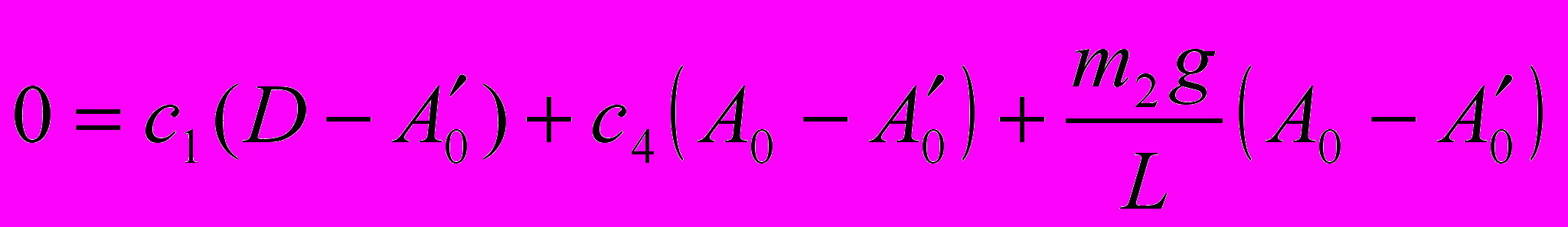(8)



.

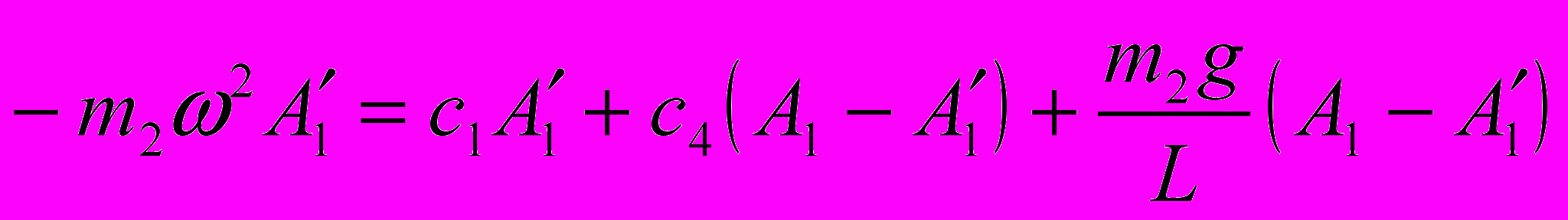
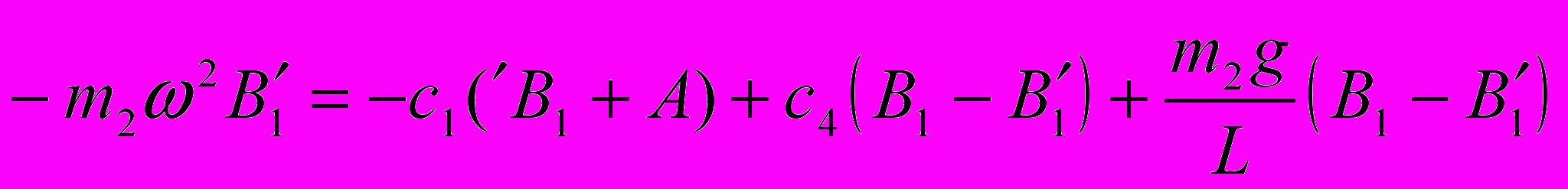Для обеспечения безотрывной работы прибора надо, чтобы амплитуда колебаний не превосходила амплитуду возмущения. Отсюда получаем условие:

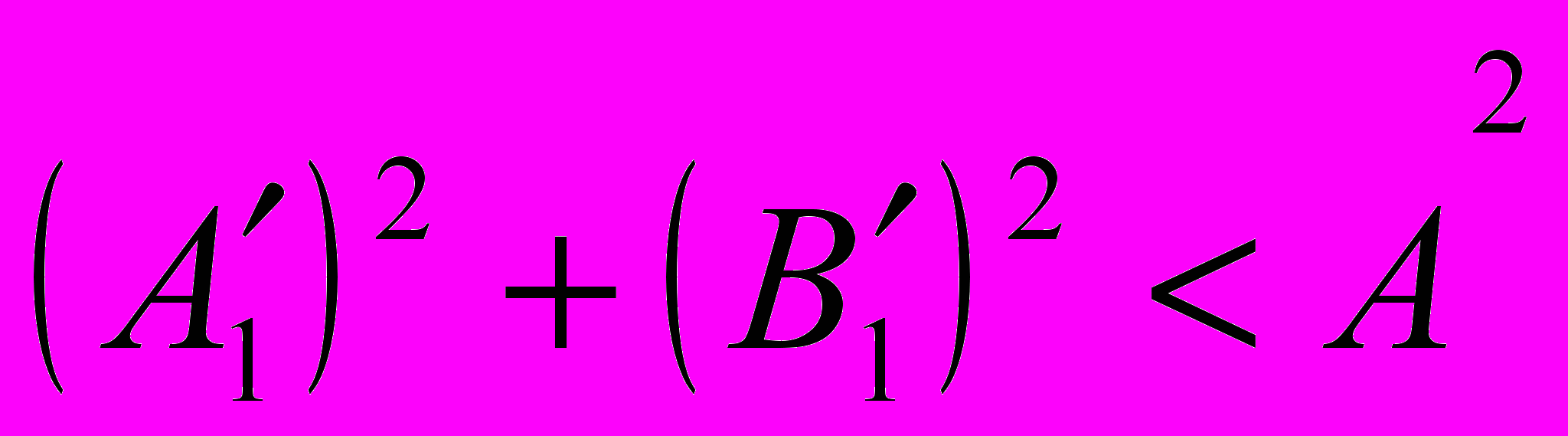. (9)

Данная математическая модель позволила с большой степенью приближения проанализировать поведение скважинных приборов в условиях различных возмущений. Полученные результаты использовались автором при создании ряда скважинных приборов различного назначения.

Динамика сейсмических источников на базе электродинамического преобразователя возвратно-поступательного движения.

В данном случае под электродинамическим преобразователем возвратно-поступательного движения понимается электромеханический преобразователь, в котором подвижная катушка размещается с возможностью осевого перемещения в зазоре магнитопровода. Развиваемое электродинамическим преобразователем возвратно-поступательного движения усилие F(t) определяется выражением

F(t) = B l i(t) (10)

Тогда передаточные функции сейсмического источника на базе электродинамического преобразователя возвратно-поступательного движения по току подвижной катушки определяются произведением соответствующей передаточной функции W_k(p) на коэффициент B l.

Передаточные функции сейсмического источника на базе электродинамического преобразователя возвратно-поступательного движения по напряжению питания подвижной катушки.

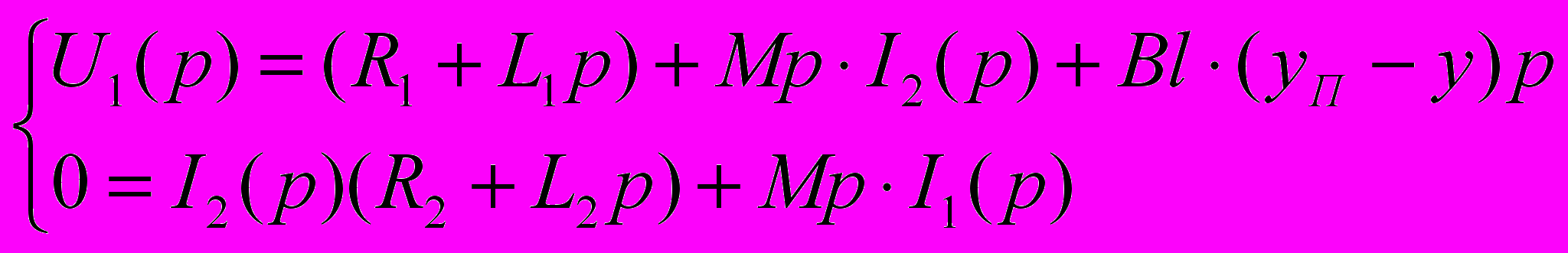. (11)

Передаточная функция виброперемещения излучающей плиты y_П(p) по напряжению питания подвижной катушки U₁(p)

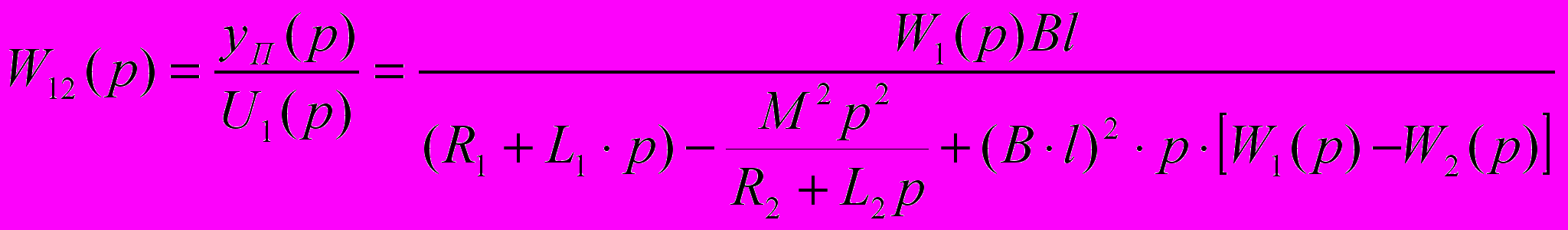. (12)

Передаточная функция виброперемещения транспортного средства y_Т(p) по напряжению U₁(p)

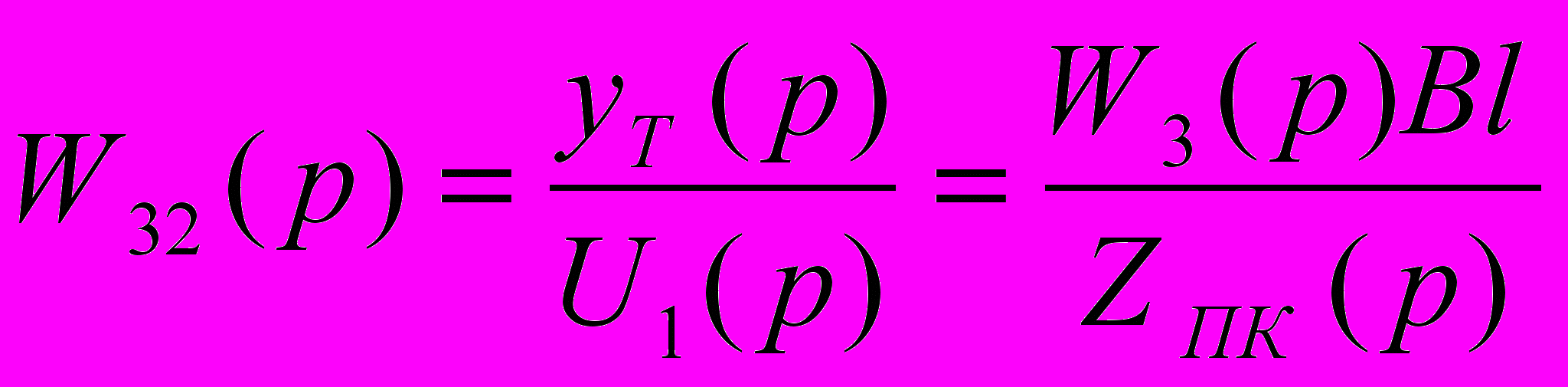. (13)

Передаточная функция виброперемещения инерционной массы y(p) по напряжению U₁(p)

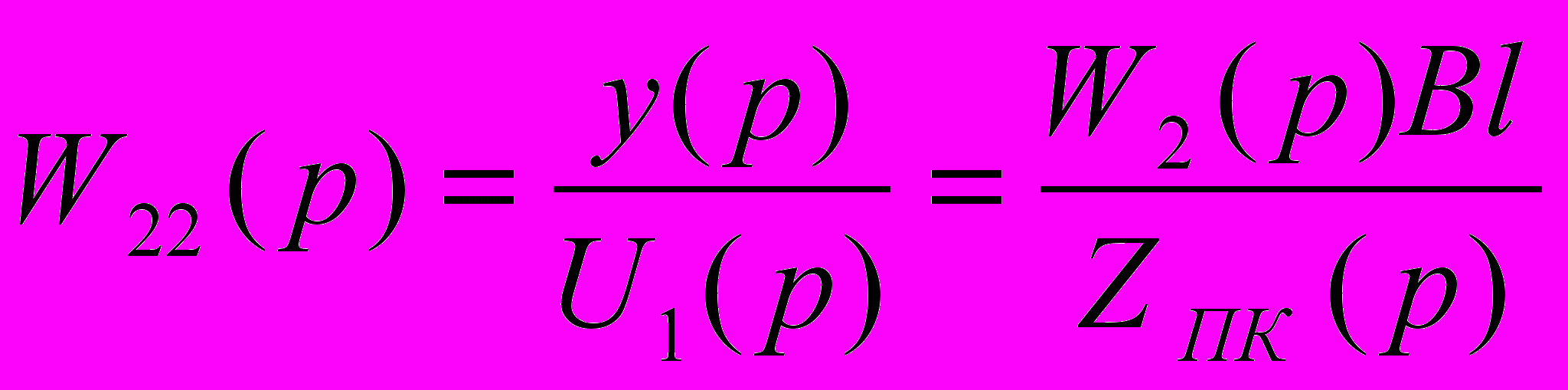. (14)

Замена в соответствующих передаточных функциях оператора p на оператор jω обеспечивает получение соответствующих частотных характеристик источника. На рис. 3. приведены амплитудно-частотные характеристики виброскорости излучающей плиты в диапазоне от 0 до 1000 Гц при различных значениях величины инерционной массы.



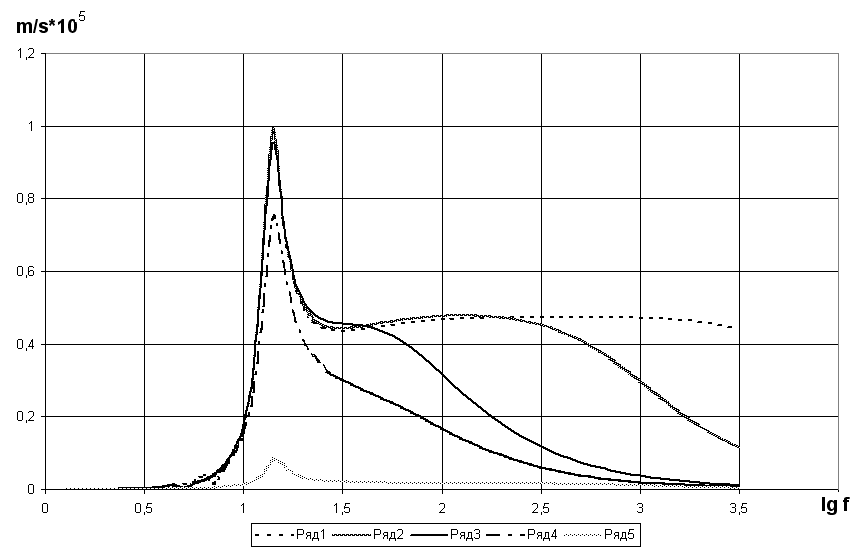
Рис. 3. АЧХ виброскорости излучающей плиты сейсмического источника


Анализ амплитудно-частотных характеристик в функции различных параметров позволил установить, что приведенные параметры грунта существенно сказываются на полосе пропускания.

Третья глава посвящена исследованию электромагнитных процессов в системе электромеханический преобразователь сейсмического источника – статический преобразователь.

На рис. 4 приведена схема системы статический преобразователь – электродинамический преобразователь возвратно-поступательного движения.

Так как при формировании гармонических колебаний широкое распространение получили системы управления с широтно-импульсной модуляцией по синусоидальному закону, представляет интерес исследование влияния глубины модуляции на гармонический состав тока подвижной катушки.

Сложность данной задачи заключается в том, что входное сопротивление электродинамического преобразователя возвратно-поступательного движения в зависимости от частоты вибрации и вида механической нагрузки значительно изменяется и может принимать как индуктивный, так и емкостный характер.

Автором предложен метод, который позволяет упростить расчет тока в нагрузке и ключах инвертора при наиболее сложных для анализа режимах работы, когда закон коммутации ключей заранее неизвестен.



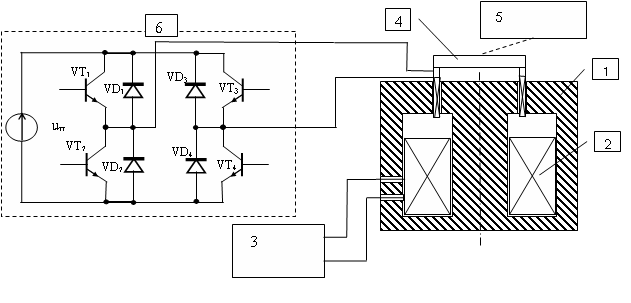
Рис. 4. Схема системы статический преобразователь – ЭДПВПД

1– магнитопровод; 2 – катушка подмагничивания; 3 – блок подмагничивания; 4 – подвижная катушка; 5 – механическая нагрузка; 6 – статический преобразователь; (VT₁-VT₄) – управляемые вентили (транзисторы); (VD1-VD4) – неуправляемые вентили обратного тока (диоды)


Суть предложенного метода заключается в том, что, предварительно задавшись гладкой составляющей тока подвижной катушки электродинамического преобразователя возвратно-поступательного движения, вычисляют ЭДС движения, наводимую в подвижной катушке, подставляют полученное значение ЭДС в выражение тока подвижной катушки и затем вычисляют мгновенные значения токов подвижной катушки и ключей инвертора.

В зависимости от аппаратурного решения формирование управляющего сигнала при широтно-импульсной модуляции осуществляется сравнением задающего сигнала требуемой формы (в частности синусоидального), взятого по модулю, и опорного сигнала, пилообразного или треугольного.

На рис. 5 показаны диаграммы сравниваемых задающего и опорного напряжений. За нулевую ординату взята ордината основания модулирующего сигнала.



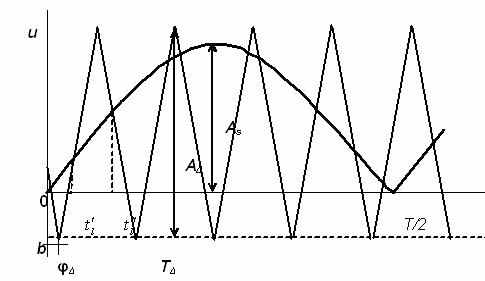
Рис. 5. Диаграммы задающего и опорного напряжений


Так как при широтно-импульсной модуляции моменты коммутации ключей автономного инвертора напряжения определяются моментами равенства задающего сигнала опорному, для определения моментов коммутации необходимо найти множество точек, когда удовлетворяется равенство

f_s(t)=f_Δ(t) , (15)

где f_s(t) – функция модулирующего сигнала; f_Δ(t) – функция опорного сигнала.

Для заданных условий получены выражения определения моментов коммутации соответствующих пересечению кривой модулирующего сигнала с восходящими отрезками опорного сигнала в нечетные полупериоды опорного сигнала

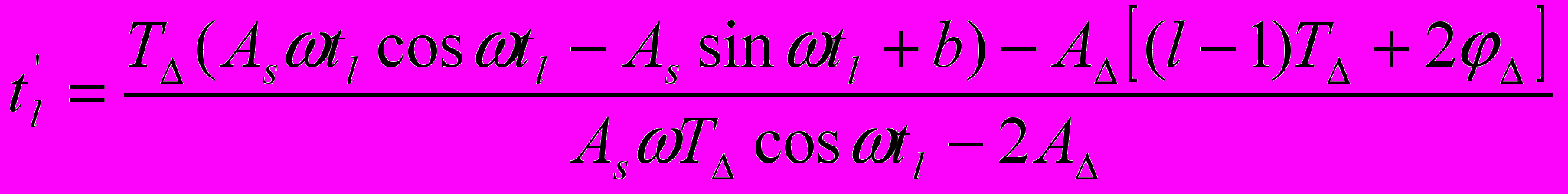( 16)

и моменты коммутации в четные полупериоды опорного сигнала


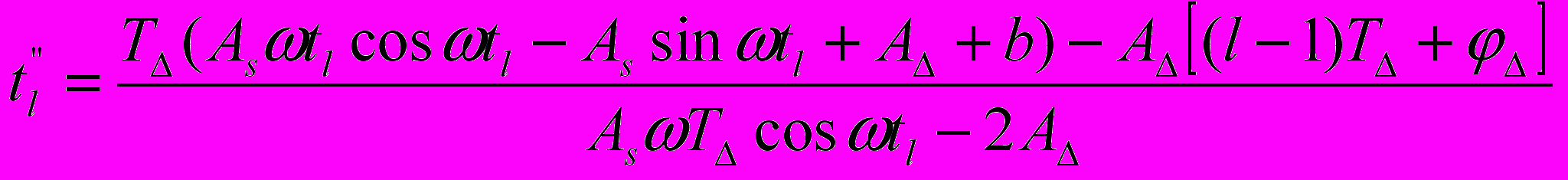(17)

Определение значений коммутационных функций производим для мостового автономного инвертора напряжения с разделением управления управляемых вентилей разных диагоналей моста по соответствующим полупериодам формируемого сигнала. Когда положительная полуволна сигнала формируется управлением вентилями v₁ и v₄ при закрытых вентилях v₂ и v₃, а отрицательная полуволна формируется управлением вентилями v₂ и v₃ при закрытых вентилях v₁ и v₄.

В идеальном случае, когда в цепи нагрузки отсутствуют реактивные элементы, коммутация будет происходить в моменты, соответствующие вычисленным по формулам (16) и (17). Коммутационная функция будет принимать значения +1 или –1 в четные полупериоды опорного сигнала и 0 в нечетные полупериоды опорного сигнала, причем значение +1 коммутационная функция приобретает при формировании положительной полуволны выходного напряжения и –1 при формировании отрицательной полуволны выходного напряжения.

При активно-индуктивной нагрузке коммутационная функция будет принимать значения +1, -1 при формировании обоих полупериодов выходного напряжения в режиме непрерывных токов, а в режиме прерывистых токов коммутационная функция будет принимать значения +1,-1 и 0.

Проведены исследования электромагнитных процессов в системе электродинамический преобразователь возвратно-поступательного движения - статический преобразователь при широтно-импульсной модуляции и частотно-токовом управлении.

Для исследования гармонического состава тока получены уравнения для вычисления коэффициентов ряда Фурье.

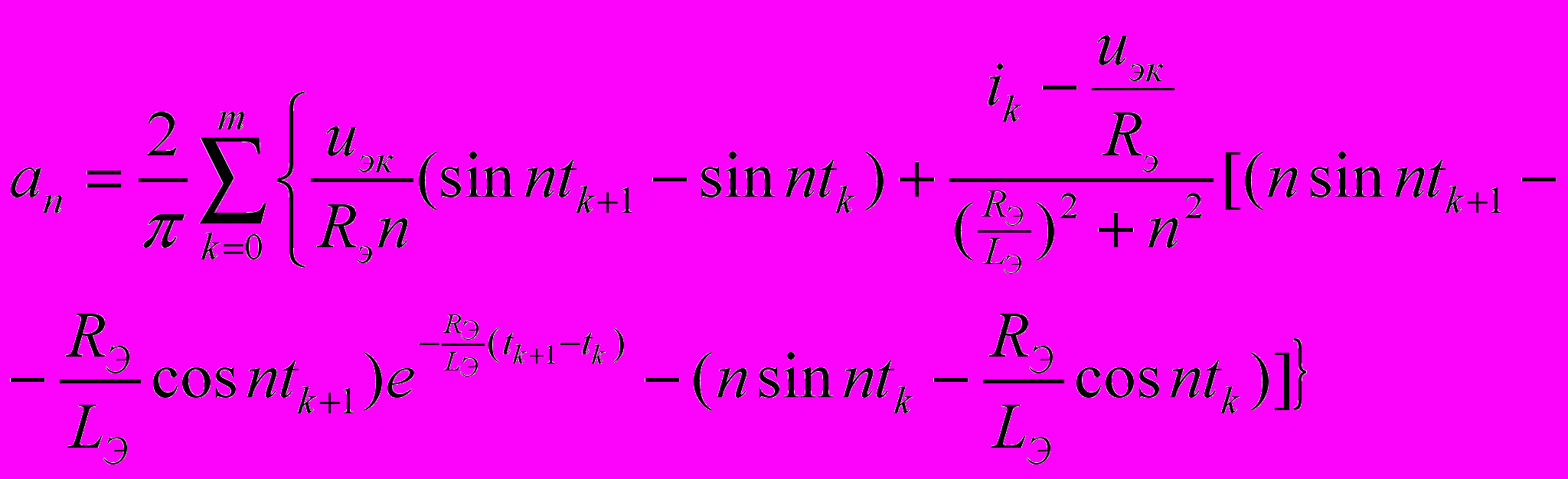; (18)


, (19)

где m – число коммутаций на полупериоде.

На основании полученных выражений разработан алгоритм расчета гармонического состава тока подвижной катушки.

На рис. 6 и 7 представлены графики зависимости гармонических составляющих от соотношения амплитуд задающего и опорного треугольного сигналов и смещения треугольного сигнала относительно нуля.



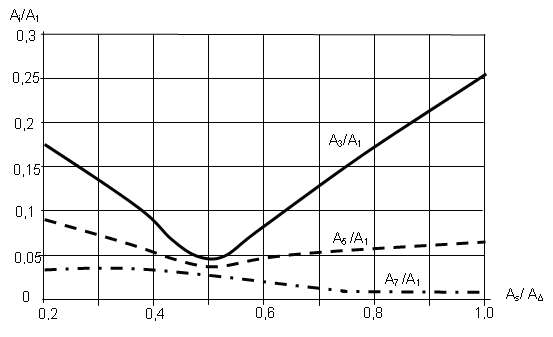
Рис.6. Графики зависимости гармонических составляющих от соотношения амплитуд задающего и опорного треугольного сигналов


На графиках приведены значения величин амплитуд высших гармонических составляющих относительно величины амплитуды первой гармонической составляющей тока подвижной катушки. Из графиков видно, что соотношение амплитуд высших гармонических составляющих тока с первой гармонической составляющей зависит от глубины модуляции и величины смещения опорного треугольного сигнала относительно оси абсцисс.

Проведенный анализ показал, что положение минимума частотных искажений в функции смещения опорного сигнала относительно нуля зависит от приведенной индуктивности подвижной катушки. Это позволило разработать способ управления напряжением питания подвижной катушки электродинамического преобразователя возвратно-поступательного движения при широтно-импульсной модуляции, обеспечивающий минимум частотных искажений тока.



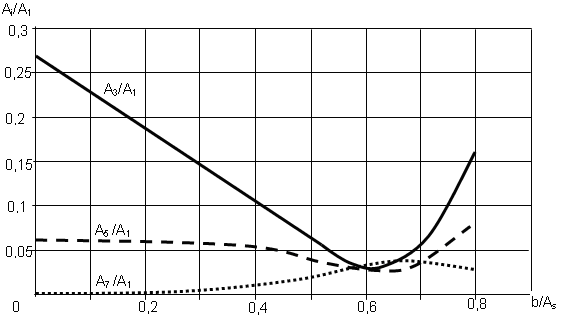
Рис. 7. Графики зависимости гармонических составляющих от смещения опорного треугольного сигнала относительно нуля


Суть способа заключается в следующем.

При широтно-импульсной модуляции напряжения питания подвижной катушки по синусоидальному закону на основании предварительного гармонического анализа выбирают амплитуду опорного сигнала и его смещение относительно оси абсцисс таким образом, чтобы обеспечить минимум высших гармонических составляющих.

На практике этот способ может быть довольно просто решен эмпирически в процессе настройки прибора.

Применение предложенного способа при управлении вибрационными сейсмическими источниками ЭДВИС-1 и ЭДВИС-2 позволило значительно снизить частотные искажения возбуждаемых сейсмических сигналов.

В четвертой главе предложен метод синтеза вибрационных приборов.

Разработан метод выбора параметров сейсмического источника, обеспечивающих требуемые АЧХ и ФЧХ, включающий построение функций сопрягающих частот от выбираемых параметров.

В процессе синтеза, исходя из заданной структуры системы и ЛАХ, обеспечивающей требуемую полосу, необходимо выбрать такие значения параметров вибрационной системы, чтобы исключить значительное различие минимумов и максимумов АЧХ в области заданной полосы.

Автором предложен метод, позволяющий находить оптимальное значение параметров механической части системы, обеспечивающих требуемую полосу.

Известно, что характер изменения аппроксимированной ЛЧХ определяется совокупностью прямолинейных отрезков различного наклона, соединяющихся в точках сопряжения. Каждой такой точке соответствует так называемая сопрягающая частота. Сопрягающие частоты соответствуют нулям и полюсам передаточной функции данной системы.

Например, система с передаточной функцией

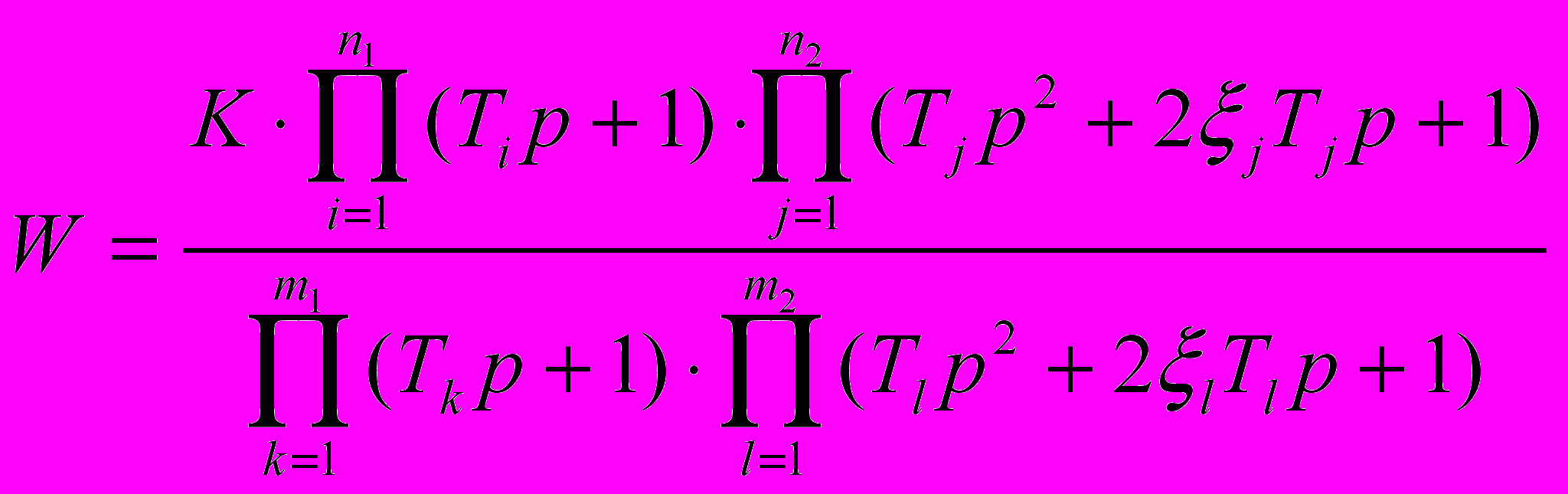, (20)

имеет сопрягающие частоты

ω_i = 1/T_i ; ω_j = 1/T_j ; ω_k = 1/T_k ; ω_l = 1/T_l

Для сопрягающих частот ω_j и ω_l могут наблюдаться существенные отклонения значения АЧХ от идеализированной аппроксимированной за счет резонансов (возрастания) и антирезонансов (провалы). Величины этих отклонений зависят от демпфирующих свойств соответствующих колебательных звеньев, характеризуемых коэффициентами затухания ξ_j и ξ_l. Очевидно, равномерность АЧХ в заданном диапазоне частот будет зависеть от значений сопрягающих частот и коэффициентов затухания ξ_j и ξ_l. Следовательно, чтобы получить максимальную полосу, необходимо задать такие параметры системы, чтобы обеспечить оптимальное расположение сопрягающих частот, соответствующих двучленам и трехчленам числителя и знаменателя передаточной функции (20).

Однако трудность задачи заключается в том, что для сложной многомассовой системы аналитическую зависимость сопрягающих частот от задаваемых параметров получить очень сложно, зачастую практически невозможно.

Поэтому автором предлагается предварительно построить функции сопрягающих частот от задаваемых параметров, и на основании полученных функций выбрать параметры, обеспечивающие оптимальные значения сопрягающих частот.

В свою очередь, для получения функций сопрягающих частот необходимо привести передаточную функцию системы к виду (20). Для этого необходимо найти корни числителя (нули) и знаменателя (полюса) передаточной функции. Нахождение корней полиномов числителя и знаменателя в настоящее время реализуется довольно просто с помощью различных программных средств, например Mathcad.

При синтезе предлагается следующий порядок решения задачи.

1. Строится физическая модель системы.
   
2. Для полученной физической модели составляется система уравнений.
   
3. На основании полученной системы уравнений получают соответствующие передаточные функции.
   
4. Задают исходные значения параметров проектируемой системы и с помощью известных программ находят корни числителя (нули) и знаменателя (полюса) передаточной функции.
   
5. Задают области вариации соответствующих параметров и для различных значений параметров получают соответствующие значения корней.
   
6. Для полученных корней определяют сопрягающие частоты и строят графики их функций в зависимости от варьируемых параметров.
   
7. На основании полученных графиков выбирают предпочтительные значения требуемых параметров.
   
8. Для полученных значений параметров строят ЛАХ и, при необходимости корректируют тот или иной параметр.
   
9. Строят окончательную ЛАХ скорректированной системы и определя­ют ее показатели качества.
   

На рис. 8 приведены графики функций сопрягающих частот по параметру подвески одной из масс (демпфирование подвески транспортного средства).




Рис. 8. Графики функций сопрягающих частот от Dt


Предложенный метод дает возможность в процессе проектирования наглядно представить влияние изменения соответствующего параметра на характеристики системы, что позволяет достаточно просто выбрать оптимальное значение данного параметра, а при необходимости параметрического управления свойствами системы определить пределы изменения управляющего параметра.

Воспользовавшись полученными графиками функций сопрягающих частот, можно довольно просто выбрать параметры сейсмического прибора, обеспечивающие желаемую полосу частот.

Для этого необходимо по графикам функций сопрягающих частот выбрать такое значение параметра, чтобы обеспечить оптимальное расположение сопрягающих частот, под которым будем понимать расположение, обеспечивающее заданную полосу пропускания, то есть необходимо так расположить сопрягающие частоты, чтобы в заданной полосе частот было минимальное изменение амплитуды колебаний. В идеале желательно иметь на данном участке горизонтальную асимптоту ЛАХ.

Построение желаемой ЛАХ осуществляется следующим образом.

1. Задается значение варьируемого параметра.
   
2. Для данного значения по графикам функций сопрягающих частот определяются значения сопрягающих частот.
   
3. Затем на основании известной методики отмечаются полученные значения сопрягающих частот на оси частот.
   
4. На частоте ω = 1 откладывается ордината, равная 20lg k, где k – коэффициент передачи системы (точка А).
   
5. Через точку А проводится прямая с наклоном, равным ν·20 Дб/дек, где ν – порядок астатизма системы.
   
6. После каждой из частот сопряжения наклон ЛАХ изменяется на -20 Дб/дек (-40 Дб/дек), если эта частота сопряжения ω_k (ω_l) определяется постоянной времени соответствующего двучлена (трехчлена) знаменателя, или на 20 Дб/дек (40 Дб/дек), если эта частота сопряжения ω_i (ω_j) определяется постоянной времени соответствующего двучлена (трехчлена) числителя.
   

В зависимости от коэффициента затухания ξ в соответствующих точках сопряжения вводятся поправки, повышающие или понижающие величину ЛАХ в этих точках. Поправки можно не вводить, если значения ξ находятся в пределах 0,38 ≤ ξ ≤ 0,7

На рис. 9 приведено семейство ЛАХ для различных значений коэффициента демпфирования подвески транспортного средства.

Пятая глава. Экспериментальные исследования сейсмических источников.

Проведены экспериментальные исследования вопросов согласования сейсмических источников с грунтом. Предложена методика определения параметров грунта, что позволило получить характеристики исследуемой среды.

В результате проведенных исследований разработан метод определения приведенного импеданса грунтов, контактирующих с источником, а также механических характеристик соответствующих грунтов.

Экспериментально доказано, что эквивалентная площадь плиты зависит от силы прижатия сейсмического источника к грунту, что определяет степень его согласования с грунтом.



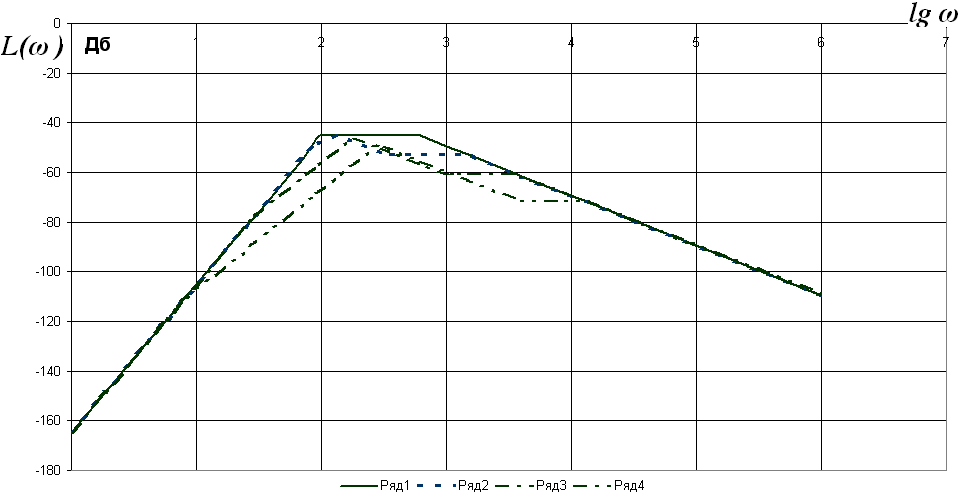
Рис. 9. Семейство ЛАХ для различных значений коэффициента демпфирования подвески транспортного средства


Полученные экспериментально механические, электромеханические и электромагнитные характеристики с высокой степенью точности (до 10 %) совпали с характеристиками, полученными аналитически.

В экспериментальных полевых работах использовался образец электродинамического источника с амплитудой усилия от 2 до 5 кН и частотным диапазоном от 40 до 600 Гц. В результате работ показано, что в условиях как высокоскоростных кристаллических пород, так и в осадочных низкоскоростных отложениях амплитуда сигнала на рабочем органе источника за областью естественного максимума от частоты меняется незначительно, что создаёт условия формирования достаточно равномерного спектра зондируемого сигнала в указанном диапазоне частот.

В точках приёма на удалении нескольких сотен метров как на поверхности, так и в скважинах (глубиной свыше 500 м) фактор частотно-избирательного поглощения незначителен. Амплитуда сигналов уменьшается с удалением от источника в основном за счет расхождения фронта волн, что не отражается на их спектральном составе. В результате в условиях кристаллических пород при наблюдениях в скважинах получена высокоразрешенная волновая картина проходящих продольных и поперечных волн, зарегистрированы и прослежены отраженные волны, прослеживание которых в низкочастотном диапазоне невозможно или сопряжено со значительными сложностями из-за неразрешенности и слабой динамической выразительности. При наблюдениях на поверхности в осадочном разрезе (скорости продольных волн 400 – 1800 м/с) уверенно зарегистрированы многочисленные отражения в диапазоне времен до 0,6 с с высоким разрешением. Их видимая частота примерно соответствует средней частоте свипа, что свидетельствует об отсутствии заметного избирательного поглощения в диапазоне до 500 Гц. При этом в диапазоне частот 120 – 500 Гц волны помехи верхней части разреза существенно ослаблены по сравнению с низкочастотным диапазоном.

Достигнуто существенное повышение эффективности метода при выявлении и оконтурировании целевых геологических неоднородностей с размерами от первых метров до первых десятков метров.

На основе большого объема наблюдений с высокочастотными невзрывными источниками в диапазоне частот 100 – 800 Гц оценены параметры затухания, свидетельствующие о высокой добротности пород разреза и отсутствии аномально высоких потерь энергии высокочастотных компонент волнового поля. Установлена реальная возможность повышения разрешающей способности сейсморазведки почти на порядок, благодаря применению высокочастотного вибрационного источника в сочетании с трехкомпонентной регистрацией и высокочастотным накоплением.

Шестая глава. Практическая реализация

Посвящена описанию приборно-аппаратного комплекса для высокочастотных сейсмических исследований, в создание которого существенный вклад внес автор.

Комплекс содержит приемо-передающую сейсмическую аппаратуру, размещаемую на поверхности земли и под землей в скважинах, шурфах и шахтах.

Также здесь приводятся разработки автора, реализованные в других отраслях народного хозяйства. Как правило, при создании всех приведенных ниже разработок автор был либо основным, либо одним из ведущих исполнителей. Личный вклад автора в каждом техническом решении, приводимом ниже, ли­бо указан в списке исполнителей соответствующего отчета о НИР, либо определен протоколом соглашения о долевом участии в изобретении.

На основании предложенных моделей и методов анализа и синтеза сложных систем найдены новые подходы к построению структурно-функциональной организации приборов и устройств, которые позволили создать и внедрить в ряд отраслей народного хозяйства:

- широкополосные вибрационные сейсмические источники для малоглубинной сейсморазведки ЭДВИС-1, ЭДВИС-2, ЭДВИС-3 превосходящие по частотным характеристикам все известные аналоги;

- широкополосные импульсные сейсмические источники, значительно превышающие известные по ширине полосы спектра излучения и КПД,

- широкополосные скважинные геофизические приборы для возбуждения и регистрации сейсмических сигналов ;

- устройства для эксплуатации и ремонта подземных водозаборов;

- системы вибрационной диагностики строительных конструкций;

- системы и устройств коррекции психофизиологического состояния человека;

- вибрационные вискозиметры.

Оригинальность предложенных способов и устройств подтверждаются авторскими свидетельствами и патентами СССР, РФ, Австралии, Великобритании, Франции, Украины.


Заключение


В диссертационной работе решена научно-техническая проблема повышения разрешающей способности сейсморазведки на основе обеспечения возбуждения и регистрации широкополосных сигналов с преобладанием высоких частот.

В рамках диссертации получены следующие результаты.

1. На базе введенных функций сопрягающих частот от выбираемых параметров разработан новый метод синтеза сложных систем автоматического управления, дающий возможность в процессе проектирования наглядно представить влияние изменения соответствующего параметра на характеристики системы. Это позволяет достаточно просто выбирать оптимальные значения проектируемых параметров, а при необходимости параметрического управления свойствами системы определить пределы изменения управляющего параметра.

2. Разработан метод анализа электромагнитных процессов в системе статический преобразователь напряжения - электрический преобразователь возвратно-поступательного движения, позволяющий значительно упростить процесс анализа электромагнитных процессов и сократить затраты времени при расчетах. На основании полученных с помощью разработанного метода результатов исследований предложен способ управления сейсмическим источником с широтно-импульсной модуляцией напряжения, обеспечивающий формирование сигнала возбуждения с минимумом высших гармоник.

3. Разработаны способ управления электрическим преобразователем возвратно-поступательного движения и устройство для его осуществления, обеспечивающие упрощение регулирования амплитуды и фазы возбуждаемого усилия в диапазоне рабочих частот, а также улучшение массогабаритных показателей.

4. В результате анализа динамики электромагнитного преобразователя возвратно-поступательного движения предложено принципиально новое решение, позволяющее повысить динамические показатели импульсного сейсмического источника на базе электромагнитного преобразователя возвратно-поступательного движения (расширение полосы спектра излучения в область верхних частот) и его КПД.

5. Разработаны обобщенные математические модели наземных и скважинных сейсмических приборов, позволяющие анализировать зависимости динамических характеристик приборов от различных параметров. Проведенный на базе полученных математических моделей анализ влияния вариаций параметров сейсмических приборов на их характеристики позволил определить направление выбора значений параметров, обеспечивающих наиболее широкую полосу частот при максимальной энергетической эффективности.

6. Предложена упруго-диссипативная модель грунта с зависимостью параметров от силы прижатия источника к грунту, которая объясняет возникновение существенных нелинейных искажений на низких частотах при соизмеримых значениях силы прижима и амплитуды развиваемой источником силы и позволяет выбирать оптимальные соотношения развиваемого источником усилия и силы прижима его к грунту для уменьшения нелинейных искажений.

7. Предложенная методика определения параметров грунта позволяет ускорить процесс оценки реальных параметров грунтов в точках установки сейсмических приборов. Разработанные стенды для исследования сейсмических источников обеспечивают возможность испытания вибрационных и импульсных сейсмических источников.

8. Установлена реальная возможность повышения разрешающей способности сейсморазведки почти на порядок благодаря применению широкополосных источников, трехкомпонентных скважинных приборов с прижимом и высокочастотным накоплением.

9. На основании предложенных моделей и методов анализа и синтеза сложных систем найдены новые подходы к построению структурно-функциональной организации приборов и устройств, которые позволили создать и внедрить в ряд отраслей народного хозяйства:

- широкополосные вибрационные сейсмические источники;

- широкополосные импульсные сейсмические источники,

- широкополосные скважинные геофизические приборы для возбуждения и регистрации сейсмических сигналов;

- устройства для эксплуатации и ремонта подземных водозаборов;

- системы вибрационной диагностики строительных конструкций;

- системы и устройства коррекции психофизиологического состояния человека;

- вибрационные вискозиметры.

Оригинальность предложенных способов и устройств подтверждаются авторскими свидетельствами и патентами СССР, РФ, Австралии, Великобритании, Франции, Украины.