Информатика, вычислительная техника и инженерное образование 2011, №1(3) эволюционное моделирование, генетические и бионические алгоритмы
| Вид материала | Решение |
- Информатика, вычислительная техника и инженерное образование. − 2011, №4 (6) раздел, 247.88kb.
- Информатика, вычислительная техника и инженерное образование. − 2011, №4 (6) раздел, 134.8kb.
- «Информатика и вычислительная техника», 723.11kb.
- Рабочая учебная программа дисциплины Моделирование рассуждений (наименование дисциплины), 166.66kb.
- Информатика, вычислительная техника и инженерное образование. 2011, 1595.3kb.
- Рабочая учебная программа по дисциплине «Информатика» Направление №230100 «Информатика, 91.73kb.
- В. Ф. Пономарев математическая логика, 3033.04kb.
- Рабочая программа дисциплины «Теория систем» по направлению подготовки дипломированного, 142.63kb.
- Рабочая программа дисциплины «Методы оптимизации» по направлению подготовки дипломированного, 132.79kb.
- Рабочая программа дисциплины «Компьютерная графика» по направлению подготовки дипломированного, 108.6kb.
Эволюционные алгоритмы синтеза при неполной информации Задача синтеза сложных систем – собрать целое из функциональных частей, предварительно подготовленных блоков или модулей разных типов. Имеется множество направлений применения синтеза в задачах социально-экономического характера, в науке об управлении, экономике, социологии, психологии, биологии и других направлениях. Важным направлением исследования таких “больших” или “сложных” систем является рассмотрение их как многоуровневых систем, или систем с иерархической структурой. Однако стройной математической теории таких иерархических систем до сих пор нет [9]. С другой стороны, “для сложных систем, как правило, существует несколько альтернативных путей развития” [10], одним из которых является применение эволюционных методов развития систем, не нуждающихся в полной мере в математическом описании или стройной теории. Эволюция природных явлений или живых организмов и их взаимосвязей (являющихся примерами сложных систем) протекает естественным образом, без оперирования математическими формулировками. Более того, до сих пор многие сложные системы, достигшие совершенства в процессе эволюционного развития, не поддаются математическому описанию. Задача эволюции – получить более приспособленную систему посредством отбора, и при этом она не использует стереотипы человеческой логики и мышления, используемые для построения моделей существующих систем или явлений. Для эволюционного процесса постановка задачи стоит нечетко, цель – найти оптимальное решение, удовлетворяющее неполным, зачастую противоречивым наборам параметров, при этом найденное решение, как правило, оптимальное, но не всегда лучшее. Поэтому решение задачи синтеза при четкой постановке задачи не вызывает затруднения для современных систем автоматизированного проектирования или эксперта, но если информация о проектируемой системе является неполной или неточной, то знания и опыт эксперта в большинстве случаев неспособны помочь при поиске решения. Решение задач с неполной информацией является затруднительным и для САПР, так же неспособных выполнить поиск в силу неопределенности параметров синтеза и необходимости поиска на множестве, неограниченном четко критериями поиска. Как показано в [1]: в системах автоматизированного проектирования интеллектуальные методы, синтезирующие новые изделия, достаточно редки, поэтому для решения задач структурного и функционального синтеза столь велико значение эволюционных методов, с развитием которых могут быть созданы действительно интеллектуальные системы автоматизированного проектирования вместо многочисленных САПР, использующих экспертную систему на ранних стадиях разработки. Классическая задача синтеза состоит в том, чтобы по закону функционирования объекта получить его проектное решение [11]. Различают параметрический и структурный синтез. Задачи параметрического синтеза – это совокупность задач, связанных с определением требований к параметрам объекта, номинальных значений параметров и их допусков, в условиях, когда известны структура объекта или его топология. Сложность задач структурного синтеза заключается в том, что формирование и отбор решений осуществляется только на основе соответствия заданных соотношений вход/выход, т.е. производится синтез структуры объекта по его параметрическому или функциональному описанию. Процедуры структурного синтеза относятся к наиболее трудноформализуемым [12,13] в процессе проектирования. В зависимости от степени формализации, задачи синтеза можно разделить на несколько уровней сложности. К первому уровню сложности необходимо отнести задачи, в которых требуется выполнение только параметрического синтеза, в то время как структура объекта задана спецификой технического задания или результатами процедур, выполненных на более ранних этапах проектирования. Второй уровень сложности представляют задачи, в которых возможен полный перебор известных решений, т.е. это комбинаторные задачи, в которых выполняется выбор элементов в конечных множествах малой мощности. В таких задачах элементы множества структур описываются заданной базой знаний, либо используется алгоритм, с помощью которого последовательно синтезируются и анализируются все возможные элементы множества за допустимое время. При увеличении мощности множества элементов, когда алгоритмы перебора не могут найти решение за приемлемое время или задача с трудом поддается четкой формализации, или становится многопараметрической, задачу синтеза следует отнести к третьему уровню сложности. Примерами таких задач могут быть задачи компоновки и размещения элементов на платах, трассировки соединений, программно-аппаратного разделения, параллельного разделения задач и процессов и др. Если мощность множества поиска становится неизвестной или отсутствует какая-либо информация, способная ввести ограничение на параметры проектирования, то такую задачу синтеза следует отнести к четвертому уровню сложности - синтезу при неполной информации. Формализация таких задач наиболее трудоемка, и одним из методов решения может быть методика, суть которой сводится к нахождению среди многих генерируемых структур такой, которая будет удовлетворять определенным (пусть и не всем) количественным требованиям. В дальнейшем, на основе найденного решения, посредством его анализа и доработки, производится поиск решения, наиболее соответствующего требованиям. Действительно, при неполной информации о синтезируемом объекте или его неполном функциональном описании, для найденных решений возможно нарушение свойства легальности и законности [14], т.е. некоторые синтезируемые решения могут соответствовать или недопустимым, или незаконным решениям. Нетрудно видеть, что возможен перевод задачи из четвертого уровня сложности в третий, при условии, что вводятся ограничения на область поиска, задаются граничные параметры синтезируемого объекта или функциональное описание дополняется множеством возможных параметров и дальнейший синтез выполняется с учетом принятых допущений. Выделив несколько уровней сложности задач синтеза, можно формализовать методики их решения. Рассматривая уровни сложности как иерархию, к самому низшему уровню необходимо отнести методы, в основе которых заложены алгоритмы перебора, способные выполнять оценку различных вариантов на основе перебора готовых законченных структур. При решении задач среднего уровня сложности целесообразно рассматривать методы последовательного синтеза, в основе которого могут быть алгоритмы, использующие какие-либо эвристики и др. На самом высоком уровне в иерархии методик решения могут быть использованы алгоритмы трансформации описаний различных аспектов, суть которых можно представить в выделении некоего базиса (скалярного критерия), объединяющего частные показатели в многокритериальных ситуациях. Другим методом решения может выступать применение методов эволюционного синтеза [8], где в качестве метода синтеза используются эволюционные алгоритмы или методы, инспирированные природными системами [15]. В последнем случае обеспечивается не только распараллеливание процесса поиска решения, но и возможность повышения эффективности алгоритмов многовариантного анализа и оптимизации. Так как основной задачей современных методов автоматизированного проектирования является задача нахождения оптимальных конструкторских и технологических решений, то применение эволюционных алгоритмов для решения задачи синтеза при неполной информации является рациональным. Эволюционные алгоритмы способны находить оптимальные решения в областях, сведения о которых недостаточно определены или в условиях, когда задача не имеет четкой формализации. Эволюционный синтез рассматривает задачу проектирования как итерационный процесс, на каждой стадии которого выполняется эволюция множества решений в соответствии с неким законом (критерием) выживания. Решение представляется в виде особи или хромосомы посредством кодирования в выбранном формате, множество хромосом определяет популяцию решений. Решение задачи эволюционного синтеза при неполной информации необходимо рассматривать с позиции применения эволюционных методов или стратегий для последовательного выполнения этапов структурного и параметрического синтеза. Поиск решения начинается с поиска структуры объекта на основе неполного функционального описания. В отсутствии полноты описания на этапе структурного синтеза выполняется поиск множества возможных структур проекта, соответствующих заданному неполному функциональному описанию. Структурный синтез выполняет поиск на неограниченном множестве параметров или неточном законе функционирования, что приводит к необходимости введения ограничений на область поиска решений, а также к выполнению поиска решений для множества различных трактовок имеющейся неполной информации. Как было показано выше, для перевода задачи из четвертого уровня сложности в третий, необходимо формализовать область поиска, для чего структурный синтез необходимо выполнять на основе дополнения множества недостающих элементов вектора параметров, например случайными величинами или с применением метода Монте-Карло [16], в пределах ограниченного или бесконечного множества возможных описаний системы. Структурный синтез будет выполняться для множества возможных наборов исходных данных. Такая постановка задачи может привести к нахождению различных решений, частично удовлетворяющих исходной постановке задачи, но не являющихся работоспособными [17] за пределами введенных ограничений. Для определения соответствия допустимым или законным решениям задачи необходимо определить параметры найденных решений и сравнить их с областью (множеством) работоспособных параметров, удовлетворяющих поставленной задаче. То есть необходимо последующее выполнение параметрического синтеза для уточнения векторов параметров, определяющих области работоспособности найденных структурных описаний. Данный этап позволит исследовать найденные структуры на наборе возможных параметров, определяя тем самым области работоспособности синтезируемых решений. Задача определения граничных условий параметров набора исходных данных может быть сведена к определению минимальных требований к проектируемой системе, при котором синтезированное решение находится в области допустимых решений. Далее необходимо обобщить найденные решения и, если требования не выполнены, возможно повторение процедур структурного и параметрического синтеза на основе полученных результатов с целью дальнейшей оптимизации по требуемому параметру или при необходимости улучшения решения в целом. По мнению О.В. Абрамова, отправной точкой при параметрическом синтезе является определение набора некоторых исходных значений параметров, при котором система считается работоспособной в узком смысле, т.е. определение номинальных значений параметров системы без учета вариаций параметров [18] или согласно утверждению Н.Г. Ярушкиной [1]: необходимы жестко заданные множества параметров. Тогда для описания множеств параметров состояния системы целесообразным является использование теории грубых множеств [19], которая основана на предположении, что каждое суждение ассоциируется с какой-нибудь информацией (данными или знаниями). Объединение нескольких множеств неразличимых объектов представляется жесткими (определенными) множествами, хотя само определение – это грубое множество, неопределенное и неточное. Грубое множество определяют нижней и верхней аппроксимациями – в виде пары множеств, где нижняя включает объекты, которые полностью соответствуют некоторому понятию, а верхняя – которые возможно ему соответствуют. Теория грубых множеств, применима к любому числу объектов, число которых для строгого исследования должно быть достаточно велико, и на практике используется для больших объемов данных. Параметрический синтез в широком смысле рассматривает наличие некоторой стратегии, управляющей параметрами системы. При этом, имеется три взаимосвязанных вопроса, на которые необходимо найти ответ: какие параметры выбрать в качестве управляемых, когда необходимо осуществлять управление и какие значения должны принять управляемые параметры [18]. На начальном этапе вопрос о выборе управляемых параметров не возникает, и в качестве исходных значений параметров выбираются расчетные величины без учета возможных отклонений. Цель данного этапа – определение номинальных значений всех параметров. Следующим шагом является определение решения, обеспечивающего некоторый запас работоспособности при возможных отклонениях действительных значений параметров от расчетных, т.е. выбор оптимальных значений внутренних параметров, выполняемый без учета производственных и эксплуатационных параметров. Для обеспечения максимальной гарантии работоспособности (максимальной вероятности безотказной работы в течении заданного времени) необходимо производить выбор номинальных значений параметров с учетом закономерностей их производственных и эксплуатационных вариаций [20]. Параметрический синтез на данном уровне соответствует задаче оптимизации при стохастических критериях. Если качество решения, полученное на данном уровне, не соответствует требуемому, то необходимо вводить возможность регулировки (настройки) некоторых параметров системы. Данная возможность позволит определить параметры работоспособности системы в некотором диапазоне, но необходимо определить совокупность параметров, наиболее оптимально влияющих на настройку управляемых параметров и определить диапазоны их изменений. Для более детального изучения системы и получения характеристик работоспособности для множества наборов параметров, необходимо итерационно исследовать систему на наборе многократно изменяемых (корректируемых) параметров. Цель данного этапа – дать ответы на поставленные вопросы: какие параметры, когда и как необходимо изменять, чтобы обеспечить заданные требования к качеству функционирования системы. Действительно, согласно Общей теории систем [21]: “Для наилучшего достижения цели система всегда должна выполнять свое действие оптимально, выдать свой результат действия в нужном месте и в нужное время”. То есть необходимо определить множества векторов параметров системы, при котором она продолжает функционировать в заданных условиях. Решение задачи параметрического синтеза позволит говорить, что найденное множество векторов параметров соответствует работоспособному состоянию системы. Каждый из параметров системы имеет некоторый набор допустимых значений, при котором система остается стабильной или функционирует в пределах допустимой погрешности. При выходе за пределы множества параметров (вектора длины n) система выходит за пределы области работоспособности. Взаимное влияние параметров друг на друга оказывает дополнительное влияние на работоспособность системы и оказывает значительное влияние на пространство области поиска, т.к. необходимость исследования влияния изменении параметров на систему в целом являются необходимыми для обеспечения максимальной гарантии работоспособности. Отсутствие четкой постановки задачи проектирования приводит к необходимости рассмотрения множества моделей, полученных на стадии структурного синтеза, для каждой из которых необходимо выполнять поиск множества векторов параметров, элементы которых так же могут являться множеством конечной длины. Несложно видеть, что вычислительная нагрузка при подобном рассмотрении вопроса будет чрезвычайно большой. Необходимо определить некоторые принципы, ограничивающие диапазоны изменения параметров, т.к. при отклонении значений параметров от допустимых, происходит выход проекта за пределы области работоспособности. В общем виде задача определения работоспособности системы может быть определена как пересечение множеств найденных параметров, при котором система остается работоспособной. Очевидно, что чем больше мощность множеств параметров, тем больший запас работоспособности имеет система. Для решения подобных задач целесообразно рассмотреть методы эволюционного поиска, обеспечивающие параллельный поиск и предоставляющие возможность одновременного оперирования множеством параметров. Кроме того, данные методы позволяют находить не одно, а множество решений, т.е. предоставляют возможность выбора различных вариантов решения с различными характеристиками, что привлекательно как для принятия решения при конечном использовании найденных решений, так и необходимости дальнейших улучшений и доработок полученных результатов по различным параметрам. Таким образом, задачу синтеза в условиях неполной информации можно определить как итерационный процесс, состоящий из этапа синтеза структуры объекта с последующим этапом параметрического синтеза для поиска вектора параметров (или множества векторов), при котором функционирование системы удовлетворяет требованиям работоспособности. Найденные решения анализируются и оцениваются согласно заданного (возможно многокритериального) алгоритма оценки, и принимается решение о выборе конечного решения или синтез повторяется вновь до тех пор, пока полученные решения не удовлетворяют поставленным требованиям. Как показано в [1], “проектирование, в том числе автоматизированное – это итерация процессов анализа и синтеза, причем анализ предшествует выбору любого технического решения”. В приведенном примере задача анализа возлагается на функцию оценки критерия и напрямую зависит от предметной области искомого решения, задача синтеза требует более детального рассмотрения, т.к. в целом специфика функционирования алгоритма синтеза остается неизменной и может транслироваться на различные задачи поиска с небольшими дополнениями. Примером разработки эволюционного алгоритма синтеза является работа [8], в которой автором представлены методы поэтапной разработки бинарного и десятичного вероятностного алгоритма синтеза комбинационных схем. Комбинационные схемы, представляют в виде множества R = {H, cF, P}, где элемент множества H определяет генотип синтезируемого решения; элемент cF определяет оценку математической модели синтезируемой схемы как критерий отбора; элемент P определяет вероятность передачи наследственной информации. Решение задачи синтеза заключается в поиске схемы, для которой cF = 1. Для алгоритма эволюционного синтеза комбинационных схем вводится понятие минимального базиса логических элементов, определенного как множество L = {Li | i = 1, 2,..., nl}, элементами которого являются стандартные двухвходовые элементы “И”, “ИЛИ”, “XOR” и одновходовые элементы “НЕ” и “WIRE”, имеющие один выход, где nl – количество элементов множества. Функциональные составляющие элементов “И”, “ИЛИ”, “XOR” и “НЕ” аналогичны соответствующим им логическим элементам. Функциональный элемент “WIRE” (перемычка) выполняет передачу сигнала, поступающего на единственный вход элемента к выходу, без каких-либо изменений функциональной составляющей входного сигнала. Кодирование элементов функционального базиса выполняется посредством назначения кода в порядке возрастания их порядкового номера. При десятичном кодировании структура хромосомы определяется как массив, элементы которого представлены матрицей конъюнкторов Сl,m, размерности l на с и матрицей дизъюнкторов Dl,q, размерности l на q, где с – количество входных переменных, количество строк 0 ≤ l <2с определяет количество дизъюнкций и q – количество входных функций, описывающих искомую схему. Кодирование хромосомы определяется на основе матричного представления схемы Mm,n (рис. 1,а), содержащей абстрактные логические элементы (АЛЭ), посредством перехода от двумерной индексации логических элементов (столбец m, строка n) в синтезируемой схеме к одномерной.  Рис. 1. Представление схемы – а) представление схемы, содержащей матрицу n на m ЛЭ Lr,t, имеющую с входов и q выходов; б) представление структуры хромосомы, кодирующей схему Число с входов xс, поступающих на схему, образуют нулевой столбец входов элементов L0,n, где n = с задает количество строк матрицы Mm,n. Количество выходов схемы yq, определяется согласно количеству q выражений, описывающих закон функционирования искомой схемы. Номера элементов Lr,t в схеме имеют сквозную нумерацию, совпадающую с нумерацией логических элементов внутри матрицы Mm,n и используемую при синтезе схемы для обозначения выхода элемента. Индексы элементов Lr,t r и t задаются согласно порядковому расположению элемента в матрице Mm,n, по возрастанию слева направо и сверху вниз, где 0 ≤ t < n и 0 ≤ r ≤ m (нулевой столбец m = 0 содержит сигналы входов схемы, т.е. количество столбцов m дополнено столбцом входов). Выходы схемы y подключаются только к выходам элементов Lr,t столбца m (r = m), при этом элемент нулевой строки Lm,0 соответствует нулевому выходу y0 схемы и т.д. Расположение АЛЭ в узлах решетки схемы остается неизменным в процессе синтеза схемы, а изменяется лишь их функциональная составляющая (код) и соединения между входами и выходами элементов. Логический элемент Lr,t, кодируемый геном gr,t, заносится в хромосому H последовательно, по столбцам, от младшего элемента t столбца r к старшему, где 0 < r ≤ m, 0 ≤ t < n (рисунок 1 б)). Каждый ген хромосомы H определяется вектором gn = {gni | i = 1,2,3}, который кодирует отдельно взятый логический элемент Lr,t, где элементы вектора gn1 и gn2 задают информацию о входах r и t логического элемента Lr,t, и gn3 задает код кодируемого логического элемента Lr,t. Локус гена в хромосоме соответствует заданной позиции кодируемого им элемента в схеме, т.о. значение, получаемое на выходе логического элемента, ассоциируется с отождествляемым ему геном. Переход к многовходовым схемам возможен посредством дополнения функционального базиса новыми элементами и модификации структуры гена хромосомы. Приведенные методы кодирования схем могут быть легко доработаны для различных представлений структуры ЦУ и включать необходимые технологические ограничения, требуемые для реализации задачи синтеза с учетом специфики функционирования цифрового устройства. Подобные ограничения достаточно отразить в структуре гена или хромосомы и в дальнейшем учитывать при анализе схемы. Для анализа синтезируемой схемы разработан метод построения математической модели схемы с ее последующим анализом на s = 2c входных наборах таблицы истинности, где с – количество входных переменных функций. Для схем на основе логических элементов метод построения математической модели определен как переход от одномерного массива логических элементов, кодирующего фенотип в виде хромосомы, к некоторому множеству двумерных массивов Zm,n (матриц размерности m на n), элементы которых отражают функциональную составляющую синтезируемого объекта. Элементы Zm,n представлены в виде матриц Zem,n, Zin1m,n, Zin2m,n и Zoutm,n, где Zem,n задает матрицу кодов ЛЭ, Zin1m,n и Zin2m,n определяют адреса ЛЭ, подключаемых к входам текущего логического элемента, Zoutm,n содержит значения выходов логических элементов. Построение математической модели схемы выполняется посредством анализа ген хромосомы и построения на их основе матрицы кодов логических элементов Zem,n и матриц адресов входов Zin1m,n и Zin2m,n. Матрицы выходов логических элементов Zoutm,n формируются для каждого набора s входных сигналов схемы на основе набора состояний входных сигналов в таблице истинности. Степень соответствия эволюционирующей и искомой схемы определена как критерий cF, значение которого изменяется в интервале от нуля до единицы, т.е. при полном соответствии эволюционирующей и искомой схемы cF принимает единичное значение. Искомая таблица истинности определяется на основе входных функций, эволюционирующая таблица истинности вычисляется посредством установки s входных значений из искомой таблицы истинности на входы математической модели схемы. Результатом построения математической модели является построение эволюционирующей таблицы истинности TTz, элементы которой сравниваются с элементами искомой таблицы истинности TTf, где таблицы истинности представлены в виде матриц: 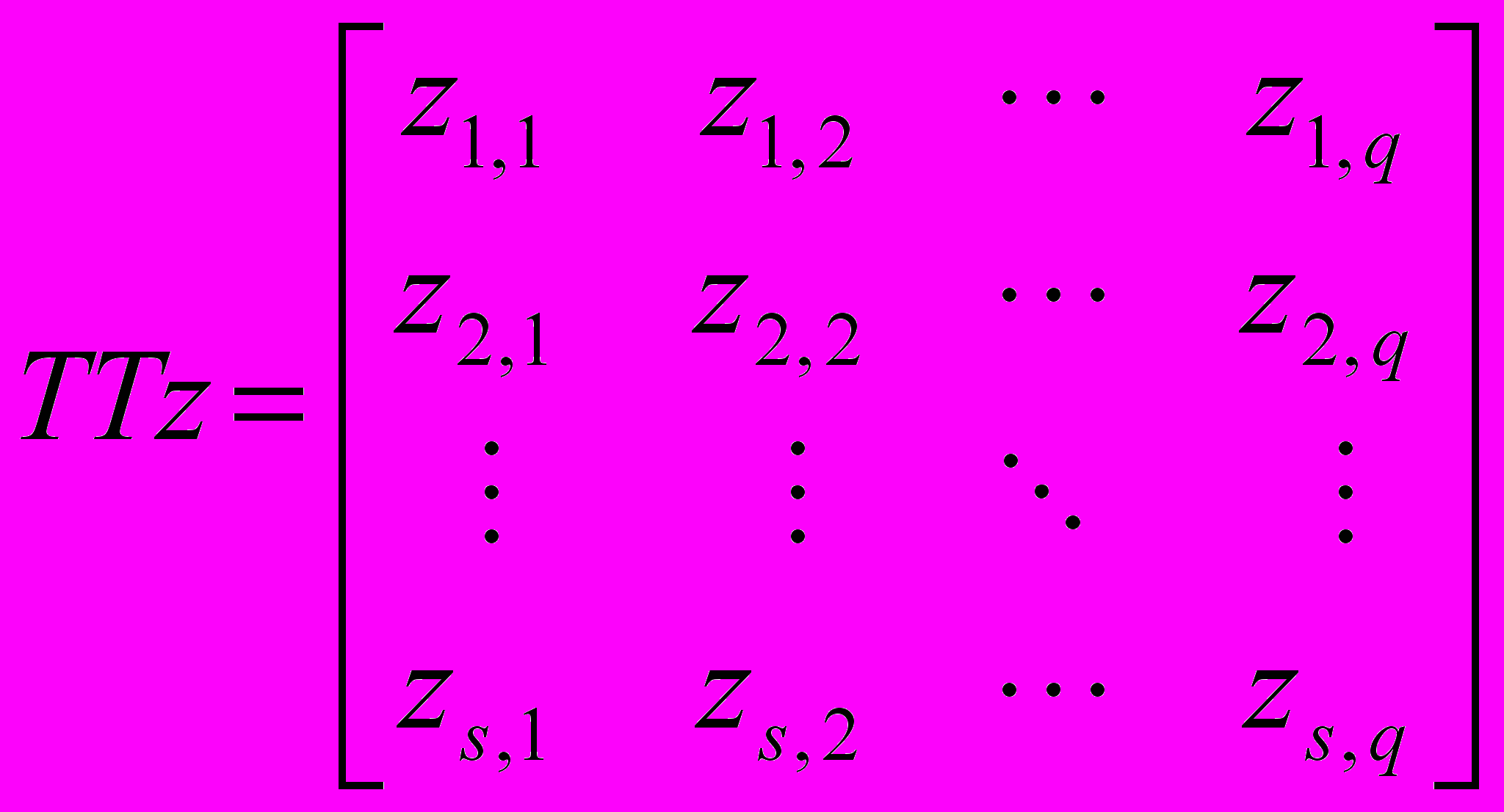 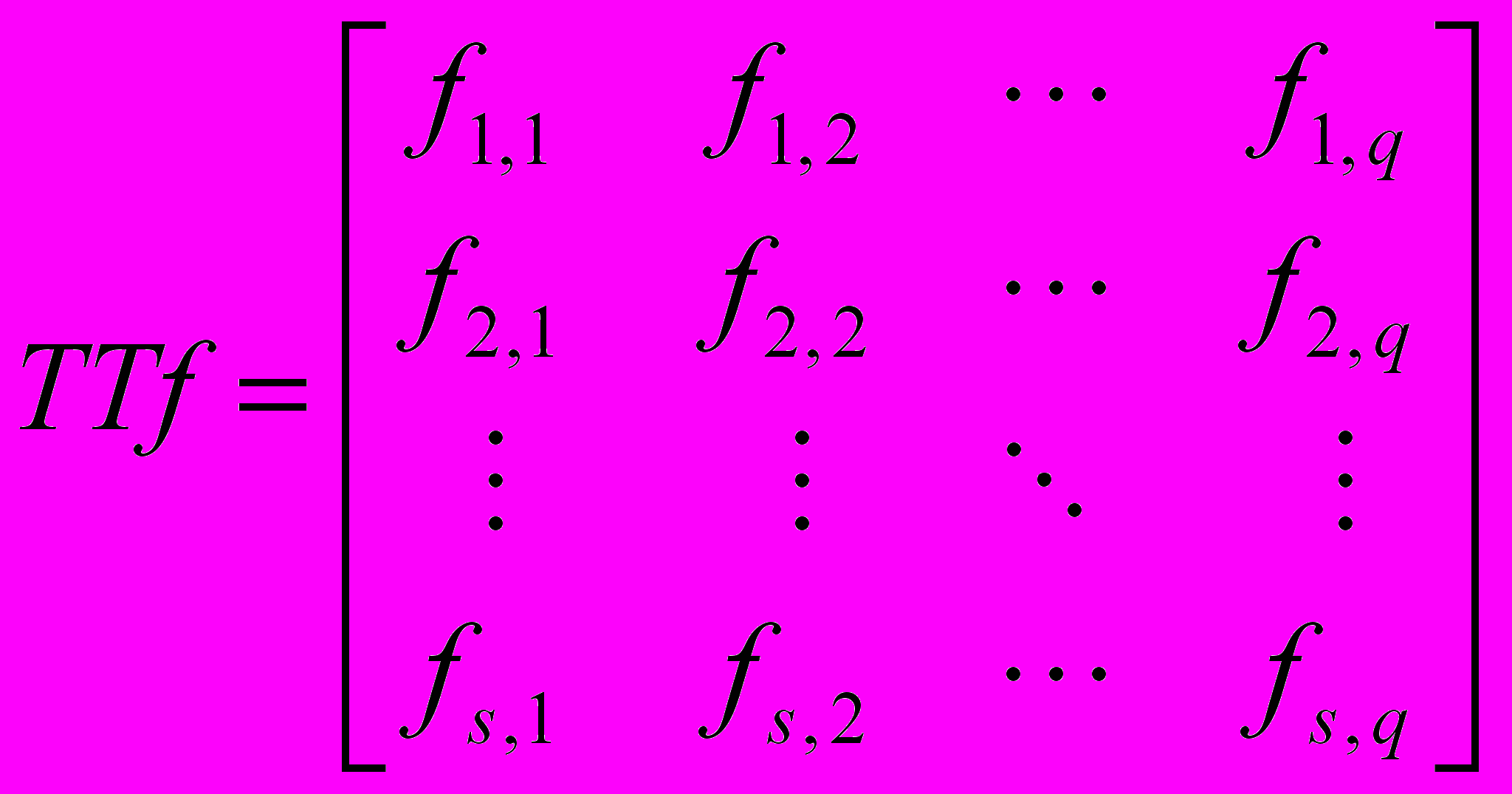 (1) (1)размерности s на q элементов. Тогда значение соответствия hiti вычисляется как: 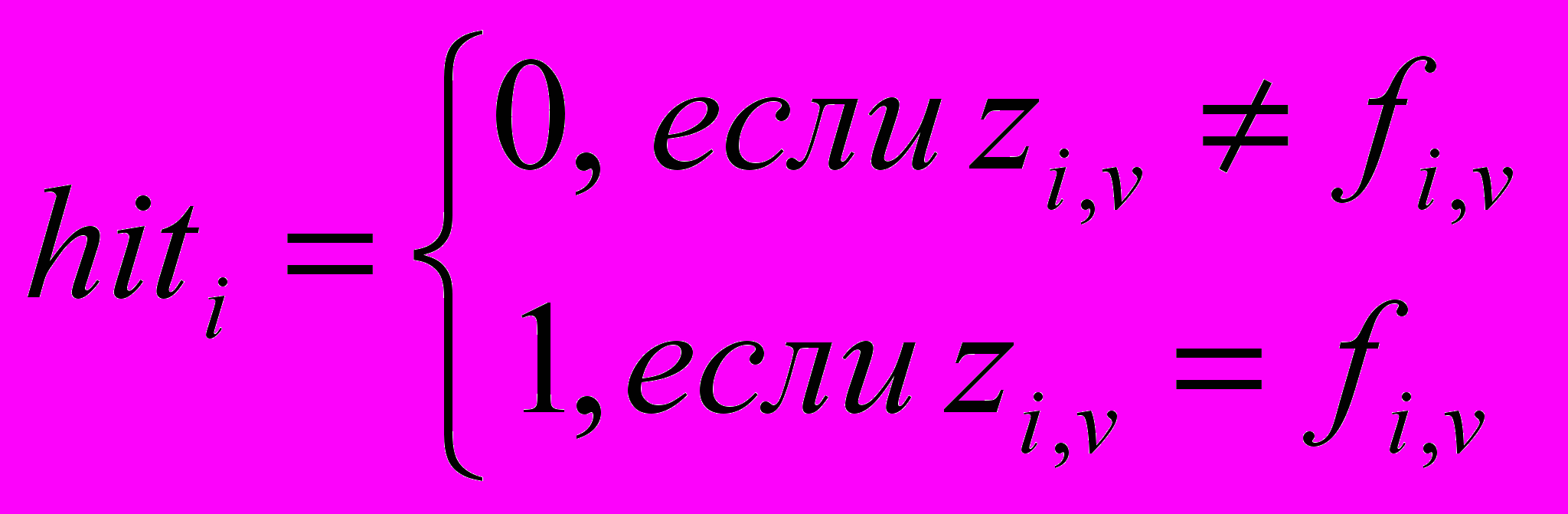 , (2) , (2)где 0 ≤ i < U, 0 ≤ j < s, 0 ≤ v < q и hiti определяет результат выполнения операции сравнения i-го элемента матриц TTz и TTf. Таким образом, критерий оценки cF для хромосомы j вычисляется на основе соотношения: 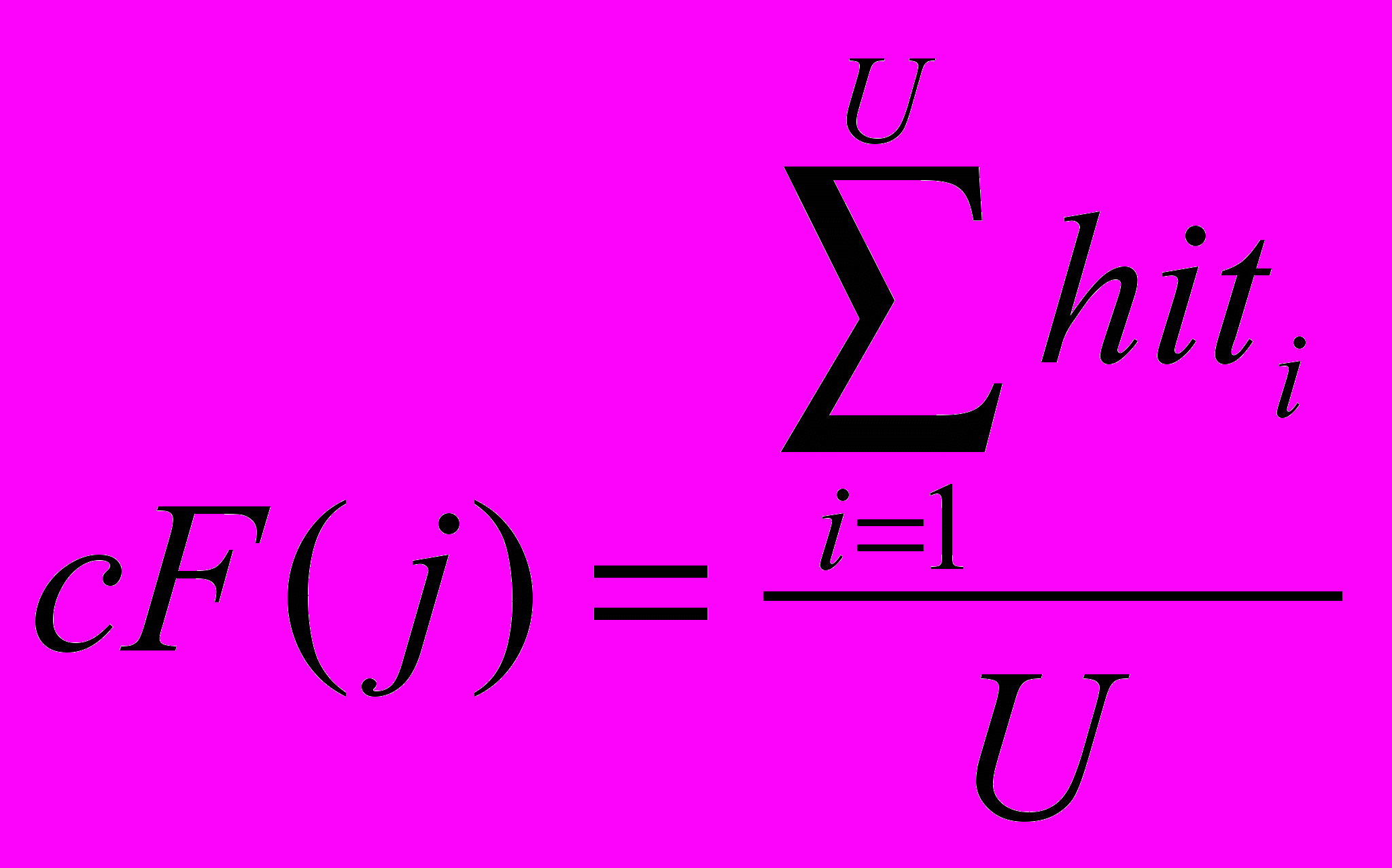 . (3) . (3)Данное значение критерия оценивает функциональную составляющую схемы и при значении 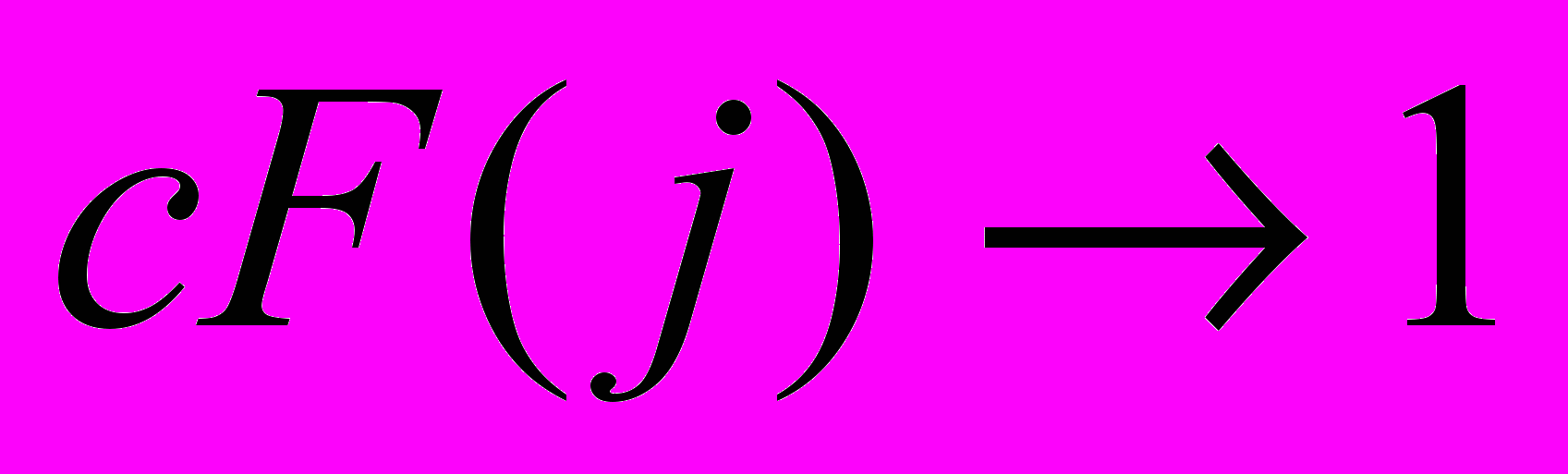 , схема j, кодируемая хромосомой H(j), стремится к искомому решению. Таким образом, параметром эволюции выступает степень соответствия схемы искомому решению. , схема j, кодируемая хромосомой H(j), стремится к искомому решению. Таким образом, параметром эволюции выступает степень соответствия схемы искомому решению. Математическая модель по ряду параметров рассматривает структурную схему с позиции идеализированной схемы с упрощением физических процессов прохождения сигнала через логические элементы. Учет в математической модели специфики функционирования цифрового устройства, а также методов оценки схем с памятью, синхронизацией по фронтам и пр., позволяет модифицировать алгоритмы синтеза для различных схем и цифровых устройств, что позволит расширить область применения разработанных алгоритмов синтеза. Передача генетического материала выполняется на основе лучших решений, для выбора которых предназначен оператор отбора, выполняющий перемещение из популяции Пcs, размера Ps, заданного количества Es хромосом el(i) с максимальным значением критерия cF(j) в порядке убывания cF(j), где 0 < i ≤ Es, 0 < j ≤ Ps и i ≤ j. Разработанный метод передачи наследственной информации определен вектором вероятности P = {pi | i = 1, 2,..., hL} наследования генетического материала из множества элитных хромосом Hel текущей популяции Псs в последующую популяцию Псs+1, где hL – длина хромосомы. Величина pi определяет степень отношения многообразия генетического материала для гена gi, представленного в локусе i хромосом элитной области, к величине Es элитной области. В случае бинарного кодирования хромосомы, величина pi определяет вероятность наследования единичных ген: 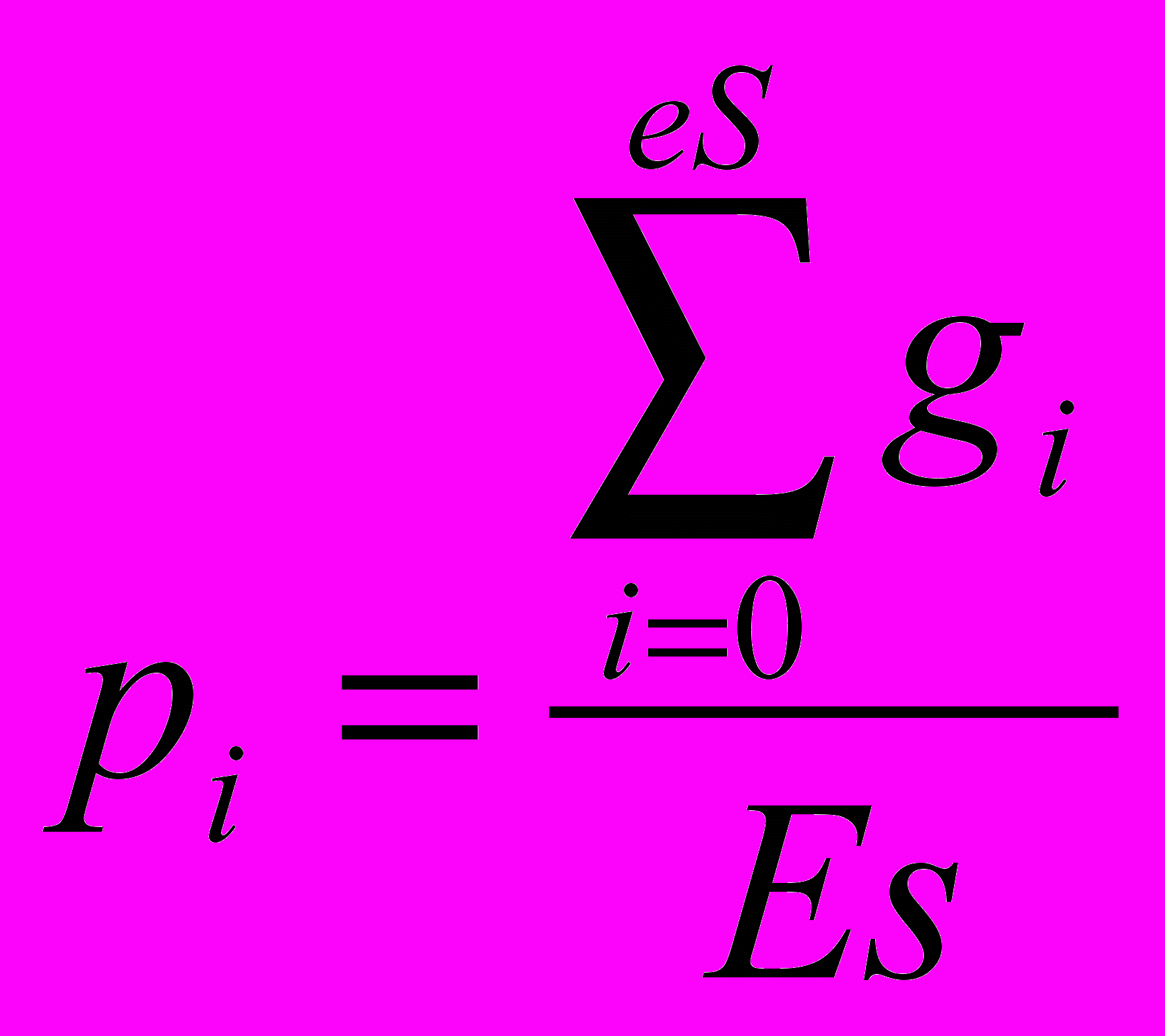 . (4) . (4)При десятичном кодировании схемы, когда ген хромосомы задает логический элемент, элементы pi вектора P определяют вероятность наследования всех возможных состояний гена gi и имеют длину, определяемую количеством состояний, которое может принимать ген gi. Значение векторов вероятности pi может изменяться в интервале от нуля до единицы и при единичном значении означает, что гены в локусе i хромосом H последующей популяции Псs+1 унаследуют доминирующее значение генетического материала данного гена. Исходная популяция из заданного количества Ps хромосом H генерируется случайным образом. В процессе эволюции генерация i-го гена хромосомы выполняется на основе выбора значений вероятности, определяющих вероятность наследования комбинаций для i-го гена хромосомы, как результат сравнения числа, сгенерированного случайным образом, и значений вектора вероятности, представленных соответствующим вектором pi. В качестве дополнительного механизма передачи генетического материала разработан метод сегрегации, в основу которого положен метод элитизма (давления элитных хромосом), позволяющий накапливать генетический материал, что оказывает существенное влияние на сходимость алгоритма. Механизмом предотвращения предварительной сходимости разработанных алгоритмов выступает разработанный метод направленной мутации, не разрушающий схему и применяемой только при попадании алгоритма в локальный оптимум. Для расширения многообразия топологий синтезируемых решений предложен метод вывода популяции из области глобального экстремума на основе метода редукции, исключающего из популяции хромосомы представляющие искомое решение. Алгоритм эволюционного синтеза комбинационных схем приведен на рис. 2. В рамке указана итерационная часть алгоритма, включающая генерацию популяции, анализ синтезированных схем посредством построения математической модели, оценку схем на основе вычисления значения критерия, проверку нахождения решений, если критерий останова не достигнут (не найденного заданного количества решений или не выполнено заданное количество итерационных циклов), то выполняется формирование элитной области и вычисление вероятности. После вычисления вероятности для всех ген хромосомы выполняется переход к следующему итерационному циклу.  Рис. 2. Алгоритм эволюционного синтеза комбинационных схем Приведенный алгоритм успешно производил синтез множества комбинационных схем для различных представлений исходной таблицы истинности. Было показано существенное превосходство в быстродействии при сравнении данного алгоритма синтеза с аналогами при решении тестовых задач. Преимуществом использования данного метода эволюционного синтеза перед традиционными методами проектирования является отсутствие необходимости использования специфических знаний об объекте синтеза: поиск решения выполняется на основе заданных условий входной и выходной информации (заданных соотношений вход-выход). При неполном или неточном представлении входной или выходной информации синтез будет выполняться для множества возможных вариаций входной информации (полученного посредством доопределения отсутствующих фрагментов данных), таки образом результатом работы алгоритма синтеза будет множество решений, для различных трактовок неполноты входных данных, на основе которого возможен выбор требуемого решения. В случае с применением знаний эксперта, при подобной постановке задачи, получить решение было бы проблематично, т.к. человек встречает затруднения при поиске решения, если постановка задачи не определена точно и возможно множество вариаций решений. Структурная схема, полученная на основе эволюционного синтеза, представляет собой материал для дальнейшего изучения и анализа. Для этого возможно применение алгоритмов параметрического синтеза, задача которых уточнить параметры функционирования схемы при различной интерпретации входных данных (введения эффекта гонок при прохождении сигнала сквозь элементы схемы) или определение временных задержек распространения сигнала при различных параметрах используемых логических элементов и типе сигнала (синхронный или асинхронный). Данный этап позволит определить наиболее стабильные (с наибольшим запасом работоспособности) схемы и выявить недостатки предложенных решений, после чего возможен дальнейший поиск с учетом полученных замечаний. Динамически изменяемые эволюционные алгоритмы Применение эволюционных алгоритмов для решения задач с неполной информацией, и в частности задачи синтеза, сталкивается с весьма интересными требованиями к структуре эволюционных алгоритмов: неполнота описаний объекта поиска (в данном случае нечеткая постановка задачи синтеза) приводит к размытости или неопределенности как граничных параметров области поиска, так и генотипа искомого решения. Действительно, при отсутствии четкой или достоверной информации о структуре синтезируемого решения возникает необходимость поиска решений на различных вариациях фенотипического пространства, обладающего различными свойствами и характеристиками структуры. То есть, можно говорить о некотором множестве пересекающихся пространств фенотипов искомого решения, для каждого элемента которого необходимо определить представление (метод кодирования) решений, а также задать правила, согласно которым будет протекать процесс эволюции. Даже если однозначно определить процесс эволюции в рамках некоторого выбранного алгоритма (т.е. условиться, что эволюция протекает для всех индивидуумов одинаково вне зависимости от их представления), то с представлением самих индивидуумов дело обстоит несколько сложнее. Различные фенотипические пространства, получаемые при доопределении множества неизвестных или неточных параметров исходной постановки задачи, приводят к различным представлениям решений на уровне генотипа. То есть, при кодировании будет иметь место наличие множества различных генотипов с различной структурой и длиной, на основе которых необходимо выполнять эволюционный процесс. Изменение структуры генотипа при протекании эволюционного процесса будет оказывать влияние на процесс оценки критерия, усложнять проблематику принятия решений при отборе, вносить изменения в параметры основных генетических операторов (кроссинговера, мутации и др.) для генетических алгоритмов, или приводить к нарушению принципов передачи наследственной информации в вероятностных алгоритмах эволюционного поиска. По сути, возникает необходимость разработки отдельной модификации эволюционного алгоритма для каждого отдельно взятого фенотипического представления искомого решения, т.к. каждое пространство фенотипа содержит набор решений, потенциально являющихся решением поставленной задачи. С другой стороны, логично предложить более “элегантный” выход из сложившейся ситуации: т.к. специфика поставленной задачи в общем и целом известна (она вытекает из общей постановки исходной задачи) и остается неизменной, а меняются лишь некоторые параметры (качественные или количественные), характеризующие или уточняющие поставленную задачу, то необходимо разработать динамически изменяемый эволюционный алгоритм, способный подстраиваться под возникающие изменения структуры фенотипического представления входных данных. Структура динамически изменяемого эволюционного алгоритма остается постоянной, меняются лишь параметры его операторов и, возможно, параметры функционирования алгоритма: величина популяции и элитной области, коэффициенты мутации, рекомбинации, параметры оператора кроссинговера и функции вычисления критерия. Для исключения противоречивости генотипов и структуры эволюционного синтеза возможно выполнение отдельного итерационного процесса для каждого элемента множества пересекающихся пространств фенотипов, когда структура алгоритма будет соответствовать генотипу решений. Изменение фенотипа для эволюционного алгоритма отражается на изменении постановки входной задачи (исходных данных). Необходим морфологический разбор исходной постановки задачи, с помощью которого будут определяться основные параметры функционирования алгоритма: длина и структура хромосомы, метод кодировки и декодировки, параметры генетических операторов и пр. На начальном этапе необходимо охватить как можно большее пространство фенотипов для исследования максимально возможной мощности множества возможных решений, что позволит определить наиболее привлекательные области поиска и исключить тупиковые ветви развития, приводящие к нарушению легальности и законности эволюционирующих решений. Возможно последовательное или параллельное исследование пространства фенотипов, при этом отобранные области поиска могут конкурировать друг с другом в поиске наилучшего (одного или множества) пространства решении. После определения (уточнения) наиболее перспективных областей поиска дальнейший поиск решений выполняется в рамках определенных фенотипических представлений. Поддержка вычислительной нагрузки эволюционных алгоритмов Общеизвестно, что основной сложностью эффективного применения эволюционных алгоритмов является сложность выбора оптимальных параметров при настройке алгоритма. NFL-теорема [22] в частности утверждает, что в среднем, все эволюционные алгоритмы идентичны с точки зрения эффективности и, как показано в [14]: “удачное применение эволюционных алгоритмов для решения той или иной задачи, во многом определяется их удачной настройкой. Строгих правил настройки параметров ЭА и кодирования решений универсальных для всех задач, согласно NFL-теореме, нет и быть не может”. Если учесть, что структура эволюционного алгоритма остается неизменной, а меняются только параметры его настройки, то задачу подборки оптимальных параметров эволюционного алгоритма можно представить в виде задачи параметрического синтеза. Тогда при помощи внешнего алгоритма параметрического синтеза итерационно выполняется последовательный или параллельный синтез параметров эволюционного процесса. В качестве основы алгоритма параметрического синтеза возможно использование различных эволюционных алгоритмов или стратегий что позволит говорить об использовании алгоритмов эволюционного синтеза для настройки параметров динамически изменяемых эволюционных алгоритмов. Так как данный вопрос является слабоизученным, то необходимо исследовать предложенные методы, что позволит с одной стороны повысить эффективность применения эволюционных методов, с другой, рассматривать иерархические структуры организации динамически изменяемых эволюционных алгоритмов, применение которых возможно для проектирования сложных систем. Предложенный подход настройки параметров эволюционных алгоритмов может быть использован для автоматизации процесса поиска оптимальных параметров эволюционных алгоритмов для различного рода задач. В случае рассмотрения предложенных методов создания вложенных иерархических эволюционных алгоритмов для проектирования сложных систем, необходимо уделить дополнительное внимание вопросу быстродействия. Отсутствие необходимого быстродействия при поиске решения и высокая вычислительная нагрузка – одни из основных причин ограничения применения эволюционных алгоритмов. Не секрет, что производительность вычислительных систем растет с каждым годом, и выходом может выступать применение многопроцессорных вычислительных систем, способных значительно ускорить эволюционный процесс. Тем более, что в последнее время широкое распространение в развитии многопроцессорных технологий получила разработка модульных систем с изменяемым количеством процессоров (в которых заказчик может по необходимости установить требуемое количество процессоров), тем самым, подгоняя вычислительные ресурсы под поставленные задачи. В подобных системах основной упор сделан на увеличение производительности при росте вычислительной нагрузки посредством параллельного выполнения задач на наборе процессоров. Однако, как уже было отмечено, производительность многопроцессорных систем растет нелинейно при росте числа процессоров, а в некоторых случаях даже начинает падать. Эффективность распараллеливания зависит от сложности взаимодействия программной и аппаратной частей многопроцессорной вычислительной системы [2]. Под практически каждый пакет анализа, и особенно под каждую область исследований, требуется индивидуальная подборка многопроцессорной вычислительной системы. Даже в случае поиска универсальной системы всегда существует единственное оптимальное решение [23], найти которое современными способами зачастую не представляется возможным в силу высокой сложности систем. Другим недостатком многопроцессорных систем является их высокая стоимость, быстрое моральное устаревание и частая неспособность соответствовать требованиям вычислительной нагрузки, т.к. возникающие в современной науке задачи существенно опережают возможности существующих технических средств, используемых для решения. Вычислительных ресурсов не бывает слишком много, более того, такого определения просто не существует. Именно поэтому применение многопроцессорных вычислительных систем зачастую ограничивается этапами разработки и первоначального тестирования эволюционных алгоритмов на небольших тестовых задачах. Для исследования реальных задач зачастую используются кластеры, но и тут возникают временные ограничения доступа к кластеру, т.к. подобных систем не так много, и время работы и кластером обычно распределяется между несколькими проектами. На первый взгляд кажется, что выход из сложившейся ситуации кроется за переходом от программной реализации эволюционных алгоритмов к их аппаратной интерпретации. Действительно, в некоторой степени это позволяет решить ряд вопросов с быстродействием, повышая скорость работы алгоритмов на 2 или 4 порядка [24,25] и переводя их в область функционирования в рамках реального времени. Но имеющийся у автора опыт разработки систем аппаратной реализации эволюционных алгоритмов [26] или методов повышения их быстродействия [27] приводит к выводу, что простого применения методов перехода от программной реализации медлительных алгоритмов к их прямой аппаратной реализации недостаточно. Дело в том, что подобные решения ограничены в своей применимости рамками тех задач, для которых они разрабатывались. Применение разработанных аппаратных структур для новых методов поиска или доработка под новые предложенные стратегии приводит к необходимости пересмотра существующей архитектуры аппаратно реализованного алгоритма. Зачастую, дешевле и быстрее разработать все заново, нежели пытаться подогнать существующие решения под новые требования. Поэтому необходим поиск более универсальных методов решения вопросов повышения быстродействия эволюционных алгоритмов, в основе которых лежат наиболее удачные примеры существующих решений, а также применение новых методов аппаратного проектирования, позволяющих достаточно просто изменять архитектуру и параметры аппаратного комплекса, иметь возможность многокритериально исследовать и оптимизировать предложенные архитектурные решения и выбирать оптимальные по требуемым параметрам (быстродействие, качество найденного решения, степень использования вычислительных ресурсов и пр.). Другим полезным свойством является возможность оставить часть решения в виде программной реализации, в то время как наиболее ресурсоемкую и статичную (одинаковую для рассматриваемого класса задач) переложить в аппаратную часть инструментального комплекса. Данное свойство позволит использовать разработанные комплексы для множества различных алгоритмов и методов, в которых совпадающие части передаются на реализацию в специализированные аппаратные базовые блоки (предварительно настраиваемые под требуемою конфигурацию), а уникальные части алгоритмов, для которых еще не выработано аппаратных решений в силу их новизны или незначительности вычислительной нагрузки, выполнять традиционными средствами. Это позволит не только повысить быстродействие (а значит расширить область применения) существующих эволюционных алгоритмов, но и проводить исследование совершенного новых алгоритмов, включающих новые стратегии и методы, не заложенные в архитектуру разработанных инструментальных комплексов. Необходимо также иметь возможность добавлять и впоследствии использовать в подобных инструментальных комплексах новые аппаратные решения какого-либо оператора, метода или алгоритма. Очевидно, что необходимость настройки базовых аппаратных блоков под требуемые параметры или конфигурацию реализуемых ими алгоритмов (операторов) приводят к необходимости разработки основных блоков с применением методов реконфигурации аппаратных структур. Реализация описанной функциональности возможна на основе применения методов построения гетерогенных микропроцессорных вычислительных структур, положенных в основу разработки предложенных программно-аппаратных инструментальных комплексов. Эволюционные методы программно-аппаратного разделения Гетерогенные многопроцессорные архитектуры являются де-факто стандартом для встроенных систем проектирования [28]. В таких системах ускорение различных частей приложений обычно выполняется с применением систем цифровой обработки сигналов (используются специализированные процессоры или реконфигурируемые устройства на базе FPGA), объединенных через различные механизмы коммуникации. При разработке встроенных систем, проектировщик должен определить когда (задать расписание) и где (составить соответствия) группы операторов (т.е. задач) и каналов передачи данных (т.е. коммуникаций) должны быть выполнены и задействованы с учетом установленных ограничений и зависимостей, в порядке оптимизации некоторых параметров проектирования, в том числе времени выполнения программы. Основными вопросами при разработке гетерогенных систем являются вопросы программно-аппаратного разделения [7], т.е. определения, какая часть программы будет реализована аппаратно в специализированном микропроцессоре, а какая будет функционировать программно и обрабатываться стандартными методами. Доказано [29], что эффективное распределение заданий между вычислительными ресурсами оказывает большое влияние на характеристики стоимости/производительности системы. Поэтому, при распределении заданий необходимо принимать во внимание системные свойства целевого устройства, а также ограничения, связанные со средой, платформой реализации и/или системными требованиями функциональных возможностей. Гетерогенные системы относятся к классу сложных систем, а задача разделения (включающая планирование и составление соответствий) – сильно зависимая NP-полная задача [30], которая не может быть эффективно решена с помощью точных алгоритмов и эвристических методов, способных находить хорошие решения за приемлемое время. В качестве методов решения подобных задач целесообразно рассматривать эволюционные алгоритмы и алгоритмы инспирированные природными системами. Задачу разделения можно свести к задаче поиска архитектуры и параметров функционирования сложной системы при неполной информации (т.к. в процессе функционирования изменяется архитектурная составляющая системы – часть ресурсов задействуется, часть высвобождается и не все параметры решения задачи могут быть известны на этапе ее постановки). Решение данного типа задач может быть рассмотрено с позиций описанных выше эволюционных алгоритмов структурного и параметрического синтеза при неполной информации. Действительно, т.к. структура системы известна, постановка задачи определена исходными данными (как правило, это текст программы или граф) и неизменна в процессе функционирования, то необходимо определить параметры функционирования системы в рамках заданных ограничений, при которых с одной стороны задействовано минимальное количество ресурсов (а, значит, достигнуто минимальное энергопотребление или имеется возможность параллельного функционирования нескольких процессов), с другой получено максимальное быстродействие при выполнении задачи. При такой постановке задачи нет необходимости искать единственно точное решение, вполне сгодится одно из лучших, удовлетворяющих временным и архитектурным требованиям, поэтому нет ограничений для применения эволюционных методов поиска с этой точки зрения. Задача программно-аппаратного разделения использовалось при проектировании встраиваемых систем с начала 90-х годов, и теперь является широко распространенной методикой оптимизации при проектировании систем. Эта методология проектирования позволяет реализовывать различные синергизмы аппаратных средств и программного обеспечения, которые могут быть получены для встроенных систем. Такие системы обычно встраиваются вокруг основного процессора, который может быть подключен к аппаратным модулям, приспособленным для определенных приложений. Это "приспосабливание" соответствует со-разработке системы и состоит из различных этапов, как определено в [31]: разделения, cо-синтеза, cо-проверки и cо-моделирования. Поскольку эта задача не нова, необходимо рассмотреть методы решения, предложенные в прошлом. Первые работы были представлены в основном “ручными” – неавтоматизированными методиками разделения [32-34]. Среди подходов автоматизированного решения задачи разделения наиболее простой является полный перебор, позволяющий находить точное решение среди заданного множества вариантов. Примерами подобных решений являются работы [34,35]. Точные алгоритмы основаны на определении и оценке всех возможных решений. В теории они позволяют, наверняка, достигнуть всех оптимальных решений. Практически, эти подходы идеальны для простых задач, неактуальных при проектировании современных систем. Их основной недостаток - время выполнения, которое растет экспоненциально с ростом числа системных задач, предназначенных к разделению. Время поиска становится несоизмеримо большим, как только количество анализируемых параметров превосходит 20 [36]. Например, исчерпывающий поиск пространства решения для подобной задачи на двухпроцессорном ПК с частотой в 3 ГГц, при допущении, что время поиска одного решения занимает один тактовый цикл, занял бы более 12 лет. К другим недостаткам существующих методов распределения можно отнести [37] следующие:
- специализированы заданному целевому типу архитектуры и невозможно применение на других платформах. На сегодняшний день, различают два направления в решении задачи разделения: структурно-ориентированные специализированные стратегии, и общая эвристика, которая не является определенной для специфической задачи или структуры. Среди специализированных стратегий, можно выделить работы по синтезу на системном уровне при использовании репрограммируемых элементов и синтез на поведенческом уровне множества процессов для смешанных программно-аппаратных систем [36,38]. Основное преимущество применения определенных подходов состоит в том, что они "приспособлены" для рассматриваемой задачи. Однако применение решений этого типа становятся сложным или невозможным, как только в рассматриваемую задачу вносятся изменения. Методы решений на основе общей эвристики [39-42] не специализированы для решения какого-либо типа задач, и широко используется в других областях исследований при решении NP-полных задач. Преимущество этого типа эвристики состоит в том, что используемая функция оценки критерия может быть легко адоптирована к изменениям в структуре решаемой задачи (т.е. присутствует элемент гибкости, позволяющий расширить область применения алгоритмов), и время поиска решения значительно сокращается в сравнении с полным перебором. Недостатком является отсутствие гарантии, что достигнутое решение – оптимум. Фактически, этот вид алгоритмов часто сходятся к локальному экстремуму, и почти никогда не достигает глобального оптимума. Поэтому разработчики алгоритмов ищут новые и более эффективные алгоритмы, способные повысить качество найденных решений, при снижении времени поиска. Недавние работы в области разделения [43-46] доказывают, что проблема поиска эффективного разделения все еще открыта. При этом работы [46,47] затрагивает проблематику разработки алгоритмов программно-аппаратного разделения для динамически реконфигурируемых систем, что является актуальным направлением. В работе [48] в качестве алгоритма поиска использовались алгоритмы моделирования отжига, в работе [49] использовалась нечеткая логика, генетические алгоритмы представлены в работах [50,51], иерархическая кластеризация [52] или запретный поиск [48] использовались как отдельная эвристика, так и в синергизме с другими перечисленными методиками. Среди успешно продемонстрированных решении методы стохастического поиска [53-55], часто биоинспирированные, которые раскрывают пространство проектирования и используют результаты успешно продемонстрированных предыдущих работ. Тем не менее, представленные методы обычно сфокусированы отдельно на одном из аспектов, и терпят неудачу при попытке получения хороших общих характеристик решений из-за ограниченного пространства проектирования. Общие подходы, новые направления и методы проектирования, способные эффективно генерировать высококачественные решения для сложных приложений на новой стадии развития гетерогенных встраиваемых архитектур, определенно необходимы. Библиографический список 1. Н.Г. Ярушкина. Основы теории нечетких и гибридных систем: Уч. пособие. – М.: Финансы и Статистика, 2004. 2. Р. Шагалиев. HPC. Что нужно сделать? Осознание проблемы. Суперкомпьютеры. – М.: Изд-во СКР-Медиа, 2010, с.– 42-46. 3. В.П. Строгалев., И.О. Толкачева. Имитационное моделирование. – М.: МГТУ им. Баумана, 2008. – С. 697-737. 4. .net/news2/?id=22880. 5. [i-russia] ru/computers/articles/354/. 6. И.А. Каляев, И.И. Левин, Е.А. Семерников, В.И. Шмойлов. Руконфигурируемые мельтиконвейерыне вычислительные структуры. – Ростов-на-Дону, ЮНЦ РАН 2009. – 344 c. 7. De Micheli G. and Gupta R., "Hardware/Software Co-design", Proceedings of the IEEE, Vol.85, N°3, 1997. – pp. 349-365. 8. В.В. Гудилов, В.М. Курейчик. Алгоритмы эволюционного синтеза комбинационных схем. – Таганрог: Изд-во ТТИ ЮФУ, 2010. – 160 с. 9. М.Месарович, Д. Мако, И. Такахара. Теория иерархических многоуровневых систем. – М.: Мир, 1973. – 344 с. 10. Е.Н. Князева, С.П. Курдюмов. Законы эволюции и самоорганизации сложных систем. – М.: Наука, 1994. 11. В.П.Корячко, В.М. Курейчик, И.П.Норенков. Теоретические основы САПР. – М.: Энергоатомиздат, 1987. 12. В.М. Курейчик. Математическое обеспечение конструкторского и технологического проектирования с применением САПР. – М.: Радио и связь, 1990. 13. И.П. Норенков, В.Б. Маничев. САПР ЭВА. – М.: Высшая школа, 1983. 14. В.В. Курейчик, С.И. Родзин. О правилах представления решений в эволюционных алгоритмах // Известия ЮФУ. – № 07, 2010. – С. 13-21. 15. В.В. Курейчик. Биоинспирированный поиск с использованием сценарного подхода // Известия ЮФУ. – 2010. – № 7. – С. 7-13. 16. И.М. Соболь. Метод Монте-Карло. – М.: Наука, 1968. – 64 с. 17. Редько В.Г. Эволюция, нейронные сети, интеллект: модели и концепции эволюционной кибернетики. – М.: Комкнига, 2005. 18. О.В. Абрамов. Методы и алгоритмы синтеза стохастических систем // Проблемы управления. – № 4, 2006. – С. 3-8. 19. Pawlak Z. Rough sets present state and further prospects // Intellegent Automation and Soft Computing. – Vol. 2, 1996. – N 2. 20. О.В. Абрамов. Параметрический синтез стохастических систем с учетом требований надежности. – М.: Наука, 1992. 21. М.А. Гайдес. Общая теория систем (системы и системный анализ). – Глобус-Пресс, 2005. – 201 с. 22. Wolpert D.H., Macready W.G. No free lunch theorems for search // Operations research: Santa Fe Institute, 1995. 23. А. Мурашов. Пакеты инженерного анализа для вычислительной гидродинамики // Суперкомпьютеры. СКР-Медиа. – М., 2010. – С. 52-58. 24. A. Chatchawit and C. Prabhas, A Hardware Implementation of the Compact Genetic Algorithm, in Proceedings of the 2001 IEEE Congress on Evolutionary Computation// Seoul, Korea, May 27-30, 2001. – pp. 624-629. 25. В.В. Гудилов, В.М. Курейчик. Устройство аппаратной реализации вероятностных генетических алгоритмов. Методы и средства обработки информации // Труды второй Всероссийской научной конференции. – М.: Изд-во МГУ им. М. В. Ломоносова. 2005. – С. 596-601. 26. В.В. Гудилов. О построении эволюционных аппаратных средств // AIS’06 CAD-2006 Интеллектуальные САПР, Том 1. – М.: Физматлит, 2005. – С. 7-15. 27. В.В. Гудилов, В.М. Курейчик. Методы повышения эффективности вероятностных алгоритмов // Перспективные информационные технологии и интеллектуальные системы. – Таганрог, 2005. – № 1. – С. 43-55. 28. W. Wolf, The future of multiprocessor systems-on-chips, in Proc. 41 st Assoc. Comput. Machinery//IEEE Design Automat, Cof. (DAC), 2004. – pp. 681-685. 29. Kumar S. Aylor J.H. Johnson B. and Wulf W.A. "The Codesign of Embedded Systems", Kluwer Academic Publishers, 1996. 30. D. Bernstein, M. Rodeh and I Gertner, On the Complexity of Scheduling Problems for Parallel//Pipelined Machines, IEEE Transactions on Computers. Vol. 38 Issue 9, September 1989, no. 9, pp.1308-1313. 31. J. Harkin, T. M. McGinnity, and L. Maguire. Genetic algorithm driven hardware-software partitioning for dynamically reconfigurable embedded systems. Microprocessors and Microsystems, 25(5), 2001.- 263–274. 32. Theissinger, M.; Stravers, P.; Veit, H.; "CASTLE: an interactive environment for HW-SW co-design", Proceedings of the Third International Workshop on Hardware/Software Codesign, GMD, St. Augustin, 1994.- pp.203-209. 33. Ismail, T.B.; Abid, M.; O'Brien, K.; Jerraya, A.; "An approach for hardware-software codesign", Proceedings of the Fifth International Workshop on Rapid System Prototyping, Shortening the Path from Specification to Prototype, 1994.- pp.73-80. 34. Edwards M.D., "A development system for hardware/software cosynthesis using FPGAs", Second IFIP International Workshop on Hw-Sw Codesign, 1993. 35. D'Ambrosio, J.G.; Xiaobo Hu; "Configuration-level hardware/software partitioning for real-time embedded systems", Proceedings of the Third International Workshop on Hardware/Software Codesign, 1994.- pp.34-41. 36. Adams, J.K.; Thomas, D.E.; "Multiple-Process behavioral synthesis for mixed hardware-software systems", in Proc. 8th Int. Symp. On System Synthesis, 1995.- pp.10-15. 37. A. Henni, M. Koudil, K. Benatchba, H. Oumsalem, K. Chaouche. A parallel environment using taboo search and genetic algorithms for solving partitioning problems in codesign, Institut National de formation en Informatique. 38 Kavalade A., Lee E.A.. "The extended partitioning problem: hardware//software mapping and implementation-bin selection", Proceedings of the Sixth International Workshop on Rapid Systems Prototyping, Chapel Hill, NC, June 1995. 39. Gupta R.K., "Co-Synthesis of Hardware and Software for digital embedded systems", Amsterdam: Kluwer, 1995. 40. Jantsch A., Ellervee P., Oberg J., HemmaniI A., Tenbunen H., "Hardware-software partitioning and minimizing memory interface traffic", Proc. of the European Design Automation Conference, Sept. 1994.- pp.226-231. 41 Gajski, D.D.; Narayan, S.; Ramachandran, L.; Vahid, F.; Fung, P.; "System design methodologies: aiming at the 100h design cycle", IEEE Trans. On VLSI Systems, Vol.4, N°1, March 1996.- pp.70-82. 42. Harenstein R., Becker J., Kress R., "Twolevel hardware/software partitioning using CoDe-X", IEEE Symposium and Workshop on Engineering of Computer-Based Systems, March 1996. 43. Chatha K.S., Vemuri R., “MAGELLAN: Multiway Hardware-Software Partitioning and Scheduling for Latency Minimization of Hierarchical Control-Dataflow Task Graphs”, Proceedings of 9th International Symposium on Hardware-Software Codesign (CODES 2001), Copenhagen, Denmark, April 25-27 2001. 44. Bolchin, C., Pomante L., Salice F., Sciuto, D. H/W embedded systems: on-line fault detection in a hardware/software codesign environment: system partitioning // Proceedings of the International Symposium on Systems Synthesis, Vol. 14, September 2001. 45. Dours S D.., "Estimations rapides pour le partitionnement fonctionnel de systemes temps-reelstricts distribues", RENPAR'14, ASF, SYMPA,Hamamet, Tunisie, 10-13 april 2002. 46. Noguera J., Badia R.M., “A hardware/software partitioning algorithm for dynamically reconfigurable architectures”, Proceedings of the International Conference on Design Automation and Test in Europe (DATE’01), March 2001. 47. J. Harkin, T. M. McGinnity, and L. Maguire. Genetic algorithm driven hardware-software partitioning for dynamically reconfigurable embedded systems. Microprocessors and Microsystems, 2001, 25(5): pp. 263-274. 48. P. Eles, K. Kuchcinski, Z. Peng, and A. Doboli. System level hardware/software partioning based on simulated annealing and tabu search. Design Automation for Embedded Systems, 1997 2:5-32. 49. V. Catania, M. Malgeri, and M. Russo. Applying fuzzy logic to codesign partitioning. IEEE Micro, 17(3):pp. 62 70, 1997. 50. R P. Dick and N.K. Jha. MOGAC: a multiobjective genetic algorithm for hardware-software cosynthesis of distributed embedded systems. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, October 1998, 17(10): pp. 920-935. 51. V. Srinivasan, S. Radhakrishnan, and R. Vemuri. Hardware/software partitioning with integrated hardware design space exploration. In DATE ’98: Proceedings of the conference on Design, automation and test in Europe, pages. 52. J. Hou and W. Wolf. Process partitioning for distributed embedded systems. In CODES ’96: Proceedings of the 4th International Workshop on Hardware/Software Co-Design, page 70. IEEE Computer Society, 1996. 53. Hidalg, J.I., Lanchares J. Functional partitioning for hardware-software codesign using genetic algorithms. in Proc/ 23rd EUROMICRO Conf, 1997, pp 631-638. 54. T. Wiangtong, P. Cheung and W. Luk, Comparing Three Heuristic Search Methods for Functional Partitioning in Hardware–Software Codesign. Design Automation for Embedded Systems, Volume 6, Number 4, pp. 425-449. 55. P. Eles, Z. Peng, K. Kuchcinski and A. Doboli. System Level Hardware/Software Partitioning Based on Simulated Annealing and Tabu Search, Design Automation for Embedded Systems, Volume 2, Number 1, pp. 5-32. |
