Лекция n16 Лекция 16

Вид материала

Лекция

Содержание Дж/К. Количество энергии, испускаемой в единицу времени (т.е. поток Закон Кирхгофа Теория атома водорода Бора Электрон вращается вокруг ядра по избранным стационарным круговым орбитам. Атом при этом не излучает и не поглощает энергии. Eb) на более близкую (с меньшей

Подобный материал:

• «Социальная стратификация и социальная мобильность», 46.19kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
• Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
• Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
• Тема Лекция, 34.13kb.
• Лекция посвящена определению термина «транскриптом», 219.05kb.
• А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.

Лекция 16.
Законы ТЕПЛОВОГО ИЗЛУЧЕНИЯ.
ГИПОТЕЗА ПЛАНКА. квантовая физика. ТЕОРИЯ БОРА ДЛЯ АТОМА ВОДОРОДА


Е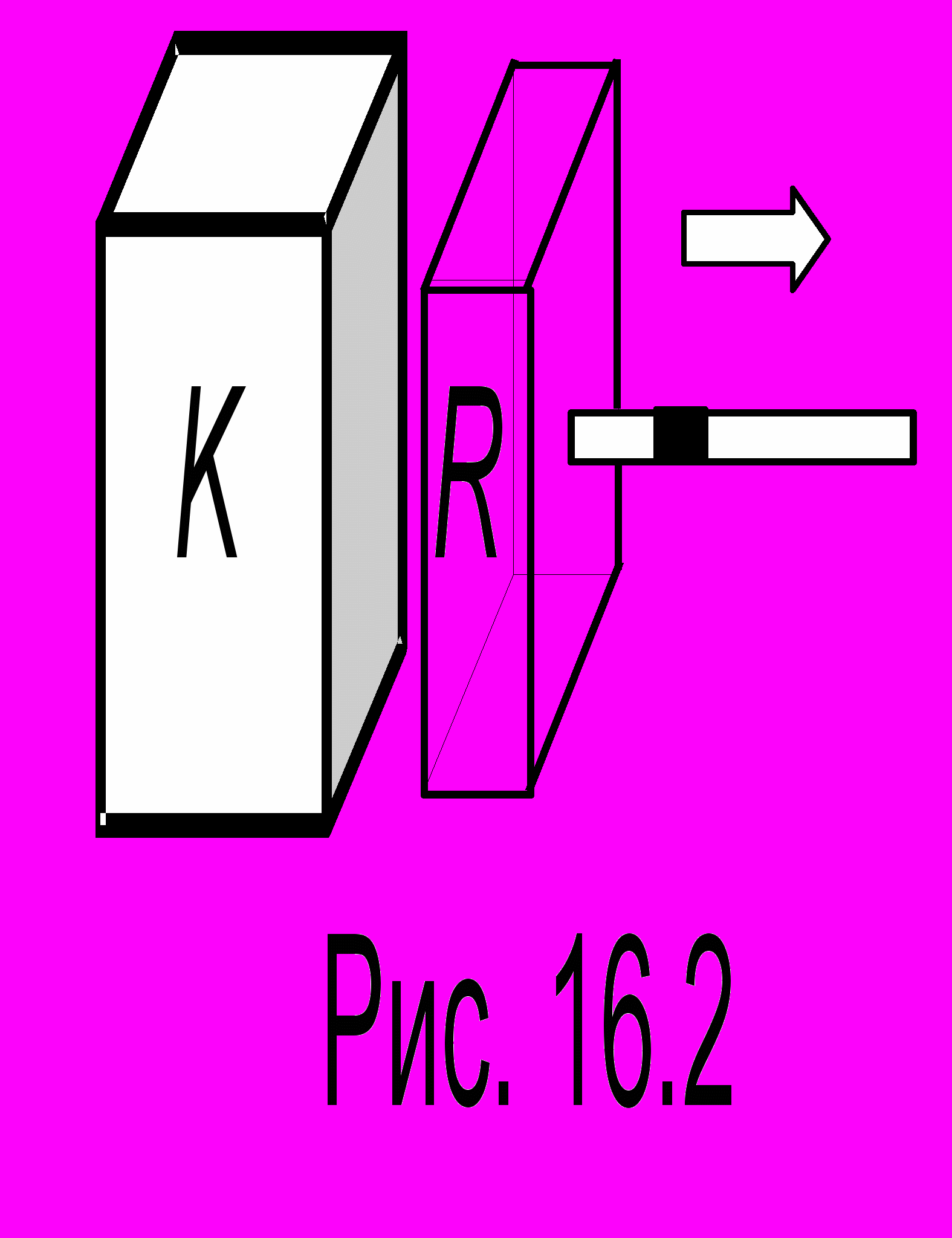сли нагревать гвоздь, то в процессе нагревания атомы железа будут переходить в возбужденное состояние. Последующий переход в основное состояние сопровождается выбросом электромагнитного излучения с длинами волн, приходящимися, в основном, на инфракрасный диапазон спектра. Это и есть тепловое излучение. Вблизи нагретой плиты или нагретого асфальта мы часто наблюдаем нечеткие колеблющиеся контуры окружающих предметов. Это есть следствие изменения от нагрева показателя преломления воздуха и связанных с этим оптических эффектов преломления света, а вовсе не потоки излучения, как некоторые ошибочно полагают. Из всех видов излучений только тепловое находится в равновесии с окружающей средой. Поместим внутрь идеально отражающей полости нагретое тело S (рис. 16.1). Если оно в единицу времени больше испускает, чем поглощает (в результате отражения от полости), то его температура снизится, и оно испускать станет меньше. Наоборот, если оно больше поглощает, чем испускает, то температура его повысится, и оно испускать станет больше. Таким образом, в любом случае равновесие восстанавливается. Если два тела поглощают в единицу времени разные количества энергии, то и испускание должно быть различным (правило Превó, 1809). Так, капелька ртути, заключенная в трубку, соединенную с воздушным резервуаром R, движется быстрее, когда к резервуару обращена зачерненная сторона куба К с горячей водой (как на рис. 16.2), чем в случае, когда куб повернут к резервуару любой другой стороной. Средняя кинетическая энергия молекул тела называется температурой. Чтобы ее не измерять, как энергию в джоулях, удобно ввести ту или иную температурную шкалу. Более подробное определение температуры будет введено в следующей части курса, а пока будем считать, что

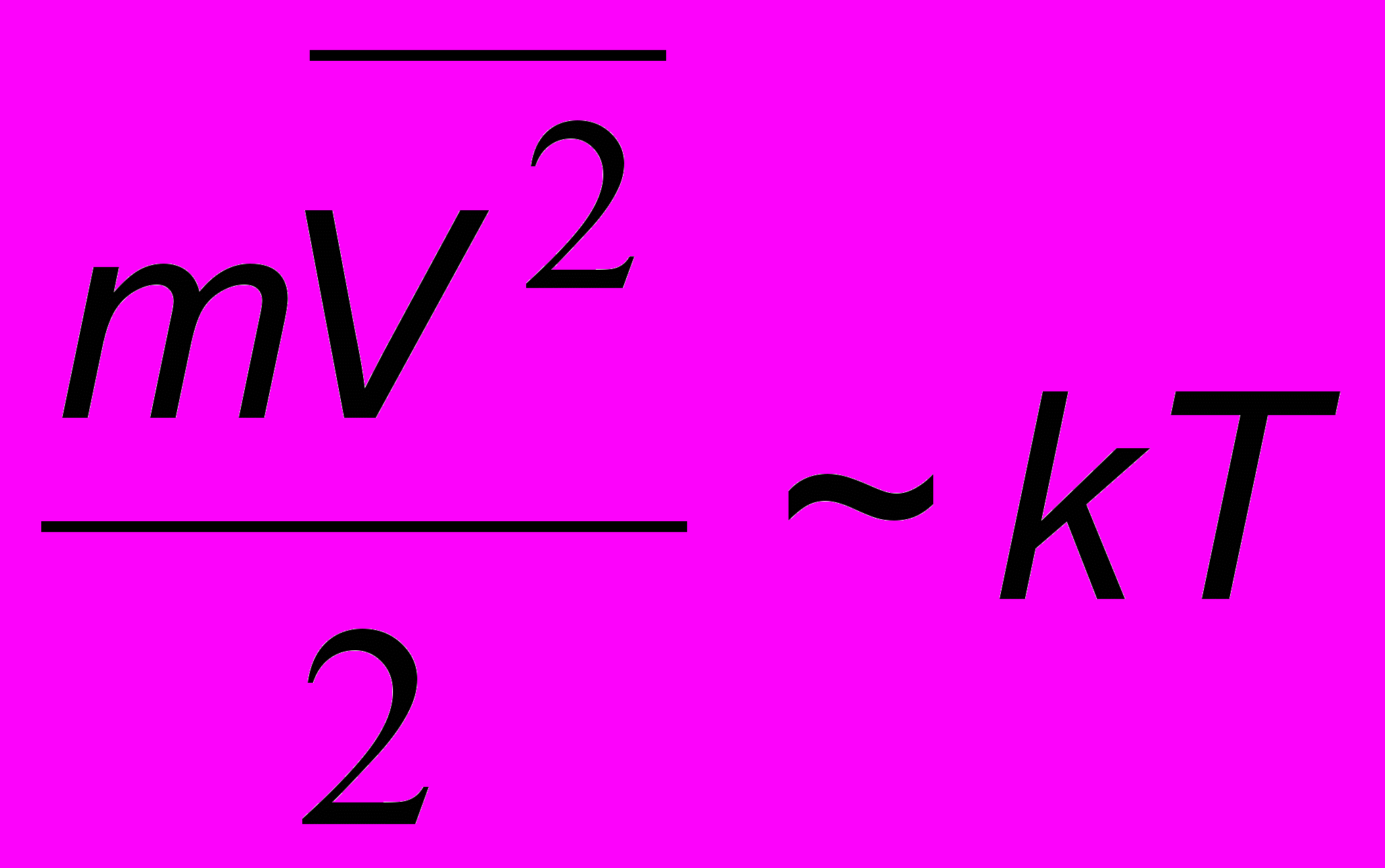, (16.1)

где k - постоянная Больцмана, переводящая Джоули в градусы Кельвина (или Кельвины) и равная 1,38  10^-23­­ Дж/К.

Количество энергии, испускаемой в единицу времени (т.е. поток) с единицы поверхности тела по всем направлениям, называется испускательной способностью . Для различных частот (длин волн) она различна, и поэтому ее относят к бесконечно малому участку d (или же d) спектрального интервала. Тогда величина потока в данном спектральном интервале при данной температуре Т равна dФ = _,T d = _,Td, а полный поток равен

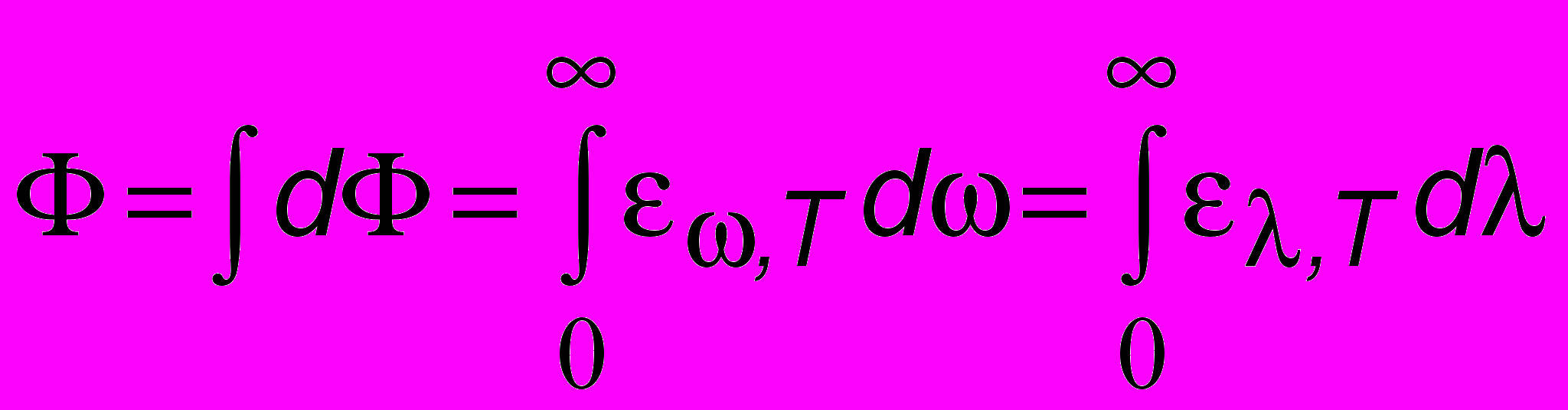
. (16.2)

Так как  = 2с/, то d/d= -2с/²
=-²/(2с). Поэтому связь между _,T и _,T имеет вид: _,T =_,T²/(2с) (Знак минус означает, что положительное приращение частоты соответствует отрицательному приращению длины волны и потому существенной роли здесь не играет.) Часть dФ' потока dФ будет поглощаться. Поглощательная способность определяется как А_,Т = dФ'/dФ. 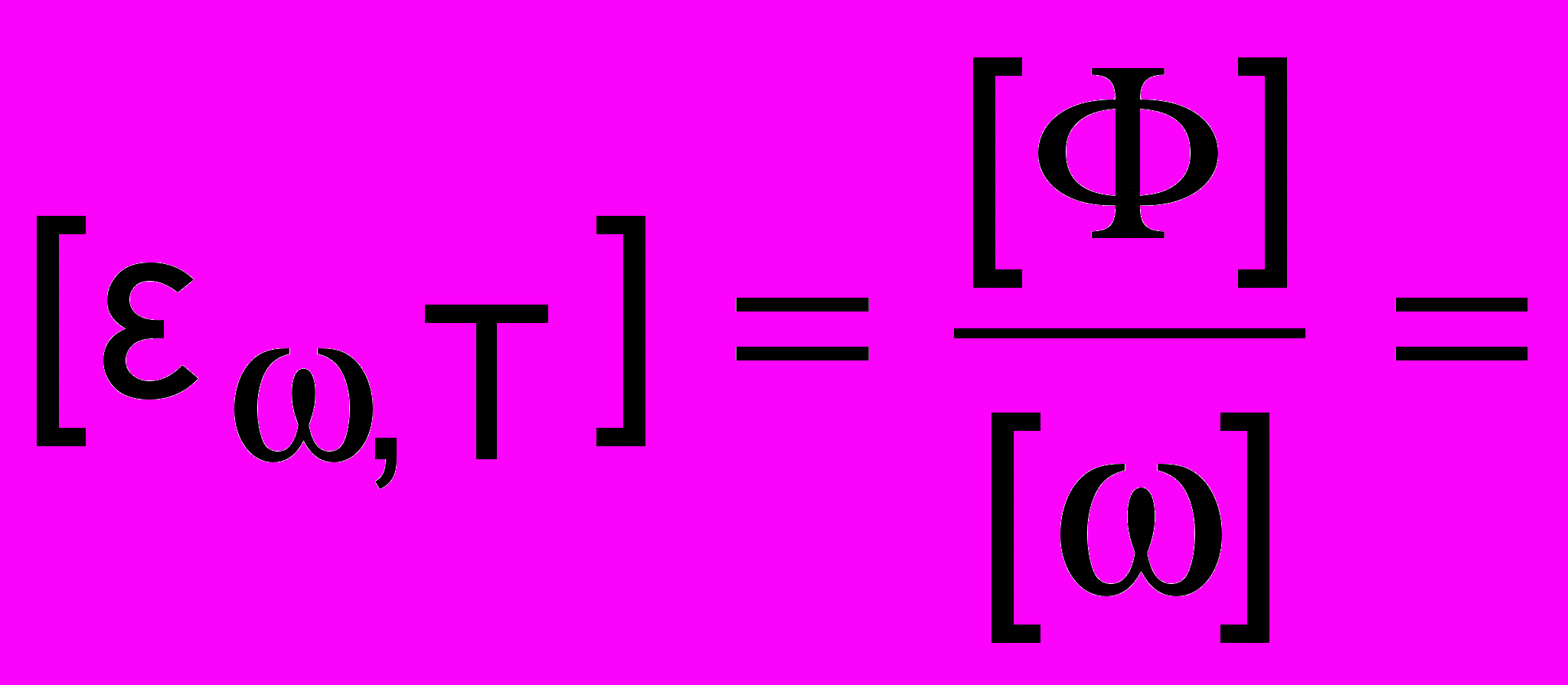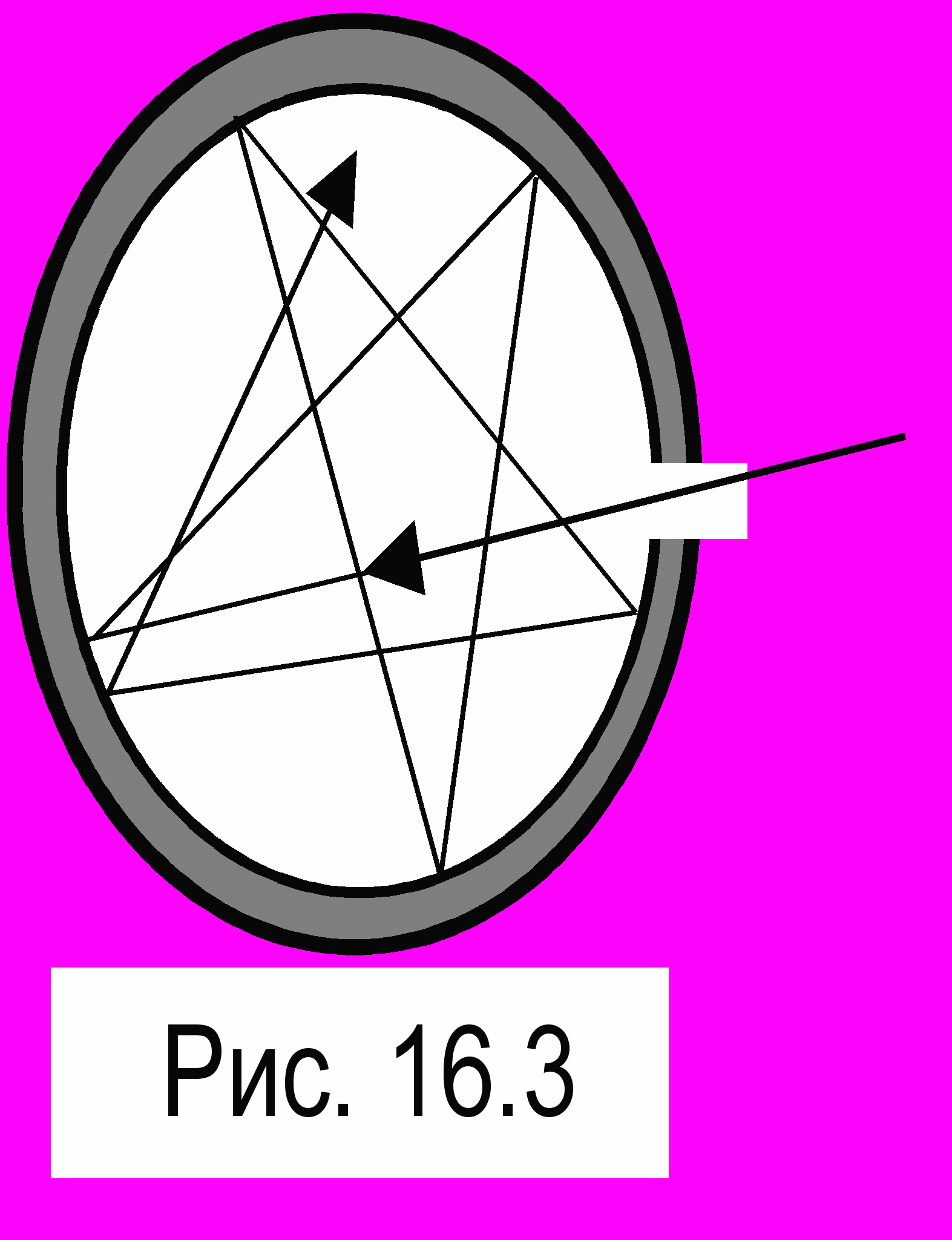Она, как и испускательная способность, зависит от частоты (длины волны) и температуры, но в отличие от нее является безразмерной величиной, в то время как испускательная способность является размерной величиной Дж/м² и 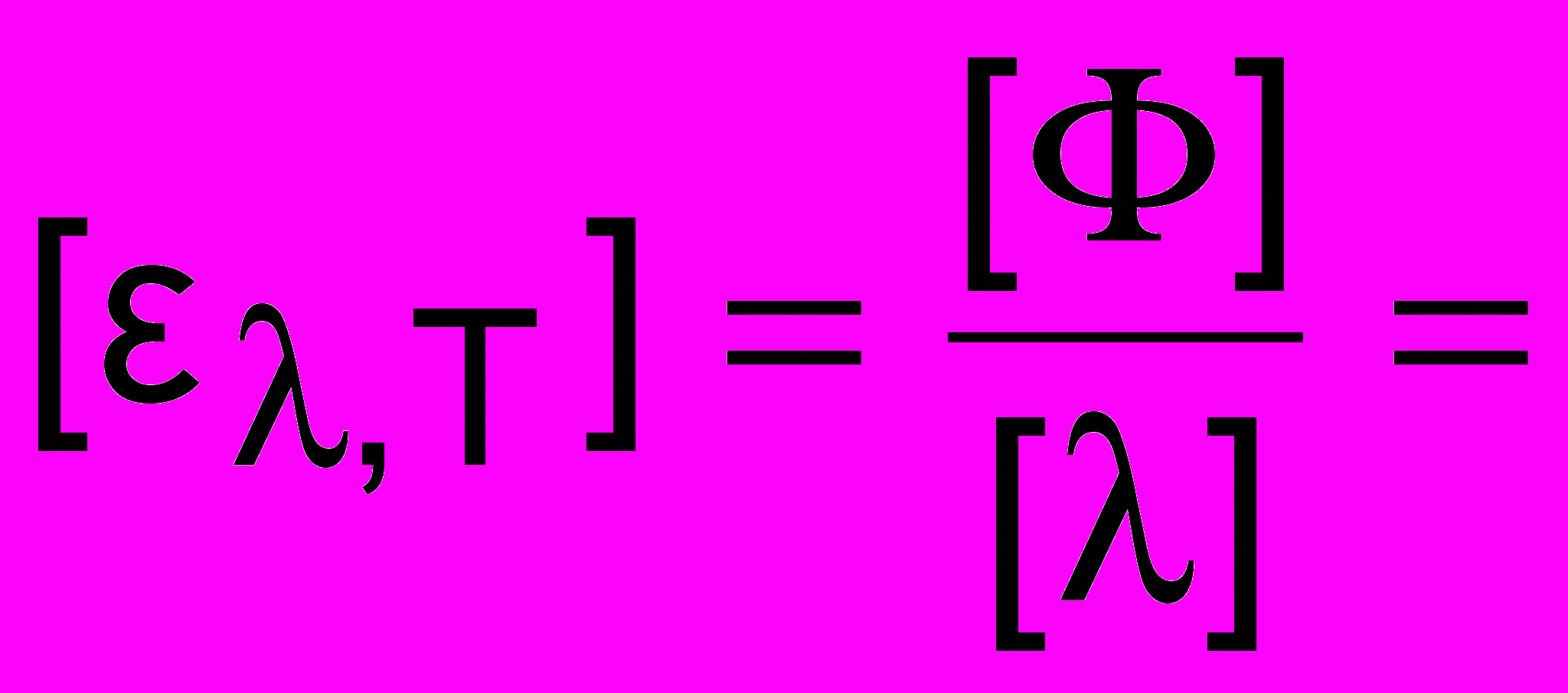Дж/(м³с). Тело, для которого А_,Т = 1 для всех частот (длин волн) и температур называется абсолютно черным (АЧТ). Понятие это является, вообще говоря, идеализацией, однако по своим свойствам к АЧТ близка сажа, а также маленькое отверстие в сферической полости – например, дырка в глобусе (рис. 16.3). Луч света, попав в полость, испытывает многократные отражения, теряя при каждом из них часть своей энергии и имея малую вероятность при очередном отражении выбраться наружу.

Закон Кирхгофа: отношение испускательной и поглощательной способностей тела не зависит от природы тела¹ и есть универсальная для всех тел функция частоты и температуры: .

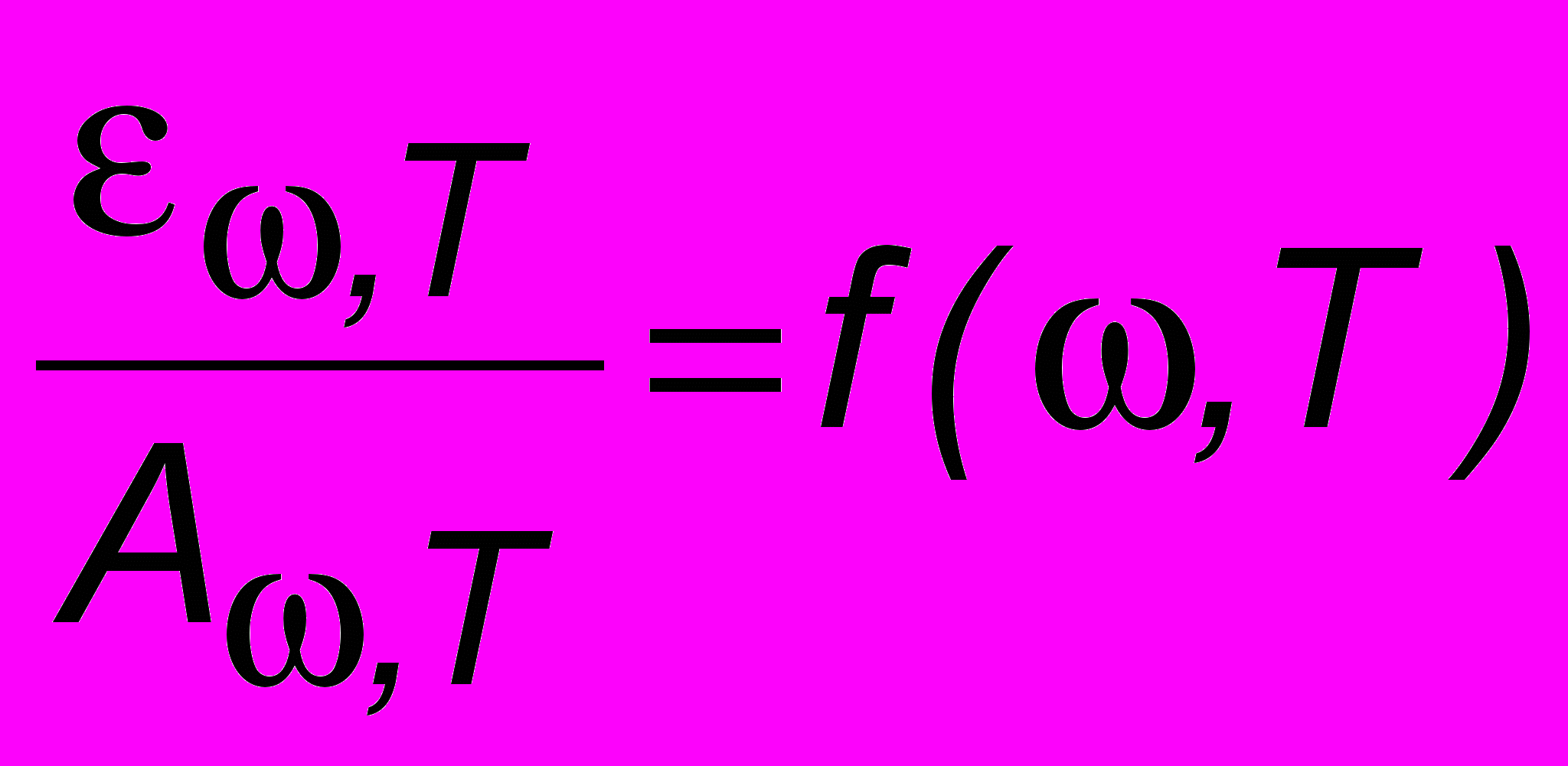Так как этот закон справедлив для любого тела, то им может быть и АЧТ. Тогда знаменатель в отношении обратится в единицу и получится, что универсальная функция Кирхгофа есть не что иное, как испускательная способность АЧТ: 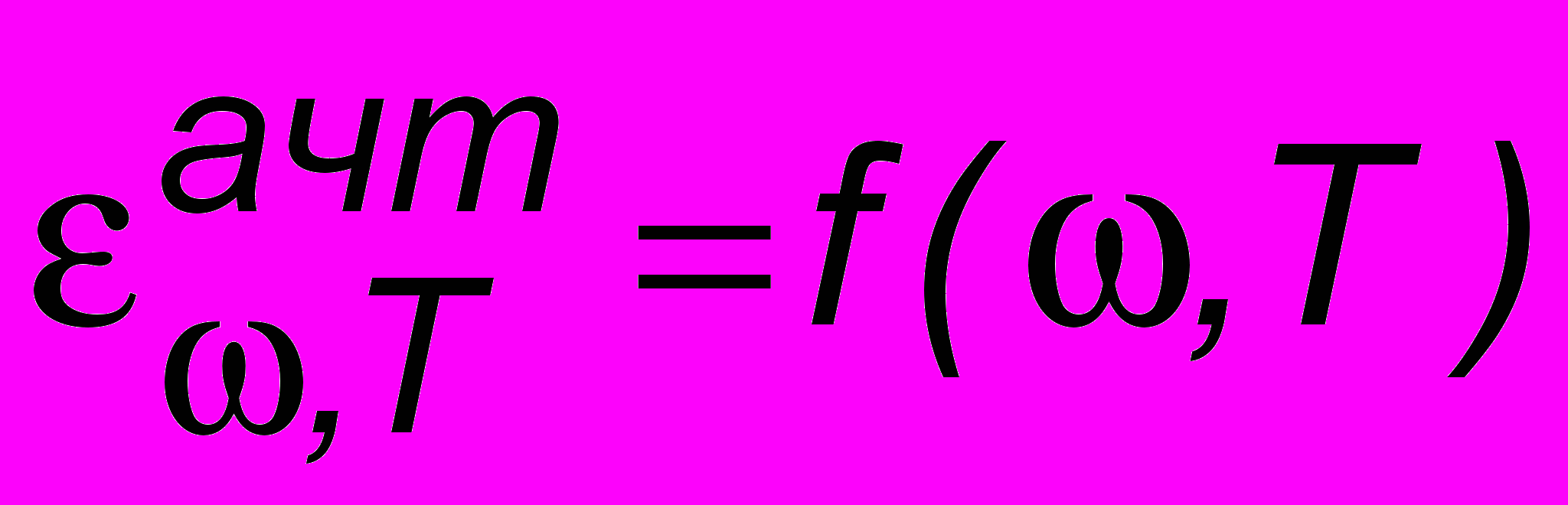. Поиски этой функции увенчались успехом лишь в начале XX века. В декабре 1900 г. Макс Планк, выдающийся немецкий физик, анализируя тепловое излучение, впервые предположил, что оно испускается отдельными порциями. Каждая такая порция стала называться квантом электромагнитного излучения (от латинского quantum - количество) или фотоном. По Планку, полная энергия кванта равна

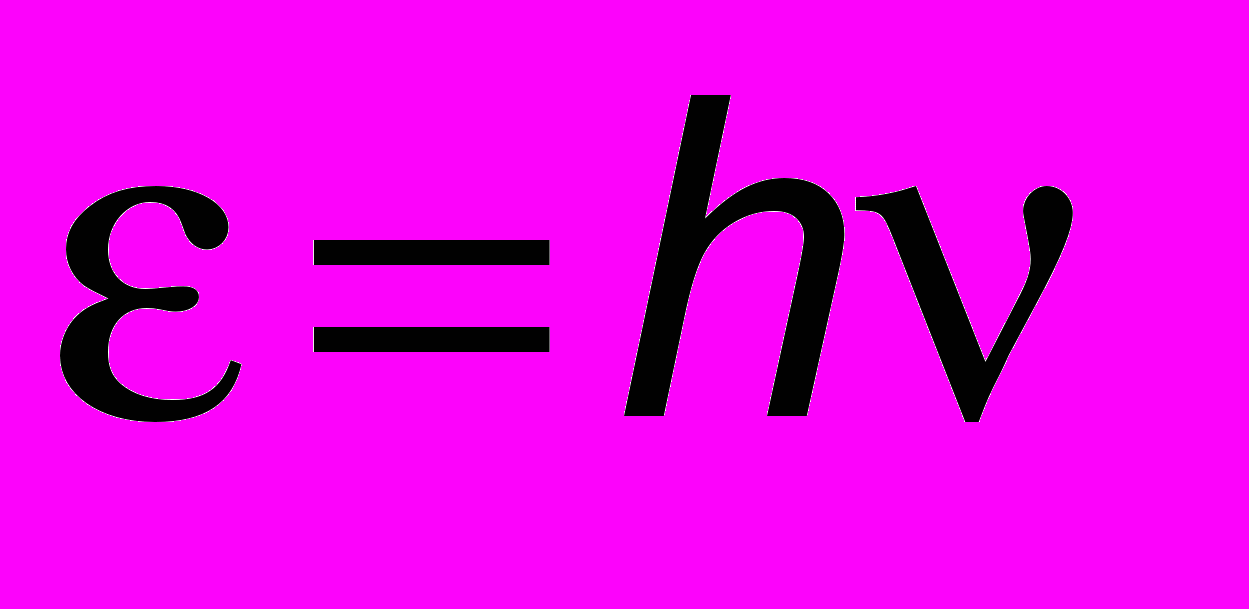, (16.3)

где  - частота излучения, а h = 6.622  10^-34 Дж с - постоянная Планка. Если пользоваться круговой частотой  = 2, то удобнее формула
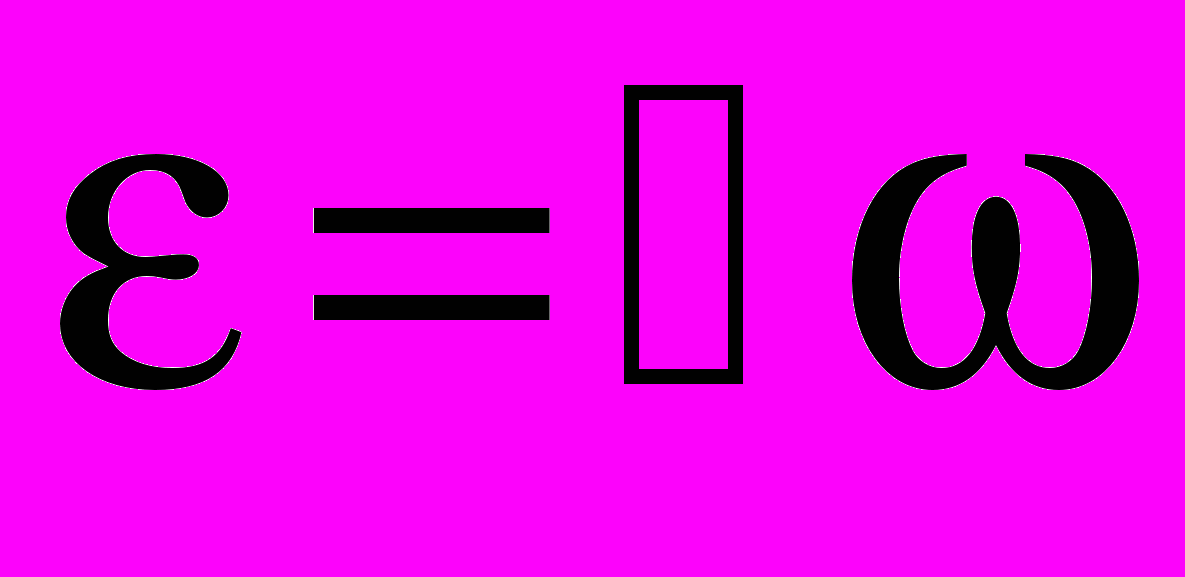, где 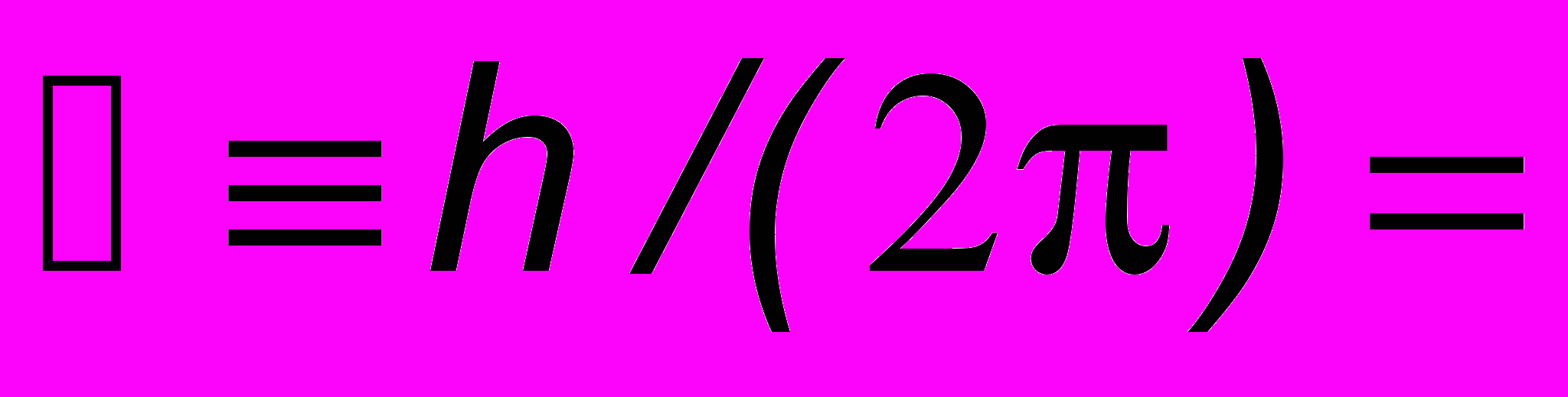1,054 10^-34 Джс.

Эта рабочая гипотеза Планка - гениальная догадка - произвела настоящую революцию в физике и ознаменовала начало новой квантовой эры. Оказалось, что отсутствие непрерывности (так называемая дискретность) в изменении физических характеристик и свойств - неотъемлемая часть микромира. Однако вернемся к тепловому излучению, а о квантовой механике подробно поговорим чуть позже.

Формула, полученная Планком, имеет вид: 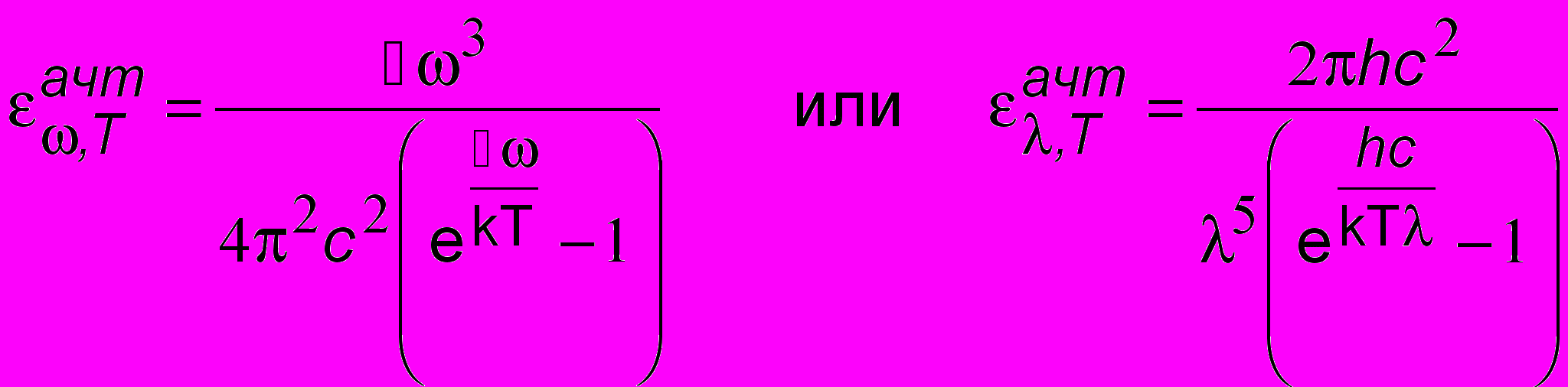. (16.4)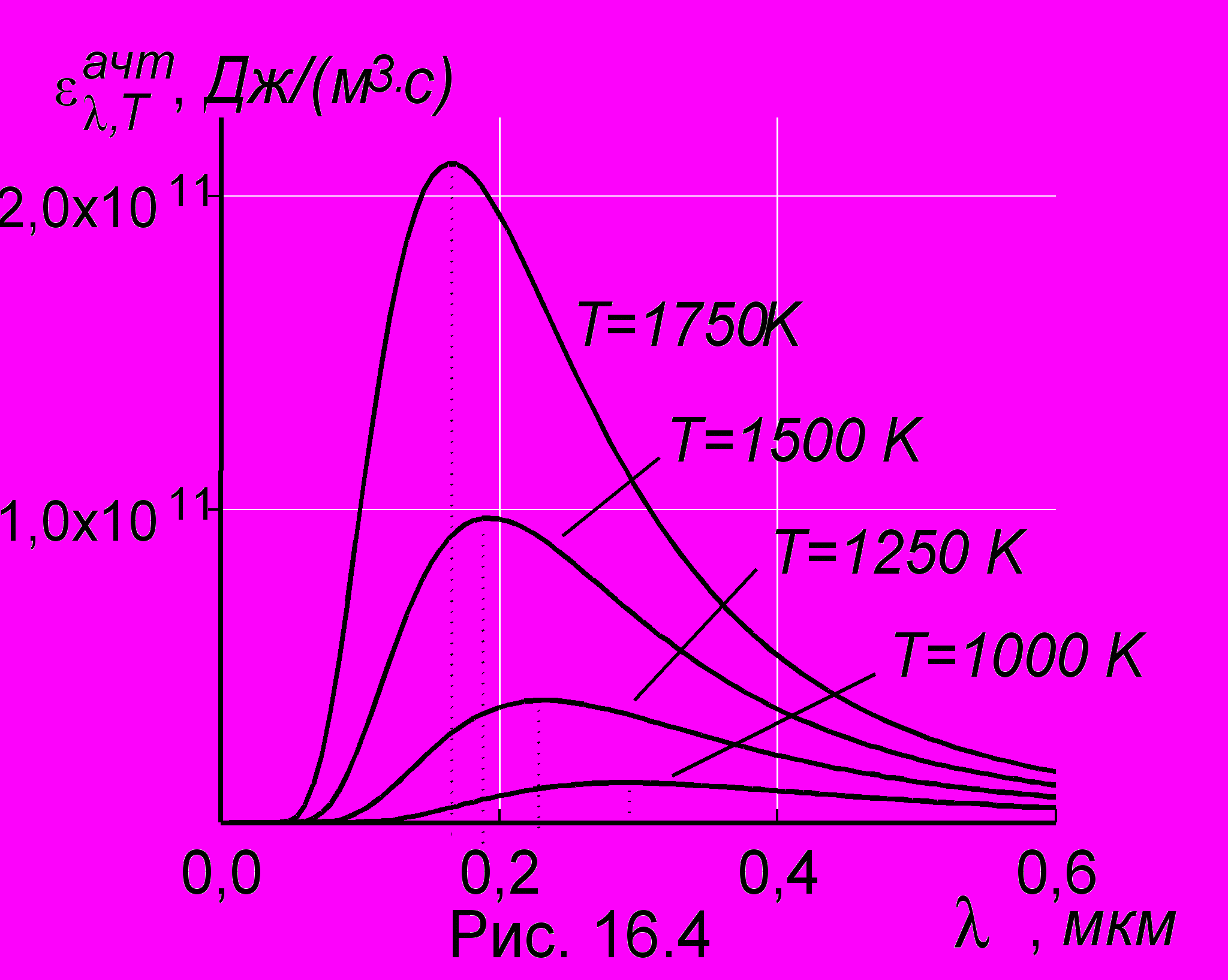




На рис. 16.4 представлено семейство функций 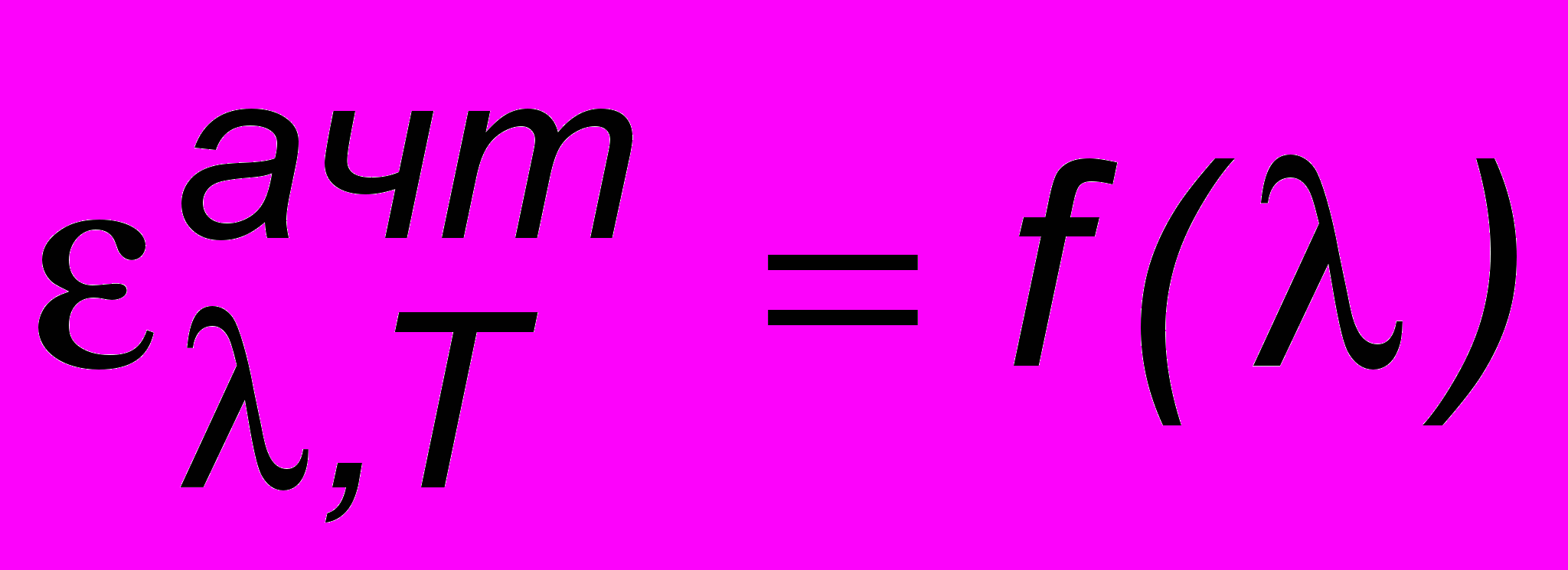для различных температур. Экспериментально кривые можно получить на установке, показанной на рис. 16.5. Излучение АЧТ преобразовывается коллиматором К в параллельный пучок и поступает на монохроматор - фильтр, вырезающий из всего спектра излучения узкую полосу вблизи некоторой длины волны . Далее излучение падает на термоэлемент, соединенный с гальванометром, показания которого пропорциональны испускательной способности в данном участке длин волн. В 1887 г., поставив аналогичный эксперимент, В. Михельсон (Москва) обнаружил, что при повышении температуры максимум испускательной способности смещается в сторону более коротких длин волн. (Известно, что тот нагретый г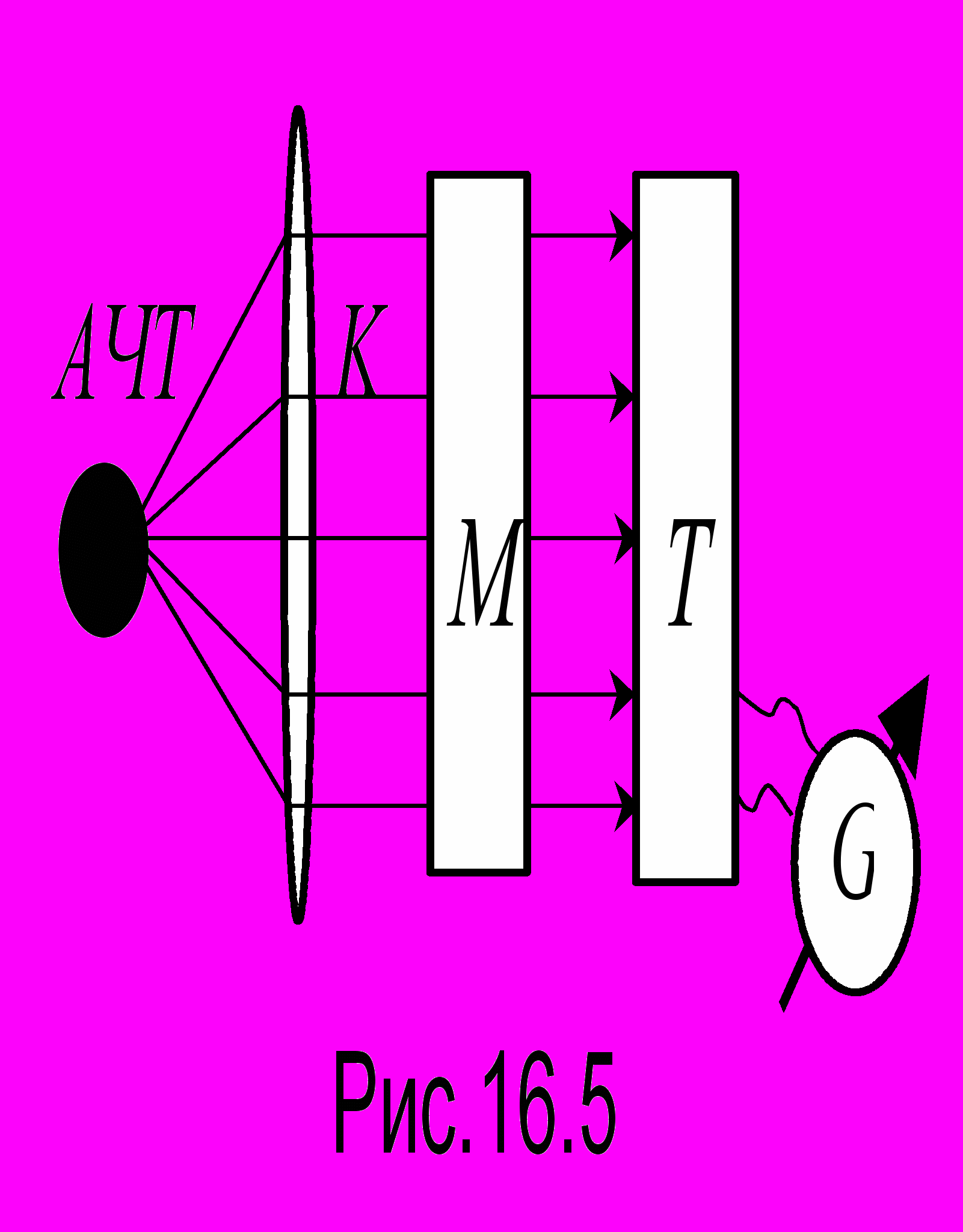
воздь сначала не светится, затем раскаляется докрасна, а потом исчезает и красный цвет, уступая более коротковолновым составляющим). Закон этот в 1893 г. был теоретически обоснован Вином и в настоящее время носит его имя. Сдвиг максимумов влево хорошо виден из рис. 16.4. Закон легко получить, применяя известное условие экстремума функции: 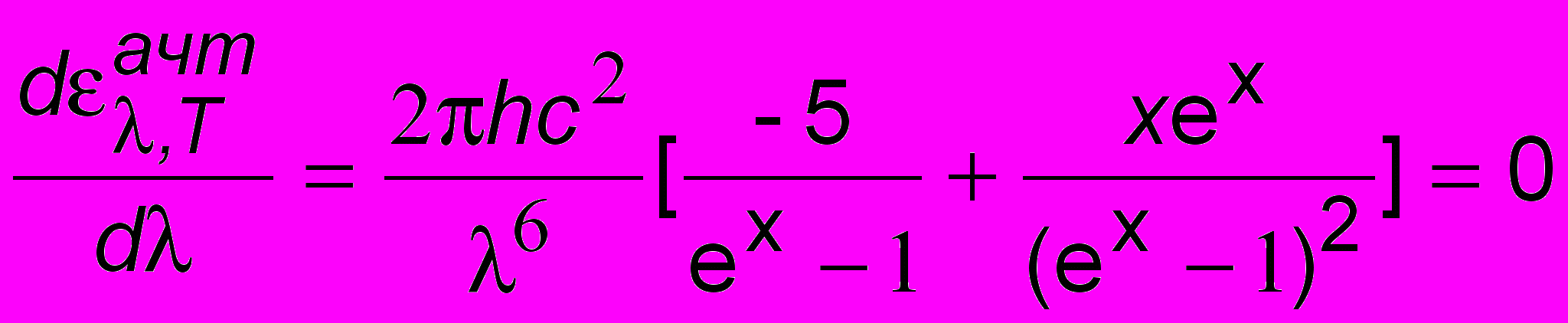, где введено обозначение x = hc/(kT). Получим трансцендентное уравнение e^x-1 = xe^x/5. "Вручн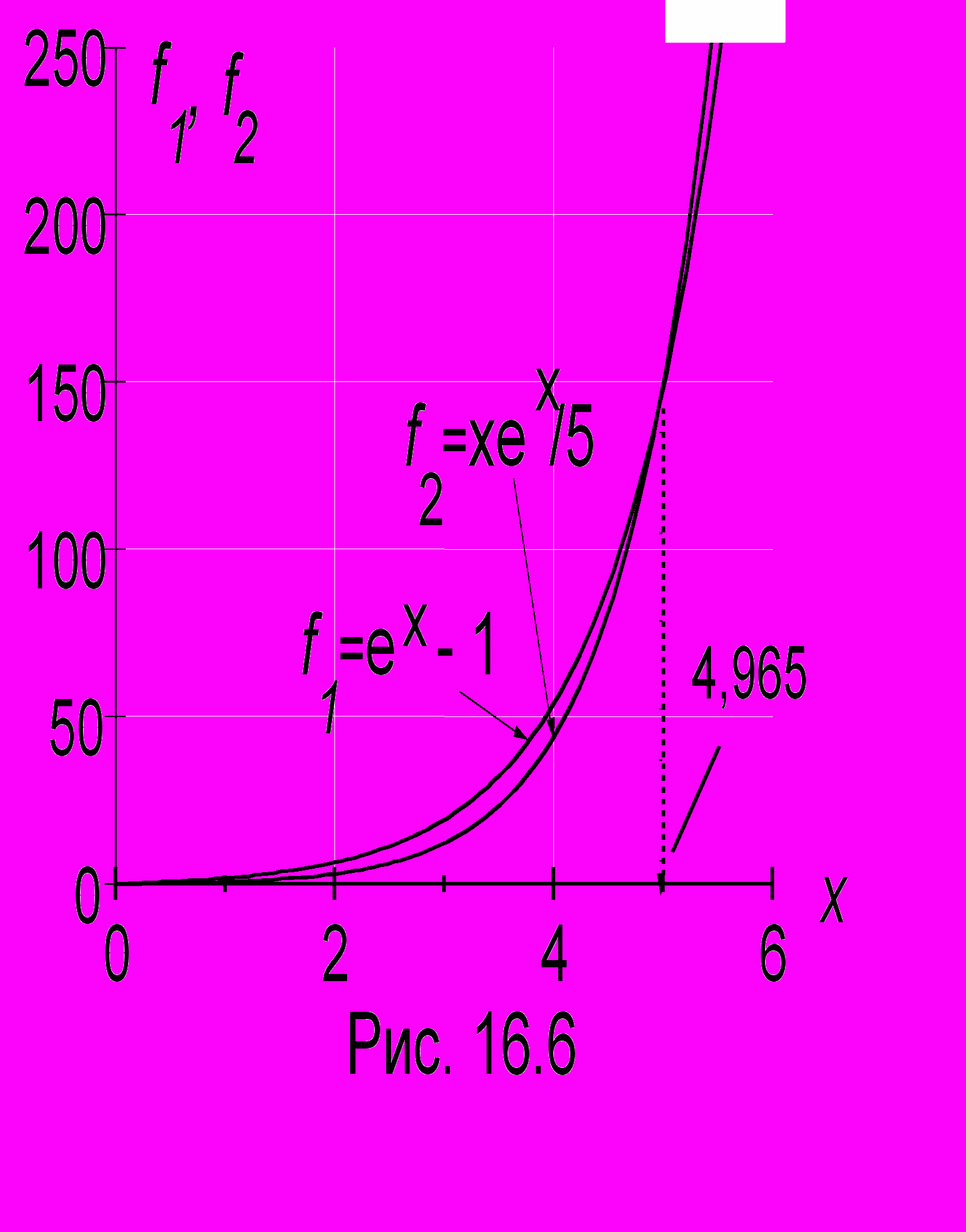ую" такое уравнение решается графически построением на одном графике функций f₁ (левая часть уравнения) и f₂ (правая часть) и определением абсциссы точки пересечения графиков (рис. 16.6). Получим х = сh/(kT_max) = 4,965, откуда T_max = B = 0,0029 мK - постоянная Вина.

И наконец вычислим суммарное излучение АЧТ по всему спектру частот при заданной температуре. Для этого достаточно вычислить интеграл (16.2):

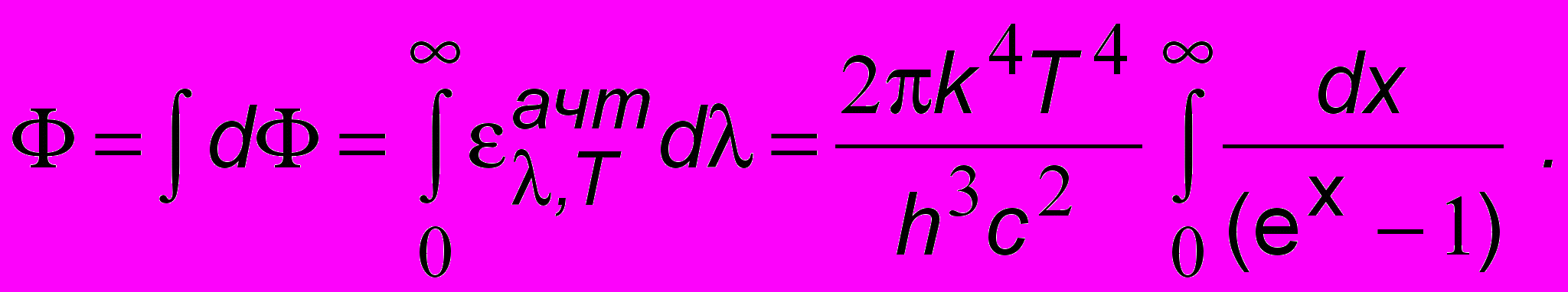Последний интеграл равен ⁴/15. Поэтому 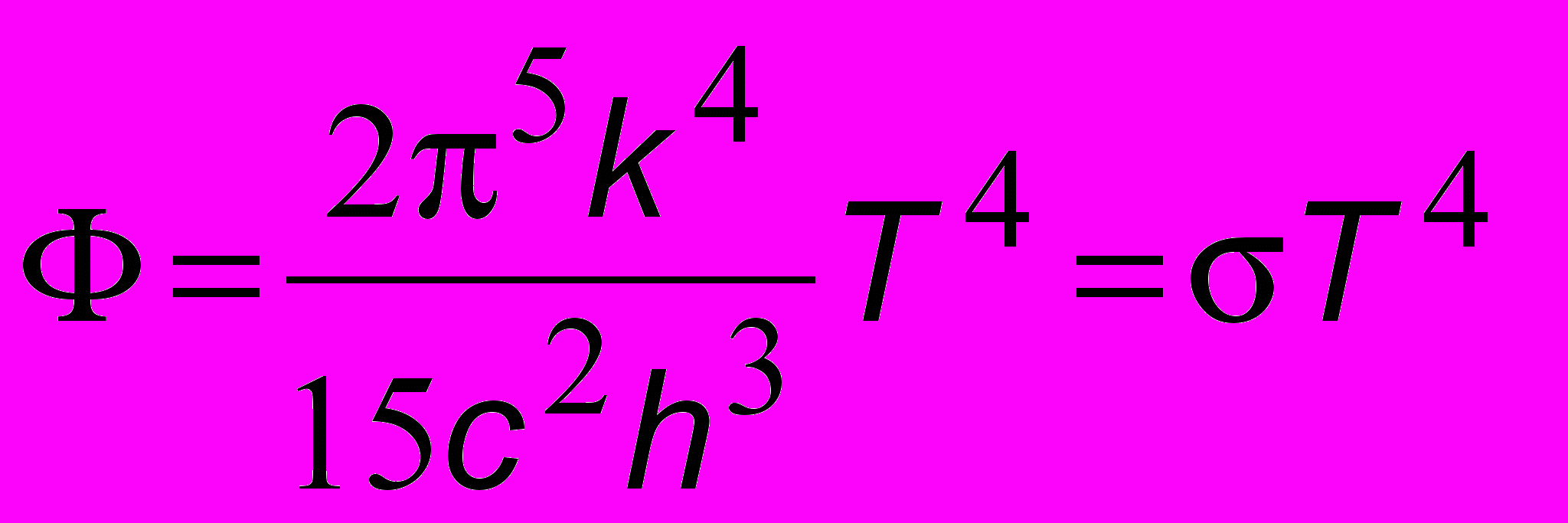- закон Стефана - Больцмана, в котором  = 5,67  10^-8 Вт/(м²К⁴) - постоянная Стефана. И этот закон, и закон Вина были получены экспериментально задолго до квантовой революции, но, как мы видели, оба этих закона являются следствием формулы Планка (16.4) что подтверждает правильность новых квантовых представлений.

Теория атома водорода Бора - триумф квантовой механики начала XX века (1913 г.). По сложившимся к тому времени понятиям атом водорода представлял собой электрон с отрицательным зарядом -e = -1,6  10^-19 Кл, вращавшийся вокруг силового центра - ядра с положительным зарядом Ze (Здесь Z = 1 - номер водорода в системе Менделеева.) Основываясь на этом представлении и гипотезе Планка, великий датский физик Нильс Бор² выдвинул два постулата:³

• Электрон вращается вокруг ядра по избранным стационарным круговым орбитам. Атом при этом не излучает и не поглощает энергии.
  
• При переходе с одной стационарной орбиты на другую происходит излучение или поглощение кванта электромагнитной энергии.
  

На рис. 16.7 схематически показаны такие орбиты и процесс излучения кванта при переходе с более отдаленной орбиты (с энергией E_b) на более близкую (с меньшей энергией E_a). Таким образом, излучается как бы излишек энергии. При обратном переходе необходима энергия извне, поэтому происходит поглощение внешней энергии; электрон переходит на более удалённую орбиту, а атом, как говорят, переходит в возбужденное состояние. Сам проц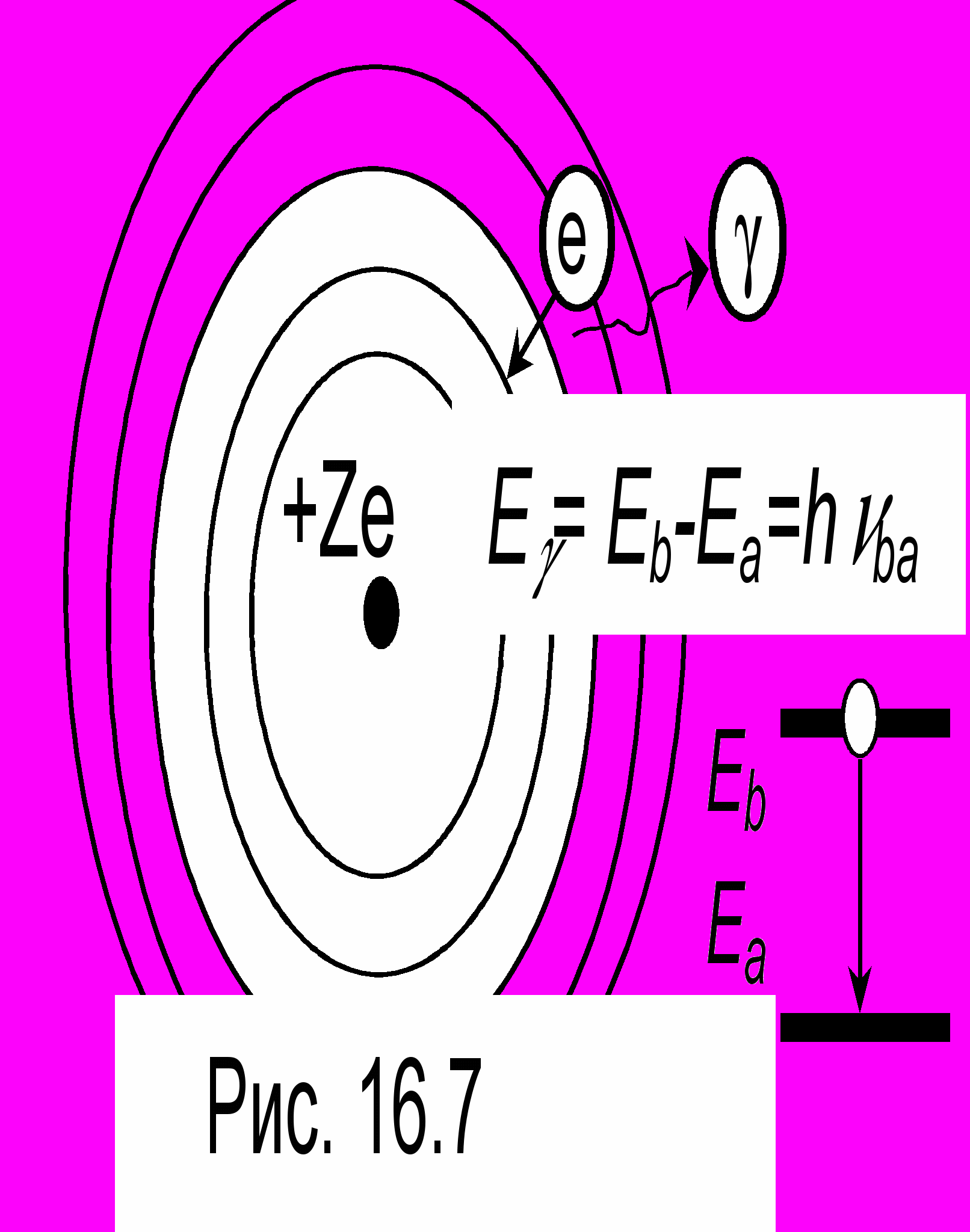есс перехода - скачкообразный. Электрон не может задержаться в промежутке между орбитами, этот промежуток - зона запрета. Разрешенные орбиты пространственно разделены. Разделены и соответствующие уровни энергии. Это и есть проявление дискретности, о которой уже говорилось в этой лекции. (Заметим в скобках, что английская булавка является отличным примером системы с двумя дискретными состояниями: булавка либо заперта, либо открыта, а в промежуточных положениях она задержаться не может.)

По Бору стационарная орбита удовлетворяет условию квантования, по которому момент импульса электрона равен целому :

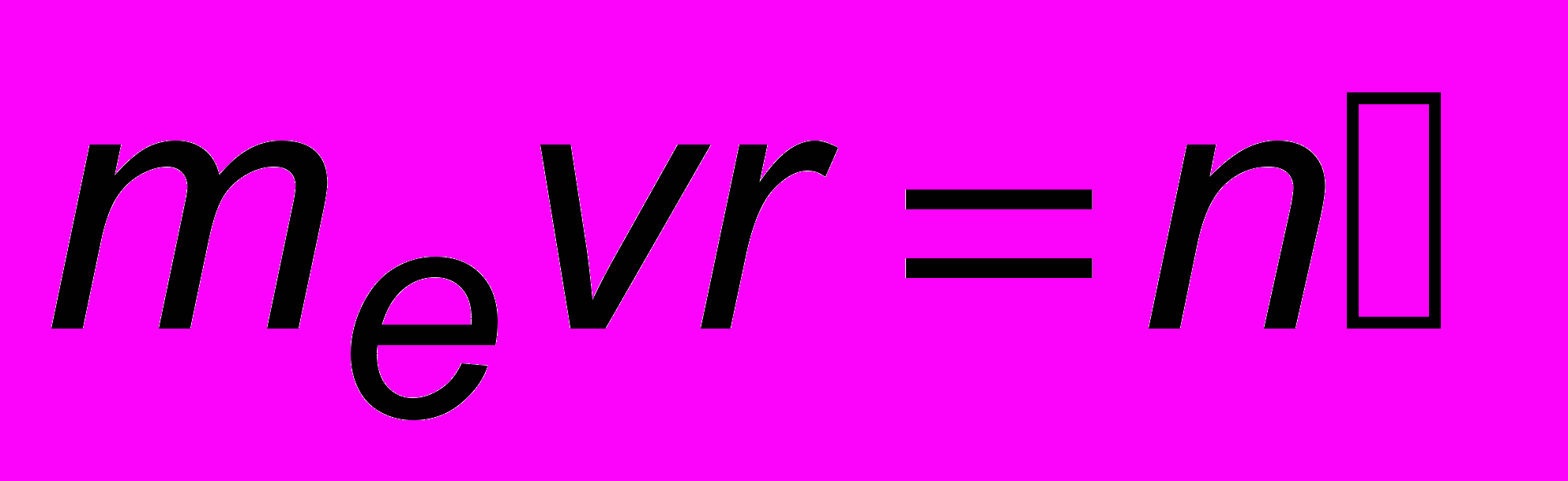, (16.5)

где r - радиус орбиты, n = 1, 2, 3, ... - целое число (квантовое число). Из второго закона Ньютона следует, что 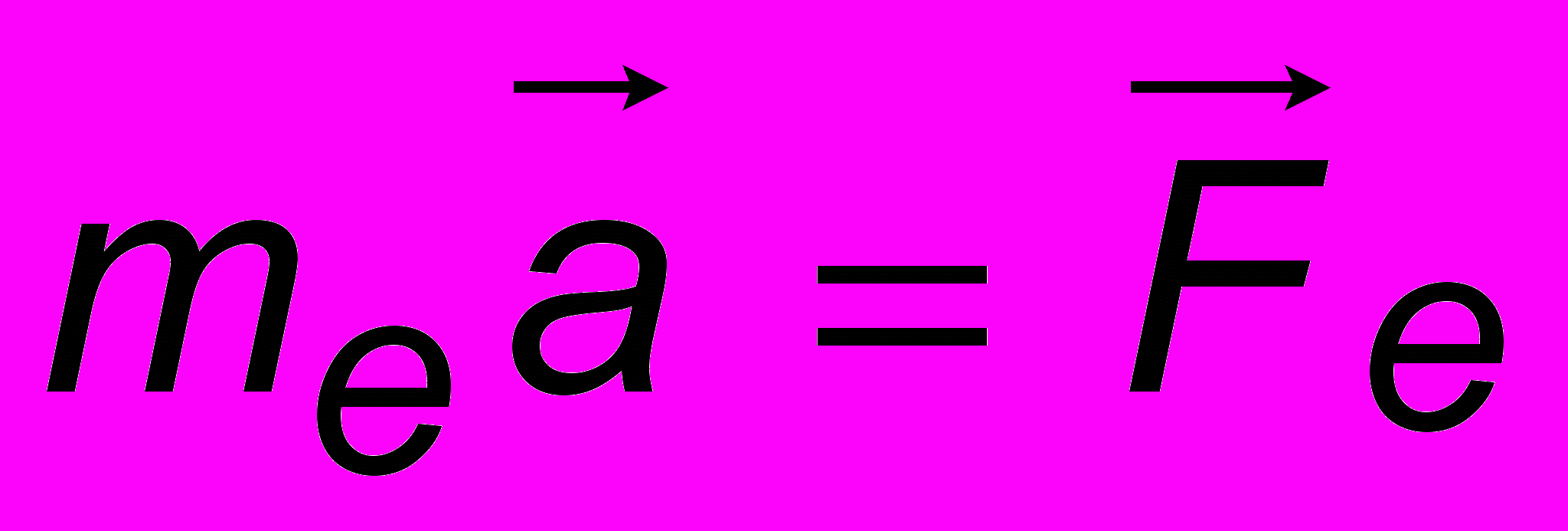. Величина силы электрического взаимодействия электрона с ядром определяется законом Кулона F_e = ke²/r², а соответствующая потенциальная энергия равна (ЧАСТЬ 1, 6.3) 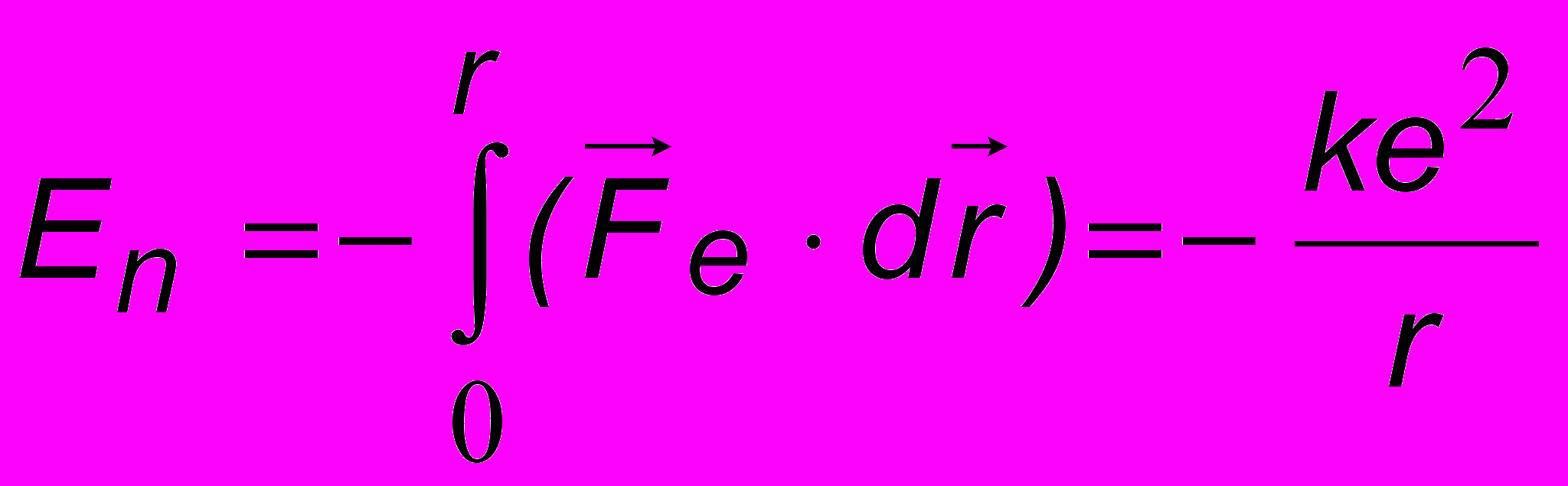. Здесь постоянная k зависит от системы единиц и в СИ определяется через электрическую постоянную _o соотношением k = 1/(4_o)  9  10⁹ м/Ф. Получим

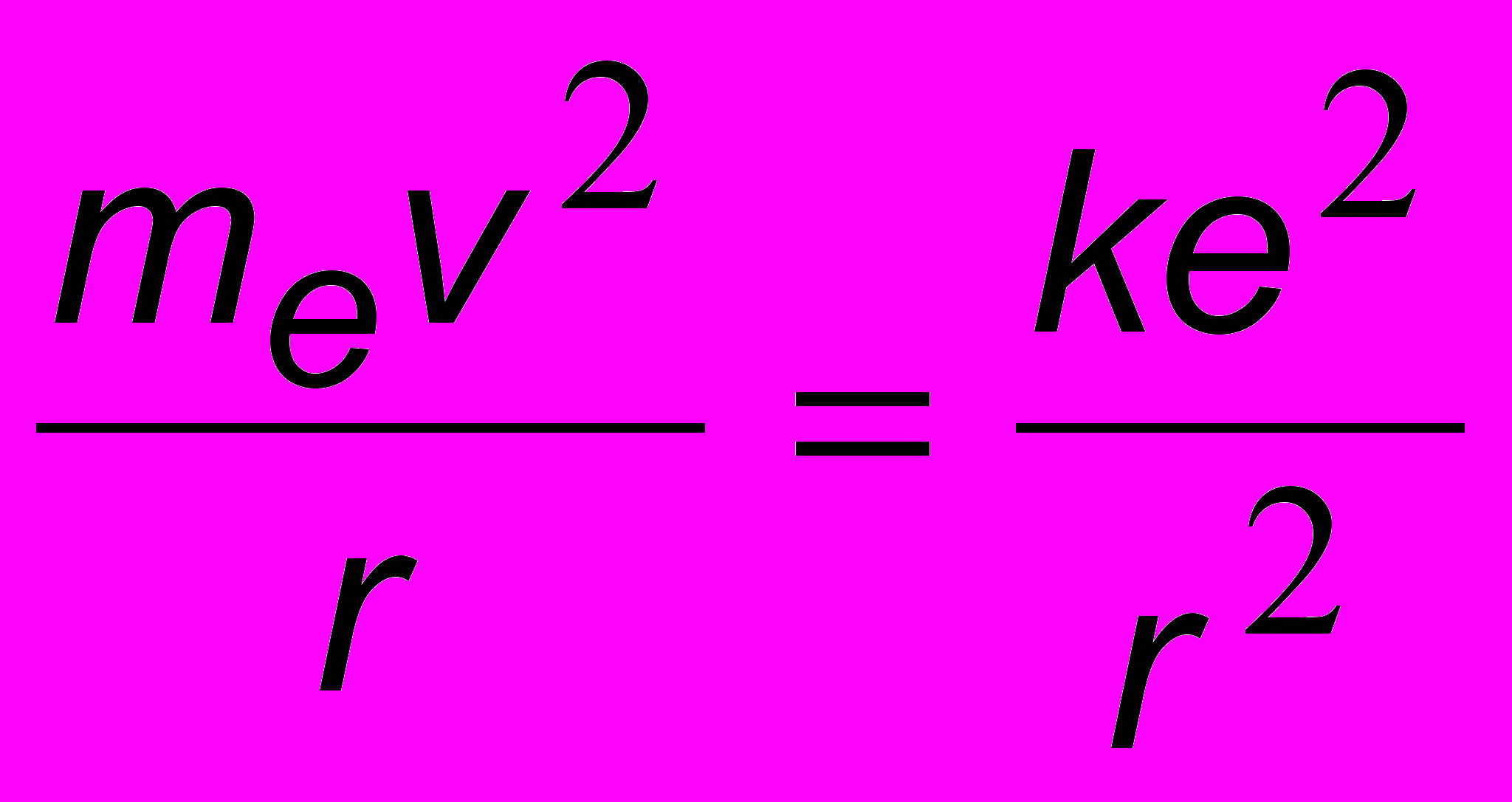. (16.6)

Здесь мы учли, что при движении по окружности центростремительное ускорение равно .

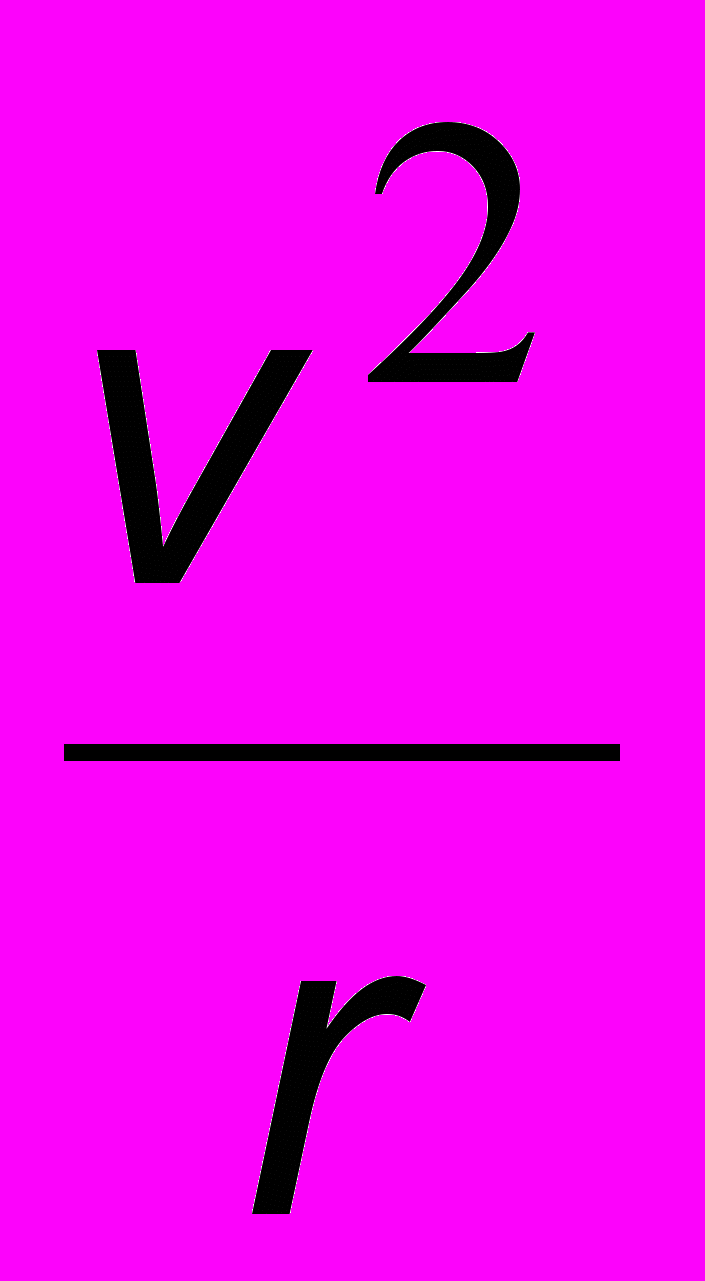Подставляя сюда выражение для V из условия квантования (16.5), получим выражение для радиуса любой орбиты с номером n:

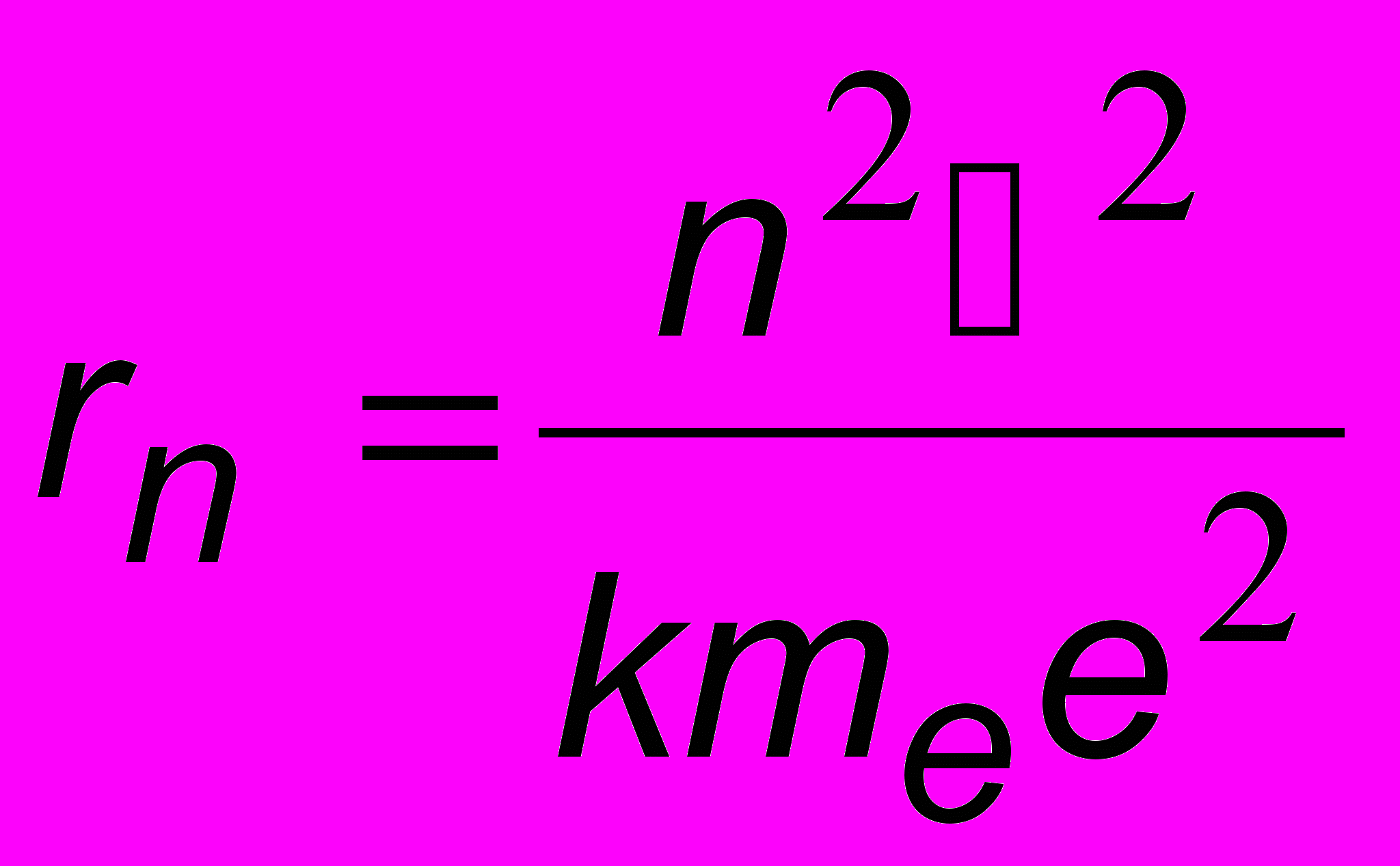. (16.7)

При n = 1 имеем самую близкую к ядру первую боровскую орбиту
r₁ = 0,529  10^-10 м = 0,529 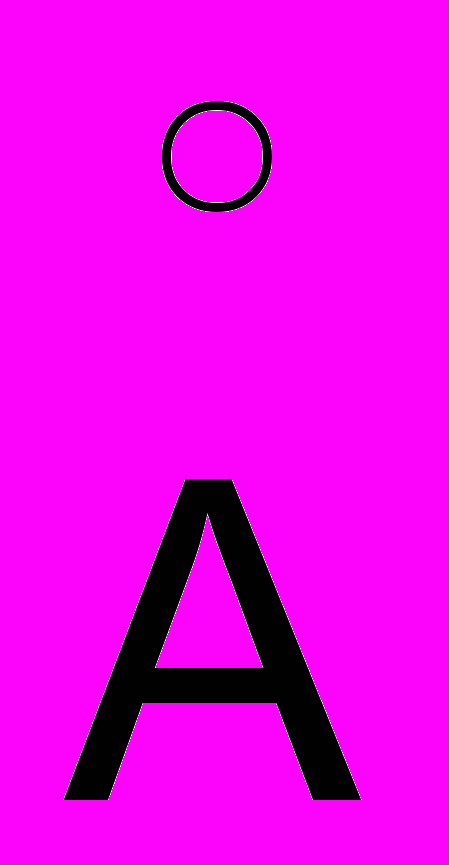. Полная энергия электрона с учетом (16.6) равна .

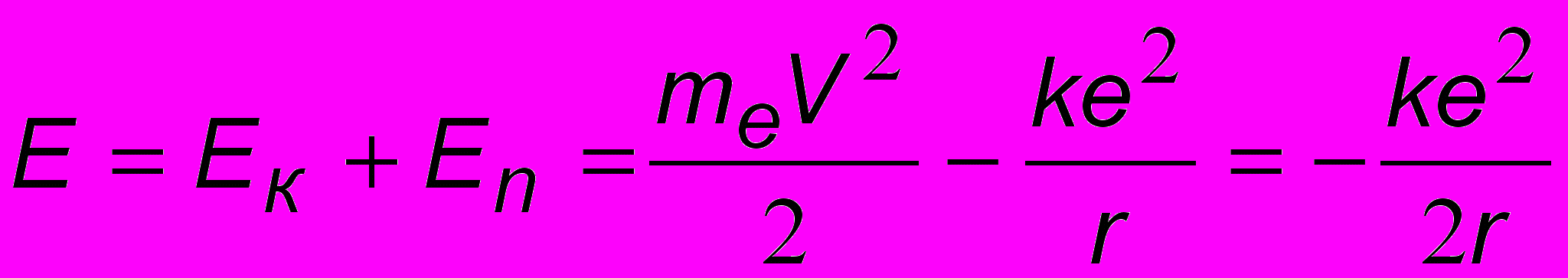Подставляя сюда (16.7), получим формулу спектра энергий атома водорода:

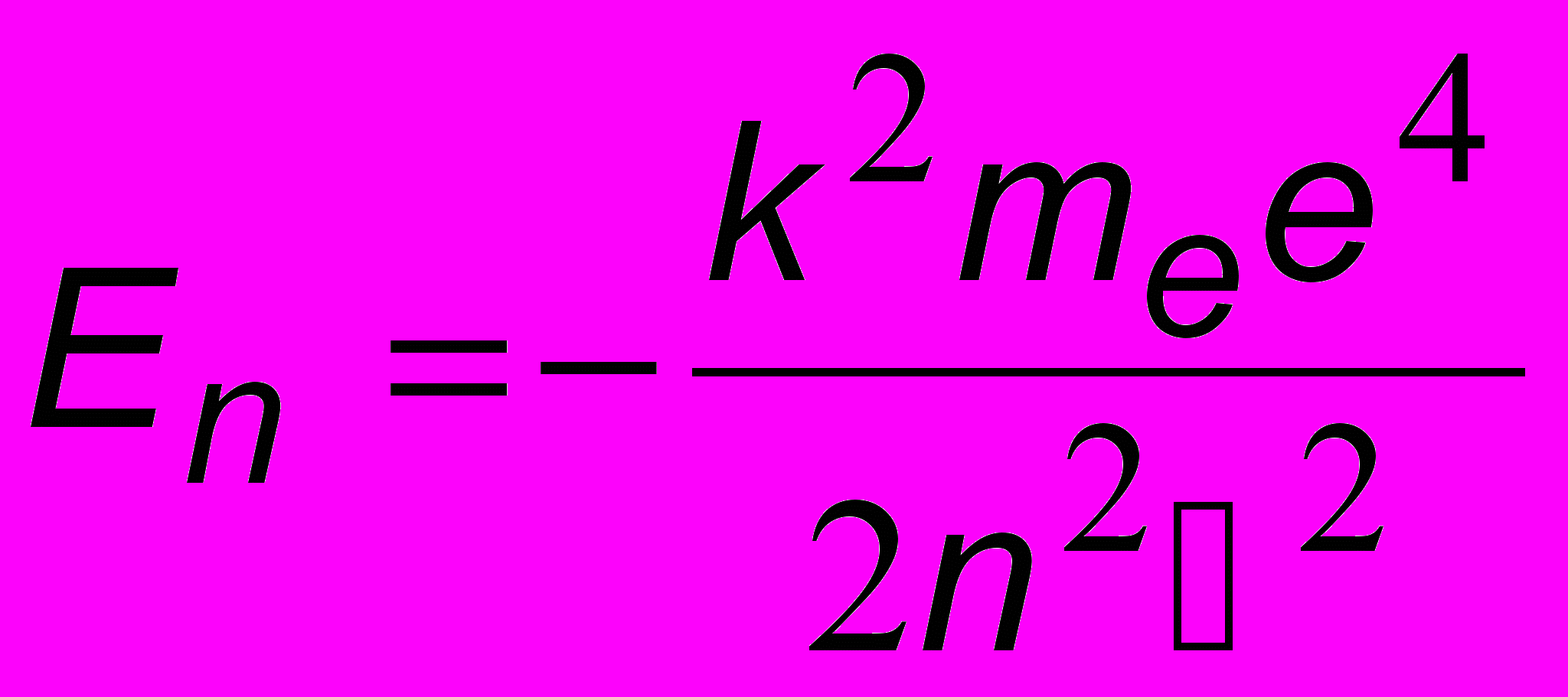. (16.8)

Самый низкий уровень энергии (основное состояние) соответствует случаю n = 1. При этом E₁ = 2,18  10^-18 Дж = 13,6 эВ. Выше размещаются уровни E₂, E₃ и т.д., как показано на рис.16.8. При n   уровни подходят к нулевой черте "снизу". Знак "минус" в (16.8) означает то, что электрон находится внутри атома: он пребывает в связанном состоянии, и его энергия отрицательна. Эти значения энергии квантуются, то есть могут принимать только дискретные значения. Если находящемуся в основном состоянии (n = 1) электрону сообщить извне энергию более 13,6 эВ, то электрон окажется вне атома. В этом случае его энергия E > 0 и может принимать любые неквантованные значения и меняться непрерывно. Атом становится ионом с зарядом q = +e. Поэтому энергию E₁ = 13,6 эВ называют энергией ионизации.

Определим теперь длины волн в спектре излучения. Рассмотрим два любые уровня E_a и E_b и пусть E_b > E_a. Тогда частота излучения равна (см. рис. 16.7):

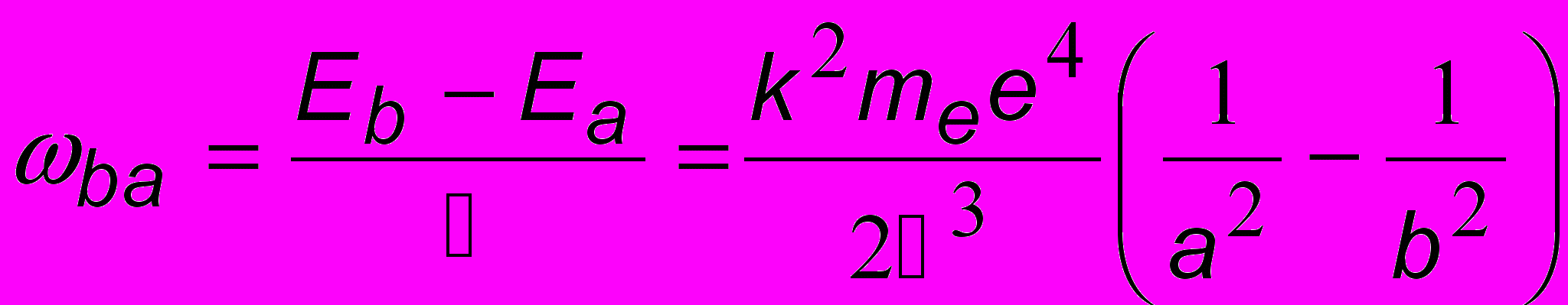. Переходя от частоты к длине волны по формуле  = 2с/, получим формулу Бальмера

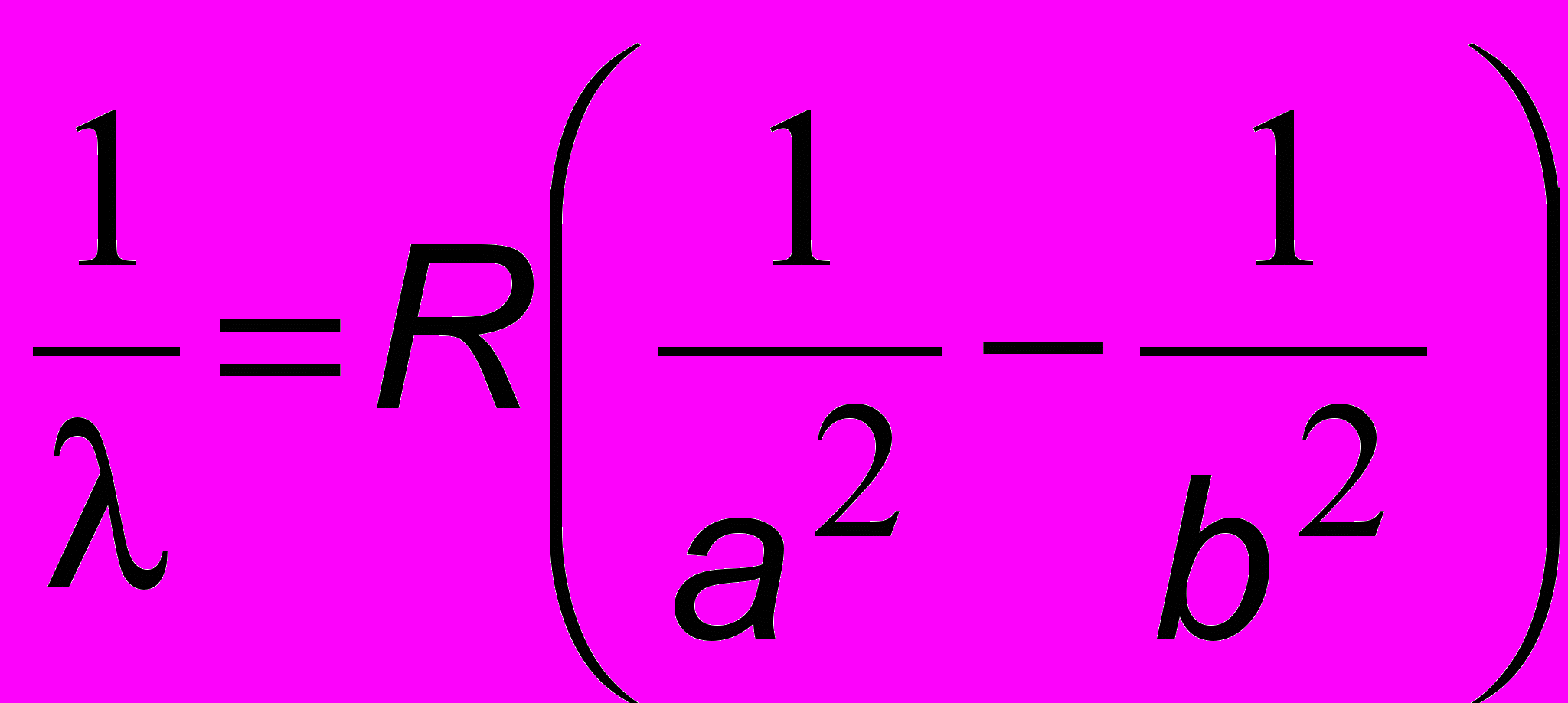, (16.9)

где 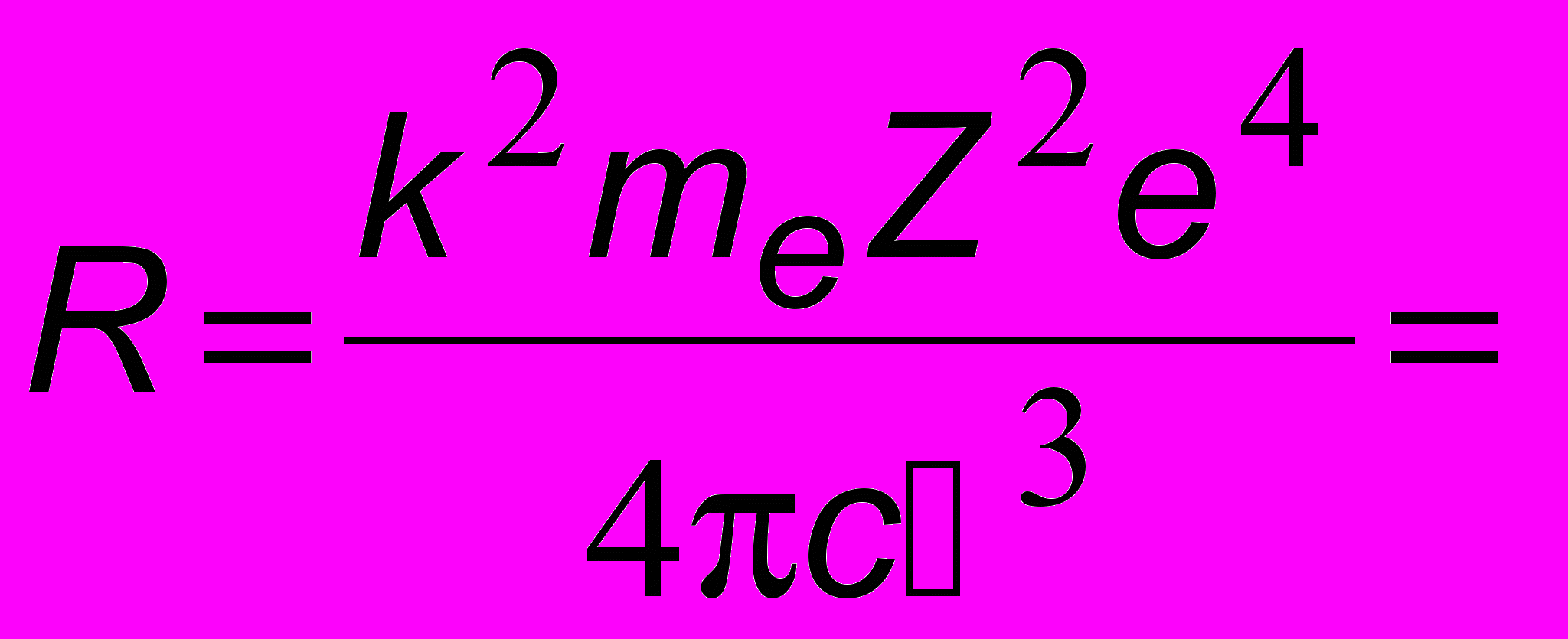1,097  10⁷ м^-1 - постоянная Ридберга.

Интересно отметить, что формула (16.9) была получена экспериментально (т.е. "подгонкой") задолго до теории Бора, то есть опытным путем на основе спектроскопических данных. Из этой формулы получаются все линии спектра водорода. Если рассмотреть переходы на какой-нибудь фиксированный уровень n = а со всех остальных, расположенных выше, то получится так называемая серия. Так, при a = 1 (основное состояние, самый нижний уровень) возможны переходы с более высоких уровней b = 2, 3, 4 ..., образующих серию Лаймана (см. рис.16.8), расположенную в ультрафиолетовой области. При а = 2 и b = 3, 4, 5, ... получается серия Бальмера. Четыре первых линии - красная, зелено-голубая, синяя и фиолетовая - приходятся на видимую часть спектра и хорошо наблюдаются при помощи спектрометров. Остальные серии лежат в инфракрасной области. К сожалению, при помощи теории Бора удалось объяснить лишь положение линий в спектре (притом только водорода!). Не удалось построить теорию гелия - следующего за водородом элемента в таблице Менделеева. Не удалось объяснить и различия в интенсивности линий (так, например, красная линия очень яркая, а синей почти не видно). По сути дела боровская теория квантовой была лишь наполовину. Но это были первые шаги новой революционной науки, не свободные от недостатков. Дальнейшее развитие физики привело к созданию более совершенной теории.