Базы данных

Вид материала

Документы

Содержание Вопрос №10 Основы теории нормализации Зависимости между атрибутами Функциональная взаимозависимость Частичной зависимостью (частичной функциональной зависимостью) В многозначно зависит от атрибута А Взаимно независимые атрибуты Выявление зависимостей между атрибутами ФИО, Предм и Группа Должн=преп и Оклад Пятая нормальная форма

Подобный материал:

• 1 научиться создавать таблицу базы данных в режиме таблицы, 54.71kb.
• Ms access Создание базы данных, 34.31kb.
• Лекция 2 10. Полнотекстовые базы данных, 133.46kb.
• Практическая работа № «Создание базы данных», 21.96kb.
• Информационные системы, использующие базы данных: оборудование, программное обеспечение,, 102.98kb.
• Конспект лекций по курсу "базы данных" (Ч., 861.92kb.
• Реферат на тему: Access. Базы данных, 274.77kb.
• Лекция №3 нормализация данных, 107.45kb.
• Курсовая работа по дисциплине «Базы данных» на тему: «Разработка базы данных для учета, 154.05kb.
• Создание базы данных “Классный, 73.09kb.

Вопрос №10 Основы теории нормализации

Проектирование БД является одним из этапов жизненного цикла информационной системы. Основной задачей, решаемой в процессе проектирования БД, является задача нормализации ее отношений. Не все отношения одинаково желательны. Таблица, отвечающая минимальному определению отношения, может иметь неэффективную или неподходящую структуру. Для некоторых отношений изменение данных может привести к нежелательным последствиям, называемым аномалиями модификации. Аномалии могут быть устранены путем разбиения (декомпозиции) исходного отношения на два или более новых отношения. Любое отношение, содержащее две или более темы, следует разбить на два или более отношения, каждое из которых будет содержать одну тему. Этот процесс составляет суть нормализации.

Общее назначение процесса нормализации заключается в следующем:

• исключение некоторых типов избыточности;
  
• устранение некоторых аномалий обновления;
  
• разработка проекта базы данных, который является достаточно «качественным» представлением реального мира, интуитивно понятен и может служить хорошей основой для последующего расширения;
  
• упрощение процедуры применения необходимых ограничений целостности.
  

1. Зависимости между атрибутами

ПРЕПОДАВАТЕЛЬ ФИО Должн Оклад Стаж ДСтаж Каф Предм Группа ВидЗан Иванов И.М. преп 500 5 100 25 СУБД 256 Практ Иванов И.М. преп 500 5 100 25 ПЛ/1 123 Практ Петров М.И. ст. преп 800 7 100 25 СУБД 256 Лекция Петров М.И. ст. преп 800 7 100 25 Паскаль 256 Практ Сидоров Н.Г. преп 500 10 150 25 ПЛ/1 123 Лекция Сидоров Н.Г. преп 500 10 150 25 Паскаль 256 Лекция Егоров В.В. преп 500 5 100 24 ПЭВМ 244 Лекция

Рис. 1. Исходное отношение ПРЕПОДАВАТЕЛЬ

Рассмотрим основные виды зависимостей между атрибутами отношений: функциональные, транзитивные и многозначные.

Понятие функциональной зависимости является базовым, так как на его основе формулируются определения всех остальных видов зависимостей.

Атрибут В функционально зависит от атрибута А, если каждому значению А соответствует в точности одно значение В. Математически функциональная зависимость В от А обозначается записью А->В. Это означает, что во всех кортежах с одинаковым значением атрибута А атрибут В будет иметь также одно и то же значение. Отметим, что А и В могут быть составными - состоять из двух и более атрибутов.

В отношении на рис. 1 можно выделить функциональные зависимости между атрибутами ФИО->Каф, ФИО->Должн, Должн->Оклад и другие. Наличие функциональной зависимости в отношении определяется природой вещей, информация о которых представлена кортежами отношения. В отношении на рис. 1 ключ является составным и состоит из атрибутов ФИО, Предмет, Группа.

Функциональная взаимозависимость. Если существует функциональная зависимость вида А->В и В->А, то между А и В имеется взаимно однозначное соответствие, или функциональная взаимозависимость. Наличие функциональной взаимозависимости между атрибутами А и В обозначим как А<->В или В<->А.

Пример. Пусть имеется некоторое отношение, включающее два атрибута, функционально зависящие друг от друга. Это серия и номер паспорта (N) и фамилия, имя и отчество владельца (ФИО). Наличие функциональной зависимости поля ФИО от N означает не только тот факт, что значение поля N однозначно определяет значение поля ФИО, но и то, что одному и тому же значению поля N соответствует только единственное значение поля ФИО. Понятно, что в данном случае действует и обратная ФЗ: каждому значению поля ФИО соответствует только одно значение поля N. В данном примере предполагается, что ситуация наличия полного совпадения фамилий, имен и отчеств двух людей исключена.

Если отношение находится в 1НФ, то все неключевые атрибуты функционально зависят от ключа с различной степенью зависимости.

Частичной зависимостью (частичной функциональной зависимостью) называется зависимость неключевого атрибута от части составного ключа. В рассматриваемом отношении атрибут Должн находится в функциональной зависимости от атрибута ФИО, являющегося частью ключа. Тем самым атрибут Должн находится в частичной зависимости от ключа отношения.

Альтернативным вариантом является полная функциональная зависимость неключевого атрибута от всего составного ключа. В нашем примере атрибут ВидЗан находится в полной функциональной зависимости от составного ключа.

Атрибут С зависит от атрибута А транзитивно (существует транзитивная зависимость), если для атрибутов А, В, С выполняются условия А->В и В->С, но обратная зависимость отсутствует. В отношении на рис. 1 транзитивной зависимостью связаны атрибуты:

ФИО->Должн->Оклад

Между атрибутами может иметь место многозначная зависимость.

В отношении R атрибут В многозначно зависит от атрибута А, если каждому значению А соответствует множество значений В, не связанных с другими атрибутами из R.

Многозначные зависимости могут быть "один ко многим" (1:М), "многие к одному" (М: 1) или "многие ко многим" (М:М), обозначаемые соответственно: А->>В, А<<-В и А<<->>В.

Например, пусть преподаватель ведет несколько предметов, а каждый предмет может вестись несколькими преподавателями, тогда имеет место зависимость ФИО<<->>Предмет. Так, из таблицы, приведенной на рис. 1, видно, что преподаватель Иванов И.М. ведет занятия по двум предметам, а дисциплина СУБД - читается двумя преподавателями: Ивановым И.М. и Петровым М.И.

Замечание. В общем случае между двумя атрибутами одного отношения могут существовать зависимости: 1:1, 1:М, М:1 и М:М. Поскольку зависимость между атрибутами является причиной аномалий, стараются расчленить отношения с зависимостями атрибутов на несколько отношений. В результате образуется совокупность связанных отношений (таблиц) со связями вида 1:1,1:М, М:1 и М:М. Связи между таблицами отражают зависимости между атрибутами различных отношений.

Взаимно независимые атрибуты. Два или более атрибута называются взаимно независимыми, если ни один из этих атрибутов не является функционально зависимым от других атрибутов.

В случае двух атрибутов отсутствие зависимости атрибута А от атрибута В можно обозначить так:

А-.->В. Случай, когда А-.->В и B-.->A, можно обозначить А-.=В.

2. Выявление зависимостей между атрибутами

Выявление зависимостей между атрибутами необходимо для выполнения проектирования БД методом нормальных форм, рассматриваемого далее.

Основной способ определения наличия функциональных зависимостей - внимательный анализ семантики атрибутов. Для каждого отношения существует, но не всегда, определенное множество функциональных зависимостей между атрибутами. Причем если в некотором отношении существует одна или несколько функциональных зависимостей, можно вывести другие функциональные зависимости, существующие в этом отношении.

Для построения полного множество функциональных зависимостей из исходного множества необходимо знать ряд правил (или аксиом) вывода одних функциональных зависимостей из других.

Существует 8 основных аксиом вывода:

• рефлексивности
  
• пополнения
  
• транзитивности
  
• расширения
  
• продолжения
  
• псевдотранзитивности
  
• объединения
  
• декомпозиции.
  

Перечисленные аксиомы обеспечивают получение всех ФЗ, т. е. их совокупность применительно к процедуре вывода можно считать "функционально полной".

Выявим зависимости между атрибутами отношения ПРЕПОДАВАТЕЛЬ, приведенного на рис. 1. При этом учтем следующее условие, которое выполняется в данном отношении: один преподаватель в одной группе может проводить один вид занятий (лекции или практические занятия).

В результате анализа отношения получаем зависимости между атрибутами, показанные на рис. 2.


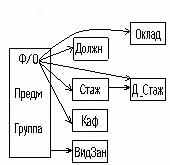
Рис. 2. Зависимости между атрибутами

ФИО->Oклад
     ФИО->Должн
     ФИО->Стаж
     ФИО->Д_Стаж
     ФИО->Каф
     Стаж->Д_Стаж
     Должн->0клад
     Оклад->Должк
     ФИО.Предм.Группа->ВидЗан



К выделению этих ФЗ для рассматриваемого примера приводят следующие соображения.

Фамилия, имя и отчество у преподавателей факультета уникальны. Каждому преподавателю однозначно соответствует его стаж, т. е. имеет место функциональная зависимость ФИО->Стаж. Обратное утверждение неверно, так как одинаковый стаж может быть у разных преподавателей.

Каждый преподаватель имеет определенную добавку за стаж, т. е. имеет место функциональная зависимость ФИО->Д_Стаж, но обратная функциональная зависимость отсутствует, так как одну и ту же надбавку могут иметь несколько преподавателей.

Каждый преподаватель имеет определенную должность (преп., ст.преп., доцент, профессор), но одну и ту же должность могут иметь несколько преподавателей, т. е. имеет место функциональная зависимость ФИО->Должн, а обратная функциональная зависимость отсутствует.

Каждый преподаватель является сотрудником одной и только одной кафедры. Поэтому функциональная зависимость ФИО->Каф имеет место. С другой стороны, на каждой кафедре много преподавателей, поэтому обратной функциональной зависимости нет.

Каждому преподавателю соответствует конкретный оклад, который одинаков для всех педагогов с одинаковыми должностями, что учитывается зависимостями ФИО->Oклад и Должн->Oклад. Нет одинаковых окладов для разных должностей, поэтому имеет место функциональная зависимость Оклад->Должн.

Один и тот же преподаватель в одной группе по разным предметам может проводить разные виды занятий. Определение вида занятий, которые проводит преподаватель, невозможно без указания предмета и группы, поэтому имеет место функциональная зависимость ФИО, Предм, Группа->ВидЗан. Действительно, Петров М.И. в 256 группе читает лекции и проводит пратические занятия. Но лекции он читает по СУБД, а практику проводит по Паскалю.

Нами не были выделены зависимости между атрибутами ФИО, Предм и Группа, поскольку они образуют составной ключ и не учитываются в процессе нормализации исходного отношения.

После того, как выделены все функциональные зависимости, следует проверить их согласованность с данными исходного отношения ПРЕПОДАВАТЕЛЬ (рис. 5.4).

Например, Должн=преп и Оклад=500 всегда соответствуют друг другу во всех кортежах, т. е. подтверждается функциональная зависимость Должн<->Oклад. Так же следует верифицировать и остальные функциональные зависимости, не забывая об ограниченности имеющихся в отношении данных.

3. Нормальные формы
   

Процесс проектирования БД с использованием метода нормальных форм является итерационным и заключается в последовательном переводе отношений из первой нормальной формы в нормальные формы более высокого порядка по определенным правилам. Каждая следующая нормальная форма ограничивает определенный тип функциональных зависимостей, устраняет соответствующие аномалии при выполнении операций над отношениями БД и сохраняет свойства предшествующих нормальных форм.

Выделяют следующую последовательность нормальных форм:

• первая нормальная форма (1НФ);
  
• вторая нормальная форма (2НФ);
  
• третья нормальная форма (3НФ);
  
• усиленная третья нормальная форма, или нормальная форма Бойса-Кодда (БКНФ);
  
• четвертая нормальная форма (4НФ);
  
• пятая нормальная форма (5НФ).
  

Рис. 3. Отношение СЕКЦИИ

НомерСтудента	Секция	Плата
100	Лыжи	200
100	Гольф	65
150	Плавание	50
175	Сквош	50
175	Плавание	50
200	Плавание	50
200	Гольф	65

1. О любой таблице данных, удовлетворяющей определению отношения, говорят, что она находится в первой нормальной форме. Отношение на рис. 3 находится в первой нормальной форме.
   
2. Отношение находится во второй нормальной форме, если все его неключевые атрибуты зависят от всего ключа.
   

Рассмотрим отношение СЕКЦИИ на рис. 3. Это отношение имеет аномалии модификации. Если мы удалим строку с данными о студенте с номером 175, мы потеряем тот факт, что абонент в секции сквоша стоит $50. Кроме того мы не сможем ввести информацию о секции, пока в эту секцию не запишется хотя бы один студент. Проблема с этим отношением состоит в том, что оно содержит зависимость, затрагивающую только часть ключа. Ключом является комбинация (НомерСтудента, Секция), но отношение содержит зависимость Секция>Плата. Детерминант этой зависимости (Секция) представляет собой лишь часть ключа (НомерСтудента, Секция). В этом случае мы можем сказать, что атрибут Плата частично зависит от ключа таблицы. Аномалий модификации не было бы, если бы Плата зависела от всего ключа. Чтобы устранить эти аномалии, мы должны разделить отношение на два отношения.


Рис. 4. Разбиение отношения СЕКЦИЯ на два отношения

НомерСтудента	Секция		Секция	Плата
100	Лыжи		Лыжи	200
100	Гольф		Гольф	65
150	Плавание		Плавание	50
175	Сквош		Сквош	50
175	Плавание
200	Плавание
200	Гольф

3. Отношение находится в третьей нормальной форме, если оно находится во второй нормальной форме и не имеет транзитивных зависимостей.
   

Рассмотрим отношение ПРОЖИВАНИЕ на рис. 5. Ключом здесь является НомерСтудента, и имеются функциональные зависимости НомерСтудента>Общежитие и Общежитие>Плата. Эти зависимости возникают потому, что каждый студент живет только в одном общежитии, и каждое общежитие взимает со всех проживающих в нем студентов одинаковую плату.

Поскольку НомерСтудента определяет атрибут Общежитие, а Общежитие определяет атрибут Плата, то косвенным образом НомерСтудента>Плата. Такая структура функциональных зависимостей называется транзитивной зависимостью, поскольку атрибут НомерСтудента определяет атрибут Плата через атрибут Общежитие.

Атрибут НомерСтудента является одиночным ключом, следовательно, отношение находится во 2НФ. Но оно имеет аномалию удаления: если мы удалим вторую строку, то потеряем не только тот факт, что студент №150 живет в Ингерсол, но и тот факт, что проживание в этом общежитии стоит $3100. И аномалию вставки: мы не можем записать тот факт, что плата за проживание в Кэрриг составляет $3500, пока туда не поселится хотя бы один студент.

Чтобы удалить аномалии, необходимо устранить транзитивную зависимость, разделив отношение ПРОЖИВАНИЕ на два отношения.


Рис. 5. Устранение транзитивной зависимости в отношении ПРОЖИВАНИЕ

НомерСтудента	Общежитие	Плата
100	Рэндольф	3200
150	Ингерсол	3100
200	Рэндольф	3200
250	Питкин	3100
300	Рэндольф	3200

НомерСтудента	Общежитие		Общежитие	Плата
100	Рэндольф		Рэндольф	3200
150	Ингерсол		Ингерсол	3100
200	Рэндольф		Питкин	3100
250	Питкин
300	Рэндольф

4. Отношение находится в НФБК, если каждый детерминант является ключом-кандидатом.
   

Рассмотрим отношение КОНСУЛЬТАНТ на рис. 6. Пусть требования к этому отношению таковы:

- студент может иметь одну или несколько специальностей,

- консультантами по одному и тому же предмету могут быть несколько преподавателей,

- каждый преподаватель может быть консультантом только по одной специальности.

Поскольку студенты могут специализироваться в нескольких областях, атрибут НомерСтудента не определяет атрибут Специальность. Более того, так как студент может иметь несколько консультантов, НомерСтудента не определяет и атрибут Преподаватель. Таким образом, НомерСтудента сам по себе не может быть ключом.

Комбинация (НомерСтудента, Специальность) определяет атрибут Преподаватель, а комбинация (НомерСтудента, Преподаватель) определяет атрибут Специальность. Следовательно, любая из этих комбинаций может быть ключом. Два или более атрибута или группы атрибутов, которые могут быть ключом, называются ключами-кандидатами. Тот из ключей-кандидатов, который выбирается в качестве ключа, называется первичным ключом.

Кроме ключей-кандидатов, есть еще одна функциональная зависимость: атрибут Преподаватель определяет атрибут Специальность (любой из преподавателей является консультантом только по одному предмету; следовательно, зная имя преподавателя, мы можем определить специальность). Таким образом, Преподаватель является детерминантом.

Несмотря на то, что отношение находится в 3НФ, оно имеет аномалии. Если мы удалим строку с информацией о студенте с номером 300, мы потеряем тот факт, что Перлс является консультантом по психологии. А записать в базу тот факт, что Кейнс является консультантом по экономике, мы не сможем, пока не появится хотя бы один студент, специализирующийся на экономике. Отношение КОНСУЛЬТАНТ можно разбить на два отношения, не имеющие аномалий.


Рис. 6. Получение нормальной формы Бойса-Кодда для отношения КОНСУЛЬТАНТ

НомерСтудента	Специальность	Преподаватель
100	Математика	Коши
150	Психология	Юнг
200	Математика	Риман
250	Математика	Коши
300	Психология	Перлс
300	Математика	Риман

НомерСтудента	Преподаватель		Преподаватель	Специальность
100	Коши		Коши	Математика
150	Юнг		Юнг	Психология
200	Риман		Риман	Математика
250	Коши		Перлс	Психология
300	Перлс
300	Риман

5. Отношение находится в четвертой нормальной форме, если оно находится в НФБК и не имеет многозначных зависимостей.
   

Рассмотрим отношение СТУДЕНТ на рис. 7. Предположим, что студенты могут иметь несколько специальностей и заниматься в нескольких различных секциях. В таком случае единственным ключом является комбинация (НомерСтудента, Специальность, Секция).

Одному и тому же значению атрибута НомерСтудента может соответствовать много значений атрибута Специальность. Помимо того, одному и тому же значению атрибута НомерСтудента может соответствовать много значений атрибута Секция.

Такая зависимость атрибутов называется многозначной зависимостью. Многозначные зависимости приводят к аномалиям модификации. Для начала надо обратить внимание на избыточность данных. Во вторых, допустим, что студентка с номером 100 решила записаться в секцию лыж, и поэтому мы добавляем в таблицу строку [100,Музыка,Лыжи]. В данный момент из отношения можно сделать вывод, что студентка 100 занимается лыжами только как музыкант, но не как бухгалтер. Чтобы данные имели согласованный характер, мы должны добавить столько строк, сколько имеется специальностей, и в каждой из них указать секцию лыж. Таким образом, мы должны добавить строку [100,Бухгалтерский учет,Лыжи], как показано на рис. 8. Это аномалия обновления: требуется слишком много модификаций, чтобы внести одно простое изменение.

Чтобы устранить эти аномалии, мы должны избавиться от многозначной зависимости. Мы сделаем это, создав два отношения, в каждом из которых будут храниться данные только по одному многозначному атрибуту, как показано на рис. 9.

Рис. 7. Отношение с многозначными зависимостями

НомерСтудента	Специальность	Секция
100	Музыка	Плавание
100	Бухгалтерский учет	Плавание
100	Музыка	Теннис
100	Бухгалтерский учет	Теннис
150	Математика	Бег

Рис. 8. Отношение СТУДЕНТ с аномалиями вставки

НомерСтудента	Специальность	Секция
100	Музыка	Лыжи
100	Бухгалтерский учет	Лыжи
100	Музыка	Плавание
100	Бухгалтерский учет	Плавание
100	Музыка	Теннис
100	Бухгалтерский учет	Теннис
150	Математика	Бег

Рис. 9. Устранение многозначной зависимости

НомерСтудента	Специальность		НомерСтудента	Секция
100	Музыка		100	Лыжи
100	Бухгалтерский учет		100	Плавание
150	Математика		100	Теннис
			150	Бег

Пятая нормальная форма. Существуют переменные отношения, для которых нельзя выполнить декомпозицию без потерь на две проекции, но которые можно подвергнуть декомпозиции без потерь на три или большее количество проекций. Подобные переменные отношения обозначим не очень удачным, но достаточно удобным термином «n-декомпонуемая переменная отношения, или отношение». Такое название применяется к переменной отношения, если можно выполнить ее декомпозицию без потерь на n проекций, но не на m проекций, где 1
В качестве примера рассмотрим переменную отношения SPJ из БД поставщиков, деталей и проектов, представленную на рис. 10. Обратите внимание на то, что эта переменная отношения состоит только из ключевых атрибутов, не содержит нетривиальных функциональных и многозначных зависимостей и поэтому находится в 4НФ. Заметим также, что на этом рисунке показаны следующие компоненты.

1. Три бинарные проекции (SP, PJ и JS), соответствующие значению отношения SPJ, показанному в верхней части рисунка.
   
2. Результат соединения проекций SP и PJ по атрибуту P#.
   
3. Результат соединения этого результата с проекцией JS по комбинации атрибутов J# и S#.
   

В результате первого соединения получается копия исходной переменной отношения SPJ с одним дополнительным (фиктивным) кортежем, а в результате второго соединения этот дополнительный кортеж исключается и восстанавливается первоначальное отношение SPJ. Иначе говоря, исходная переменная отношения SPJ является 3-декомпонуемой.

Переменная отношения R находится в пятой нормальной форме (5НФ), которую иногда иначе называют проекционно-соединительной нормальной формой (ПСНФ), тогда и только тогда, когда каждая нетривиальная зависимость соединения в переменной отношения R определяется потенциальным ключом (ключами) R, если соблюдаются приведенные ниже условия.

1. Зависимость соединения *{A,B,…,Z} в переменной отношения R является тривиальной тогда и только тогда, когда по крайней мере одно из подмножеств A,B,…,Z множества атрибутов является множеством всех атрибутов R.
   
2. Зависимость соединения *{A,B,…,Z} в переменной отношения R определяется потенциальным ключом (ключами) R тогда и только тогда, когда каждое из подмножеств A,B,…,Z множества атрибутов является суперключом для R.
   

Переменная отношения SPJ не находится в 5НФ. Она удовлетворяет некоторой зависимости соединения, а именно – ограничению 3-Д, которое не определяется ее единственным потенциальным ключом (этот ключ является комбинацией всех ее атрибутов). Иначе говоря, переменная отношения SPJ не находится в 5НФ, поскольку она может быть 3-декомпонована и возможность такой декомпозиции не обусловлена тем фактом, что комбинация атрибутов {S#,P#,J#} является ее потенциальным ключом. Напротив, после 3-декомпозиции три проекции SP, PJ и JS находятся в 5НФ, поскольку в них вообще нет нетривиальных зависимостей соединения.

Как следует из определения, 5НФ является окончательной нормальной формой по отношению к операциям проекции и соединения. Таким образом, если переменная отношения находится в 5НФ, то гарантируется, что она не содержит аномалий, которые могут быть исключены посредством ее разбиения на проекции.

Идеи нормализации чрезвычайно полезны для проектирования БД, но они отнюдь не являются универсальным средством:

• Нормализация действительно позволяет реализовать определенные ограничения целостности, но на практике, помимо зависимостей соединения, функциональных и многозначных зависимостей, существуют и другие типы ограничений.
  
• Декомпозиция может быть неуникальной, но существует очень мало объективных критериев, позволяющих выбрать один из альтернативных вариантов декомпозиции.
  
• Преследование одновременно двух целей (т.е. приведение к НФБК и сохранение зависимостей) в некоторых случаях приводит к конфликтной ситуации.
  
• Процедура нормализации позволяет избавиться от избыточности за счет разбиения на проекции, но не всякую избыточность можно устранить таким образом.