Блок 1: Рост стоимости вложений за счет присоединения процентов 4
| Вид материала | Анализ |
- Возмещение затрат по уплате процентов по кредитам и лизинговых платежей по договорам, 80.46kb.
- Правила определения таможенной стоимости товаров, действующие в рамках вто, 38.09kb.
- Биржевые спекулянты на российском фондовом рынке: в чем различия между новичками, 274.71kb.
- Капитального строительства, 96.76kb.
- В. А. Баумгертнер «Конкурентоспособность российских производителей минеральных удобрений,, 69.53kb.
- Ежедневный мониторинг сми 29 декабря 2011, 202.46kb.
- О реализации приоритетного национального проекта "Развитие апк в северных субъектах, 178.05kb.
- Темы рефератов по дисциплине: «Инвестиции» Принципы и методы оценки стоимости недвижимости, 147.42kb.
- Инструкция Возврат основного долга по кредиту осуществляется на счет №47422810300000000117, 61.51kb.
- Правила определения стоимости активов и величины обязательств, подлежащих исполнению, 58.04kb.
3.1.2 Дисконтирование по простым процентам
Прорабатывая материал предыдущих глав вы уже убедились, что важнейшей характеристикой любой финансовой операции является современная стоимость (величина) потоков платежей PV, определяемая методом дисконтирования.
В зависимости от вида процентной ставки, при анализе краткосрочных финансовых операций применяют два метода дисконтирования – математическое и коммерческое (т.н. банковский учет).
В первом случае в качестве нормы приведения используют ставку r, применяемую при наращении (3.1). Во втором случае в роли нормы приведения выступает т.н. учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.
Математическое дисконтирование
Математическое дисконтирование представляет собой задачу обратную наращению и сводится к определению величины PV по известным значениям величин FV, r, n. С учетом принятых обозначений формула дисконтирования по ставке r будет иметь следующий вид:
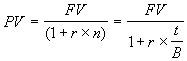. (3.4) Разность FV - PV называют дисконтом или скидкой, а используемую норму приведения r – декурсивной ставкой процентов.
Банковский или коммерческий учет
Этот метод дисконтирования применяется, в основном, при банковском учете векселей, смысл которого будет рассмотрен ниже. Суть данного метода заключается в том, что проценты начисляются на сумму, подлежащую уплате в конце срока операции. При этом применяется учетная ставка d. Формула дисконтирования по учетной ставке имеет следующий вид:
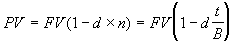. (3.5) При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 360/365. Используемую при этом норму приведения d называют антисипативной ставкой процентов.
Нетрудно заметить, что применение двух рассмотренных методов дисконтирования приводит к разным результатам, даже при r = d. Учетная ставка d дает более быстрый рост задолженности, чем обычная ставка r.
Учетная ставка d иногда применяется и для наращения по простым процентам. Необходимость в таком наращении возникает при определении будущей суммы контракта, например – общей суммы векселя. Формула определения будущей величины в этом случае имеет следующий вид:
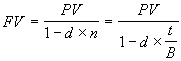. (3.6) 3.1.3 Определение процентной ставки и срока проведения операции
Величина процентной ставки r или учетной ставки d может быть определена из соотношений (3.1) и (3.5). Решив соответствующие уравнения относительно r или d получим:
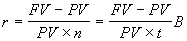. (3.7) 
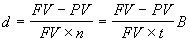. (3.8) Соответственно срок операции в днях определяется как:
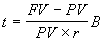. (3.9) 
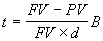. (3.10) 3.1.4 Эквивалентность процентных ставок r и d
Принцип эквивалентности процентных ставок широко применяется в финансовом анализе. Его используют при сравнении условий сделок, замене одного вида ставок на другой, определении эффективности операций и т.д.
В общем случае две различные процентные ставки считаются эквивалентными, если их использование при одинаковых условиях сделки приводит к одному и тому же финансовому результату.
В настоящей работе мы ограничимся рассмотрением условий эквивалентности ставки наращения r и учетной ставки d, исчисляемых по методу простых процентов.
Вывод формул эквивалентности базируется на равенстве соответствующих множителей наращения:
1 + nr = (1 - nd)-1 . (3.11)
С учетом n = t / B, для операций с продолжительностью менее года соотношения эквивалентности примут следующий вид:
а) временная база ставок одинакова и равна В (360 или 365 дней)
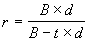. (3.12) 
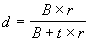. (3.13) б) временная база ставки r равна 365 дням, а d – 360 дням
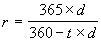. (3.14) 
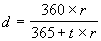. (3.15) Детальное изложение методов процентных вычислений и их применения в финансовом анализе можно найти в [7, 13].
В дальнейшем, рассматривая методы анализа краткосрочных ценных бумаг, мы будем использовать ставку наращения r и математическое дисконтирование. Техника применения учетной ставки d и соответствующего ей метода дисконтирования будет показана при рассмотрении анализа операций с векселями