Методические указания, лабораторные работы для студентов заочной формы обучения по специальности 140211

Вид материала

Методические указания

Содержание Контрольные вопросы Лабораторная работа №2 Программа работы Пояснения и указания к работе Схема Y/Y Y – трехпроводная. Поэтому в первичную обмотку трансформируются только токи прямой и обратной последовательности I Схема D/Y Экспериментальная часть М1. Им же после установления номинального напряжения измеряют линейные токи первичной обмотки IА,В,С (А). С помощью тестера М2 Обработка опытных данных Лабораторная работа №3

Подобный материал:

• Программа и методические указания по выполнению контрольной работы для студентов заочной, 326.82kb.
• Методические указания к дисциплине и задания к контрольной работе для студентов заочной, 126.92kb.
• Методические указания к дисциплине и темы рефератов для студентов заочной формы обучения, 102.72kb.
• Методические указания для написания курсовой работы по дисциплине «Деньги, кредит,, 162.15kb.
• Методические указания к выполнению контрольной работы для студентов заочной формы обучения, 193.46kb.
• Методические указания по выполнению контрольной работы по дисциплине «Оценка недвижимости», 678.32kb.
• Методические указания к выполнению контрольной работы для студентов заочной формы обучения, 150.65kb.
• Методические указания для выполнения контрольной работы по дисциплине "Налоговое планирование", 278.39kb.
• Методические указания по выполнению курсовой работы по дисциплине «Маркетинг» для специальности, 226.22kb.
• А. Н. Косыгина Учебно-методический комплекс по специальности 080502 «Экономика и управление, 905.25kb.

Контрольные вопросы

1. Объясните принцип работы трансформатора. Что происходит с током первичной обмотки трансформатора при изменении тока во вторичной обмотке?

2. Что такое коэффициент трансформации? Как определить коэффициент трансформации расчетным и опытным путем?

3. Какие потери определяют потребляемую в режиме холостого хода активную мощность и в каких конструктивных элементах трансформатора они выделяются?

4. В опыте холостого хода первичной обмоткой являлась обмотка ВН. Как изменятся потери и ток холостого хода, если в качестве первичной обмотки использовать обмотку НН (на обмотку НН подается номинальное ее напряжение)?

5. Какие параметры схемы замещения трансформатора определяются по результатам опыта холостого хода? Как рассчитываются значения этих параметров?

6. Какие потери определяют потребляемую в режиме короткого замыкания активную мощность и в каких конструктивных элементах трансформатора они выделяются?

7. Что называется номинальным напряжением короткого замыкания и в каких единицах оно выражается?

8. Из каких соображений выбирается большее или меньшее значение напряжения короткого замыкания при проектировании систем электроснабжения?

9. Какие параметры схемы замещения трансформатора определяются по результатам опыта короткого замыкания? Как рассчитываются значения этих параметров?

10. Какие данные необходимы для расчета изменения напряжения трансформатора в функции его нагрузки?


Лабораторная работа №2

Исследование несимметричной нагрузки

трансформатора


Краткие теоретические сведения

Нагрузка трехфазного трансформатора называется несимметричной, если не равны токи фаз, если сдвиг токов по фазе во времени не равен 120° или если наблюдается и то и другое. Это может происходить при включении мощных однофазных потребителей энергии, в аварийных режимах однофазных и двухфазных коротких замыканий в линии электропередачи или на зажимах трансформатора, а также, когда сопротивления нагрузки в фазах различны — по модулю, по фазе или по обеим этим величинам.

Анализ и расчет характеристик трансформаторов в несимметричных режимах проводится с помощью метода трехфазных симметричных составляющих. Сущность метода состоит в том, что любая несимметричная система трехфазных величин (токов, напряжений и т. д.) может быть представлена в виде суммы трех систем. Две из них симметричные трехфазные (прямая и обратная последовательности), а третья содержит переменные, равные по величине и совпадающие по фазе во всех фазах трехфазной обмотки трансформатора (нулевая последовательность).

Для симметричной составляющей прямой последовательности справедливо выражение

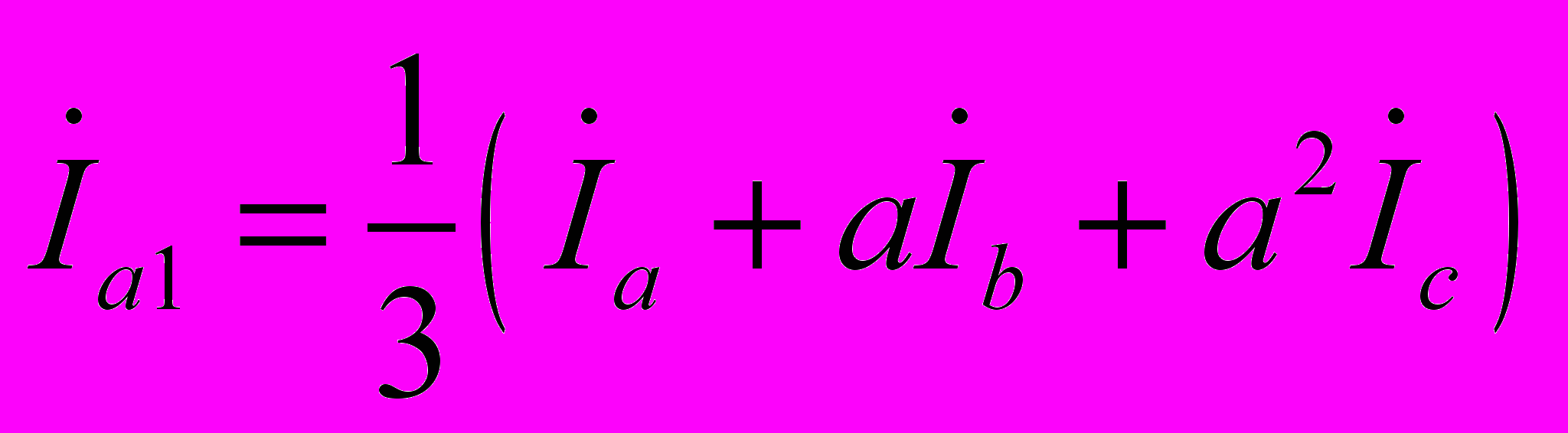, (2.1)

где 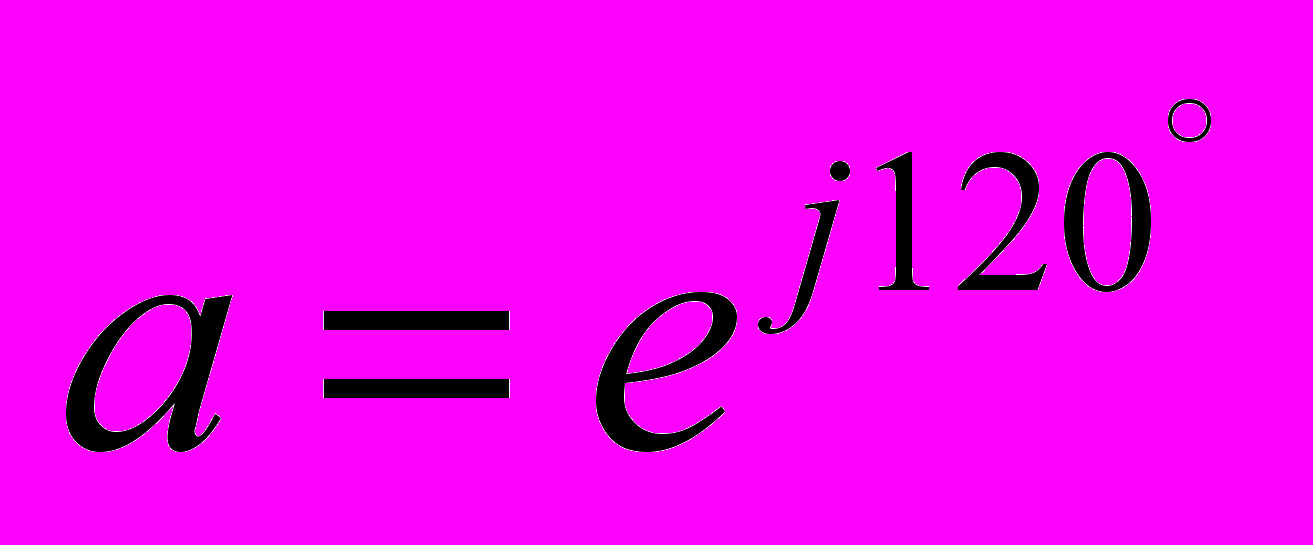, , 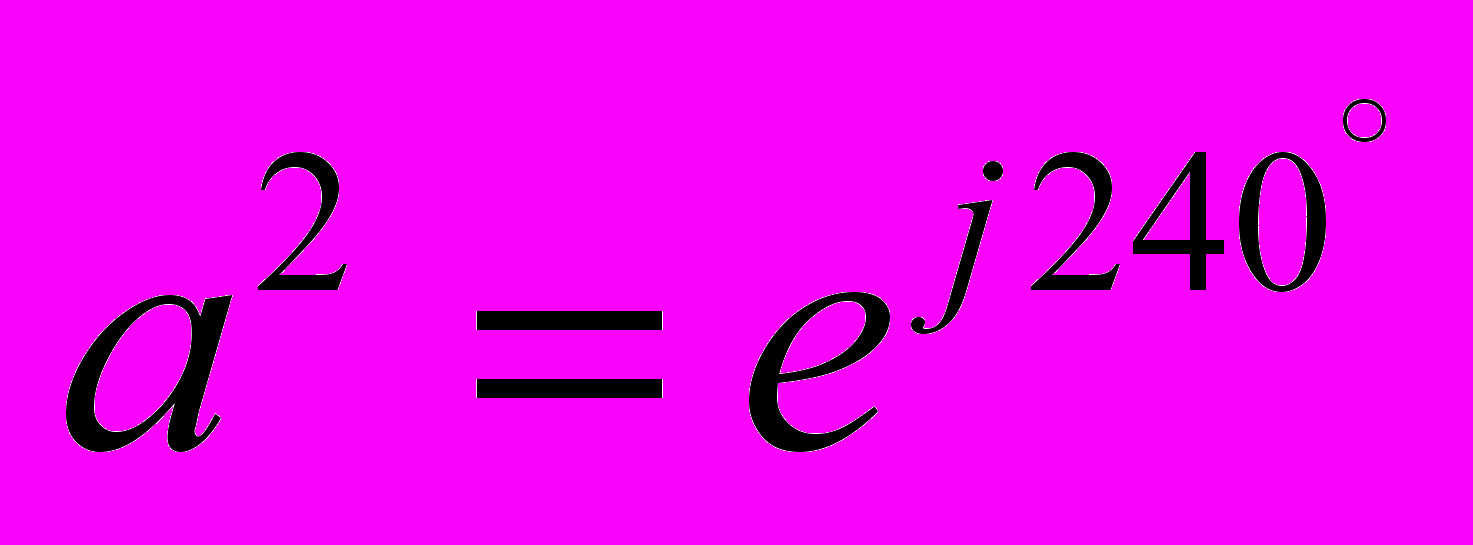I_a,b,c – токи фаз.

Для симметричной составляющей обратной последовательности справедливо выражение

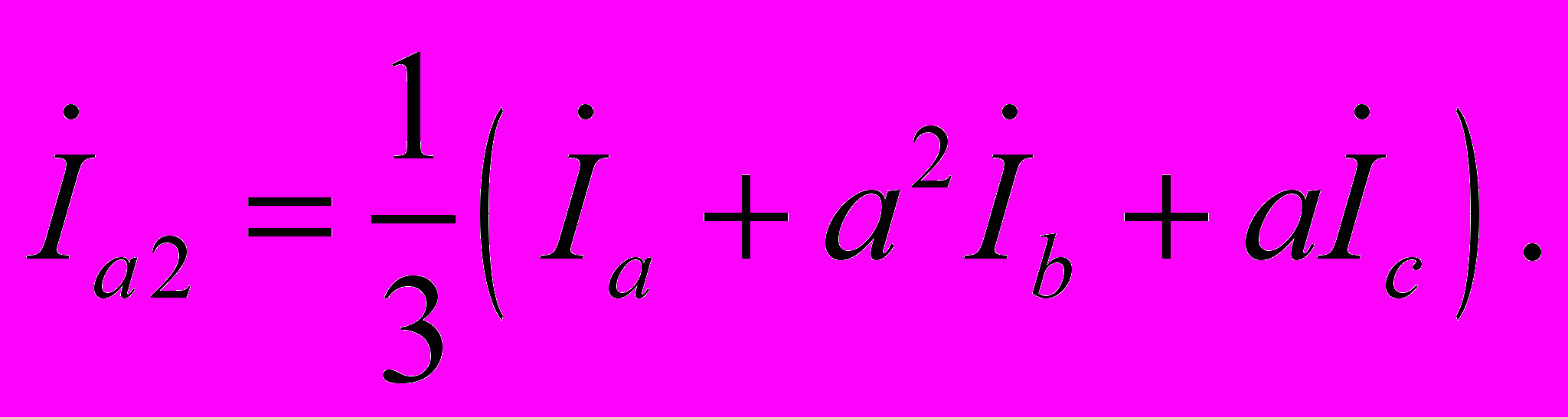(2.2)

Для симметричной составляющей нулевой последовательности справедливо выражение

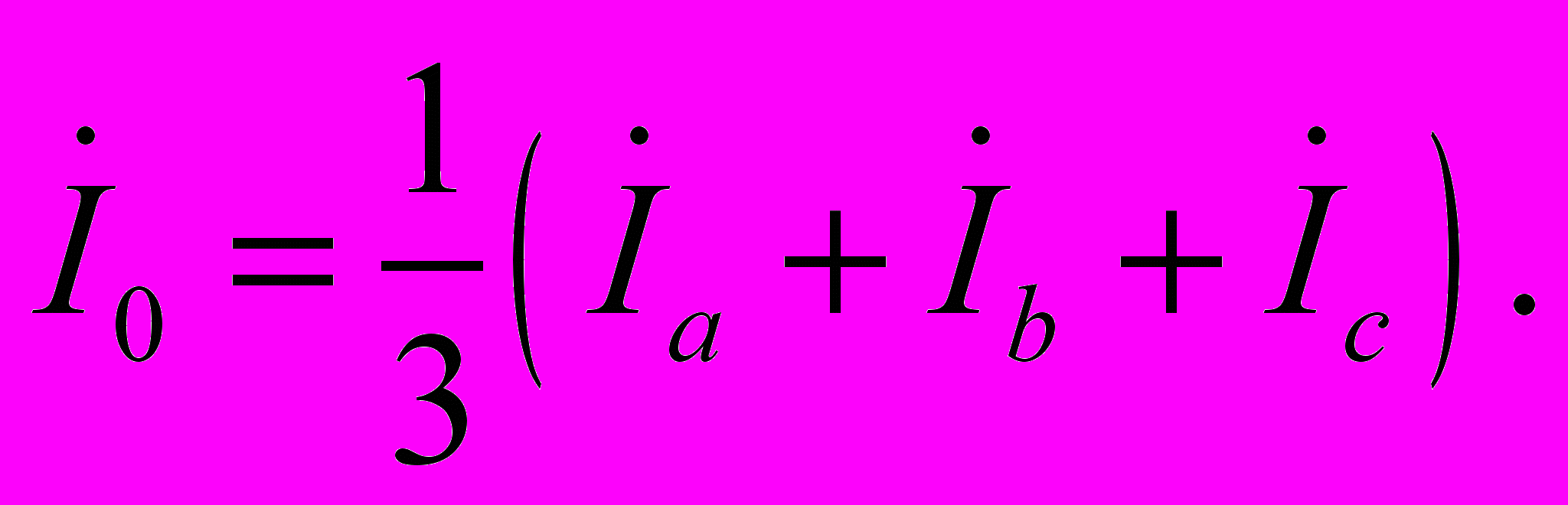(2.3)

При расчете характеристик методом симметричных составляющих решаются уравнения для каждой последовательности в отдельности. В трансформаторе магнитные потоки разных последовательностей не влияют друг на друга, если не учитываются насыщение и гистерезис стали сердечника. Ясно, что для определения симметричной составляющей любой переменной достаточно решить уравнения одной фазы трансформатора. После того как найдены симметричные составляющие, результирующие значения переменных определяются их геометрическим сложением .

Таким образом, метод симметричных составляющих основан на использовании принципа наложения, а он справедлив только для линейных систем. Поэтому принимается допущение, что сердечник трансформатора имеет линейные характеристики.

Все, что говорилось о симметричных режимах, в равной мере относится к прямой и обратной последовательностям по отдельности. То есть для них одинаковы и равны параметры схемы замещения, которые соответствуют параметрам схемы замещения в симметричном режиме работы (см. лабораторную работу №1).

Иначе обстоит дело с нулевой последовательностью. Параметры и все переменные нулевой последовательности зависят от схемы соединения обмоток трансформатора. Возможны два принципиально различных случая: когда токи нулевой последовательности протекают в одной обмотке трансформатора и когда они протекают в обеих обмотках. К первому случаю относится схема соединения У/У₀, ко второму — Д/У₀. В первом случае токи нулевой последовательности протекают только во вторичной обмотке, так как первичная обмотка является трехпроводной. Поэтому составляющая нулевой последовательности МДС вторичной обмотки F₂₀ не компенсируется МДС первичной обмотки. Это приводит к появлению больших некомпенсированных магнитных потоков нулевой последовательности 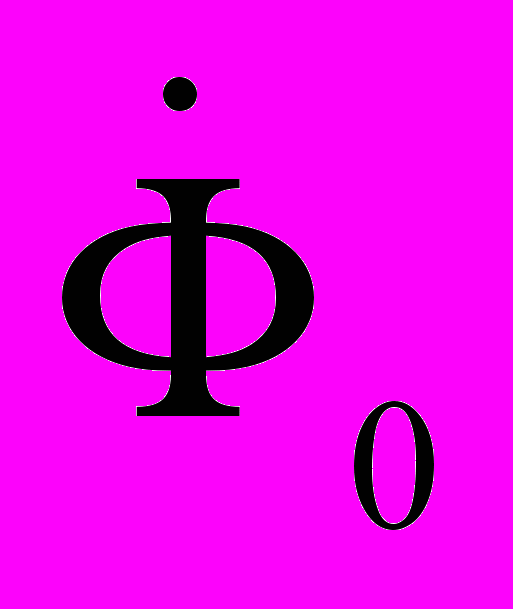, совпадающих по величине и фазе во всех стержнях. В стержневом трансформаторе такие потоки могут замыкаться только по воздуху и металлическим частям конструкции трансформатора. По сердечнику поток Ф₀ замыкаться не может, потому что в любом контуре, замыкающемся по сердечнику, сумма МДС от токов I₀ равна нулю. Поток Ф₀ индуцирует во всех фазах обмотки высшего напряжения одинаковую ЭДС нулевой последовательности 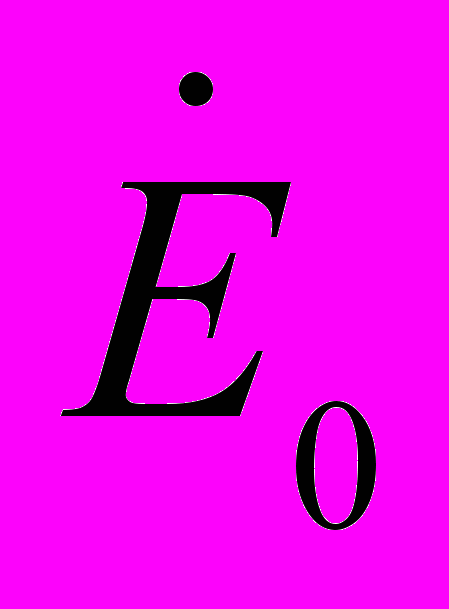, что приводит к искажению симметрии звезды первичных и вторичных фазных напряжений и ЭДС, как показано на рис.2.1. Из рис.2.1 видно, что симметричная тройка фазных напряжений Ua1₀, U_b10, U_c10 превращается в несимметричную  U_a10', U_b10', U_c10'. На рис.2.1 ЭДС E₀ численно равна отрезку 00'.

Во втором случае поток нулевой последовательности вторичной обмотки индуцирует в фазах первичной обмотки ЭДС нулевой последовательности. Поскольку эти ЭДС совпадают по величине и фазе, то в замкнутом контуре треугольника возникнет ток нулевой последовательности. Этот ток почти на 90° отстает по фазе от вызвавшей его ЭДС, а создаваемый им поток нулевой последовательности находится практически в противофазе с потоком вторичной обмотки. Поэтому результирующий поток нулевой последовательности и наведенные им ЭДС в фазах обмоток будут малы, а искажение звезды фазных напряжений и ЭДС будет незначительным.


Программа работы

Подготовка к работе

Рассчитать распределение линейных токов в первичной обмотке трансформатора при однофазной нагрузке для номинального тока вторичной обмотки I_a = I_н = 2,75 А и занести результаты расчетов в журнал лабораторных работ.


Экспериментальная часть

1. Определить распределение токов в первичной обмотке трансформатора и искажение вторичных фазных напряжений для случая однофазной нагрузки при схеме соединения обмоток трансформатора Y/Y₀.

2. Определить распределение линейных токов в первичной обмотке трансформатора и искажение вторичных фазных напряжений для случая однофазной нагрузки при схеме соединения обмоток трансформатора D/Y₀.



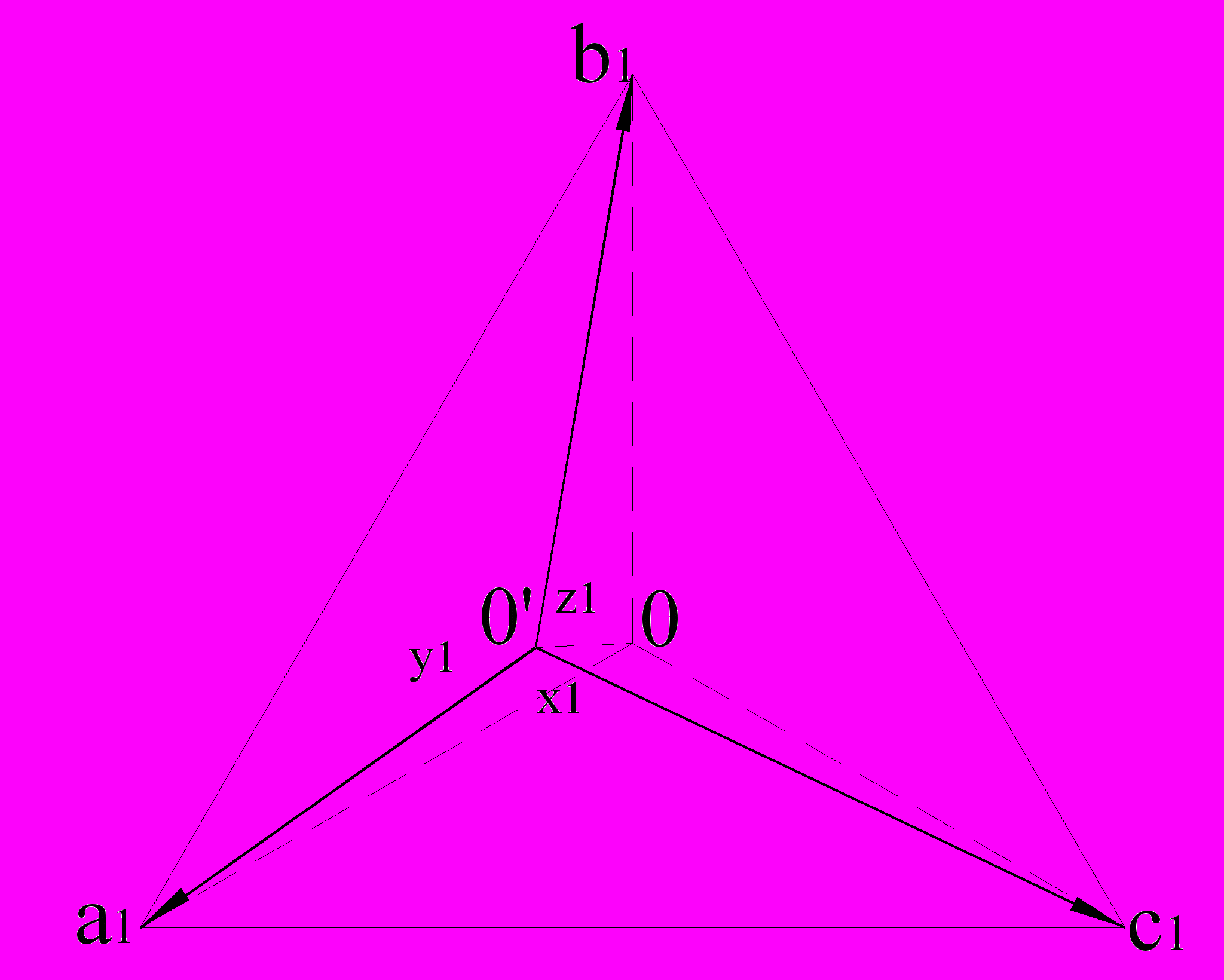
Рис.2.1. Векторная диаграмма напряжений для случая
несимметричной нагрузки, соединенной по схеме Y₀.

Обработка опытных данных

1. По данным опытов построить векторные диаграммы вторичных фазных и линейных ЭДС и определить искажение фазных напряжений ∆U_ф (В) и ∆U_ф* (о.е).

2. Сравнить полученные значения ∆ U_ф* для двух схем соединения обмоток и сделать вывод о предпочтительности применения одной из них.

Пояснения и указания к работе

Подготовка к работе

Расчет распределения линейных токов в первичной обмотке, если пренебречь током холостого хода (справедливо для силовых трансформаторов), проводится по следующим формулам.

Схема Y/Y_o

Во вторичной цепи трансформатора в этом случае будут токи всех трех последовательностей. Значение тока нулевой последовательности любой фазы равно

I_a0 = I_b0 = I_с0 = ⅓I_нг,

а токи в фазах вторичной обмотки равны

I_a = I_нг, I_b = I_c = 0.

Здесь I_нг – ток нагрузки, А.

Токи нулевой последовательности в первичной обмотке протекать не могут, так как схема Y – трехпроводная. Поэтому в первичную обмотку трансформируются только токи прямой и обратной последовательности

I_A = ⅔I_нг/k, I_B = ⅓I_нг/k, I_C = ⅓I_нг/k, (2.4)

где k – коэффициент трансформации, полученный в лабораторной работе №1.

Схема D/Y₀

В первичную обмотку будут трансформироваться токи всех трех последовательностей, но токи нулевой последовательности будут замыкаться только внутри треугольника (будут в фазных токах). В линейных токах токов нулевой последовательности, как и в предыдущем случае, не будет, поскольку сеть осталась трехпроводной. Поэтому линейные токи при такой схеме соединения обмоток будут равны

I_A = I_нг/k, I_B = I_нг/k, I_C = 0. (2.5)

Поскольку трансформаторы, установленные на лабораторном стенде, имеют мощность всего 0,16 кВА и ток холостого хода около 20%, то расчет токов по приведенным формулам также имеет погрешность порядка 20%.

Экспериментальная часть

Целью исследования несимметричной нагрузки трансформатора является изучение влияния токов нулевой последовательности на искажение симметрии фазных напряжений при различных схемах соединения первичной обмотки.

Объектом исследования является трехфазный групповой трансформатор, собранный из трех однофазных, описание которых приведено во введении. В качестве первичной трехфазной обмотки используются обмотки ВН однофазных трансформаторов, собранные по схеме Y или Д. В качестве вторичной трехфазной обмотки используются обмотки НН однофазных трансформаторов, собранные по схеме Y₀. Однофазная активная нагрузка подключается к фазе «a» трансформатора – обмотка a₁-x₁.

1. Схема Y/Y₀. Опыт проводится по схеме, представленной на рис.2.2, где Т – испытуемый 3-фазный групповой трансформатор, А_~ – щитовой амперметр переменного тока; остальные обозначения соответствуют работе №1.



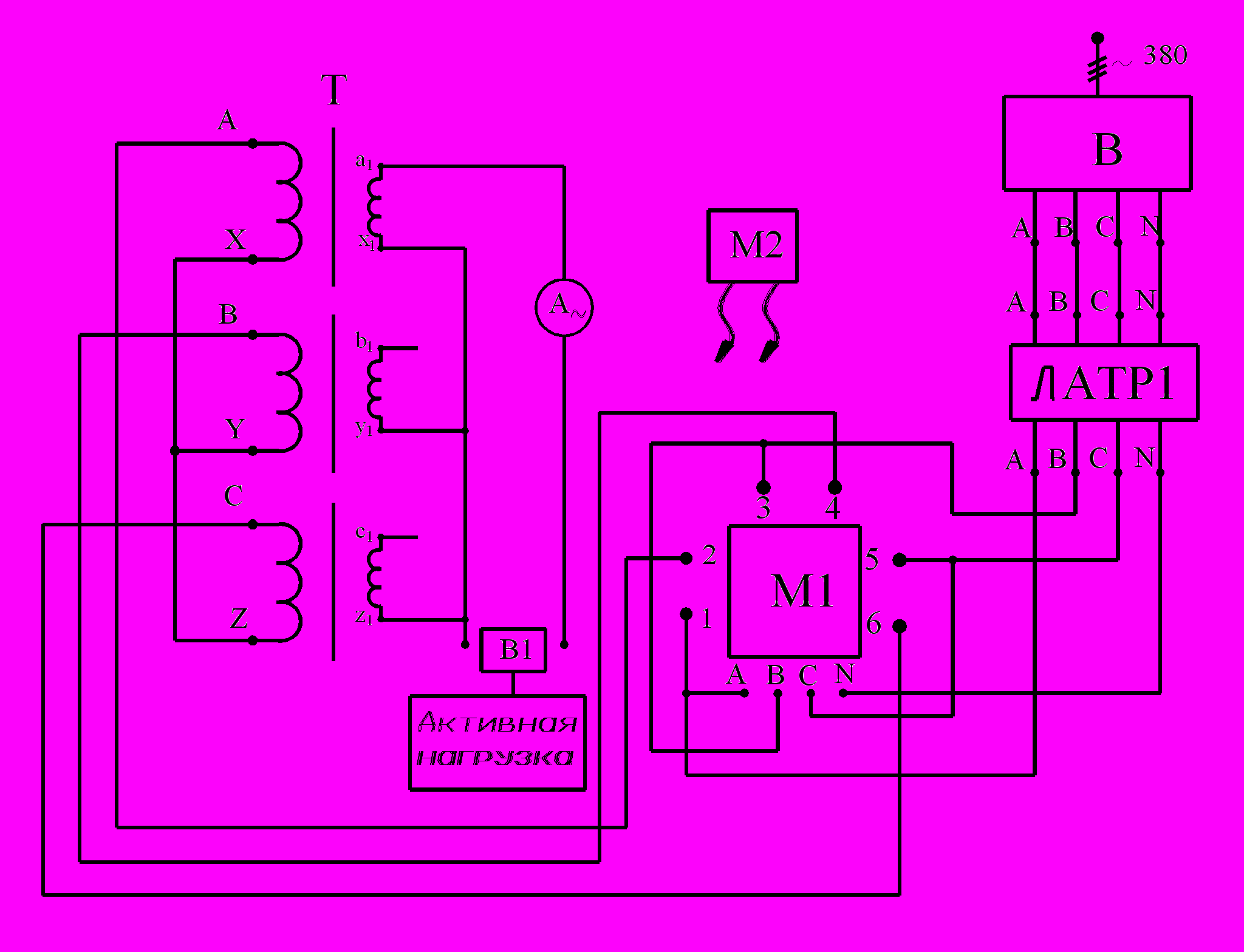
Рис.2.2. Соединение обмоток группового
трехфазного трансформатора по схеме Y/Y₀


Перед включением стенда следует убедиться, что ручка автотрансформатора ЛАТР1 установлена в нулевое положение, а выключатель В находится в положении «откл» (off). После включения стенда (на лицевой панели загорается красная лампа) выключателем В подают напряжение на собранную схему. С помощью автотрансформатора ЛАТР1 устанавливают на обмотке ВН (обмотка A-X, B-Y, C-Z) трехфазного трансформатора Т номинальное линейное напряжение 380 В. Затем с помощью встроенного выключателя В1 к фазе «a» трансформатора подключают активную нагрузку и, изменяя ее, устанавливают по амперметру А_~ ток, близкий к номинальному (2,75 А).

Контроль величины напряжения обмотки ВН осуществляют с помощью мультиметра М1 (см. табл. 1.1). Им же после установления номинального напряжения измеряют линейные токи первичной обмотки I_А,В,С (А). С помощью тестера М2 измеряют фазные (U_а0,в0,с0) и линейные (U_ab,_bc,_ca) напряжения обмотки НН. Полученные данные заносят в журнал лабораторных работ.

По окончании опыта необходимо отключить схему (выключатель В), установить в нулевое положение ручку автотрансформатора ЛАТР1 и отключить активную нагрузку.

2. Схема D/Y₀. По сравнению с предыдущим опытом необходимо лишь изменить схему соединения обмотки ВН в соответствии с рис.2.3. После включения стенда (на лицевой панели загорается красная лампа) выключателем В подают напряжение на собранную схему. С помощью автотрансформатора ЛАТР1 устанавливают на обмотке ВН (обмотка A-X, B-Y, C-Z) трехфазного трансформатора Т номинальное линейное напряжение 220 В. Затем с помощью встроенного выключателя В1 к фазе «а» трансформатора подключают активную нагрузку и устанавливают по амперметру А_~ ток, близкий к номинальному (2,75 А).

Контроль величины напряжения обмотки ВН осуществляют с помощью мультиметра М1. Им же после установления номинального напряжения измеряют линейные токи первичной обмотки I_А,В,С (А). С помощью тестера М2 измеряют фазные (U_а0,в0,с0) и линейные (U_ab,_bc,_ca) напряжения обмотки НН. Полученные данные заносят в журнал лабораторных работ.

По окончании опыта необходимо отключить схему (выключатель В), установить в нулевое положение ручку автотрансформатора ЛАТР1 и отключить активную нагрузку.


Обработка опытных данных

1. Сравнить расчетные и экспериментальные значения токов в первичной обмотке.
   

2. Векторные диаграммы вторичных линейных напряжений представляют собой треугольники, построенные по имеющимся значениям линейных напряжений с помощью циркуля. Рекомендуемый размер 100 мм на сторону треугольника линейных напряжений U_ab,_bc,_ca (В). Тогда масштаб напряжений равен m_U = 100/U_лин.

Центр звезды вторичных фазных напряжений (точка О’ на рис.2.1) определяют графически. Для этого откладывают циркулем в выбранном масштабе известные фазные напряжения из соответствующих вершин треугольника линейных напряжений.




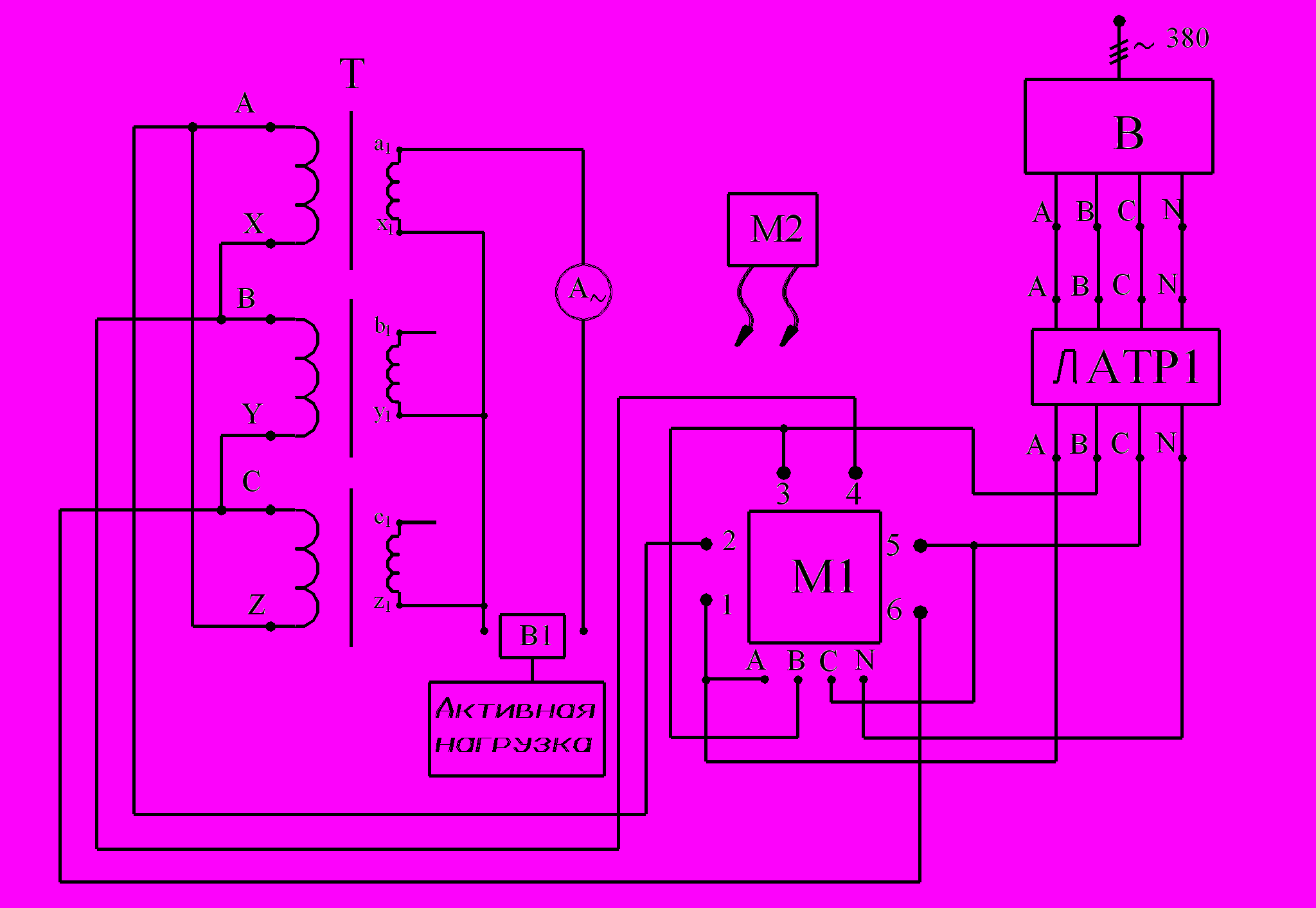
Рис.2.3. Соединение обмоток группового
трехфазного трансформатора по схеме Д/Y₀


3. Смещение нулевой точки звезды фазных напряжений ∆U_2ф определяется графически как расстояние (в мм) между центром тяжести треугольника линейных напряжений (т. О) и центром звезды фазных напряжений (т. О’), как показано на рис.2.1. Тогда

∆U_2ф = 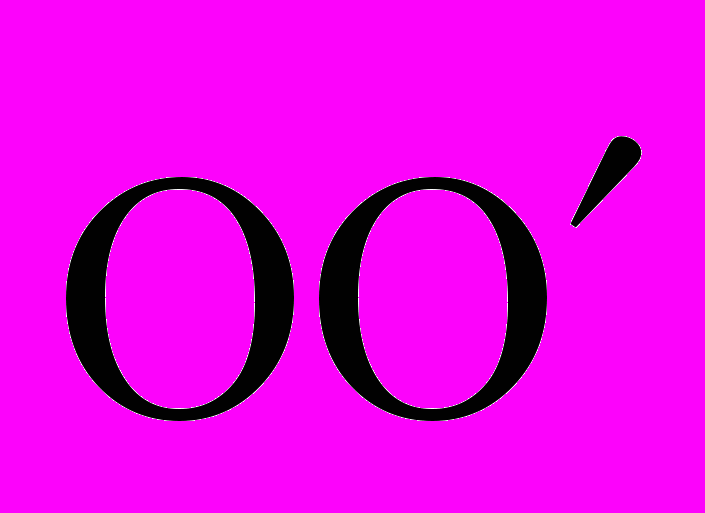m_U , В,

где m_U ― выбранный для построения векторной диаграммы масштаб напряжений, В/мм.

Относительное значение этого смещения равно

∆ U_ф* = 100(∆U_2ф/ U_2ф.ср), %.

Здесь U_2ф.ср = ⅓(U_a0 + U_b0 + U_c0) , В.


Контрольные вопросы

1. Что понимается под термином «несимметричная нагрузка» трансформатора?

2. К каким неприятным последствиям для потребителей и для трансформатора приводит несимметрия нагрузки?

3. В каких случаях при несимметричной нагрузке появляется ток нулевой последовательности?

4. Как и почему первичная обмотка трансформатора, соединенная по схеме треугольник, влияет на величину искажения фазных напряжений при несимметричной нагрузке?

5. В чем состоит метод симметричных составляющих? Для каких систем он применим?

6. Какой должна быть схема соединения первичной обмотки, чтобы в нее трансформировался (не трансформировался) ток нулевой последовательности из вторичной обмотки?

7. Какие магнитные системы трехфазных трансформаторов Вы знаете? По какому пути замыкаются потоки нулевой последовательности в этих магнитных системах?

8. Применение какой трехфазной магнитной системы дает минимальное искажение фазных напряжений?


Лабораторная работа №3

Исследование асинхронного двигателя


Краткие теоретические сведения

Обмотка статора асинхронного двигателя подключается к сети переменного тока. Под действием напряжения сети в ней протекает переменный ток, создается МДС и вращающееся магнитное поле. Рабочий поток взаимной индукции проходит по ярму (спинке сердечника) и зубцам статора, через воздушный зазор, по зубцам и ярму (спинке сердечника) ротора, замыкаясь через полюс другой полярности (рис. 8-2). Поле при вращении пересекает проводники обмотки ротора, цепь которой всегда замкнута. В каждом проводнике наводится ЭДС, под действием которой в проводнике возникает ток. В результате взаимодействия этого тока с вращающимся полем статора появится тангенциальная сила, действующая на проводник.

Проводники обмотки ротора распределены по пазам сердечника ротора Произведение тангенциальной силы на плечо — расстояние до оси вращения — равно моменту. Суммирование моментов от всех проводников даст результирующий электромагнитный момент, действующий на ротор. Если электромагнитный момент больше момента сопротивления нагрузки, то ротор начнет вращаться.

Поле статора всегда вращается с постоянной скоростью n₁, не зависящей от нагрузки. Начав вращаться под действием электромагнитного момента, ротор будет «догонять» поле статора. Но скорость вращения ротора n не может стать равной синхронной скорости вращения поля n₁. Предположим, что эти скорости стали равны; тогда проводники ротора (и сам ротор) будут неподвижны относительно поля статора. В этом случае ЭДС проводника станет равной нулю, а, следовательно, нулю станут ток проводника, действующая на него сила и электромагнитный момент. Под действием момента сопротивления нагрузки ротор начнет тормозиться.

Таким образом, у асинхронного двигателя всегда n < n₁, т.е. ротор «отстает» от поля статора, вращается медленнее его. Это несинхронное вращение ротора и стало причиной происхождения названия «асинхронный» двигатель. Скорость относительного скольжения ротора и поля статора равна n_ск = n₁ — n. На практике обычно используется ее относительная величина, называемая скольжением

s = n_ск/n₁ = (n₁ —n)/n₁. (3.1)

Отметим некоторые характерные значения скольжения. При пуске асинхронного двигателя в первый момент после включения в сеть ротор еще неподвижен, n = 0, s = 1. При холостом ходе, т.е. работе без нагрузки на валу, скорость ротора n весьма близка к n₁ , но не равна ей, т.е. s ≈ 0. Работе с номинальным моментом нагрузки соответствует номинальное скольжение s_ном = 0,02 —0,05.

Частота ЭДС в обмотке ротора f₂. определяется скоростью n_ск и равна

f₂ = p n_ск/60 = sf₁, (3.2)

где f₁ – частота токов в статоре, Гц.

Таким образом, поле статора наводит в роторе ЭДС переменной частоты f₂, которую называют частотой скольжения. Преобразование частоты — одно из полезных свойств асинхронной машины, используемое на практике. При пуске асинхронного двигателя частота в роторе наибольшая, так как при n = 0, s = 1 и f₂ = f₁.

При холостом ходе двигатель преодолевает только незначительный момент трения в подшипниках, момент сопротивления собственного вентилятора, находящегося на валу двигателя, щеток о контактные кольца у двигателя с фазным ротором, и трения поверхности ротора о воздух. В сумме этот момент называется моментом холостого хода. По принципу действия электромагнитный момент M в асинхронном двигателе создается за счет взаимодействия вращающегося поля с током ротора. Следовательно, M ~ ФI₂.

Рабочий магнитный поток в асинхронном двигателе, как и в трансформаторе, определяется приложенным напряжением, он практически одинаков при любой нагрузке. Для преодоления момента холостого хода нужен маленький ток в роторе. Токи ротора и статора связаны между собой таким же соотношением, как в трансформаторе. Поэтому при холостом ходе ток в каждой фазе обмотки статора I₁₀ тоже мал, он содержит намагничивающую (реактивную) составляющую и небольшую активную, обусловленную потерями холостого хода. С увеличением момента нагрузки на валу асинхронного двигателя скорость вращения ротора снижается, а скольжение растет. При переходе от холостого хода к режиму номинальной нагрузки у серийных асинхронных двигателей это снижение скорости невелико. Одновременно с возрастанием скольжения увеличиваются ЭДС и ток в роторе, а также развиваемый двигателем электромагнитный момент.

Физический смысл приведения обмотки ротора к статору такой же, как в трансформаторе. При этом также выравнивают количества витков и обмоточные коэффициенты статора и ротора, а инвариантами остаются МДС, мощности и потери в роторе. Из этого следует, что приведенная ЭДС в фазе обмотки ротора E₂^' равна ЭДС фазы статора E₁.

После приведения роторные величины стали иметь те же порядки, что и статорные. Замена вращающегося ротора на эквивалентный неподвижный выровняла их частоты, они равны частоте сети. Теперь можно описать асинхронную машину единой системой комплексных уравнений. Основные уравнения асинхронной машины с короткозамкнутым ротором после приведения имеют вид

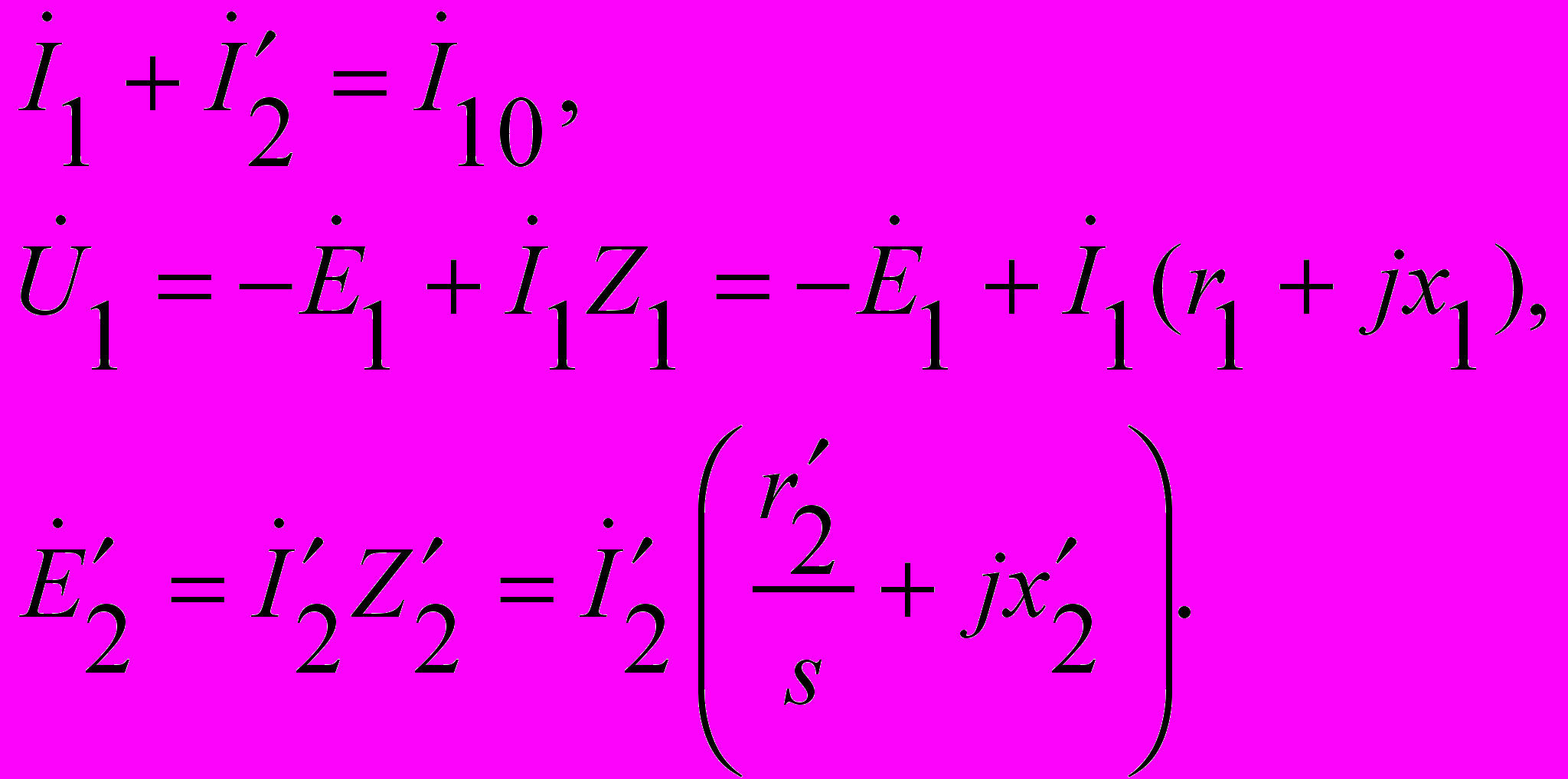(3.3)

Поскольку основные уравнения асинхронной машины (3.3) и трансформатора – (1.4), (1.5) подобны, то аналогичными оказываются и их схемы замещения. Различие состоит в том, что в двигателе помимо магнитных и электрических потерь существуют механические потери (учитываются в сопротивлении r₁₂), а его вторичная обмотка ― обмотка ротора ― замкнута накоротко (в схеме замещения двигателя вместо сопротивления нагрузки стоит сопротивление r₂'(1 ― s)/s, потери в котором численно равны его механической мощности.

Физический процесс возбуждения асинхронного двигателя, т.е. образования в нем магнитного поля, не отличается от процесса в трансформаторе и тоже требует реактивного намагничивающего тока. Асинхронный двигатель забирает реактивную мощность из сети для создания, как рабочего магнитного потока, так и потоков рассеяния. Она равна

Q₁ = m₁U₁I₁ sinφ₁. (3.4)

Кстати, подчеркнутое произведение полного тока статора на sinφ₁ как раз и является реактивной составляющей этого тока. А намагничивающим током машины называется геометрическая сумма (т.е. арифметическая разность) реактивных составляющих токов статора и ротора. Из-за наличия воздушного зазора между статором и ротором намагничивающий ток в асинхронном двигателе значительно больше, чем в трансформаторе. По этой причине у асинхронных двигателей с бóльшим числом полюсов более низкий cosφ, т.к. рабочий поток в машине пересекает воздушный зазор 2p раз.

КПД и cosφ асинхронного двигателя называются его энергетическими показателями. Они решающим образом влияют на количество электроэнергии, которую двигатель потребляет за время эксплуатации. Поэтому энергетические показатели определяют экономичность и потребительский уровень качества асинхронных двигателей. Даже незначительное повышение энергетических показателей может дать существенный экономический эффект потому, что они потребляют около 40% всей вырабатываемой электроэнергии. Этим объясняется большое внимание, уделяемое сейчас различным методам компенсации реактивной мощности в асинхронных двигателях и созданию высокоэффективных машин с повышенным КПД.