Лекция №1 Содержание курса физики система научного знания

Вид материала

Лекция

Содержание Ядро теории Теоретические и экспериментальные методы физики. Второй этап познания Колебания и волны Глава 4. Законы движения Глава 1. Общие сведения о движении. В заключении (9 класс) Содержание избранных вопросов курса соответствует фундаментальным теориям: механике, молекулярной физике, электродинамике, квант Теоретическая схема В замкнутой цепи постоянный ток может существовать, если в ней действуют сторонние силы. В и площади поверхности S Ф (фи). Тогда можно записать: Ф = В S Вб). Вебер равен потоку, создаваемому однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м Магнитный поток. Измерение физических величин Экспериментальное исследование Задания и упражнения Правило Ленца. Экспериментальное исследование A/q. Аналогично сила тока в контуре прямо пропорциональна ЭДС: I ... Полное содержание

Подобный материал:

• Лекция №1 Содержание курса физики система научного знания, 539.84kb.
• Физика, 212.85kb.
• Физика, 200.62kb.
• Основные методологические программы построения научного знания. 11. Основные концепции, 928.96kb.
• Темы курсовых работ по дисциплине «Теория и методика обучения физике» Межпредметные, 19.14kb.
• «Индустриальный сектор мировой экономики», 35.79kb.
• Содержание курса разделы курса Методологические и исторические аспекты политической, 142.3kb.
• Входящей в базовый курс изучения физики, необходимо сориентировать учащегося на новые, 106.41kb.
• Лекция №2 Тема: характеристика социологического знания, 195.16kb.
• disk/11850131001/%D0%9F%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B0%20-%20%D1%82%D0%B5%D0%BC%D1%8B%20-%20%D1%80%D0%B5%D1%84%D0%B5%D1%80%D0%B0%D1%82%D0%BE%D0%B2%20%D0%BF%D0%BE%20%D0%98%D0%9C%D0%A2%D0%, 252.78kb.

Лекция №1

Содержание курса физики – система научного знания


§ 1. Физическая теория – система научных знаний

Фундаментом построения содержания курсов физики, формирования соответствующей системы знаний учащихся основной и профильной старшей школы является физическая теория. Она является формой выражения и определённой системой научных знаний. Теория отличается от понятий, гипотез, законов, но содержит их в качестве своих элементов. В теории научные знания взаимосвязаны с методами познания. Они обладают свойством тождественности и различия. Различия теории и метода состоит в том, что теория – результат предыдущей деятельности поколений, метод – исходный объект и предпосылка познавательной деятельности освоения теории. По утверждению философов, теория является системой идеального, отражающая сущность объектов, метод - система правил, регуляторов, предписаний, выступающих в качестве средств познания. Метод не может использоваться вне связи с содержанием теории, с реальной действительностью, практикой. В педагогических целях выявим структуру и основные элементы физических теорий, которые необходимы для конструирования содержания разделов и тем курса физики основной и средней школы, чтобы сформировать системные знания и способы научного познания.

Один из основателей квантовой механики, немецкий учёный В. Гейзенберг, выделил четыре фундаментальных теоретических направлений, объединяющих родственные физические теории по исходным идеям, понятиям, математическим моделям, объектам природы. Такими направлениями являются классическая механика, статистическая физика, электродинамика и квантовая физика. Указанные направления иногда называют фундаментальными физическими теориями. В соответствии с указанными направлениями курсы физики основной и средней школы имеют четыре раздела: классическую механику; молекулярную (статистическую) физику; электродинамику и квантовую физику.

А.Эйнштейн различал в теории следующие составляющие: понятия, основные принципы, следствия, вытекающие из них путём дедукции. Вслед за ним, В. Гейзенберг подчеркивал наличие такого отличительного признака теории от простой совокупности элементов, как замкнутость системы понятий, законов, следствий из них. Они исчерпывающе описывают определённый круг физических явлений.

В любой физической теории различают следующие части (этапы): основание, ядро, выводы. Эти части теории сопоставимы с элементами гносеологического цикла познания: предметная деятельность, содержательные обобщения, восхождения от абстрактного к конкретному результату. Каждый из этапов познавательной деятельности охватывает группу элементов теории. Над ними «надстраивается» общая интерпретация содержания теории. Рассмотрим подробнее части теории.

Основание теории содержит группу экспериментальных фактов (явлений), которые в процессе развития науки отбираются, осмысливаются, сопоставляются, образуя эмпирический базис теории. Анализ фактов, общенаучных понятий (категорий) приводит к созданию исходных абстракций, а в дальнейшем к содержательным обобщениям.

Абстрактные объекты наделяются определёнными свойствами и структурой, например, идеальный газ, квантово-механическая модель атома Бора, силовые линии поля. Они в модельной форме воплощают сущность, особенности исследуемой области теории. Их иногда называют «клеточкой» познания. В основание теории входят и правила операций с физическими величинами, например, векторами, функциональными связями между величинами (таблица 1).

Разработка свойств идеализированного объекта сопровождается введением системы физических величин, каждая из которых характеризует определённое свойство объекта или связь с другими объектами.

Таблица 1

Интерпретация	Интерпретации связаны с моделью материи и взаимодействием. Анализ связей теории с другими теориями Границы применимости теории
Выводы	Объяснение и предсказание новых фактов. Получение количественных выводов – функциональных зависимостей между физическими величинами. Теория указывает общие методы для решения широкого круга задач
Ядро	Система законов (уравнений), определяющая связи и изменения фундаментальных физических величин. Совокупность законов сохранения. Мировые постоянные. Принципы симметрии и инвариантности. Законы связей новых и старых теорий.
Основание	Правила действия над физическими величинами. Правила соотнесения физических величин с опытом. Система фундаментальных понятий и величин. Эмпирические факты (эмпирический базис)

Физические величины, как характеристики идеализированного объекта, абстрактны. Конкретное содержание они обретают через связь с реальными объектами в процессе измерения. Составным элементом основания теории входят физические измерения, заданные правилами определённых предметных действий.

Ядро теории есть общая математическая модель связей и отношений, заложенных в теоретическом обобщении и относящихся к идеализированному объекту. Как правило, современная физическая теория содержит группу дифференциальных уравнений. Таким образом, ядро теории составляет система законов, которые определяют связи между физическими величинами.

Ядро соотносится с основанием теории. Оно обусловлено основанием, так как связи между величинами характерны лишь для идеализированных объектов основания. Форма выражения связей в законах диктуется характером величин, заданным в основании. Вместе с тем ядро в процессе развития теории даёт основанию новые физические интерпретации.

В ядре выделяются постулаты и принципы, тесно связанные с основными уравнениями. Это либо словесные формулировки самих уравнений, либо положения приводящие к ним. Особая роль в ядре физической теории принадлежит законам сохранения энергии, импульса, момента импульса, чётности, электрических и других зарядов и чисел. Они относятся к ядру теории в качестве самостоятельного элемента. Теория даёт возможность сделать конкретные выводы благодаря измерению входящих в уравнение констант.

Выводы. Назначение теории состоит в получении из ядра конкретных выводов и прежде всего количественных функциональных зависимостей между физическими величинами. С развитием физики определился общий критерий истинности теории. Он лежит в области теоретических обобщений более высокого уровня, включающих данную теорию как частный случай.

Конкретные выводы теории не абсолютно конкретны. Они обладают некоторой общностью, охватывая главные совокупности явлений. Эти выводы справедливы только на уровне данных теоретических обобщений. В этом отношении, как известно, процесс познания не исчерпаем.

В выводах отчётливо проявляется познавательный характер теории. Она указывает общие методы для решения широкого круга задач, формируя способ их решения. Теория «учит» решать их.

Характерная особенность теории состоит в предсказании новых фактов. Ядро теории обобщения содержат в себе неизмеримо больше, нежели конкретные факты эмпирического базиса. В выводах раскрываются связи явлений, недоступные для эмпирических обобщений. Они показывают, что из теории вытекают факты, а не факты «подводятся» под теорию. Такой структурой диктуется определённая последовательность изучения теоретического материала школьного курса.

Следующий этап теоретического обобщения - интерпретация физических теорий. Каждая теория содержит определённые физические идеи, а также интерпретации математического аппарата и выводов. Во всех фундаментальных теориях идеи и интерпретации связаны с моделью материи и взаимодействия. При интерпретации теории прослеживаются связи её с другими теориями, четко очерчиваются рамки.

Чтобы сформировать у учащихся системные знания о физической теории, содержание обучения физике должно быть сконструировано на базе фундаментальных физических теорий и современной их интерпретации на основе идей, принципов и общенаучных понятий физической картины мира. Учебный материал разделов курса физики группируется в соответствии с предметными областями научного знания классической механики, молекулярной физики, электродинамики, квантовой физики.

§ 2. Составляющие фундаментальной теории

(на примере классической механики).


Важнейшими функциями фундаментальных теорий, в том числе и классической механики, является объяснительная и предсказательная функции. Познание реального физического мира начинается с описания наблюдаемых в реальном мире эмпирических закономерностей. Эмпирические законы, полученные индуктивным обобщением экспериментальных данных, не объясняют конкретное механическое явление.

Объяснение явления осуществляется с помощью дедуктивных следствий, выведенных из основных законов механики. Из обобщённых результатов эксперимента по наблюдению за свободным падением тел у поверхности Земли формулируется эмпирический закон свободного падения: все тела в отсутствии сопротивления воздуха падают с одинаковым ускорением. Теория раскрывает экспериментально не наблюдаемую сущность явления. Эмпирический закон свободного падения в рамках классической механики объясняется вторым законом Ньютона, законом всемирного тяготения и эквивалентностью инертной и гравитационной массы.

Предсказательная функция механики проявляется в том, что она предсказывает и объясняет результаты экспериментов с ранее не изученными механическими системами. Успешное применение законов механики и их следствий при разработке и конструировании технических устройств подтверждают предсказательную силу механики.

Теоретические и экспериментальные методы физики. Научить учащихся объяснять и предсказывать явления – это значит сформировать методы познания природы, которыми учёные – физики используют в процессе своего исследования. Как известно, методы познания условно разделяются на эмпирические и теоретические. Рассмотрим на примере свободного падения эмпирические методы, которыми пользовался Галилей - основатель общенаучного экспериментального метода познания. Затем обратимся к теоретическому методу, с помощью которого объясняет классическая механика свободное падение тел.

На рубеже ХVI – XVII веков Г.Галилей, обобщая опыт исследований, открыл новый научный метод опытного познания природы Впоследствии этот метод получил название метода Галилея или естественнонаучного, так как применяется во всех естественных науках. Галилей показал, каким образом из опыта можно прийти к научному выводу, открытию закона.

Вначале определяется объект исследования, разрабатывается план и собирается экспериментальная установка для проведения опытов. Посредством анализа результатов наблюдения и опытов формулируется предположение, называемое эмпирической гипотезой.

Научная гипотеза, выдвигаемая в результате индуктивного обобщения экспериментальных и наблюдаемых данных, называется эмпирической гипотезой и выражается эмпирическим законом. Она хотя и является обобщением опытов, включает элементы нового, не изученного в науке. Гипотеза позволяет вывести следствия, предсказать новые факты и проверить их на опыте. Схема естественнонаучного метода познания такова: опытные факты –эмпирическая гипотеза – следствия - эксперимент.

Естественнонаучный метод взаимосвязан с общелогическими методами, включая в себя методы наблюдения, воспроизведение явлений в эксперименте, метод эмпирических гипотез, моделирование, анализ и др. Рассмотрим пример применения естественнонаучного метода при исследовании Галилеем свободного падения тел. При этом будем использовать современную терминологию.

Известно, что свободное падение тел происходит под действием силы тяжести. Однако в обычных условиях падающее тело у поверхности Земли испытывает и другие воздействия. Так, на него действует сопротивление воздуха. Для тел разной формы сила сопротивления, действующая на тело, может быть различной. На падение тел влияет также ветер. Галилей стремился устранить эти сопутствующие падению тел воздействия.

Наблюдая и анализируя опыты с падающими телами, Галилей выдвинул предположение о том, что у поверхности Земли тело, в отсутствие сил сопротивления, совершает свободное падение с постоянным ускорением, т.е. движется равноускоренно. В этом состояла эмпирическая гипотеза исследования. Хотя она и основана на непосредственных наблюдениях и некоторых соображениях, все же является догадкой.

Гипотезу Галилея можно выразить математически: υ  ~ t, где υ – модуль скорости падения тела из состояния покоя в момент времени t. Это означает, что при свободном падении скорость движения пропорциональна времени.

Техника эксперимента не позволила Галилею осуществить прямую зависимость между указанными величинами. В то время ещё не были изобретены приборы для определения скорости движения, а также маятниковые часы. Можно было лишь использовать для отсчёта времени песочные или водяные часы. Тогда Галилей решает проверить гипотезу посредством эксперимента для случая движения тела по наклонной плоскости. По его предположению, движение по наклонной плоскости, как и свободное падение, является равноускоренным.

Из выдвинутой гипотезы Галилей выводит следствие. Для этого он использует специальный прием. Суть его состоит в том, что, исходя из прямой пропорциональной зависимости скорости от времени при равноускоренном движении (υ  ~ t), теоретически можно установить связь между длиной пройденного пути и временем движения.

С подобным приёмом учащиеся знакомятся в курсе физики 7 класса. Напомним его. Пусть шарик (материальная точка) движется по прямолинейной траектории равноускоренно. Путь, пройденный шариком при переменном движении, можно выразить через среднюю скорость υ_ср и время t: s = υ_срt. Средняя скорость равноускоренного движения равна среднему арифметическому значению скоростей в начале и конце пути:

. (1)

В случае движения шарика из состояния покоя начальная скорость υ₀ равна нулю (υ₀ = 0), а скорость в конце пути υ = аt, где а – ускорение шарика.

Тогда средняя скорость, согласно формуле (1), равна

,

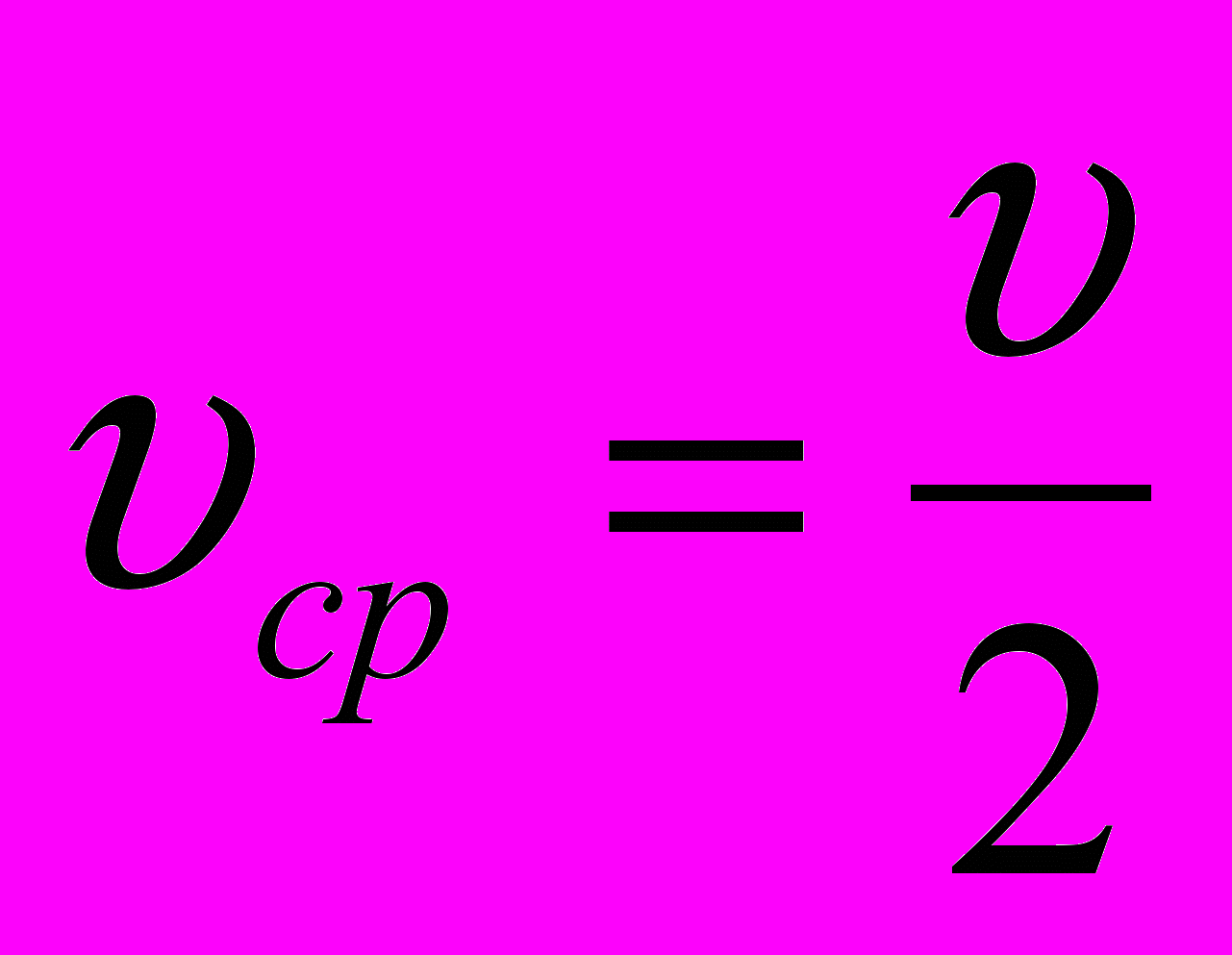а пройденный путь

s =. (2)

Формула (2) показывает, что при равноускоренном движении пройденный путь пропорционален квадрату времени: s  ~ t² .

Прямую пропорциональную зависимость между пройденным путем и квадратом времени Галилей мог проверить экспериментально. Он берёт длинную доску с жёлобом. Под один конец доски укрепляет подставку. Доска вместе с подставкой образуют наклонную плоскость. Чтобы уменьшить сопротивление при скольжении шарика, желоб в доске выстилался пергаментом. В эксперименте использовались одинаковые по объему шарики, изготовленные из разных материалов, например, из дерева, золота, слоновой кости. В опытах Галилей измерял время скольжения шарика водяными часами по количеству воды, вытекающей через малое отверстие из сосуда.

Галилей экспериментально установил, что пройденные шариком пути по наклонной плоскости пропорциональны квадрату времени. Следовательно, тела, изготовленные из разных материалов, движутся по наклонной плоскости равноускоренно. Данный вывод оказался справедливым для наклонных плоскостей с разными углами наклона.

Учёный обнаружил, что ускорение тел, соскальзывающих с гладкой наклонной плоскости, зависит от угла наклонной плоскости. Чем больше угол α ее наклона, тем большее ускорение сообщает сила тяжести шарикам. Отсюда Галилей делает вывод, что данное положение справедливо и для свободного падения. Действительно, вертикальное движение тела вниз можно рассматривать как движение его по наклонной плоскости, когда угол наклона α стремится к 90^о. Так эксперимент подтвердил основную гипотезу: все тела независимо от их массы в отсутствие сил сопротивления воздуха падают на Землю с одинаковым ускорением, называемым ускорением свободного падения.

Схема исследования свободного падения Галилея такова: факты - эмпирическая гипотеза – следствие экспериментю

Впоследствии были созданы вакуумные насосы, которые позволили осуществить свободное падение тел. Особенно убедителен опыт с так называемой трубкой Ньютона (рис.1).




В 1656 г. Х.Гюйгенс с помощью изобретённых им маятниковых часов измерил ускорение свободного падения.

Отметим, что эмпирический закон может быть сформулирован словесно словами или в форме функциональной зависимости между величинами.

Эмпирические законы не объясняют сущности явлений, в эксперименте наблюдается лишь внешнее проявление этой сущности. Действительно, сколько бы экспериментов по измерению ускорения свободного падения не было бы поставлено, эти эксперименты не ответят на вопрос, почему все тела падают с одинаковым ускорением.



Рис. 1

Объяснение явления происходит на теоретическом этапе познания. С помощью второго закона Ньютона F = mg и закона всемирного тяготения F = 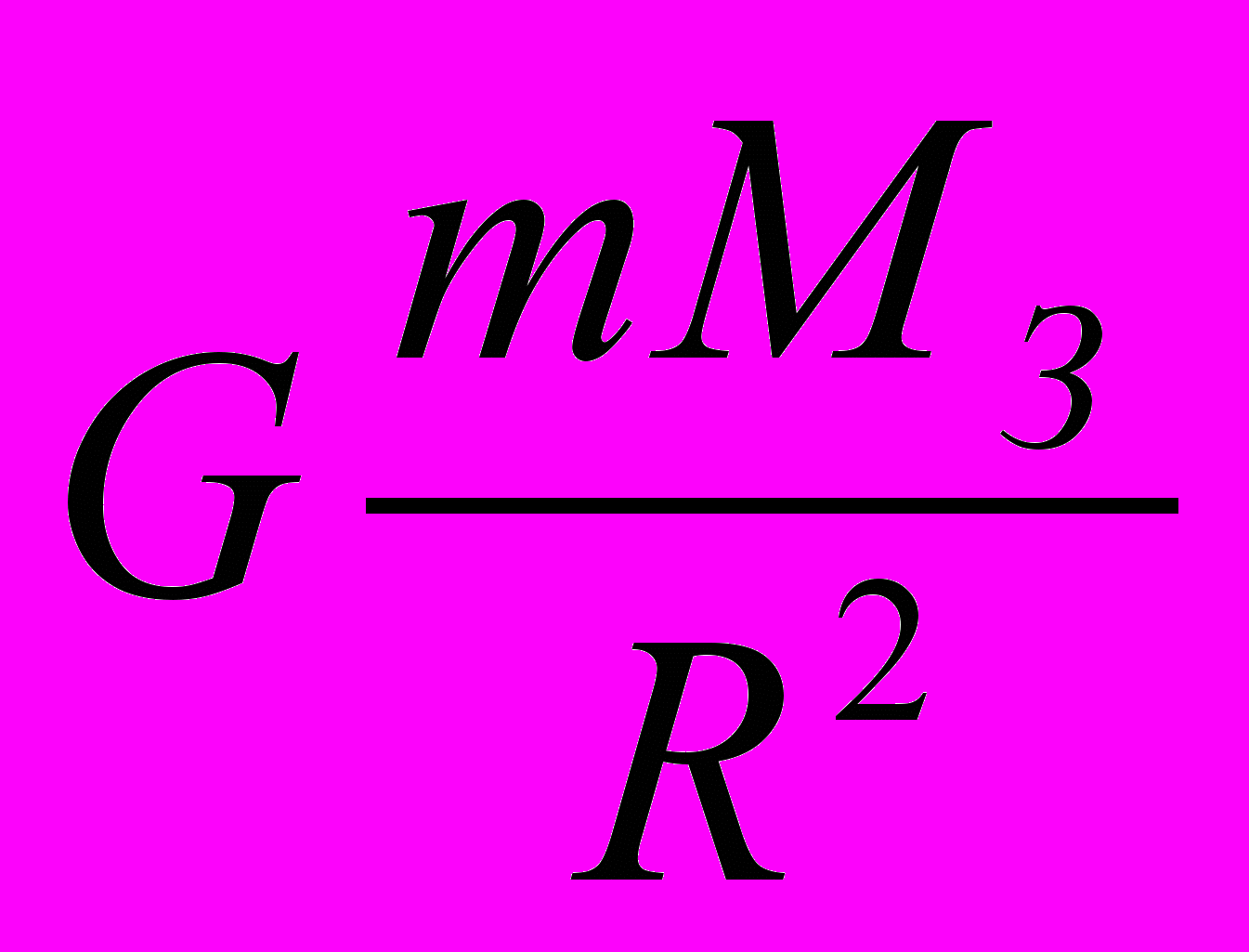доказывается, что у поверхности Земли сила тяжести сообщает всем телам, не зависимо от их массы, одинаковое ускорение, называемое ускорением свободного падения. Действительно:

mg =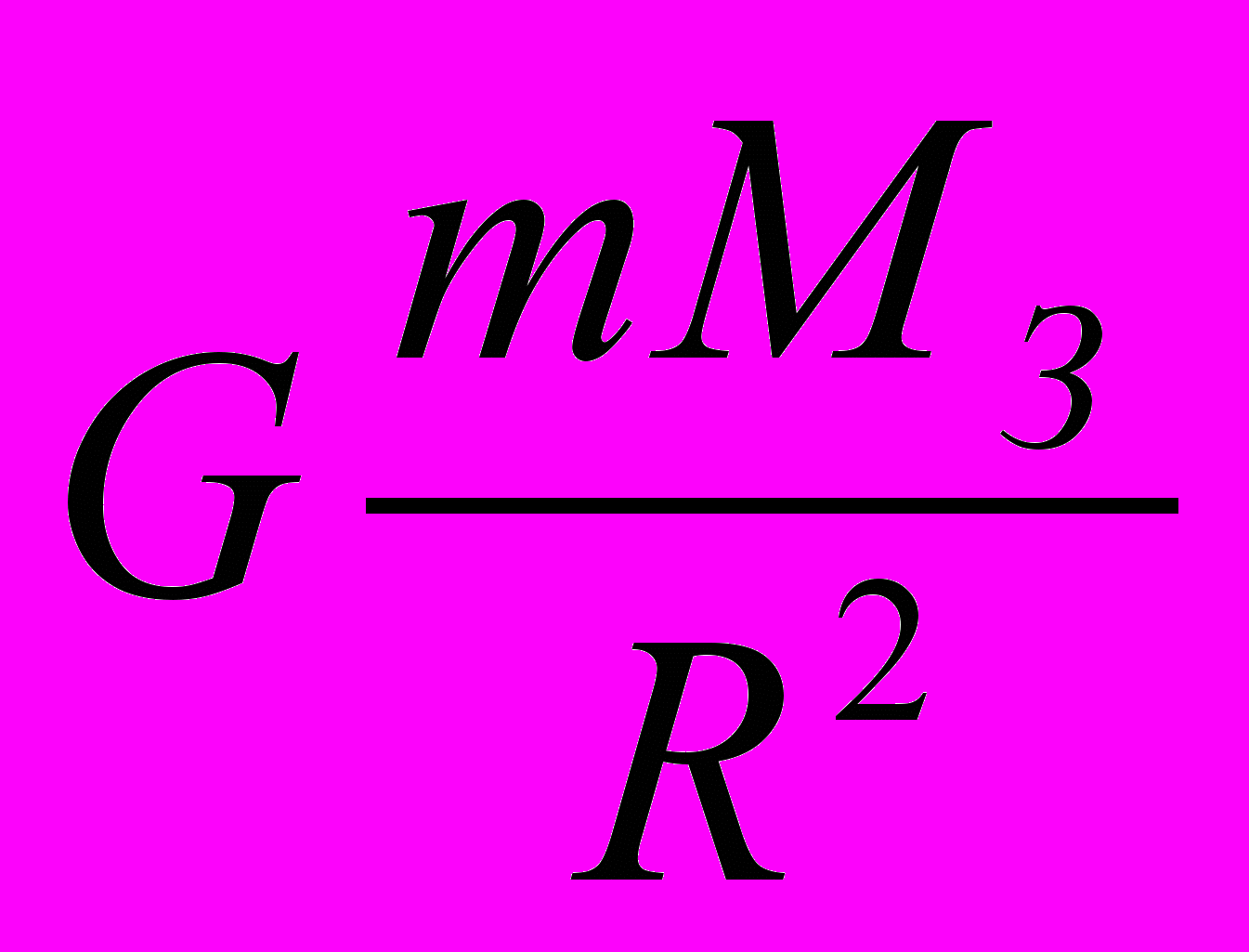, т.е g =.

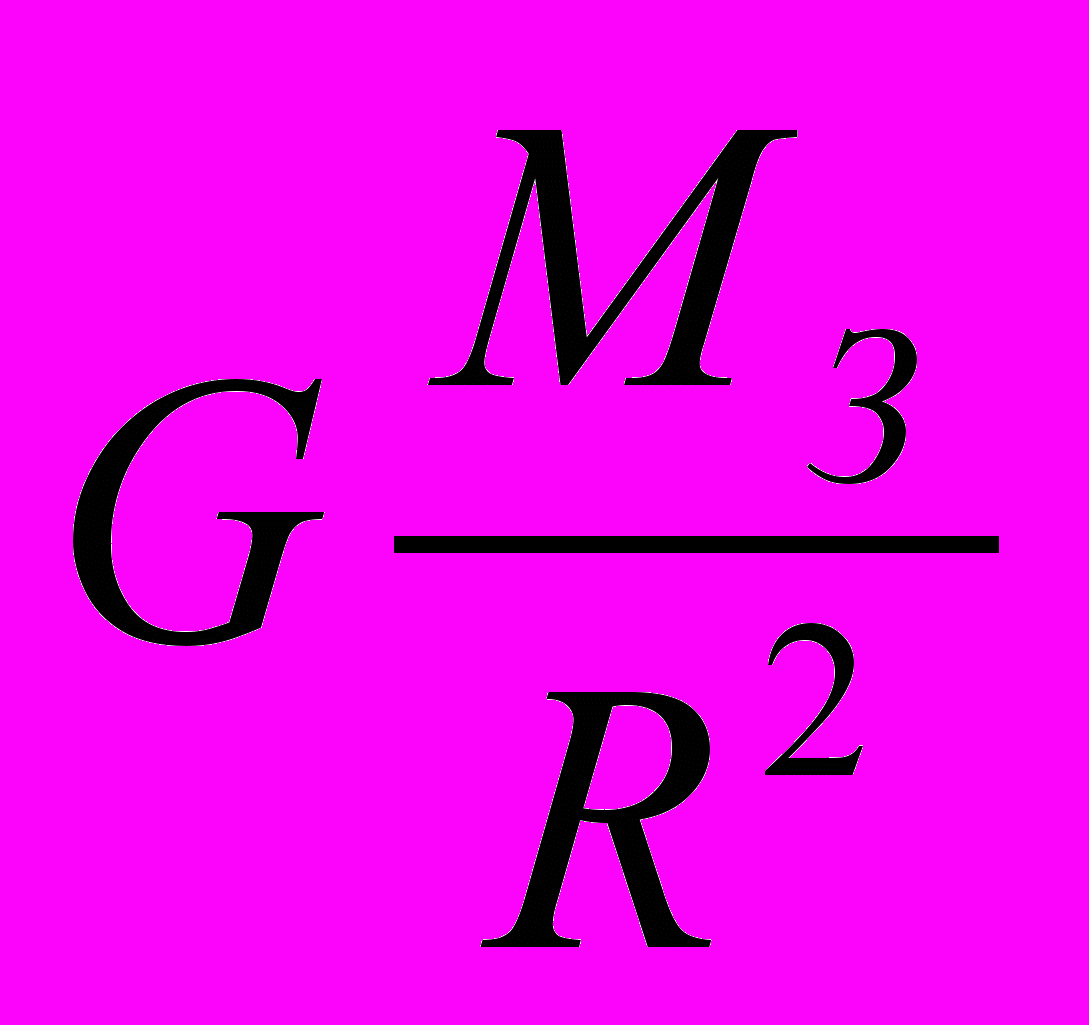Другой пример того, что предсказательная функция классической механики реализуется вторым законом Ньютона, - это решение основной задачи механики. Оно начинается с нахождения ускорения по известным массе тела и силе, действующей на него: а_x = F_x/m. Зная начальную скорость υ₀ движения, можно найти скорость движения тела в любой момент времени t:

υ_x = υ_0x +a_x t = υ_0x + (F_x/m)t.

По известной скорости υ_x движения и начальной координате х₀ находят положение тела относительно выбранной системы отсчёта при равноускоренном движении: х = х₀ + υ_0xt + a_x t²/2.

Процесс познания механического фрагмента реального мира можно разбить на три этапа. На первом этапе изучаются эмпирические закономерности механического движения с помощью эмпирических методов познания: экспериментальных методов и общелогических методов обобщения результатов экспериментов. На этом этапе, как это было уже сказано выше, внутренняя сущность явления не может быть раскрыта.

Второй этап познания – это этап теоретического осмысления экспериментально ненаблюдаемой внутренней сущности механических явлений. На этом этапе выдвигаются теоретические гипотезы об основных свойствах материальных объектов, а также о причине протекания явления в заданных условиях. Осуществляются теоретические обобщения эмпирического материала с помощью общелогических и теоретических методов познания - метода анализа и синтеза, методов аналогий, абстрагирования, моделирования, метода мысленного эксперимента, гипотетико-дедуктивного метода и др. Результатом познавательной деятельности второго этапа является формулировка фундаментальных законов классической механики, описывающих причинно-следственную сущность протекания механического явления. Законы могут быть сформулированы словесно (именно так формулируется первый закон) или в форме математического уравнения (второй закон Ньютона, теорема об изменение кинетической энергии тела и т.д.).

Третий этап познания – этап дедуктивного вывода следствий из основных законов в применении к конкретным механическим системам. Заметим, что именно дедуктивные следствия поддаются экспериментальной проверке. Соответствие дедуктивных следствий результатам экспериментов является критерием того, что основные законы отражают сущность механических явлений.

К основным законам классической механики относятся законы Ньютона, которые оперируют теоретическими модельными объектами. Законы Ньютона сформулированы для материальной точки, совершающей механическое движение в инерциальной системе отсчёта. В этой связи законы Ньютона не могут быть непосредственно проверены экспериментально. Так, первый закон Ньютона утверждает, что существует хотя бы одна инерциальная система отсчёта. Для непосредственной экспериментальной проверки этого утверждения необходимо иметь в распоряжении изолированную материальную точку, которая, разумеется, в природе отсутствует. Это же касается и остальных законов Ньютона. Второй закон сформулирован для материальной точки, находящейся в инерциальной системе отсчёта; третий закон - для изолированной механической системы, состоящей из двух материальных точек.

Однако из законов Ньютона можно дедуктивно (формально-логически с использованием математического аппарата) получить следствия, которые поддаются проверке. Примером могут служить динамика вращательного движения, колебательного движения, соударение шаров. Все математические выражения являются дедуктивными следствиями из основных законов классической механики, которые поддаются экспериментальной проверке. Оказалось, что эти следствия согласуется с данными физического эксперимента. Итак, критерием того, что классическая механика верно описывает фрагмент реального физического мира, является практика успешного применения теоретических следствий классической механики к описанию реальных механических явлений.

Классическая механика – система научных знаний. Знания о природе – это отражение объективных законов природы в мышлении, поэтому научные знания относятся к классу идеальных систем. (Для сравнения: механическая система взаимодействующих тел относится к классу материальных систем.)

Таким образом, содержательную структуру классической механики можно представить в виде цепочки трёх взаимосвязанных элементов: эмпирическое основание - теоретическое ядро – дидактические теоретические следствия - интерпретация законов и их практические применения. Содержательная модель классической механики курса физики средней школы представлена в форме таблицы 2.

Таблица 2

Составляющие Теории	Классическая механика	Содержательные блоки, главы курса
Следствие	Теоретические следствия классической механики: вопросы небесной механики, механика твёрдого тела, теория колебаний иволн.	Колебания и волны Глава 8. Механические колебания Глава 9. Волны
Ядро	Теоретические объекты классической механики (материальная точка, ньютоновское пространство, ньютоновское время). Законы Ньютона. Законы сил. Принцип относительности Галилея. Принцип независимости взаимодействий. Динамическое уравнение движения. Законы сохранения. Гравитационная постоянная. Ускорение свободного падения у поверхности Земли. Мировые постоянные. Принципы симметрии и инвариантности. Законы связей новых и старых теорий	Основы динамики Глава 4. Законы движения Глава 5. Силы в природе и движения тел. Законы сохранения Глава 6. Закон сохранения импульса. Гллава 7. Закон сохранения энергии.
Основание	Эмпирическое основание классической механики: правила действия с векторными величинами, координатный метод описания движения тел, свободное падение тел, периодическое движение. Кинематические понятия и величины.	Кинематика Глава 1. Общие сведения о движении. Глава 2. Прямолинейное неравномерное движение. Глава. 3. Криволинейное движение

§ 3. Конструирование содержательных блоков

раздела курса «Механика»

Содержательные блоки курса физики строятся с учётом того, к какой составляющей фундаментальной теории относится учебный материал этого блока. При этом систематизирующим фактором учебного материала выступает общенаучный метод познания. Если материал относится к основанию теории, то структура содержательного блока соответствует схеме: факты – эмпирическая гипотеза – модель– следствие – эксперимент.

Так, в начале кинематики учащиеся рассматривают общие сведения о движении, используя эмпирические и общелогические методы. К этим сведениям относятся следующие вопросы: механическое движение, тело отсчета, прямолинейное и криволинейное движение, понятия материальной точки, системы отсчёта, относительности механического движения.

Эмпирические гипотезы используются при изучении закономерностей равноускоренного движения, свободного падения тел, а также периодических движений. При этом наряду с эмпирическими методами применяются математические (теоретические) методы для вывода формулы равноускоренного движения с помощью метода предельного перехода.

В качестве следствий и эксперимента кинематики служат решение задач и выполнение лабораторных работ.

Содержательный блок «Основы динамики» также использует общенаучный метод познания природы. При этом меняется роль фактов и эксперимента в учебном познании.

Как было показано выше, законы Ньютона оперируют теоретическими модельными объектами. В этой связи законы Ньютона не могут быть непосредственно проверены экспериментально. Поэтому роль наглядных средств и эксперимента состоит в том, чтобы приблизить ситуации, на основании которых можно подвести к мысленному эксперименту, а затем и к теоретическим моделям динамики. Таким опытом является опыт с шариком, скатывающимся с наклонной плоскости (рис. 2). На небольшом расстоянии от конца наклонной плоскости насыпана горка песка. Шарик, скатившись на стол и попав в песок, быстро останавливается. Выровним песок и вновь пустим шарик по желобу с прежней высоты. Шарик, прежде чем остановиться, пройдет большее расстояние по столу (рис. 2,б). Если совсем убрать песок, то до остановки шарик пройдет ещё большее расстояние (рис.2, в). Следовательно, чем меньше действие горки песка на шарик, тем дольше сохраняется его движение. Если убрать песок, то движение шарика по поверхности стола можно считать равномерным. Рассмотренный опыт иногда называют «моделями приближения». Затем делается вывод: тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Подобные опыты позволяют сформировать абстрактное понятие о свободном теле, а следовательно и сущность, выраженную в первом законе Ньютона.

Из законов Ньютона дедуктивно получают выводы, используя законы сил, которые экспериментально проверяются в процессе экспериментальных задач и проведения лабораторных работ.



Рис. 2

Сконструированные таким образом содержательные блоки учебного материала курса условно называют частными теоретическими схемами. Содержательный блок обладает свойством системного выражения научного знания. Ему, как системе, присуща определенная структура и систематизирующий фактор.





Рис.3

На рисунке 3 показано распределение учебного материала содержательного блока «Законы Ньютона. Силы в механике» (курс физики 7класса). На вертикальной оси представлен объем учебного материала (в %) по каждой составляющей теоретической схемы. На горизонтальной оси указаны составляющие теоретической схемы. Первый столбик (36%) диаграммы показывает относительный объем текста учебного материала с описанием физических явлений, соответствующего эксперимента, второй (44%) – объяснения сущности понятий и закона, третий (13%) – выводов и следствий из них, четвертый (8%) – практических приложений.


§ 4. Психолого-педагические основы формирования

теоретических обобщений


При построении содержания учебного материала курса следует исходить из психологической установки: знания, как токовые, не обеспечивают развития, в то же время являются его предпосылкой.

Согласно Л.В.Занкову, развитие – это появление новообразований в психике обучаемого, не связанных на прямую с обучением, а возникающие в результате внутренних, глубоких интеграционных процессов. Ведущим в развитии является обучение. Л.В.Занков утверждает, что обучение ведёт за собой развитие. Ведущей целью обучения им признается освоение способов умственных действий. Применительно к обучению физике это означает, что ведущим в развитии учащихся является освоение методов познания природы, структурных составляющих физических теорий.

Основа гармонического развития человека закладывается исключительно общим развитием, когда появляются новообразования во всех сферах психики –ума, воли, чувств. При этом отдельное новообразование получается благодаря взаимодействию всех указанных сфер, продвигая личность в целом.

Система Л.В. Занкова опирается на психологическое понятие когнитивных (познавательных) структур – схем. По его мнению, с помощью этих структур человек воспринимает окружающий мир, отдавая приоритет в процессе обучения не знаниям, умениям, навыкам, а их возникновению. Именно когнитивные структуры становятся субстратом умственного развития. В этом положении психолога Д.В. Занкова мы видим подтверждение важности познавательных схем в конструировании разделов, тем и других составляющих содержания курса физики. Перечислим некоторые из схем, применяемых при написании учебников для основной школы.

Схема систематического курса физики основной школы. Он в целом систематизирован и обобщён на основании элементов физических теорий и физической картины мира, методов познания природы по схеме: объекты и методы исследования физики – избранные вопросы фундаментальных теорий – элементы физической картины мира.

Во введении (7 класс) рассмотрены объекты изучения физики: явления, физическое тело, вещество, электромагнитное поле. Показана взаимосвязь физических явлений, особенности агрегатных состояний вещества, примеры физического поля на конкретных экспериментальных установках. Обобщены ранее изученные в курсах естествознания, окружающего мира формы научного знания: физическая величина, открытие законов – задача физики, физическая теория – система научных знаний на примере основных положений молекулярно- кинетической теории. Основное внимание в главе обращено на два основных метода познания- физический эксперимент и моделирование.

В заключении (9 класс) подведен итог изучения курса физики основной школы. Итоговая глава «Элементы физической картины мира» знакомит учащихся с моделью природы в физике, в которую входят физические величины, связи между ними, законы, теории, общенаучные понятия, например о материи и взаимодействии. В ней представлен материал показывающий, что по мере открытия новых законов картина мира неизбежно усложняется. В данной главе представлен материал о делении окружающего мира с точки зрения науки (мегамир, макромир и микромир), рассмотрены примеры объектов макромира и микромира (Солнечная система, фотон, электрон и позитрон). Обобщены знания о методах познания природы, приведены примеры, из которых следует вывод о неисчерпаемости знаний о мире.

Содержание избранных вопросов курса соответствует фундаментальным теориям: механике, молекулярной физике, электродинамике, квантовой физике.

Из этих теорий, с учетом возрастных особенностей учащихся, отбирается такой материал для соответствующих разделов курса физики, который относится к эмпирическому базису, ее ядру, следствиям, их практическим применениям и философской интерпретации. В курсе физики основной школы такая схема построения содержания разделов курса называется теоретической схемой.

Теоретическая схема – целостная система научных знаний определённой предметной области физической теории, объединённая главными элементами физической теории и циклом научного познания. Составные элементы теоретической схемы следующие: физический эксперимент, модели объектов изучения, понятия, законы, выражающие связи между объектами, логические следствия, вытекающие из законов, их практические применения и философская интерпретация теоретического материала..

Содержание каждого раздела курса включает несколько блоков учебного материала, каждый из которых соответствует структуре частной теоретической схеме, которая воплощает в себе основные способы умственной деятельности, характерные для общенаучного метода познания.

При изучении каждого содержательного блока курса физики основной школы неоднократно повторяются мыслительные операции, характерные для изучения природных явлений на основе общенаучного метода, что содействует овладению теоретическими и экспериментальными методами познания.


§ 5. Особенности конструирования содержания темы «Электромагнитная индукция» курса физики

В учебниках используются два способа введения электромагнитной индукции. Согласно первому формулировка закона Фарадея даётся без вы

вода со ссылкой на результаты проделанных учёными выводов:


§ 14. Разделение разноименных зарядов в проводнике,

движущемся в однородном магнитном поле

Постоянный электрический ток может существовать лишь в замкнутой цепи при наличии в ней источника тока. Замкнутая (или полная) электрическая цепь состоит из внутреннего и внешнего участка цепи. Источник тока образует внутренний участок цепи. Внешний участок составляют различные потребителя тока и подводящие провода. Источник тока поддерживает напряжение на внешнем участке цепи и, создавая в нем электрическое поле, обеспечивает упорядоченное движение носителей электрического заряда (рис.41, стрелкой указано направление тока, т.е. направление движения положительно заряженных частиц).

Известно, что работа электростатических сил по замкнутому контуру равна нулю. Однако создание тока в проводниках сопровождается выделением внутренней энергии, т.е. проводник нагревается. Поэтому в любой цепи должен быть источник энергии, поставляющий ее в цепь. Для того чтобы ток в цепи не прекращался, заряженные частицы, перемещающиеся от положительного полюса к отрицательному полюсу по внешнему участку цепи, должны вновь возвращаться на положительный полюс источника. Следовательно, на внутреннем участке цепи они должны двигаться против действующих на них электростатических сил. Для этого на заряды должны действовать внешние силы неэлектростатической природы, называемые сторонними силами. Сторонние силы внутри источника направлены противоположно электростатическим силам. Работа этих сил вдоль замкнутого контура должна быть отличной от нуля. Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника энергию и затем отдают ее проводникам электрической цепи. Природа сторонних сил может быть самой разнообразной.

Действие источника тока в электрической цепи подобно действию насоса для перекачивания жидкости. Течение жидкости, движущейся из верхнего резервуара по наклонной трубе, сопровождается потерями энергии на трение. Для перемещения жидкости в системе используется насос. Под его действием скорость течения жидкости увеличивается. Жидкость возвращается в резервуар. В этом случае сила давления на жидкость в насосе выполняет роль сторонней силы.

Выясним, например, почему возникает ток в установке, показанной на рисунке 42. Установка состоит из дугообразного магнита на подставке и гальванометра, который служит для измерения силы тока порядка нескольких микроампер. К клеммам гальванометра присоединим гибкий длинный изолированный проводник. Проводник вместе с гальванометром образует электрическую цепь (замкнутый контур).

Стрелка прибора стоит на нуле, значит, в цепи нет источника тока. Возьмем провод двумя руками и начнем перемещать его в вертикальной плоскости между полюсами дугообразного магнита. Мы видим, что стрелка гальванометра отклонится от нуля, показывая, что в цепи появился электрический ток.

Для объяснения наблюдаемого явления воспользуемся рисунком 43, на котором изображен участок провода, находящийся в области магнитного поля дугообразного магнита, и несколько электронов проводимости внутри проводника. Магнитное поле между полюсами дугообразного магнита можно считать однородным. Точки на рисунке означают, что линии магнитной индукции этого поля направлены перпендикулярно плоскости рисунка к нам.

Вместе с проводом, движущимся относительно Земли со скоростью 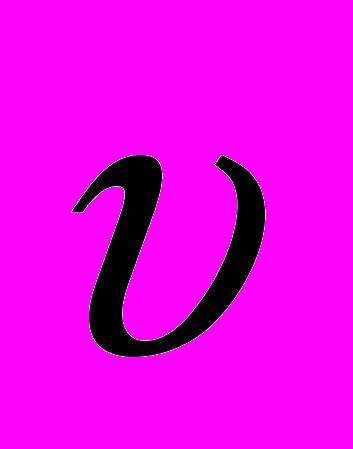вверх, движутся и свободные электроны. На каждый из них действует сила , направление которой определяется правилом левой руки. Под действием этой силы электроны будут ускоряться, смещаясь влево вдоль провода.

В результате перемещения электронов проводимости на левом конце участка провода появляется избыток электронов, а на правом - их недостаток (рис. 44). Следовательно, действие силы Лоренца привело к появлению напряжения между концами участка провода, т.е. движущийся участок провода стал «источником тока» с положительным полюсом на конце 1 и отрицательным – на конце 2.

Внутри участка провода создается электрическое поле. Когда участок замыкается на гальванометр, под действием этого поля электроны проводимости начинают двигаться по внешнему участку цепи от правого конца к левому концу провода. Стрелка гальванометра при этом отклоняется от нулевого деления. По участку 2-1 электроны движутся под действием магнитного поля.

В замкнутой цепи постоянный ток может существовать, если в ней действуют сторонние силы.


Экспериментальное исследование


Определите знаки полюсов электрической батареи, на которой отсутствуют их обозначения. В вашем распоряжении имеется следующее оборудование: лампа на подставке, кусок проволоки, компас, электрическая батарея – источник постоянного тока.

Разработайте план, сделайте пояснительные рисунки и защитите свой проект исследования. α

Вопросы


1. Каковы условия существования электрического тока в цепи? 2. По условным обозначениям элементов электрической цепи (см. рис. 41.) назовите их. 3. Какова роль сторонних сил в источнике электрического тока? 4. Какие частицы являются носителями электрического заряда в металлическом проводнике? 5. Почему возникает избыток электронов на одном конце участка проводника и их недостаток на другом (см. рис. 44.)?


Задания и упражнения


1. Укажите направление в точке С линии индукции магнитного поля, создаваемого током проводника АВ (рис. 45).

2. На рисунке 46 показаны сечения двух проводников с током, расположенных перпендикулярно к чертежу. Как направлена в точке А: а) индукция магнитного поля, созданного током I₁; б) индукция магнитного поля, созданного током I₂?

На основании какого принципа определяется вектор индукции магнитного поля в точке А, образованного токами I₁ и I₂?

3. В однородное магнитное поле влетает частица, траектория которой - дуга окружности (рис. 47). Каков заряд частицы?

4. В однородное магнитное поле влетает частица, траектория которой - дуга окружности (рис. 48). Как направлен вектор магнитной индукции (к нам или от нас)?

5. По внешней цепи переносится заряд q (см. рис. 41). Чему равна работа сил электрического поля, если напряжение на внешнем участке цепи U?


§ 15. Электродвижущая сила


Предположим, что два параллельных проводника в виде пластин с одной стороны подключены к амперметру, а с другой замкнуты металлической перемычкой bc (рис. 49), которая может перемещаться вдоль пластин. Электрическая цепь (проводящий контур) помещена в однородное магнитное поле. Линии магнитной индукции перпендикулярны плоскости контура и направлены к нам. Будем перемычку перемещать вправо с постоянной скоростью 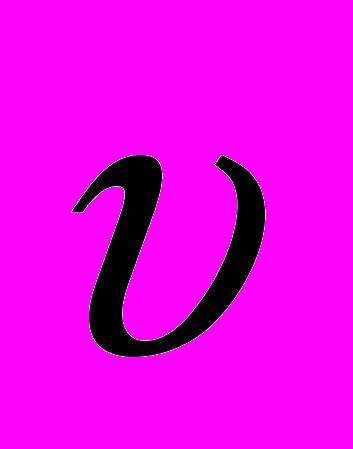. По показанию амперметра мы видим, что в цепи возник электрический ток. Перемычку можно рассматривать как «источник тока». В предыдущем параграфе мы выяснили, что выше, положительным полюсом «источника» служит конец перемычки 1, а отрицательным полюсом – конец 2.

При перемещении зарядов в источнике, от одного конца перемычки до другого на расстояние l, сторонними силами совершается работа. Она равна произведению модуля силы Лоренца на длину l перемычки:

A = F_Л l = qυBl, (1)

где q – модуль заряда электрона проводимости.

Для характеристики источника тока вводят физическую величину – электродвижущую силу.

Электродвижущей силой (ЭДС) называют физическую величину, равную отношению работы сторонних сил по перемещению положительного заряда вдоль замкнутой цепи к этому заряду.

Обозначается ЭДС буквой ℰ. Таким образом,

ℰ = А/q. (2)

Из этой формулы видно, что единицей ЭДС, так же как и электрического напряжения, является вольт.

ЭДС в замкнутом контуре определяет работу сторонних сил по перемещению положительного заряда, равного 1 Кл, вдоль контура.

На практике ЭДС источника тока измеряют с помощью вольтметра в разомкнутой цепи. Для этого к его зажимам параллельно присоединяют вольтметр и измеряют ЭДС.

Мы уже отмечали, что происхождение сторонних сил может быть различным. Но во всех случаях они создают и поддерживают напряжение на зажимах цепи. Например, в гальванических элементах и аккумуляторах ЭДС возникает за счет химических процессов, в магнитоэлектрических генераторах ЭДС возникает на концах проводящей обмотки, вращающейся в магнитном поле. В рассмотренном нами случае ЭДС возникла в проводнике, движущемся в магнитном поле перпендикулярно самому себе и линиям магнитной индукции. Но во всех случаях ЭДС определяется по формуле (2).

ЭДС – это алгебраическая величина, она может быть как положительной, так и отрицательной. Чтобы установить знак ЭДС, произвольно выбирают направление обхода контура. Пусть направление обхода контура противоположно направлению хода часовой стрелки (рис.50,а).

Выбранное направление обхода совпадает с направлением перехода зарядов от отрицательного полюса к положительному полюсу источника тока. В этом случае значение ЭДС считают положительным. При этом легко установить, что направление тока совпадает с направлением обхода.

ЭДС считается положительной, если внутри источника тока обход совершается от отрицательного полюса к положительному. Если обход внутри источника тока совершается от положительного полюса к отрицательному, то ЭДС отрицательна. На рисунке 50, б изображена цепь, в которой ЭДС имеет отрицательное значение. Электрический ток в цепи течет в сторону, противоположную направлению обхода.

ЭДС перемычки (см. рис. 49) отрицательна. Определим ее. Из формулы (1) и (2) следует, что:

ℰ = - qυB .

Источник тока характеризуется электродвижущей силой.


Теоретическое исследование


При записи формулы работы (1) использовалась упрощенная модель мысленного опыта (см. рис. 49). Уточним эту модель.

1. Следовало бы учесть тот факт, что сила Лоренца в действительности перпендикулярна не скорости перемычки 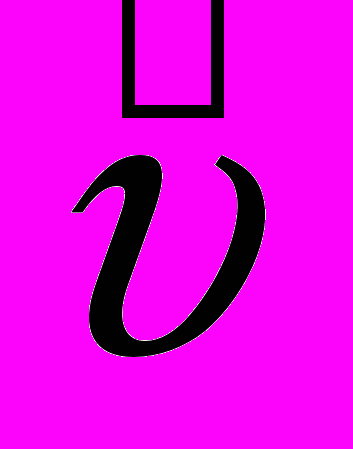, а полной скорости электронов 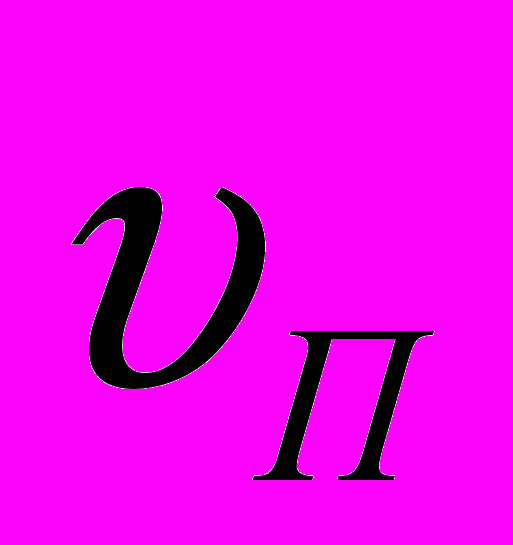, равной векторной сумме скорости перемычки 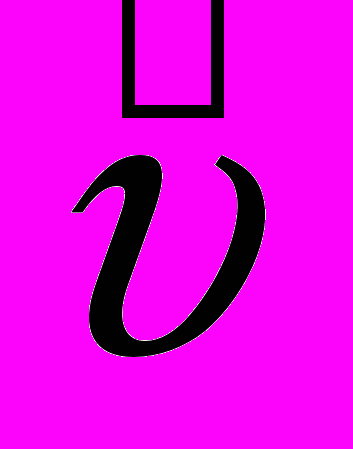и скорости движения электронов вдоль проводника : 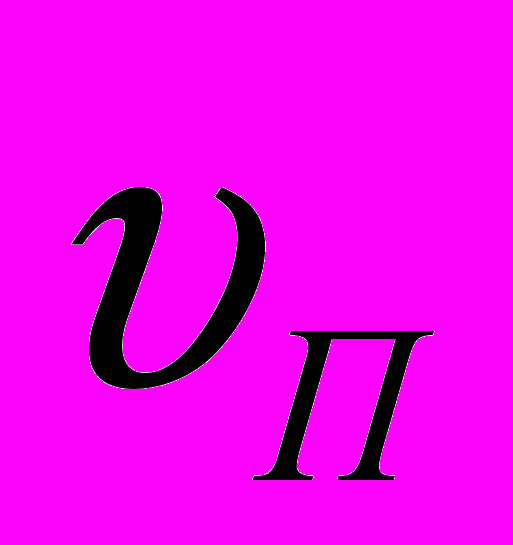=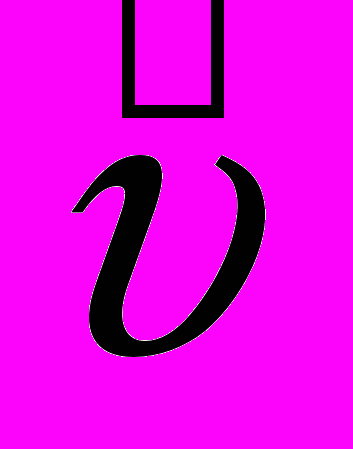+ .(рис. 2). Поэтому в формулу (1) для вычисления работы нужно поставить силу, равную по модулю проекции силы Лоренца F_y на направление проводника, а вместо скорости перемычки 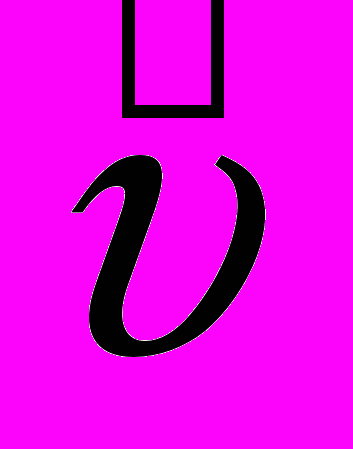- полную скорость электронов.

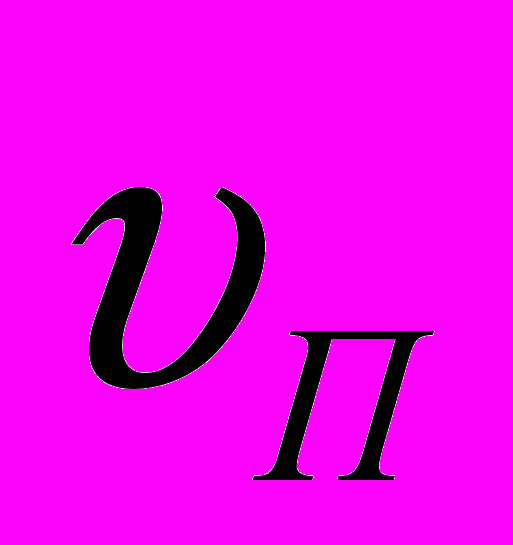Докажите, если учесть оба уточнения, то все равно получим для работы ту же формулу (1).

2. Как следует из рисунка 51, не равна нулю проекция силы Лоренца на направление, перпендикулярное проводнику. Предположим, что перемычка движется равномерно и прямолинейно вдоль пластин.

Чему равна внешняя сила, действующая на перемычку вдоль оси OX, если проекция силы Лоренца равна F_x?

Что произойдет, если перемычку предоставить самой себе, т.е. на неё перестанет действовать внешняя сила?


Вопросы


1. Какая физическая величина характеризует источник тока? 2. Укажите на рисунке (см. рис. 134 уч.) источник тока и его полюсы. 3. По какой формуле определяют ЭДС? 4. Какую работу совершают сторонние силы «источника тока» (движущейся перемычки) по перемещению положительного заряда 1 Кл вдоль перемычки? 5. При каком обходе замкнутого проводящего контура (см. рис. 41.) знак ЭДС положительный?


Задания и упражнения


1. На источнике тока написано 1,5 В. Что это означает?

2. Проводник движется в магнитном поле (рис. 52). Возникает ли на его концах ЭДС?

3. В цепи (см. рис. 49) длина перемычки равна 26 см, индукция магнитного поля составляет 0,1 Тл. Перемычка равномерно движется со скоростью 0,3 м/с. Найдите ЭДС индукции и ее знак.

4. ЭДС аккумулятора равна 6 В. Какую работу совершают сторонние силы за 30 с, если сила тока в цепи равна 0,5 А.

5. Изобразите простейшую электрическую цепь, состоящую из гальванического элемента или аккумулятора, лампочки накаливания, соединительных проводов. Выберите направление обхода контура и найдите знак ЭДС. Что нужно сделать, чтобы изменить знак ЭДС?


§ 16. Магнитный поток


Максимальный магнитный поток. Магнитное поле характеризуется также величиной, называемой магнитным потоком.

Поместим плоский замкнутый контур в однородное магнитное поле (рис. 53, а, б, в). Он ограничивает поверхность площадью S. Как видно из рисунка 53, а, модуль вектора магнитной индукции В₁ меньше модуля вектора магнитной индукции В₂ (рис. 53, б), так как число линий магнитной индукции не одинаково. Это означает, что магнитные потоки, пронизывающие контуры различны.

Произведение модуля вектора магнитной индукции В и площади поверхности S контура характеризует максимальный магнитный поток, пронизывающий данный контур.

Обозначим магнитный поток греческой буквой Ф (фи). Тогда можно записать:

Ф = В S.

Эта формула позволяет установить единицу магнитного потока.

Единицей магнитного потока в СИ служит в е б е р ( Вб). Вебер равен потоку, создаваемому однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции. Эта единица названа в честь немецкого физика В.Э. Вебера (1804 – 1891).

Исходя из формулы Ф_мак= ВS, магнитный поток можно истолковать как величину, прямо пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S, перпендикулярную линиям индукции.

Чем больше линий магнитной индукции пронизывает контур, тем больше магнитный поток.

Магнитный поток. Поместим плоский замкнутый контур в однородное магнитное поле так, чтобы линии магнитной индукции, пронизывающие контур, проходили через него под некоторым углом α (рис. 54). Значение магнитного потока зависит от угла α между вектором магнитной индукции 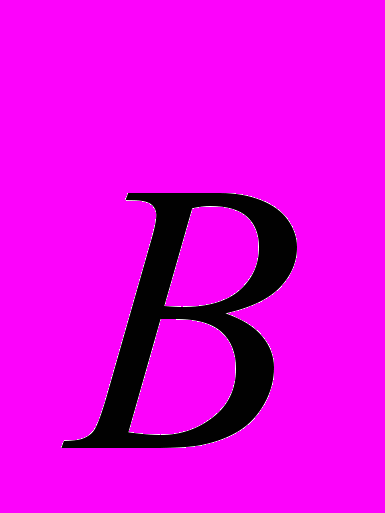и нормалью к плоскости контура 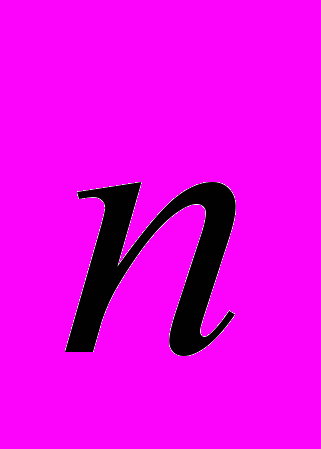. Нормаль – это вектор. Его направление определяется направлением обхода контура, которое выбирается произвольно. Если вращать рукоятку буравчика по направлению обхода контура, то направление его поступательного перемещения указывает направление вектора .

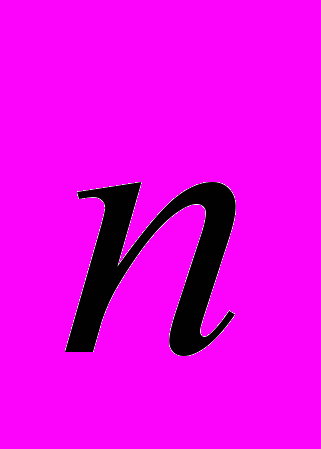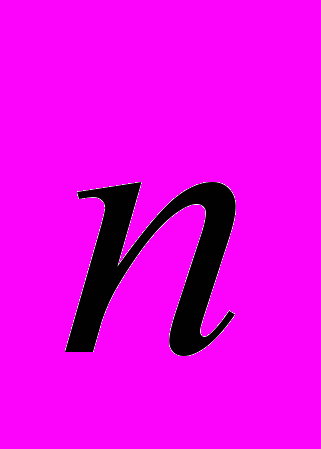Магнитным потоком через поверхность называют величину, равную произведению модуля вектора магнитной индукции, площади поверхности, ограниченной контуром, и косинуса угла между вектором и нормалью к поверхности.

Тогда с учетом угла α можно записать:

Ф = В S cos α.

Если α = 0^о, т.е. векторы и 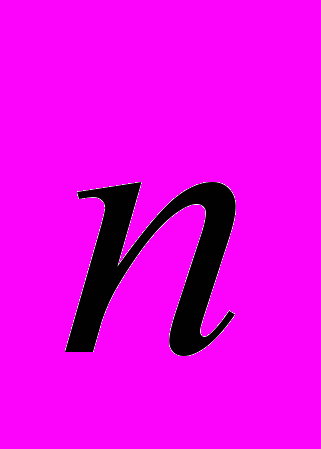параллельны и сонаправлены, то магнитный поток положителен и имеет максимальное значение, равное Ф_мак= В S.

Если линии индукции параллельны плоскости контура ( = 90^о), то они не пронизывают в контур. Так как cos 90^о = 0, то и магнитный поток равен нулю. Если линии индукции образуют с нормалью к контуру угол, равный 180^о, то магнитный поток через контур отрицателен: Ф = - ВS.

Для удобства направление обхода контура мы будем выбирать таким образом, чтобы магнитный поток был положительным.


Измерение физических величин


Выразите единицу магнитного потока 1 Вб через основные единицы СИ.

Вопросы

1. От каких физических величин зависит магнитный поток, пронизывающий контур? 2. Чему равен максимальный магнитный поток? 3. Почему можно утверждать: чем больше площадь контура, находящегося в магнитном поле, тем больше будет магнитный поток? 4. В каком случае магнитный поток через контур равен нулю? 5. Как выбирается направление обхода контура?


Задания и упражнения


1. Чему равен магнитный поток в случае, когда плоскость контура расположена вдоль линий магнитной индукции?

2. Как изменится магнитный поток, пронизывающий контур, если модуль вектора магнитной индукции увеличить в 4 раза, а площадь поверхности контура уменьшить в 2 раза?

3. В однородном магнитном поле с индукцией 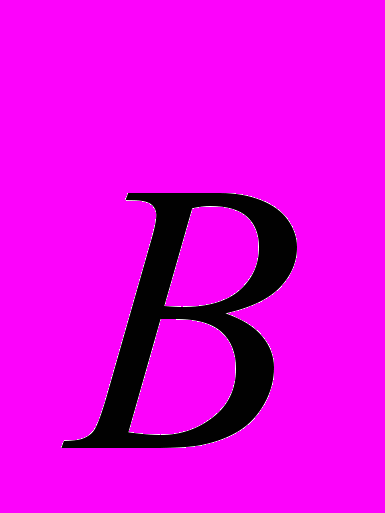находится проводящий контур, охватывающий поверхность площадью S. Чему равен магнитный поток через эту поверхность, если угол между нормалью к поверхностью и вектором магнитной индукции составляет: а) 0^о, б) 90^о, в) 180^о?

4. Магнитный поток, пронизывающий контур, равен 0,3 мВб. Площадь контура 30 см². Чему равна магнитная индукция однородного магнитного поля, если контур расположен перпендикулярно линиям магнитной индукции?

5. В однородном магнитном поле с индукцией 5 мТл находится проводящий контур площадью 50 см². Чему равен магнитный поток через контур, если угол между нормалью к поверхностью и вектором магнитной индукции составляет: а) 0^о, б) 90^о, в) 30^о?