Н. Ф. Шемяков Лекция
| Вид материала | Лекция |
- «Социальная стратификация и социальная мобильность», 46.19kb.
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
- Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
- Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
- Тема Лекция, 34.13kb.
- Лекция посвящена определению термина «транскриптом», 219.05kb.
- А. И. Мицкевич Догматика Оглавление Введение Лекция, 2083.65kb.
Постоянный ток Н. Ф. Шемяков
__________________________________________________________________________________________________________________
Лекция 9
5.22. Приближения слабой и сильной связи. Функция Блоха
Дальнейшее развитие квантовая теория проводимости металлов получила в зонной теории Зоммерфельда.
Согласно этой теории кристаллическое тело рассматривается, как периодическая структура, в которой ионы, расположенные в узлах кристаллической решетки, создают электрическое поле. Для описания поведения электрона в этом поле используются методы приближения сильной и слабой связи. По методу «приближения сильной связи» каждый электрон имеет свою систему дискретных энергетических уровней, а энергия связи электрона с атомами значительно больше их кинетической энергии движения в кристалле. Изза сильной связи электрона с атомами только внешние (валентные) электроны при сближении атомов на расстояние сравнимое с размерами самих атомов (r 1010 м), переходят от одного атома к другому. Согласно метода «приближения слабой связи» считается, что энергия взаимодействия
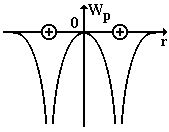
Рис. 5.19
электрона с решеткой много меньше их кинетической энергии, что позволяет считать электроны свободными. Если два изолированных атома находятся на расстоянии много больше их диаметра, то потенциальный барьер для внешних электронов у этих атомов настолько широк, что вероятность просачивания электрона сквозь потенциальный барьер близка к нулю (рис. 5.19).
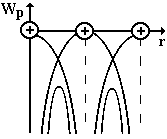
Рис. 5.20
При сближении атомов на расстояние, сравнимое с периодом кристаллической решетки твердого тела происходит перекрытие электрических полей изза сильного взаимодействия атомов.
Потенциальные кривые накладываются друг на друга (рис. 5.20), происходит их сужение и понижение. Поэтому получают свободу перемещения по кристаллу не только валентные, но и электроны, расположенные на более глубоких энергетических уровнях, за счет туннельного прохождения сквозь потенциальный барьер, отделяющий соседние атомы друг от друга. Основной задачей теории твердого тела является определение энергетического спектра электронов в кристалле. Для свободного электрона все точки пространства эквивалентны и вероятность его обнаружения в той или иной области этого пространства одинакова и не зависит от координат электрона.
Иначе обстоит дело с электронами, движущимися в периодическом поле правильной кристаллической решетки, образованной ионами, расположенными в ее узлах (рис. 5.21).
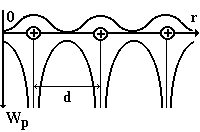
Рис. 5.21
Вероятность обнаружения электрона в данной точке кристалла должна быть периодической функцией координаты, например х. Положения, отличающиеся друг от друга на величину, кратную постоянной решетки d, для электрона являются одинаково вероятными. Различными будут только положения в пределах одного периода.
Следовательно, амплитуда волновой функции электрона (х), движущегося в периодическом электрическом поле решетки, не остается постоянной, а периодически изменяется (модулирована с периодом, равном d) с течением времени.
Если обозначить амплитуду волновой функции через u(x), то волновую функцию электрона, движущегося в направлении оси Х, можно представить в виде функции Блоха: (х) = u(x)e i k x ,
где е основание натуральных логарифмов; i = 1; k = 2 / волновое число; длина волны электрона.
Таким образом, на распределение электронов по энергетическим уровням в твердых телах влияет: 1. внутреннее периодическое электрическое поле ионов кристаллической решетки; 2) взаимодействие между атомами (происходит перекрытие волновых функций валентных электронов).
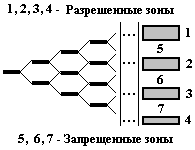
Рис. 5.22
В результате этого влияния происходит объединение энергетических уровней в зоны разрешенных энергий, разделенных запрещенными зонами (рис. 5.22).
Вывод: При объединении N атомов вещества в кристалл вместо отдельных энергетических уровней, в энергетическом спектре электронов, возникают зоны разрешенных энергий из (2
 +1)N дискретных уровней (
+1)N дискретных уровней ( орбитальное квантовое число).
орбитальное квантовое число). Расстояние между уровнями в разрешенной зоне кристалла очень мало.Например, при ширине разрешенной зоны в 1 эВ (1эВ = 1,61019 Дж) это расстояние составляет примерно 1022 эВ. Но число уровней в разрешенных зонах конечно, что оказывает влияние на распределение электронов по энергетическим состояниям.
5.23. Проводники, диэлектрики
и полупроводники в зонной теории
Зонная теория один из основных разделов квантовой теории твердых тел, которая описывает движение электрона в кристаллах. Согласно этой теории электроны внешних энергетических зон имеют примерно одинаковую свободу движения во всех твердых телах независимо от того, являются они металлами или диэлектриками. Действительно их движение осуществляется путем туннельного перехода от одного атома к другому. Современные представления о строении диэлектриков существенно отличаются от представлений о связанных зарядах, лежащих в основе классической теории.
Наличие свободных электронов является лишь необходимым условием проводимости у тел, но не достаточным.
В зонной теории проводники, диэлектрики и полупроводники по электрическим свойствам отличаются расположением разрешенных и запрещенных зон энергии и заполнением этих зон электронами.
Чем больше энергия электрона в изолированном атоме, тем шире разрешенная зона и меньше ширина запрещенной зоны.
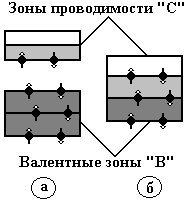
Рис. 5.23
Последняя полностью заполненная электронами зона называется валентной зоной.
Следующая за валентной зоной свободная зона или частично заполненная электронами при Т = 0 К, называется зоной проводимости.
Электропроводность твердого тела зависит не от числа валентных электронов, а от отношения числа электронов в зоне проводимости к общему числу энергетических уровней в этой зоне.
К проводникам относятся тела, у которых над полностью заполненной электронами валентной зоной располагается частично заполненная электронами зона проводимости.
Такие зоны возникают в том случае, если энергетический уровень, из которого она возникает, заполнен в атоме не полностью, например, у щелочных элементов и металлов (рис. 5.23, а).
Частично заполненная электронами зона может образоваться изза перекрытия валентной зоны и зоны проводимости (гибридная зона), что имеет место у бериллия и щелочноземельных элементов (рис. 5.23, б).
Следовательно, достаточным условием проводимости тел является наличие в их энергетическом спектре разрешенных зон, заполненных электронами лишь частично.
Поэтому даже слабое электрическое поле способно перевести электроны на свободные энергетические уровни в зоне проводимости, т. е. появится электрический ток.
К диэлектрикам и полупроводникам относятся тела, у которых при Т = 0 К над полностью заполненными электронами валентными зонами находятся свободные зоны (зоны проводимости). Эти зоны разделены широкими запрещенными зонами. К ним относятся химические элементы, например, алмаз, кремний, германий, а также многие химические соединения окислы металлов, нитриды и т. д. К диэлектрикам относятся вещества, у которых валентная зона отделена от зоны проводимости широкой запрещенной зоной (W 23 эB).
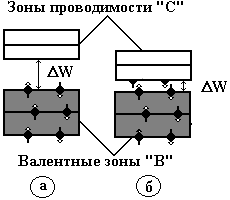
Рис. 5.24
Например, у алмаза W = 5,2 эB, у нитрида бора W = 4,6 эB, у Al2O3 W 7 эB и т. д. (рис. 5.24, а). К полупроводникам относятся вещества, у которых имеется более узкая запрещенная зона между валентной зоной и зоной проводимости, чем у диэлектриков ее энергия W 23 эB.
Например, у германия ширина запрещенной зоны W = 0,66 эB, у кремния W = 1,08 эB, у арсенида галлия W =1,4 эB (рис. 5.24, б).
Под действием электрического поля напряженностью Е = 105 В/м (обычные источники тока) может быть сообщена электронам энергия W 103 эВ, что значительно меньше ширины запрещенной зоны в диэлектриках и полупроводниках. В табл. 5.1 приведены значения ширины запрещенной зоны (энергии активации) W и концентрации электронов n в металлах, диэлектриках и полупроводниках.
Таблица 5.1
| W, эВ | 10 | 5 | 3 | 2 | 1 | 0,75 | 0,5 | 0,1 | 0,01 |
| n, м 3 | 1059 | 1029 | 10 | 108 | 1017 | 1019 | 1021 | 1024 | 1029 |
| | Диэлектрики | Полупроводники | Металлы | ||||||
9.13. Понятие о сверхпроводимости
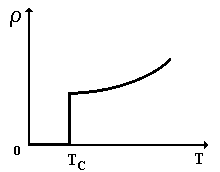
Рис. 9.29
Сверхпроводимость свойство многих веществ, в том числе и проводников и многих сплавов и др., состоящее в том, что их электрическое сопротивление скачком уменьшается до нуля при охлаждении образцов ниже критической температуры ТС, характерной для данного материала (рис. 9.29).
Впервые сверхповодимость обнаружена Камерлинг-Оннесом при охлаждении ртути ниже ТС = 4,3 К. Удельное сопротивление веществ в сверхпроводящем состоянии мало ( < 1022 Омм), в то время как, например, у чистых образцов меди или серебра при температуре жидкого гелия 10 11 Омм.
Классическая физика не смогла объяснить это явление, и сверхпроводимость оставалась загадкой до 1957 г., когда оно получило теоретическое объяснение в работах Бардина, Купера, Шриффера и Боголюбова с использованием квантовой теории.
Одним из удивительных квантовых свойств микрочастиц является существенное различие в их поведении в зависимости от того, обладают они целым или полуцелым спином.
Ансамбль N квантовых частиц с полуцелым спином называют фермионами, к которым относятся электроны.
Фермичастицы подчиняются принципу Паули.
Согласно этому принципу в твердых телах при Т = 0 К на каждом энергетическом уровне в разрешенной зоне могут находиться одновременно только два электрона с противоположными спинами.
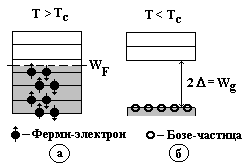
Рис. 9.30
В металлах число валентных электронов таково, что, разместив все электроны по разрешенным уровням, начиная с низшего, можно получить частично заполненную зону (зона проводимости “С”), в которой наивысший занятый электронами уровень называют уровнем Ферми (рис. 9.30, а).
Электропроводность обычных металлов определяется свойствами фермиэлектронов и процессами их рассеяния на ионах кристаллической решетки, совершающих тепловые колебания; примесях; дислокациях и других структурных несовершенствах кристалла.
При низких температурах сопротивление кристалла определяется в основном примесным рассеянием.
Даже в идеальном кристалле сопротивление всегда конечно, хотя и достаточно мало изза слабого взаимодействия электронов с решеткой, что действительно наблюдается в серебре, меди и других наилучших проводниках вплоть до температур Т 1017 К.
Иначе ведут себя частицы с целым спином (бозоны). При Т = 0 К они заполняют один, самый низший энергетический уровень, так как бозоны не подчиняются принципу Паули (рис.9.30, б).
Если спектр возбуждений такой системы удовлетворяет критерию Ландау, то движение бозечастиц при достаточно слабых возмущениях (низкие температуры, слабые электрические и магнитные поля и т. д.) происходит без потерь энергии, что эквивалентно обращению в нуль электросопротивления и возникновению сверхпроводимости (рис. 9.29).
Электроны в металлах взаимодействуют друг с другом двояко.
Вопервых, они отталкиваются как одноименные заряженные частицы (диэлектрическая проницаемость среды > 1).
Вовторых, электроны взаимодействуют с колебаниями решетки и обмениваются фононами.
Если один из электронов за счет кулоновского притяжения к положительным ионам решетки слегка ее деформирует, то второй электрон может взаимодействовать с этой областью деформации решетки, притягиваясь к ней.
В результате между этими электронами возникает эффективное притяжение, т. е. кристаллическая решетка является средой, диэлектрическая проницаемость которой < 1.
Притяжение объединяет электроны в куперовские пары с целым спином (S = 0), т. е. в бозечастицы.
В теории Бардина-Купера-Шриффера суммарный спин пары равен нулю, а импульсы электронов, составляющих пару, противоположны.
Причем спаренные электроны могут находить друг друга на расстояниях, равных многим периодам кристаллической решетки.
За счет принципа Паули спаривание двух электронов с одинаковыми спинами оказывается энергетически менее выгодным, чем образование пары с нулевым спином.
В 1950 г. экспериментально обнаружен изотопический эффект. Откуда следует, что
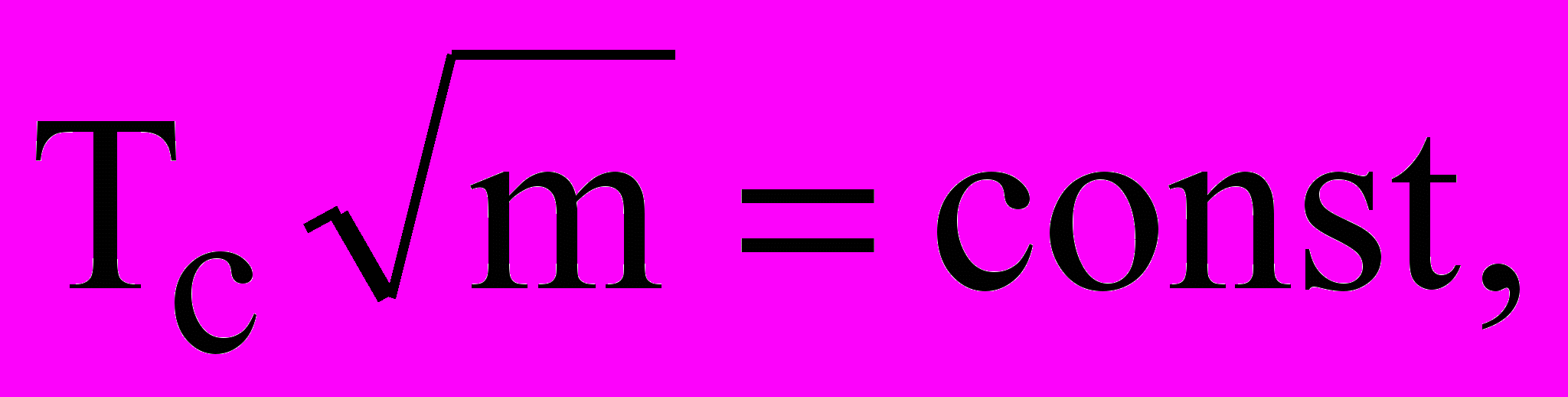 где m масса одного атома металла; Тc критическая температура сверхпроводимости.
где m масса одного атома металла; Тc критическая температура сверхпроводимости.Следовательно, чем тяжелее металл, тем больше сужается температурный диапазон 0 < T Тc, в котором металл находится в сверхпроводящем состоянии.
Но чем массивнее атомы, тем труднее возбуждать колебания, т. е. сверхпроводимость связана с колебаниями кристаллической решетки металла, в которой электроны проводимости взаимодействуют с фононами.
Согласно теории сверхпроводимости, например, один из электронов притягивая положительные ионы металла, создает вокруг себя повышенную плотность положительного заряда, который, в свою очередь, притягивает к себе другой электрон. Возникает как бы слабое притяжение между этими электронами.
Изза колебаний ионов металла, притяжение между электронами приводит к их рассеянию на колебаниях кристаллической решетки металла (эти колебания не прекращаются даже при абсолютном нуле температуры, при котором они являются нулевыми).
Квантовый механизм рассеяния электронов проводимости заключается в обмене фононами этими электронами, которые они испускают и поглощают.
Изза вырождения электронного газа в рассеянии участвуют только электроны с противоположно направленными импульсами из малой окрестности сферы Ферми (радиусом R =
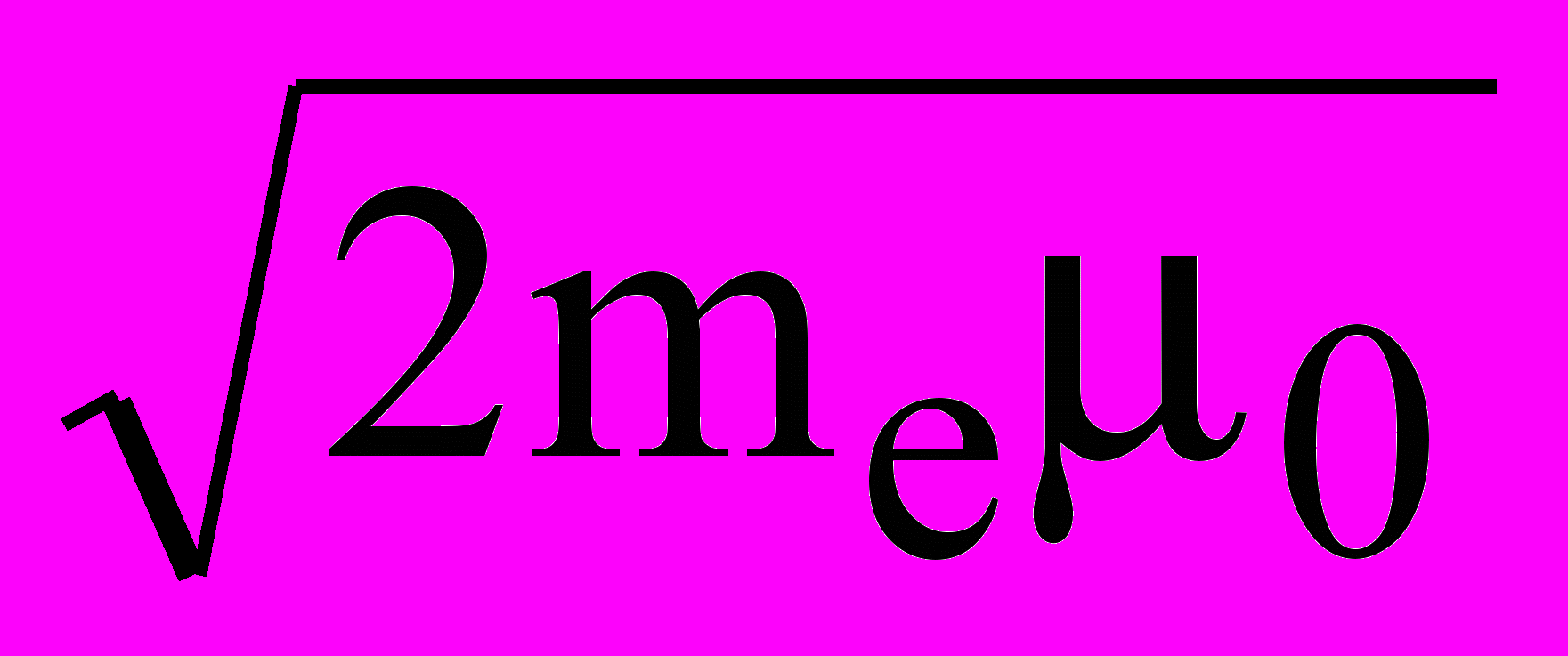 , равному максимальному абсолютному значению импульса электрона проводимости при температуре Т = 0 К), которая находится в импульсном пространстве, и описывается уравнением
, равному максимальному абсолютному значению импульса электрона проводимости при температуре Т = 0 К), которая находится в импульсном пространстве, и описывается уравнением Р2 / (2me) = 0,
где 0 химический потенциал электронов при температуре абсолютного нуля.
Обмен фононами наиболее интенсивен между электронами с противоположно направленными импульсами и спинами.
Если это притяжение преобладает над кулоновским отталкиванием электронов, то при низких температурах, при которых разрушающее действие теплового движения ослабевает, образуются куперовские пары.
Такая пара, не имея спина, подчиняется статистике Бозе Эйнштейна, имеет энергию связи порядка 103 104 эВ.
Благодаря этому куперовская пара оказывается носителем тока, которому металл не оказывает сопротивление.
Это происходит следующим образом. Когда металл охлаждается ниже критической температуры и в нем создан ток куперовских пар, т. е. возбуждено движение пар относительно кристаллической решетки металла.
Если связать это движение с системой отсчета, в которой пары покоятся, то кристаллическая решетка будет перемещаться.
При выключении электрического поля, создавшего ток, этот ток прекратиться, если электрическое поле решетки разрушит состояние покоя куперовских пар. Но для этого нужно затратить конечную энергию.
При слабых токах решетка движется медленно, и у нее нет необходимого запаса энергии, чтобы разрушить куперовскую пару.
Поэтому ток сохраняется, а металл оказывается сверхпроводником.
Характерный размер куперовской пары
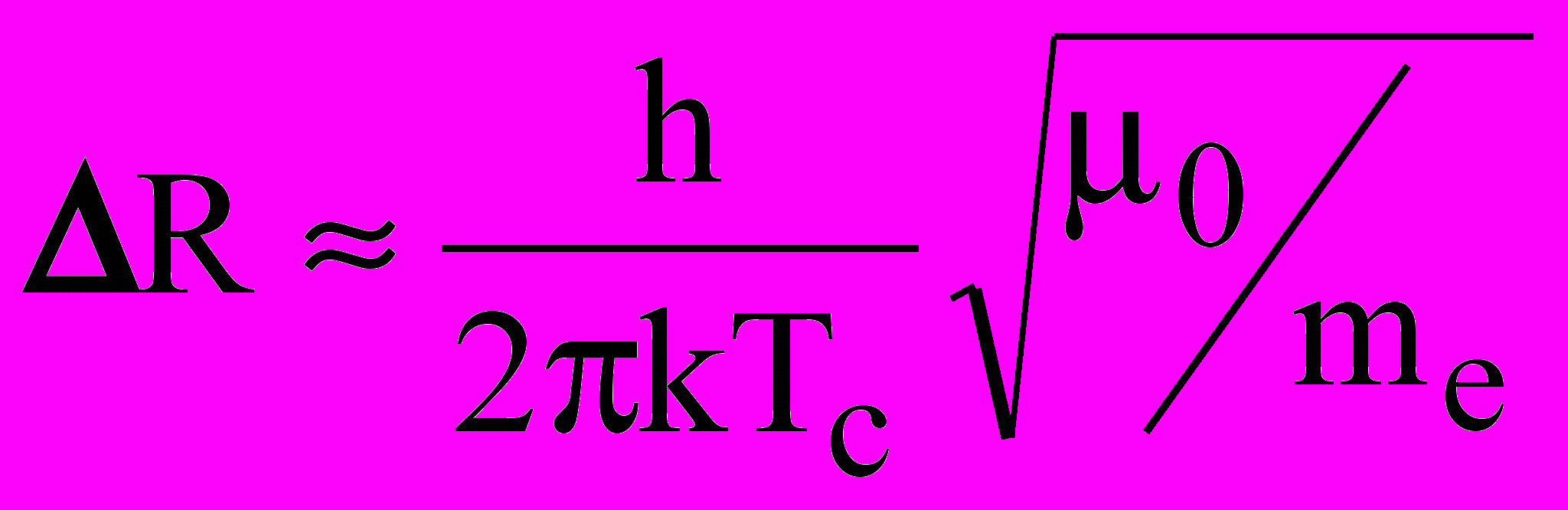
определяется длиной когеретности
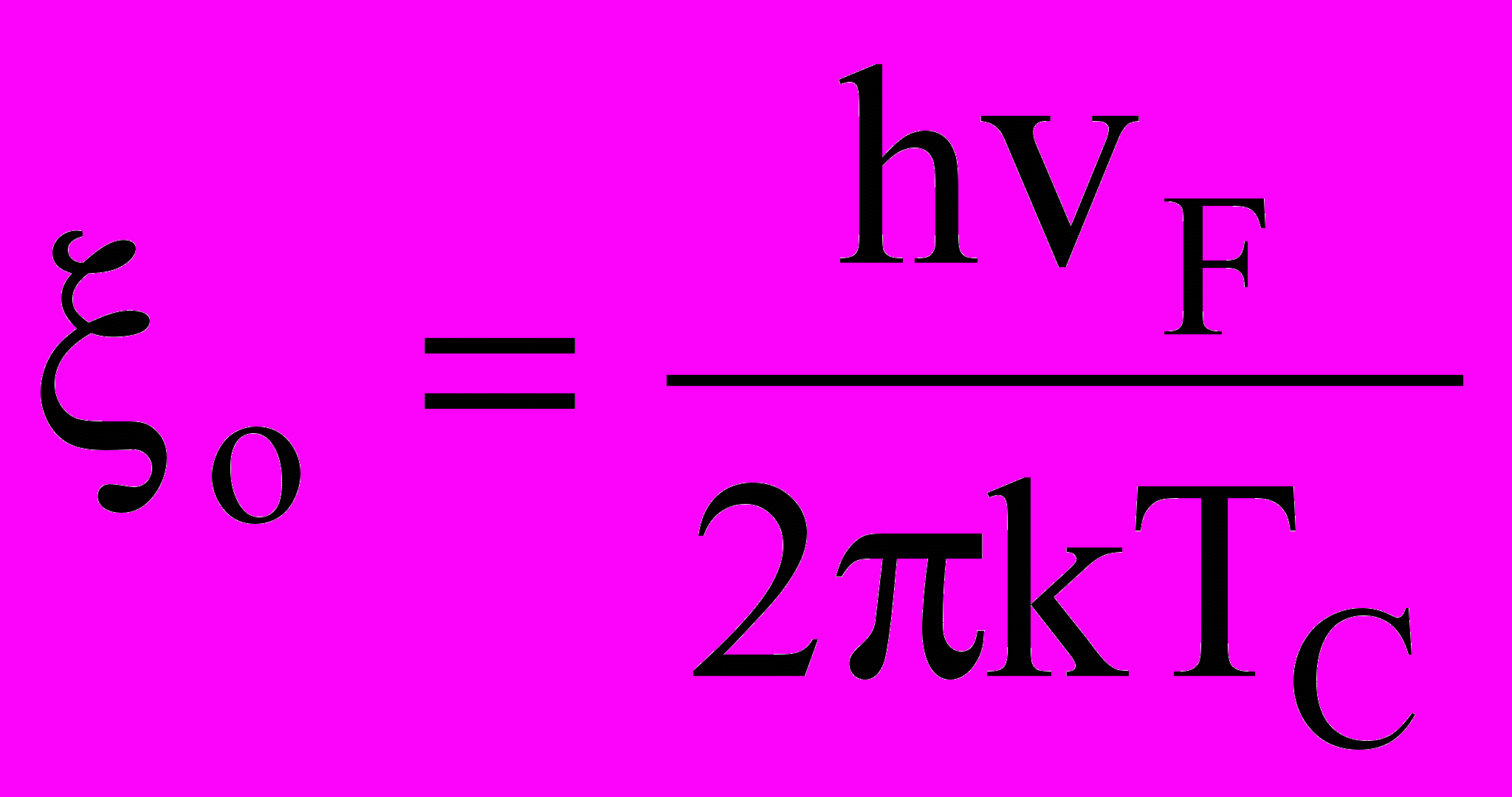 , (9.34)
, (9.34)где vF скорость электронов на уровне Ферми; h постоянная Планка; k постоянная Больцмана; ТС температура перехода в сверхпроводящее состояние.
При Тc 10 К и 0 5 эВ значение R106 м, что на четыре порядка превышает среднее межатомное расстояние в кристалле.
Энергия связи электронов в паре мала, т. е. 1,7kTC, и определяет величину щели в плотности состояний Wg = 2, образующуюся в энергетическом спектре на уровне Ферми при переходе в сверхпроводящее состояние (рис. 9.30, б).
Эта щель и отделяет уровень, на котором сконденсировались куперовские пары (бозечастицы), от ближайшего разрешенного уровня, расположенного выше уровня Ферми (в результате и оказывается выполненным критерий Ландау критерий сверхтекучести).
При температурах ниже ТС сопротивление сверхпроводника оказывается равным нулю.
Другим необычным свойством сверхпроводников является их способность полностью выталкивать слабое магнитное поле.
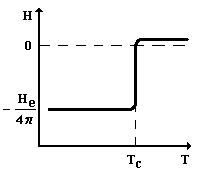
Рис. 9.31
Внешнее магнитное поле Не не проникает в глубь сверхпроводящего образца независимо от того, было ли это поле включено выше или ниже ТС.
Вследствие того, что магнитное поле Нi внутри образца равно сумме внешнего поля и поля намагничивания 4J, то сверхпроводник представляет собой идеальный диамагнетик с Нi = 0 и 4J = Не (рис. 9.31). В этом заключается эффект Мейснера.
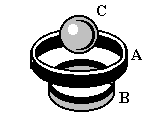
Рис. 9.32
Физически эффект Мейснера связан с тем, что у сверхпроводника, помещенного в слабое магнитное поле, в поверхностном слое толщиной L 1001000 Å наводятся круговые незатухающие токи, которые компенсируют внешнее магнитное поле (братья Лондоны, 1934 г.).
Такие сверхпроводники характеризуются механическим отталкиванием (“гроб Магомета”, рис. 9. 32), где над сверхпроводящими кольцами А и В, в которых циркулирует ток, зависла сфера С из сверхпроводника.
Это явление используют для сверхпроводящих подвесов в гироскопах, двигателях и т. д. КПД таких машин близок к 100%.
Поскольку сверхпроводимость бездиссипативное токовое состояние бозе конденсата куперовских пар, у которых спины электронов направлены противоположно друг другу, то в достаточно сильном магнитном поле оба спина стремятся к одинаковой ориентации вдоль, что и приводит к подавлению сверхпроводимости при
Н ≥ Нр,
где Нр парамагнитное критическое поле (парамагнитный эффект).
В сверхпроводниках первого рода, у которых 0 > 1,4L, при увеличении магнитного поля до Н = Не энергетически выгоднее разрушить сверхпроводимость сразу же во всем объеме образца, когда поле скачком проникает в него и весь образец переходит в нормальное состояние (рис. 9.33, а, б).
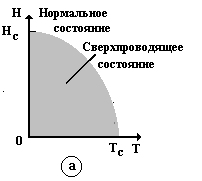
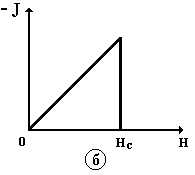
Рис. 9.33
Критическое поле НС зависит от температуры: при Т = 0 К оно имеет максимальное значение, затем монотонно убывает до нуля вплоть до ТС.
В 1952 г. Абрикосовым предложен другой метод разрушения сверхпроводимости магнитным полем.
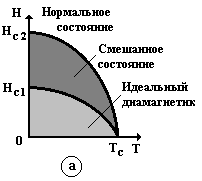
Рис. 9.34
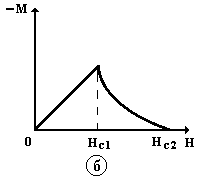
При более значительной глубине проникновения магнитного поля в сверхпроводник (в случае 0 < 1,4L) поверхностная энергия границы раздела нормальная фаза сверхпроводник отрицательна и энергетически выгодно не скачкообразное проникновение поля в объем всего образца, и формирование смешанного состояния (рис. 9. 34, а, б).
В этом состоянии сверхпроводник как бы пронизан нитями диаметром 0 (абрикосовские вихри).
Каждая нить представляет собой тонкую область нормальной фазы, ориентированной вдоль вектора
 , причем каждой нити соответствует один квант магнитного потока Ф0.
, причем каждой нити соответствует один квант магнитного потока Ф0. Смешанные состояния реализуются в сверхпроводниках II рода.
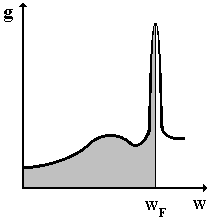
Рис. 9.35
В них полное выталкивание силовых линий магнитного поля происходит только в полях до НС1.
Выше этого поля начинается рождение областей нормальной фазы в форме нитей абрикосовских вихрей, их число увеличивается вплоть до Н = НС2.
Магнитное поле H > НС2 полностью разрушает сверхпроводящее состояние.
Хотя существование сверхпроводимости и ферромагнетизма невозможно, их конкуренция может привести к появлению нового типа магнитного порядка в сверхпроводящей фазе доменной магнитной структуры.
В последнее время существование сверхпроводимости обнаружено в системах тяжелых фермионов (например, СеСu2Si2, UРt3).
Действительно, при низких температурах эффективная масса фермиевских электронов велика
[m* (1001000)m0].
Так как величина эффективной массы электронов обратно пропорциональна ширине энергетической зоны, то в таких системах на уровне Ферми имеется очень узкий пик плотности состояний большой амплитуды, т. е. возникает резонанс (рис. 9. 35).
Функция g(W) определяет число разрешенных энергетических уровней, приходящихся на единичный интервал энергий состояний.
Величину g (при W = WF) можно определить из данных по измерению теплоемкости образца при низких температурах.
Сверхпроводимость обнаружена и в органических соединениях за счет экситонного механизма образования куперовских пар электронов.
В 1986 г. открыта высокотемпературная сверхпроводимость в различных соединениях, критическая температура которых ТС 100 К.
Существуют различные модели, объясняющие существование высокотемпературной сверхпроводимости.
Повышение ТС сверхпроводимости несомненно требует меньших затрат энергии.
9.14. Эффект Джозефсона
Согласно квантовой теории электроны проводимости проходят через диэлектрик в результате туннельного эффекта (просачивание сквозь потенциальный барьер). Если создать туннельный контакт, образованный двумя сверхпроводниками, пространство между которыми заполнено тонким слоем диэлектрика (109 м), то возможны два различных типа туннелирования джозефсоновское и одночастичное. Первое связано с туннелированием куперовских сверхпроводящих пар электронов сквозь слой изолятора, где через контакт протекает электрический ток. Второе одночастичное представляет собой просачивание сквозь потенциальный барьер микрочастиц. Когда ток через контакт не превышает критического, то на контакте отсутствует падение напряжения. Это явление называют стационарным эффектом Джозефсона.
При прохождении через контакт тока больше критического на нем возникает падение напряжения, и контакт начинает излучать электромагнитные волны. Это явление получило название нестационарного эффекта Джозефсона. Известно, что излучать электромагнитные волны может переменный ток. Поэтому через контакт при постоянном падении напряжения протекает переменный ток. Частота электромагнитного излучения связана с падением напряжения соотношением
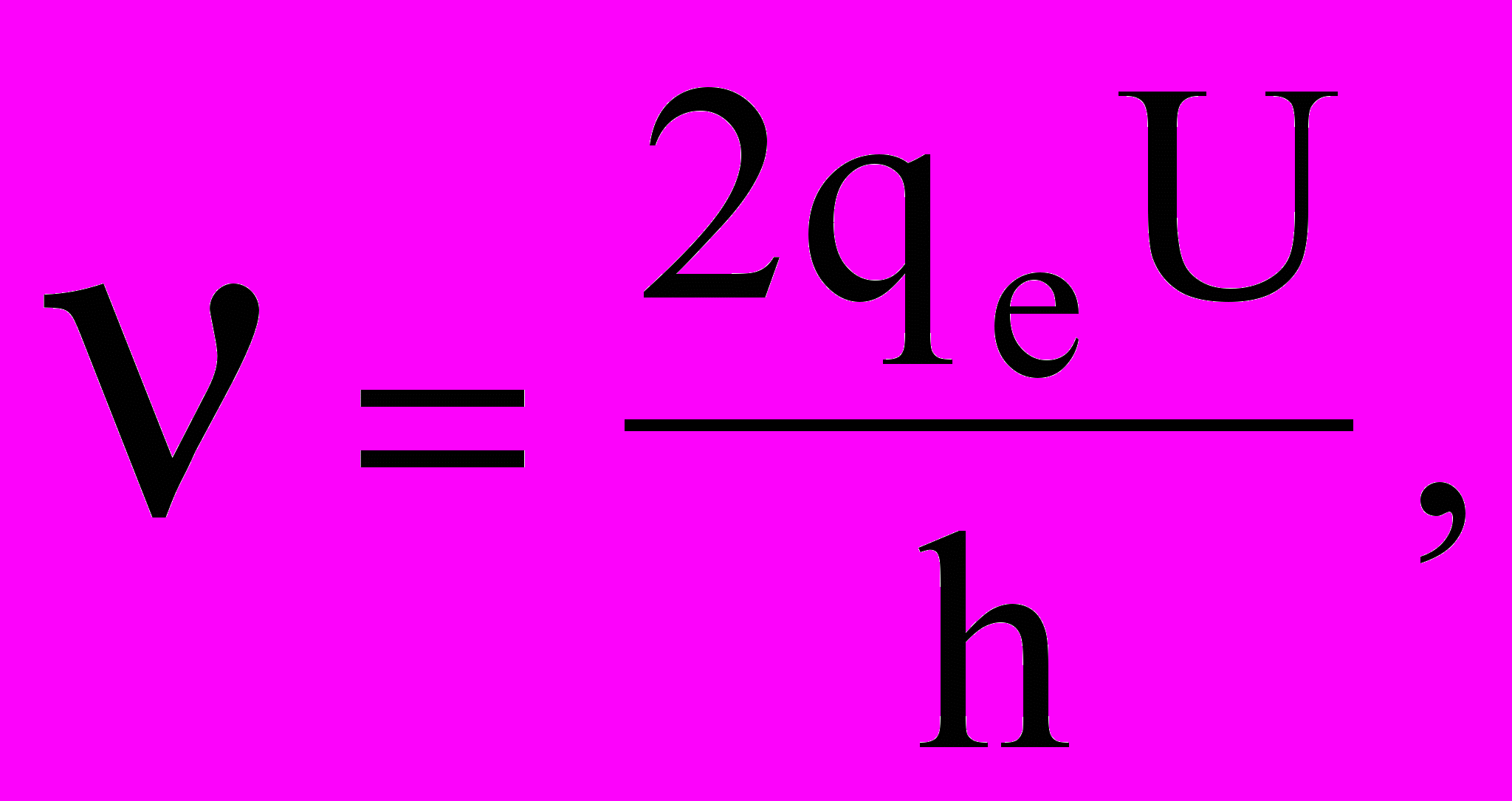 (9.35)
(9.35)где qe заряд электрона; h постоянная Планка; U падение напряжения.
Электроны, создающие сверхпроводящий ток, объединяются в куперовские пары и при переходе через контакт получают некоторую энергию WД = 2qeU. Такое состояние является возбужденным. Поэтому при переходе куперовской пары электронов в основное состояние сверхпроводника излучается квант света (фотон) с энергией = h.
Таким образом, нестационарный эффект Джозефсона является экспериментальным доказательством существования куперовских электронных пар в сверхпроводниках, о чем свидетельствует удвоенный заряд электрона в формуле (9.35). В стационарном и нестационарном эффектах Джозефсона волновая функция электрона, описывающая его квантовомеханические свойства, проявляется в макроскопических явлениях существовании тока и излучения.
Причем плотность тока Джозефсона jД пропорциональна градиенту волновой функции. В обычных металлах при отсутствии в них электрического поля ток равен нулю. При случайных изменениях разностей фаз волновых функций в металлах среднее значение плотности тока также равно нулю. Аналогичная ситуация наблюдается и в оптике, где при случайных изменениях разности фаз складываемых электромагнитных волн интерференция отсутствует.
Вывод: В эффекте Джозефсона впервые экспериментально обнаружено, что макроскопическое явление электрический ток определяется микроскопической характеристикой фазой волновой функции электрона и квантуется, т. е. принимает лишь дискретные значения.
Следовательно, границы между макро и микрофизикой “размываются”.
9.15. Квантование магнитного потока
Согласно основным положениям квантовой механики следует, что квантование энергии, заряда, импульса и других физических величин происходит только в микромире и свойственно процессам, протекающим в молекулах, атомах, ядрах.
Изучение явлений, происходящих при температурах, близких к Т = 0 К, показало, что возможно и макроскопическое квантование.
Действительно, экспериментально наблюдается квантование величин, характеризующих свойства макроскопических тел, размеры которых в 105 раз превосходят размеры атомов.
Если электрический ток протекает по сверхпроводящему металлическому кольцу, то он становится незатухающим изза отсутствия сопротивления и потерь на выделение теплоты ДжоуляЛенца.
Классическая теория природу этого явления объяснить не смогла.
Сверхпроводящее кольцо позволило наблюдать в большом масштабе квантовый эффект.
Сила тока в сверхпроводящем кольце не принимает любые значения и не изменяется непрерывно.
Как и всякий ток, сверхпроводящий ток создает магнитное поле. Квантование тока приводит к квантованию индукции магнитного поля, т. е. она может принимать только ряд дискретных значений, а не любые, как это следует из классической физики.
Это, в свою очередь, приводит к квантованию магнитного потока сквозь сечение сверхпроводящего кольца, т. е.
Фм = NФ0,
где N = 1, 2, 3, ...;
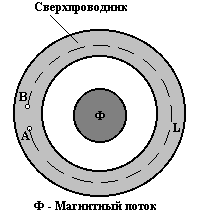
Рис. 9.36
Ф0 =
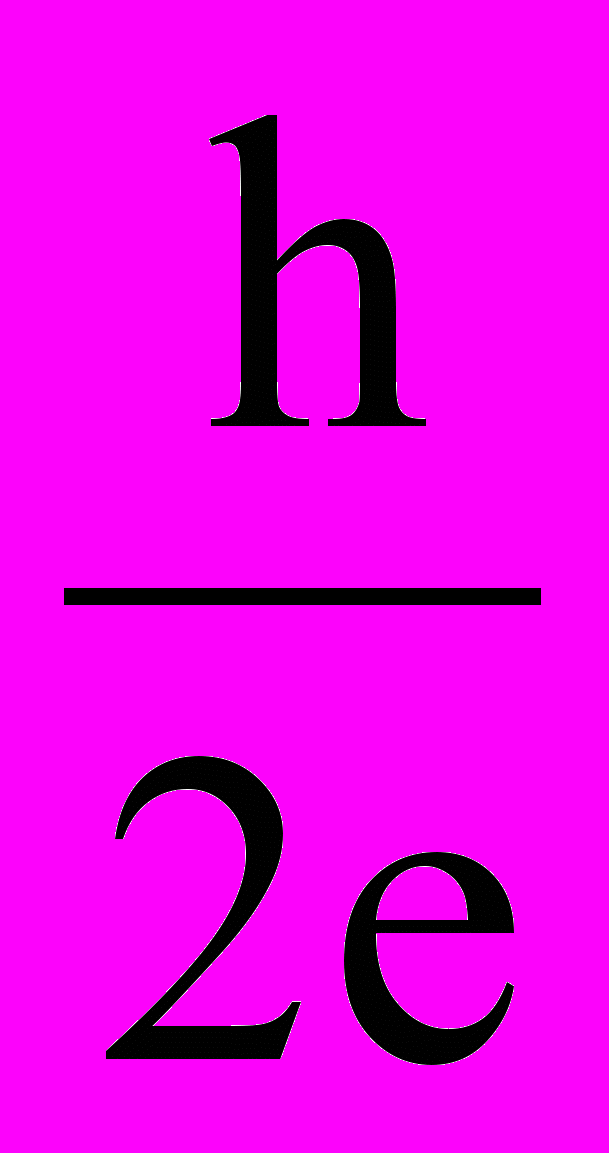 (9.36)
(9.36)Ф0 = 2,0678506(54)1015 Вб квант магнитного потока.
Магнитный поток макроскопическая величина, и возможность его квантования означает переход к большим, по сравнению с атомными, масштабам квантования.
Экспериментально квант магнитного потока определен на основе эффекта Джозефсона. При некоторых условиях критический ток через сверхпроводящий контакт оказывается периодически зависящим от внешнего магнитного потока с периодом, равным кванту магнитного потока Ф0.
Согласно теории сверхпроводимости куперовские электроны, создающие ток (Купера эффект), описываются единой волновой функцией, характеризующейся некоторой фазой фазовой когерентностью сверхпроводящих электронов, которая и приводит к квантованию магнитного потока.
В замкнутом сверхпроводящем кольце (рис. 9.36) разность фаз волновой функции между точками А и В
АВ = А В,
удовлетворяет соотношению Джозефсона
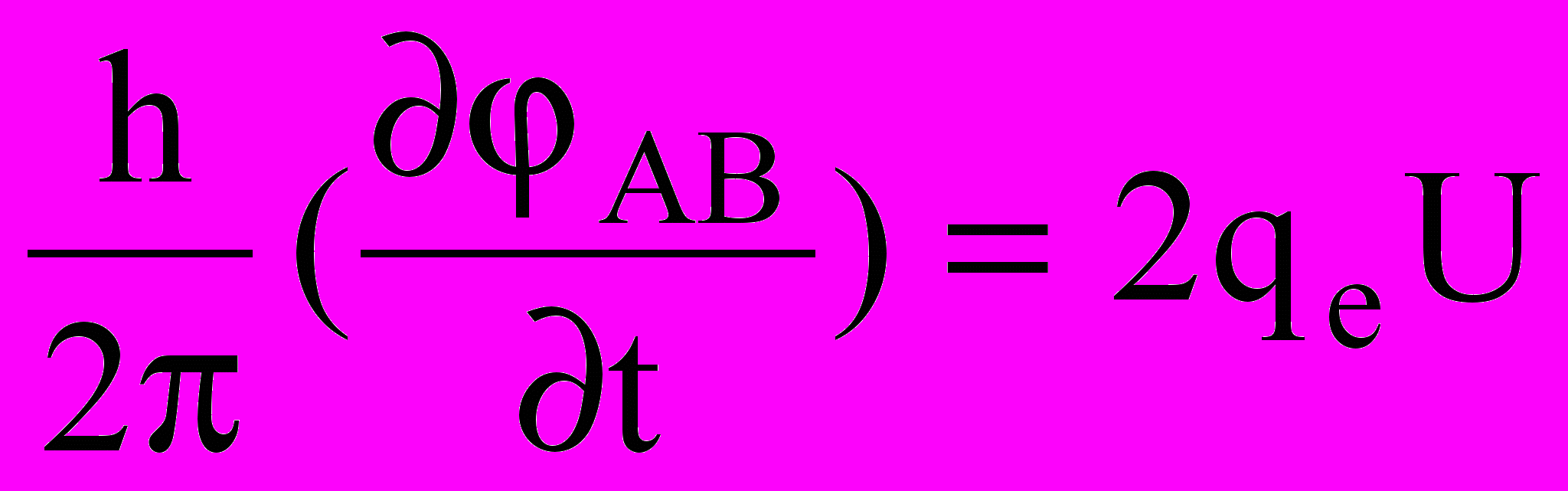 , (9.37)
, (9.37)где U разность потенциалов между точками А и В контура L (штриховая линия, рис. 9.36).
Согласно закону электромагнитной индукции напряжение между т. А и В (рис. 9.36)
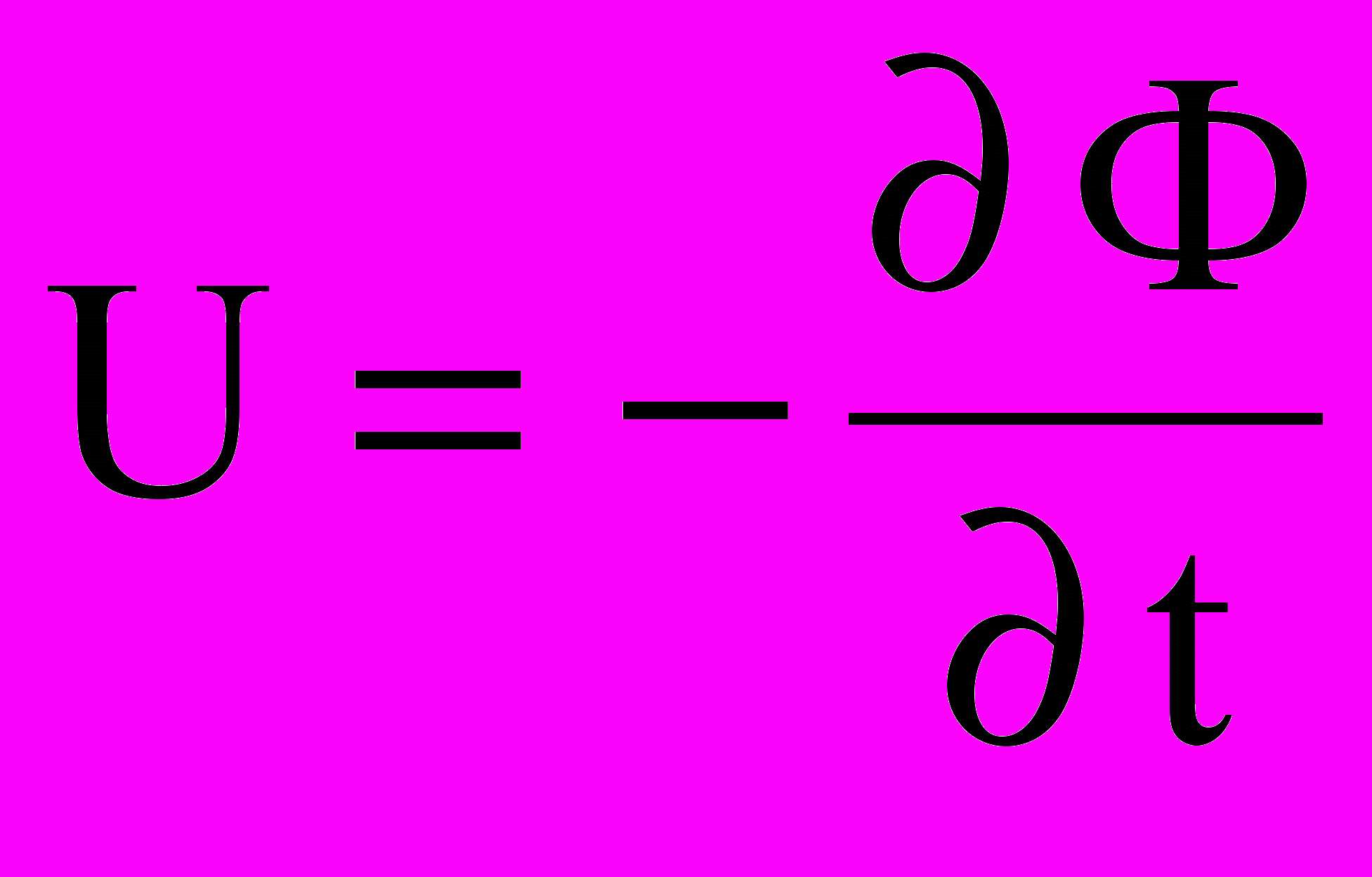 , (9.38)
, (9.38)где Ф магнитный поток, охваченный контуром L.
Из уравнений (9.37) и (9.38) следует, что
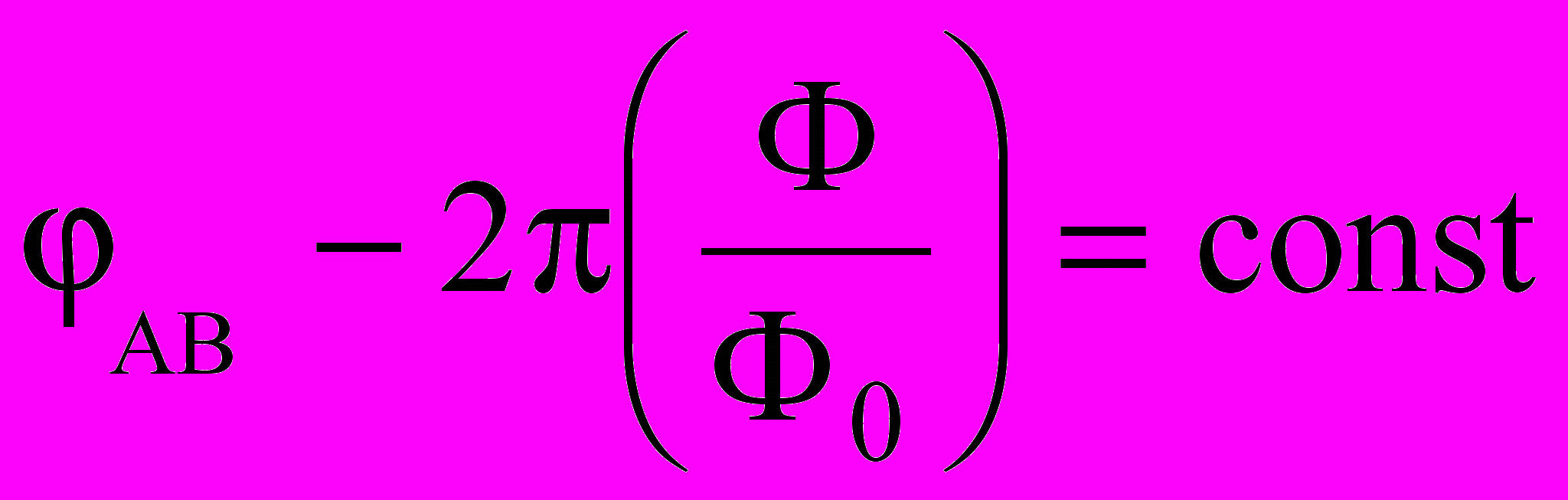 . (9.39)
. (9.39)Постоянная интегрирования в этом выражении связана со скоростью движения сверхпроводящих электронов, что следует из квантовомеханического выражения для скорости куперовских пар:
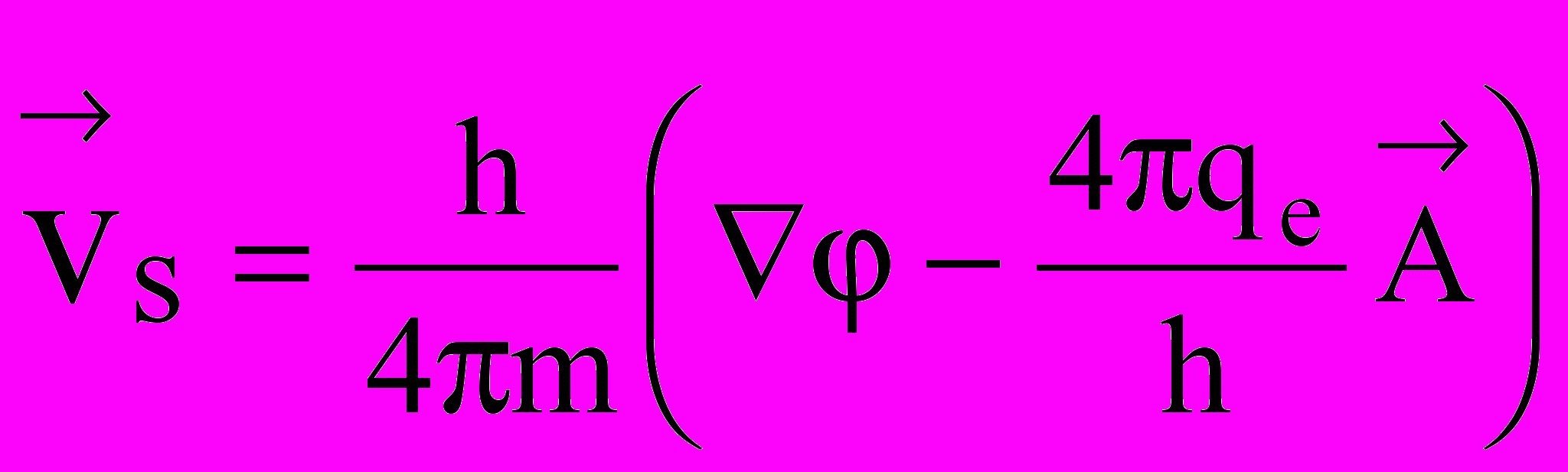 , (9.40)
, (9.40)где m масса электрона;
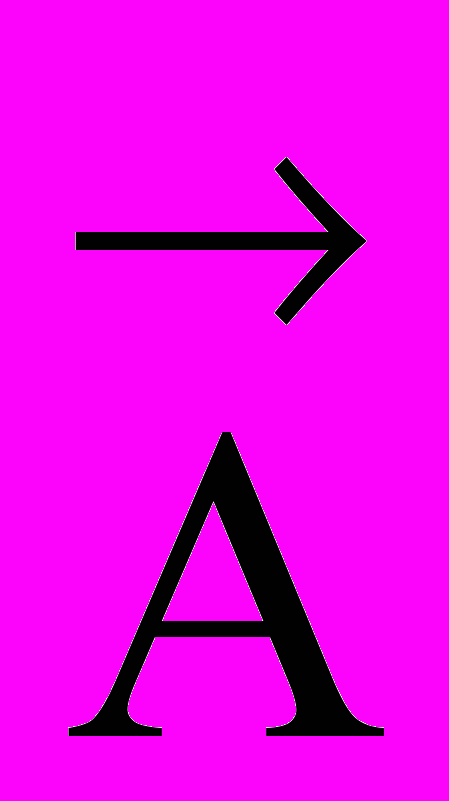 векторный потенциал электромагнитного поля.
векторный потенциал электромагнитного поля.Интегрируя
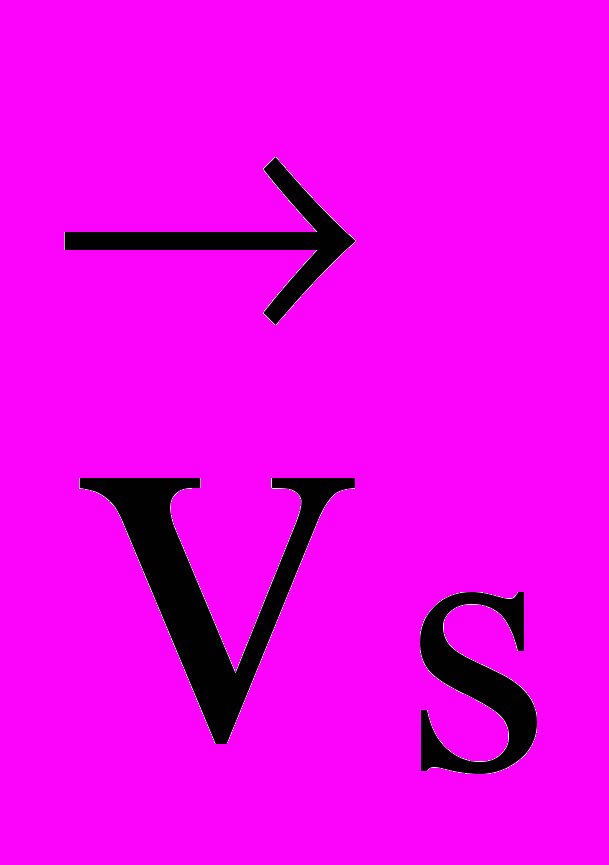 по контуру L между точками А и В, получаем следующее выражение:
по контуру L между точками А и В, получаем следующее выражение: 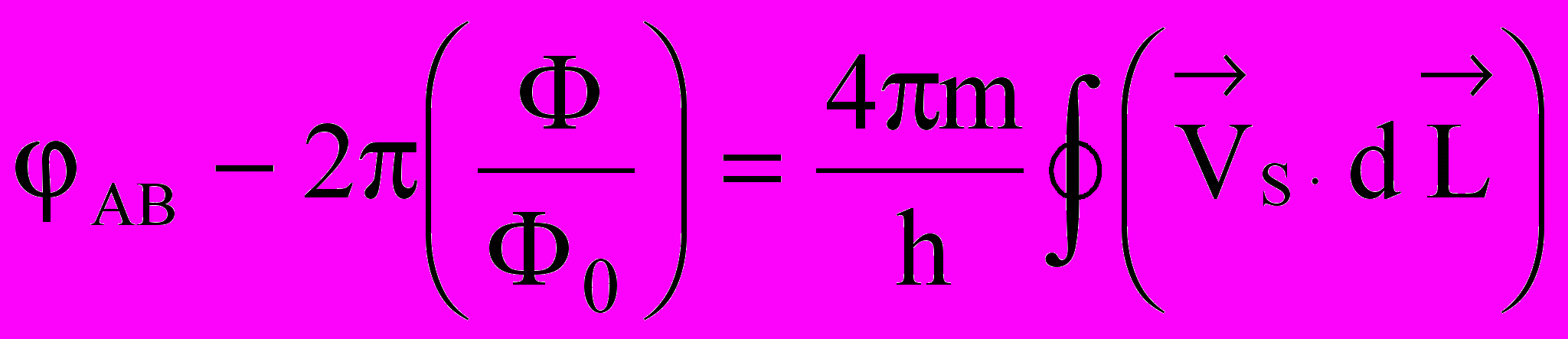 . (9.41)
. (9.41) Фундаментальность явления квантования магнитного потока сказывается, например, в существовании квантовых вихрей в сверхпроводниках II рода, определяющих магнитные свойства большого класса сверхпроводников.
Квантование магнитного потока наряду с эффектом Джозефсона составляет основу работы сверхпроводящих квантовых интерферометров.
В настоящее время ведутся работы по созданию суперкомпьютора нового поколения на основе эффекта Джозефсона.
