Элементы квантовой физики атомов и молекул
| Вид материала | Лекция |
- Элементы квантовой механики и физики атомов, молекул, твердых тел, 156.85kb.
- Элементы квантовой механики Атом Резерфорда – Бора и гипотеза де Бройля Ядерная модель, 38.71kb.
- 14. Элементы квантовой статистики и зонной теории твердого тела, 460.81kb.
- Программа дисциплины дпп. Ф. 02 Строение молекул и основы квантовой химии, 160.77kb.
- Реферат Отчет 177 с., 3 ч., 199 рис., 12 табл., 72 источников, 1 прил, 33.16kb.
- Д. И. Менделеева Строение молекул и основы квантовой химии Магистерская программа, 307.43kb.
- X международная конференция Импульсные лазеры на переходах атомов и молекул ampl, 299.2kb.
- Магнитные свойства молекул, 29.04kb.
- Моделирование структур молекул по Огжевальскому, 61.04kb.
- Рабочая программа утверждаю: по курсу общей физики (основы квантовой физики) для студентов, 85.65kb.
Лекция 13. Элементы квантовой физики атомов и молекул
13.1 Атом водорода. Квантование
Собственные значения энергии. Рассмотрим систему, состоящую из электрона е, который движется в кулоновском поле неподвижного ядра с зарядом Ze (водородоподобная система). Потенциальная энергия взаимодействия электрона с ядром в такой системе равна
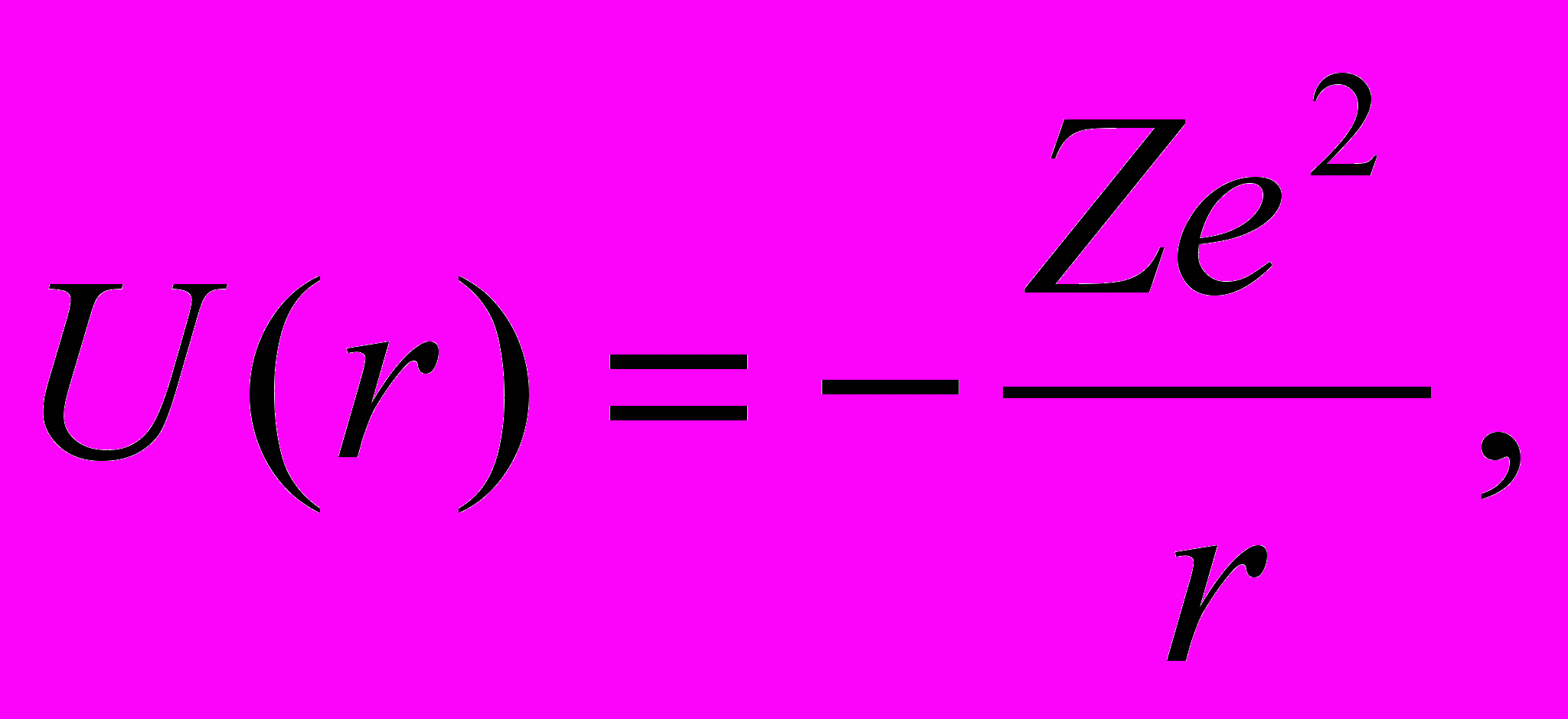 | (13.1) |
где r — расстояние между электроном и ядром, которое в первом приближении будем считать точечным. Графически функция U(r) изображена жирной кривой на рис. 13.1 а. U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает. Уравнение Шрёдингера в этом случае имеет вид
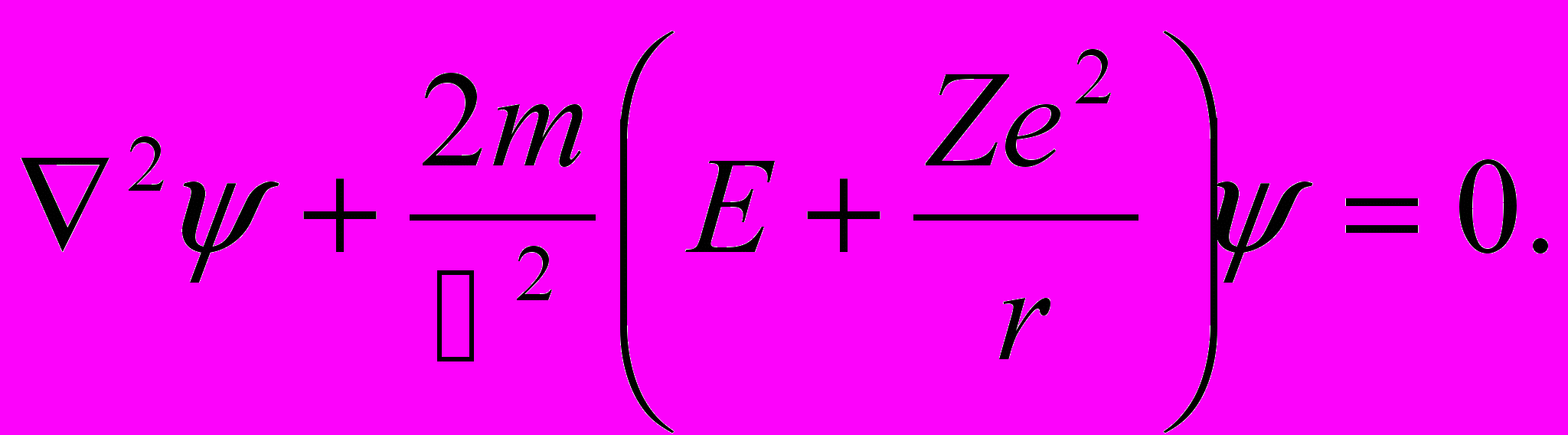 | (13.2) |
Поле (13.1), в котором движется электрон, является центрально-симметричным, т. е. зависит только от r. Поэтому решение уравнения (13.2) наиболее целесообразно проводить в сферической системе координат r,θ,φ, где оператор Лапласа
 имеет следующий вид:
имеет следующий вид: 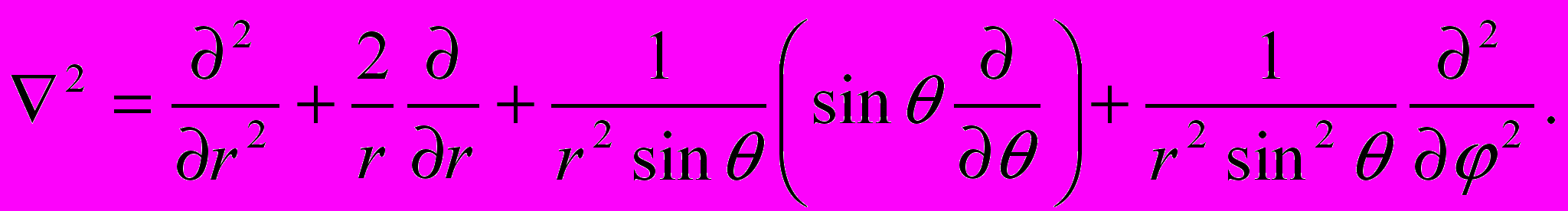 | (13.3) |
Не будем воспроизводить здесь этапы решения уравнения (13.2), поскольку оно слишком громоздко. Остановимся лишь на сути процесса решения и на анализе окончательных результатов. Решение уравнения (13.2) проводят методом разделения переменных с учетом естественных требований, налагаемых на ψ-функцию: она должна быть однозначной, конечной, непрерывной и гладкой. В теории дифференциальных уравнений доказывается, что решения уравнения (13.2) являются непрерывными, однозначными и конечными в следующих случаях:
- при любых положительных непрерывных значениях энергии;
- при дискретных отрицательных значениях энергии.
Первый случай соответствует свободному электрону (заштрихованная область на рис. 13.1 б), второй — получаемым из уравнения Шредингера собственным значениям энергии
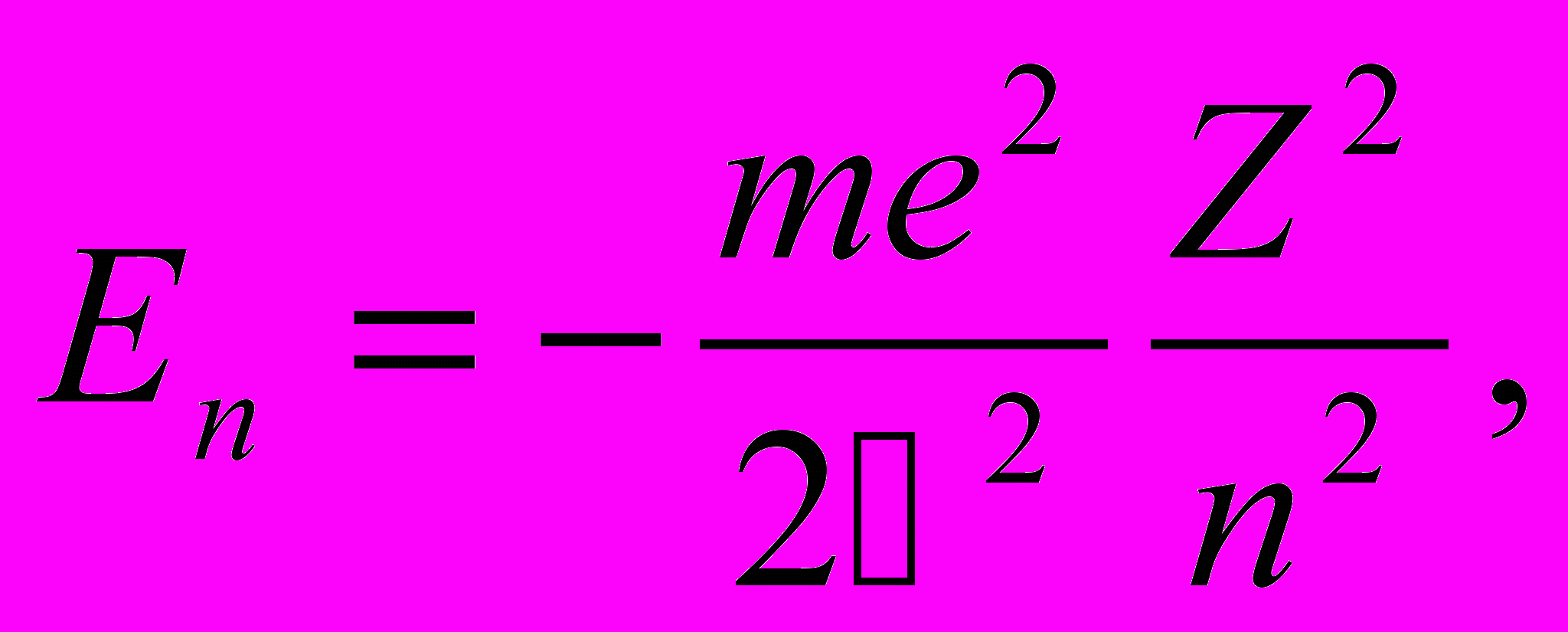 n = 1, 2, 3, … n = 1, 2, 3, … | (13.4) |
Случай (Е < 0) соответствует связанным состояниям электрона в атоме.
Решение уравнения Шредингера приводит в случае Е < 0 к формуле (13.4) для энергетических уровней без использования каких-либо дополнительных постулатов (в отличие от первоначальной теории Бора). Кроме того, совпадение с формулой Бора означает, что мы пришли к той же самой системе энергетических уровней, как в теории Бора. Это же относится и к частотам излучения при переходах между уровнями.
Таким образом, решение уравнения Шредингера приводит для атома водорода к появлению дискретных энергетических уровней Е1, Е2, ..., Еп, показанных на рис. 13.1 б в виде горизонтальных прямых.
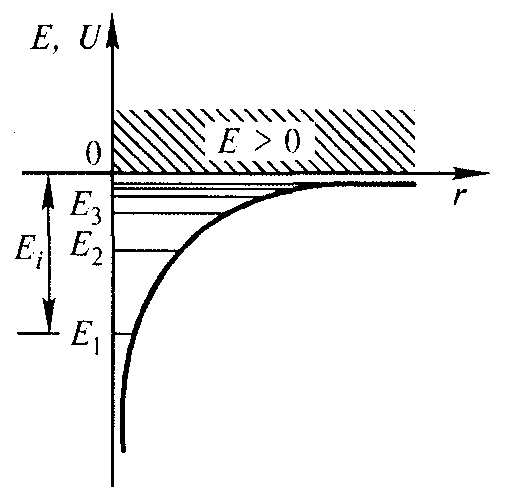

а) б)
Рис. 13.1 . а - потенциальная энергия U(r) и б - собственные значения энергии Е электрона в атоме водорода.
Самый нижний уровень Е1, отвечающий минимальной возможной энергии, — основной, все остальные (Еп > Е1 , п = 2, 3, ...) — возбужденные. При Е < 0 движение электрона является связанным — он находится внутри гиперболической потенциальной ямы. Из рисунка следует, что по мере роста главного квантового числа п энергетические уровни располагаются теснее и при п → ∞ Е∞ → 0.
При Е > 0 движение электрона является свободным; область непрерывного спектра Е > 0 (заштрихована на рис. 13.1 б) соответствует ионизированному атому.
Различие в интерпретации с теорией Бора относится только к состояниям электрона: в теории Бора это движение по стационарным орбитам, здесь же орбиты теряют физический смысл, их место занимают ψ-функции.
Квантовые числа и кратность вырождения. Собственные функции уравнения (13.2), т. е. ψ-функции, содержат, как выяснилось, три целочисленных параметра — п, ℓ, т:
| ψ = ψnℓ m(r θ,φ), | (13.5) |
где п называют главным квантовым числом (это то же п, что и в выражении для Еп). Параметры же ℓ и m — это орбитальное (азимутальное) и магнитное квантовые числа, определяющие по формулам (12.58) и (12.59) модуль момента импульса М и его проекцию Мг. В процессе решения выясняется, что решения, удовлетворяющие естественным условиям, получаются лишь при значениях ℓ, не превышающих (п – 1). Таким образом, при данном п квантовое число ℓ может принимать п значений:
| ℓ = 0, 1, 2, …, n – 1. | (13.6) |
В свою очередь, при данном ℓ квантовое число т согласно (12.59) может принимать 2ℓ + 1 различных значений:
| т = 0, ±1, ±2, ...,± ℓ | (13.7) |
Энергия Еп электрона (13.4) зависит только от главного квантового числа п. Отсюда следует, что каждому собственному значению Еп (кроме случая п = 1) соответствует несколько собственных функций ψnℓ m, отличающихся значениями квантовых чисел ℓ и т. Это означает, что электрон может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Например, энергией Е2 (п = 2) обладают четыре состояния: ψ200, ψ21-1, ψ210, ψ21+1.
Состояния с одинаковой энергией называют вырожденными, а число различных состояний с определенным значением энергии Еп - кратностью вырождения данного энергетического уровня. Кратность вырождения n-го уровня водородоподобной системы можно определить, учитывая число возможных значений ℓ и т. Каждому из п значений квантового числа ℓ соответствует 2ℓ + 1 значений т. Поэтому полное число N различных состояний для данного п равно
| N = 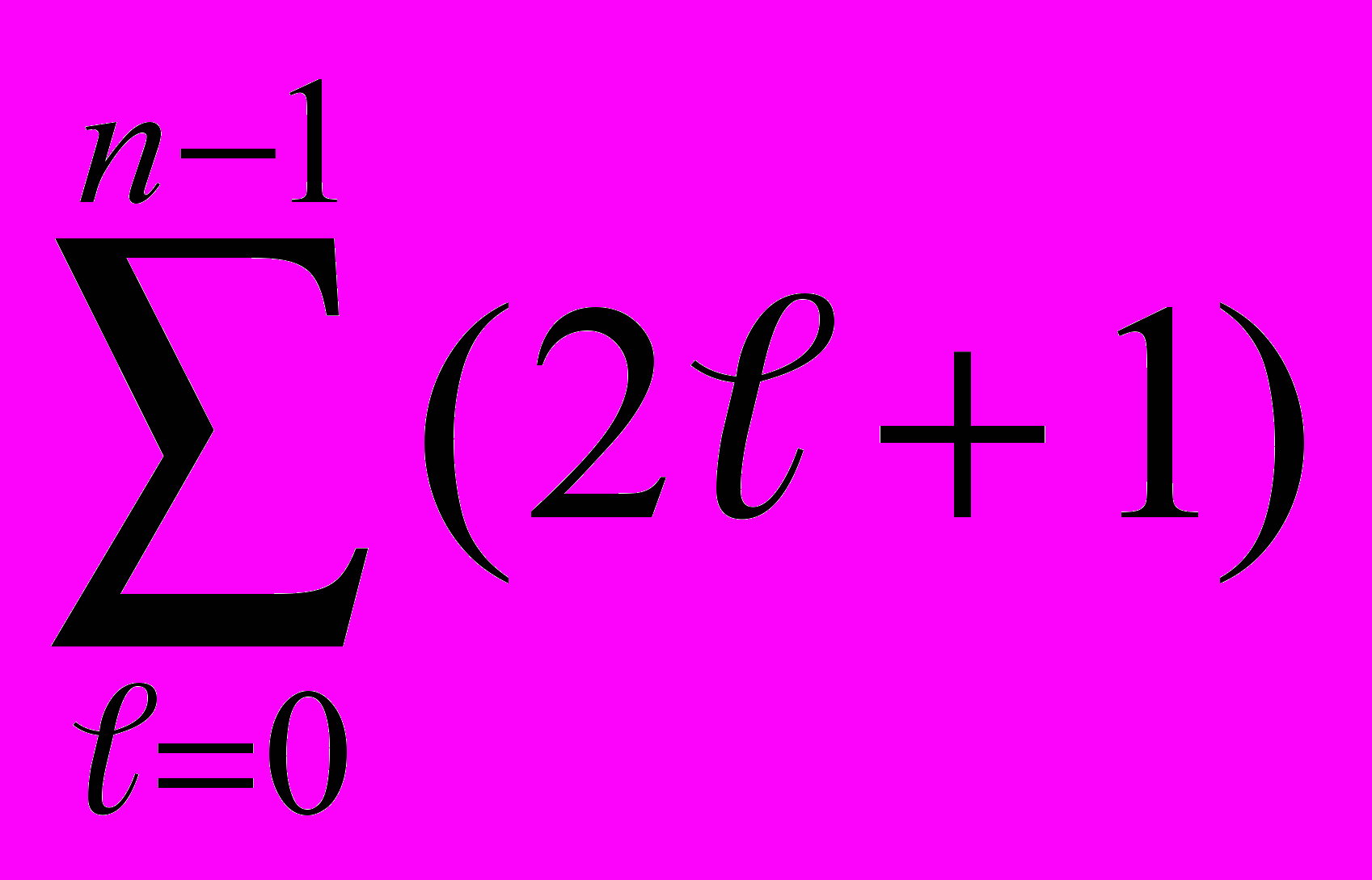 = 1 + 3 + 5 + ... + (2п - 1) = п2. = 1 + 3 + 5 + ... + (2п - 1) = п2. | (13.8) |
Как будет показано в дальнейшем, это число надо удвоить из-за наличия собственного момента (спина) у электрона. Таким образом, кратность вырождения n-го энергетического уровня
| N = 2п2. | (13.9) |
Описание состояния электрона. Поскольку в квантовой механике определяют лишь вероятность местонахождения электрона, то для наглядности применяют образ электронного облака. Плотность электронного облака в каждой точке пространства вокруг ядра пропорциональна плотности вероятности обнаружения электрона в этой точке, которая в свою очередь определяется квадратом модуля волновой функции. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число m – ориентацию электронного облака в пространстве.
В квантовой механике, по аналогии со спектроскопией, применяются условные обозначения для состояний с различными l, как указано ниже в (13.10).
| Значения l | 0 1 2 3 4 5 (13.10) s p d f g h (13.10) |
| Состояния |
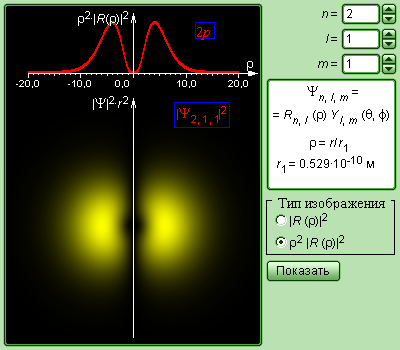
Распределение электронной плотности (радиальное и пространственное) для состояний электрона в атоме водорода при n = 1 и n = 2 показано на рис. 13.2 для s и p состояний.
Испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что для азимутального квантового числа l имеется правило отбора
| ∆l = ± 1 | (13.11) |
Это означает, что возможны только такие переходы, при которых l изменяется на единицу. Это означает, что разрешенными являются переходы лишь между s- и р-состояниями, между р- и d-состояниями и т. д.. При этом главное квантовое число п может изменяться на любое целое число. С точки зрения квантовой теории правила отбора связаны с вероятностью перехода из одного квантового состояния в другое. Оказывается, вероятность переходов, не разрешенных правилами отбора, практически равна нулю.
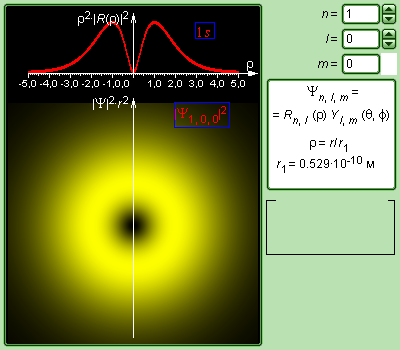
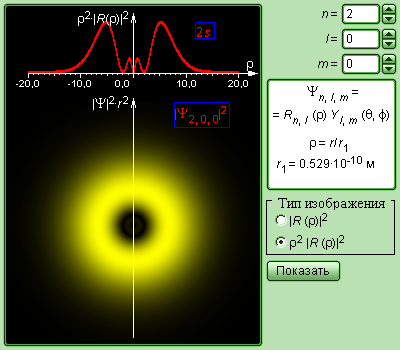
а) б)

в) г)
Рис. 13.2. Радиальное (красные кривые вверху каждого рисунка) и пространственное (жёлтые области внизу каждого рисунка) распределение вероятности |ψ|2 (электронное облако) для электронных состояний: а) 1s m = 0, б) 2s m = 0, в) 2p m = 0, г) 2p m = 1.
Правило (13.11 ) обусловлено тем, что фотон обладает собственным моментом импульса (спином), равным примерно ћ. При испускании фотон уносит из атома этот момент, а при поглощении привносит, так что правило отбора (13.11) есть просто следствие закона сохранения момента импульса.
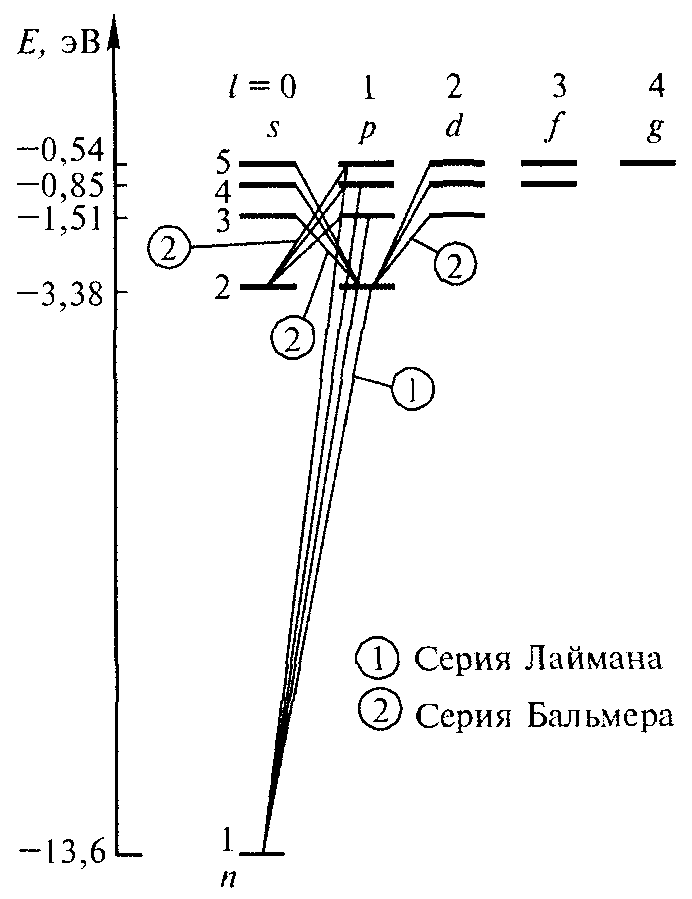
Переходы, разрешенные правилом (13.11), показаны на рис. 13.3. Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно написать в виде
np → 1s (n = 2, 3, …);
серии Бальмера соответствуют переходы
np → 2s, ns → 2p, nd → 2p (n = 3,4, …),
и т.д.
Переход электрона из основного состояния в возбужденное связан с увеличением
 энергии атома и может происходить только при сообщении атому энергии извне.
энергии атома и может происходить только при сообщении атому энергии извне.Это может быть осуществлено за счет теплового соударения атомов, или за счет столкновения атома с достаточно быстрым электроном, или, наконец, за счет поглощения атомом фотона. Так как поглощающий атом при нормальных условиях находится в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1s—> пр (п = 2, 3, ...), что находится в полном согласии с опытом.
Рис. 13.3.
Собственные функции уравнения (13.2) представляют собой произведение двух функций, одна из которых зависит только от r, а другая — только от углов θ и φ:
| Ψn ℓ m (r,θ,φ) = Rnℓ(r)·Υℓm(θ,φ), | (13.12) |
где первый сомножитель вещественный и зависит от квантовых чисел п и ℓ, второй же — комплексный и зависит от ℓ и т. Функция Υℓm(θ,φ) является собственной функцией оператора квадрата момента импульса
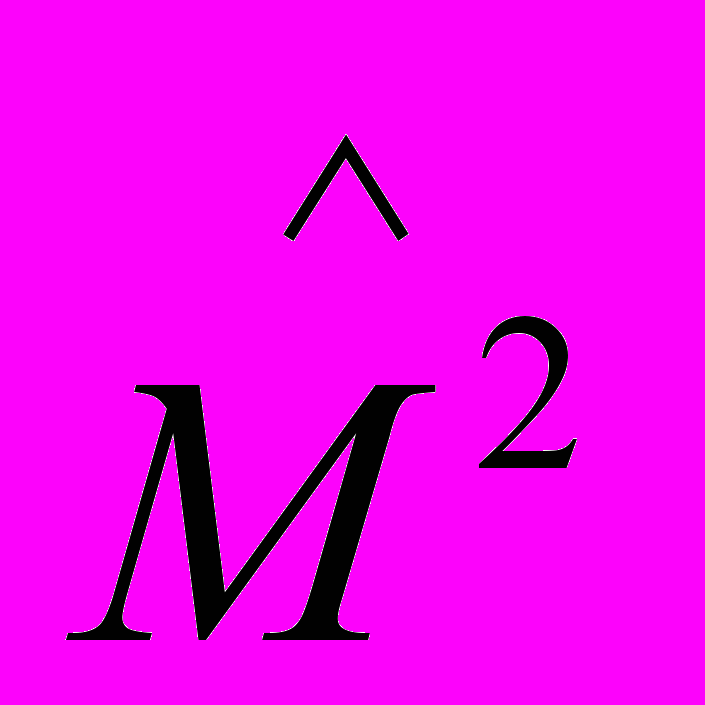 . Для s-состояний (ℓ = 0) эта функция является константой, так что ψ-функция вида ψn00 зависит только от r. Вообще же
. Для s-состояний (ℓ = 0) эта функция является константой, так что ψ-функция вида ψn00 зависит только от r. Вообще же| Υℓm(θ,φ) = Θℓ |m|(θ) eimφ . | (13.13) |
Распределение плотности вероятности. Плотность вероятности местонахождения электрона дается квадратом модуля волновой функции |ψ|2 или ψ ψ *. Ограничимся для простоты рассмотрением основного состояния электрона 1s атома водорода, которое является сферически-симметричным, т. е. его ψ -функция зависит только от r:
| Ψ1 s ~ e -α r, | (13.14) |
где α = 1/r1, r1 – боровский радиус.
Вероятность нахождения электрона в объеме dV равна |ψ|2dV. Возьмем в качестве элементарного объема d V сферический слой толщиной dr и радиусом r: dV = 4πr2dr. Тогда вероятность dP нахождения ls-электрона в этом слое
| dP=Ar2|ψ|2dr, | (13.15) |
где А — нормировочный коэффициент. Отсюда плотность вероятности ρ(r) = dP/dr, т. е. вероятность местонахождения электрона в сферическом слое единичной толщины вблизи радиуса r есть
| ρ(r) = dP/dr = Ar2e- 2 α r ~ r2е- 2α r. | (13.16) |
Эту плотность вероятности не следует смешивать с плотностью вероятности dP/dV, отнесенной к единице объема вблизи точки с радиусом r и равной |ψ|2.
Видно, что (13.16) обращается в нуль при r → 0 и при r → ∞. Найдем значение r, при котором (13.16) достигает максимума. Для этого продифференцируем (13.16) по r и приравняем нулю полученное выражение (после сокращения на экспоненту). В результате получим наиболее вероятное расстояние электрона от ядра, равное боровскому радиусу:
| rm = 1/α = r1 | (13.17) |
На рис. 13.4 изображены кривые распределения вероятности ρ(r) = 4πr2|ψ|2 обнаружения электрона в атоме водорода на различных расстояниях от ядра в состояниях 1s и 2s. Как видно электрон в состоянии 1s (основное состояние атома водорода) может быть обнаружен на различных расстояниях от ядра. С наибольшей вероятностью его можно обнаружить на расстоянии r/r1 = 1, т.е. равном радиусу r1 первой боровской орбиты.
Вероятность обнаружения электрона в состоянии 2s максимальна на расстоянии r = 4r1 от ядра. В обоих случаях атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро. Пространственная симметрия распределения вероятности для 1s и 2s состояний показана на рис. 13.2 а и 13.2 б, соответственно. С классической точки зрения s- состояния, для которых орбитальный момент электрона равен нулю (l =0), соответствует движению электрона вдоль радиуса, т.е. электрон при своем движении должен был бы пересекать область, занятую ядром. Это в классике невозможно. В квантовой же теории состояние с нулевым орбитальным моментом существует – это s-состояния электрона, в которых распределение «плотности» электронного облака сферически-симметрично.
Р
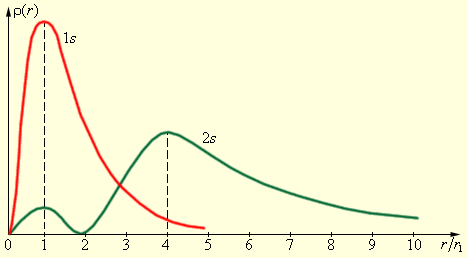 ис. 13.4.
ис. 13.4.Распределении электронного облака в других состояниях (p, d, …). уже не сферически-симметрично и в сильной степени зависит от угла θ. Вместе с тем, выяснилось, что при усреднении по углу θ остается зависимость ψ-функции только от r, и максимумы распределения в состояниях с ℓ = n – 1 (т. е. наиболее вероятные расстояния электрона от ядра) приходятся на соответствующие боровские орбиты.
13.2. Щелочные металлы. Уровни энергии
Атом щелочного металла имеет Z электронов и можно считать, что (Z – 1) электронов вместе с ядром образуют сравнительно прочный остов, в электрическом поле которого движется внешний (валентный) электрон, довольно слабо связанный с остовом атома. В некотором смысле атомы щелочных металлов являются водородоподобными, однако, не полностью. Дело в том, что внешний электрон несколько деформирует электронный остов и тем самым искажает поле, в котором движется. В первом приближении поле остова можно рассматривать как суперпозицию поля точечного заряда +е, и поля точечного диполя, расположенного в центре остова. При этом ось диполя направлена все время к внешнему электрону. Поэтому движение последнего происходит так, как если бы поле остова, несмотря на искажение, сохранялось сферически-симметричным.
Это позволяет представить потенциальную энергию внешнего электрона в поле такого остова как
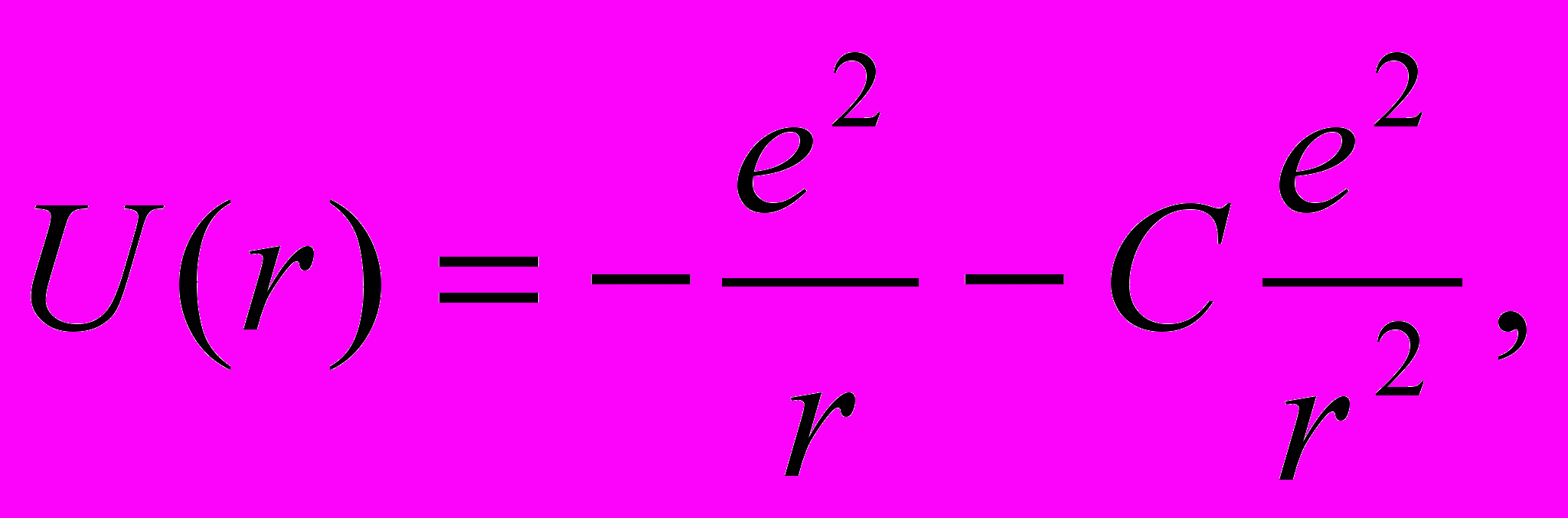 | (13.18) |
где С — некоторая постоянная.
Решение уравнения Шредингера для электрона с потенциальной энергией (13.18) приводит к тому, что теперь дозволенные значения энергии Е в области Е < 0 (для связанных состояний внешнего электрона) будут зависеть не только от главного квантового числа п (как в случае атома водорода), но и от орбитального квантового числа ℓ:
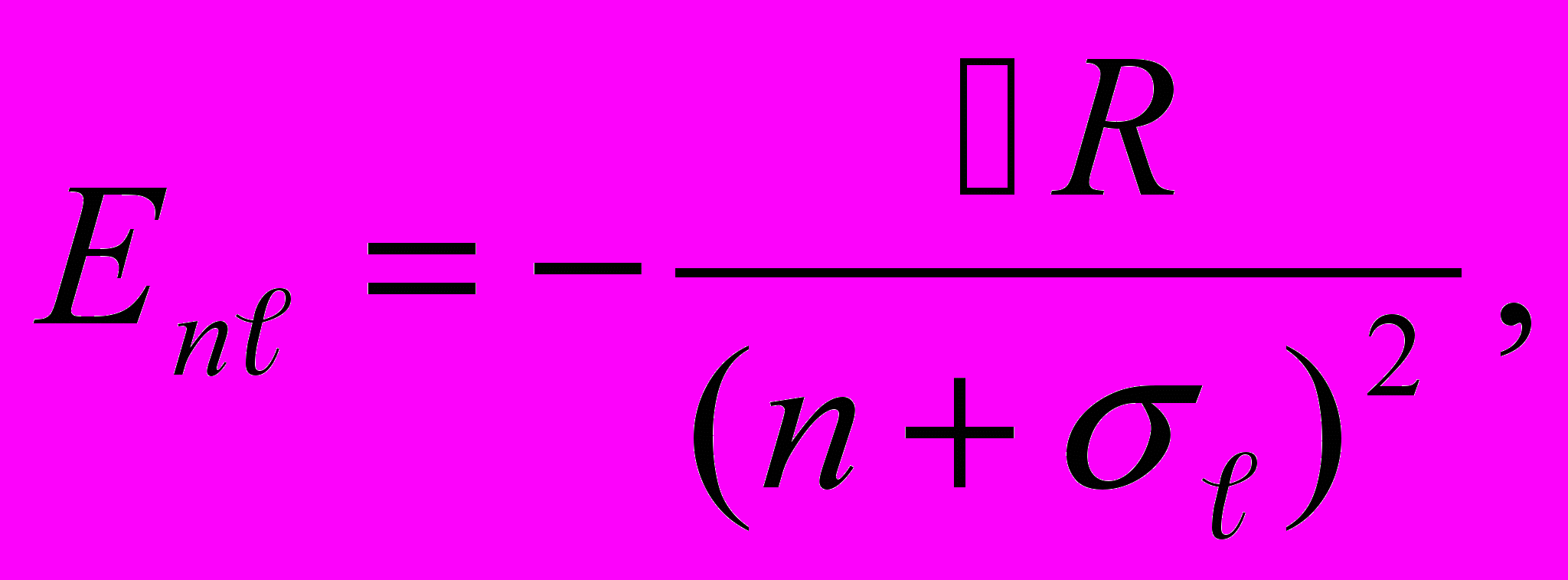 | (13.19) |
где R – постоянная Ридберга, σ ℓ — ридберговская поправка (или квантовый дефект), зависящая от l. Заметим, что у лития основным состоянием является 2s, поскольку состояние с п = 1 уже занято двумя электронами, входящими в состав остова.
Систему энергетических уровней атома принято называть и иначе – системой термов. Терм Т – это величина, определяемая как
| Тn = R/n2 = |En|/ћ. | (13.20) |
Энергетическому уровню (13.19) соответствует терм, имеющий согласно (13.20) вид
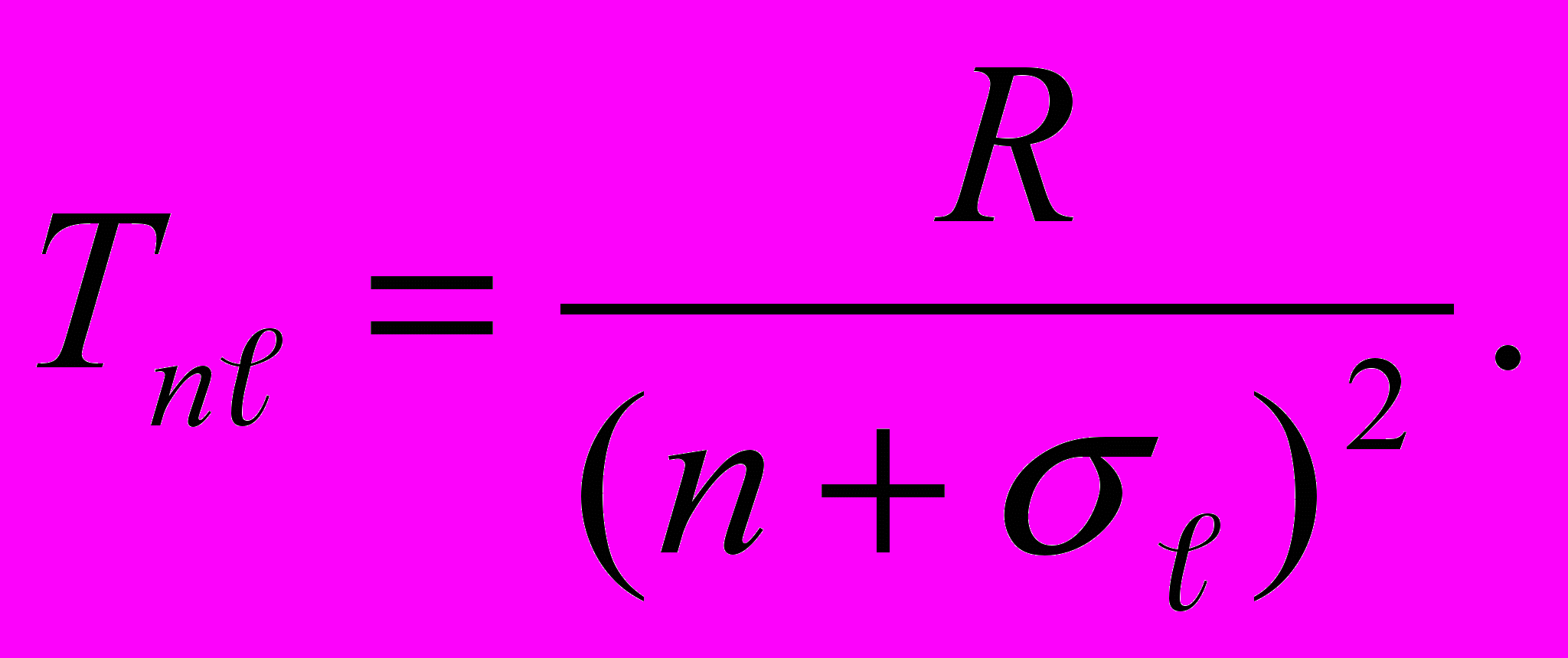 | (13.21) |
Зависимость энергии электрона от орбитального квантового числа l является принципиальным отличием уровней энергии атомов щелочных металлов от уровней энергии атома водорода. Эта зависимость означает, что в данном случае снимается вырождение по l . Физически это связано с тем, что в атомах щелочных металлов внешний электрон находится в электрическом поле атомного остова. Заряд последнего не точечный, и распределение его несколько отличается от сферически-симметричного. Электрическое поле остова уже не кулоновское (не ~ 1/r2). Благодаря этому и получается зависимость энергии Е электрона не только от п, но и от l.
Исследование спектров ионов щелочных металлов показало, что момент импульса атомного остова (т. е. ядра и Z-1 электронов) равен нулю. Следовательно, орбитальный момент атома щелочного металла оказывается равным моменту его внешнего электрона и определяется квантовым числом l.
Для l валентного электрона атомов щелочных металлов действует такое же правило отбора, как и для l электрона водородного атома, т.е.
| ∆l = ± 1. | (13.22) |
Главное квантовое число n может изменяться на любое целое число.
Тонкая структура спектральных линий. Исследование спектральных линий атомов щелочных металлов приборами с большой разрешающей способностью обнаружило, что эти линии являются двойными (дублетами), т. е. образуют тонкую структуру.
Спектральные линии, состоящие из нескольких компонент, называют мультиплетами. Число компонент в мультиплете различных атомов может быть равно двум (дублеты), трем (триплеты), четырем (квартеты) и т. д. В частности, спектральные линии могут быть и одиночными (синглеты).
Тонкая структура, т. е. расщепление спектральных линий, очевидно, вызвана расщеплением самих энергетических уровней (термов). Вместе с тем, это никак не следует из решения уравнения Шредингера. В чем же причина такого загадочного расщепления? Ответ на этот вопрос дается ниже.
13.3. Спин электрона. Мультиплетность
Собственный момент импульса электрона (спин). Расщепление спектральных линий обусловлено расщеплением энергетических уровней. Для объяснения расщепления уровней Гаудсмит и Уленбек (1925) выдвинули гипотезу о наличии у электрона собственного момента импульса Ms, не связанного с движением электрона в пространстве. Этот собственный момент импульса был назван спином.
Спин ничего общего не имеет с представлением о вращающейся частице, как первоначально предполагали (отсюда и название). Спин характеризует внутреннее свойство электрона подобно массе и заряду. Выяснилось, что спин является свойством одновременно квантовым и релятивистским. Дирак (1928) показал, что спин электрона автоматически содержится в его теории электрона, основанной на релятивистском волновом уравнении. В отличие от орбитального момента, спин всегда сохраняется (как внутреннее свойство).
Спин электрона определяется по общим законам квантовой теории. Аналогично орбитальному моменту, определенные значения в одном и том же состоянии могут иметь квадрат спина
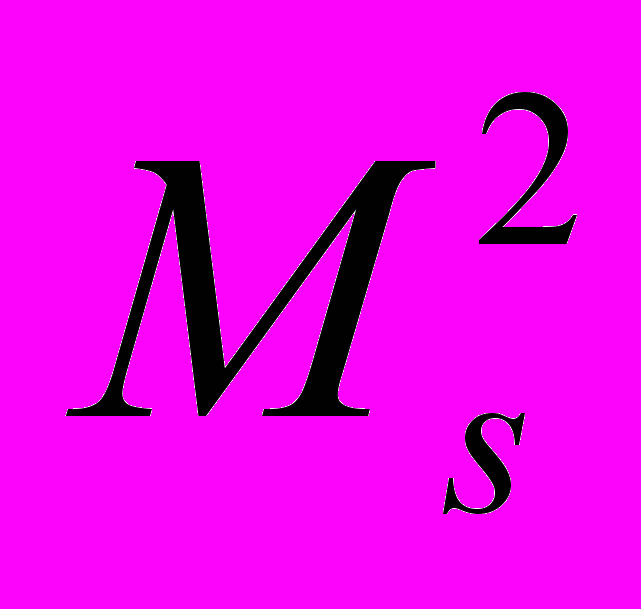 , (а значит и модуль спина Ms), и одна из его проекций Msz на произвольно выбранную ось Z.
, (а значит и модуль спина Ms), и одна из его проекций Msz на произвольно выбранную ось Z. 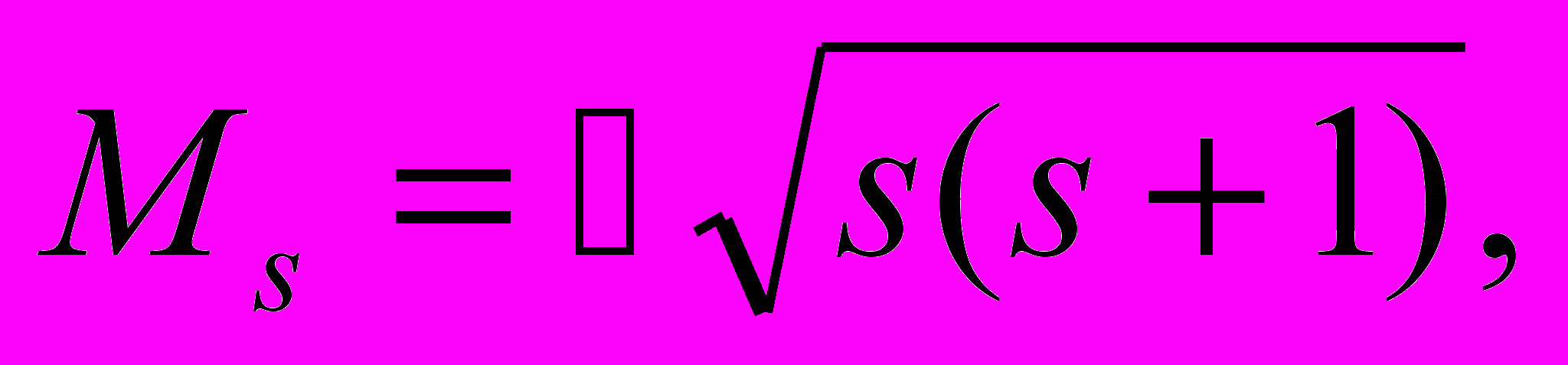 …..s = 1/2, …..s = 1/2, | (13.23) |
где s — спиновое квантовое число, и
| Msz=ћms, ms = ±s = +1/2 и -1/2. | (13.24) |
Значение s = 1/2 получено из следующих соображений. Аналогично орбитальному моменту число возможных значений проекции ms, соответствующих данному значению s, равно 2s + 1. Экспериментально было установлено, что это число для электрона равно двум, т. е. 2s + 1 = 2, откуда s = 1/2.
Отметим, что спином обладает подавляющее большинство частиц. Например, у протона и нейтрона s = 1/2, а у фотона s = 1.
Поскольку спин электрона s = 1/2, а его проекции ms равны 1/2 и -1/2, то становится понятным, почему кратность вырождения n-го энергетического уровня атома водорода равна не n2, а 2п2.
Полный механический момент электрона. С механическими моментами (орбитальным и спиновым) связаны магнитные моменты. В результате их взаимодействия происходит сложение моментов — возникает полный момент импульса электрона. Символически это записывают так: Мj = Mℓ+ Ms, где j - квантовое число полного момента.
Правила сложения угловых моментов в квантовой теории не зависят от того, являются ли моменты орбитальными или спиновыми. Поэтому полный момент электрона Мj определяется формулой, аналогичной формулам для орбитального и спинового моментов, а именно
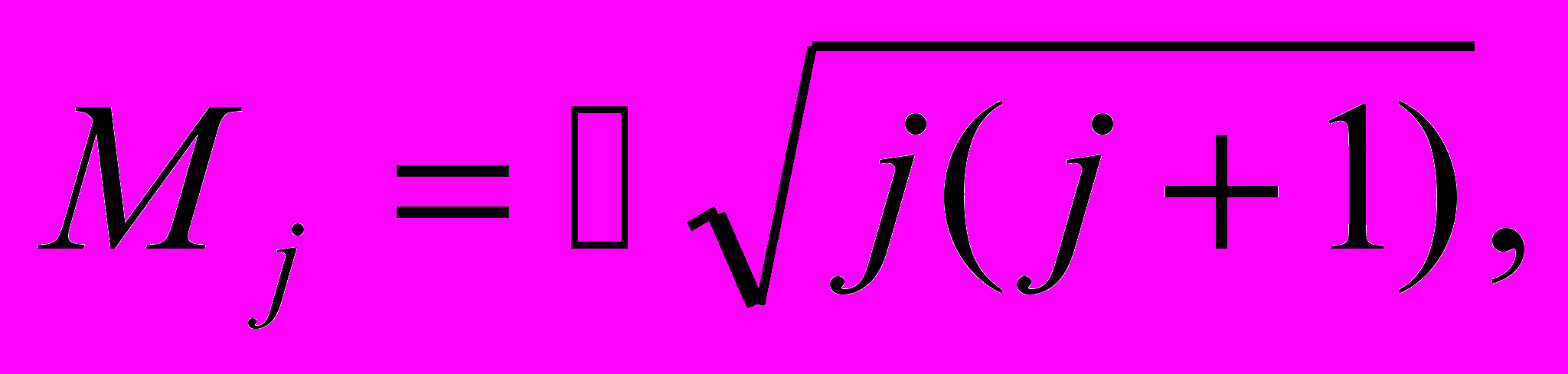 j = l + s = l ± 1/2. j = l + s = l ± 1/2. | (13.25) |
Таким образом, квантовое число j является полуцелым, поскольку l — целое, причем, если l = 0, то j = s = 1/2. Кроме того, j всегда положительно.
В связи со знаками ± перед спином s в (13.25) условно принято говорить, что спиновый момент либо «сонаправлен» с орбитальным моментом (знак +), либо они взаимно противоположны «по направлению» (знак -).
Возможные проекции момента (13.25) на ось Z определяются как
| М jz=ћтj, тj = j, j - 1, j – 2, …,-j, | (13.26) |
т. е. при данном j возможны 2j + 1 квантовых состояний, отличающихся значениями mj. Например, при l = 1
j1 = 1 + 1/2 = 3/2, mj = 3/2, 1/2, -1/2, -3/2,
j2 = 1- 1/2 = 1/2, тj = 1/2, -1/2.
Если же l = 0, то весь момент импульса чисто спиновый.
Выпишем собственные значения угловых моментов (орбитального, спинового и полного) и их проекций на ось Z в одной таблице.
Таблица 13.1
 l = 0, 1, 2, … l = 0, 1, 2, …Mℓz = ћml, ml = 0, ± 1, ± 2, …, ± l. | (13.27) |
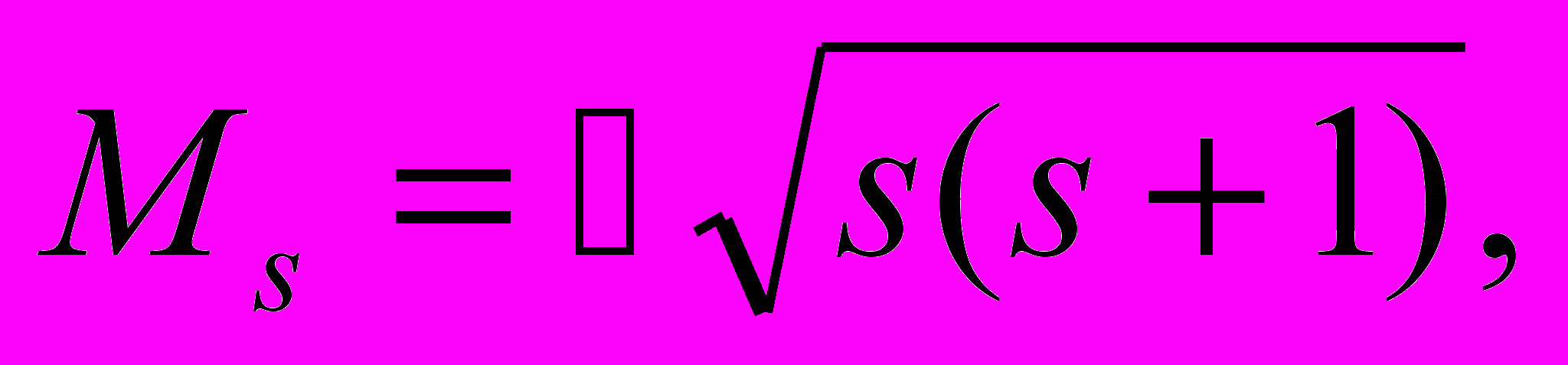 s = 1/2, s = 1/2,Msz = ћms, ms = + 1/2, - 1/2. | (13.28) |
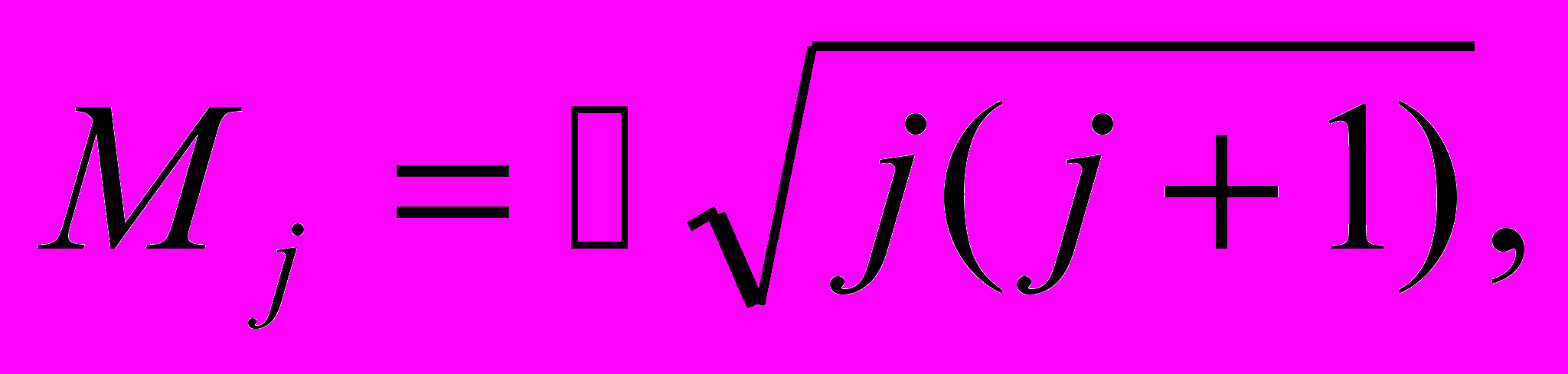 j = l ± s = l ± 1/2, j = l ± s = l ± 1/2,Mjz = ћmj, mj = j, j-1, …, - j. | (13.29) |
