Элементы квантовой физики атомов и молекул

Вид материала

Лекция

Содержание К, как видно из рис.13.6, непременно сопровождается появлением и остальных серий, поскольку при испускании ее линий освобождаютс Закон Мозли R — постоянная Ридберга, Z — порядковый номер в Периодической системе элементов σ K-край полосы поглощения (λ K -терм остается одиночным. L 13.9. Магнитный момент атома. Опыт Штерна и Герлаха Р имел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщепление J, то число компонент будет равно 2J Спиновый магнитный момент Полный магнитный момент атома 13.9. Атом во внешнем магнитном поле. Эффект Зеемана J расщепляются в магнитном поле на 2J +

Подобный материал:

•  Элементы квантовой механики и физики атомов, молекул, твердых тел, 156.85kb.
• Элементы квантовой механики Атом Резерфорда – Бора и гипотеза де Бройля Ядерная модель, 38.71kb.
• 14. Элементы квантовой статистики и зонной теории твердого тела, 460.81kb.
• Программа дисциплины дпп. Ф. 02 Строение молекул и основы квантовой химии, 160.77kb.
• Реферат Отчет 177 с., 3 ч., 199 рис., 12 табл., 72 источников, 1 прил, 33.16kb.
• Д. И. Менделеева Строение молекул и основы квантовой химии Магистерская программа, 307.43kb.
• X международная конференция Импульсные лазеры на переходах атомов и молекул ampl, 299.2kb.
• Магнитные свойства молекул, 29.04kb.
• Моделирование структур молекул по Огжевальскому, 61.04kb.
• Рабочая программа утверждаю: по курсу общей физики (основы квантовой физики) для студентов, 85.65kb.

Особенности характеристических спектров.

1. В отличие от оптических линейчатых спектров с их сложностью и разнообразием, рентгеновские характеристические спектры различных элементов отличаются простотой и однообразием. С ростом атомного номера Z элемента они монотонно смещаются в коротковолновую сторону.

2. Характеристические спектры разных элементов имеют сходный характер (однотипны) и не меняются, если интересующий нас элемент находится в соединении с другими. Это можно объяснить лишь тем, что характеристические спектры возникают при переходах электронов во внутренних частях атома, частях, имеющих сходное строение.

3. Характеристические спектры состоят из нескольких серий: К, L, М, ... Каждая серия — из небольшого числа линий: К_а, К_β, К_γ, ... L_a, L_β, L_y, ... и т. д. в порядке убывания длины волны λ.

Анализ характеристических спектров привел к пониманию, что атомам присуща система рентгеновских термов К, L, М, ...(рис.13.6). На этом же рисунке показана схема возникновения характеристических спектров. Возбуждение атома возникает при удалении одного из внутренних электронов (под действием электронов или фотонов достаточно большой энергии). Если вырывается один из двух электронов K-уровня (n = 1), то освободившееся место может быть занято электроном из какого-либо более высокого уровня: L, M, N, и т. д. В результате возникает K-серия. Подобным же образом возникают и другие серии: L, М, ...

С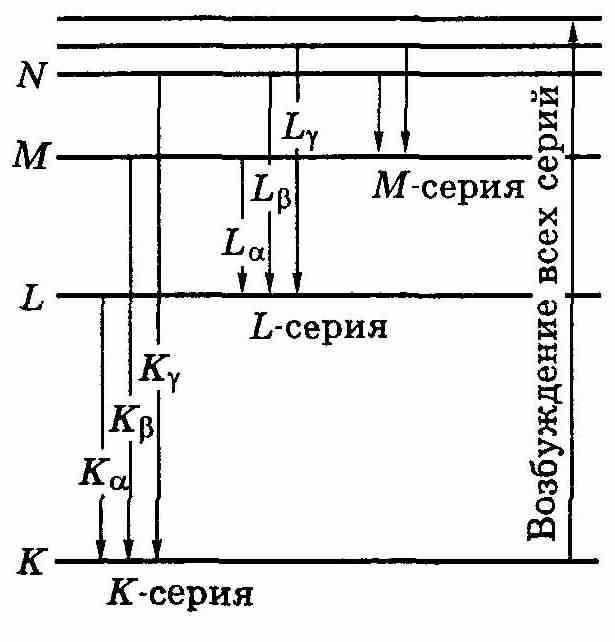ерия К, как видно из рис.13.6, непременно сопровождается появлением и остальных серий, поскольку при испускании ее линий освобождаются электроны на уровнях L, М и др., которые в свою очередь будут заполняться электронами с более высоких уровней.


Рис. 13.6.

Закон Мозли. Частоты ν линий характеристического рентгеновского излучения подчиняются закону Мозли (1913):

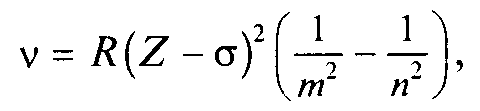(13.43)

R — постоянная Ридберга, Z — порядковый номер в Периодической системе элементов σ — постоянная экранирования, т = 1, 2, 3, ... (определяет рентгеновскую серию), п = т + 1, т + 2, ... (определяет линию соответствующей серии).

Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, действует не весь заряд ядра Ze, а заряд (Z — σ)е, ослабленный экранирующим действием других электронов. Закон Мозли сыграл в свое время важную роль при уточнении расположения элементов в периодической системе. Этот закон достаточно точно выполняется для легких элементов. Для тяжелых же элементов поправка σ значительно отличается от единицы.

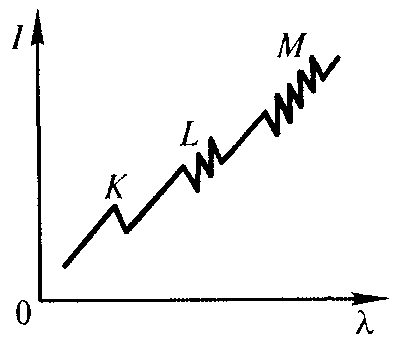Рентгеновские спектры поглощения отличаются от рентгеновских спектров излучения: они состоят из нескольких полос с резким длинноволновым краем (рис. 13.7). В результате поглощения рентгеновского фотона атомом может произойти вырывание электрона с одной из внутренних оболочек атома (процесс фотоионизации), причем каждая из полос поглощения

Рис. 13.7.


соответствует вырыванию электрона из определенной оболочки атома (K-полоса

соответствует выбиванию электрона из самой внутренней оболочки и т. д.). Резкий длинноволновый край полос соответствует началу процесса фотоионизации. Из рисунка также следует, что полосы поглощения обладают тонкой структурой: в K-полосе — один максимум, в L-полосе — 3 максимума, в M-полосе — 5 максимумов. Отметим, что структура рентгеновских спектров поглощения тяжелых атомов аналогична, что говорит об идентичности строения внутренних оболочек атомов тяжелых элементов.

Итак, например, K-край полосы поглощения (λ_K) связан с прекращением возбуждения K-уровня. Это значит, что длина волны λ_K характеризует энергию связи K-электрона (Е_K):

Е_K = ћω_K = (2πћc)/ λ_K .

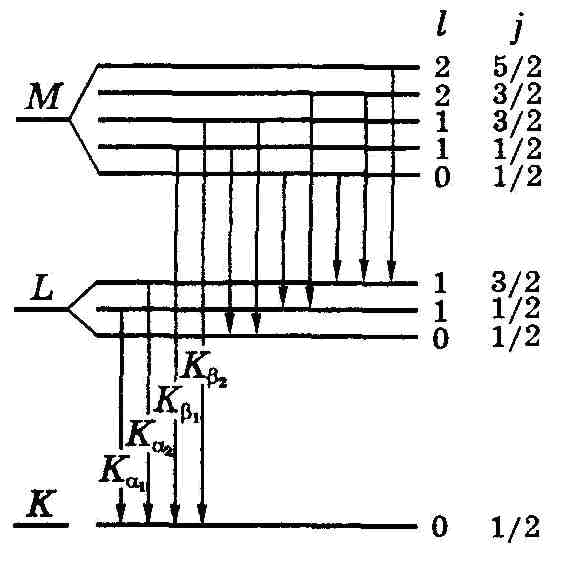
Детальный анализ характеристических спектров привел к уточнению структуры рентгеновских термов (рис. 13.8). K -терм остается одиночным. L-терм оказался тройным, М-терм — пятикратным. Мы встречаемся здесь со случаем jj-связи, которая осуществляется в глубинных слоях тяжелых атомов. У K-оболочки п = 1, значит каждый электрон имеет l = 0, s = 1/2 и j = 1/2 (это единственное значение). У L-оболочки п = 2, каждый электрон имеет l = 0 или 1. При l = 0 j = 1/2, а при l = 1 согласно (13.29) j = 1/2 и 3/2. Итак, мы имеем здесь три подуровня в точном соответствии с кратностью L-края полосы поглощения. А именно, при п = 2 (L-оболочка)

l		0	1
j		1/2	1/2, 3/2

Аналогично для М-оболочки и т. д. (см. рис. 13.8).

Кроме того, необходимо учесть, что возможны только те переходы между термами, которые подчиняются правилу отбора:


Рис. 13.8.

Δl = ±1, Δj = 0, ±1.

(13.44)

Теперь должны быть понятными изображенные на рис. 13.8 переходы: только они удовлетворяют этим правилам отбора. Мы видим, что линии K-серии имеют дублетную структуру. Компоненты дублетов обозначают индексами α₁, α₂; β₁, β₂ и т. д. Например, К_а-линия представляет собой дублет К_а1 и К_а2. Серия L и другие имеют более сложную мультиплетную структуру.

13.8. Молекулярные спектры.

Молекула является квантовой системой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания атомов молекулы, вращение молекулы. Решение этого уравнения - очень сложная задача, которая обычно разбивается на две: для электронов и ядер.

Для приближенного решения задачи используют адиабатическое приближение, согласно которому квантово-механическая система разделяется на тяжелые и легкие частицы — ядра и электроны. Так как массы и скорости этих частиц сильно различаются, то считается, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле электронов. Следовательно, в адиабатическом приближении уравнение Шредингера для молекулы распадается на два уравнения — для электронов и ядер.

Из решения уравнения Шредингера для молекул водорода при указанных выше предположениях получается зависимость собственных значений энергии от расстояния R между ядрами, т. е. Е = E(R).

Энергия молекулы

Е ≈ Еэл + Екол + Евращ,

(13.45)

где Е_эл — энергия движения электронов относительно ядер; Е_кол — энергия колебаний ядер (в результате которых периодически изменяется относительное положение ядер); Е_вращ — энергия вращения ядер (в результате которых периодически изменяется ориентация молекулы в пространстве).

В формуле (13.45) не учтены энергия поступательного движения центра масс молекул и энергия ядер атомов в молекуле. Первая из них не квантуется, поэтому ее изменения не могут привести к возникновению молекулярного спектра, а вторую можно не учитывать, если не рассматривать сверхтонкую структуру спектральных линий.

Доказано, что Е_эл >> Е_кол >> Е_вращ, при этом Е_эл ≈ 1 – 10 эВ. Каждая из входящих в выражение (13.45) энергий квантуется и им соответствует набор дискретных уровней энергии. При переходе из одного энергетического состояния в другое поглощается или 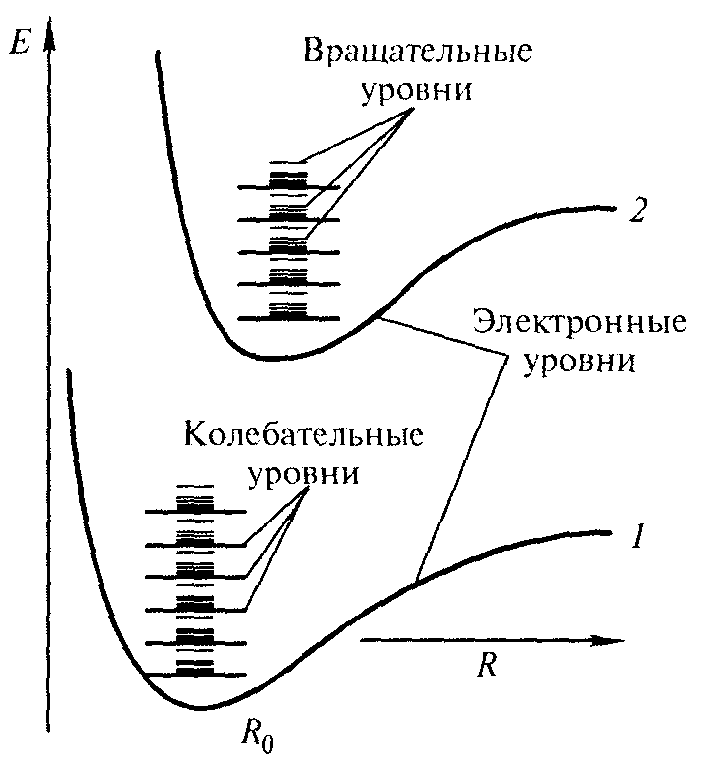испускается энергия ΔЕ = hν. Из теории и эксперимента следует, что расстояние между вращательными уровнями энергии Δ Е_вращ гораздо меньше расстояния между колебательными уровнями Δ Е_кол, которое, в свою очередь, меньше расстояния между электронными уровнями Δ Е_эл. На рис. 13.9 схематически представлены уровни энергии двухатомной молекулы (для примера рассмотрены только два электронных уровня — показаны жирными линиями).


Рис. 13.9.

Строение молекул и свойства их энергетических уровней проявляются в молекулярных спектрах - спектрах излучения (поглощения), возникающих при квантовых переходах между уровнями энергии молекул. Спектр излучения молекулы определяется структурой ее энергетических уровней и соответствующими правилами отбора (например, изменение квантовых чисел, соответствующих как колебательному, так и вращательному движению, должно быть равно ± 1). При разных типах переходов между уровнями возникают различные типы молекулярных спектров. Частоты спектральных линий, испускаемых молекулами, могут соответствовать переходам с одного электронною уровня на другой (электронные спектры) или с одного колебательного (вращательного) уровня на другой [колебательные (вращательные) спектры].

Кроме того, возможны и переходы с одними значениями Е_кол и Е_вращ на уровни, имеющие другие значения всех трех компонентов, в результате чего возникают электронно-колебательные и колебательно-вращательные спектры. Поэтому спектр молекул довольно сложный.

Типичные молекулярные спектры - полосатые, представляют собой совокупность более или менее узких полос в ультрафиолетовой, видимой и инфракрасной областях. Применяя спектральные приборы высокой разрешающей способности, можно видеть, что полосы представляют собой настолько тесно расположенные линии, что они с трудом разрешаются.

Структура молекулярных спектров различна для разных молекул и с увеличением числа атомов в молекуле усложняется (наблюдаются лишь сплошные широкие полосы). Колебательными и вращательными спектрами обладают только многоатомные молекулы, а двухатомные их не имеют. Это объясняется тем, что двухатомные молекулы не имеют дипольных моментов (при колебательных и вращательных переходах отсутствует изменение дипольного момента, что является необходимым условием отличия от нуля вероятности перехода).

Молекулярные спектры применяются для исследования строения и свойств молекул, используются в молекулярном спектральном анализе, лазерной спектроскопии, квантовой электронике и т.д.

13.9. Магнитный момент атома. Опыт Штерна и Герлаха

Орбитальный магнитный момент. В квантовой теории магнитный момент μ и механический момент М атома следует заменить операторам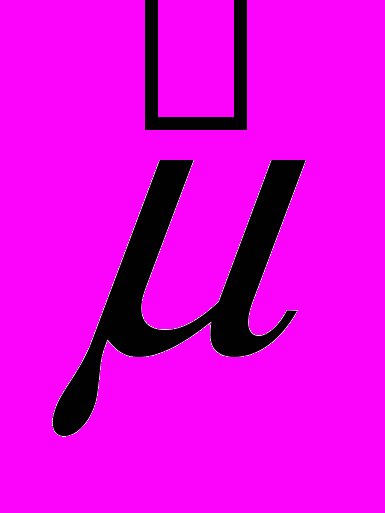и и :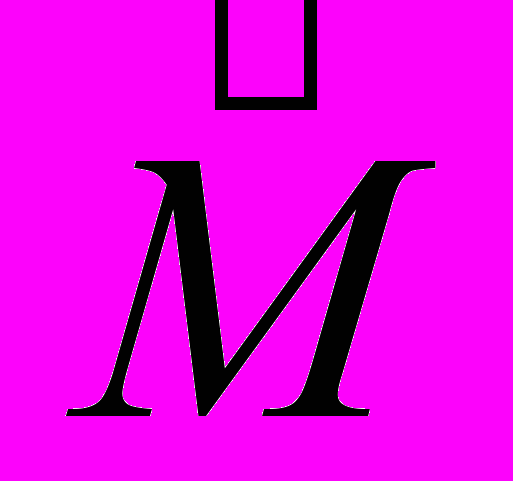

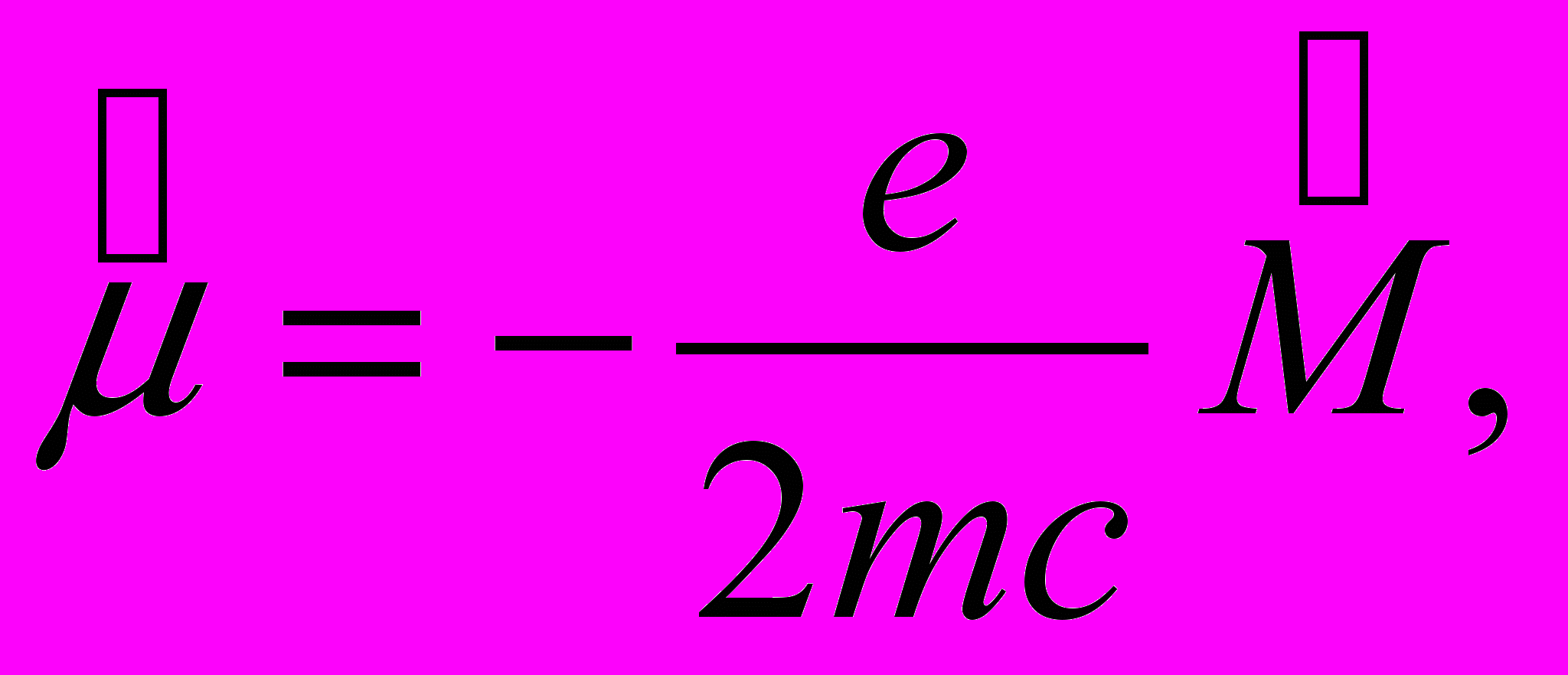(13.46)

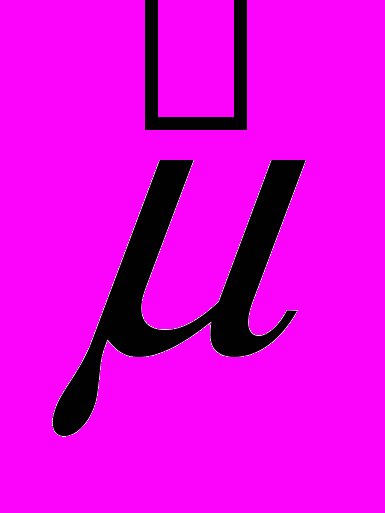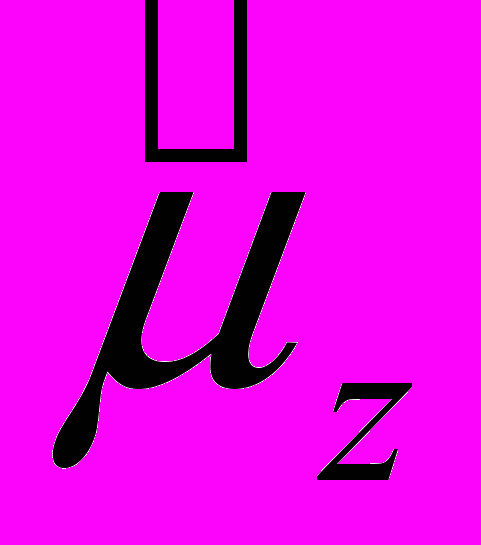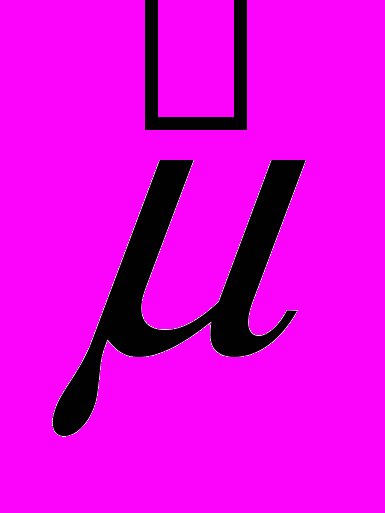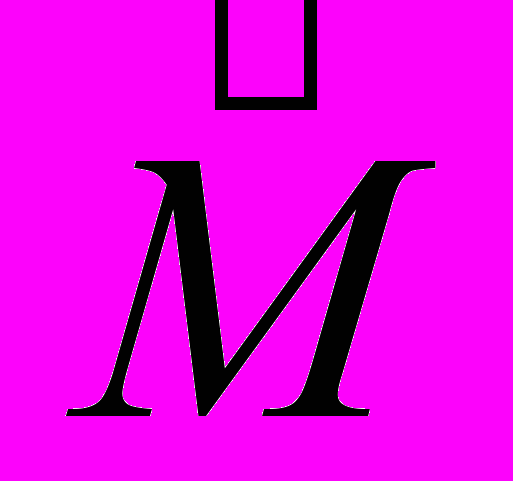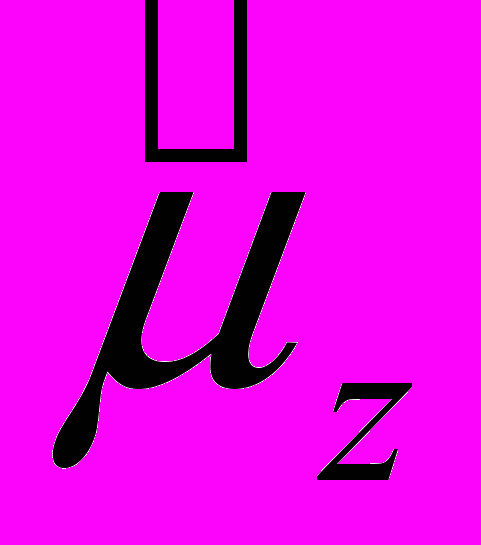Отсюда следует, что изучение свойств магнитного момента электрона сводится к изучению свойств операторов и . А так как операторы и , и 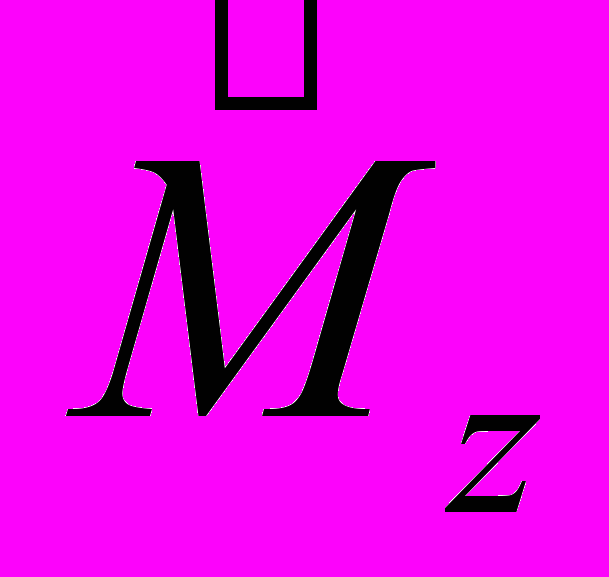отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.

В стационарном состоянии определенные значения могут иметь только модуль магнитного момента 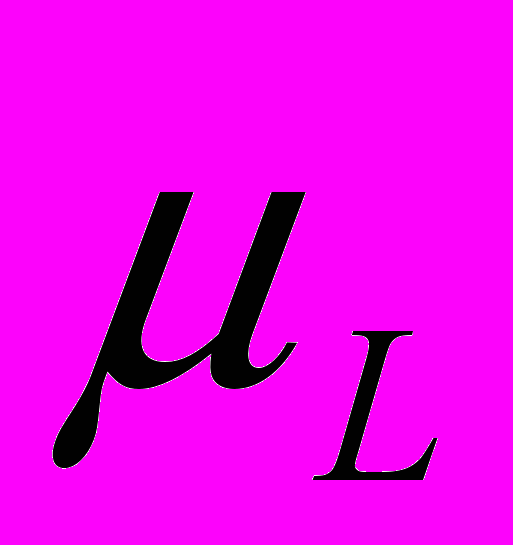и одна из его проекций на произвольную ось Z. Имея в виду (13.46), а также (13.34) и (13.36), запишем собственные значения операторов 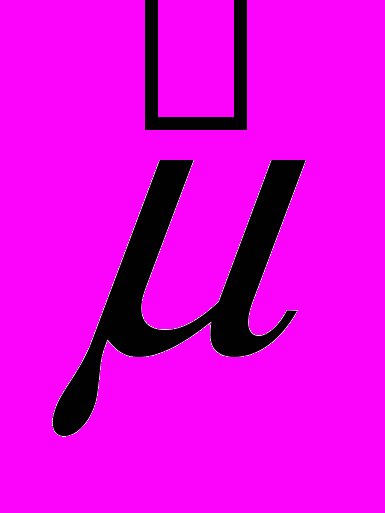и :

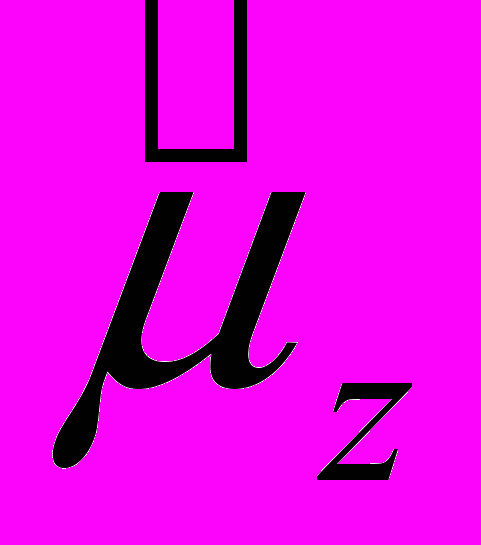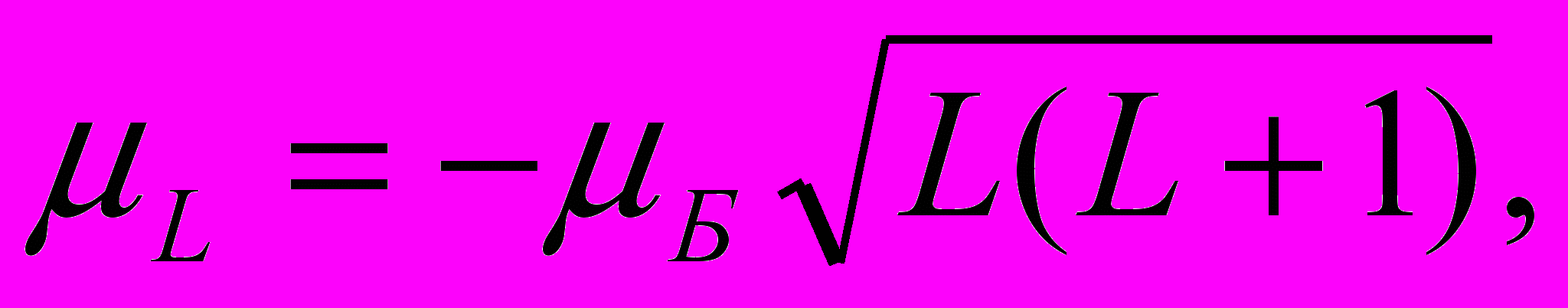L = 0, 1, 2, ...	(13.47)
μLz = -μБ mL, mL = 0, ± 1, ± 2, …, ± L,		(13.48)

где μ_Б — магнетон Бора: μ_Б = eћ/2mc. Он играет роль кванта магнитного момента (точнее его проекции μ_z).




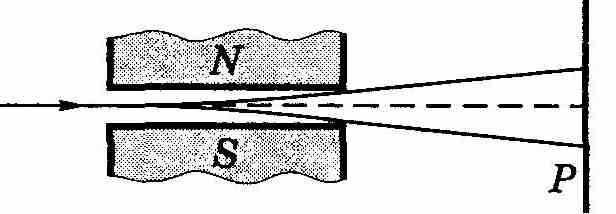
Опыты Штерна и Герлаха. Наличие у атомов магнитных моментов и их квантование было доказано экспериментально Штерном и Герлахом (1921). В их опытах пучок атомов пропускался сквозь сильно неоднородное поперечное магнитное поле (рис. 13.10, а). Необходимая степень неоднородности поля достигалась с помощью специальной формы полюсных наконечников N и S электромагнита (рис. 13.10, б). После прохождения магнитного поля пучок атомов попадал на фотопластинку Р и оставлял на ней след.







а)

Рис. 13.10.

Если атомы обладают магнитным моментом, то согласно электродинамике на них будет действовать сила, проекция которой на ось Z (см. рис. 13.10, б)

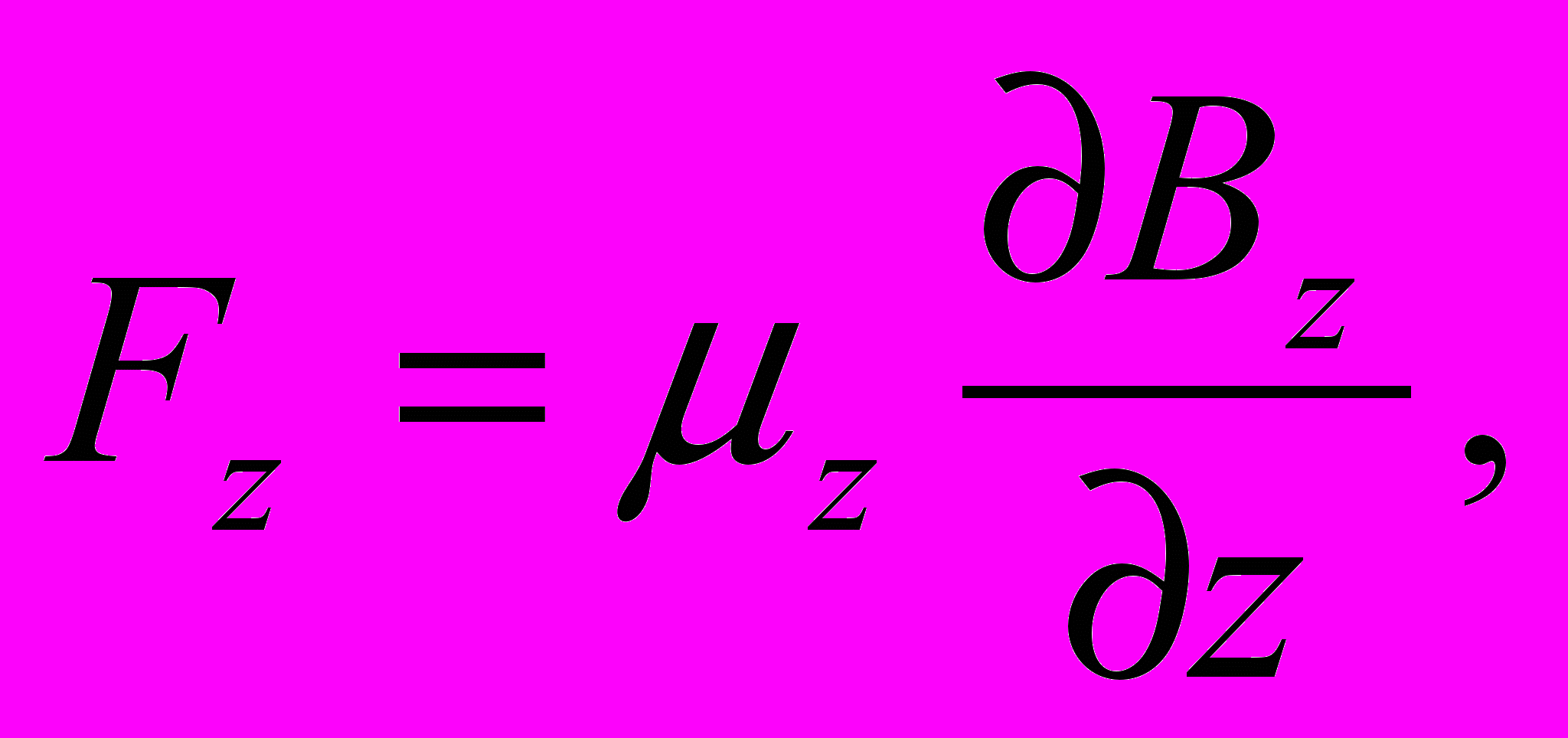(13.49)

где μ_z — проекция магнитного момента атома на ось Z. Из этой формулы видно, что для получения необходимого эффекта при малых значениях μ_z нужно обеспечить достаточно большую не­однородность поля, т. е. ∂B_z/∂z. Это и достигалось с помощью указанной формы полюсных наконечников.

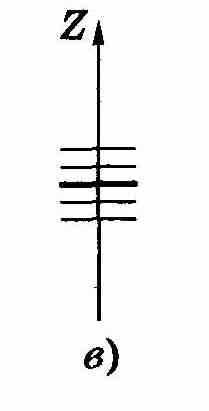
В отсутствие магнитного поля след пучка на фотопластинке Р имел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщепление пучка (рис. 13.10, в), что являлось следствием квантования проекции магнитного момента μ_z в формуле (13.49): μ_z может принимать только ряд дискретных значений. В опытах обнаружилось также, что для разных атомов число компонент, на которые расщеплялся пучок, было или нечетным, или четным. Анализ полученных результатов показал, что нечетное число компонент возникает у атомов, обладающих только орбитальным механическим моментом M_L, тогда магнитное поле снимает вырождение по L и число компонент (значений m_L) будет равно 2L + 1, т. е. нечетным.

Если же момент атома является суммой орбитального и спинового, т. е. определяется квантовым числом J, то число компонент будет равно 2J+ 1, и в зависимости от того, полуцелым или целым будет значение J, число компонент будет соответственно четным или нечетным.

Спиновый магнитный момент. Зная степень неоднородности магнитного поля, т. е. дВ_г/дг, Штерн и Герлах по величине расщепления пучка на фотопластинке рассчитали значение проекции спинового магнитного момента на направление магнитного поля, μ_B. Выяснилось, что μ_B равен одному магнетону Бора. Этот результат приводит к гиромагнитному отношению вдвое превышающему гиромагнитное отношене для орбитальных моментов. В связи с этим говорят, что спин обладает удвоенным магнетизмом.

Итак, спиновый магнитный момент и его проекция на произвольную ось Z определяются как

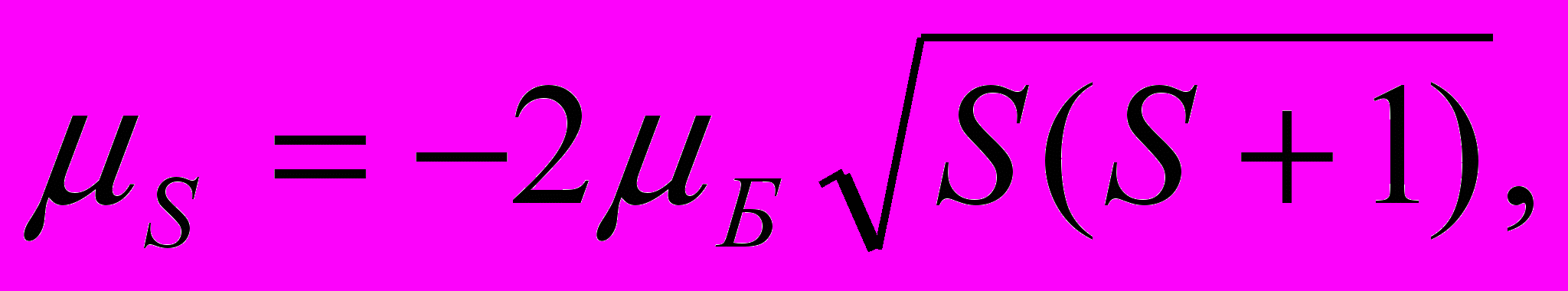(13.50)

μSz = -2μБ ms, ms=S,S-1, …, -S.

(13.51)

При S = 1/2 m_s = +1/2 и -1/2.

Принято говорить, что спиновый магнитный момент электрона равен одному магнетону Бора. Такая терминология обусловлена тем, что при измерении магнитного момента мы обычно измеряем его проекцию, а она как раз и равна одному μ_Б. Опыты Штерна и Герлаха явились еще одним убедительным доказательством наличия у электрона спина. Помимо этих опытов следует упомянуть и о так называемых магнитомеханических явлениях — опытах Эйнштейна и де Хааса, а также опыте Барнетта. И в этих опытах было обнаружено, что гиромагнитное отношение спиновых моментов тоже вдвое больше отношения орбитальных.

Полный магнитный момент атома. Вследствие удвоенного магнетизма спина гиромагнитное отношение полных моментов μ/M_J оказывается значительно более сложным. Оно зависит от квантовых чисел L, S и J. Соответствующий расчет, проводимый в квантовой теории, позволил найти магнитный момент μ и его проекцию на ось Z:

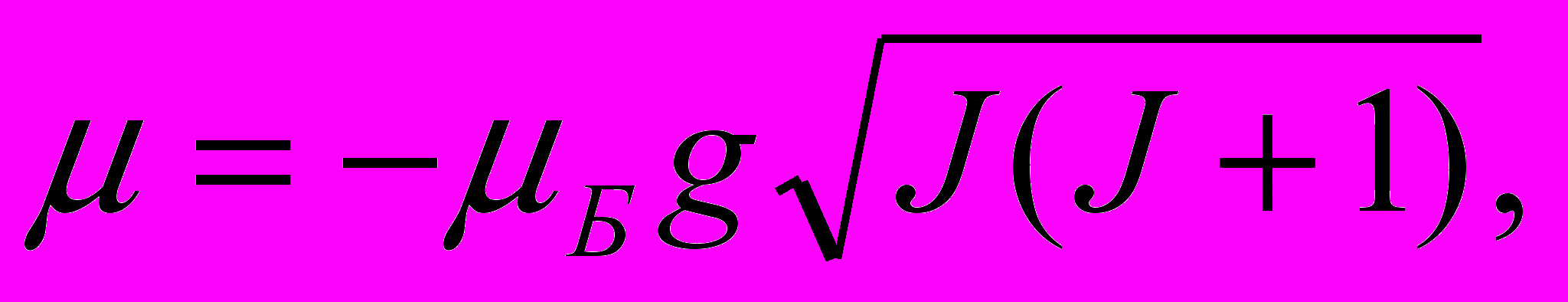(13.52)

μ z = - μБgmJ, mJ = J, J-1, …, -J,

(13.53)

где g — множитель (или фактор) Ланде

В частности, в синглетных состояниях (S = 0) J = L, g = 1, и мы приходим к формулам (13.47) и (13.48). А при L = 0 (J = S, g = 2) — к формулам (13.50) и (13.51).

13.9. Атом во внешнем магнитном поле. Эффект Зеемана

Расщепление в магнитном поле энергетических уравнений атомов, приводящее к расщеплению спектральных линий в спектрах, называют эффектом Зеемана. Различают эффект Зеемана: нормальный (простой), когда каждая линия расщепляется на три компонента, и аномальный (сложный), когда каждая линия расщепляется на большее, чем три, число компонентов.

Эффект Зеемана характерен для атомов парамагнетиков, так как только эти атомы обладают отличным от нуля магнитным моментом и могут взаимодействовать с внешним магнитным полем.

Атом, обладающий магнитным моментом, приобретает в магнитном поле дополнительную энергию

∆E = -μJBB,

(13.54)

где μ_JB — проекция полного магнитного момента атома на направление поля В. Имея в виду формулу (13.53), запишем выражение для энергии каждого подуровня:

E = E0 + ∆E = E0 + μБgBmJ , mJ = J, J-1, …, -J,

(13.55)

где Е₀ — энергия уровня в отсутствие магнитного поля.

Отсюда следует, что уровни с квантовым числом J расщепляются в магнитном поле на 2J + 1 равноотстоящих друг от друга подуровней, причем величина расщепления зависит от множителя Ланде g, т. е. интервалы δЕ между соседними подуровнями пропорциональны g: δЕ ≈ g. Таким образом, магнитное поле в результате расщепления уровней снимает вырождение по m_J.

Кроме этого, необходимо учесть, что возможны только такие переходы между подуровнями, принадлежащими разным уровням, при которых выполняются следующие правила отбора для квантового числа т_J:

∆mJ = 0, ±1.

(13.56)

Если в (13.55) B = 0, то энергетический уровень определяется только первым членом, если В ≠ 0, то необходимо учитывать возможные значения m_J , а оно может принимать 2J + 1 значений. Это означает расщепление первоначального энергетического уровня на 2J+ 1 подуровней.

Теперь можно понять происхождение мультиплетов Зеемана. На рис. 13.11 рассмотрены возможные переходы в атоме водорода между состояниями р (l = 1)иs(l=0) для двух случаев:

1. когда В = 0 (внешнее магнитное поле отсутствует);
   
2. когда В ≠ 0.
   

В 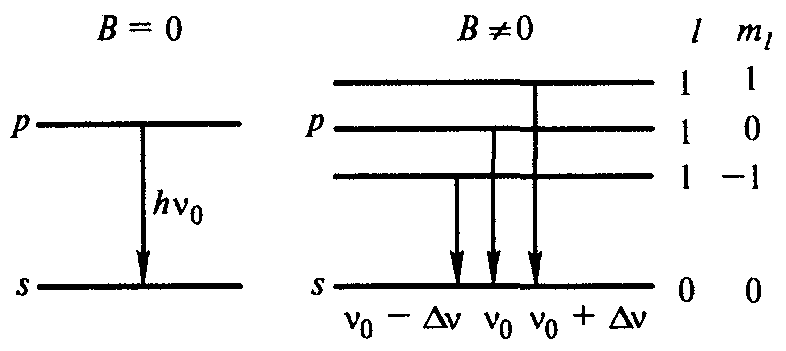отсутствие поля наблюдается одна линия с частотой v₀. В магнитном поле p-состояние расщепляется на три подуровня (при l = 1, m_l, = 0, ± 1), с каждого из которых могут происходить переходы на уровень s, и каждый переход характеризуется своей частотой: v₀ - ∆v, v₀, v₀ + ∆v. Следовательно, в спектре появляется триплет (наблюдается нормальный эффект Зеемана).


Рис. 13.11.


Не вдаваясь в подробности, отметим, что нормальный эффект Зеемана наблюдается в том случае, если исходные линии не обладают тонкой структурой (являются синглетами). Если исходные уровни обладают тонкой структурой, то в спектре появляется большее число компонентов и наблюдается аномальный эффект Зеемана.