Geum.ru

Лекция n10 Лекция 10

Вид материалаЛекция

Содержание


Электромагнитное излучение в вакууме
V = c /n зависит
ЭМ волны в ионосфере
Подобный материал:



ЛЕКЦИЯ N10


Лекция 10.
Электромагнитные волны. Шкала электромагнитных волн.

групповая скорость и дисперсия


Как уже было сказано выше, возникновение электромагнитной (ЭМ) волны обусловлено тем, что изменяющееся магнитное поле порождает в непосредственной окрестности изменяющееся электрическое поле, которое, в свою очередь, снова порождает изменяющееся магнитное и т.д. Применение уравнений Максвелла для среды даст уравнения Даламбера для волны, распространяющейся вдоль направления х:

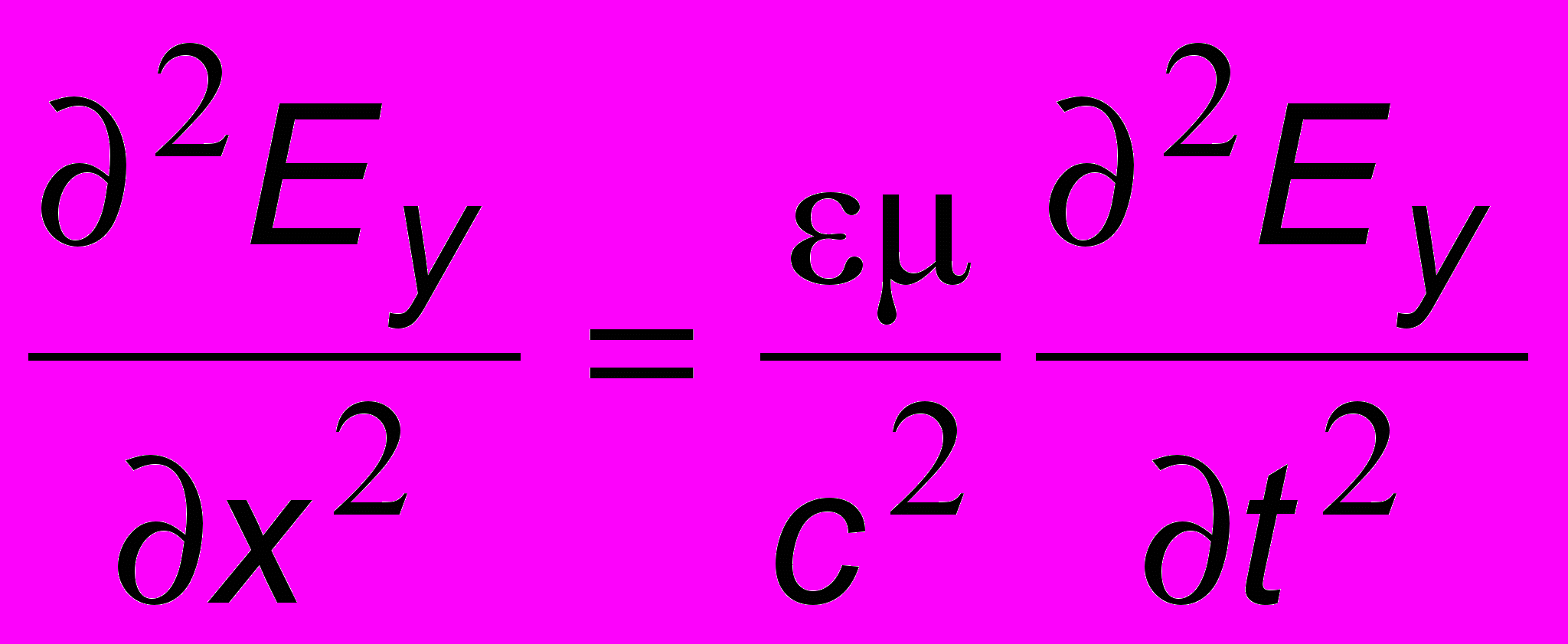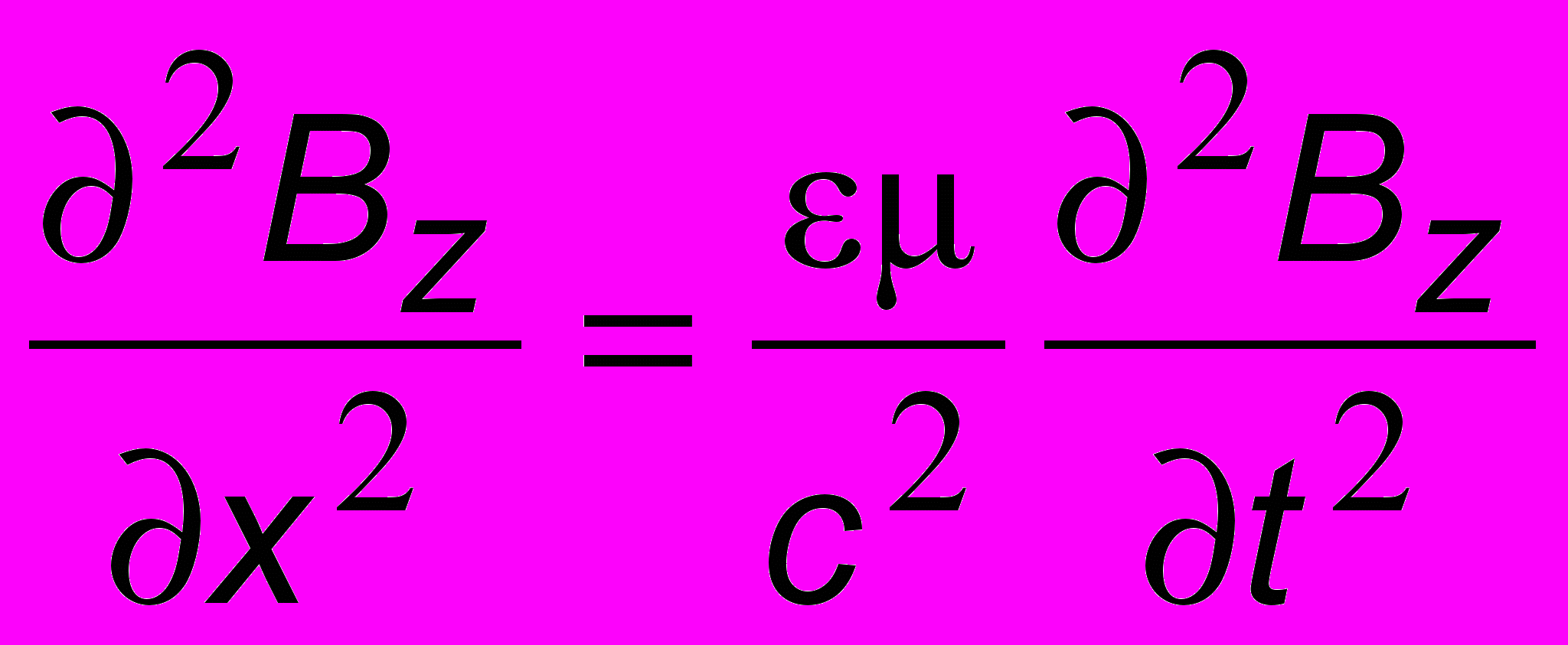; , (10.1)

г
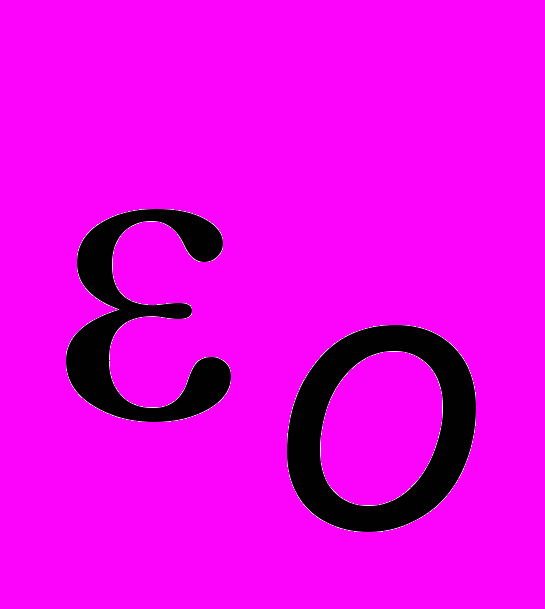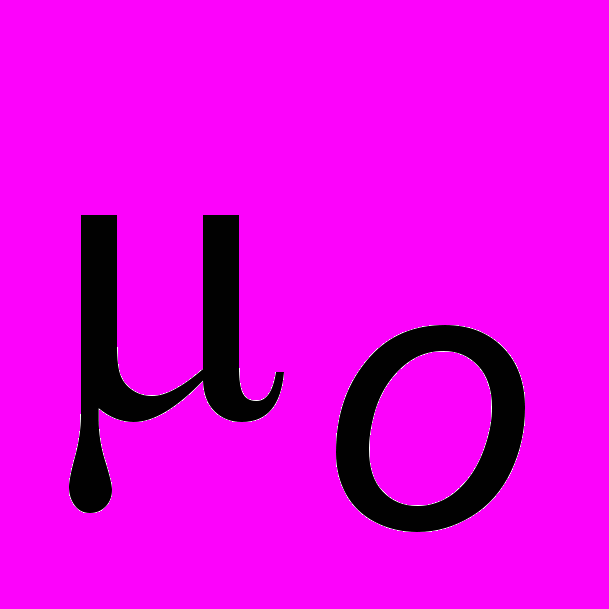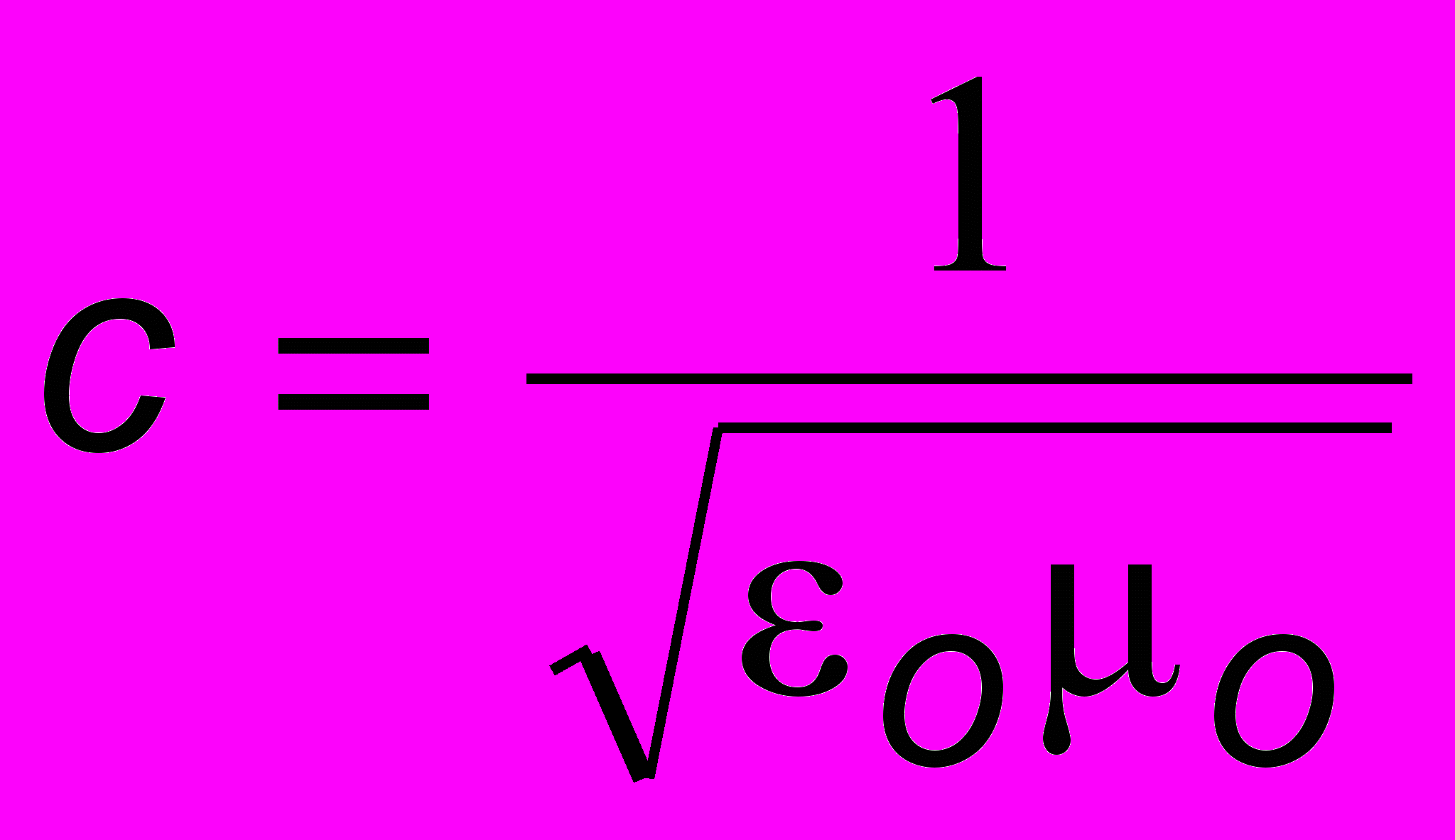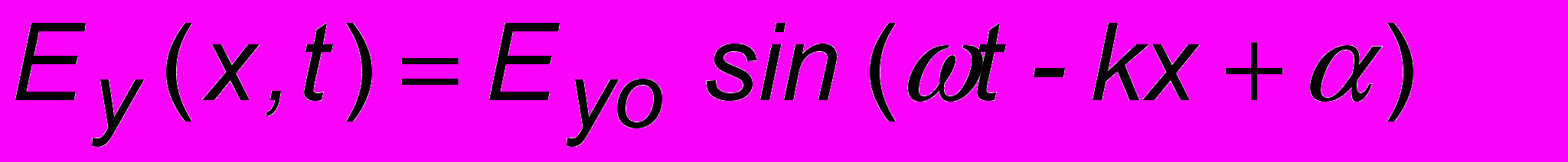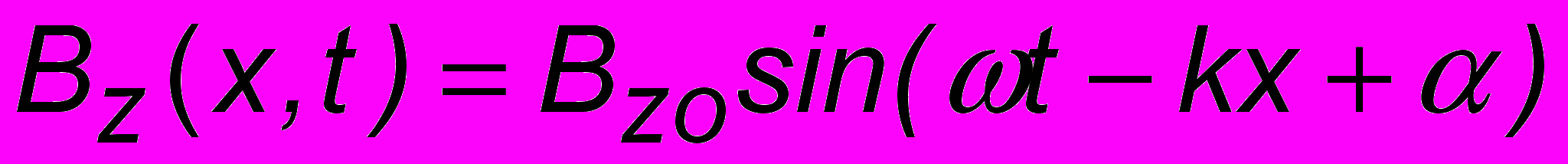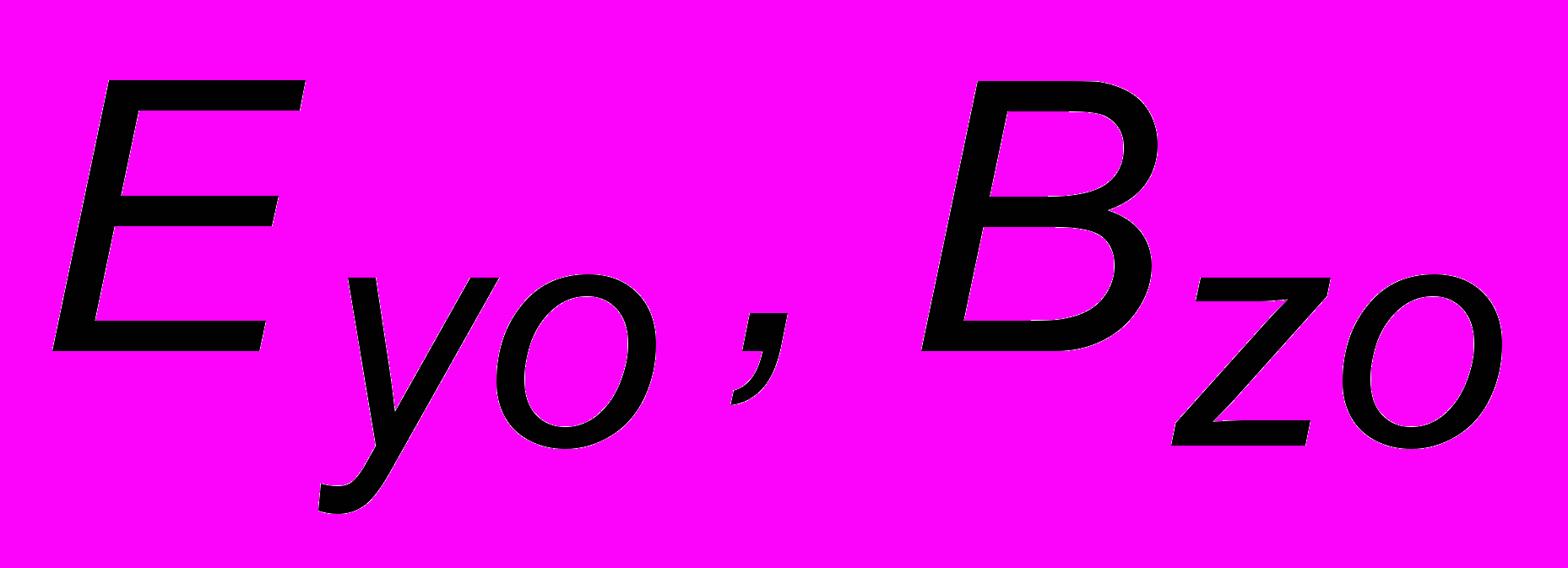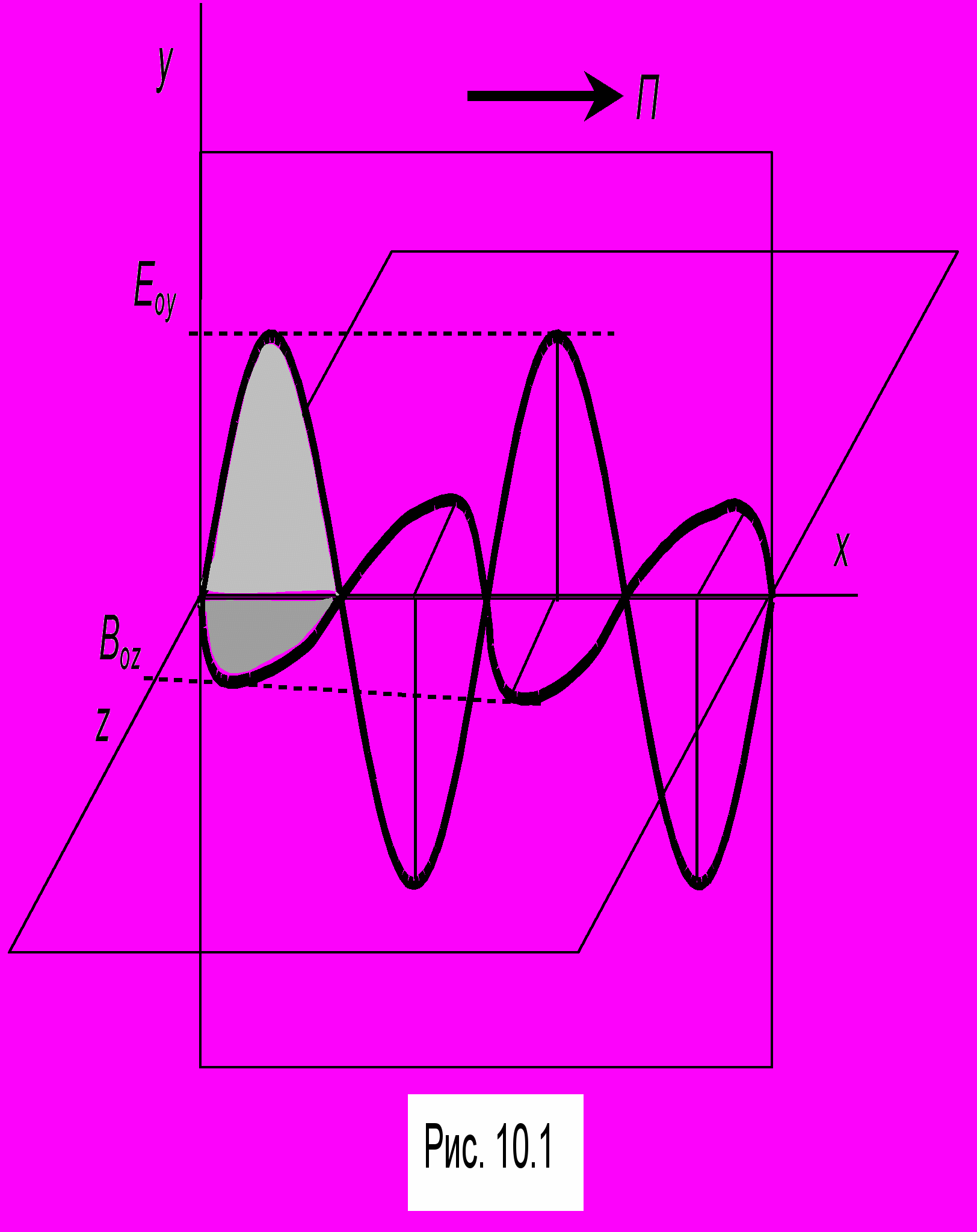
де ,  - соответственно диэлектрическая и магнитная проницаемости; с - скорость света в вакууме, связанная с электрической и магнитной постоянными соотношением (см. ЧАСТЬ 2). Для гармонических волн решение уравнений (10.1) имеет вид: и , где - амплитуды компонент поля. Как видно из этих соотношений, колебания векторов 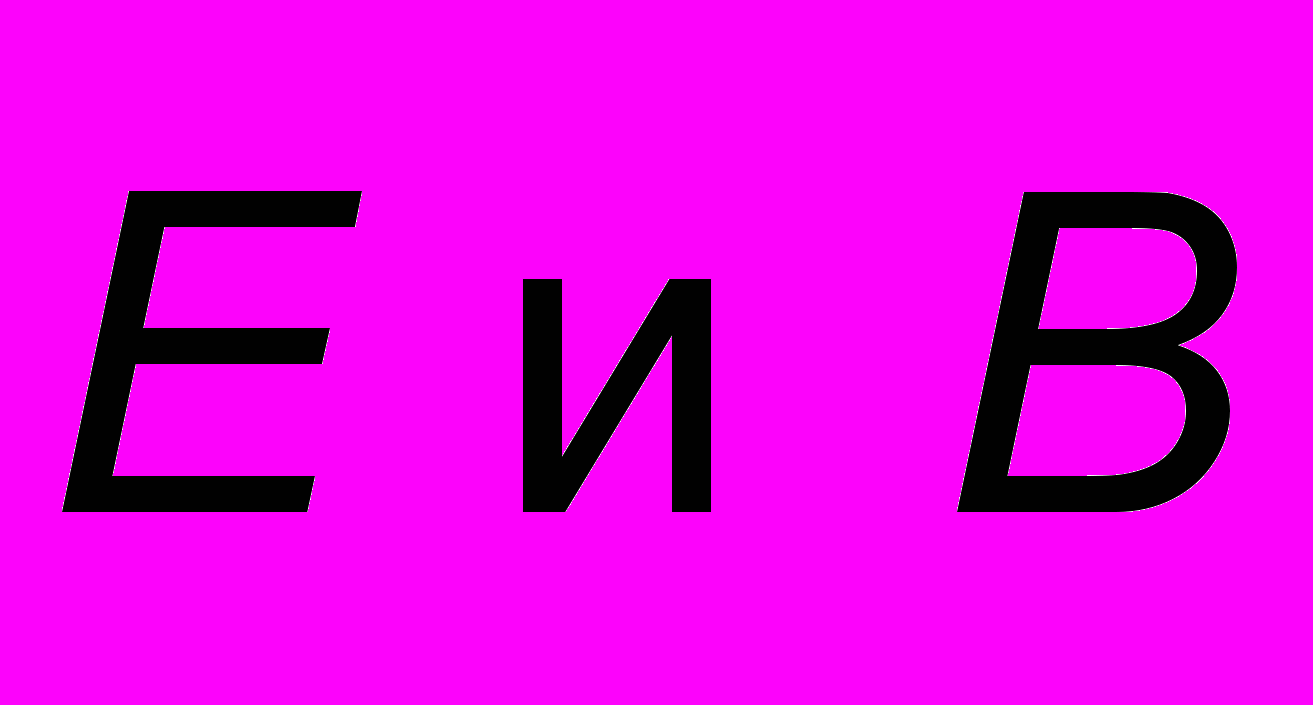происходят в направлениях, перпендикулярных направлению распространения х. Таким образом, ЭМ волны поперечны и всегда 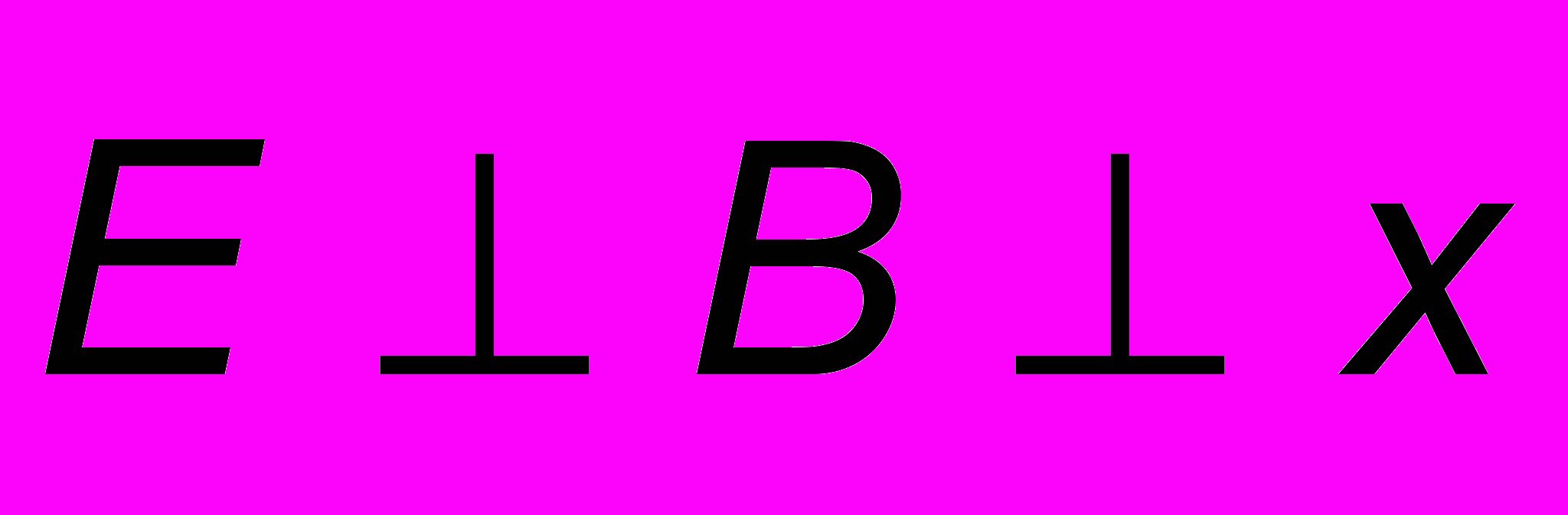, как это показано на рис. 10.1. Колебания векторов 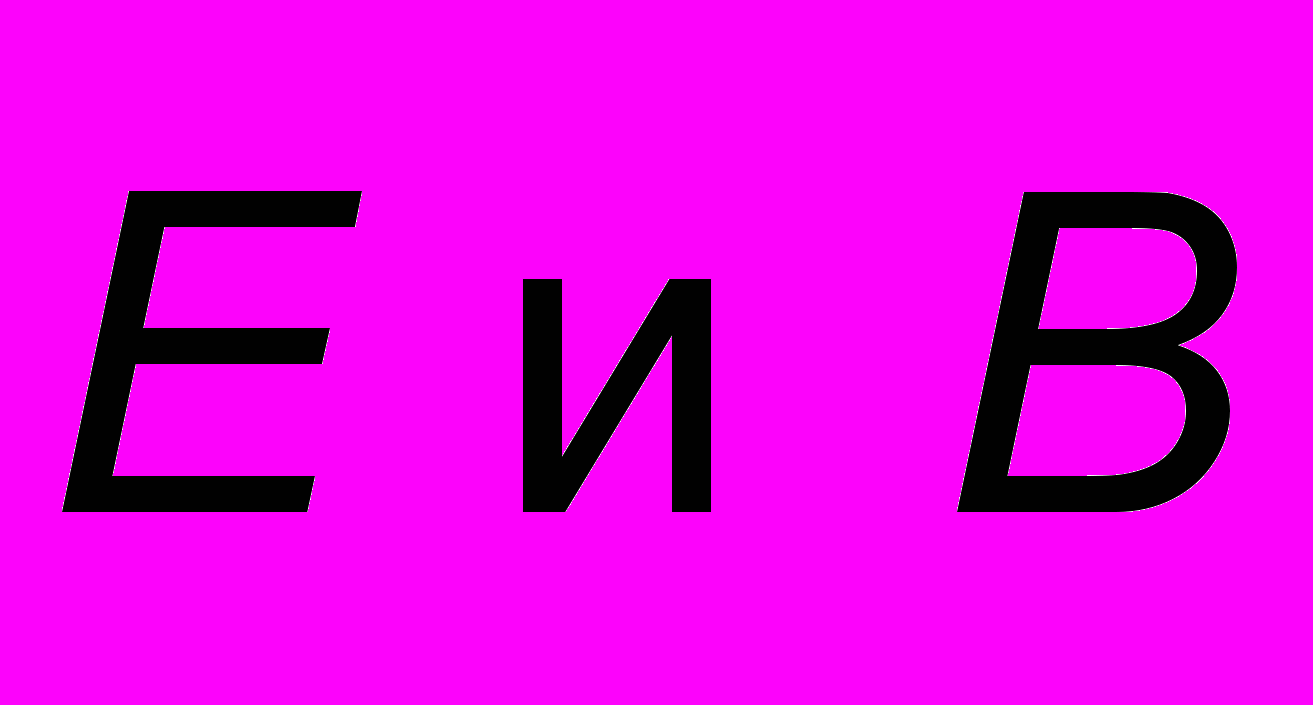происходят в одной фазе: их значения через нуль или через экстремальные точки проходят одновременно. Сравнивая (10.1) с (9.3), найдем, что фазовая скорость в среде 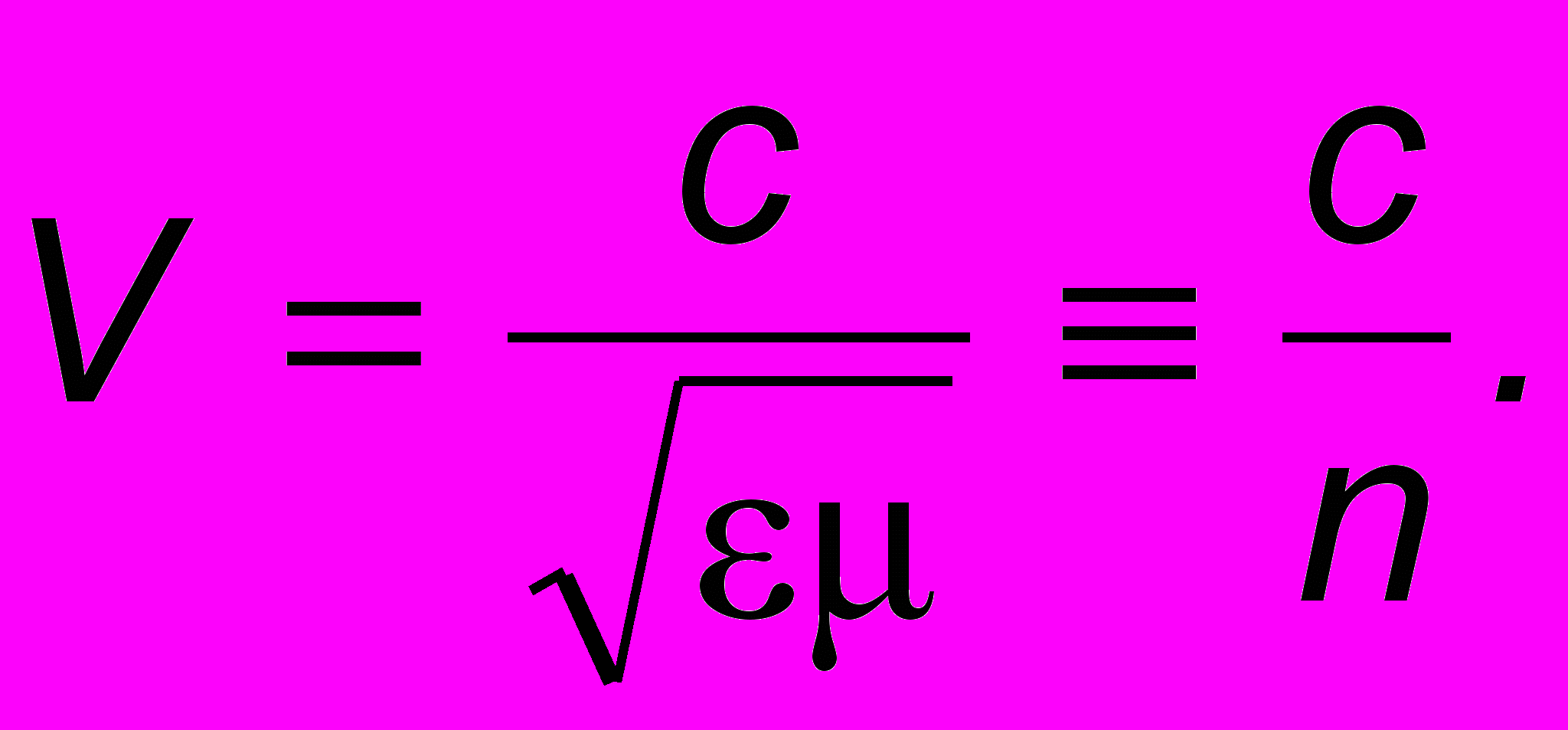Величина n, показывающая, во сколько раз фазовая скорость ЭМ волны в среде меньше, чем в вакууме, называется опт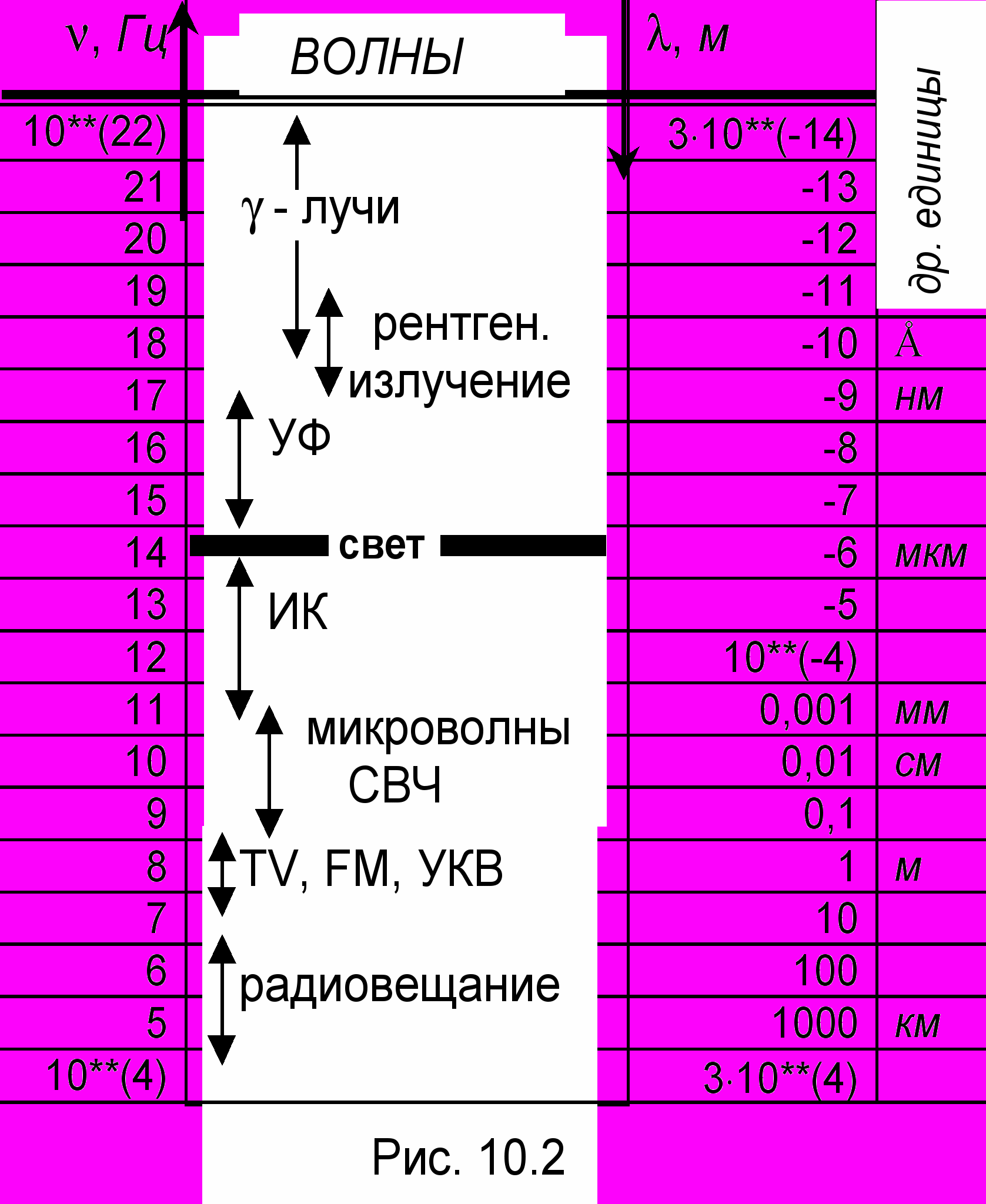ическим показателем преломления. При этом мы имеем в виду среды, свойства которых одинаковы по всем направлениям - изотропные среды. Если это не так (анизотропные среды; например, кварц), то n будет тензорной величиной и задаваться матрицей1. Для вакуума  = = 1 и V = c.

Для ЭМ волны плотность энергии определяется суммой электрической и магнитной компонент: 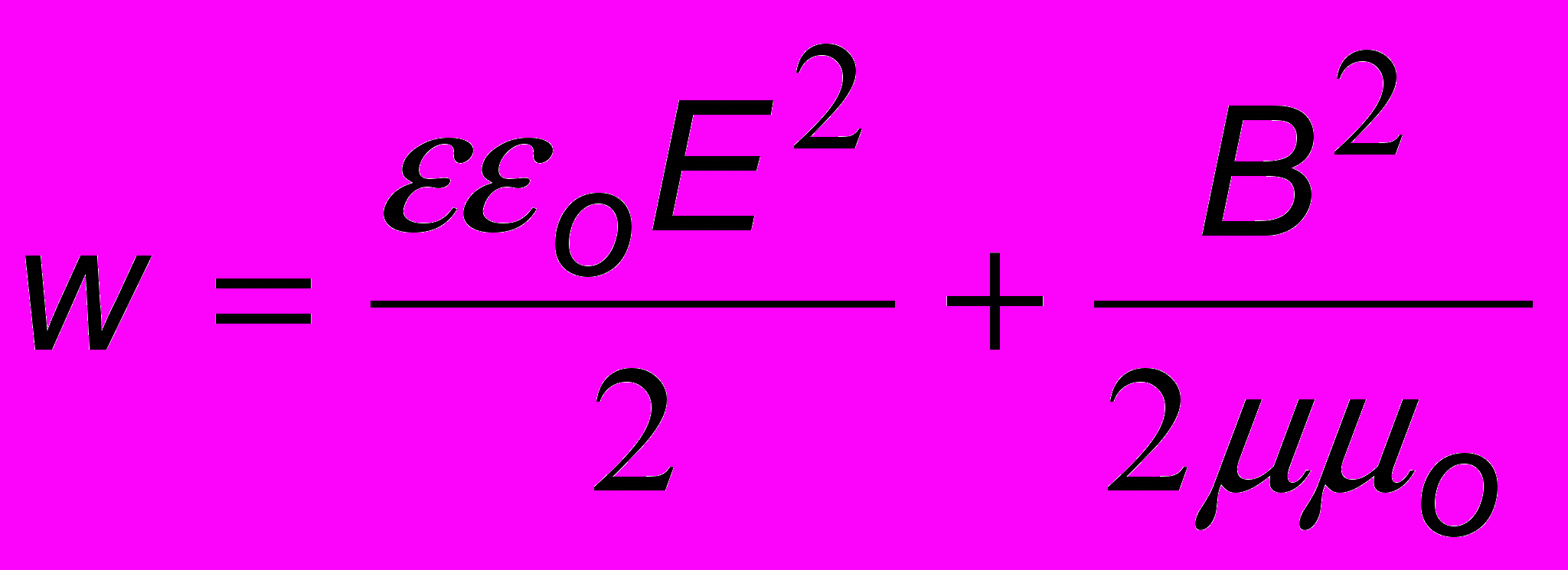, плотность потока энергии - вектором Пойнтинга 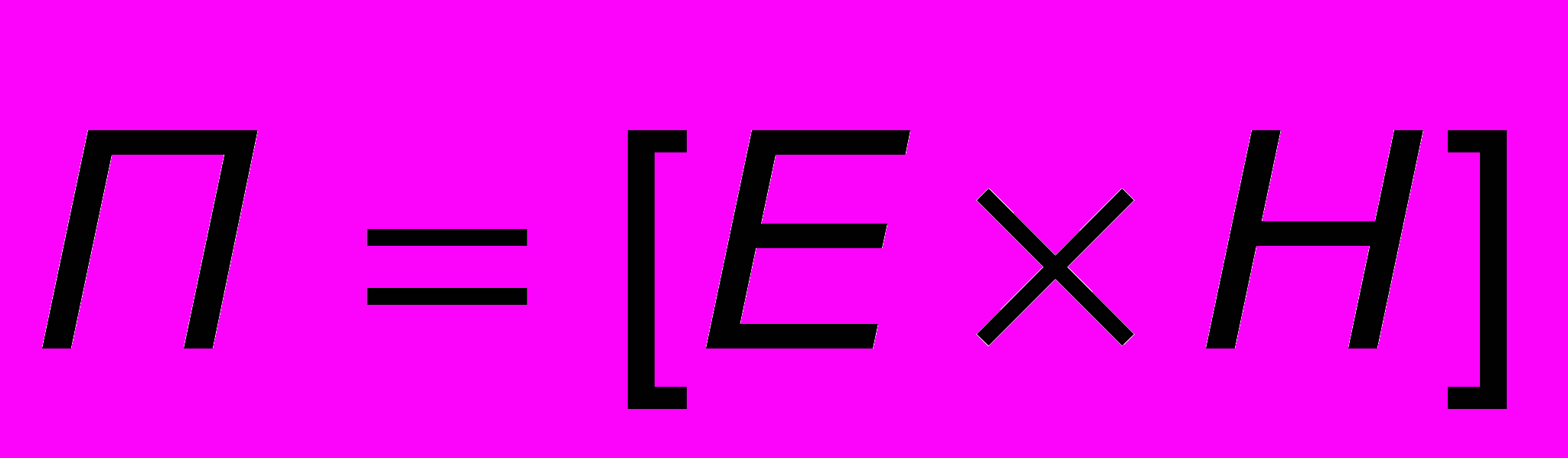, где - напряжённость магнитного поля, связанная с магнитной индукцией соотношением 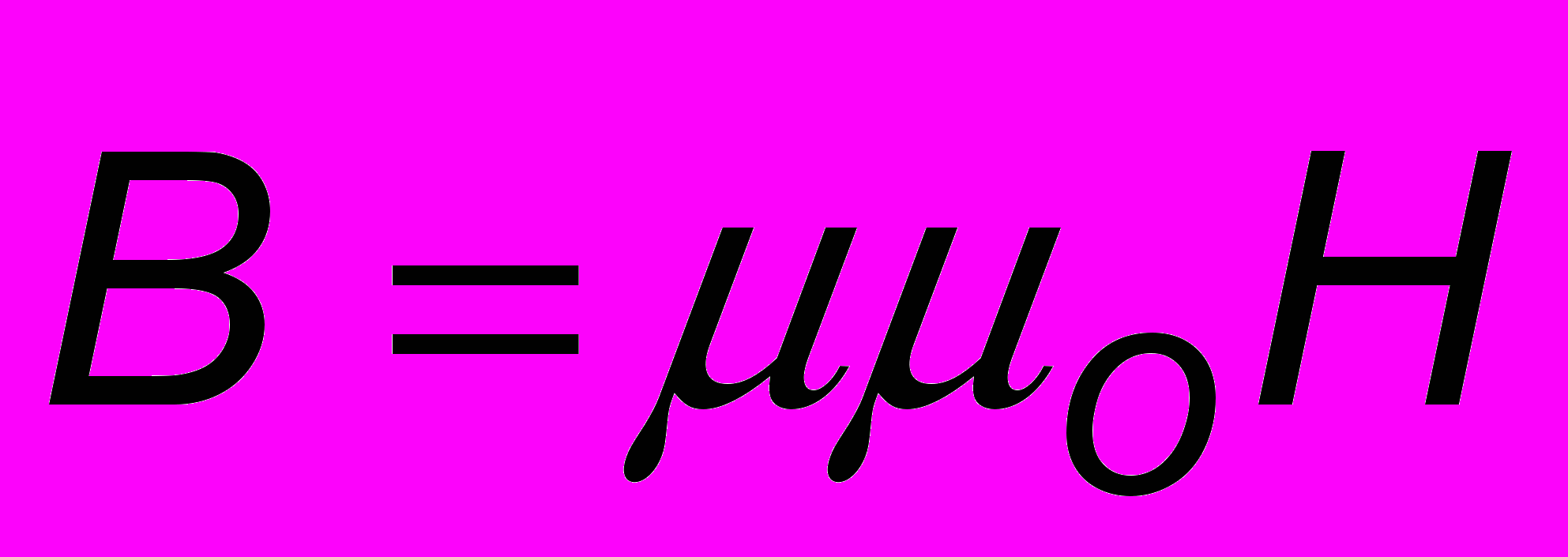(см. ЧАСТЬ 2, ЛЕКЦИЯ 7). Вектор Пойнтинга, как и вектор Умова в случае упругих волн, определяет направление распространения энергии ЭМ волны.

Шкала ЭМ волн представлена на рис. 10.2. Следует отметить, что границы диапазонов весьма условны. Видимый свет занимает узкую полоску в этом континууме: от 4000 Å (фиолетовый свет) до 7500 Å (красный). Здесь мы употребили принятую в оптике единицу длины ангстрем: 1 Å = 10-10 м. Шкала ЭМ волн прекрасно иллюстрирует закон философии о переходе количественных изменений в качественные. Однако более глубокие спекуляции по этому поводу оставим философам-профессионалам.

Д
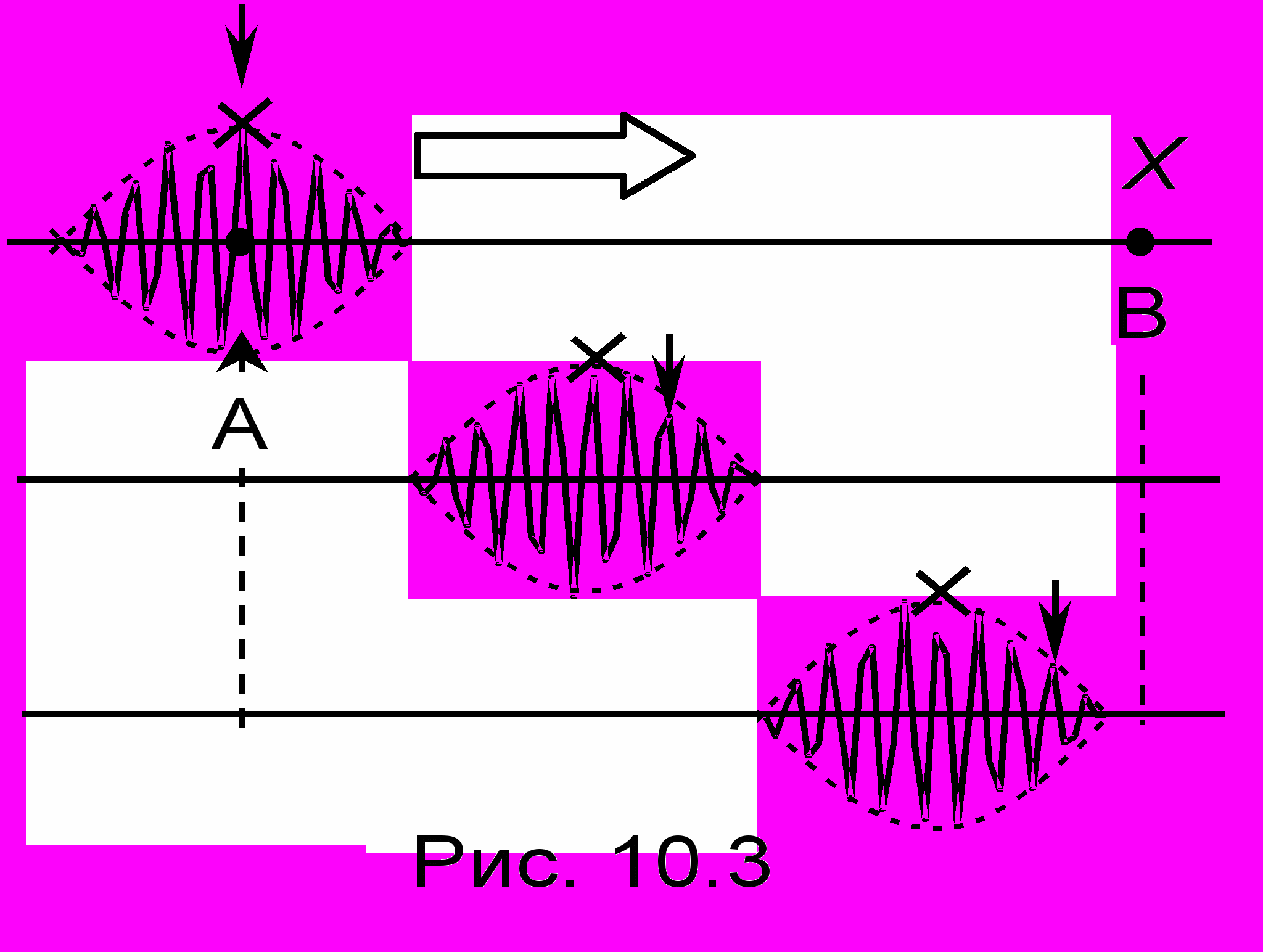
о сих пор, говоря о скорости распространения волны, мы имели в виду скорость изменения волновой картины - фазовую скорость
V = /k. Наблюдатель, сидя на гребне (или впадине) бесконечной гармонической волны и перемещаясь вместе с ней с такой же скоростью, видит вокруг себя неподвижную картину горбов и впадин. Однако в инженерной радиоэлектронике приходится иметь дело с передачей информации и распространением энергии. Как уже отмечалось в ЛЕКЦИИ 5, для передачи информации сигнал должен быть промодулирован, а как следует из теории Фурье, любой негармонический сигнал состоит из бесконечного числа гармонических составляющих, каждая из которых необязательно будет распространяться с одной и той же скоростью. Передача некоторого количества энергии (или "сгустка") осуществляется передачей в пространстве и времени так называемого волнового пакета. Предположим, что мы хотим передать без искажения такой волновой пакет (рис. 10.3) из пункта А в пункт В и будем для простоты рассматривать "водную аналогию", т.е. считать, что картинки на рис. 10.3 наблюдаются на поверхности воды. Поместим мысленно наблюдателя на вершину пунктирной огибающей сигнала и будем считать, что при распространении пакета он всегда сидит на самом его верху (положение его отмечено на рисунке крестом). "Набивка" пакета (сплошная линия) - это не просто синусоида, а несметное их количество, причем каждая составляющая может распространяться со своей скоростью. Что же увидит наблюдатель? Сначала ему покажется, что он неподвижно сидит на вершине горки, окруженной невозмущенной водой, но, приглядевшись вниз, он обнаружит под собой мелкие волны, убегающие вперед. Волны будут появляться сзади, набирать амплитуду, убегать вперед и, убывая, исчезать. На рис. 10.3 вертикальной стрелкой прослежено положение горба, который находился под наблюдателем в начале путешествия. На нижней картинке видно, что по мере продвижения к пункту В горб убегает вперед от наблюдателя. Форма огибающей в целом претерпит изменение. То же наблюдается, когда группа бегунов берет старт. Общая форма всей группы как целого постепенно расплывается по мере удаления бегунов от стартовой точки. Таким образом, чтобы волновой пакет распространялся через среду без изменения формы огибающей необходимо, чтобы все его гармонические спектральные составляюшие распрострянялись с одной и той же фазовой скоростью. Возвращаясь к проблеме передачи сигнала, отметим, что волна внутри волнового пакета может распространяться со скоростью V (фазовая скорость), которая, вообще говоря, отличается от скорости распространения u всего пакета как целого (групповая скорость), причем всегда uc, а V может иметь любые значения. Противоречия с теорией относительности здесь нет, поскольку фазовая скорость передает процесс распространения самой волновой картины, а не реального носителя энергии.

Зависимость фазовой скорости от частоты [или длины волны] V = f () [или V = f ()] называется дисперсией2. Дисперсия - это свойство среды, в которой распространяется сигнал. В вакууме дисперсия отсутствует.

Чтобы найти формулу для групповой скорости u, необходимо определить скорость распространения огибающей волнового пакета. Точное аналитическое выражение для функции, изображенной на рис. 10.3 сложно. Однако вместо одиночного пакета можно рассмотреть суперпозицию двух бегущих волн, вполне адекватно моделирующую свойства пакета. Пусть складываются две гармонические волны 1 = A cos (1t - k1x) и 2 = A cos (2t - k2x), такие что 1  2 и k1k2. Складывая волны и пользуясь тождеством 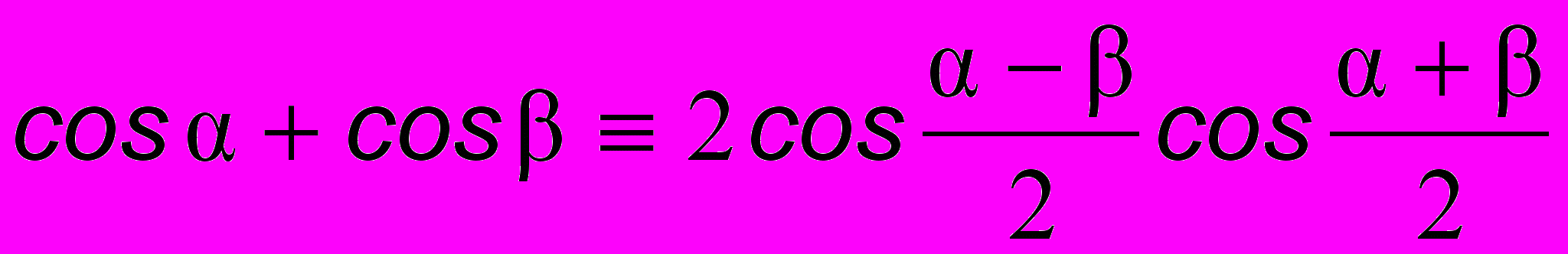, получим

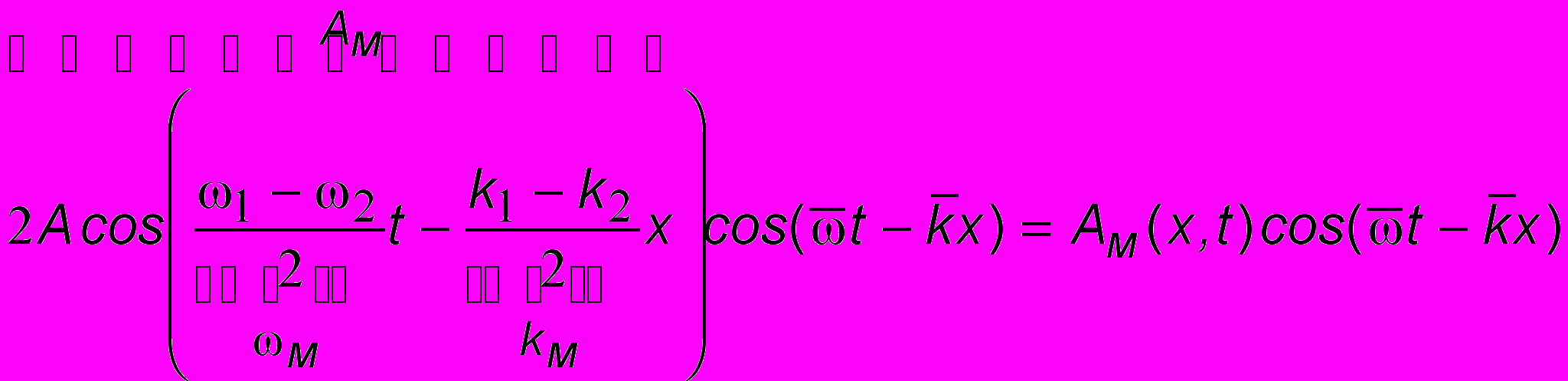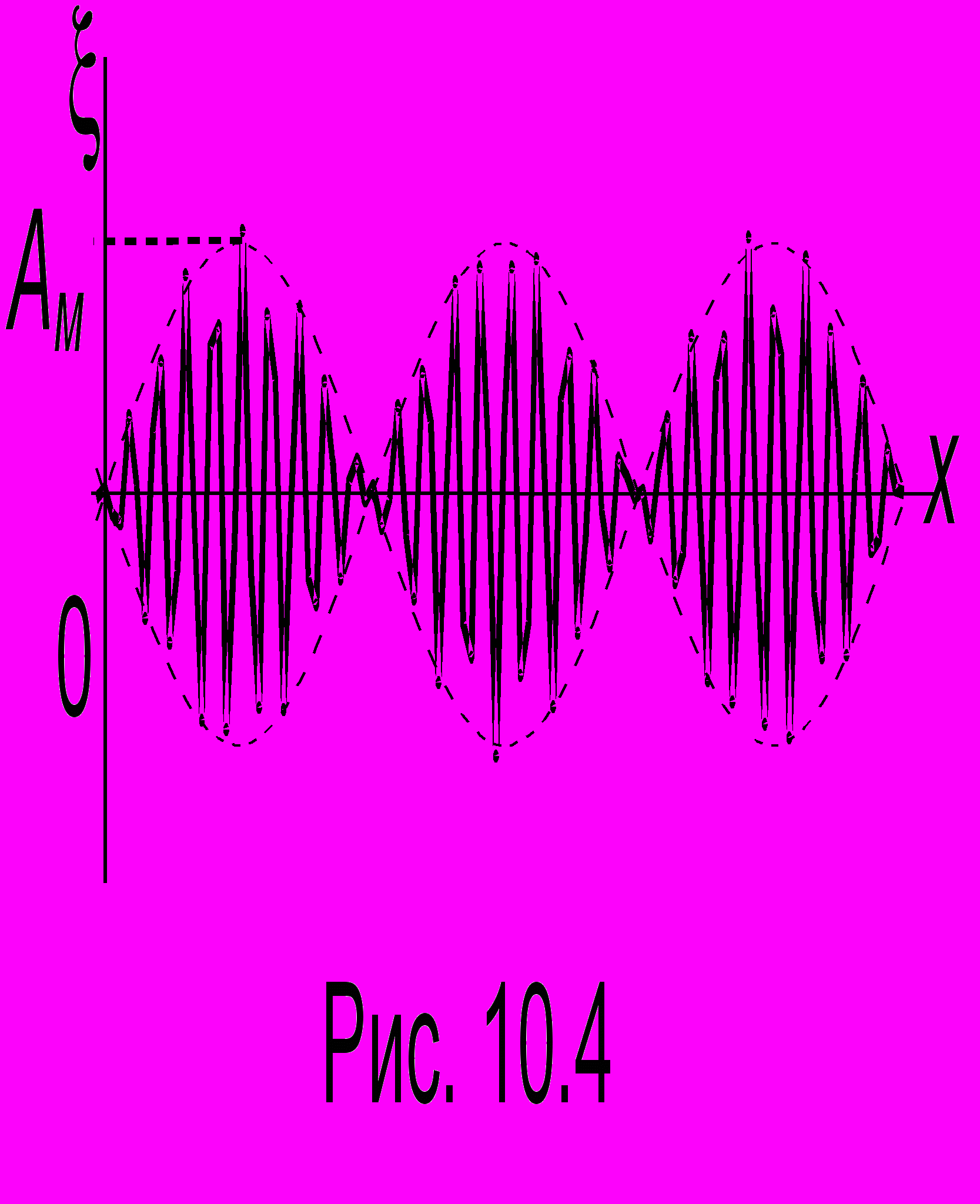
 = 1 + 2 = =, (10.2)

где индекс "м " означает модулированное значение параметра, а черта над символом - усреднение. Результат сложения для фиксированного момента времени показан на рис. 10.4. Здесь колебания пунктирной огибающей происходят с частотой модуляции 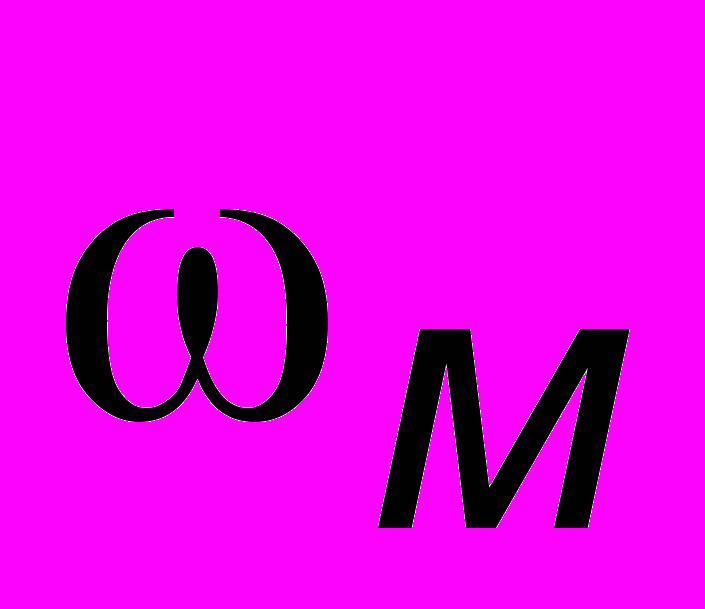, а колебания внутри пакета - со средней частотой 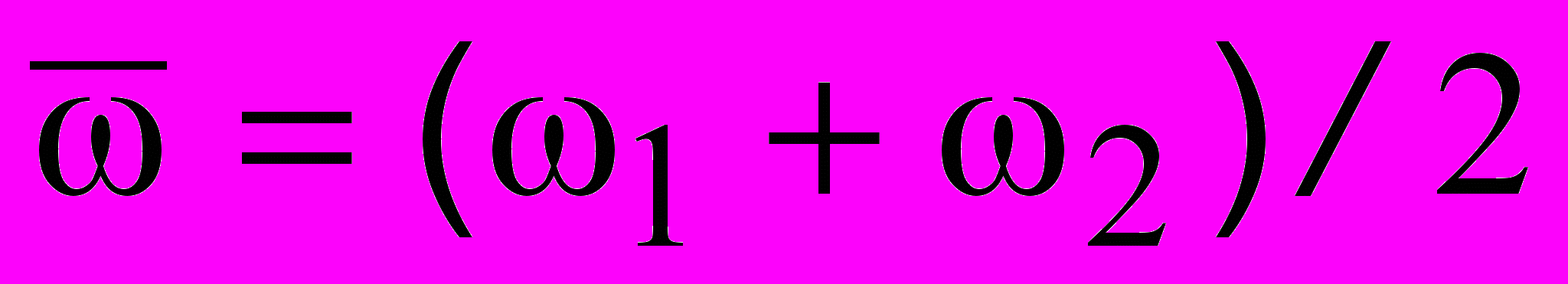, которой соответствует усредненное волновое число 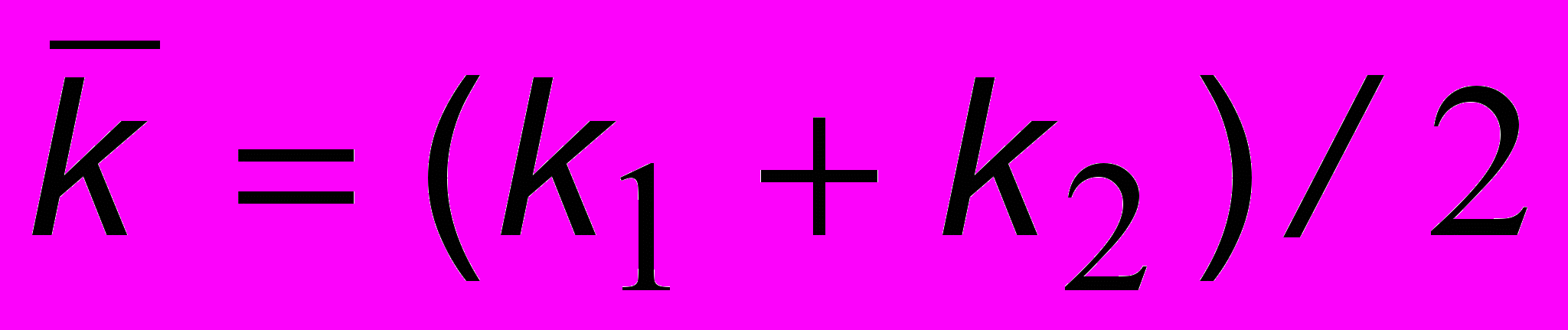. Скорость перемещения огибающей (креста на рис. 10.3) определится из условия 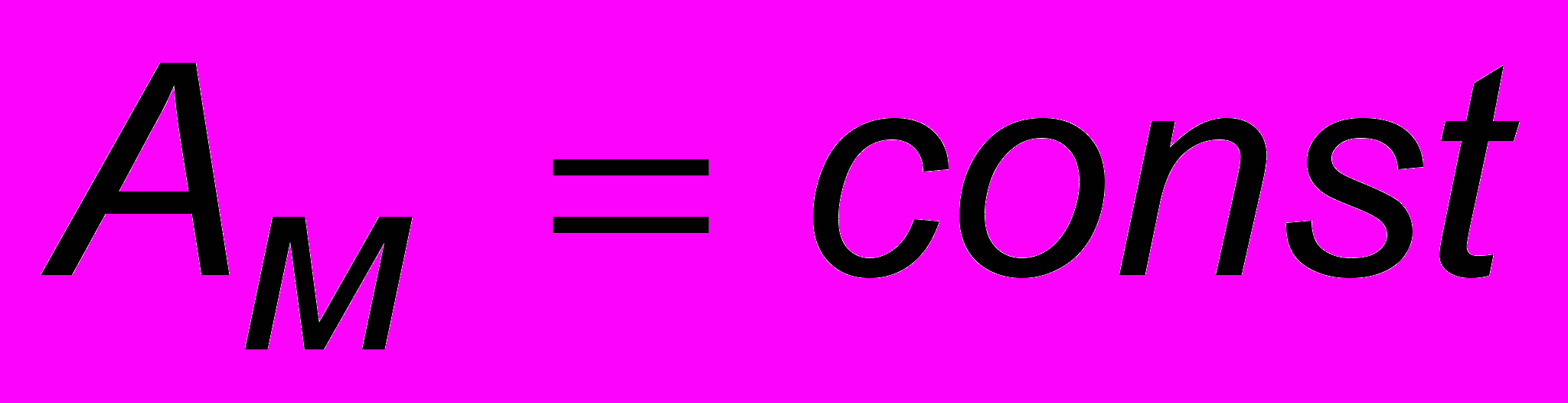. Для этого в (10.2) надо считатьть первые скобки константой: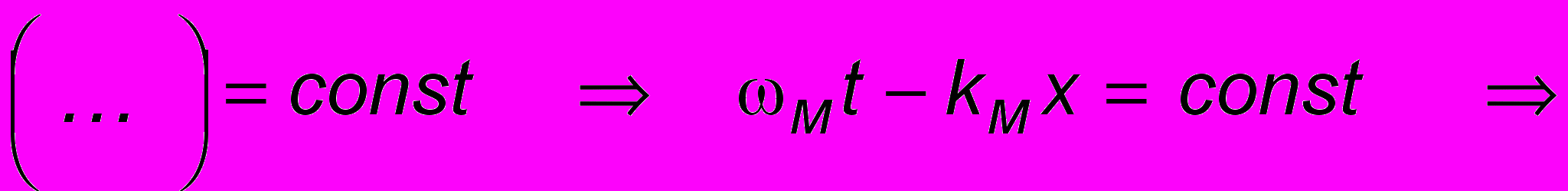

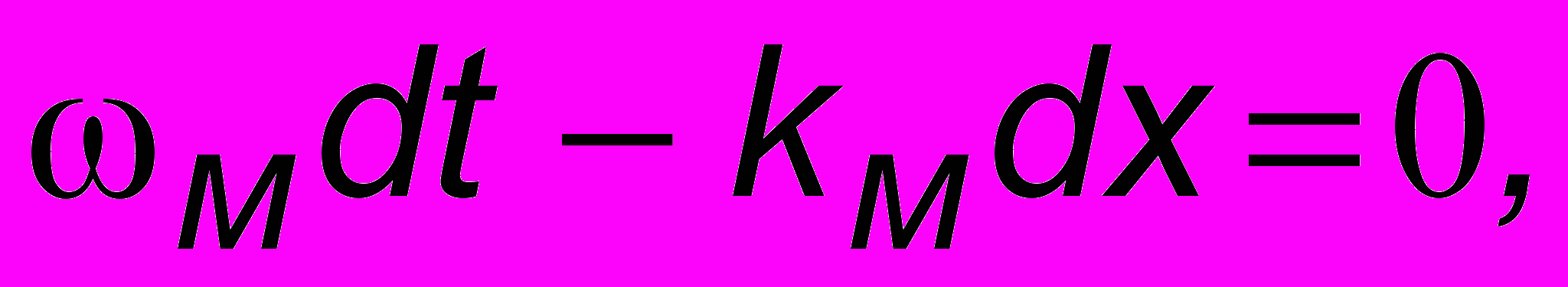откуда следует что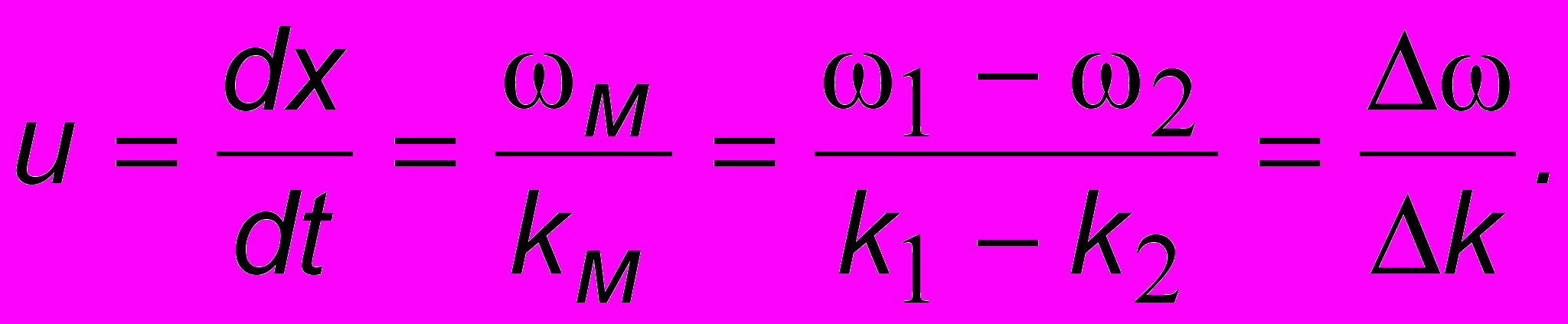
Более точный результат при более строгом выводе имеет вид:

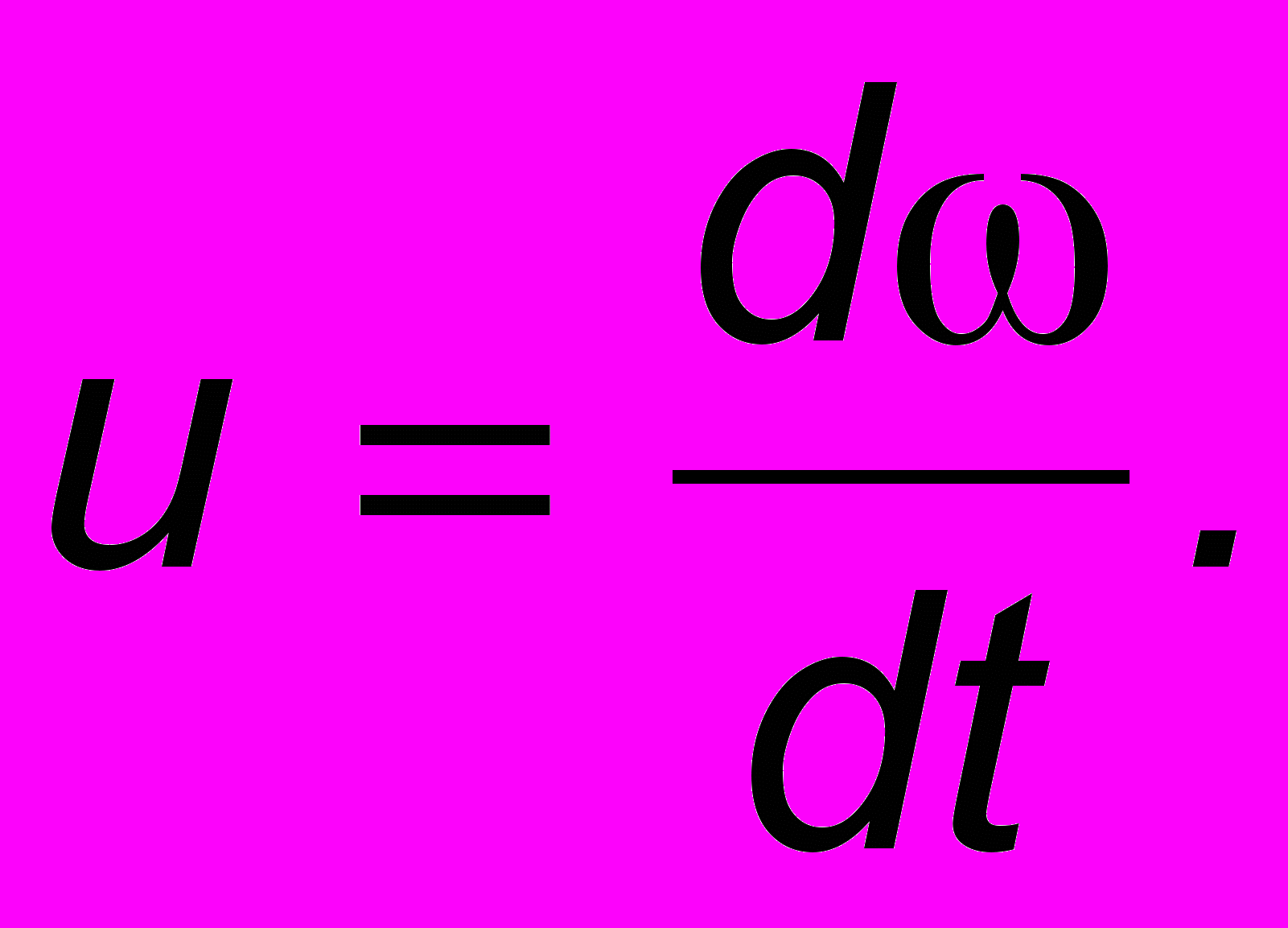(10.3)

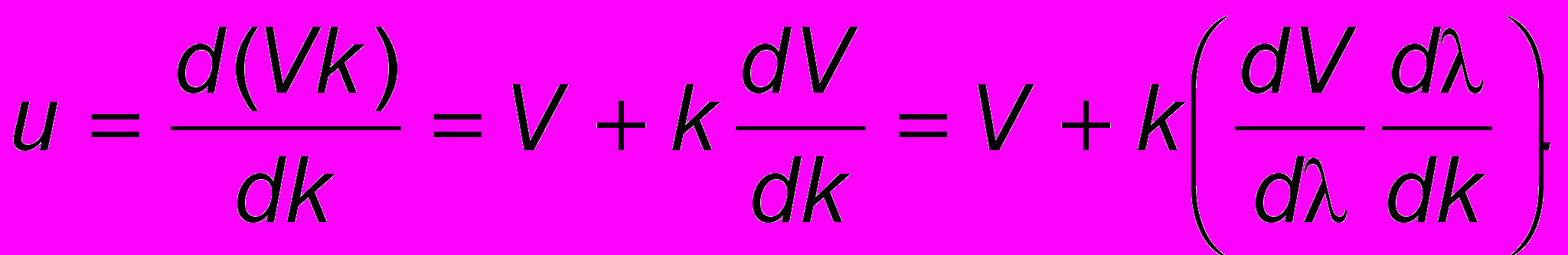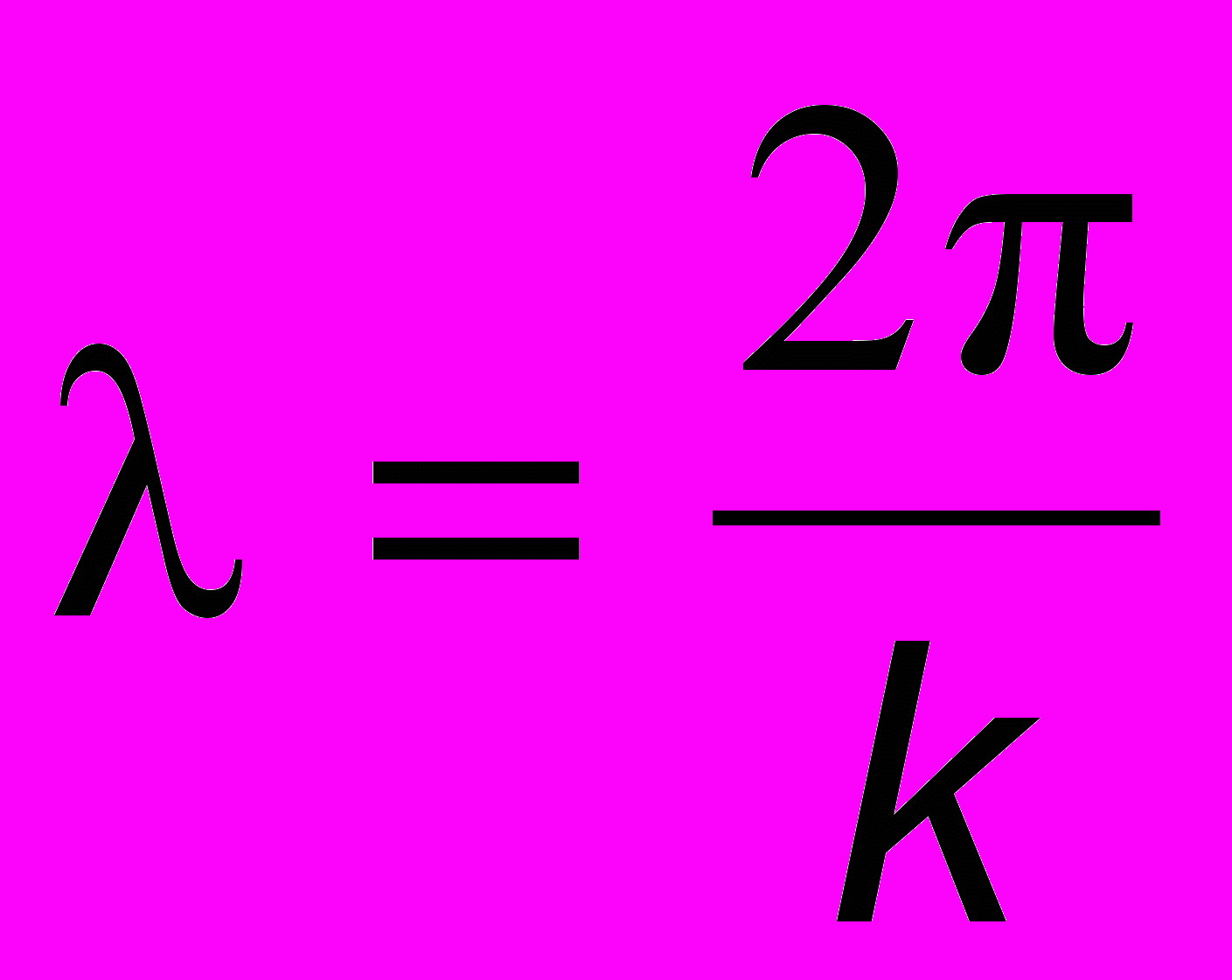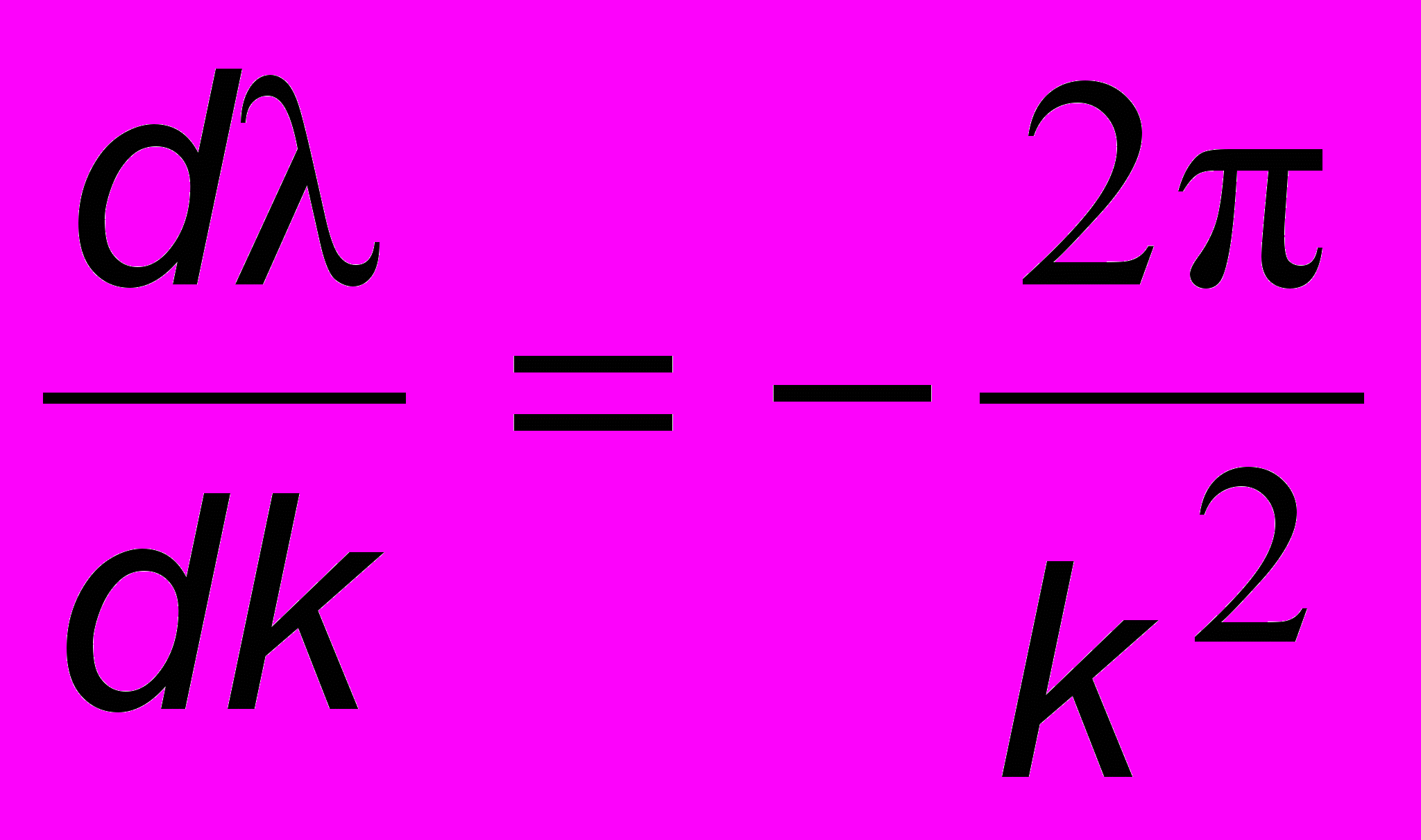Так как  = Vk, то Поскольку и , то 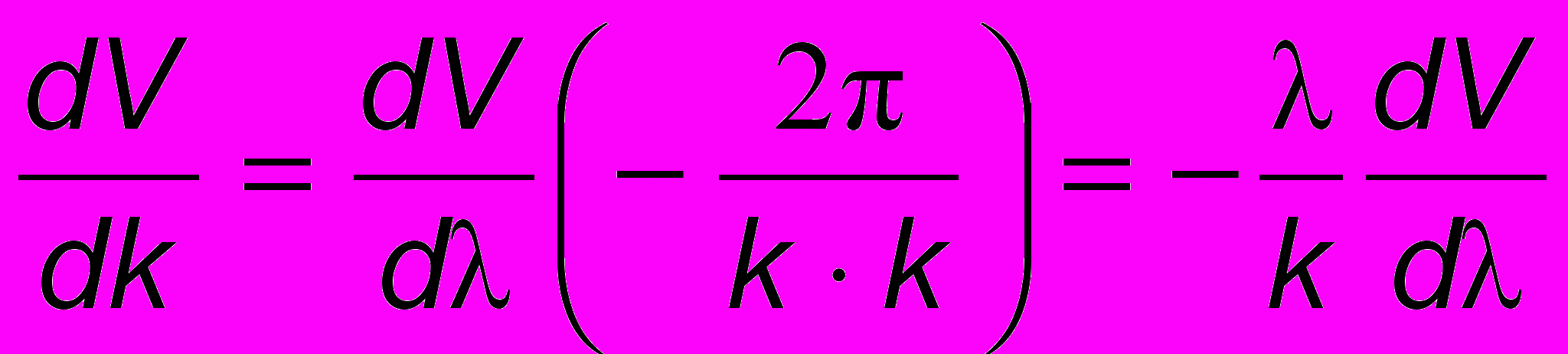, и окончательно

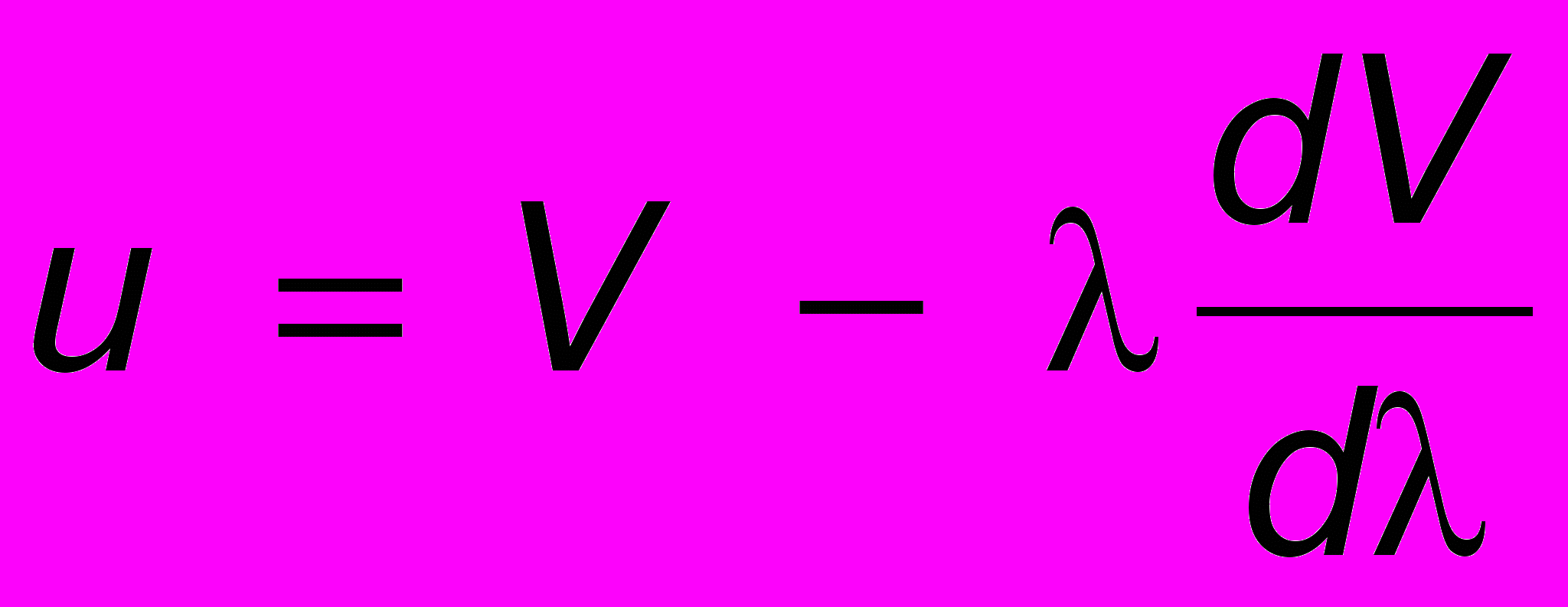. (10.4)

Таким образом, если V не зависит от  (т.е. 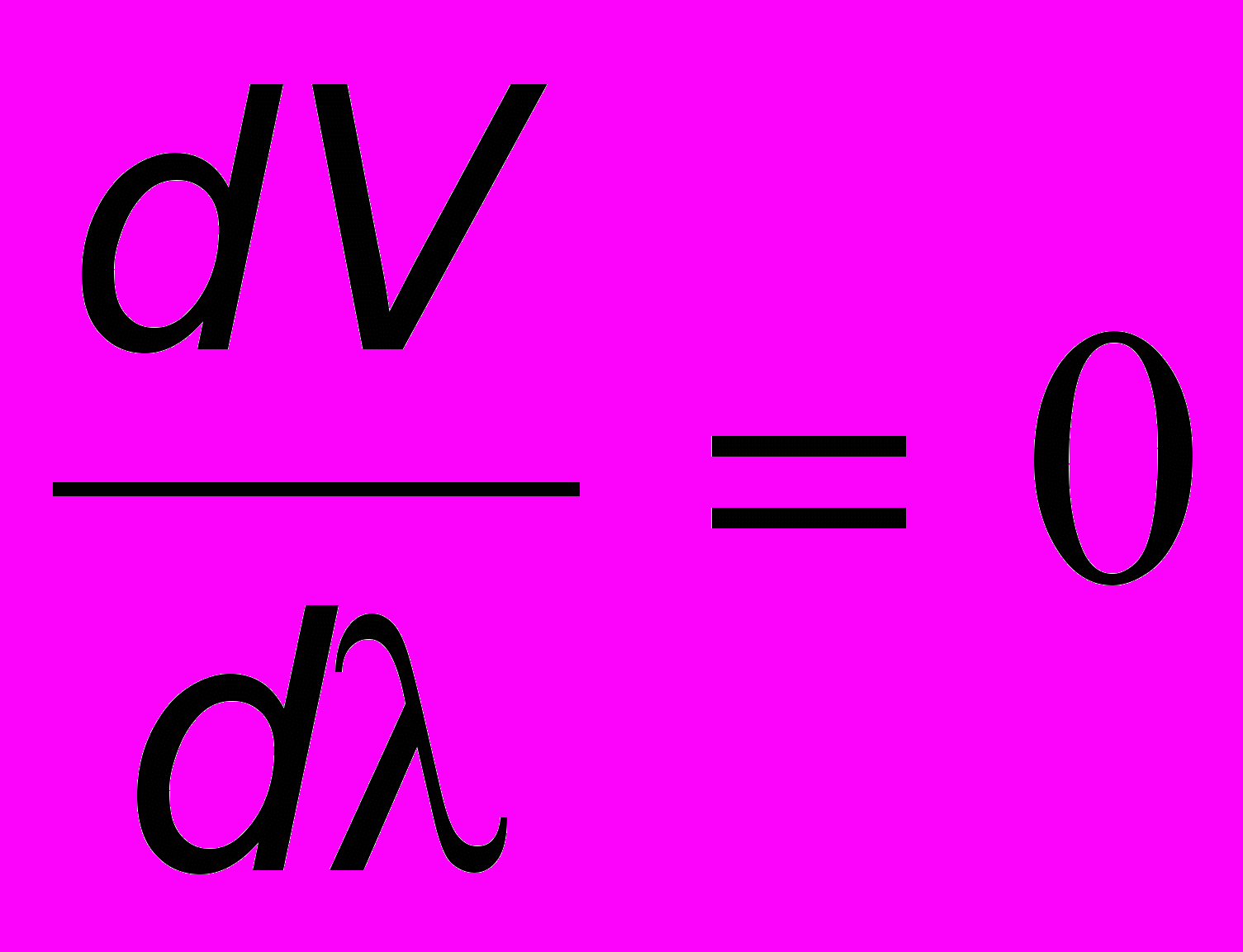), то дисперсии нет и u = V. На практике часто бывает известна зависимость 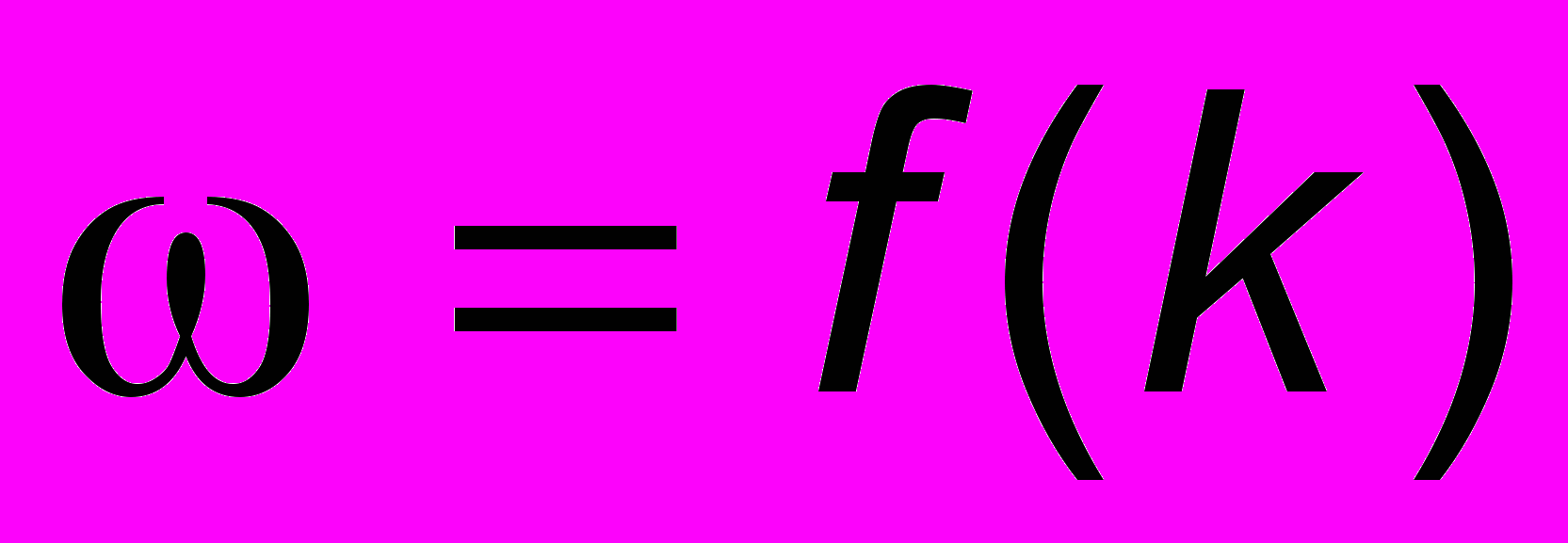, называемая дисперсионным соотношением. Рассмотрим примеры.

1. Электромагнитное излучение в вакууме:  = сk. В этом случае фазовая скорость V = /k = c = сonst и не зависит от частоты или волнового числа. Групповая скорость 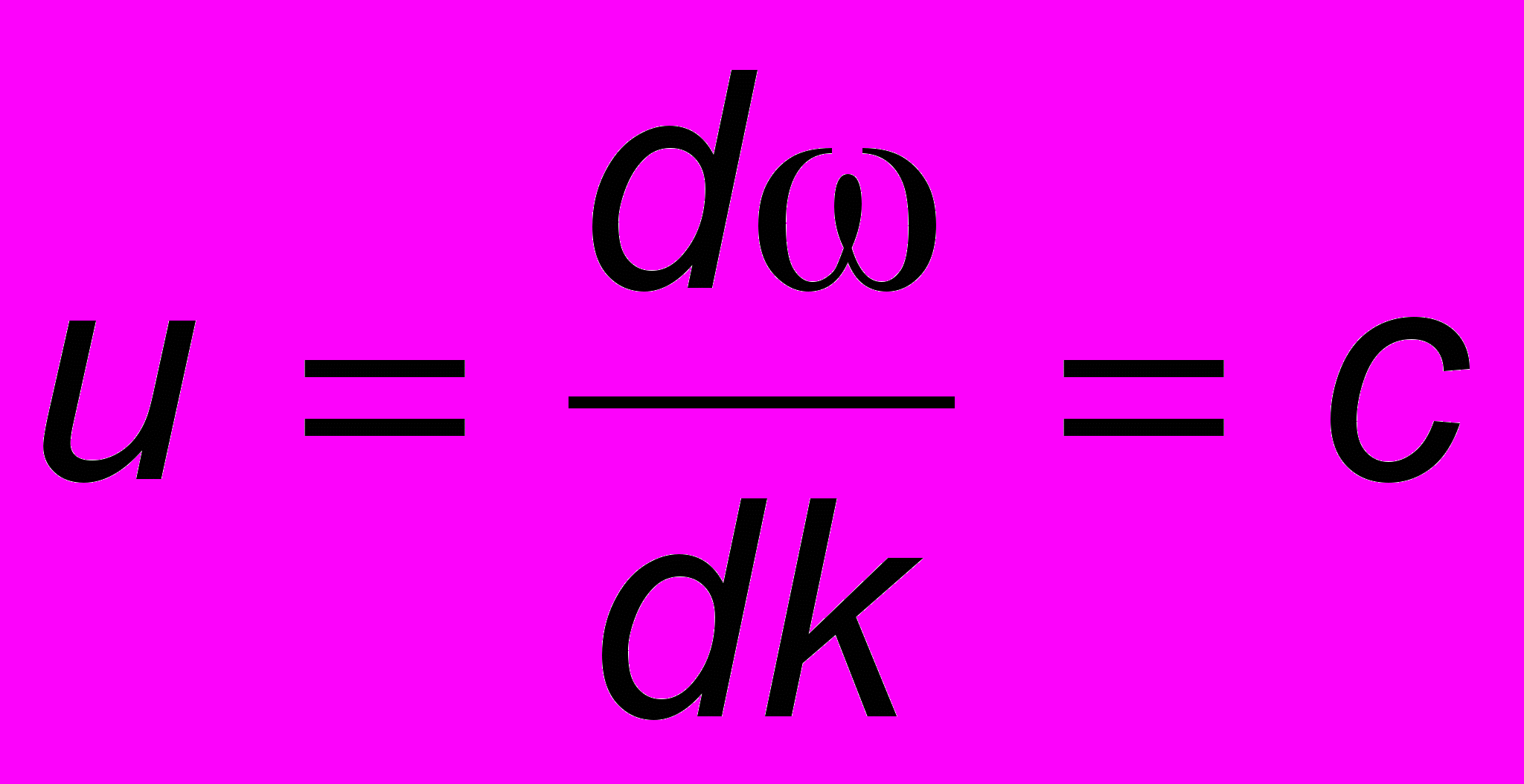также константа. Имеем для вакуума V = u = c и, следовательно, дисперсия отсутствует. При наступлении затмения Солнца белое свечение солнечного диска, проходящее через громадный вакуум космоса, прекращается и затем возобновляется мгновенно. Если бы дисперсия имела место, цвета спектра достигали бы Земли в своей последовательности один за другим и затем рекомбинировали, образуя белый свет.

В среде фазовая скорость распространения V = c /n зависит от , поэтому n = f (), т.е. в данной среде для каждой составляющей спектра будет свой показатель преломления, что и обусловливает разложение призмой белого света на цветную полоску. Особенности оптической дисперсии будут рассмотрены ниже (ЛЕКЦИЯ 15).

2. ЭМ волны в ионосфере. Ионосфера является слоистой средой, расположенной на расстоянии более 50 км над Землей и состоящей из положительных и отрицательных ионов. Такая проводящая среда - плазма - действует как гигантское зеркало, отражая поступающее электромагнитное излучение, что позволяет осуществлять сверхдальнюю радиосвязь и телекоммуникации. Дисперсионное соотношение для ионосферы имеет вид: 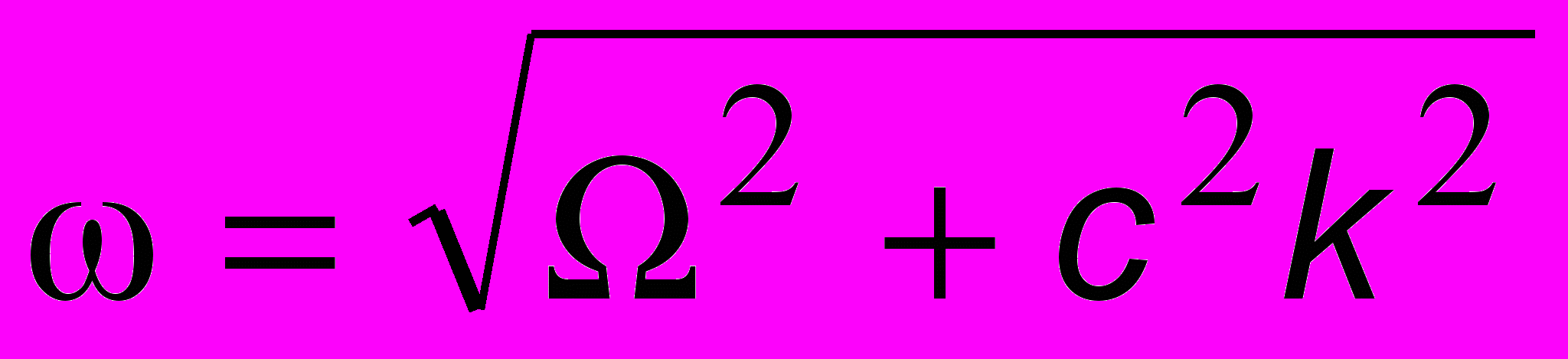, где  = const - так называемая плазменная частота, зависящая от концентрации частиц, их масс и температуры. Найдем вначале фазовую скорость:

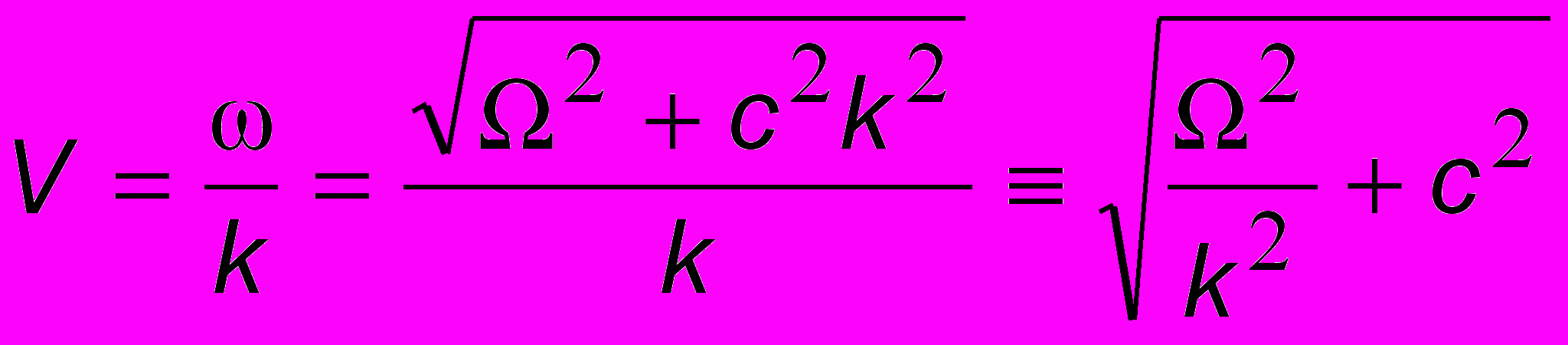. Так как под корнем к с2 прибавляется еще некоторая положительная величина, то получим V > c (!) Противоречия с теорией относительности, как уже говорилось, нет, поскольку реальной скорости распространения энергии эта величина не соответствует. Найдем теперь групповую скорость:

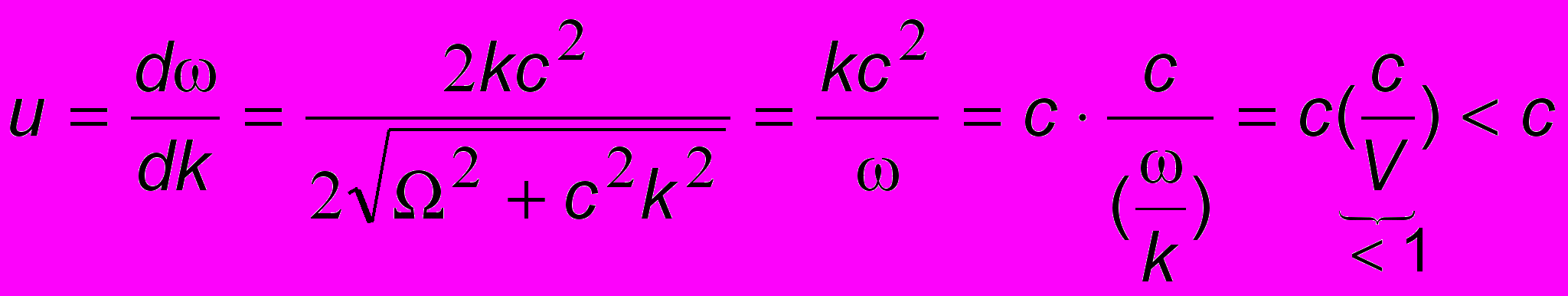. Таким образом, групповая скорость не превышает скорости света, чего и следовало ожидать.

1 В Части 1 мы уже имели дело с такой величиной - это момент инерции.

2 Вместо этой функции дисперсией можно считать фукции n = f() или же
 = f(k), эквивалентные данному определению.