Xxvii уральский (XIV кировский) турнир юных математиков
| Вид материала | Документы |
СодержаниеПервая лига Вторая лига Высшая юниорская лига |
- Международный турнир по хоккею «Золотая шайба» среди юных хоккеистов 1998-1999гг, 116.13kb.
- Госкомимущества Российской Федерации путем реорганизации государственного предприятия, 147.46kb.
- Открытый Уральский Турнир по программированию в Белорецке 3 Иванов а 10 диплом, 214.62kb.
- Информационное сообщение, 207.09kb.
- Закон україни, 1242.64kb.
- Турнир проводился при организационной поддержке компании Руспортинг, 26.02kb.
- Оценка эффективности методики развития выносливости юных лыжников, на основе применения, 154.07kb.
- I. общие положения, 71.78kb.
- Итоги xxvii-й Всероссийской конференции обучающихся «юность, наука, культура», 77.05kb.
- Цель: 1 познакомить учащихся с краткой биографией ученых математиков, 343.88kb.
ПЕРВАЯ ЛИГА
1. Пусть n > 10 — натуральное число. Докажите, что среди чисел, меньших, чем 10n, чисел с суммой цифр 9(n–2) больше, чем чисел с суммой цифр
9(n–1). (VIII Олимпиада Cono Sur, 1997)
2. В четырехугольнике ABCD АDС = 90, BCD = 78, CAB = CBA, и AB = 2AD. Найдите CAD. (IMTS)
3. 16-значное число a делится на 999 999 999. Докажите, что никакое число, которое можно получить из a перестановкой цифр, не может делиться на 100 000 001. (СПб 2006, 1 тур)
4. Докажите, что для произвольного треугольника со сторонами x, y, z и произвольных чисел a, b, c, сумма любых двух из которых положительна, справедливо неравенство ax+by+cz > 0. (Харьковская областная олимпиада 2005/06 года)
5. В треугольнике ABC угол A — тупой, D — произвольная точка на стороне AB, E — произвольная точка на стороне AC. Докажите, что CD+BE > BD+DE+EC. (KoMaL-2005)
6. Дед Мороз подарил каждому из 102 детей по 100 конфет. Конфеты бывают трех видов: красные, синие и зеленые. Докажите, что найдутся двое, чьи наборы конфет либо полностью одинаковы, либо полностью различны. (Два набора конфет считаются полностью одинаковыми, если в них поровну конфет каждого вида, и полностью различными, если никакого вида конфет в них не поровну.) (СПб-2006, 2 тур, 8 класс)
7. В каждой вершине шестиугольника лежит некоторое количество фишек (возможно, ни одной). Разрешается убрать из одной вершины любое количество фишек и добавить вшестеро большее количество фишек в любую из двух соседних вершин. Пусть в начале в одной вершине одна фишка, а в остальных вершинах фишек нет. Можно ли с помощью разрешенных операций добиться того, чтобы во всех вершинах оказалось поровну фишек? (по мотивам отбора на олимпиаду Cono Sur, 2002)
8. Вычислите сумму
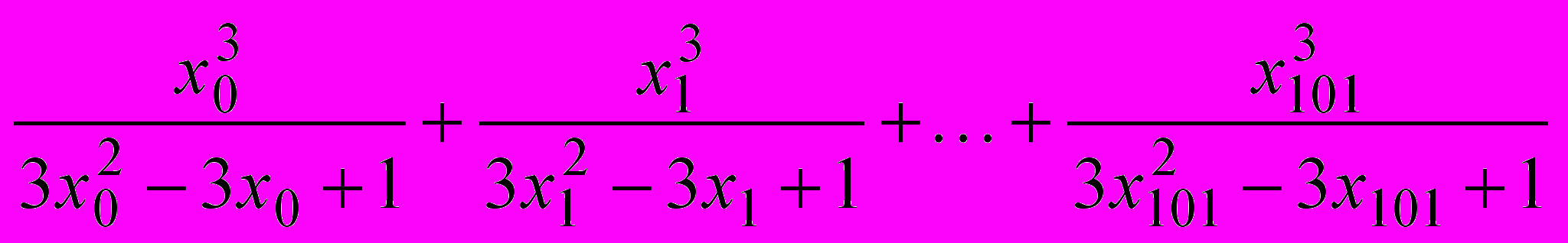, где 
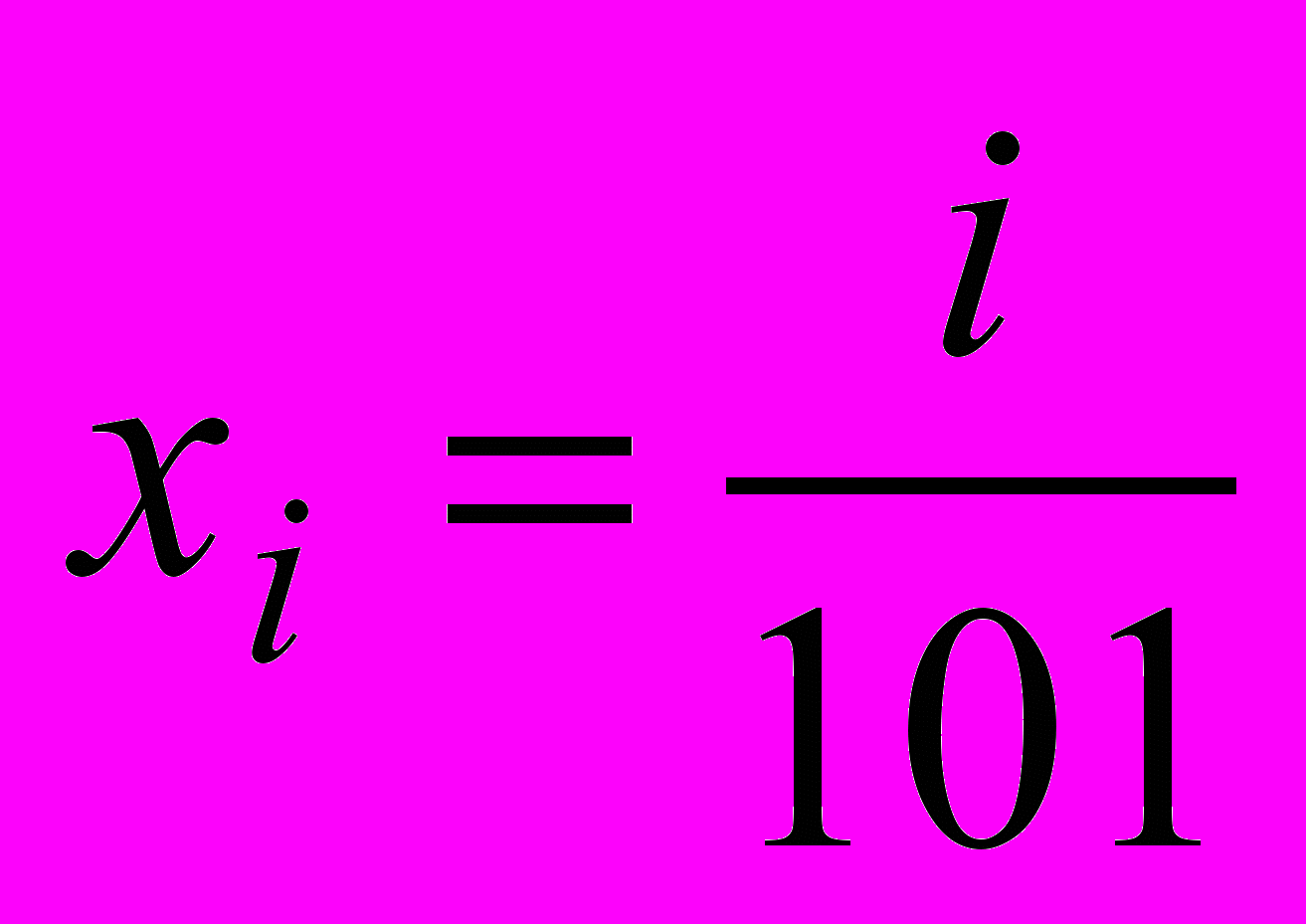. (APMO)МАТЕМАТИЧЕСКИЙ БОЙ №1. 19.02.2006
ВТОРАЯ ЛИГА
1. Пусть n > 10 — натуральное число. Докажите, что среди чисел, меньших чем 10n, чисел с суммой цифр 9(n–2) больше, чем чисел с суммой цифр
9(n–1). (VIII Олимпиада Cono Sur, 1997)
2. Докажите, что для произвольного треугольника со сторонами x, y, z и произвольных чисел a, b, c, сумма любых двух из которых положительна, справедливо неравенство ax+by+cz > 0. (Харьковская областная олимпиада 2005/06 года)
2. В четырехугольнике ABCD АDС = 90, BCD = 78, CAB = CBA, и AB = 2AD. Найдите CAD. (IMTS)
4. В вершинах квадрата стоят числа: три нуля и единица. Можно вычитать из любого числа единицу, одновременно прибавляя шестёрку к числу, написанному в одной из соседних вершин. Можно ли сделать все числа равными?(Омские городские олимпиады; BMO-1998)
5. В треугольнике ABC угол A — тупой, D — произвольная точка на стороне AB, E — произвольная точка на стороне AC. Докажите, что CD+BE > BD+DE+EC. (KoMaL-2005)
6. Вычислите сумму
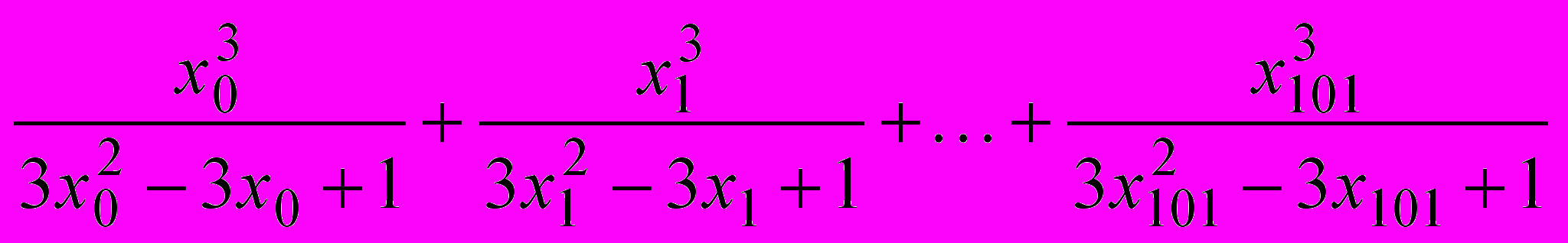, где 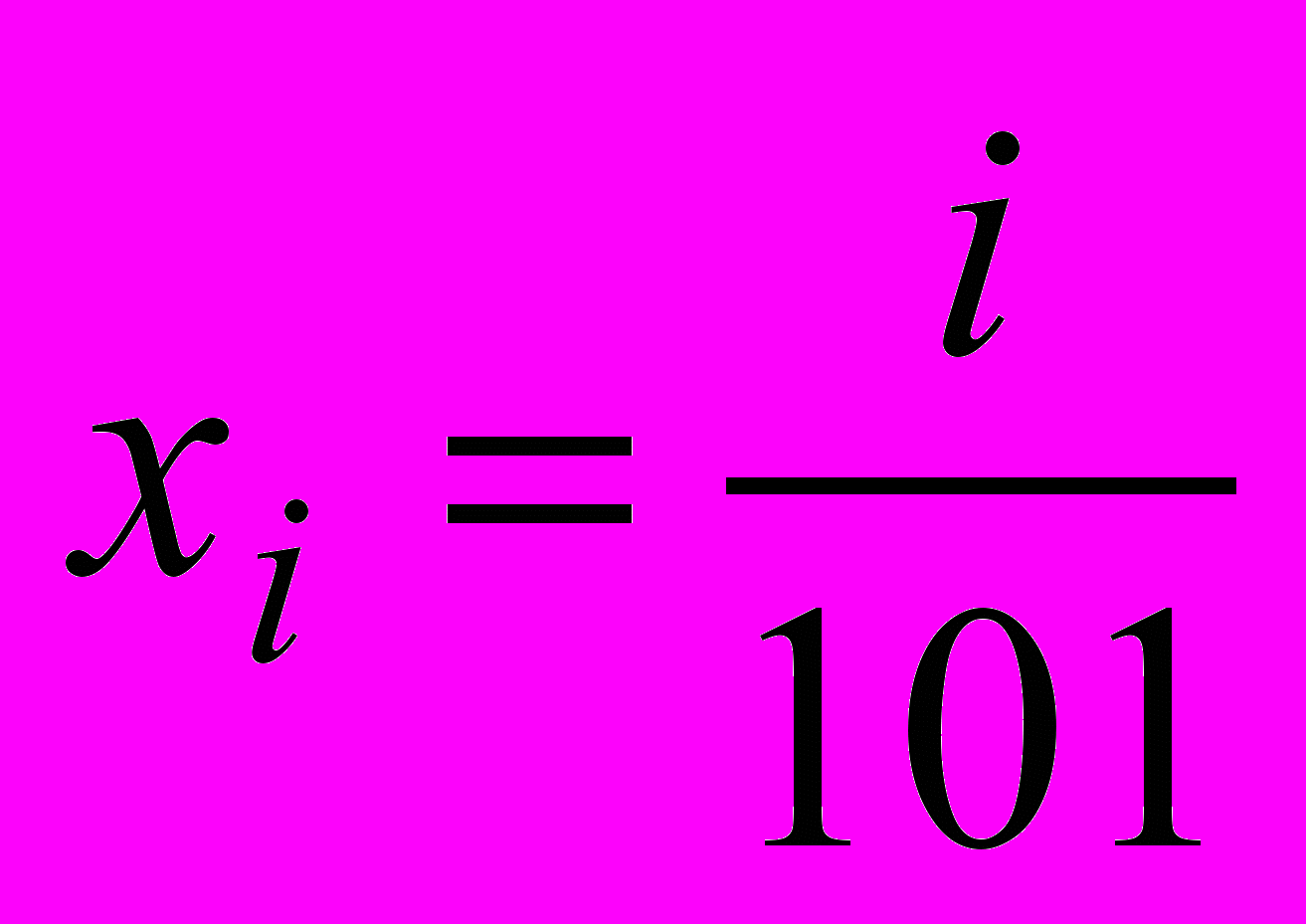. (APMO)7. В парламент прошли 99 представителей двух партий: «красные» и «синие». На первом заседании парламента каждый депутат сделал следующее заявление: «в парламенте представители моей партии составляют большинство». Известно, что каждый красный говорит правду, если перед ним выступает синий, и обманывает, если перед ним выступает однопартиец. А каждый синий, наоборот, говорит правду после однопартийца, и обманывает после человека из чужой партии. К какой партии принадлежал первый выступавший? (В парламенте присутствуют представители обеих партий и выступают по одному.) (Омские городские олимпиады)
8. Делитель натурального числа называется собственным, если он не равен этому числу и единице. Натуральное число называется редким, если самый большой из его собственных делителей равен произведению самого маленького на следующий по величине. Сколько редких чисел оканчивается цифрой 5? (А.С. Штерн)
МАТЕМАТИЧЕСКИЙ БОЙ №2. 20.02.2006
ВЫСШАЯ ЮНИОРСКАЯ ЛИГА
1. Пусть n > 10 — натуральное число. Докажите, что среди чисел, меньших чем 10n, чисел с суммой цифр 9(n–2) больше, чем чисел с суммой цифр 9(n–1). (VIII Олимпиада Cono Sur, 1997)
2. Докажите, что для произвольного треугольника со сторонами x, y, z и произвольных чисел a, b, c, сумма любых двух из которых положительна, справедливо неравенство ax+by+cz > 0. (Харьковская областная олимпиада 2005/06 года)
3. В каждой клетке квадрата 101101 стоит одно из натуральных чисел от 1 до 101. При этом в каждой строке, в каждом столбце и в каждой из двух больших диагоналей все числа различны. Докажите, что на 100 клетках, стоящих под диагональю, идущей из левого верхнего угла в правый нижний, не может быть 99 совпадающих чисел. (СЛ..Берлов по мотивам BMO-1998)
4. В парламент прошли 99 представителей двух партий: «красные» и «синие». На первом заседании парламента каждый депутат сделал следующее заявление: «в парламенте представители моей партии составляют большинство». Известно, что каждый красный говорит правду, если перед ним выступает синий, и обманывает, если перед ним выступает однопартиец. А каждый синий, наоборот, говорит правду после однопартийца, и обманывает после человека из чужой партии. К какой партии принадлежал первый выступавший? (В парламенте присутствуют представители обеих партий и выступают по одному.) (Омские городские олимпиады)
5. В остроугольном треугольнике ABC угол A больше 45, BE и CD – биссектрисы. Докажите, что CD+BE > BD+DE+EC. (С. Берлов по мотивам KoMaL-2005)
6. Рассмотрим таблицу из n строчек и 4 столбцов. Во всех клетках первой строки стоят нули. Каждая строчка, начиная со второй, строится по такому правилу: в одну из клеток вписывается такое же число, какое стоит в клетке над ней, а в каждой из остальных клеток пишется 1, если над ней стоит 0, 2, если над ней стоит 1, и 0, если над ней стоит 2. Какое наибольшее количество попарно различных строк можно получить в этой таблице (некоторые строчки таблицы могут совпадать)? (VIII Олимпиада Cono Sur, 1997)
7. В вершинах шестиугольника стоят числа: пять нулей и единица. Можно вычитать из любого числа единицу, одновременно прибавляя шестерку к числу, написанному в одной из соседних вершин. Можно ли такими операциями сделать все числа равными? (Отбор на Cono Sur 2002)
8. Вове дали задание расставить натуральные числа от 1 до 99 следующим образом: одно число ставится в центр окружности, а остальные расставляются по окружности на одинаковом расстоянии друг от друга так, чтобы суммы трех чисел, находящихся на каждом диаметре, образовывали 49 последовательных натуральных чисел. Какое число может стоять в центре окружности? Найдите все возможности и докажите, что других нет. (О.Ю.Ланин, С.Л.Берлов)
МАТЕМАТИЧЕСКИЙ БОЙ №2. 20.02.2006