Математика и искусство

Вид материала

Содержание

Подобный материал:

Математика и искусство

Пристальное, глубокое изучение природы

есть источник самых плодотворных

открытий математики

Ш. Фурье

Учитель: У школьников обычно складывается впечатление, что математика занимается исключительно числами и измерениями. Однако, на самом деле, математика – это нечто гораздо большее, чем просто наука для счетоводов и кассиров. Математика и искусство: сегодня эти две великие сферы культуры многими воспринимаются как два полюса или даже как две противоборствующие духовные силы, тогда как на самом деле они тесно переплетены крепкими незримыми узами.

1. Математика и музыка.

Учитель: Почтенный Пифагор отвергал оценку музыки, основанную на свидетельстве чувств. Он утверждал, что достоинства ее должны восприниматься умом, и потому судил о музыке не по слуху, а на основании математической гармонии и находил достаточным ограничить изучение музыки пределами одной октавы.

Математика и музыка.

Необходимую, существенную связь музыки и числа обнаружили, как известно, еще пифагорейцы, которые, открыв числовые соотношения, лежащие в основе музыкальных созвучий, явились, собственно говоря, родоначальниками музыкальной теории.

Пифагор создал свою школу мудрости, положив в ее основу два искусства – музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга.

Возьмем для примера так называемую «гармоническую пропорцию». Говорят, что три числа образуют гармоническую пропорцию, если обратные им числа удовлетворяют непрерывной арифметической пропорции.

Оказывается, длины трех струн, дающих ноты до, ми, соль, которые составляют один из наиболее благозвучных аккордов — мажорный, удовлетворяют гармонической пропорции, а числа колебаний этих струн образуют непрерывную арифметическую пропорцию. Следовательно, числа предшествуют гармонии, так как их неизменные законы управляют всеми гармоническими пропорциями.

Пифагорейский музыкальный строй, определивший на столетия судьбу европейской музыки, — это математика.

ИНТЕРВАЛЫ И ГАРМОНИИ СФЕР

В пифагорейской концепции музыки сфер интервал между Землей и сферой неподвижных звезд рассматривался в качестве диапазона - наиболее совершенного гармонического интервала. Наиболее принятым порядком музыкальных интервалов планет между сферой Земли и сферой неподвижных звезд является такой: от сферы Земли до сферы Луны - один тон; от сферы Луны до сферы Меркурия - полтона; от Меркурия до Венеры - полтона; от Венеры до Солнца - полтора тона; от Солнца до Марса - один тон; от Марса до Юпитера -полтона; от Юпитера до Сатурна - полтона; от Сатурна до неподвижных звезд - полтона. Сумма этих интервалов равна шести тонам октавы.

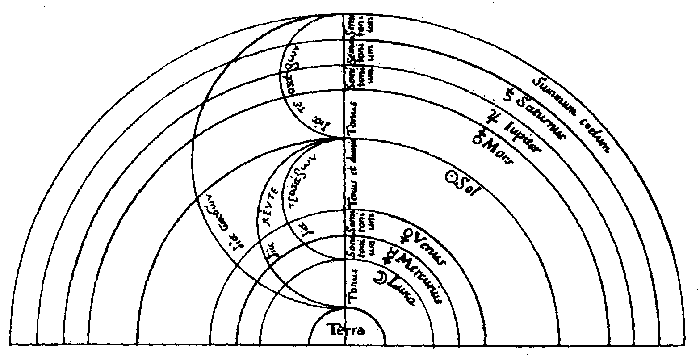
Создание логарифмически равномерной 12-тонной музыкальной шкалы - итог совместной деятельности музыкантов и математиков. Она могла появиться только после разработки общей теории отношений в V книге «Начал» Евклида и теории логарифмов в XVII в.

Не случайно на протяжении всего этого столетия в теории сохраняется точка зрения на музыку как на науку о числах, т. е. как на раздел математики. Такому взгляду способствовал авторитет «Гармонии мира» Кеплера. И позже, в начале XVIII в., Лейбниц в своих многочисленных заметках о музыке еще всюду утверждает, что природа музыкальных созвучий строится на основе числовых пропорций. Однако, сводя природу музыки к математическим пропорциям, Лейбниц тем не менее высказывал совершенно новую мысль: исчисление пропорций, которое совершается при восприятии музыки, происходит скрытным, неосознанным образом. В письме Гольбаху от 17 апреля 1712 г. Лейбниц дает следующее знаменитое определение музыки: «Музыка есть арифметическое упражнение души, которая исчисляет себя, не зная об этом».

В свое время английский математик Д. Сильвестр называл музыку математикой чувств, а математику — музыкой разума. Он же выражал надежду, что каждая из них должна получить завершение со стороны другой, и предвидел в будущем появление личности, в которой соединятся гении Бетховена и Гаусса.

Основанием для подобной надежды могла быть только математическая точность музыки, которая всегда была ее неотъемлемым свойством. Очень важно, что и современные течения не поколебали этой фундаментальной ее черты.

"Если что есть приятное в музыке, — говорит анонимный автор средневекового трактата, — то это от числа зависит; то же и в ритмах, как музыкальных, так и иных. Звуки быстро проходят, числа же, телесным существом звуков и движений украшенные, останутся".

2. Ученые и поэзия.

Учитель: Математика и поэзия. Что роднит их, казалось, на первой взгляд они такие разные… Ученым не чужда поэзия. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.

Ж. Дьедонне говорил: “Стимулы математиков всех времен: любознательность и стремление к красоте”. Большое математическое дарование нередко сочетается с проявлением творческого интереса к поэзии.

Ученые и поэзия.

Женщина-математик Софья Васильевна Ковалевская говорит о математике так: “Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе”.

Она – великий математик, она – признанный писатель и поэт. Вот одно из ее стихотворений.

“ЕСЛИ ТЫ В ЖИЗНИ…”

Если ты в жизни, хотя на мгновенье

Истину в сердце своем ощутил,

Если луч правды сквозь мрак и сомненье

Ярким сияньем твой путь озарил:

Чтобы в решеньи своем неизменном

Рок ни назначил тебе впереди –

Память об этом мгновеньи священном

Вечно храни, как святыню, в груди.

Тучи сберутся громадой нестройной,

Небо покроется черною мглой,

С ясной решимостью, с верой спокойной

Бурю ты встреть и померься с грозой.

Великий русский ученый М. В. Ломоносов говорил о математике так: “Математику уже затем учить надо, что она ум в порядок приводит”. И вот отрывок из его стихотворения:

О вы, которых ожидает

Отечество от недр своих

И видеть таковых желает,

Каких зовет от стран чужих,

О, ваши дни благословенны!

Дерзайте ныне ободрены

Раченьем вашим показать,

Что может собственных Платонов

И быстрых разумом Невтонов

Российская земля рожать.

Писал стихи и великий русский геометр Лобачевский. Ректор Казанского университета и известный математик вдруг в 1834 году “рискнул” опубликовать свое стихотворение “Разлив Волги при Казани”. Вот отрывок его:

“Ты поражаешь ли поля опустошеньем?

Ты похищаешь ли надежды поселян?

Нет! На водах твоих всегда благословенье

Почиет благодарных стран,

Тобой, питаемых, тобой обогащенных!

Ты и земли безвредная краса,

И светлые в струях твоих невозмущенных,

Как в чистой совести, сияют небеса.

Вот образ мирного могущества России!

Ее разлив не страшен никому.

Великодушие обуздывает силы,

Всегда, везде покорные ему.

Эта публикация, по-видимому, связана с приездом Пушкина в Казань в сентябре 1833 года, где он собирал материалы о восстании Пугачева. Жена Лобачевского – сестра Великопольского, давнишнего приятеля Пушкина, на вечерах которого бывали Пушкин и Лобачевский. Встретились два гения. Может быть, после встречи с Лобачевским Пушкин сказал: “Вдохновение нужно в поэзии, как в геометрии”.

3. Пушкин и математика.

Учитель: Широко распространено мнение, что А.С. Пушкин был не совсем в ладах с математикой. На самом деле, из воспоминаний старшей сестры Ольги, мы узнаем, что в детстве бывало он плакал над задачами по математике.

На страницах гениальных творений Пушкина нашли отражение математические понятия, термины и идеи. Связи поэта с современной ему математикой весьма многообразны.

Пушкин и математика.

По результатам вступительных экзаменов в лицей об Александре Пушкине записано: что «в познании языков: российского – очень хорошо, французского – хорошо, немецкого – не учился, в арифметике – знает до тройного правила, в познании общих свойств тел – хорошо.

В воспоминаниях об учебе в лицее «первый друг» и «друг бесценный» Иван Пущин рассказывал: «Учитель физики и математики Яков Иванович Карцев вызвал Пушкина к доске решать алгебраическую задачу. Переминаясь с ноги на ногу, Пушкин молча делал на доске какие-то записи чисел. На вопрос учителя: «Ну, что же у Вас получилось? Чему равняется икс?» - ученик улыбнулся и ответил: «Нулю!». «Хорошо, - подытожил Карцев. – У вас, Пушкин, все в моем классе кончается нулем. Садитесь на место и пишите лучше стихи».

Как видно в лицейские годы математика не всегда принималась юным А. Пушкиным как «милые сердцу предметы». Зато в последствии, когда он писал о своем стремлении «в просвещении стать с веком на равнее», поэт несомненно проявлял большой интерес к математике, что нашло отражение в его гениальных творениях.

В материалах записных книжек Пушкина за 1835 год содержится гипотеза о происхождении формы цифр: «Форма цифр арабских составлена из следующей фигуры: AD (1), ABDC (2), ABECD (3), ABD+AE (4). Русские цифры составлены по тому же образцу». Хотя, существует мнение об индийском происхождении «арабских» цифр.

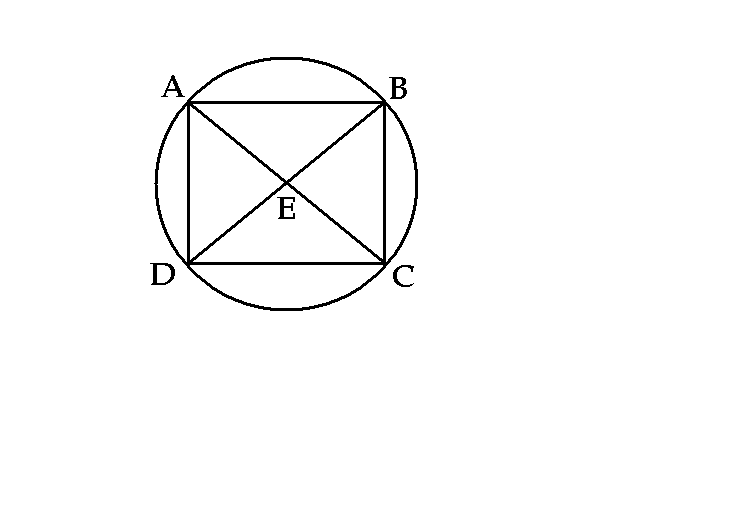
Индийские цифры попади в Европу от арабов в 12 в. через Мавриатнию. Пушкин, сравнивая татарское иго с игом мавританским в Испании, отметил: «Татары не походили на мавров. Они, завоевав Россию, не подарили ей ни алгебры, ни Аристотеля».

Поистине крылатыми стали слова из трагедии «Моцарт и Сальери» «проверил я алгеброй гармонию». Считается, что эта фраза проводит разделение между искусством Моцарта и ремесленничеством Сальери и сводится к противопоставлению искусства и науки.

В творчестве Пушкина в различных вариациях встречаются слова, загадочным образом связанные с наукой о случайном.

Дар напрасный, дар случайный,

Жизнь, зачем ты мне дана?

Иль зачем судьбою тайной

Ты на казнь осуждена?

В незаконченном стихотворении о научном творчестве Пушкин дает глубокие определения случаю, опыту и гению:

О, сколько нам открытий чудных

Готовят просвещенья дух

И опыт, сын ошибок трудных,

И гений, парадоксов друг,

И случай, бог изобретатель

Глубину этих определений специально отмечал еще академик С.И. Вавилов

В настоящее время на основе произведений Пушкина авторы современных задачников по теории вероятностей с удовольствием включают задачи на классическое определение вероятности. Например: Из колоды карт (52 карты) Герман наугад извлекает три карты. Найдите вероятность того, что это будут 3, 7 и туз.

Друг поэта П.А. Вяземский писал о Пушкине, что от был «страстен и к наукам естественным и особенно математическим, которые составляли значительный каптал его познаний и были до конца любимым предметом его ученых занятий и глубоких исследований».

4 . Золотое сечение в искусстве.

Учитель: Вопрос о предпосылках прекрасного, о роли математики в искусстве волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций. В наше время геометрия – необходимый элемент общего образования и культуры, представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой. Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем.

Золотое сечение в искусстве.

Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому.

Золотым сечением (делением) и даже “божественной пропорцией” называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей. Это отношение приближенно равно 0,618 или 5/8. Цифры, выражающие длины отрезков, оставляют ряд Фибоначчи. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.

Замечательный пример “золотого сечения” представляет собой правильный пятиугольник – выпуклый и звездчатый, который называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и опознавательным знаком.

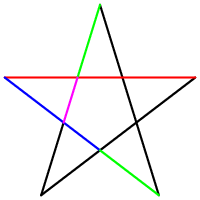
К примеру, в правильной пятиконечной звезде, каждый сегмент делится пересекающим его сегментом в золотом сечении (т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к к фиолетовому, равны 1.618.

В 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.

В строении стихотворений также проявляются элементы золотого сечения. Начнем с величины стихотворения, то есть количества строк в нем. Казалось бы, этот параметр стихотворения может изменяться произвольно. Однако оказалось, что это не так. Например, проведенный Н. Васютинским анализ стихотворений А.С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи).

Многими исследователями было замечено, что в стихотворениях существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения.

Рассмотрим, например, стихотворение А.С. Пушкина "Сапожник":

Картину раз высматривал сапожник

И в обуви ошибку указал;

Взяв тотчас кисть, исправился художник,

Вот, подбочась, сапожник продолжал:

"Мне кажется, лицо немного криво ...

А эта грудь не слишком ли нага?

Тут Апеллес прервал нетерпеливо:

"Суди, дружок, не выше сапога!"

Есть у меня приятель на примете:

Не ведаю, в каком бы он предмете

Был знатоком, хоть строг он на словах,

Но черт его несет судить о свете:

Попробуй он судить о сапогах!

Проведем анализ этой притчи. Стихотворение состоит из 13 строк. В нем выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 - числа Фибоначчи).

Представляет несомненный интерес анализ романа "Евгений Онегин", сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава. В ней 51 стих. Вместе с письмом Евгения к Татьяне (60 строк) это точно соответствует числу Фибоначчи 55!

5. Золотое сечение в живописи.

Учитель: Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.

Золотое сечение в живописи.

В эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

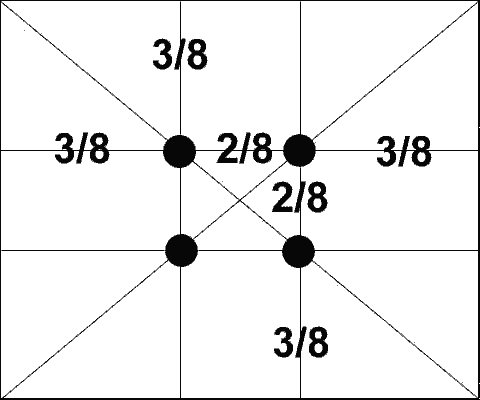
Данное открытие у художников того времени получило название"золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.

Золотое сечение в картине И. И. Шишкина"Сосновая роща"

На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.

Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника. Когда же замысел художника иной, если, скажем, он создает картину с бурно развивающимся действием, подобная геометрическая схема композиции (с преобладанием вертикалей и горизонталей) становится неприемлемой.

Золотая спираль в картине Рафаэля"Избиение младенцев"

В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре - спирали. Многофигурная композиция, выполненная в 1509 - 1510 годах Рафаэлем как раз отличается динамизмом и драматизмом сюжета.

На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции - точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается ...золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.

Золотое сечение в картине Леонардо да Винчи "Джоконда"

Портрет Моны Лизы привлекает тем, что композиция рисунка построена на"золотых треугольниках" (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

6. Золотое сечение у человека, в архитектуре.

Учитель: Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Золотое сечение у человека

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

Д

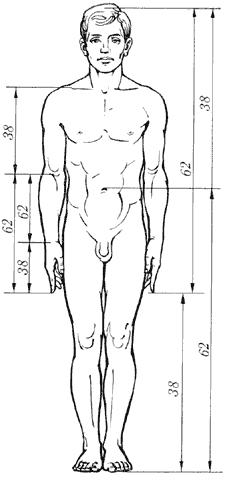еление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6.

У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.

Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

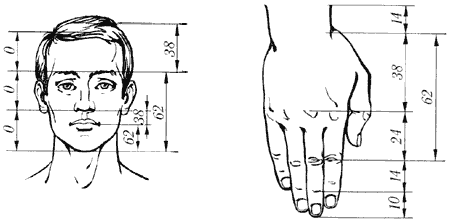
Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

В эпоху Возрождения математическое понятие – золотая пропорция было возведено в ранг главного эстетического принципа. Леонардо да Винчи именовал ее Sectio aurea, откуда и получил начало термин “золотое сечение”.

Золотое сечение в архитектуре

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

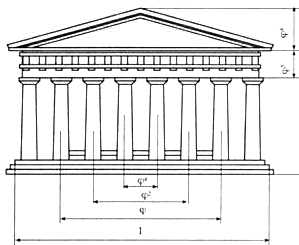
На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...

На плане пола Парфенона также можно заметить "золотые прямоугольники":

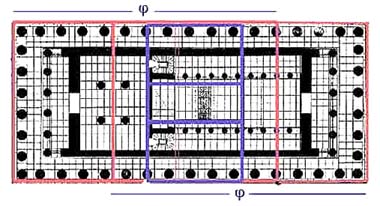
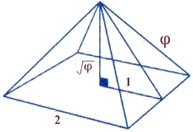
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Известный русский архитектор М. Казаков в своем творчестве широко использовал “золотое сечение”.

Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Ленинский проспект, д. 5).

Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова. Прекрасное творение В. Баженова прочно вошло в ансамбль центра современной Москвы, обогатило его. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.

Многие высказывания зодчего заслуживают внимание и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания... К достижению сего служит руководством знание пропорции, перспектива, механика или вообще физика, а всем им общим вождем является рассудок”.

7. Золотое сечение и симметрия в природе.

Учитель: Можно ли “поверить алгеброй гармонию”? “Да”, – считал Леонардо и указал, как это сделать. “Золотое сечение” – не середина, а пропорция – несложное математическое соотношение, содержащее в себе “закон звезды и формулу цветка”, рисунок на хитиновом покрове животных, длину ветвей дерева, пропорции человеческого тела.

Золотое сечение и симметрия в природе.

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.

Хорошо известна "золотая" пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Трудно найти человека, который не имел бы какого-то представления о симметрии. “Симметрия” - слово греческого происхождения. Оно, как и слово “гармония”, означает соразмерность, наличие определенного порядка, закономерности в расположении частей. Известный немецкий математик Герман Вейль дал определение симметрии таким образом: “Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство”.

Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.

Если сверху посмотреть на любое насекомое и мысленно провести посередине прямую (плоскость), то левые и правые половинки насекомых будут одинаковыми и по расположению, и по размерам, и по окраске. Ведь мы ни разу не видели, чтобы у жука или стрекозы, у любого другого насекомого лапы слева были бы ближе к голове, чем справа, а правое крыло бабочки или божьей коровки было бы больше, чем левое. Такого в природе не бывает, иначе бы насекомые не смогли бы летать. Свойство симметричности, присущее живой природе, человек использовал в своих достижениях: изобрел самолет, создал уникальные здания архитектуры. Да и сам человек является фигурой симметричной.

Однако симметрия существует и там, где ее не видно на первый взгляд. Физик скажет, что всякое твердое тело – кристалл. Знаменитый кристаллограф Евграф Степанович Федоров сказал: “Кристаллы блещут симметрией”. Химик скажет, что все тела состоят из молекул, а молекулы состоят из атомов. А многие атомы располагаются в пространстве по принципу симметрии.

Таким образом, данное преобразование фигур (симметрия) вошло в математику в результате наблюдения человека за окружающим миром. Оно встречается часто и повсеместно. Поэтому даже не искушенный человек обычно легко усматривает симметрию в относительно простых ее проявлениях.

Симметрии посвящены такие строчки:

О, симметрия! Гимн тебе пою!

Тебя повсюду в мире узнаю.

Ты в Эйфелевой башне, в малой мошке,

Ты в елочке, что у лесной дорожки.

С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!

8. Заключение.

С давних пор человек стремится окружать себя красивыми вещами. Уже предметы обихода жителей древности, которые, казалось бы, преследовали чисто утилитарную цель - служить хранилищем воды, оружием на охоте и т.д., демонстрируют стремление человека к красоте. На определенном этапе своего развития человек начал задаваться вопросом: почему тот или иной предмет является красивым и что является основой прекрасного? Уже в Древней Греции родилось представление о том, что основой прекрасного является гармония. Красота и гармония стали важнейшими категориями познания, в определенной степени даже его целью, ибо в конечном итоге художник ищет истину в красоте, а ученый - красоту в истине.

Blog

Математика и искусство

Содержание