Geum.ru

Составление программы на языке программирования. Отладка и тестирование программы

Вид материалаДокументы

Содержание


3.9. Функции, связывающие различные типы данных
3.10. Логические выражения в управляющих операторах
Подобный материал:
1   ...   5   6   7   8   9   10   11   12   ...   21

3.9. Функции, связывающие различные типы данных


В табл. 3.6 приводится список стандартных функций, обеспечивающих связь между различными типами данных.

Таблица 3.6



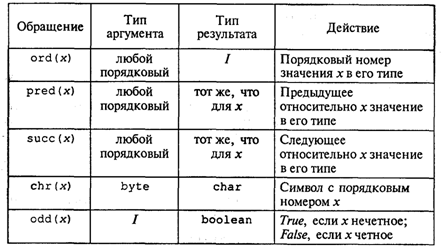
Функции ord, pred и succ применимы только к порядковым типам. Из простых типов это все, кроме вещественного.

Функция ord, применяемая к целому числу, дает его собственное значение. Например,

ord(-35)=-35; ord(128)=128

Если аргумент целый, то, например, оператор y:=pred(x) эквивалентен у:=х-1, а у:=succ(x) эквивалентен у:=х+1.

Для символьного типа аргумента эти функции дают соответственно предыдущий и следующий символ в таблице внутренней кодировки. Поскольку латинский алфавит всегда упорядочен по кодам, т.е.

ord('a')
то, например,

pred('b')='a', a succ('b')='c'

То же относится и к цифровым литерам:

pred('5')='4'; succ('5')='6'

Функция chr (x) является обратной к функции ord(x), если х — символьная величина.

Это можно выразить формулой

chr(ord(x))=х,

где х — символьная величина.

Например, для кода ASCII справедливо

ord('a')=97; chr(97)='a'

В некоторых случаях возникает задача преобразования символьного представления числа в числовой тип. Например, нужно получить из литеры '5' целое число 5. Это делается так:

N:=ord('5')-ord('0'),

где N — целая переменная. Здесь использован тот факт, что код литеры '5' на пять единиц больше кода '0'.

Булевский тип также является порядковым. Порядок расположения двух его значений таков: false, true. Отсюда справедливы следующие отношения:

ord(false)=0, succ(false)=true,

ord(true)=1, pred(true)=false

Вот интересный пример. Пусть х, у, z — вещественные переменные. Как вы думаете, какую задачу решает следующий оператор:

z:=x*ord(x>=y)+y*ord(y>x)

Ответ такой: z = mах(х, у). Как видите, эту задачу можно решить, не используя условного оператора if...then...else.

3.10. Логические выражения в управляющих операторах


Алгоритмическая структура ветвления программируется в Паскале с помощью условного оператора. Раньше мы его описывали в таком виде:

If <условие> Then <оператор 1> Else <оператор 2>;

Кроме того, возможно использование неполной формы условного оператора:

If <условие> Then <оператор>;

Теперь дадим строгое описание условного оператора в форме синтаксической диаграммы (рис. 20).



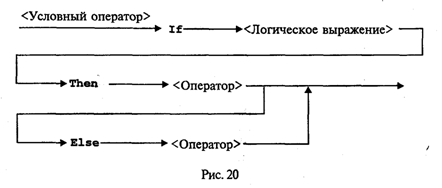
То, что мы раньше называли условием, есть логическое выражение, которое вычисляется в первую очередь. Если его значение равно true, то будет выполняться <оператор 1> (после Then), если false, то <оператор 2> (после Else) для полной формы или сразу следующий оператор после условного для неполной формы (без Else).

Пример 1. По длинам трех сторон треугольника а, b, с вычислить его площадь.

Для решения задачи используется формула Герона



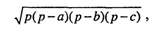
где р = (а + b + с) / 2 — полупериметр треугольника. Исходные данные должны удовлетворять основному соотношению для сторон треугольника: длина каждой стороны должна быть меньше длин двух других сторон.

Имея возможность в одном условном операторе записывать достаточно сложные логические выражения, мы можем сразу «отфильтровать» все варианты неверных исходных данных.

Program Geron;

Var A,B,C,P,S: Real;

Begin

WriteLn('Введите длины сторон треугольника:');

Write('а='); ReadLn(A) ;

Write('b='); ReadLn(В);

Write ('c='); ReadLn(C);

If (A>0) And (B>0) And (00) And (A+B>C)

And (B+С>A) And (A+C>B)

Then Begin

P:=(A+B+C)/2;

S:=Sqrt(P*(P-A)*(P-B)*(P-C));

WriteLn('Площадь=',S)

End

Else WriteLn('Неверные исходные данные')

End.

Теперь рассмотрим синтаксическую диаграмму оператора цикл-пока, или цикл с предусловием (рис. 21).



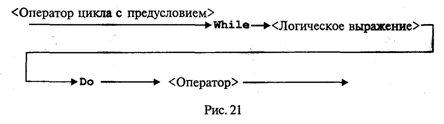
Сначала вычисляется <Логическое выражение>. Пока его значение равно true, выполняется <0ператор> — тело цикла. Здесь может быть как простым, так и составным.

Пример 2. В следующем фрагменте программы на Паскале вычисляется сумма конечного числа членов гармонического ряда



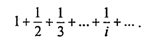
Суммирование прекращается, когда очередное слагаемое становится меньше ε или целая переменная i достигает значения MaxInt.

S:=0;

I:=l;

While (l/I>=Eps) And (I
Begin

S:=S+1/I;

I:=1+1

End;

Синтаксическая диаграмма оператора цикл-до, или цикл с постусловием, представлена на рис. 22.



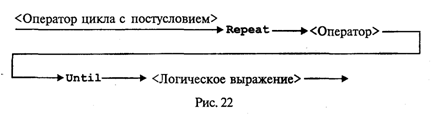
Исполнение цикла повторяется до того момента, когда <Логическое выражение> станет равным true.

Предыдущая задача с использованием цикла с постусловием решается так:

S:=0;

I:=1;

Repeat

S:=S+1/I; I:=I+1

Until (1/I=MaxInt);