Geum.ru

Составление программы на языке программирования. Отладка и тестирование программы

Вид материалаДокументы

Содержание


3.8. Логические величины, операции, выражения. Логический оператор присваивания
Операции отношения
Логическое выражение
Подобный материал:
1   ...   4   5   6   7   8   9   10   11   ...   21

3.8. Логические величины, операции, выражения. Логический оператор присваивания


Прямое отношение к программированию имеет дисциплина, которая называется математической логикой. Основу математической логики составляет алгебра логики, или исчисление высказываний. Под высказыванием понимается любое утверждение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, «Луна — спутник Земли» — истинно; «5 > 3» — истинно; «Москва — столица Китая» — ложно; «1 = 0» — ложно. Истина или ложь являются логическими величинами. Логические значения приведенных выше высказываний однозначно определены; другими словами, их значения являются логическими константами.

Логическое значение неравенства х < 0, где х — переменная, является переменной величиной. В зависимости от значения х оно может быть либо истиной, либо ложью. В связи с этим возникает понятие логической переменной.

Основы формального аппарата математической логики создал в середине XIX в. английский математик Джордж Буль. В его честь исчисление высказываний называют булевой алгеброй, а логические величины — булевскими.

Одиночные высказывания могут быть объединены в составные логические формулы с помощью логических операций.

Имеются три основные логические операции: отрицание, конъюнкция (логическое умножение) и дизъюнкция (логическое сложение).

Операция отрицания обозначается в математической логике значком ¬ и читается как частица не. Это одноместная операция.

Например, ¬ (x = у) читается «не (х равно y)». В результате получится истина, если х не равно у, и ложь, если х равно у. Отрицание изменяет значение логической величины на противоположное.

Операция конъюнкции обозначается значком & и читается как частица и. Это двухместная операция. Например, (х > 0) & (х < 1) читается «х больше 0 и х меньше 1». Данная логическая формула примет значение истина, если х



 (0,1), и ложь — в противном случае. Следовательно, результат конъюнкции — истина, если истинны оба операнда. Знак операции дизъюнкции v читается как частица или. Например, (х = 0) v (х = 1) читается «х равно 0 или х равно 1». Формула дает истину, если х — двоичная цифра (0 или 1). Следовательно, дизъюнкция дает в результате истину, если хотя бы один операнд — истина.

В Паскале логические значения обозначаются служебными словами false (ложь) и true (истина), а идентификатор логического типа — boolean.

Кроме величин (констант и переменных) типа boolean логические значения false, true принимают результаты операций отношения.

Операции отношения осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними.

Примеры записи отношений: х<у; a+b>=c/d; abs(m-n)<=l. Примеры вычисления значений отношений:



Логические операции выполняются над операндами булева типа. Имеются четыре логические операции: Not — отрицание; And — логическое умножение (конъюнкция); Or — логическое сложение (дизъюнкция). Кроме этих трех обязательных операций в Турбо Паскале имеется еще операция — исключающее ИЛИ. Ее знак — служебное слово Хоr. Это двухместная операция, которая в результате дает значение истина, если оба операнда имеют разные логические значения.

Операции перечислены в порядке убывания приоритетов. Результаты логических операций для различных значений операндов приведены в табл. 3.5.

Таблица 3.5



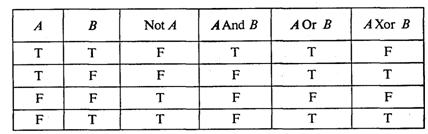
Операции отношения имеют самый низкий приоритет. Поэтому если операндами логической операции являются отношения, то их следует заключать в круглые скобки. Например, математическому неравенству 1 ≤ х ≤ 50 соответствует следующее логическое выражение:

(1<=X) And (X<=50)

Логическое выражение есть логическая формула, записанная на языке программирования. Логическое выражение состоит из логических операндов, связанных логическими операциями и круглыми скобками. Результатом вычисления логического выражения является булева величина (false или true). Логическими операндами могут быть логические константы, переменные, функции, операции отношения. Один отдельный логический операнд является простейшей формой логического выражения.

Примеры логических выражений (здесь d, b, с — логические переменные; х, у — вещественные переменные; k — целая переменная):



Если d=true; b=false; c=true; x=3.0; y=0.5; k=5, то результаты вычисления будут следующими:



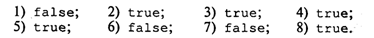
В примере использована логическая функция odd(k). Это функция от целого аргумента k, которая принимает значение true, если значение k нечетное, и false, если k четное.

Логический оператор присваивания имеет структуру, представленную на рис. 19.



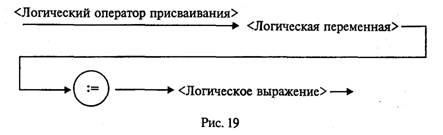
Примеры логических операторов присваивания:

1) d:=true;

2) b:=(x>y) and (k<>0);

3) c:=d or b and not (odd(k) and d).