Geum.ru

Составление программы на языке программирования. Отладка и тестирование программы

Вид материалаДокументы

Содержание


3.14. Вычисление рекуррентных последовательностей
Программирование вычислений рекуррентных последовательностей.
Подобный материал:
1   ...   8   9   10   11   12   13   14   15   ...   21

3.14. Вычисление рекуррентных последовательностей


Рекуррентная последовательность. Из курса математики известно понятие рекуррентной последовательности. Это понятие вводится так: пусть известно k чисел a1, ..., аk. Эти числа являются первыми числами числовой последовательности. Следующие элементы данной последовательности вычисляются так:



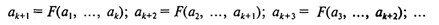
Здесь F— функция от k аргументов. Формула вида



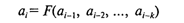
называется рекуррентной формулой. Величина k называется глубиной рекурсии.

Другими словами, можно сказать, что рекуррентная последовательность — это бесконечный ряд чисел, каждое из которых, за исключением k начальных, выражается через предыдущие.

Примерами рекуррентных последовательностей являются арифметическая (1) и геометрическая (2) прогрессии:



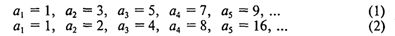
Рекуррентная формула для указанной арифметической прогрессии:



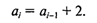
Рекуррентная формула для данной геометрической прогрессии:



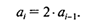
Глубина рекурсии в обоих случаях равна единице (такую зависимость еще называют одношаговой рекурсией). В целом рекуррентная последовательность описывается совокупностью начальных значений и рекуррентной формулы. Все это можно объединить в одну ветвящуюся формулу. Для арифметической прогрессии:



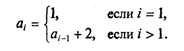
Для геометрической прогрессии:



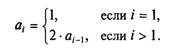
Следующая числовая последовательность известна в математике под названием чисел Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Начиная с третьего элемента каждое число равно сумме значений двух предыдущих, т. е. это рекуррентная последовательность с глубиной равной 2 (двухшаговая рекурсия). Опишем ее в ветвящейся форме:



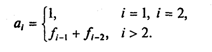
Введение представления о рекуррентных последовательностях позволяет по-новому взглянуть на некоторые уже известные нам задачи. Например, факториал целого числа п! можно рассматривать как значение n-го элемента следующего ряда чисел:



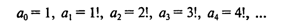
Рекуррентное описание такой последовательности выглядит следующим образом:



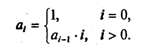
Программирование вычислений рекуррентных последовательностей. С рекуррентными последовательностями связаны задачи такого рода:

1) вычислить заданный (n-й) элемент последовательности;

2) математически обработать определенную часть последовательности (например, вычислить сумму или произведение первых n членов);

3) подсчитать количество элементов на заданном отрезке последовательности, удовлетворяющих определенным свойствам;

4) определить номер первого элемента, удовлетворяющего определенному условию;

5) вычислить и сохранить в памяти заданное количество элементов последовательности.

Данный перечень задач не претендует на полноту, но наиболее часто встречающиеся типы он охватывает. В четырех первых задачах не требуется одновременно хранить в памяти множество элементов числового ряда. В таком случае его элементы могут получаться последовательно в одной переменной, сменяя друг друга.

Пример 1. Вычислить п-й элемент арифметической прогрессии (1).

Var M,I: 0..Maxint;

A: Real;

Begin

Write('N=');

ReadLn(N);

A:=l;

For I: =2 To N Do

A:=A+2;

WriteLn('A(',N:l,')=',A:6:0)

End.

Рекуррентная формула ai = ai-­1 + 2 перешла в оператор А := А + 2.

Пример 2. Просуммировать первые п элементов геометрической прогрессии (2) (не пользуясь формулой для суммы первых n членов прогрессии).

Var N,1: 0..Maxint;

A,S: Real;

Begin

Write('N='); ReadLn(N);

A:=l;

S:=A;

For I: =2 To N Do

Begin

A:=2*A;

S:=S+A

End;

WriteLn('Сумма равна',S:6:0)

End.

При вычислении рекуррентной последовательности с глубиной 2 уже нельзя обойтись одной переменной. Это видно из следующего примера.

Пример 3. Вывести на печать первые п (п ≥ 3) чисел Фибоначчи. Подсчитать, сколько среди них четных чисел.

Var N,I,K,F,F1,F2: 0..Maxint;

Begin

Fl:=l; F2:=l;

K:=0;

WriteLn('F(l)=',Fl,'F(2)=',F2);

For I:=3 To N Do

Begin

F:=F1+F2;

WriteLn('F(',I:l,')=',F);

If Not Odd(F) Then K:=K+1;

F1:=F2; F2:=F

End;

WriteLn('Количество четных чисел в последовательности равно',К)

End.

Понадобились три переменные для последовательного вычисления двухшаговой рекурсии, поскольку для нахождения очередного элемента необходимо помнить значения двух предыдущих.

Пример 4. Для заданного вещественного х и малой величины ε (например, ε = 0,000001) вычислить сумму ряда




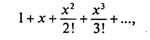
включив в нее только слагаемые, превышающие ε. Известно, что сумма такого бесконечного ряда имеет конечное значение, равное еx, где е = 2,71828... — основание натурального логарифма. Поскольку элементы этого ряда представляют собой убывающую последовательность чисел, стремящуюся к нулю, то суммирование нужно производить до первого слагаемого, по абсолютной величине не превышающего ε.

Если слагаемые в этом выражении обозначить следующим образом:



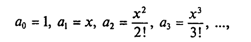
то обобщенная формула для i-го элемента будет следующей:



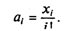
Нетрудно увидеть, что между элементами данной последовательности имеется рекуррентная зависимость. Ее можно найти интуитивно, но можно и вывести формально. Правда, для этого нужно догадаться, что рекурсия — одношаговая, и что каждый следующий элемент получается путем умножения предыдущего на некоторый множитель, т.е.



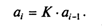
Используя обобщенную формулу, имеем:



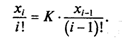
Отсюда:



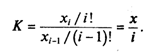
Действительно:



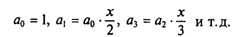
Следовательно, данная рекуррентная последовательность может быть описана следующим образом:



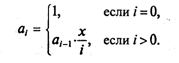
И наконец, приведем программу, решающую поставленную задачу.

Var A,X,S,Eps: Real;

I: Integer;

Begin

Write('X ='); ReadLn(X);

Write('Epsilon ='); ReadLn(Eps);

A:=l; S:=0; I:=0;

While Abs(A)>Eps Do

Begin

S:=S+A;

I:=I+1;

A:=A*X/I

End;

WriteLn('Сумма ряда равна', S:10:4)

End.

Как и прежде, значения одношаговой рекуррентной последовательности вычисляются в одной переменной.

Каждое повторное выполнение цикла в этой программе приближает значение S к искомому (уточняет значащие цифры в его записи). Такой вычислительный процесс в математике называется итерационным процессом. Соответственно, циклы, реализующие итерационный вычислительный процесс, называются итерационными циклами. Для их организации используются операторы While или Repeat.

Пример 5. Для заданного натурального N и вещественного х (х > 0) вычислить значение выражения:



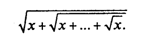
В этом случае рекуррентность не столь очевидна. Попробуем найти ее методом индукции. Будем считать, что искомое выражение есть N-й элемент последовательности следующего вида:



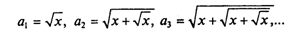
Отсюда видна связь:



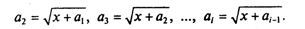
Теперь поставленная задача решается очень просто:

Var A,X: Real; I,N: Integer;

Begin

Write('X='); ReadLn(X);

Write('N='); ReadLn(N);

A:= Sqrt(X);

For I:=2 To N Do

A:=Sqrt(X+A);

WriteLn('Ответ:',А)

End.

К решению всех перечисленных выше задач можно подойти иначе.

Вспомним о рекурсивно определенных подпрограммах. Посмотрите на описание арифметической прогрессии в форме рекуррентной последовательности. Из него непосредственно вытекает способ определения функции для вычисления заданного элемента прогрессии.

Сделаем это для общего случая, определив арифметическую прогрессию с первым членом а0 и разностью d:



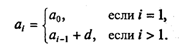
Соответствующая подпрограмма-функция выглядит так:

Function Progres(АО,D: Real;I: Integer): Real;

Begin

If I=1

Then Progres:=AO

Else Progres:=Progres(A0,D,I-1)+D

End;

Следующая программа выводит на экран первые 20 чисел Фибоначчи, значения которых вычисляет рекурсивная функция Fibon.

Var К: Byte;

Function Fibon(N: Integer): Integer;

Begin

If (N=1) Or (N=2)

Then Fibon:=1

Else Fibon:=Fibon(N-1)+Fibon(N-2)

End;

Begin

For K:=l To 20 Do WriteLn(Fibon(K))

End.

Необходимо отметить, что использование рекурсивных функций ведет к замедлению счета. Кроме того, можно столкнуться с проблемой нехватки длины стека, в котором запоминается «маршрут» рекурсивных обращений.

Рекуррентные последовательности часто используются для решения разного рода эволюционных задач, т.е. задач, в которых прослеживается какой-то процесс, развивающийся во времени. Рассмотрим такую задачу.

Пример 6. В ходе лечебного голодания масса пациента за 30 дней снизилась с 96 до 70 кг. Было установлено, что ежедневные потери массы пропорциональны массе тела. Вычислить, чему была равна масса пациента через k дней после начала голодания для k = 1, 2, ..., 29.

Обозначим массу пациента в i-й день через рi (i = 0, 1, 2, ..., 30). Из условия задачи известно, что р0 = 96 кг, p30 = 70 кг.

Пусть К— коэффициент пропорциональности убывания массы за один день.

Тогда



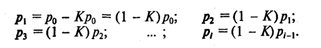
Получаем последовательность, описываемую следующей рекуррентной формулой:



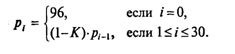
Однако нам неизвестен коэффициент К. Его можно найти, используя условие p30 = 70.

Для этого будем делать обратные подстановки:



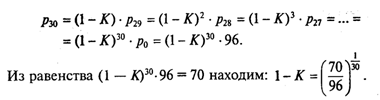
Далее программирование становится тривиальным.

Var I: Byte; P,Q: Real;

Begin

P:=96;

Q:=Exp(l/30*Ln(70/96));

For I:=l To 29 Do

Begin

P:=Q*P;

WriteLn(I,'-й день-',Р:5:3,'кг')

End

End.