Лекция №4-5 Измерение информации Пример

Вид материала

Лекция

Содержание ПОДХОД I. Неизмеряемость информации в быту (информация как новизна) ПОДХОД II —технический, или объемный. ПОДХОД III — вероятностный. N = 2 (выбор из двух возможностей), то I N, но уже не равновероятных Что учащемуся необходимо знать Что учащемуся необходимо уметь Информация как снятая неопределенность Расширь свой кругозор Общая характеристика информационных процессов Информация не существует сама по себе, она проявляется в информационных процессах. Что учащемуся необходимо знать Наиболее общими информационными процессами являют­ся сбор, преобразование, использование информации. Что учащемуся необходимо уметь Кодирование информации Конец фильма. М различных символов кодом по­стоянной длины с помощью алфавита из k Интересный факт Хранение информации Интересный факт ... Полное содержание

Подобный материал:

• «измерение», 44.31kb.
• Тема классификационный анализ лекция, 63.18kb.
• Измерение информации. Количество информации. Единицы измерения информации, 328.73kb.
• Дискретных Марковских Цепей) в анализе данных. Пример применения. (лекция, 7.29kb.
• Муниципальное образовательное учреждение Пошатовская средняя общеобразовательная школа, 201.78kb.
• Карпов Дмитрий Анатольевич лекция, 472.96kb.
• Vi. Измерение вредных производственных факторов рабочих мест, 43.78kb.
• Учебный план курсовой подготовки по пользователю, 46.52kb.
• Методические указания к лабораторной работе, 454.05kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.

Лекция №4-5

Измерение информации

Пример. Не правда ли, истрепанная книжка, если в ней нет вы­рванных страниц, несет для вас ровно столько же инфор­мации, сколько такая же новая? Каменная скрижаль весом в три тонны несет для архео­логов столько же информации, сколько ее хороший фо­тоснимок в археологическом журнале. Не так ли? Когда московская радиостудия передает последние изве­стия, то одну и ту же информацию получает и подмос­ковный житель и житель Новосибирска. Но поток энер­гии радиоволн в Новосибирске намного меньше, чем в Москве.

Следовательно, мощность сигнала, так же как и размер, вес и качество носителя, не могут служить оценкой коли­чества информации, переносимой сигналом. Как же оценить это количество?

Из курса физики вы знаете, что прежде, чем измерять значение какой-либо физической величины, надо ввести единицу измерения. У информации тоже есть такая едини­ца — бит, но смысл ее различен при измерении информации в рамках разных подходов к определению понятия «инфор­мация». Соответственно, можно выделить 3 подхода к изме­рению информации.

ПОДХОД I. Неизмеряемость информации в быту (информация как новизна)

Пример. Вы получили некоторое сообщение, например, прочита­ли статью в любимом журнале. В этом сообщении содер­жится какое-то количество информации. Как оценить, сколько информации вы получили? Другими словами, как измерить информацию? Можно ли сказать, что чем больше статья, тем больше информации она содержит? Разные люди, получившие одно и то же сообщение, по-разному оценивают его информационную ёмкость, то есть количество информации, содержащееся в нём. Это происхо­дит оттого, что знания людей о событиях, явлениях, о кото­рых идет речь в сообщении, до получения сообщения были различными. Поэтому те, кто знал об этом мало, сочтут, что получили много информации, те же, кто знал больше, могут сказать, что информации не получили вовсе. Количество ин­формации в сообщении, таким образом, зависит от того, на­сколько ново это сообщение для получателя.

В таком случае, количество информации в одном и том же сообщении должно определяться отдельно для каждого получателя, то есть иметь субъективный характер. Но субъ­ективные вещи не поддаются сравнению и анализу, для их измерения невозможно выбрать одну общую для всех едини­цу измерения.

Таким образом, с точки зрения информации как новиз­ны, мы не можем однозначно и объективно оценить коли­чество информации, содержащейся даже в простом сооб­щении. Что же тогда говорить об измерении с этой точки зрения количества информации, содержащейся в научном открытии, новом музыкальном стиле, новой теории обще­ственного развития.

Поэтому, когда информация рассматривается как новиз­на сообщения для получателя, не ставится вопрос об измере­нии количества информации.

ПОДХОД II —технический, или объемный.

Измерение информации в технике

(информация как сообщения в форме знаков или сигналов, хранимые, передаваемые и обрабатываемые с помощью технических устройств)

В технике, где информацией считается любая хранящая­ся, обрабатываемая или передаваемая последовательность знаков, сигналов, часто используют простой способ опреде­ления количества информации, который может быть назван объемным. Он основан на подсчёте числа символов в сооб­щении, то есть учитывает только длину сообщения, но не его содержание.

Длина сообщения зависит от числа знаков, употребляе­мых для записи сообщения. Например, слово «мир» в рус­ском алфавите записывается тремя знаками, в англий­ском — пятью (peace), а в коде ДКОИ-8 (двоичный код обмена информацией длиной 8) — двадцатью четырьмя би­тами (111011011110100111110010).

В вычислительной технике применяются две стандарт­ные единицы измерения информации: бит (от англ, binary digit — двоичная цифра) и байт (byte).

Конечно, будет правильно, если вы скажете: «В слове «Рим» содержится 24 бита информации, а в сообщении «Миру мир!» — 72 бита». Однако для того чтобы измерить информацию в битах, вы определяете количество символов в этом сообщении. Нам привычнее работать с символами. Для ввода в компьютер символы надо кодировать. Каждый сим­вол в настоящее время в вычислительной технике кодирует­ся 8-битным или 16-битным кодом. Поэтому для удобства была введена более крупная единица информации в технике (преимущественно вычислительной) — байт. В байтах лег­че подсчитать количество информации в техническом сооб­щении — оно совпадает с количеством символов в нём.

Пример.

Исходное сообщение		Количество информации
На языке	В машинном представлении (ДКОИ-8)	В символах	В битах	В байтах
рим	1111001011101001 11101101	3	24	3
мир	11101101 11101001 11110010	3	24	3
миру мир!	11101101 11101001 1111001011110101 0010000011101101 1110101 11110010 00100001	9	72	9
(** */	00101000 00101010 00101010 00100000 0010101000101111	6	48	6

Поскольку компьютер предназначен для обработки боль­ших объемов информации, то используют производные еди­ницы — килобайт (КБ), мегабайт (МБ), гигабайт (ГБ).

Обычно приставка «кило» означает тысячу, а приставка «мега» — миллион, но в вычислительной технике осуществляется привязка к принятой двоичной системе ко­дирования.

В силу этого один килобайт равен не 1000 байтов, а 2¹⁰ = = 1024 байта.

Аналогично, 1 Мб = 2¹⁰ Кб = 1024 Кб = 2²⁰ байтов = = 1 048 576 байтов.

1 Гб = 2¹⁰ Мб = 2²⁰ Кб = 2³⁰ байтов = 1 073 741 824 байта.

Пример. Если у вас есть дискета ёмкостью 100 Мб, то на ней мож­но сохранить:

Вид хранимой информации	Объем (количество)	информации
Страниц текста	50 000 страниц или	150 романов
Цветных слайдов высочайшего качества	150
Аудиозапись речи видного политического деятеля	1,5 часа
Музыкальный фрагмент качества CD-стерео	10 мин
Фильм высокого качества записи	15с
Протоколы операций с банковским счетом	за 1000 лет

ПОДХОД III — вероятностный.

Измерение информации в теории информации

(информация как снятая неопределённость)

Получение информации (ее увеличе­ние) одновременно означает увеличение знания, что, в свою очередь, означает уменьшение незнания или информаци­онной неопределённости.

За единицу количества информации принимают выбор одного из двух рав­новероятных сообщений («да» или «нет», «1» или «0»). Она также названа битом. Вопрос ценности этой информа­ции для получателя — это уже из иной области.

Пример. Известно, что книга лежит на одной из двух полок — верхней или нижней. Сообщение о том, что книга лежит на верхней полке, уменьшает неопределённость ровно вдвое; в этом случае говорят, что оно несет 1 бит инфор­мации.

Сообщение о том, как упала монета после броска — «ор­лом» или «решкой», несет 1 бит информации. В соревновании участвуют 4 команды. Сообщение о том, что третья команда набрала большее количество очков, уменьшает первоначальную неопределённость ровно в 4 раза (дважды по два) и несет 2 бита информации. Очень приближенно можно считать, что количество ин­формации в сообщении о каком-то событии совпадает с ко­личеством вопросов относительно ситуации, разрешаемой одним из некоторого набора событий, ответом на которые могут быть лишь «да» или «нет», которые необходимо за­дать, чтобы получить ту же информацию. Причем события должны быть равновероятны.

Пример. Сколько вопросов надо задать, чтобы отгадать одну из 32 карт (колода без шестерок), если ответами могут быть лишь «да» или «нет»?

Оказывается, достаточно задать всего лишь 5 вопросов, но задавать их надо так, чтобы после каждого ответа можно было исключить из рассмотрения ровно половину карт, среди которых задуманной не может быть. Таки­ми, например, являются вопросы о цвете масти карты («Задуманная карта красной масти?»), о типе карты («Задуманная карта — «картинка»?») и т. п. То есть сообщение о том, какая конкретно карта из 32 за­думана, несет 5 битов информации.

В приведенных примерах число равновероятных собы­тий, об одном из которых идет речь в сообщении, кратно степени числа 2 (4 = 2², 32 = 2⁵). Поэтому сообщение несет количество битов информации, являющееся целым числом. Но на практике могут встречаться и другие ситуации.

Пример. Сообщение о том, что на светофоре красный сигнал, не­сет в себе количество информации большее, чем 1 бит. Попробуйте объяснить, почему.

Пример. Известно, что Иванов живет на улице Весенней. Сообще­ние о том, что номер его дома есть число чётное, умень­шило неопределённость. Получив такую информацию, мы стали знать больше, но информационная неопре­делённость осталась, хотя и уменьшилась. Почему в этом случае мы не можем сказать, что первона­чальная неопределённость уменьшилась вдвое (иными словами, что мы получили 1 бит информации)? Если вы не знаете ответа на этот вопрос, представьте себе улицу, на чётной стороне которой, например, четыре дома, а на нечётной — двадцать. Такие улицы не такая уж большая редкость.

Научный подход к оценке сообщений был предложен еще в 1928 году Р. Хартли. Расчетная формула имеет вид:

I= Iog₂ N или 2^I = N,

где N — количество равновероятных событий (число воз­можных выборов),

I — количество информации.

Если N = 2 (выбор из двух возможностей), то I = 1 бит. Иногда формула Хартли записывается иначе. Так как на­ступление каждого из N возможных событий имеет одина­ковую вероятность р = 1/N, то N = 1/р и формула имеет вид

I = Iog₂ (1/p) = - Iog₂ p.

Последние 2 примера показывают, что данное выше опре­деление количества информации слишком упрощено. Уточ­ним его. Но прежде разберем еще один пример.

Пример. Пылкий влюблённый, находясь в разлуке с объектом своей любви, посылает телеграмму: «Любишь?». В ответ приходит не менее лаконичная телеграмма: «Да!». Сколь­ко информации несет ответная телеграмма? Альтернатив здесь две — либо «да», либо «нет». Их можно обозначить символами двоичного кода 1 и 0; Таким образом, ответ­ную телеграмму можно было бы закодировать всего од­ним двоичным символом.

Можно ли сказать, что ответная телеграмма несет одну единицу информации?

Если влюблённый уверен в положительном ответе, то от­вет «да» почти не даст ему никакой новой информации. Аналогично безнадёжному влюблённому, уже привык­шему получать отказы, ответ «нет» также принесет очень мало информации. Но внезапный отказ уверенно­му влюблённому (неожиданное огорчение) или ответ «да» безнадёжному влюблённому (нечаянная радость) не­сет сравнительно много информации, настолько много, что радикально изменяется все дальнейшее поведение влюблённого, а, может быть, его судьба!

Таким образом, с точки зрения взгляда на информацию как на снятую неопределённость количество информации зависит от вероятности получения того или иного сооб­щения. Причем, чем больше вероятность события, тем мень­шее количество информации содержится в сообщении о та­ком событии.

Иными словами, количество информации в сообщении о каком-то событии зависит от вероятности свершения данно­го события.

Научный подход к более общему случаю вычисления ко­личества информации в сообщении об одном из N, но уже не равновероятных событий был предложен К. Шенноном в 1948 году.

Пусть имеется текст, содержащий 1000 букв. Буква «о» в тексте встречается примерно 90 раз, буква «р» 40 раз, буква «ф» 2 раза, буква «а» 200 раз. Поделив 200 на 1000, мы по­лучим величину 0,2, которая представляет собой среднюю частоту, с которой в рассматриваемом тексте встречается буква «а». Вероятность p_a появления буквы «а» в тексте мо­жем считать приблизительно равной 0,2. Аналогично р_р = 0,04, р_ф = 0,002, р_о = 0,09.

Далее поступаем согласно К. Шеннону. Берем двоичный логарифм от величины 1/0,2 и называем то, что получилось, количеством информации, которую несёт появление буквы «а» в рассматриваемом тексте. Точно такую же операцию проделаем для каждой буквы. Тогда количество информа­ции, которую несёт появление i-ro символа алфавита, равно

h_i = Iog₂ (1/p_i) = - Iog₂ p_i

где p_i — вероятность появления в сообщении i-гo символа алфавита.

Удобнее в качестве меры количества информации пользо­ваться не отдельными значениями h_i, а средним значением количества информации, приходящейся на один символ ал­фавита:

Н = Σ p_i h_i = - Σ p_i Iog₂ p_i.

Значение Н достигает максимума при равновероятных событиях, то есть при равенстве всех p_i :

p_i = 1/N.

В этом случае формула Шеннона превращается в формулу Хартли.

Между техническим и вероятностным подходами к изме­рению информации существует следующая корреляция.

С точки зрения вероятностного подхода принято считать, что двумя двоичными словами исходной длины k битов или словом длины 2k битов можно передать в 2 раза больше ин­формации, чем одним исходным словом длины k битов. Чис­ло возможных равновероятных выборов при этом увеличи­вается в 2^k раз, значит, количество информации удваивается.

Что учащемуся необходимо знать

В технике (теория кодирования и передачи сообщений) под количеством информации понимают количество кодиру­емых, передаваемых или хранимых символов.

Бит — двоичный знак двоичного алфавита {0, 1}.

Бит — минимальная единица измерения информации.

Байт — это восьмиразрядный двоичный код, с помощью которого можно представить один символ.

Байт — единица количества информации в системе СИ.

Информационный объем сообщения (информационная емкость сообщения) — количество информации в сообще­нии, измеренное в битах, байтах или производных единицах (килобайтах, мегабайтах и так далее).

В теории информации количеством информации назы­вают числовую характеристику сигнала, которая не зависит от его формы и содержания и характеризует уменьшение не­определенности после получения сообщения в виде данного сигнала. В этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.

Для абсолютно достоверного события (событие обязатель­но произойдет, поэтому его вероятность равна 1) количество информации в сообщении о нем равно 0. Чем невероятнее событие, тем большее количество информации несет сообще­ние о нем. Лишь при равновероятных ответах ответ «да» или «нет» несет один бит информации.


Что учащемуся необходимо уметь

Технический аспект измерения информации

Задание 1

Измерьте информационный объем сообщения «Ура! Закончи­лись каникулы!!» Выразите этот объем в битах, байтах, килобай­тах.

Задание 2

Измерьте примерную информационную емкость 1 страницы учебника; всего учебника.

Подсказка. Подсчитайте, сколько символов в одной строке и сколько строк на странице, и перемножьте полученные числа. Сколько таких учебников может поместиться на дискете емко­стью 360 Кб; 1,44 Мб; на винчестере ёмкостью 420 Мб; 6,4 Гб?

Информация как снятая неопределенность

Задание 3

Сколько следует задать вопросов и как их следует формулиро­вать, чтобы количественно оценить сообщение о том, что вагон стоит на одном из 16 путей?

Задание 4

Шарик находится в одном из 64 ящичков. Сколько единиц инфор­мации будет содержать сообщение о том, где находится шарик?

Задание 5

Определите, сколько битов информации несет сообщение о том, что на светофоре горит зеленый свет.

Задание 6

Вы бросаете два кубика с нанесенными на гранях цифрами от 1 до 6. Определите, сколько битов информации несет сообщение о том, что на одном кубике выпала тройка, а на другом — пятерка.

Задание 7

Предположим, вероятность того, что вы получите за контрольную работу оценку «5», равна 0,6; вероятность получения оценки «4» равна 0,3; вероятность получения оценки «3» — 0,1. Определите, сколько битов информации будет нести сообщение о результатах контрольной работы в каждом из возможных случаев.

Задание 8

Проанализируйте таблицу и предложите возможные подходы к измерению количества информации (для незаполненной области таблицы).


Расширь свой кругозор

На памятнике немецкому ученому Л. Больцману высече­на формула, выведенная в 1877 году и связывающая вероят­ность состояния физической системы и величину энтропии этой системы.

Энтропия (греч. en — в, внутрь; trope — превращение, смысловой перевод: то, что внутри, неопределенно) — физи­ческая величина, характеризующая тепловое состояние тела или системы, мера внутренней неупорядоченности системы.

Так вот, формула для энтропии Больцмана совпадает с формулой, предложенной Шенноном для среднего количест­ва информации, приходящейся на один символ в сообще­нии. Совпадение это произвело столь сильное впечатление, что Шеннон назвал количество информации энтропией. С тех пор слово «энтропия» стало чуть ли не синонимом сло­ва «информация».

Чем больше энтропия системы, тем больше степень ее не­определенности. Поступающее сообщение полностью или час­тично снимает эту неопределенность. Следовательно, количе­ство информации можно измерять тем, насколько понизилась энтропия системы после поступления сообщения.

Таким образом, за меру количества информации прини­мается та же энтропия, но с обратным знаком.

Уменьшая неопределенность, мы получаем информа­цию, — в этом весь смысл научного познания.

Общая характеристика информационных процессов

Если обратиться в далекое прошлое, то жалобы на обилие информации обнаруживаются тысячелетия назад.

Пример. На глиняной дощечке (шумерское письмо IV тысячеле­тия до нашей эры) начертано: «Настали тяжелые време­на. Дети перестали слушаться родителей, и каждый но­ровит написать книгу».

Особенно модным стало жаловаться на непереносимость информационного бремени с XVII века. В XX веке заговори­ли ни более, ни менее, как об информационной катастрофе. Информационный кризис — это возрастающее противоречие между объемом накапливаемой в обществе информации и ограниченными возможностями ее переработки отдельно взя­той личностью. По оценкам специалистов в настоящее время количество информации, циркулирующей в обществе, удваи­вается примерно каждый год. Появилась уверенность в том, что для того, чтобы справиться с такой лавиной инфор­мации, недостаточно возможностей человеческого организма. Для этого нужны специальные средства и методы обработки информации, ее хранения и использования. Сформировались новые научные дисциплины — информатика, кибернетика, бионика, робототехника и др., имеющие своей целью изуче­ние закономерностей информационных процессов, то есть процессов, цель которых — получить, передать, сохранить, обработать или использовать информацию.

В наиболее общем виде информационный процесс (ИП) определяется как совокупность последовательных действий (операций), производимых над информацией (в виде дан­ных, сведений, фактов, идей, гипотез, теорий и пр.) для по­лучения какого-либо результата (достижения цели).

Информация не существует сама по себе, она проявляется в информационных процессах.

Информационные процессы всегда протекают в каких-ли­бо системах.

Информационные процессы могут быть целенаправлен­ными или стихийными, организованными или хаотичными, детерминированными или вероятностными, но какую бы мы ни рассматривали систему, в ней всегда присутствуют ин­формационные процессы, и какой бы информационный про­цесс мы ни рассматривали, он всегда реализуется в рамках какой-либо системы — биологической, социальной, техни­ческой, социотехнической.

Пример. «Танец» пчел — процесс передачи информации от пчел-разведчиков пчелам-сборщикам меда. Обучение в школе — это процесс передачи информации, накопленной предыдущими поколениями людей, подрас­тающему поколению.

Электронная почта (как совокупность соответствующих аппаратных средств и программ) предназначена для обес­печения передачи данных между компьютерами.




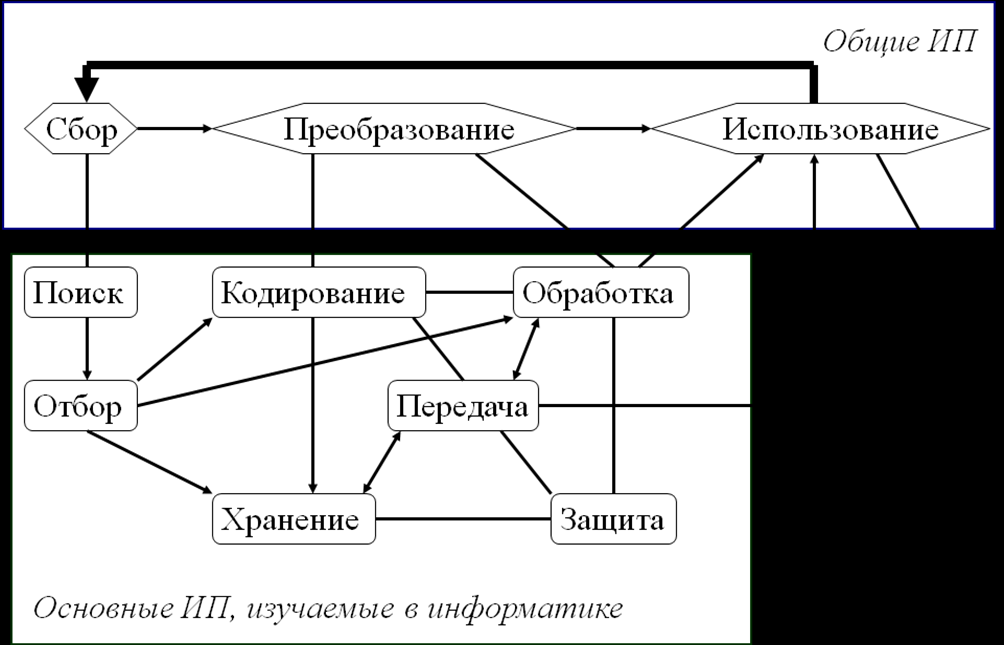
В зависимости от того, какого рода информация является предметом информационного процесса и кто является его субъектом (техническое устройство, человек, коллектив, об­щество в целом), можно говорить о глобальных информаци­онных процессах, или макропроцесссах, и локальных ин­формационных процессах, или микропроцессах.

Схема взаимосвязи информационных процессов показана на рисунке, где линиями без стрелок показаны включения одних процессов в другие (нижних на схеме в верхние), а линиями со стрелками — последовательность выполнения процессов.

Пример. Процесс познания, распространение информации посред­ством средств массовой информации (СМИ), информационные войны, организация ар­хивного хранения информации — глобальные ИП. Сравнение данных, двоичное кодирование текста, запись порции информации на носитель — локальные ИП.

Наиболее общими информационными процессами явля­ются три процесса: сбор, преобразование, использование информации.

Каждый из этих процессов распадается, в свою очередь, на ряд процессов, причем некоторые из последних могут входить в каждый из выделенных обобщенных процессов.

Так, сбор информации состоит из процессов поиска и от­бора. В свою очередь поиск информации осуществляется в результате выполнения процедур целеполагания и использо­вания конкретных методов поиска.

Методы поиска бывают «ручные» или автоматизирован­ные. Они включают в себя такие процедуры, как формирова­ние поискового образа (в явном или неявном виде), про­смотр поступающей информации с целью сравнения её с поисковым образом.

Отбор информации производится на основе ее анализа и оценки ее свойств (объективность, достоверность, актуаль­ность и пр.) в соответствии с выбранным критерием оценки. Отобранная информация сохраняется.

Хранение информации — это распространение её во вре­мени. Хранение информации невозможно без выполнения процессов кодирования, формализации, структурирова­ния, размещения, относящихся к общему процессу преобра­зования информации.

В то же время кодирование, формализацию, структуриро­вание можно вполне обоснованно отнести к процессам обра­ботки информации. Наряду с вышеперечисленными к про­цессам обработки информации относятся также информаци­онное моделирование, вычисления по формулам (численные расчеты), обобщение, систематизация, классификация, кла­стеризация, схематизация и т. п.

Обработка информации составляет основу процесса пре­образования информации.

Информация может быть передана (распространена в пространстве) для её последующего использования, обработ­ки или хранения. Процесс передачи информации включает в себя процессы кодирования, восприятия, расшифровки и пр.

Важнейшим процессом использования информации субъ­ектом является процесс подготовки и принятия решений. Наряду с этим часто использование информации сводится к процессам формирования документированной информа­ции (документов в том смысле, в каком этот термин исполь­зуется в делопроизводстве) с целью подготовки информаци­онного или управляющего воздействия.

Пример. Бухгалтер на основании имеющихся первичных доку­ментов (накладных, нарядов, табелей учета времени, ин­струкций по налогообложению и пр.) составляет сводную ведомость.

Сообщение о крупной аварии может стать основой для подготовки пакета документов о введении чрезвычайного положения.

В реальной практике широко используются процедуры, входящие в процесс защиты информации. Защита инфор­мации — важный компонент процессов хранения, обработ­ки, передачи информации в системах любого типа, особенно в социальных и технических системах. К ней относятся раз­работка кода (шифра), кодирование (шифрование), сравне­ние, анализ, паролирование и т. п.

После того, как процесс использования информации за­вершен, например, решение принято и субъект приступил к его реализации, как правило, возникает новая задача и не­обходимы новая информация либо уточнение уже имеющейся. Это приводит к тому, что субъект вновь обращается к процедуре сбора информации и пр. Поэтому, говоря об ин­формационных процессах, следует подчеркивать не только их взаимосвязь, но и цикличность. Отсюда ясно происхож­дение понятий «информационный цикл», «жизненный цикл информации».

Человек всегда стремится автоматизировать выполнение рутинных операций и операций, требующих постоянного внимания и точности. То же справедливо и по отношению к информационным процессам.

Универсальным устройством для автоматизированного выполнения информационных процессов в настоящее время является компьютер. Немалую роль в этом играют вычисли­тельные системы и сети.

Что учащемуся необходимо знать

Информационный процесс — совокупность последовате­льных действий (операций), производимых над информа­цией (в виде данных, сведений, фактов, идей, гипотез, тео­рий и пр.) для получения какого-либо результата (достиже­ния цели).

Информация проявляется именно в информационных процессах.

Информационные процессы всегда протекают в каких-ли­бо системах (социальных, социотехнических, биологиче­ских и пр.).

Наиболее общими информационными процессами являют­ся сбор, преобразование, использование информации.

К основным информационным процессам, изучаемым в курсе информатики, относятся: поиск, отбор, хранение, пе­редача, кодирование, обработка, защита информации.

Информационные процессы, осуществляемые по опреде­ленным информационным технологиям, составляют основу информационной деятельности человека.

Компьютер является универсальным устройством для ав­томатизированного выполнения информационных процес­сов.