Лекция n17 Лекция 17

Вид материала

Лекция

Содержание Эффект Комптона В пользу волновой теории Эффект Допплера Теория де-Бройля Волновая функция

Подобный материал:

• «Социальная стратификация и социальная мобильность», 46.19kb.
• Первая лекция. Введение 6 Вторая лекция, 30.95kb.
• Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
• Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
• Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
• Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
• Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
• Тема Лекция, 34.13kb.
• Лекция посвящена определению термина «транскриптом», 219.05kb.
• Энергоснабжениеапк лекция, доц. Уринцова Л. В. 2/309, 28.44kb.

Лекция 17.
ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА. ДИФРАКЦИЯ ЭЛЕКТРОНОВ. КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ ГЕЙЗЕНБЕРГА. -ФУНКЦИЯ


Фотоэффект, открытый в 1887 году Г. Герцем и затем подробно исследованный А.Г. Столетовым, долго не удавалось объяснить существовавшими в то время теориями. Два электрода – цинковая пластинка и медная сетка, помещенные в вакуумированную колбу, включены последовательно с микроамперметром и источником регулируемого постоянного напряжения U порядка киловольта (рис. 17.1). При освещении цинковой пластинки светом через цепь протекает ток, регистрируемый микроамперметром. Было обнаружено, что наибольший эффект достигается при облучении ультрафиолетом, что ток возрастает при увеличении освещенности и что возникающий ток обусловлен отрицательными частицами, появляющимися между электродами (законы Столетова). Изменяя напряжение между электродами и отслеживая показания микроамперметра, можно получить вольт-амперную характеристику (рис. 17.1). Участок нарастания тока при увеличении напряжения плавно переходит в насыщение, когда ток J_нас перестает зависеть от U. При U = 0 наблюдается очень малый ток, который можно обратить в ноль, прикладывая напряжение U_зап обратной полярности, называемое потенциалом запирания.

Объяснить фотоэффект удалось только в 1905 г. А. Эйнштейну, применившему гипотезу Планка: кванты света (фотоны), каждый из которых несет энергию h, бомбардируют цинк, выбивая из него электроны. Полученная формула описывает распределение энергии фотонов: часть ее расходуется на работу выхода А_вых – энергию, которую нужно сообщить связанным в атоме электронам, чтобы вывести их из атома в свободное состояние, а другая часть передается выбитым электронам в виде кинетической энергии:

, (17.1)

где 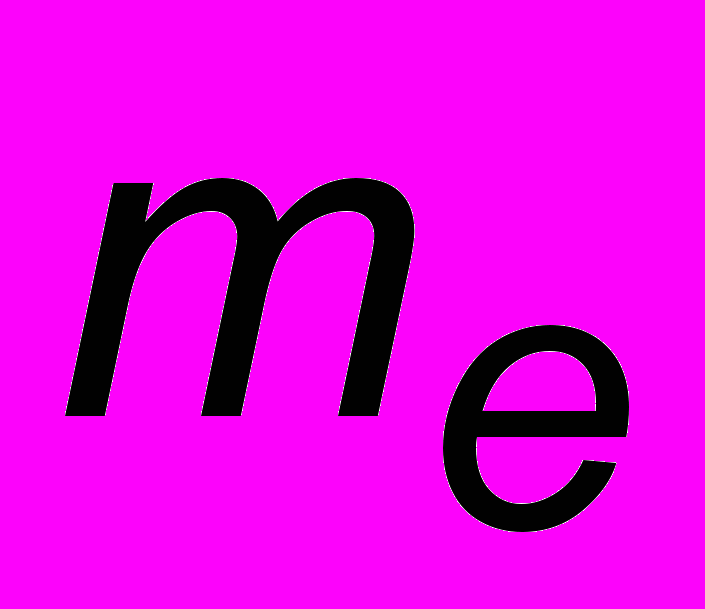- масса электрона. Выбитые из цинка нейтральными фотонами отрицательные электроны и образуют фототок. Становится также понятно, что фотоэффект наблюдается лучше при ультрафиолетовом излучении: его частота, а стало быть энергия падающих фотонов, больше. При некоторой частоте в красной части спектра энергии фотонов хватает только на преодоление работы выхода. Такая частота (или длина волны) называется красной границей фотоэффекта и определяется из соотношения . При облучении катода светом с длиной волны 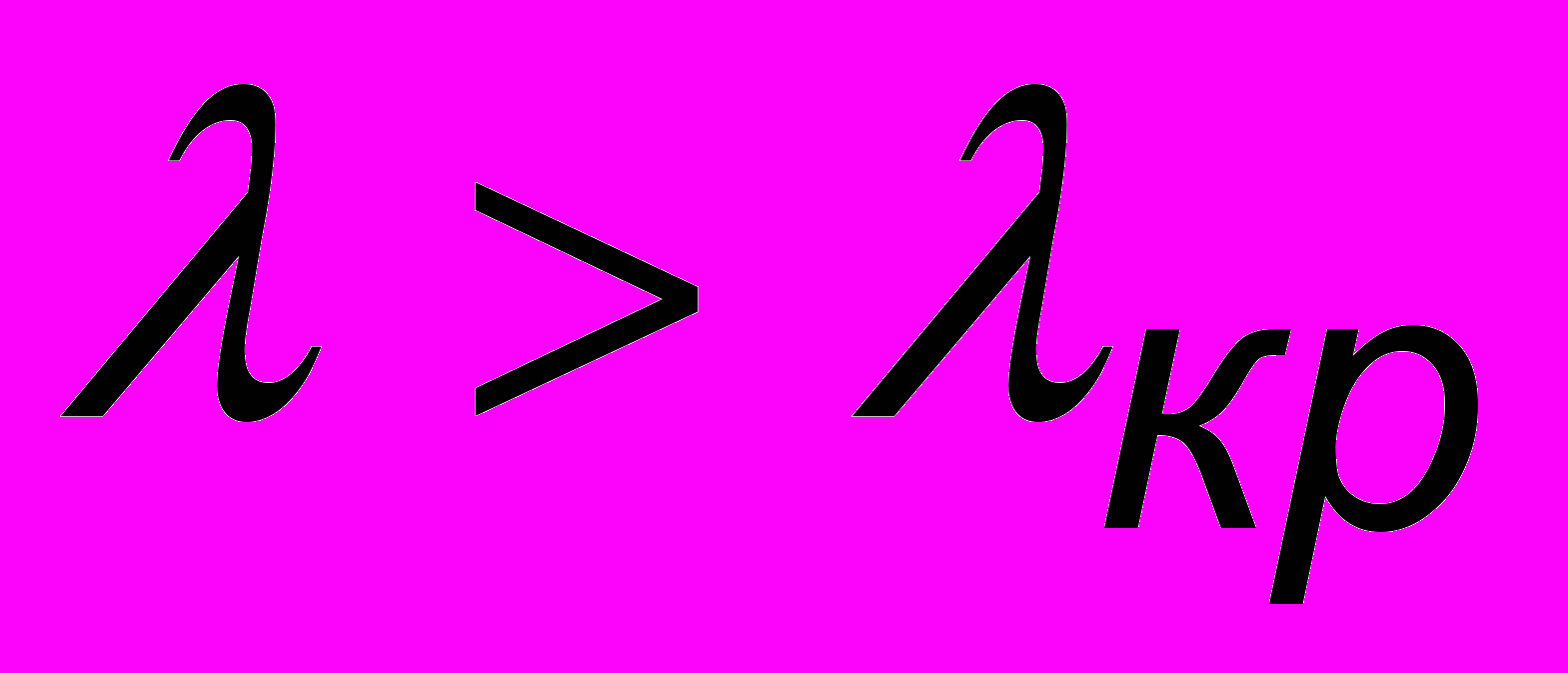фототока не будет. Нетрудно получить и соотношение для потенциала запирания, когда электроны полностью затормозятся создаваемым полем: .

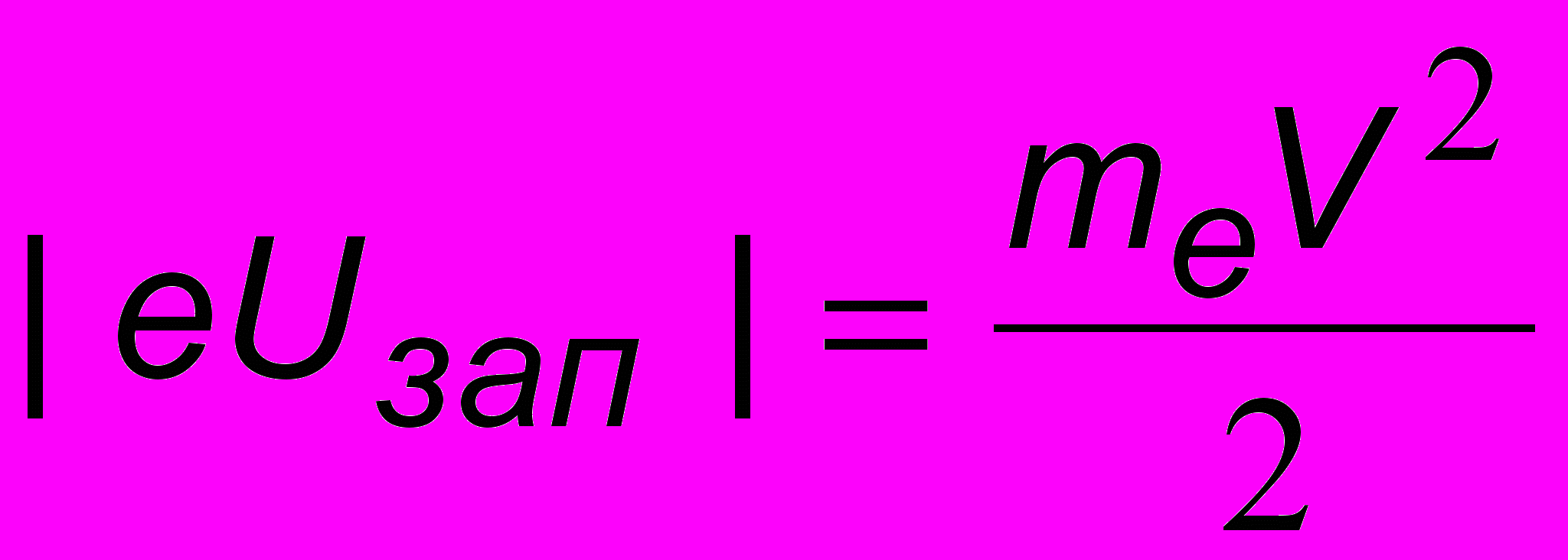В инженерной практике существует много приборов, использующих фотодатчики, представляющие собой описанный двухэлектродный фотоэлемент. Такие датчики, использующие прерывание луча и возникающий при этом импульс тока, включаются в схемы, содержащие механизмы срабатывания - фотореле - применяемые в счетчиках на конвейере, в турникетах метро и т.п. Более чувствительны многоэлектродные системы – фотоэлектронные умножители (ФЭУ), в которых возникающий первичный электронный поток падает на третий электрод, вызывая появление новых, вторичных, электронов. Те, в свою очередь, продолжают движение внутри ФЭУ, вызывая лавинообразный процесс, позволяющий получать фототоки порядка сотен миллиампер. ФЭУ используются в телевидении и других областях электроники для преобразования оптического излучения в электрический сигнал.

Э
ффект Комптона (1923 г.) является даже более убедительным доказательством квантовой природы электромагнитного излучения. Тонкий пучок монохроматического рентгеновского излучения с длиной волны  от рентгеновской трубки S (рис. 17.2) падает на металлическую мишень M и ею рассеивается по всевозможным направлениям. Детектор D, являющийся анализатором спектра, может размещаться в произвольном месте за мишенью и исследовать спектр излучения, рассеянного под некоторым углом . Было обнаружено, что, кроме исходного излучения с длиной волны , в спектре рассеянного излучения присутствует новая компонента
' > , причем разность между ' и  не зависит от материала мишени, а лишь зависит от угла рассеяния:

(17.2)

где - так называемая комптоновская длина волны. Будем считать, что взаимодействие излучения с мишенью происходит как абсолютно упругий удар шаров: налетающий фотон  (рис. 17.3) с импульсом р соударяется с покоящимся электроном е атома мишени и рассеивается им. При этом импульс фотона становится равным p', а п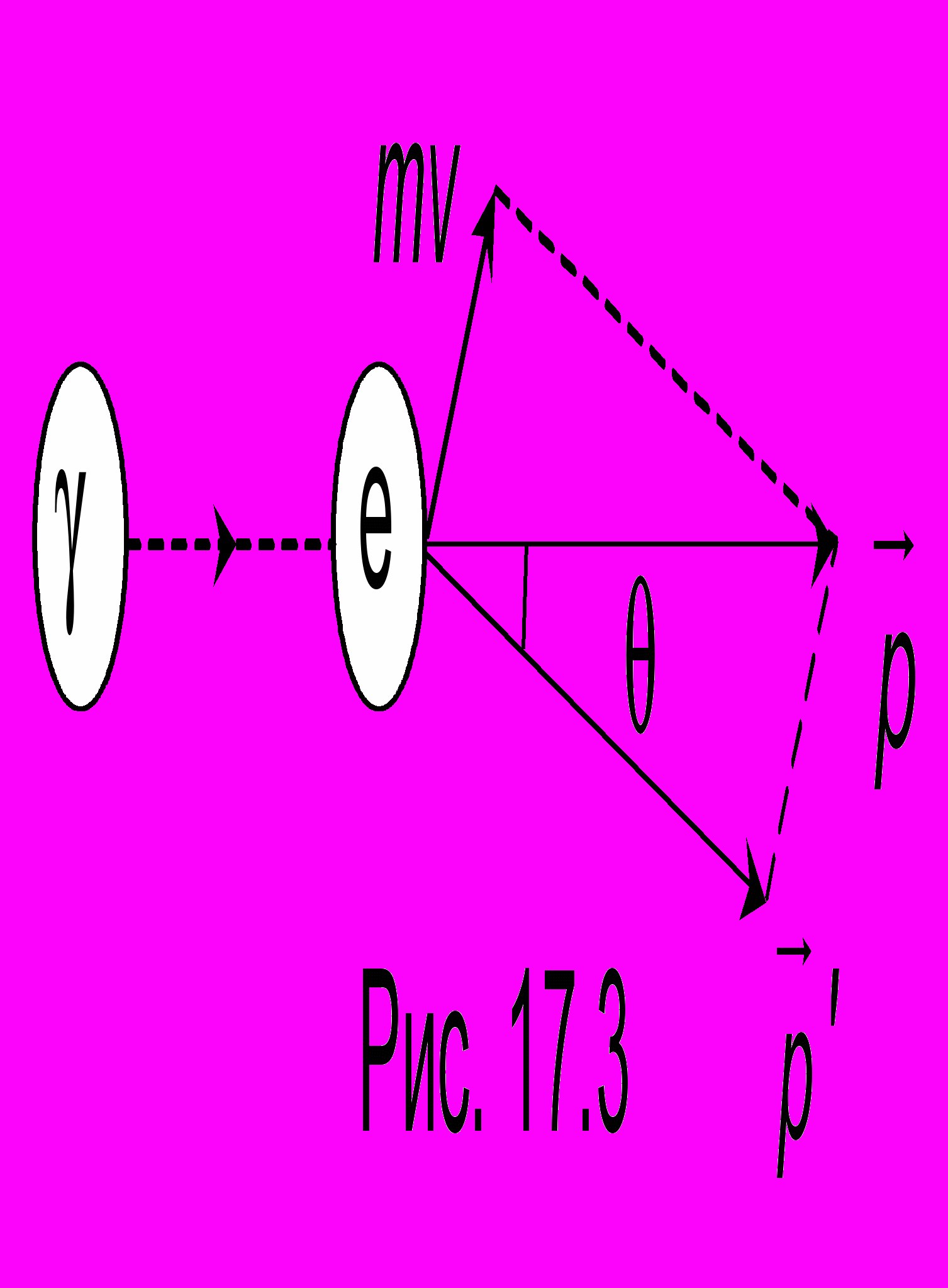
окоившийся прежде электрон отскакивает в сторону со скоростью V. Так как эта скорость велика, то масса электрона после удара определяется релятивистским соотношением 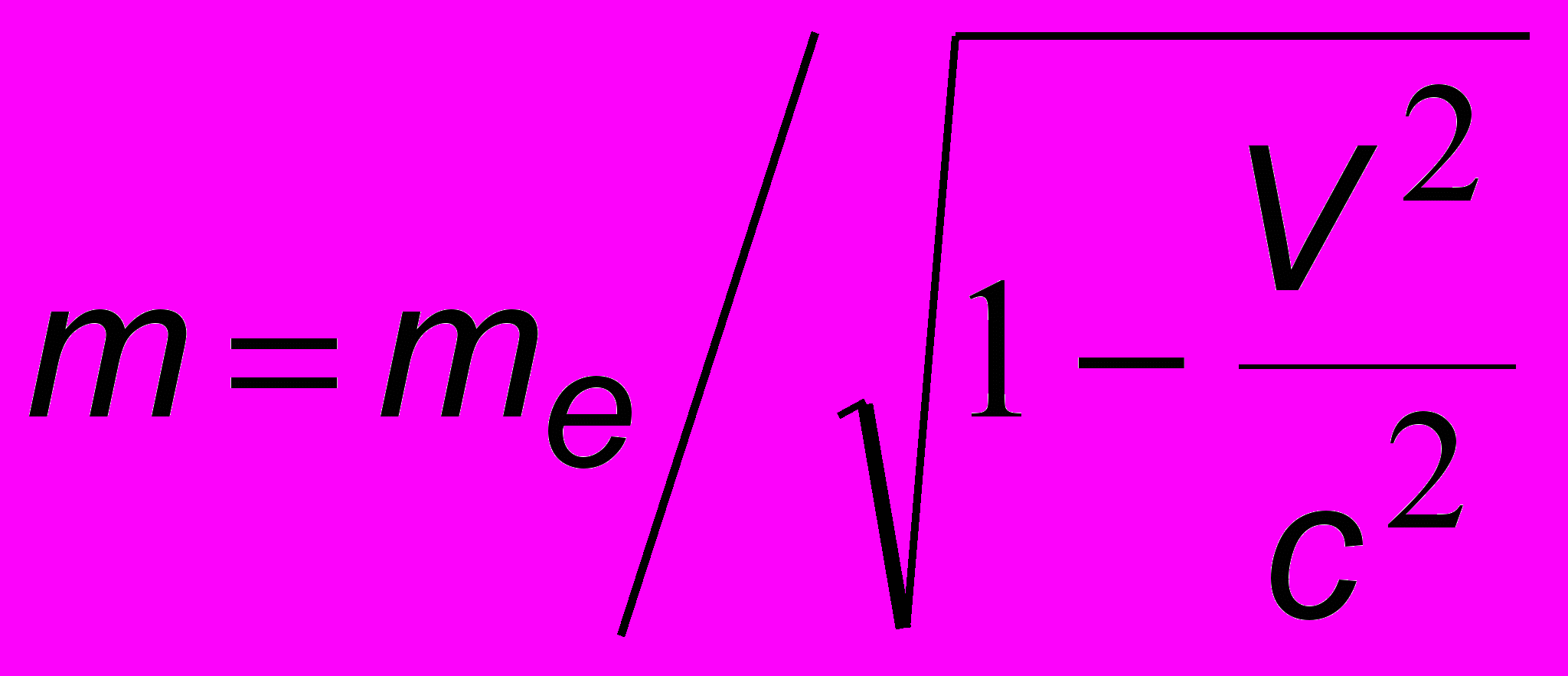. В этой вполне механической задаче, похожей на задачу об ударе бильярдных шаров, следует иметь в виду, что фотон движется с скоростью света с, и в этом случае его импульс выражается через его энергию по формуле (7.4) части 1: p = E_ /c = h/с. Соответственно для рассеянного фотона p' = E_'/c = h'/с. Законы сохранения энергии и импульса имеют вид: , где E = mc² - полная энергия электрона после соударения. Последнее векторное соотношение наглядно иллюстрируется чертежом на рис. 17.3 и может быть расписано в скалярном виде при помощи теоремы косинусов. Получим систему уравнений: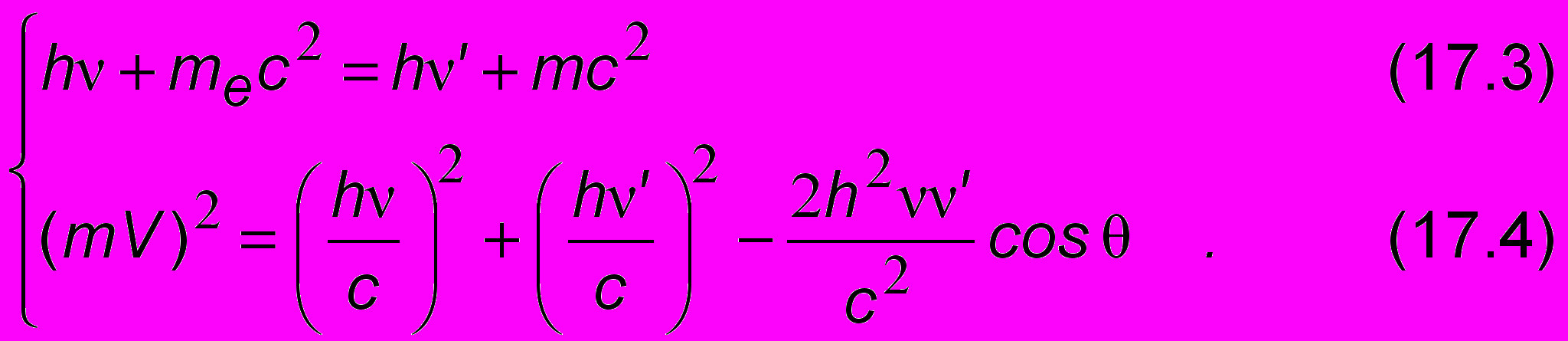




Перенося h' в (17.3) в левую часть и возводя в квадрат, получим

m ²с ⁴ = h ²² + h ²'² - 2h ²' + m_e ²c ⁴ + 2hm_ec ²( - '). (17.5)

Приводя (17.4) к общему знаменателю и вычитая результат из (17.5), получим m ²c ²(c ²- V ²)=m_e ²c ⁴-2h ²'(1- cos )+2hm_ec ²(-').

Поскольку ,

то h'(1-cos) = m_ec²(- ').

Подставляя  = с/ и ' = c/', получим следующее основополагающее соотношение:

,

то есть формулу Комптона (17.2).

Идея о существовании "частиц света" - то самое новое, что является хорошо забытым старым. Этой идеи придерживались античные атомисты во главе с Демокритом (V в. до н.э.), а также Ньютон. Однако с начала XIX века, с первых интерференционных опытов Юнга и Френеля активно начала развиваться волновая концепция, согласно которой свет имеет волновую природу.

Интересно, что эту же точку зрения, по-видимому, разделял Эйлер (1707 – 1783), считавший свет колебаниями эфира, и его современник Ломоносов (1711-1765), который писал: "Вокруг алмаза можно поставить тысячу свечей, так что тысяча пучков света будут пересекать друг друга и при этом ни один луч не будет мешать другому...".

К концу XIX века почти не оставалось сомнений, что свет - электромагнитные волны. Однако позже один за другим стали появляться подтверждения корпускулярной¹ теории, согласно которой свет - частицы. Поместим в одну колонку таблицы эксперименты в пользу волновой теории, а в другую - в пользу корпускулярной.


Таблица

В пользу волновой теории	В пользу корпускулярной теории
Интерференционные явления, опыты Юнга и Френеля	Фотоэффект
Дифракция	Теория теплового излучения
Голография	Эффект Комптона
Поляризация
Эффект Допплера
Давление света

Давление света, открытое в 1899 г. Лебедевым² на уникальной экспериментальной установке в виде вертушки, сначала объяснили с позиций корпускулярной теории, получив формулу, подтвержденную результатами эксперимента, а затем та же самая формула была получена с помощью волновой теории! Какова же современная позиция по этому вопросу? Какая теория справедлива? И та, и другая. В различных ситуациях свет может проявлять и корпускулярные, и волновые свойства. Такая двойственность поведения называется корпускулярно-волновым дуализмом. Ему есть аналог в христианской религии: троица есть не что иное как существование Бога в трех ипостасях - Отец, Сын и Святой Дух, которые образуют неразрывное триединство.

Теория де-Бройля (1924) есть попытка создания мостика между корпускулярными и волновыми свойствами. Так как импульс фотона p = E/c, а энергия по Планку E = h = hc/, то  = h/p. Луи де-Бройль обобщил эту идею на все микрочастицы. Поэтому, согласно его гипотезе, микрочастице с массой m, и скоростью V соответствует длина волны порядка 1 Å, определяемая по формуле

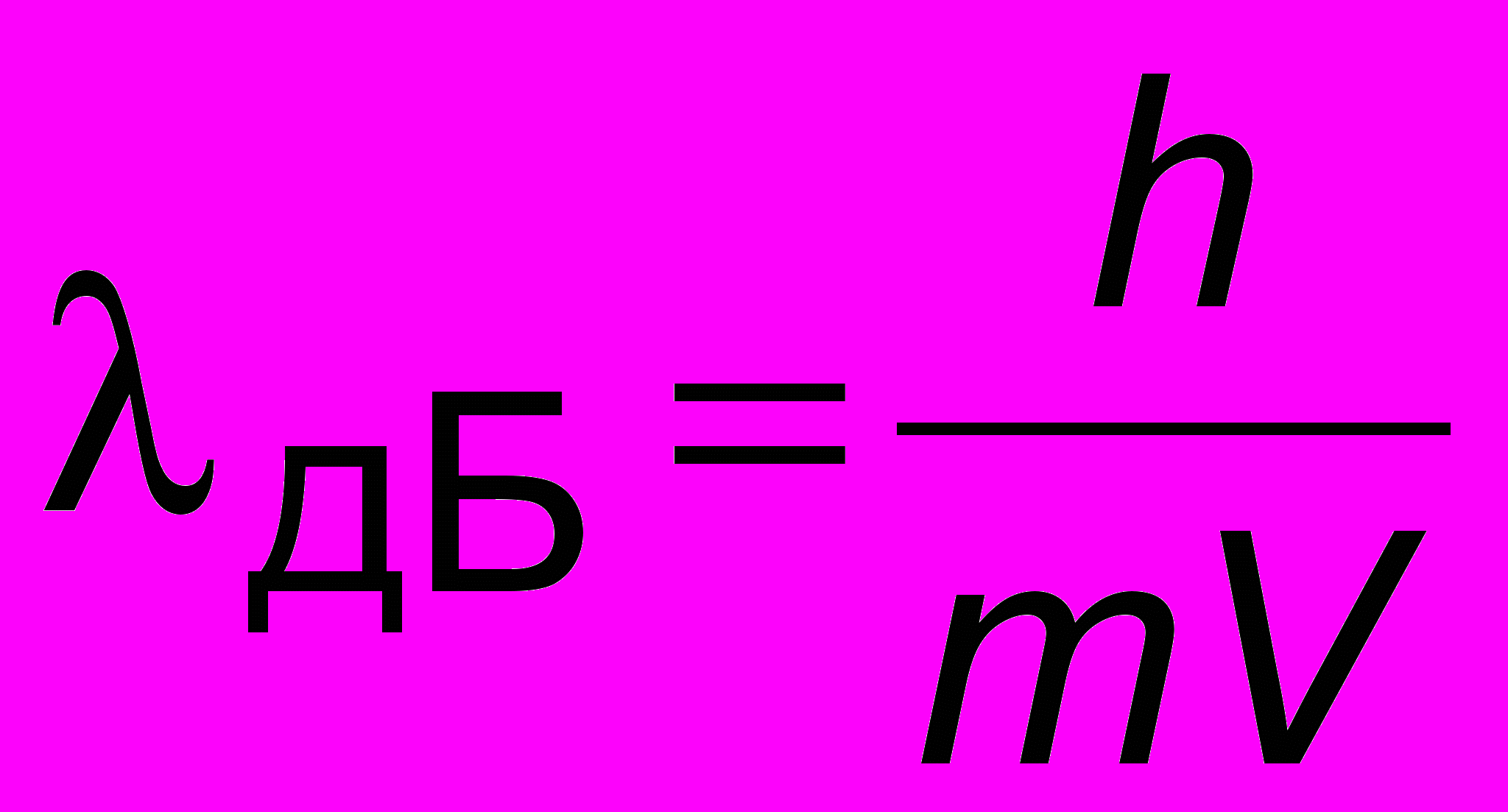. (17.6)

Это и есть тот самый мостик: слева длина волны - чисто волновой параметр, а справа импульс - параметр механический.

В 1927 г. Дэвиссоном и Джермером, а позднее и другими физиками (из советских - Тартаковским и Фабрикантом) были поставлены опыты по взаимодействию пучка электронов с естественными кристаллическими периодическими структурами. Результатом такого взаимодействия явилась дифракционная картина, полученная на фотопластинке, с максимумами и минимумами, положение которых определяется углом дифракции и длиной волны излучения по формуле (14.1), куда следует подставить де-Бройлевскую длину волны (17.6). Таким образом, электроны, поначалу ведущие себя как частицы, попадая на кристалл, начинают вести себя как волны, образуя привычную дифракционную картину.

Согласно де-Бройлю частице можно поставить в соответствие плоскую волну (x,t) = Acos(t - kx) c волновым числом k = 2/_дБ.

Если в классической физике можно совершенно определенно говорить о том, как поведет себя камень, брошенный под углом к горизонту, то в квантовой физике, описывающей поведение микрочастиц, этого делать, как оказалось, нельзя.

Камень (несмотря на то, что размерами его можно пренебречь и рассматривать его как материальную точку) имеет вполне определенную траекторию, определенные импульс и координату. Он четко локализован, и движение его предсказуемо. Волна в точке находиться не может. Поэтому не может быть определенности в поведении микрочастицы. В этом и заключается основное различие между классической и квантовой физикой, математическим выражением которого является принцип неопределенности Гейзенберга (1927 г.), который утверждает принципиальную невозможность точного одновременного определения импульса и координаты микрочастицы. Согласно этому принципу координаты x, y, z и соответствующие проекции импульса p_x, p_y, p_z имеют как бы "допуски"³, а точнее, неопределенности, связанные соотношениями

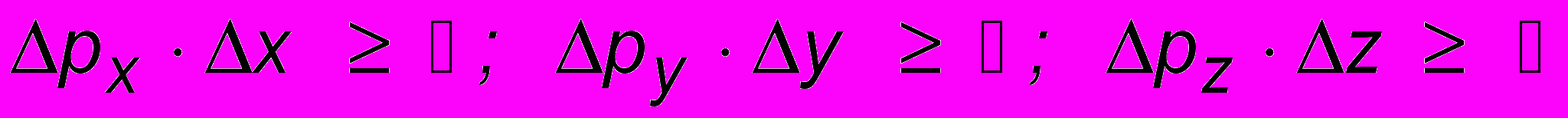. (17.7)

Таким образом, постоянная Планка определяет возможный предел точности одновременного измерения этих величин. Не следует, однако, полагать, что эта неопределенность вызвана несовершенством приборов, которыми пытаются вести измерения в микромире. Допуски при изготовлении детали на станке действительно связаны с неидеальностью макроскопической техники, но соотношения неопределенности - это проявление внутренней природы микромира.

Упростить сложный математический аппарат квантовой механики можно с помощью несуществующих для бухгалтерий, но очень удобных для физики комплексных чисел z, состоящих из действительной (Re) и мнимой (Im) частей: z = Re + i Im, каждая из которых является самым обыкновенным числом, а i = - формальность. Число z* = Re - i Im называется комплексно сопряженным. Учитывая, что
i ²= -1, получим zz*= (Re + i Im)( Re - i Im) = (Re)²+(Im)² = |z|² .

Есть еще и тригонометрическая форма комплексного числа, задаваемая формулой Эйлера:

, где Re =  cos, Im =  sin,  = |z|. (17.8)

Oперации над комплексными числами проще, чем умножение тригонометрических функций. Иначе говоря, вместо волны (x,t) = Acos(t - kx) можно писать

(x,t) = A 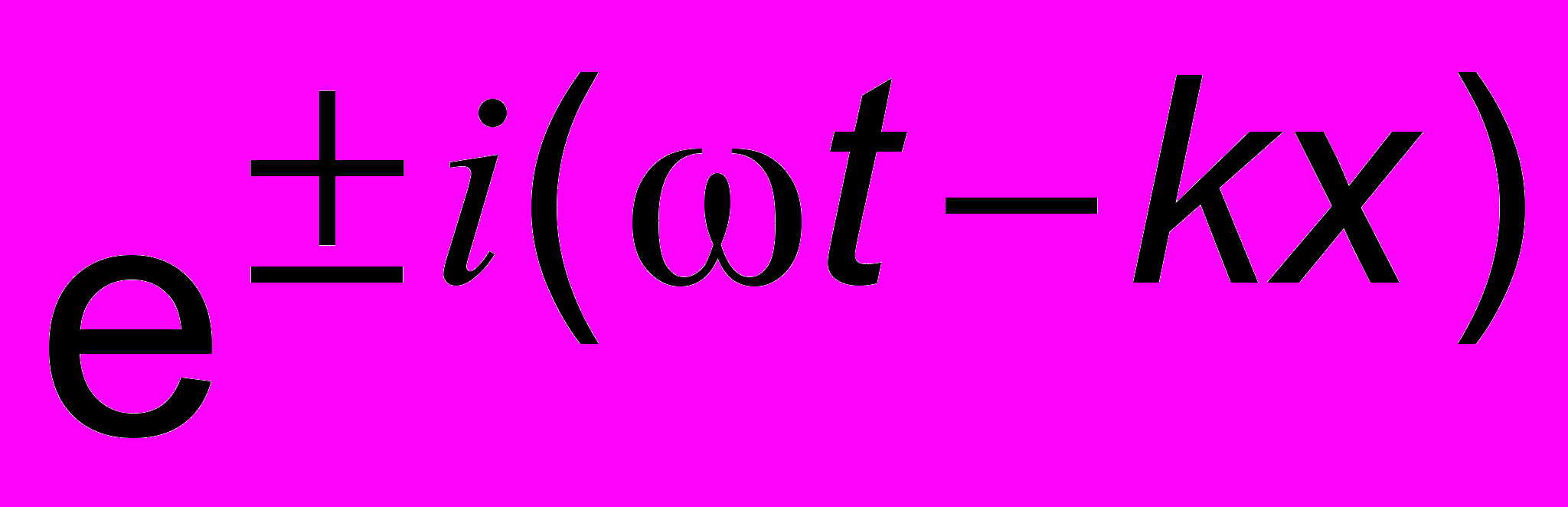(17.9)

и делать далее различные математические операции, а в конце концов отделить от полученного выражения действительную часть.

Волновая функция  = (x,y,z;t) играет в квантовой механике очень важную роль; квадрат её модуля является мерой вероятности нахождения микрочастицы в некотором заданном объеме пространства. Пусть, например, в некоторой комнате объемом V имеется микрочастица, состояние которой описывается функцией . Тогда вероятность обнаружить эту частицу в пределах малого элемента объема dV равна

dW = ||²dV. (17.10)

Это свойство волновой функции - самое важное. Рассмотрим еще несколько главных свойств -функции:

• Интеграл, взятый по всему объему пространства, где находится частица:
  

. (17.11)

Он называется условием нормировки волновой функции и соответствует достоверному событию обнаружить частицу где-нибудь в пределах данной комнаты. (Если известно, что частица в ней есть, то вероятность того, что она где-то да находится равна 100%.) Сама же величина ||², являющаяся интенсивностью волны де-Бройля, называется плотностью вероятности.

• Если частица способна находиться в состоянии, описываемом функцией _1, и в другом состоянии, описываемом функцией ₂, то она может находиться и в состоянии с функцией  = С₁₁ + С₂₂ , где С₁, С₂ - константы. (И вообще, можно взять сколько угодно волновых функций: 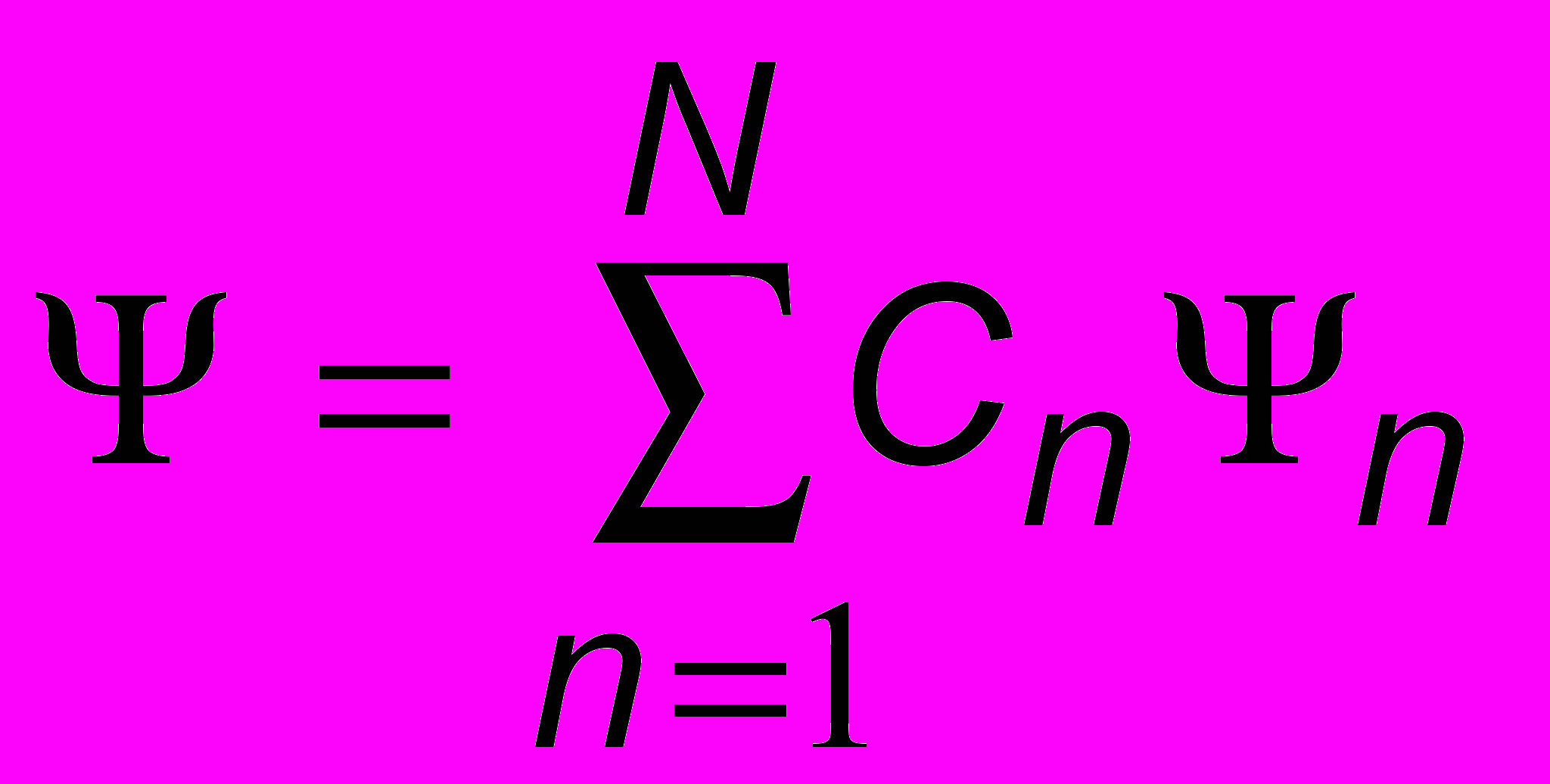- принцип суперпозиций волновых функций.)
  
• Среднее значение некоторой физической величины 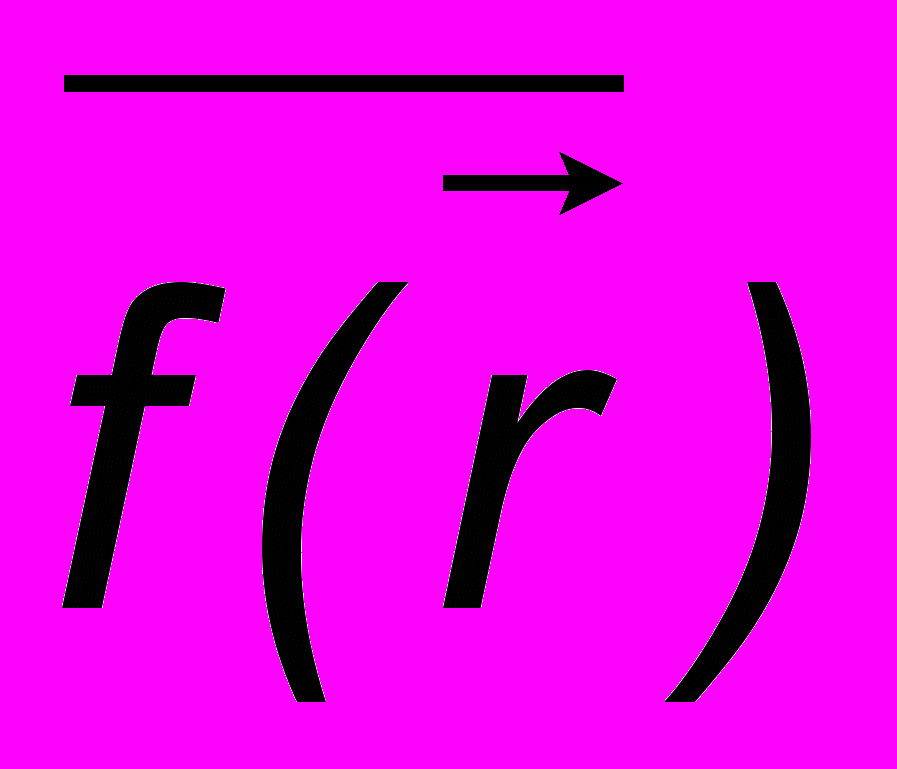равно .
  

Постепенно становилось ясным, что для волновой функции должно существовать универсальное уравнение, которое играло бы в квантовой механике такую же роль, какую в классической механике играет уравнение второго закона Ньютона. Таким уравнением явилось уравнение Шредингера.