Курс за второй семестр. Абстрактные типы данных
| Вид материала | Задача |
- Программа дисциплины программирование на языке С++ для направления 080700. 62 «Бизнес-информатика», 131.2kb.
- Методические указания для студентов 1 курса факультета математики, механики и компьютерных, 439.36kb.
- Курс биологи,1 семестр ) фен 26 ч. ((1 курс химики, 2 семестр 2 курс биологи, 2 семестр, 45.56kb.
- Структура программы. Часть Структуры данных. 24. Классификация структур данных. Операции, 41.26kb.
- Курс лекций "Базы данных и субд" Ульянов В. С. Лекция Язык sql. Создание таблиц и ограничений, 146.46kb.
- Borland Turbo Pascal, знать простые основные алгоритмы работы с простыми типами данных, 316.19kb.
- Курс, 1 поток, 5-й семестр лекции (34 часа), экзамен, 52.85kb.
- Программа дисциплины Анализ данных средствами ms excel для направления 080102. 65 Мировая, 121.98kb.
- Крыштановский А. О. Анализ социологических данных, 34.07kb.
- Пояснительная записка, 258.04kb.
Деревья поиска.
Задача поиска значения по ключу существенно более простая: в бинарном дереве – это идея дихотомического поиска. Продолжим эту идею на обратную задачу.
Бинарное дерево называется деревом поиска, если для каждой вершины дерева слева от него хранятся меньшие, а справа – большие значения в некотором порядке на типе хранимых значений.





Procedure Dpoisk (root:pNode;x:tInfo;var pt:pNode;var found:boolean);
Begin
found:=false;
pt:=root;
while not found and (pt<>nil) do
begin
if pt.info=x then found:=true
else
if pt.info>x then pt:=pt.left
else pt:=pt.right;
end;
end;
Замечание. Данный поиск будет действительно дихотомическим, если исходное дерево полное (идеально сбалансированное).
Включение в дерево поиска.
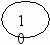
В

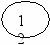




 ключим 13 в дерево.
ключим 13 в дерево. Procedure Vstavka(var root:pNode;x:tInfo);
var found:boolean;
begin
pt:=root;
found:=false;
while not found and (pt<>nil) do
begin
if pt.info…
Аналогична задаче поиска, но сохраняет ссылку на предыдущую вершину pt.pred:pNode. Как только pt=nil – pt.pred – ссылка на вершину, после которой надо вставить данное значение.
Завести дополнительную ссылку pt.pred, указывающую на последнюю пройденную вершину.
pt.pred:=pt;
Когда pt=nil pt.pred указывает на нужный элемент, то есть pt.pred указывает на вершину, после которой нужно вставить вершину.
Упражнение: завершить реализацию вставки в дерево поиска. Построить дерево поиска.
Тривиальное решение: создать из первого элемента входной последовательности корень, затем, пока не кончилась входная последовательность, включать очередной элемент в построенное к этому шагу дерево.
К сожалению, предыдущее решение не строит сбалансированное дерево. Вставка с сохранением сбалансированности – сложная задача (в этом случае используются специальные типы деревьев). Хотя задача построения сбалансированного дерева не столь сложна:
1) Найти среднее значение во входной последовательности и сделать его корнем дерева.
2) Сделать то же для всех элементов, меньших корня (левое поддерево) и больших корня (правое поддерево).
Формулировка алгоритма рекурсивная. (см. Рекурсия)
Другие обходы дерева. Обход в ширину.
Есть задачи, в которых порядок обхода важен. В задаче о вычислении нижние вершины должны быть обработаны раньше, чем верхние.


 Л П
Л П




 К<Л<П Л П К - корень КЛП-обход
К<Л<П Л П К - корень КЛП-обходПорядок обработки: корень, левая ветка, правая ветка.
ЛПК-обход – задача о вычислении (ПЛК).
Обход КЛП даёт самую простую спецификацию обхода дерева.
1) КЛП – наиболее важный (см. Рекурсия).
2) Обходы “в ширину”, то есть такие порядки, в которых последовательности одинаковой длины соседствуют друг с другом (сгруппированы).
Задача. Найти в дереве вхождение заданного значения от ближайшего корня.
Procedure Поиск_в_ширину (root:pNode;x:tInfo;var found:boolean;var pt:pNode);
var level:{последовательность вершин одного уровня};









Л П
Л П
Begin
found:=false;
put(level,root);
while {не кончились уровни} and not found and level<>0 do
begin
{искать на текущем уровне нужные значения}
{обеспечить доступ на следующий уровень}
while not {кончились вершины уровня} and not found and level<>0 do
begin
get(level,pt);
{достать текущую вершину уровня}
if pt.info=x then found:=true
else begin
if pt.left<>nil then put(newlevel,pt.left);
ifpt.right<>nil then put(newlevel,pt.right);
end;
level:=newlevel;
end;
end;
end;
Структура tLevel – последовательность (динамическая) с двумя операциями – get и put и проверка пустоты. В данном случае неважно, стек это или очередь.
Другой вариант того же алгоритма:
uses Queue;
var q:tQueue;
begin
put(q,root);
found:=false;
{q содержит ссылки на все не пройденные вершины списка}
while not empty(q) and not found do
begin
get(q,pt);
if pt.info=x then found:=true
else begin
if pt.left<>nil then put(q,pt.left);
if pt.right<>nil then put(q,pt.left);
end;
end;
end;
Это непременно очередь. Потомки текущей вершины должны обрабатываться после всех вершин текущего уровня.
Рекурсивные процедуры и функции.
Примеры применения.
Паскаль допускает обращение функции внутри её определения (прямая рекурсия), либо обращение друг к другу двух или более определяемых функций – процедур (косвенная рекурсия).
Многие алгоритмы и структуры данных рекурсивно формируются просто. В частности, графы и деревья просто определяются рекурсивно и соответственно этому функции их обработки.
Граф называется деревом, если он имеет вид:
 - вершина.
- вершина. 



- деревья
Пример: Рекурсивный вариант обхода дерева.
procedure Print(root:pNode);
begin
if root<>nil then
begin
write(root.info);
print(root.left);
print(root.right);
end;
end;
КЛП-обход, в случае дерева-выражения получим префиксную запись выражения.
Аналогично можно получить ЛПК и другие порядки, например, инфиксную и постфиксную записи выражения.
Рекурсивная версия задачи о вычислении:
function ExpVal(root:pNode;VarVal:tVarVal:integer);
begin
if term(root) then result:=TermVal(root);
else begin
result_1:=ExpVal(root.left,VarVal);
result_2:=ExpVal(root.right,VarVal);
result:=AtomVal(root.info,result_1,result_2);
end;
end;
Поиск в дереве.
procedure Poisk(root:pNode;x:tInfo;var found:boolean;var pt:pNode);
begin
found:=false;
if root.info=x then
begin
found:=true;
pt:=root;
end
else if root.left<>nil then Poisk(root.left,x,found,pt)
else if not found and root.right<>nil then
Poisk(root.right,x,found,pt);
end;
end;
Поиск в дереве поиска:
procedure Poisk(root:pNode;x:tInfo;var found:boolean;var pt:pNode);
begin
if root=nil then found:=false
else if root.info=x then
begin
found:=true;
pt:=root;
end
else if x
else Poisk(root.right,x,found,pt);
end;
Пример с факториалом:
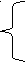
1, n=0
fact(n)=
fact(n-1)*n, n>0
function fact(n integer):longint;
begin
if n=0 then fact:=1
else fact:=n*fact(n-1);
end;
Проблемы с семантикой рекурсии.
В случае не рекурсивных вызовов семантика обращений строилась с помощью замены обращения модифицированным телом процедуры. Фактически мы описывали её (семантику) как построение некоторого выражения – программы на базовом Паскале. Этот способ работал и для кратных обращений.
Использование процедуры процедурой:
P
P1
P2

 Чётко выделялись два этапа:
Чётко выделялись два этапа: 1) Построение выражения;
2) Его вычисление.
В этом случае такое дерево не может быть построено.
Вспомним алгоритм вычисления выражения. Как показал наш анализ, для того, чтобы вычислить значение выражения, необязательно строить его полностью. Более того, мы не обязаны для этого обходить всё дерево.
Пример: Если значение левого терма – ноль, а операция у нас – умножение, то значение правого терма вычислять не нужно.
Любая рекурсия связана с последовательным построением и вычислением выражения. Действительно, в любом случае можно считать, что рекурсивный вызов выполняется в случае истинности некоторого условия. При каждом рекурсивном вызове вычисляется выражение, и дерево достраивается лишь в случае его истинности.
Таким образом, любой рекурсивный алгоритм эквивалентен построению и обходу некоторого дерева.
P1
P1
P2
P1
P2
P2

 1 2 B1+ B2+ if B1 then P1 if B2 then P2
1 2 B1+ B2+ if B1 then P1 if B2 then P2 1 2 2
B1+ B2+ B2+
В случае двух вызовов получаем бинарное дерево.
КЛП-обход или стековый обход.
Описали семантику рекурсии с помощью циклов. Теоретически возможно описание семантики циклов через рекурсию.
 S, B(s)=false
S, B(s)=falsewhile B do S(s)
S, while B do S, B(s)=true
Теоретически можно программировать без циклов в терминах лишь рекурсии.
Функциональным программированием называется программирование в терминах рекурсивного определения функций. Логическим программированием: языки основаны на рекурсивном определении булевых функций.
Введение в машинно-ориентированное (ссылочное) программирование.
Оператор Goto.
Синтаксис: goto k, где k – метка (имя, указатель) на некоторый оператор программы, соответствующее обозначение оператора. Выглядит как k:S.
В стандартном Паскале метками могут являться натуральные числа (не связаны с характером выполняемых действий). Все метки обязаны быть объявлены в программе в специальной области label. В стандартном Паскале это самая первая область объявлений, то есть до const.
Неформальная семантика: «Я нарушаю естественный ход выполнения программы, после меня выполняется не следующий оператор, а оператор, помеченный соответствующей меткой».
Создание новых структурных операторов.
Разбор случаев (нечто вроде case):
B1:S1;
…….
Bn:Sn
иначе Sn+1
где Bi – условие (предикат), Si – оператор.

S1


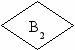
S2


Sn
Sn+1



if B1 then S1;
goto 1;
if B2 then S2;
goto 1;
…………..
if Bn then Sn
else Sn+1
1:
Другой вариант: вложенный if.
c:char;
read(c);{чтение цифры}
if not c in [‘0’..’9’] then
begin
write(‘ожидалась цифра’);
goto 1;
end;
1:end;
Все подобные естественные использования goto в развитых языках программирования возлагаются на новые операторы с отличным синтаксисом.
Третий пример: программирование неструктурных алгоритмов.
while uslovie1 and uslovie2 do
begin
{что-то}
{проверка условия uslovie1}
if not uslovie1 then goto 1;{побочный выход из цикла}
{проверка условия uslovie2}
end;
В целом использование goto свидетельствует о плохом стиле программирования.
Формальная семантика goto и неструктурных программ.
Оператор goto не изменяет пользовательские переменные. В реальности goto изменяет системную переменную, счетчик команд, содержащую указатель (метку, имя, адрес) следующего в порядке выполнения оператора.
В
 терминах блок-схем goto – это просто стрелка.
терминах блок-схем goto – это просто стрелка. Такая семантика даёт возможность точно определить семантику произвольных блок-схем. Пусть блок-схема B содержит n блоков S1,…,Sn. Неявно мы ввели нумерацию блоков (вместо индексов подошли бы любые иные указатели). Наша задача: построить структурную блок-схему, функционально эквивалентную данной.
Procedure StrucruredB ( );
var BlockName: tBlockName; {указатель на выполняемый блок}
bool:boolean;{значени текущего условного блока}
BlockEnd:tBlockName;{ещё один указатель на блок}
{этих переменных нет в исходной блок-схеме}
begin
BlockName:=cFirstBlockName;{указатель на кружок «н»}
while BlockName<>cLastBlockName {указатель на кружок «К»}do
begin
{Разбор случаев – для каждого операторного блока два случая}
BlockName=ThisBlock : SThisBlock;
BlockName:=ThisBlockEnd;
BlockName=ThisBlockName : BlockName:=NextBlockName;
{метка оператора следующего блока}
{С каждым условным блоком связываем 3 случая}
BlockName=ThisBlock : Bool:=BThisBlock;
BlockName:=ThisBlockEnd;
BlockName=ThisBlockEnd and Bool=true : BlockName:=PlusBlockName;
{
 метка на блок, на который указывает стрелка + }
метка на блок, на который указывает стрелка + }BlockName=ThisBlockName and Bool=false : BlockName:=MinusBlockName;
end;
end;
Данная программа пошагово эквивалентна исходной.
Наши рассуждения фактически доказываю более сильные утверждения:
1) Любая программа может быть записана с единственным циклом и единственным разбором случаев. Такая форма программы называется нормальной.
2) Этот переход можно осуществить алгоритмически – написать интерпретатор блок-схем, который по произвольной блок-схеме (для него – входные данные) исполняет алгоритм, описанный этой блок-схемой.
Procedure Structure(B:tFlowChart);
Упражнение*. Сделай это! ;)
В теории программирования этот результат называется теоремой об универсальной функции (теоремой о существовании компьютера).
Каковы же минимальные средства программирования? Сколько операторов, типов данных, переменных и так далее должен содержать язык программирования, чтобы на нём можно было написать любую программу?
Для прояснения этого вопроса создадим искусственный машинный язык с «паскалеобразным» синтаксисом.
