Курс за второй семестр. Абстрактные типы данных

Вид материала

Содержание

Записи типов с вариантами.
Создание дерева. Перевод из префиксной записи.
Анализ алгоритма вычисления.
Задача синтаксического анализа.
Шаблоном атома
Формальным вычислением
Раздельное описание абстрактных типов.
Проблема с кратным использованием модулей.
Деревья как структуры данных.

Подобный материал:

1 2 3 4 5 6 7 8

Различные объединения типов.

Записи типов с вариантами.

Синтаксис: список полей есть выражение вида

L=N₁:T₁,…,N_m:T_m.

где N_i – список идентификаторов

T_i – произвольный тип, кроме файла.

record

L

end;

Общий синтаксис типа record:

record

L₀ {Знакомый нам синтаксис – общая часть записи. В любой переменной данного типа присутствуют поля из этого списка}

case S:T_s of

c₁:(L₁); Поле S типа T_s также присутствует во всех значениях типа.

. . .

c_m:(L_m); вариантная часть записи

end; S – селектор

end;

c₁,…,c_m – значения типа T_s

Предполагается, что в значении данного типа присутствуют лишь поля одного из списков L_i в зависимости от значения поля S.

* x.S=c_i 

x:record

L₀, S : T_s: L_i

end;

N₁ N₂ N₃

type

tInfo=record

case этоInteger:boolean of

true: (IntInfo:integer);

false: (CharInfo:char);

end;

end;

Условие * не проверяется автоматически.

x.этоInteger:=true;

write(x.CharInfo);

Примечание. Записи с вариантами хороши для объединения нескольких явно заданных типов, но не для описания всех типов, например, всех типов, обладающих каким-либо свойством.

Пример: невозможно параметрическое определение типа: stack of T.

Создание дерева. Перевод из префиксной записи.

Представление записи.

Дан текстовый файл exp, содержащий правильно построенное выражение.

Требуется создать дерево:

((x+1)*y)/2

/*+x1y2

Пока в выражении идут имена функций идём налево.

Натыкаемся на старую проблему: нужно вернуться на предыдущую вершину.

Р

ешение: сохранять ссылки на вершины со свободным правым концом в стеке.

procedure Create(var exp:text;var root:pNode);

var stack:tStack {Стек ссылок на вершины}

c:char;

begin {Корень создаём отдельно}

reset(exp);

read(exp,c);

root:=NewNode(c); {Создаём вершину с содержимым атрибутом c}

push(stack,root);

while not eof(exp) do

begin

read(c);

while c in [‘+’ , ’-‘ , ’/’ , ’*’] do

begin

pt.left:=NewNode(c);{Ссылка на текущую вершину дерева}

pt:=pt.left;

push(stack,pt);

read(exp,c);

end;

pt.left:=NewNode(c);

read(exp,c);

pop(stack,pt);

pt.right:=NewNode(c);

pt:=pt.right;

end;

end;

Анализ алгоритма вычисления.

Дерево как последовательность ветвей.

Дано выражение в текстовом файле. Вычислить значение выражения.

Дерево – естественная форма представления выражений, но неэффективно по расходу памяти. Если алгоритм сводится к последовательной обработке компонент некоторой последовательности в естественном порядке, не нужно держать в памяти всю последовательность. В алгоритме вычисления в каждый момент времени используются сведения лишь об одной ветке дерева (ссылка на которую хранится в стеке).

function NewNode(c:char):pNode;

var NewPt:pNode;

begin

new(NewPt);

pt.info:=c;

pt.left:=nil;

pt.right:=nil;

end;

type

tInfo=record

case этоInteger:boolean of

true (IntInfo:integer);

false (CharInfo:char);

end;

end;

function ExpVal(var exp:text;VarVal: tVarVal):integer;

var stack:tStack; {tStack of tInfo}

begin

create(stack); {Стек символов}

ReadChar(exp,f);

ReadChar(exp,x);

push(stack,f);

push(stack,x);

while not eof(exp) do

begin

{Пока не нашли атом, читай символы и складывай в стек}

pop(stack,x);

pop(stack,f); {/*+x1y2}

ReadChar(exp,c);

while not Atom(f,x,y) do

begin

push(stack,f);

push(stack,x);

push(stack,y);

pop(stack,f);

pop(stack,x);

pop(stack,y);

end;

push(stack,AtomVal(f,x,y));

end;

pop(stack,x);

ExpVal:=x.IntInfo;

end;

Мы упоминали об относительности взгляда на структуры (деревья, графы) как на структуры данных и структуры управления. То, что раньше мы воспринимали как структуру данных (в первом алгоритме), стало трассой вычисления.

Задача синтаксического анализа.

На первый взгляд эта задача кажется совсем не похожей на задачу о вычислении. В реальности это практически та же задача.

Дана произвольная символьная последовательность. Выяснить, является ли она правильно построенным выражением.

/*+x1y2 – true

-*+x1y23 – false

Шаблоном текста c₁,…,c_n назовём текст c₁^|,…,c_n^| , где

‘t’, c_i – терм

c_i^|= ‘f’, c_i – знак операции

‘’, c_i – чужой (посторонний) символ.

Шаблоном атома назовём строку c₁,c₂,c₃. Это либо строка f,t,t, где c₁=f, c₂=t, c₃=t, либо хотя бы один их них равен .

Формальным вычислением назовём переход от шаблона атома c₁,c₂,c₃ к символу ‘t’ в случае ftt, либо к символу ‘’ во втором случае. (?)

Последовательность есть выражение, если его можно преобразовать формальным вычислением к символу ‘f’.

procedure ReadMask(var exp:text;var m:char);

{Определение шаблонов атомов}

begin

if eof(exp) then m:=’’

else

begin

read(c);

if c in [‘+’ , ’-‘ , ’/’ , ’*’] then m:=’f’

else if c in [‘a’..’z’]+[‘0’..’9’] then m:=’t’

else m:=’’;

end;

end;

function CorrectExp(var exp:text):boolean;

begin

reset(exp);

create(stack);

ReadMask(exp,f);

push(stack,f);

b:=(f<>’’) and (f<>’t’) or eof(exp);

ReadMask(exp,x);

push(stack,x);

b:=b and (x<>’’);

while b and not eof(exp) do

begin

pop(stack,f);

pop(stack,x);

ReadMask(exp,y);

while not AtomMask(f,x,y) do

begin

push(stack,f);

push(stack,x);

push(stack,y);

pop(stack,x);

pop(stack,f);

ReadMask(exp,y);

end;

result:=AtomMaskVal(f,x,y);

push(stack,result);

b:=result<>0;

end;

CorrectExp:=(x=’t’) and empty(stack);

end;

Графы-выражения.

(x+1)*(x+1)²+(x+1)*x

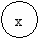
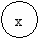
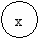
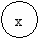
Дерево хранит многократно каждое вхождение, но не собственно выражение.

Ациклический граф.

Такие графы соответствуют выражениям

частичного порядка.

Задача вычисления выражения, представленного графом, аналогична случаю дерева.

Подзадача «поиск атома, значения атома» аналогична. Но уничтожить терм теперь можно лишь в случае, когда на него нет других ссылок.

способ – хранить обратные ссылки и, в случае удаления, проверять, присутствуют ли они.
способ – хранить в каждой вершине счётчик ссылок на эту вершину. При каждом вычислении уменьшать значение счётчика. В случае равенства нулю – удалять вершину.

Упражнение. Завершить задачу о вычислении выражения.

* Преобразовать выражение из представления деревом в представление графом и обратно.

Раздельное описание абстрактных типов.

Модульное программирование.

Технологичное программирование предполагает определение абстрактных типов, важных для решения широкого круга задач, повторное использование. Такое использование можно осуществить копированием фрагментов программ, относящихся к определённым абстрактным типам. Такое решение порождает серьёзные проблемы их согласования при редактировании.

Паскаль предлагает более эффективное решение – выделить определение типов в отдельный (и даже отдельно проверяемый и транслируемый) файл или модуль. Фактически модуль представляет собой совокупность областей описания, относящихся к определённым типам. Но, в отличие от областей описания, в модуле чётко различаются интерфейс пользователя модуля (interface; перечень объявлений данных и операций над ними) и реализация (список их определений).

unit {имя модуля}; {заголовок}

В Дельфи имя модуля обязано совпадать с именем файла с расширением *.pas, содержащего текст этого модуля.

Interface {Объявление языковых объектов, констант, типов, процедур и функций, редко – переменных, доступных для пользователей модулей, то есть программ, включавших в свои определения предложение uses}

Объявление констант, типов и переменных совпадает со знакомым. Объявление процедур и функций содержит только их заголовок.

Implementation.

Определение процедур и функций в знакомом виде, объявление в интерфейсе, а также, возможно, и других языковых объектов, нужных для этого в отличие от объектов интерфейса последние недоступны пользователю модуля (скрытые или инкапсулированные), в отличие от функций интерфейса, который наследуется пользователем.

Программа, которая ссылается на модуль, ведёт себя точно так же, как программа, содержащая описание этого модуля.

[initialization] – перечень операторов, относящихся к инициализации или созданию объекта абстрактного типа.

[finalization] – последовательность операторов, относящихся к уничтожению объекта данного типа.

Программа, которая хочет получить доступ к интерфейсу модуля, содержит опцию uses.

Uses <логическое имя модуля> in <физическое имя модуля>

Unit stackunit;

Interface

Procedure Destroy(var top:pComponent);

Procedure Create(var top:pComponent);

Procedure Push(var top:pComponent;x:tInfo);

Implementation

{Определение процедур push, pop, empty, create, destroy}

Модули могут использовать друг друга. Типы можно описать либо в самом модуле, либо в используемом. Интерфейс и реализация могут ссылаться на разные модули.

type pComponent=tComponent;

tComponent=record

info:tInfo;

next:pComponent;

end;

Определение типа tInfo естественно выделить в определённый модуль, поскольку понятие стека логически не зависит от типа входящих в него элементов.

Проблема с кратным использованием модулей.

Концепция модульного программирования предполагает создание уже не одной программы (текстового файла), а проекта – иерархически связанной совокупности модулей.

unit

unit

program

uses

з
unit

unit

кщпкфь

Объекты в разных модулях могут называться одинаково, что порождает конфликт имён.

Деревья как структуры данных.

Как обычно, структуры данных мы ассоциируем с некоторым семейством функций: fIT, где I – некоторое множество “индексов” (указателей или ключей) со следующими основными операциями: выборка, поиск, вычисление значения по ключу, поиск ключа по значению (вычисление обратной функции), сохранение значения по ключу (переопределение функции в заданной точке), создание нового ключа (расширение области определения), удаление ключа (сужение области определения). Реализация всех этих операций связана с некоторым порядком перечисления ключей.

Дерево как структуру данных естественно рассматривать как функцию на путях, «словах».

Пример. Декодирование текста, записанного азбукой Морзе.

Центральная проблема: найти по коду Морзе его значение (букву в латинском алфавите).

Как хранить таблицу соответствий кодов и букв?

F={0,1}^*Last[‘a’..’z’]

…………….

1 1 1  ‘s’

0 0 0  ‘o’

…………….

0 1 1

Упражнение. 1) Завершить задачу декодирования.

2) Выяснить, сколько раз встречается каждое слово в тексте. Результатом должно быть [‘a’..’z’]^*Cardinal

3) Что за функция «дерево выражений»?

В применении к деревьям эта задача формулируется как задача обхода дерева в некотором или заданном порядке. Рассмотрим задачу на примере задачи поиска.

Procedure Poisk(root:pNode;x:tInfo;var key:pNode;var found:boolean);

Begin

found:=false;

pt:=root;

push(root);

while not found and {не кончились вершины} do

begin

pop(stcak,pt);

if pt.info=x then

begin

found:=true;

key:=pt;

end

else {перейти к следующему}

end;

if pt.left<>nil then

begin

push(stack,pt.right);

if pt.right<>nil then pt:=pt.left;

end

else if pt.right<>nil then pt:=pt.right;

end; {Завести стек и хранить в нём ссылки на ещё не пройденные вершины дерева, то есть правые ссылки пройденных на данном пути вершин}

Очевидно, порядок обхода – знакомый лексикографический порядок.

Blog

Курс за второй семестр. Абстрактные типы данных

Содержание