Курс за второй семестр. Абстрактные типы данных

Вид материала

Задача

Содержание Словарный порядок на последовательностях произвольной длины Переход к следующей раскраске при новом определении словарного порядка Статическая реализация стеков. Очереди. Статическая реализация. Get(q:tQueue;var x:T) Статическая реализация деревьев. Автоматы как структуры данных Статическая реализация графов. Проблема фрагментации памяти. Общая схема реализации автомата как списка. Обработка кучи. Динамическая реализация абстрактных типов ссылками.

Подобный материал:

• Программа дисциплины программирование на языке С++ для направления 080700. 62 «Бизнес-информатика», 131.2kb.
• Методические указания для студентов 1 курса факультета математики, механики и компьютерных, 439.36kb.
• Курс биологи,1 семестр ) фен 26 ч. ((1 курс химики, 2 семестр 2 курс биологи, 2 семестр, 45.56kb.
• Структура программы. Часть Структуры данных. 24. Классификация структур данных. Операции, 41.26kb.
• Курс лекций "Базы данных и субд" Ульянов В. С. Лекция Язык sql. Создание таблиц и ограничений, 146.46kb.
• Borland Turbo Pascal, знать простые основные алгоритмы работы с простыми типами данных, 316.19kb.
• Курс, 1 поток, 5-й семестр лекции (34 часа), экзамен, 52.85kb.
• Программа дисциплины Анализ данных средствами ms excel для направления 080102. 65 Мировая, 121.98kb.
• Крыштановский А. О. Анализ социологических данных, 34.07kb.
• Пояснительная записка, 258.04kb.

Словарный порядок на последовательностях произвольной длины

c₁…c_k  c₁^|…c^|_L, т.е.  i₀ (c_i0c_i0^| & ii₀ (c_i=c^|_I) or (i (c_i=c_i^|) and k
Технический приём: дополнить меньшее слово фиктивным элементом, например пробелом, наименьшим по определению.

Можно:=false;

Раскраска:=Первая раскраска; {<первый цвет>}

While (не кончилась раскраска) do begin

{Пустая раскраска – последовательность длины 0}

If правильная (раскраска) then if полная (раскраска) then begin

Можно:=true {печать (раскраска)}

Else {раскраска правильная, но не полная}

{дополнить} раскраска:=раскраска + первый цвет

else {возврат} раскраска:=succ(раскраска);

Переход к следующей раскраске при новом определении словарного порядка:

1. Выбрасывать все последние значения с конца последовательности до тех пор, пока не выкинем первый элемент, у которого есть следующий. Если такого нет, то раскраска кончилась.
   
2. Если раскраски не кончились, возвратить следующий за последним, выкинутым в раскраску.
   

Последовательность, из конца которой можно выкидывать и в конец которой можно добавлять элементы, называется стеком (stack).

Стеком называется абстрактный тип данных, множеством значений которого является множество всех последовательностей произвольной длины (динамический тип) элементов некоторого базового типа Т со следующими операциями:

1. Push ([x:tStack], y:T), х – имя стека – затолкнуть y в стек.
   

Семантика: x:=x+y (добавление элементов в конец последовательности)

2. Pop ([x:tStack]):T
   

If x=c₁…c_n then pop=c_n. Длина стека уменьшается на 1: x=c₁…c_n-1.

Попытка взять элемент из пустого стека считается ошибкой.

3. Empty ([x:tStack]):boolean; – стек пуст.
   

If Empty([x:tStack]){=true} then {длина стека равна нулю}.

4. Характерные для динамических типов операции Create([x:tStack]) и Destroy([x:tStack]) рассмотрим позднее.
   

Стеки также называют «магазинной» памятью.

Переход к следующей раскраске, если такой нет, то к пустой.


Procedure Новая (var раскраска:tStack);

Var x:tЦвет;

Begin

Pop(stack,x);

while not empty(stack) and (x=последний цвет) do pop(stack,x);

if not empty(stack) then push(succ(x));

End;


Дополнить раскраску=push(stack,первый цвет)

Кончились раскраски – empty(stack)

Упражнение. Завершить реализацию перебора с возвратом, написав процедуру «Правильная».

c₁…c_k+1 – правильная, то c₁…с_k – правильная.

i[1,k] (соседи(c_k,c_k+1))

раскраска(1)раскраска(k+1)

(Выходим за пределы стековых операций).


Статическая реализация стеков.

Стек – динамический тип данных – количество элементов, которое можно положить в стек, не ограничено (в идеале), но во многих случаях, в том числе в задаче о раскраске карты, известна максимальная глубина стека, то есть стек можно понимать статически. Стандартный приём оперировать с такими типами (абстрактными, но статическими) – моделировать их массивами и переменными стандартных типов.


top heap

  nMax

Куча

Type index=1..nMax{ };

T={базовый тип стека};

TStack= record

content:array[index] of T;

heap:index;{указатель на начало «кучи», первую свободную компоненту массива}

end;

procedure push(var stack:tStack;x:T);

begin

with Stack do

begin

content[heap]:=x;

inc(heap);

end;

end;


Реализация не защищена от ошибки – переполнения стека. Предполагается, что ситуацию контролирует пользователь.


Procedure Pop(stack:tStack;var x:T);

Begin

with stack do

begin

dec(heap);

x:=content[heap];

end;

end;


Снова незащищённая реализация: контроль за пустотой стека возлагается на пользователя.


Function Empty(stack:tStack):boolean;

Begin

empty:=stack.heap=1;

end;


Procedure Init(stack:tStack);{инициализация стека}

Begin

stack.heap:=1;

end;


Очереди. Статическая реализация.

Ещё один популярный абстрактный тип данных с простой реализацией.

Множество значений: все конечные последовательности t₁,…,t_n – значения некоторого типа T.

Операции: get и put

Put(q:tQueue;x:T) – поставить в очередь.

Семантика:

{q1,…,t_n>,xX}

{q1,…,t_n>,xX}

Get(q:tQueue;var x:T) – вывести из очереди.

Семантика:

{q1,…,t_n>,xX}

{q1,…,t_n-1>,xt_n}


function Empty(q:tQueue):boolean;

procedure Init(q:tQueue);

Семантика как у стеков.

Упражнение. Используя очередь, обратить файл (небольшой длины), то есть вывести его элементы в обратном порядке. Осуществить циклический сдвиг последовательности на заданное количество разрядов.

c₁c_2…c_k



c_kc₁…c_k-1

Реализация:

Const cStart=1;cFinish={максимальная длина очереди};

Type tIndex=cStart..cFinish;

T={ };

TQueue=record

content:array[tIndex] of T;

heap:index;

first:index;{указатель на первый элемент – начало очереди}

end;

procedure Put(q:tQueue;x:T);

Begin

with q do

begin

content[heap]:=x;

if heap
else heap:=cStart;

end;

end;

Реализация не защищена от переполнения.


Procedure Get(q:tQueue;var x:T);

Begin

with q do

begin

x:=content[first];

if first
else first:=cStart;

end;

end;


Статическая реализация деревьев.

Рассмотрим случай бинарных деревьев (остальные – аналогично).

1

о

2 3 Нумерация в ширину

о о

4 5 6 7

о о о о


const cEmpty=-1; {Признак отсутствия вершины}

type tNodeInfo={Атрибуты вершины и, если нужно, единственные исходящие из неё стрелки}

tIndex=0..nMax; {=2ⁿ, n-число уровней (поколений) дерева}

tTree=record

content=array[1..nMax] of tNodeInfo;

root:index;

end;

function Left(t:tTree;c:tIndex):tIndex;

{Найти индекс левого потомка}


Автоматы как структуры данных

Одни и те же структуры можно рассматривать как структуры управления, так и структуры данных. Основная функция графа как автомата – последовательный переход от одной (начальной) вершины к другой, обеспечение доступа к вершине. Все преобразования можно проводить только над доступными вершинами.

Возможные операции над доступными вершинами:

1. Чтение атрибутов вершины и исходящих из неё стрелок.
   
2. Запись новых атрибутов.
   
3. Добавить/удалить вершину (стрелку) (с пустыми атрибутами).
   

Понятие доступа продолжается и на возможность выполнения операций: доступ для чтения/записи и т.д. Понятие доступа обычно формулируется в терминах некоторого набора элементов (маркеров) или головок автомата, значениями которых служат вершины автомата и некоторые могут передвигаться в соответствие с (функцией переходов) определением автомата. Фактически мы пришли к знакомому понятию состояния. Поэтому вместо «состояния» используют понятие конфигурации автомата (чтобы не путать с вершинами).


Статическая реализация графов. Проблема фрагментации памяти.

Списочные структуры.

До сих пор в реализации абстрактных типов мы старались жёстко зафиксировать некоторую нумерацию компонентов этого типа, связав её с естественной нумерацией самого массива. Такой подход не позволяет эффективно реализовать характерные для динамических типов операции вставки и удаления компонентов. Это хронический дефект массивов даже в их основной роли – хранение последовательностей.

Упражнение. Написать процедуры вставки и удаления символа и слова в тексте.

Дилемма: Либо тратить на не имеющие логического смысла технические сдвиги – дефрагментацию памяти, либо мириться с дырками фрагментированной памяти.

Начальная идея проста – ставить новые компоненты не в конец или начало памяти (массива), а на первое попавшее свободное место.

a5

a4

a1

a2

a3

a6

Проблема. Теперь порядок компонентов-хранителей последовательности не будет совпадать с естественным порядком, следовательно, его нужно запоминать отдельно. Самый популярный способ сделать это – использовать списковую структуру, в которой вместе с каждым значением компоненты (члена последовательности) хранится индекс (указатель – имя) – следующая компонента.

1 2 3 4 5 6 7 8

‘а’

‘н’

‘б’

‘а’

‘н’

2 7 1 8 


5 – индекс 1-й буквы

 - специальное значение – признак конца списка.

Второй вариант – функция предшествования. Получаем понятия прямого, обратного и двукратного списков.


succ succ

последовательность одна, но автоматы разные.

pred pred


Общая схема реализации автомата как списка.

Атрибуты вершин графа.

На каждую стрелку отдельное поле, хранящее указатель на вершину, к которой ведёт эта стрелка.


Светофор











1 2 3 4 5 6 7 8

К

З

Ж

5 7 3

7. 5
   

type tIndex=1..nMax;

tList=record

content:array[tIndex] of tNode;

head:tIndex;

end;

tNode=record

info:tInfo; {Атрибуты вершины}

next:tIndex;

end;

tGraphNode=record

info:tInfo[tIndex] of tNode;

left,right:tIndex;

end;

Варианты – перечень полей-указателей. Например, для бинарного дерева – left,right:tIndex. Либо массив-указатель, либо список.

Новый способ требует больше памяти. Окупится ли «жертва» эффективной вставки и удаления? Убедимся в этом (оставим на время проблемы, связанные с обработкой кучи).

Задача. Включить в список List компоненту Х после компоненты.


Procedure Include(var List:tList;x:tInfo;AfterPtr:tIndex);

Var NewPtr:tIndex;

Begin

{Взять первый свободный индекс NewPtr из кучи}

GetHeap(List,NewPtr); After NewPtr

with List do  

ai

x

begin

content[NewPtr].info:=x;

content[AfterPtr].next:=NewPtr;

content[NewPtr]:=

end;

end;


Замечание: процедура Include корректно работает, если известна ссылка на предыдущую компоненту, после которой надо вставлять.

Техническая проблема: она не может включать в пустой список. Не хочется писать отдельную процедуру для включения в пустой список. Проверять же непустоту списка в процедуре Include неэффективно.

Решение: расширить тип Index до 0..nMax и при инициализации списка поставить в него фиктивную нулевую компоненту («болванчик» или «фантом»).

Procedure Init(List:tList);

Begin

with list do

begin

content[0].next:=0;

head:=o;

end;

{Инициализировать кучу}

end;

{Удаление элемента из списка, стоящего после компоненты AfterPtr}


procedure Exclude(var list:tList;AfterPtr:tIndex);


AfterPtr

 j

a_i+1


j₂

a_i+2
a_i
a_i


j₁









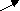
 (удаление)


{Работает в предположении, что удалённая компонента существует}

var ThisPtr:tIndex;

begin

with list do

begin

ThisPtr:=content[AfterPtr].next;

Content[AfterPtr].next:=content[ThisPtr].next;

{Сборка мусора – возвратить освободившуюся компоненту в кучу}

PutHeap(List,ThisPtr);

end;

end;


Обработка кучи.

Нас интересует лишь возможность доставлять и класть в кучу указатели, индексы свободных компонент. С логической точки зрения для этого подходят стек или очередь.


HeapHead

   

a_i

a_i+1


a_i+2



Эффективное решение – связать свободные компоненты в список.


{Инициализация кучи}

procedure InitHeap(List:tList);

{Связать все компоненты от 1 до nMax}

begin

with list do

begin

for Ptr:=1 to nMax do content[Ptr].next:=succ(Ptr);

content[nMax].next:=; {Признак конца стека}

end;

end;


procedure GetHeap(var list:tList;NewPtr:tIndex);

{Взять указатель на свободную компоненту из кучи}

begin

with list do

begin

NewPtr:=HeapHead;

HeapHead:=content[HeapHead].next;

end;

end;


procedure PutHeap(var list:tList;Ptr:tIndex);

{Кладёт элемент в кучу}

begin

with list do

begin

content[Ptr].next:=HeapHead;

HeapHead:=Ptr;

end;

end;

Упражнение. Реализовать вставку и удаление из обработанного и двусвязного списка.


Динамическая реализация абстрактных типов ссылками.

Ссылочные типы Паскаля.

Статическая реализация абстрактных типов страдает недостатками как с точки зрения логики, так и эффективности реализации. С точки зрения логики - нахождение ограничений на размер используемых структур данных. Расход памяти также неэффективен – запрашиваемых ресурсов больше, чем используемых.

Мы явно предпочли бы сосредоточиться на логике решения задачи, не замечая конечности памяти и автоматизировать технические проблемы распределения памяти (вроде обработки кучи).

Ссылочные типы обеспечивают мощный и гибкий аппарат конструирования абстрактных типов, но иногда слишком мощный и далёкий от логики решаемых нами задач.

указатели





Пример.


  

члены последовательности




указатели на следующий член


Имена как значения:


Имя Отчество Наиль Раисович

  

Наиль Раисович


Имена – специфический тип данных.

a[i]:=b[j]

• 
  

имя значение

Основные из них – разыменование – по переменной определить её имя (не значение, как обычно).

Пример: Как тебя зовут?

Косвенная ссылка: определить значение имени, являющегося значением данной переменной.