Geum.ru

Курс за второй семестр. Абстрактные типы данных

Вид материалаЗадача

Содержание


Синтаксис типов.
Реализация очередей.
Обработка деревьев. Деревья выражений.
Задача по вычислению
Подобный материал:
1   2   3   4   5   6   7   8

Ссылочные типы Паскаля.

Синтаксис типов.

Синтаксис:

p1: T, где T – произвольный тип

p2: integer; char;

Множество значений: множество всех имён-указателей на значение соответствующего типа.

Реализация: стандартным именем-значением является его номер, адрес в линейно-упорядоченной области памяти.

Единственной стандартной константой, общей для ссылочных типов, является константа nil – фиктивное значение, обозначающее отсутствие указателя.

Основные операции: разыменование и косвенная ссылка.

@x – разыменование – указатель (адрес) на переменную x.

Если x:integer, то p:integer;

p - косвенная ссылка (значение той переменной, имя (адрес) которой хранится в p).

p:=x – ошибка несогласования типов.

x:=0;

p:=@x;

p:=1;

write(x);

Мы получили 2 имени одного и того же значения.

Пример: Что выведет следующая программа? Единицу.

p:=1  x:=1;

write(x);

Вывод: использование ссылок грозит побочными эффектами.

Нет никакого смысла связывать переменные ссылочного типа с уже имеющимися переменными. В стандарте отсутствует.

Истинное преимущество ссылок – возможность определять новые переменные динамически в ходе выполнения программ. До сих пор мы определяли переменные до выполнения программы в области var.

p:T;

Процедура New(p) ссылочного типа порождает новую переменную типа T и кладёт её стандартное имя (адрес) в P. В результате получаем новую переменную типа Т с уникальным пользовательским именем p.

Реализация: см. GetNewPtr (предыдущая лекция).

Процедура Dispose(p) имеет обратный эффект – уничтожает, возвращает в кучу переменную с именем p. Значение Р становится неопределённым. В отличие от массивов, никакой контроль за семантикой не производится автоматически.

Реализация: см. PutHeap.

Замечание: никаких других функций над ссылочными типами в стандартном Паскале нет, в частности не разрешены арифметические операции над адресами..

Наличие процедуры New лежит в основе моделирования динамических типов данных. Можно порождать не только переменные известных типов, но и переменные, компонентами которых служат ссылки.


New










Объявление списочной структуры в Паскале.

Type T={базовый тип, компонента списка}

component=record

info:T;

next:component;

end;

Определение такого типа недопустимо в синтаксисе Паскаля, но возможно описание следующего вида:

type T={ };

pComponent=tComponent;

tComponent=record

info:tInfo;

next:pComponent;

end;

Базовое правило «тип можно определять лишь в терминах уже описанных типов» имеет единственное исключение – ссылку на тип можно определять раньше, чем сам тип. Это единственная форма рекурсивного определения, допустимая в Паскале.


Реализация стеков.

Procedure Push(top:pComponent;x:T);

{Стек задаётся списком, top, в свою очередь, - ссылкой на первый элемент (голову списка)}

top






nil



var p:pComponent;

begin

new(p);

p.info:=x;

top:=p;

end;


procedure Pop(var top:pComponent;varx:T);

var p:pComponent;

begin

p:=top;

x:=top.info;

top:=top.next;

dispose(p);

end;


function Empty(top:pComponent):boolean;

begin

empty:=top=nil;

end;

{Соответствует инициализации в случае, когда стек ещё не существует и уже существует}


procedure Create(var top:pComponent);

{Создать пустой стек}

begin

top:=nil;

end;


procedure Destroy(var top:pComponent);

begin

while top<>nil do

begin

p:=top.next;

dispose(top);

top:=p;

end;

end;


Реализация очередей.

{Дан член последовательности, который надо исключить и сама последовательность}

procedure Put(a:T;b:pComponent);

var p:pComponent;

begin

new(p);

p.info:=a;

p.next:=nil;

b.next:=p;

b:=p;

end;


procedure Create(b,c:pComponent);

{Указатели на начало и конец очереди}

var p:pComponent;

begin

new(p);

p.info:=zero; {zero=const – нулевой элемент}

p.next:=nil;

b:=p;

c:=p;

end;


procedure Get(a:T;var b:pComponent);

{Ссылка на «болванчик»}

var first:tComponent;

{Ссылка на первый элемент}

begin

first:=b.next;

a:=first.info;

b.next:=first.next;

dispose(first);

end;


function Empty(b:pComponent):boolean;

begin

empty:=b.next=nil;

end;


Основные операции над стеками.

Операции:
  1. Конкатенация списка;
  2. Вставка компоненты после, до или вместо заданной;
  3. Выделение подсписка.

Во всех случаях списки задаются ссылкой на начало и конец.


firsta lasta

 






firstb lastb

concat

lasta.next:=firstb;


Вставка после:


firsta vstavka lasta

  






firstb lastb

 



lastb.next:=vstavka.next;

vstavka.next:=firstb;


Вставка до:

lastb.next:=vstavka.next;

vstavka.next:=firstb.next;

x:=vstavka.info;

vstavka.info:=first.info;

firstb.info:=x;

firstb.next:=lastb.next;

lastb.next:=firstb;

Упражнение. Выделение и включение подсписка, если задана ссылка на конец подсписка и

а) голову (первый компонент);

б) стоящий перед ним.

В этих задачах удобнее считать, что у каждой компоненты, хранящей члены последовательности, есть следующая и предыдущая.

Обработка деревьев. Деревья выражений.

Несмотря на очень сложный вид (синтаксис), выражения обозначают функции и можно считать (если нужно привести – преобразовать), что выражения заданы в стандартном синтаксисе, в функциональной или префиксной нотации. Таким выражением будет элементарное выражение (терм) (обычно константа или переменная). Если e1,…en – выражение, а f – знак операции, то строка вида f(e1,…,en) – также выражение.

Деревом называется граф, состоящий либо из одной вершины, либо имеющий вид:







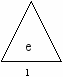
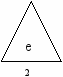
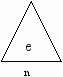
где e1,…,en – деревья


Примеры:


ax2+bx+c












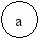
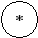
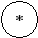
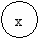
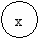
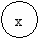
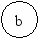
p:=1; for I:=1 to n do p:=p*a;










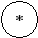
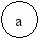
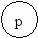
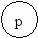
С обработкой выражений связаны три классические задачи программирования:
  1. Синтаксический анализ: выяснить, является ли произвольный текст правильно построенным выражением.
  2. Трансляция: по заданному выражению построить семантически эквивалентные выражения в другом синтаксисе (как правило более низкого уровня).
  3. Выполнение: вычислить значение данного выражения.


Для точной постановки задачи надо строго определить синтаксис и семантику конкретного языка. Для наших целей выберем язык с минимальным по возможностям синтаксисом и очевидной семантикой.

Константы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Переменные: a, b, c, d, …, z

Знаки операций: + , - , * , /.

Выражение рассматривается в стандартной функциональной нотации.

ax2+bx+c – уже недопустимо

*a*xx+*b*c

Семантика: арифметика целых чисел.

Задача по вычислению. Даны правильно построенное выражение и значения входящих в него переменных. Вычислить значение выражения.

type tVariable=array[‘a’..’z’] of integer;

pComponent=tComponent;

tComponent=record

info:char; {?}

left, right:pComponent; {Ссылки на левый и правый аргументы

(потомков)}

end;

function ExpVal(root:pComponent;variable:tVariable);

ax+2b +*ax*2b






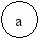
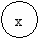
a1

x2

b3





АТОМ

Идея: свести вычисление выражения к последовательному вычислению атомов, то есть выражений с одним знаком операции.





left right






АТОМ


left

var pt:pComponent; {ссылка на следующий (next) вычисляемый атом}

begin

while {пока есть атомы} do

begin

{pt:= }

{Найти ссылку на первый атом, положить его в pt}

Вычисление атомов в лексикографическом порядке. (left
{Сократить дерево, заменить атом на его значение}

pt.info:=AtomVal(pt);

dispose(pt.left);

dispose(pt.right);

pt.left:=nil;

pt.right:=nil;

Конечно, можно не удалять вершины физически, а лишь помечать как удалённые.


Поиск атома.

Черновик.



pt found:=false;
  1. 1 while not found do begin

if not терм(pt.left) then pt:=pt.left

else if not терм(pt.left) then
  1. 1 pt:=pt.right else

found:=true;


  1. 1



Начинать каждый раз с корня неэффективно. Нужно искать ближайший к вычисленному атом. Всё прекрасно, если в дереве есть обратная ссылка на родителей. В нашем представлении их нет. Как вернуться к предыдущей вершине? Сохранять ссылки на предыдущую, а затем возвращаться к последней сохранённой.

pt:=root;

found:=false;

while not found do

begin

if not терм(pt.left) then

begin

push(stack,pt);

pt:=pt.left;

end;

else if not терм(pt.right) then

begin

push(stack,pt);

pt:=pt.right;

end

else found:=true;

(***) pop(stack,pt);

{Каждый раз начинаем с последней сохранённой вершины}

До начала цикла (инициализация стека):

create(stack);

push(stack,root);

Условия окончания цикла:

not терм(root);

not empte(stack);

Упражнения:
    1. Решить задачу вычисления в случае, когда в дереве хранится ссылка на родителей.
    2. То же самое, но вершины содержат только ссылки на родителей.

Дерево задаётся списком листьев.

Подзадача: вычислить значения атомов.


function AtomVal(pt:pNode):integer;

var arg1,arg2:integer;

begin

arg1:=TermVal(pt.left);

arg2:=TermVal(pt.right);

case pt.info of

‘+’: AtomVal:=arg1+arg2;

‘*‘: AtomVal:=arg1*arg2;

‘/’: AtomVal:=arg1/arg2;

‘-‘: AtomVal:=arg1-arg2;

end;

end;


Вернёмся здесь к вопросу об определении типа Info. Сначала он char, затем должен содержать значения типа integer. Типом поля Info по нашему алгоритму должно служить объединение типов. Мы должны не только хранить в этом поле значеня разных типов, но и уметь определять, какого типа значение там хранится в текущий момент. Это помеченное объединение.

function TermVal(pt:pNode):integer;

begin

if {тип Info=integer} then TermVal:=pt.info

else if pt.info in [‘0’..’9’] then TermVal:=ord(pt.info)-ord(0)

else TermVal:=VarVal[pt.info];

Очевидный вариант определения типа tInfo – запись.

record

это integer:boolean;

CharInfo:char;

IntInfo:integer;

end;

Этот вариант хорош, если мы не хотим фактически уничтожать дерево. Условие “это integer=true” означает, что это выражение уже вычислено. Но если мы хотим уничтожить дерево, то такое определение типа неэффективно. Паскаль предлагает более эффективное решение.