10. Статистические параметры логических элементов. К статистическим параметрам
| Вид материала | Документы |
- Микросхемная реализация логических элементов, 31.42kb.
- Анализ линейных электрических цепей при гармоническом воздействии, 22.75kb.
- 1. Понятие и виды корпоративных облигаций, 253.6kb.
- Rs – Триггер, 228.9kb.
- Конференция продолжает серию конференций, посвященных современным статистическим технологиям, 30.72kb.
- Конференция продолжает серию конференций, посвященных современным статистическим технологиям, 30.71kb.
- Методические указания по выбору темы и написанию курсовых проектов по дисциплине «Эконометрика, 94.91kb.
- Классификация и основные параметры, 145.52kb.
- Лекция 12. Архитектура компьютера, 124.05kb.
- Тема: Использование логических функций в пакете Excel, 14.85kb.
10. Статистические параметры логических элементов.
К статистическим параметрам, характеризующим логические и схемотехнические возможности логическим элементам (ЛЭ) микросхем и больших интегральных схем (БИС), относятся:
— реализуемая логическая функция;
— нагрузочная способность n, характеризующая возможность подключения определенного числа идентичных ЛЭ;
— коэффициент объединения по входу m (mи — для реализации логической функции И; mили — для реализации логической функции ИЛИ);
— средняя задержка передачи сигнала tср (полу сумма времени задержек передачи сигналов 1 и 0 со входа ЛЭ на его выход);
—предельная рабочая частота fр (частота переключения триггера, составленного из рассматриваемых ЛЭ);
— помехоустойчивость;
— потребляемая мощность.
По виду реализуемой логической функции ЛЭ условно могут быть разбиты на два класса. К первому классу относятся функциональные элементы одноступенчатой логики. Это простейшие ЛЭ, реализующие функции: И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ. Ко второму классу относятся функциональные элементы двухступенчатой логики, реализующие более сложные функции: И—ИЛИ, ИЛИ—И, НЕ—И—ИЛИ, И—ИЛИ—НЕ, И—ИЛИ—И, и др.
Нагрузочная способность ЛЭ n определяет число входов идентичных элементов, которое может быть подключено к выходу каждого из них. При этом обеспечивается неискаженная передача двоичных символов 0 и 1 в цифровом устройстве по цепи из произвольного числа последовательно включенных элементов при наихудших сочетаниях дестабилизирующих факторов. Дестабилизирующими факторами могут быть: изменение питающих напряжений, разброс параметров компонентов, изменение температуры и т. п.
Часто нагрузочная способность n называется коэффициентом разветвления элементов по выходу и выражается целым положительным числом (n =4, 5, 7, 10 и т. д.). Чем выше нагрузочная способность ЛЭ, тем шире их логические возможности и тем меньше затраты при построении цифрового устройства. Однако увеличение параметра n возможно до определенных пределов, поскольку при этом ухудшаются другие параметры ЛЭ: снижается быстродействие, ухудшается помехоустойчивость и увеличивается потребляемая мощность. По этой причине в состав одной серии интегральной микросхемы часто входят ЛЭ с различной нагрузочной способностью: основные ЛЭ с n =4...10 и буферные элементы — так называемые усилители мощности с n =20...50. Это позволяет более гибко проектировать цифровые устройства, достигая оптимальных показателей по потребляемой мощности и числу ЛЭ.
В зависимости от частного диапазона работы логических МДП-микросхем их нагрузочная способность может изменяться в широких пределах (n = 10 ... 100).
Коэффициент объединения по входу m характеризует максимальное число логических входов функционального элемента. С увеличением параметра m расширяются логические возможности микросхемы за счет выполнения функций с большим числом аргументов на одном типовом элементе И—НЕ, ИЛИ—НЕ и т. п. Однако при увеличении числа входов, как правило, ухудшаются другие параметры функционального элемента, такие как быстродействие, помехоустойчивость и нагрузочная способность.
С точки зрения возможности увеличения коэффициента объединения по входу И или по входу ИЛИ логические схемы существенно отличаются друг от друга. В существующих сериях интегральных микросхем основные логические элементы выполняются, как правило, с небольшим числом входов (mи =2...6, mили=2... 4). Увеличение числа входов m обеспечивается за счет введения в серию ЛЭ специального логического расширителя.
Помехоустойчивость. Базовый элемент интегральной микросхемы в статическом режиме может находиться в одном из двух устойчивых состояний (0 или 1). По этой причине различают статическую помехоустойчивость ЛЭ по уровню 0 Uпо и по уровню 1 Uп1.
Определение 10.1: Статическая помехоустойчивость базовых элементов ИМС определяется значением напряжения, которое может быть подано на вход ИМС относительно уровня 0 или 1, не вызывая ее ложного срабатывания (например, переход из состояния 1 в состояние 0 или наоборот).
ИМС, принадлежащие одной и той же серии, спроектированы взаимно согласованными. То есть уровни выходных сигналов одного логического элемента (даже при их изменении в допустимых пределах) могут использоваться в качестве уровней входного сигнала следующего элемента без каких-либо согласующих устройств.
Потребляемая мощность. При работе в реальном устройстве каждый ЛЭ может находиться в следующих состояниях: в состоянии
— выключено;
— в стадии включения;
— в состоянии включено;
— в стадии выключения.
Под этим параметром понимают среднюю мощность, потребляемую схемой за достаточно большой промежуток времени. Так как эта мощность отводится (рассеивается) в виде теплоты, ее называют также мощностью рассеяния.
Некоторые ЛЭ большую мощность потребляют в статических состояниях (включено, выключено) и сравнительно незначительную - во время переходного процесса из состояния включено в состояние выключено и наоборот.
Для ИМС на биполярных транзисторах, предполагая, что схема примерно одинаковое время находится в состояниях 0 и 1, среднюю мощность рассчитывают по формуле:
Рср=(Р0+Р1)/2,
где P1 — мощность, потребляемая микросхемой в состоянии включено; Р0—мощность, потребляемая микросхемой в состоянии выключено.
Для ИМС на МДП-транзисторах мощность, потребляемая ими в процессе переключения, в десятки раз и более превышает мощность, потребляемую в статических состояниях, поэтому для них Рср оценивают при максимально допустимой частоте переключения.
По потребляемой мощности ИМС можно разделить на относительно мощные (Рср от сотен до единиц милливатт), маломощные (от единиц милливатт до микроватта) и еще меньшей мощности, называемые «нановаттными» (Рср <1 мкВт).
11. Быстродействие цифровых устройств.
Определение 11.1: Быстродействием цифрового устройства называется среднестатистическое число операций, выполняемых устройством в единицу времени (номинальное быстродействие).
Быстродействие является одним из основных параметров устройства, характеризующим её производительность.
Эффективное быстродействие (Vэ) связано с номинальным быстродействием (Vн) соотношением: Vэ = vVн, где v - некоторый обобщённый коэффициент, учитывающий влияние медленно действующих компонентов, логическую структуру устройства, особенности системы команд, влияние надёжности устройства и потери за счёт контрольных процедур и диагностико-восстановительных мероприятий.
Цифровые устройства, микросхемы которых основаны преимущественно на триггерах, являются самыми быстродействующими. Так же быстродействие устройства определяется поставленной задачей и реализацией этой задачи наиболее подходящими компонентами. Помимо этого быстродействие определяется ещё и материалами, из которых выполнены компоненты.
Однако построение микросхем цифровых устройств на базовых логических элементов приводит к большому числу внешних соединений, сложности конструкций и больших габаритов печатных плат. Более того, большая длина соединительных проводников, сложность построения устройств с высокой тактовой частотой являются причинами низкой надёжности. Поэтому задача достижения максимально возможного быстродействия устройства должна решаться вкупе с задачей максимальной надёжности устройства.
19. Базовые логические элементы.
Логические элементы — это наиболее простые цифровые микросхемы. Именно в этой простоте и состоит их отличие от других микросхем.
Обычно каждый логический элемент имеет несколько входов (от одного до двенадцати) и один выход. При этом связь между выходным сигналом и входными сигналами (таблица истинности) предельно проста. Каждой комбинации входных сигналов элемента соответствует уровень нуля или единицы на его выходе. Никакой внутренней памяти у логических элементов нет. Но в отличие от более сложных комбинационных микросхем логические элементы имеют входы, которые не могут быть разделены на группы, различающиеся по выполняемым ими функциям.
Главные достоинства логических элементов, по сравнению с другими цифровыми микросхемами, — это их высокое быстродействие (малые времена задержек), а также малая потребляемая мощность (малый ток потребления). Недостаток же их состоит в том, что на их основе довольно трудно реализовать сколько-нибудь сложные функции.
Инверторы.
Самый простой логический элемент — это инвертор (логический элемент НЕ, "inverter"). Определение 10.1: Инвертор — логический элемент, выполняющий простейшую логическую функцию инвертирование, то есть изменение уровня входного сигнала на противоположный. Он имеет всего один вход и один выход. Выход инвертора может быть типа 2С или типа ОК.
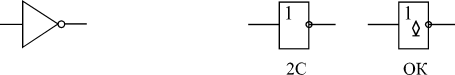
Рис. 10.1. Условные обозначения инверторов: зарубежные (слева) и отечественные (справа).
| Таблица истинности инвертора | |
| Вход | Выход |
| 0 | 1 |
| 1 | 0 |
Две основные области применения инверторов — это изменение полярности сигнала и изменение полярности фронта сигнала. То есть из положительного входного сигнала инвертор делает отрицательный выходной сигнал и наоборот. Еще одно важное применение инвертора — буферирование сигнала (с инверсией), то есть увеличение нагрузочной способности сигнала.
Элементы И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Самые распространенные логические функции — это И, И-НЕ, ИЛИ и ИЛИ-НЕ. Присутствие слова НЕ в названии элемента обозначает только одно — встроенную инверсию сигнала. Объединяет все эти элементы то, что у них есть несколько равноправных входов (от 2 до 12) и один выход, сигнал на котором определяется комбинацией входных сигналов.
Определение 10.2: Элемент И — логический элемент, который формирует на выходе единицу тогда и только тогда, если на всех его входах (и на первом, и на втором, и на третьем и т.д.) присутствуют единицы. Если речь идет об элементе И-НЕ, то на выходе формируется нуль, когда на всех входах — единицы.
Определение 10.3: Элемент ИЛИ – логический элемент, который формирует на выходе единицу тогда и только тогда, когда хотя бы на одном из его входах присутствует единица. Если речь идёт об элементе ИЛИ-НЕ, то на выходе формируется единица только в том случае, когда на все входах присутствуют все нули, в остельных случаях на выходе формируется ноль.
| Вход 1 | Вход 2 | Выход И | Выход И-НЕ | Выход ИЛИ | Выход ИЛИ-НЕ |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
20. Синтез комбинационных ЦУ.
Комбинационные микросхемы выполняют более сложные функции, чем простые логические элементы. Их входы объединены в функциональные группы и не являются полностью взаимозаменяемыми. Например, любые два входа логического элемента И-НЕ совершенно спокойно можно поменять местами, от этого выходной сигнал никак не изменится, а для комбинационных микросхем это невозможно, так как у каждого входа — своя особая функция.
Комбинационные микросхемы не имеют внутренней памяти. То есть уровни их выходных сигналов всегда однозначно определяются текущими уровнями входных сигналов и никак не связаны с предыдущими значениями входных сигналов. Любое изменение входных сигналов обязательно изменяет состояние выходных сигналов.
Этапы синтеза.
- Входы и выходы получают двоичную кодировку.
- Выбираются элементный базис, а также триггерные элементы.
- Проводят построение в заданном базисе таблицы сигналов возбуждения и выходов автомата, руководствуясь таблицей переходов и выходов соответственно. Аргументами в таблице являются текущие состояния и входы автомата, выходы получают из обратной таблицы переходов (триггеров).
- Наносят результаты на карту Карно, минимизируют логическое выражение, с помощью полученной записи формируют схему.
Пример комбинационной схемы.
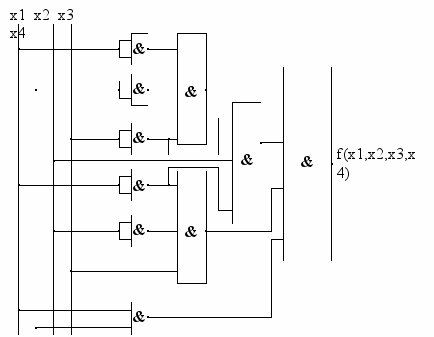
21. Понятие конечного автомата, автомата с памятью: синхронный и асинхронный автоматы.
Определение 21.1: Конечные автоматы являются математической моделью устройств, перерабатывающих дискретную входную информацию в режиме "реального времени", т.е. в темпе ее поступления.
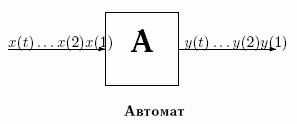
На такие устройства в последовательные дискретные моменты времени 1,2, …, t, t+1,… поступают входные сигналы x(1),x(2), …, x(t),x(t+1),… и в ответ на них автомат A вырабатывает выходные сигналы y(1) y(2), …, y(t), y(t+1),…. Конечные автоматы характеризуются двумя особенностями.
Отсутствие предвосхищения: выходной сигнал y(t), выдаваемый автоматом в момент t, зависит лишь от полученных к этому времени входов x(1),x(2), …, x(t), т.е. автомат не может предвосхитить будущие входы и заранее на них отреагировать. Таким образом, имеется некоторая функция выходов
(x(1),x(2), …, x(t))= y(t), определяющая очередной выход по предшествующему входу. Конечная память: в каждый момент t информация в автомате о полученном к этому моменту входе x(1),x(2), …, x(t) конечна. Это свойство удобно интерпретировать следующим образом: автомат имеет конечное множество состояний Q и в каждый момент находится в одном из этих состояний. При получении очередного входа состояние может измениться. Таким образом, состояние q
Q, в котором находится автомат после получения входной последовательности x(1),x(2), …, x(t), и представляет информацию об этой последовательности, используемую в дальнейшей работе автомата при определении следующего состояния и выхода.Определение 22.2: Асинхронный автомат - конечный автомат, в котором выходные сигналы считываются в любое время, а переход в новое состояние определяется лишь временем срабатывания всех логических элементов, входящих в логический преобразователь.
Определение 22.3: Синхронный автомат - конечный автомат, в котором:
- генератор тактовых импульсов воздействует на автомат;
- выходные сигналы считываются только во время выдачи тактовых импульсов, когда под воздействием входных и промежуточных сигналов автомат уже перешел в новое состояние.
22. Функции переходов и выходов синхронного автомата Мили.
Определение 22.1: В случае синхронного автомата входные сигналы действуют в строго определённые моменты времени при Т=const, определяемые генератором синхронизирующих импульсов, в которые возможен переход автомата из одного состояния в другое.
Поведение автомата Мили описывается с помощью следующих уравнений:
zt+1 =
(xt,zt);yt =
(xt,zt);здесь функция перехода
определяет следующее внутреннее состояние автомата (состояние перехода) zt+1, а функция выхода - формируемый выходной набор yt. Характерным для автомата Мили является то, что выходной набор yt зависит как от входного набора xt, так и от внутреннего состояния zt. Индекс t – временной показатель, определяет поведение автомата в момент времени t.23. Функции переходов и выходов синхронного автомата Мура.
В автомате Мура функция выходa зависит только от состояния zt и не зависит от входного набора, поэтому поведение автомата Мура описывается следующими уравнениями:
zt+1 =
(xt, zt);yt =
(zt). - функция перехода; - функция выхода.24. Особенности таблиц переходов и выходов асинхронного автомата.
Определение 24.1: Более сложное определение асинхронного автомата. Асинхронным автоматом будем называть шестерку m=(V,v0,X,e,Y,T), где:
- Z - множество состояний;
- z0Z – начальное состояние;
- X - входной алфавит стимулов;
- e X - пустой символ, X`=X{e} – расширенный алфавит символов;
- Y – выходной алфавит; будем считать, что входной и выходной алфавиты не пересекаются X`Y=;
- T = R`SI - множество переходов, где:
- R` V х X` х V - принимающие переходы,
- S V х Y х V - посылающие переходы,
- I V х V - пустые переходы.
- R` V х X` х V - принимающие переходы,
Принимающие переходы можно разделить на два вида: R = R` V х X х V – принимающие переходы по непустым символам или x-переходы, и E = R` V х {e} х V – принимающие переходы по пустым символам или e-переходы.
Для определения особенностей таблицы переходов и выходов рассмотрим более простой случай. Пусть дан асинхронный автомат, в котором Х={x0(t), x1(t)……, xn(t)} – входной алфавит, Y={y0(t),y1(t),…… ,yn(t)} – выходной алфавит, Z={z0(t), z1(t), ……,zn(t)} – множество состояний автомата, f(zi(t), xk(t)) – функция перехода и g(zi(t), xk(t)) – функция выхода.
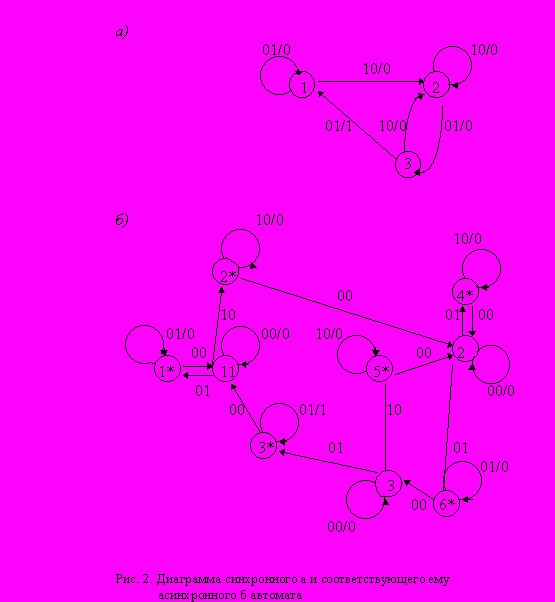
В асинхронном автомате все переходы осуществляются между устойчивыми состояниями, что создает дополнительные сложности при построении таблицы переходов. Если состояние zi(t) является устойчивым, то в клетке таблицы переходов, определяемой строкой, отмеченной состоянием zi(t), и столбцом, отмеченным входным сигналом xk, должен быть записан символ состояния zi(t), поскольку f(zi(t), xk(t))=zi(t). Таким образом, для устойчивых состояний в таблице переходов асинхронного автомата необходимы дополнительные средства, указывающие, в какое состояние должен перейти автомат при изменении входного сигнала. Это затруднение решается следующим образом. Процесс изменения состояния автомата разбивается на два этапа, полагая, что вначале происходит изменение входных сигналов, а состояние автомата остается неизменным, а затем уже происходит изменение состояния при новых значениях входных сигналов. Первому этапу этого процесса соответствует перемещение по строке таблицы переходов, отмеченной старым состоянием, в столбец, отмеченный новыми значениями входных сигналов. Итак, первый этап однозначным образом определяет новую клетку таблицы, которая соответствует переходному состоянию автомата. Такие состояния будем называть транзитивными. B этой клетке записывается символ того состояния, в которое должен перейти автомат. При этом второму этапу изменения состояния соответствует перемещение по столбцу, определяемому новыми входными сигналами, в строку, отмеченную тем состоянием, в которое автомат должен перейти. Для того чтобы не путать устойчивые состояния с указателями перехода, используемыми на втором этапе, условимся заключать символы, соответствующие устойчивым состояниям, в круглые скобки. Примером таблицы переходов и выходов асинхронного автомата является табл. 1. Эта таблица построена по графу, приведенному на рис. 2(б) (вопрос 25).
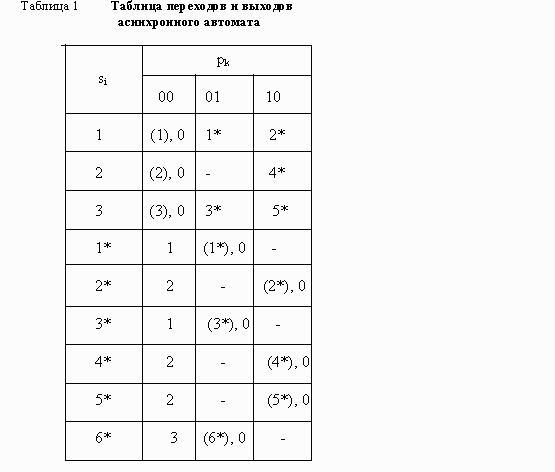
Рассмотрим, как выполняются переходы в табл. 24.1 на примере. Допустим, что автомат находится в состоянии 3 под действием входных сигналов 00. Согласно таблице переходов, это состояние является устойчивым. Если теперь значение входных сигналов изменится на 10, то для того, чтобы найти в какое состояние перейдет автомат, необходимо выполнять перемещение по третьей строке в столбец, отмеченный сигналами 10. В определенной таким образом клетке таблицы находится номер состояния, в которое переходит автомат - это состояние 5*. Перемещаясь по вертикали в столбце 10 до строки 5*, находим, что это состояние является устойчивым. Следовательно, переход завершен. В рассмотренном примере при переходе из одного устойчивого состояния в другое автомат миновал одно транзитное состояние. В общем случае изменение состояния автомата может происходить с переходом через несколько транзитных состояний, которые, конечно, должны быть расположены в одном и том же столбце таблицы переходов.
25. Графы переходов и выходов.
Работа асинхронного автомата, так же как и автомата синхронного типа, может быть описана с помощью таблицы переходов и выходов или с помощью графа. Однако переход к сигналам, обладающим ненулевой длительностью, несколько усложняет такое описание.
Остановимся вначале на способе построения графа асинхронного и синхронного автомата. Пусть задан синхронный автомат со следующей таблицей переходов-выходов.
Таблица 25.1
| Z\X | 01 | 10 |
| 1 | 1/0 | 2/0 |
| 2 | 3/0 | 2/0 |
| 3 | 1/1 | 2/0 |
Видим, что в заголовках столбцов находятся символы входного алфавита, в заголовках строк – состояния автомата, содержимым ячеек является состояние, в которое автомат переходит из текущего под действием входного возмущения, с соответствующим значением выходного результата (запись через знак дроби). Построим по данной таблице граф автомата. Вершинами графа служат состояния автомата, построчно определяются дуги, идущие от одного состояния к другому, над которыми осуществляются записи входных возмущений с соответствующими выходами. Граф представлен на рисунке 2(а).
При построении этого графа длительность входных сигналов не учитывалась. Если же считать, что импульсные сигналы, подаваемые на вход, обладают конечной длительностью, то необходимо уточнить, в каком состоянии должен находиться автомат в момент действия каждого сигнала. Это можно сделать путем введения дополнительных состояний в заданный граф для каждого перехода, как это показано на рис. 2(б). Полученный граф определяет асинхронный автомат, поскольку все состояния автомата являются устойчивыми. Принцип построения графа такой же.
Таблица переходов-выходов асинхронного автомата представлена в вопросе 24 (таблица 1).
Таким образом, можем построить определение:
Определение 25.1: Граф автомата - это сигнальный граф, вершины которого обозначают состояния автомата, на дугах отражены условия перехода из состояния в состояние и значения выходных сигналов в виде дроби: над косой чертой - xj, под ней - yj.
26. Матрицы переходов.
Конечный автомат можно также описать с помощью матрицы переходов. Это аналог графа в табличной форме.
Определение 26.1: Матрица переходов представляет собой квадратную матрицу размерности число состояний на число состояний, в которой отражены условия перехода из состояния в состояние аналогично изображённым на графе.
Построим матрицу переходов на примере синхронного автомата и его таблицы переходов-выходов, рассмотренного в вопросе 25.
| 01 | 10 | х |
| х | 10 | 01 |
| 01 | 10 | х |
Из матрицы видно, что элемент, стоящий в первом столбце на первой строке переводит автомат из состояния 1 в состояние 1. Таким же образом нетрудно догадаться, что ни один элемент не может перевести автомат из состояния 1 в состояние 3, поэтому в третьем столбце первой строки стоит крестик.
27. Триггеры.
Триггеры являются простейшими представителями цифровых микросхем, имеющих внутреннюю память. Если выходные сигналы логических элементов и комбинационных микросхем однозначно определяются их текущими входными сигналами, то выходные сигналы микросхем с внутренней памятью зависят также еще и от того, какие входные сигналы и в какой последовательности поступали на них в прошлом, то есть они помнят предысторию поведения схемы. Именно поэтому их применение позволяет строить гораздо более сложные и интеллектуальные цифровые устройства, чем в случае простейших микросхем без памяти. Микросхемы с внутренней памятью называются еще последовательными или последовательностными, в отличие от комбинационных микросхем.
Триггеры сохраняют свою память только до тех пор, пока на них подается напряжение питания. Иначе говоря, их память относится к типу оперативной (в отличие от постоянной памяти и перепрограммируемой постоянной памяти, которым отключение питания не мешает сохранять информацию). После выключения питания и его последующего включения триггеры переходят в случайное состояние, то есть их выходные сигналы могут устанавливаться как в уровень логической единицы, так и в уровень логического нуля. Это необходимо учитывать при проектировании схем.
Большим преимуществом триггеров перед другими типами микросхем с памятью является их максимально высокое быстродействие (то есть минимальные времена задержек срабатывания и максимально высокая допустимая рабочая частота). Однако недостаток триггеров в том, что объем их внутренней памяти очень мал, они могут хранить только отдельные сигналы, биты.
Триггер можно рассматривать как одноразрядную ячейку памяти.
В основе любого триггера (англ. — "тrigger" или "flip-flop") лежит схема из двух логических элементов, которые охвачены положительными обратными связями (то есть сигналы с выходов подаются на входы). В результате подобного включения схема может находиться в одном из двух устойчивых состояний, причем находиться сколь угодно долго, пока на нее подано напряжение питания.
В стандартные серии цифровых микросхем входит несколько типов микросхем триггеров, различающихся методами управления, а также входными и выходными сигналами. Наиболее распространены три типа:
- RS-триггер (обозначается ТР) — самый простой триггер, но редко используемый.
- JK-триггер (обозначается ТВ) имеет самое сложное управление, также используется довольно редко.
- D-триггер (обозначается ТМ) — наиболее распространенный тип триггера.
28. RS-триггер.
У схемы есть два инверсных входа: –R — сброс (от английского Reset), и –S — установка (от английского Set), а также два выхода: прямой выход Q и инверсный выход –Q. Отрицательный импульс на входе –R перебрасывает выход в нуль, а отрицательный импульс на входе –S перебрасывает выход в единицу. Одновременные сигналы на входах –R и –S переводят выход в единицу, а после окончания импульсов триггер попадает случайным образом в одно из своих устойчивых состояний.
| Таблица 7.2. Таблица истинности RS-триггера | |||
| Входы | Выходы | ||
| -R | -S | Q | -Q |
| 1 | 1 | 1 | Без изменения |
| X | 0 | 1 | 1 |
| 0 | X | 1 | 1 |
| 1 | 1 | 0 | 0 |
| X | 0 | 0 | Не определен |
| 0 | X | 0 | Не определен |
Входные сигналы -R и -S не должны приходить одновременно, иначе состояние триггера будет неопределенным. Длительность сигналов -R и -S также не должна быть слишком малой, иначе триггер может на них не среагировать. Сигнал –R должен начинаться с определенной задержкой после окончания сигнала –S, и наоборот. В первом приближении можно считать, что минимально допустимые временные интервалы между входными сигналами должны равняться 1–2 задержкам логического элемента соответствующей серии.
29. JK-триггер.
JK-триггер значительно сложнее по своей структуре, чем RS-триггер. Он относится к так называемым тактируемым триггерам, то есть он срабатывает по фронту тактового сигнала.
Входы -R и -S работают точно так же, как и в RS-триггере, то есть отрицательный импульс на входе -R устанавливает прямой выход в нуль, а инверсный — в единицу, а отрицательный импульс на входе -S устанавливает прямой выход в единицу, а инверсный — в нуль.
Однако состояние триггера может быть изменено не только этими сигналами, но и сигналами на двух информационных входах J и K и синхросигналом С. Переключение триггера в этом случае происходит по отрицательному фронту сигнала С (по переходу из единицы в нуль) в зависимости от состояний сигналов J и K. При единице на входе J и нуле на входе К по фронту сигнала С прямой выход устанавливается в единицу (обратный — в нуль). При нуле на входе J и единице на входе К по фронту сигнала С прямой выход устанавливается в нуль (обратный — в единицу). При единичных уровнях на обоих входах J и K по фронту сигнала С триггер меняет состояние своих выходов на противоположные (это называется счетным режимом).
| Таблица 7.3. Таблица истинности JK-триггера | ||||||
| Входы | Выходы | |||||
| -S | -R | C | J | K | Q | -Q |
| 0 | 1 | Х | Х | Х | 1 | 0 |
| 1 | 0 | Х | Х | Х | 0 | 1 |
| 0 | 0 | Х | Х | Х | Не определено | |
| 1 | 1 | 1  0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 0 | 0 | 0 | Не изменяется | |
| 1 | 1 | 1 0 | 1 | 1 | Меняется на противоположное | |
| 1 | 1 | 1 | Х | Х | Не изменяется | |
| 1 | 1 | 0 | Х | Х | Не изменяется | |
| 1 | 1 | 0 1 | Х | Х | Не изменяется | |
30. D-триггер.
Cамый распространенный D-триггер занимает, можно сказать, промежуточное положение между RS-триггером и JK-триггером. Помимо общих для всех триггеров входов установки и сброса –S и –R, он имеет один информационный вход D (вход данных) и один тактовый вход C.
| Таблица 7.4. Таблица истинности D-триггера | |||||
| Входы | Выходы | ||||
| -S | -R | C | D | Q | -Q |
| 0 | 1 | Х | Х | 1 | 0 |
| 1 | 0 | Х | Х | 0 | 1 |
| 0 | 0 | Х | Х | Не определено | |
| 1 | 1 | 0 1 | 1 | 1 | 0 |
| 1 | 1 | 0 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | Х | Не меняется | |
| 1 | 1 | 1 | Х | Не меняется | |
| 1 | 1 | 1 0 | Х | Не меняется | |
Тактируется триггер (то есть меняет свое состояние) по положительному фронту сигнала С (по его переходу из нуля в единицу) в зависимости от состояния входа данных D. Если на входе D единичный сигнал, то по фронту сигнала С прямой выход триггера устанавливается в единицу (инверсный — в нуль). Если же на входе D — нулевой сигнал, то по фронту сигнала С прямой выход триггера устанавливается в нуль (инверсный — в единицу).
31. Регистры.
Регистры представляют собой, по сути, несколько D-триггеров (обычно от 4 до 16), соединенных между собой тем или иным способом. Триггеры, входящие в состав регистров, не имеют большого количества разнообразных управляющих входов, как одиночные триггеры.
Все регистры делятся на две большие группы:
- Параллельные регистры;
- Регистры сдвига (или сдвиговые регистры).
Существуют регистры и других типов, но они применяются гораздо реже, чем параллельные и сдвиговые, так как имеют узкоспециальное назначение.
В параллельных регистрах (а) каждый из триггеров имеет свой независимый информационный вход (D) и свой независимый информационный выход. Тактовые входы (С) всех триггеров соединены между собой. В результате, параллельный регистр представляет собой многоразрядный, многовходовый триггер.
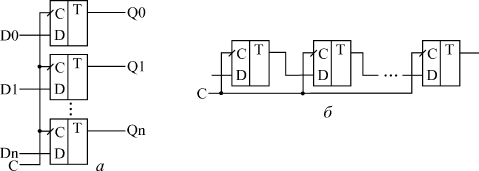
Рис. 31.1. Структура параллельного регистра (а) и сдвигового регистра (б).
В сдвиговых регистрах (б) все триггеры соединены в последовательную цепочку (выход каждого предыдущего триггера соединен с входом D следующего триггера). Тактовые входы всех триггеров (С) объединены между собой. В результате такой триггер может рассматриваться как линия задержки, входной сигнал которой последовательно перезаписывается из триггера в триггер по фронту тактового сигнала С. Информационные входы и выходы триггеров могут быть выведены наружу, а могут и не выводиться - в зависимости от функции, выполняемой регистром.
Параллельные регистры, в свою очередь, делятся на две группы:
- Регистры, срабатывающие по фронту управляющего сигнала С (или тактируемые регистры).
- Регистры, срабатывающие по уровню управляющего сигнала С (или стробируемые регистры).