10. Статистические параметры логических элементов. К статистическим параметрам

Вид материала

Документы

Содержание Синхронные счетчики с асинхронным переносом. Синхронные счетчики с асинхронным 34. Автоматы с распределёнными состояниями. Матрица переходов. 35. Устойчивые предельные состояния распределенных автоматов. 36. Эквивалентные автоматы. Минимизация автоматов. Минимизация автоматных форм

Подобный материал:

• Микросхемная реализация логических элементов, 31.42kb.
• Анализ линейных электрических цепей при гармоническом воздействии, 22.75kb.
• 1. Понятие и виды корпоративных облигаций, 253.6kb.
• Rs – Триггер, 228.9kb.
• Конференция продолжает серию конференций, посвященных современным статистическим технологиям, 30.72kb.
• Конференция продолжает серию конференций, посвященных современным статистическим технологиям, 30.71kb.
• Методические указания по выбору темы и написанию курсовых проектов по дисциплине «Эконометрика, 94.91kb.
• Классификация и основные параметры, 145.52kb.
• Лекция 12. Архитектура компьютера, 124.05kb.
• Тема: Использование логических функций в пакете Excel, 14.85kb.

Синхронные счетчики с асинхронным переносом.

Синхронные (или параллельные) счетчики характеризуются тем, что все их разряды в пределах одной микросхемы переключаются одновременно, параллельно. Это достигается существенным усложнением внутренней структуры микросхемы по сравнению с простыми асинхронными счетчиками. В результате полная задержка переключения синхронного счетчика примерно равна задержке одного триггера, то есть синхронные счетчики гораздо быстрее асинхронных, причем их быстродействие не падает с ростом количества разрядов выходного кода (до определенных пределов).

Управление работой синхронного счетчика гораздо сложнее, чем в случае асинхронного счетчика, а количество разрядов синхронных счетчиков обычно не превышает четырех. Возможностей у синхронных счетчиков, как правило, гораздо больше, чем у асинхронных, например, они обеспечивают параллельную запись информации в счетчик и инверсный режим счета.

Для объединения нескольких синхронных счетчиков с целью увеличения числа их разрядов (для каскадирования) используется специальный выходной сигнал переноса. В зависимости от принципов формирования этого сигнала и от принципов его использования синхронные счетчики делятся на счетчики с асинхронным переносом и счетчики с синхронным переносом.

Синхронные счетчики с асинхронным переносом занимают промежуточное положение по быстродействию между асинхронными счетчиками и полностью синхронными счетчиками. Управление их работой проще, чем у синхронных счетчиков, но сложнее, чем у асинхронных. Работают данные счетчики по положительному фронту входного сигнала (или, что то же самое, по заднему фронту отрицательного сигнала). Основная суть их работы сводится к следующему: все разряды одного счетчика переключаются одновременно, но при каскадировании каждый следующий счетчик (дающий более старшие разряды) переключается с задержкой относительно предыдущего счетчика (дающего более младшие разряды). То есть задержка переключения многоразрядного счетчика увеличивается в данном случае не с каждым новым разрядом (как у асинхронных счетчиков), а с каждой новой микросхемой.

Сигнал переноса у этих счетчиков при прямом счете вырабатывается тогда, когда все разряды равны единице (достигнут максимальный код) и когда приходит входной сигнал. Поэтому сигнал переноса, повторяющий входной сигнал, будет задержан относительно входного сигнала. И именно этот сигнал переноса используется в качестве входного для следующего счетчика при каскадировании. То есть входной сигнал второго счетчика задержан относительно входного сигнала первого счетчика, входной сигнал третьего счетчика задержан относительно входного сигнала второго счетчика и т.д.

33. Распознаватели.

Пусть Σ={a₁, …, a_m} - это алфавит, который состоит из конечного множества элементов, называемых символами (буквами).

Слово в алфавите Σ - это конечная последовательность символов этого алфавита: w =w₁… w_n, w_i Σ при i=1, …, n. Число букв в этой последовательности называется длиной слова и обозначается |w|. Имеется одно специальное "пустое" слово длины 0. Будем обозначать его через ε. Для слова определена операция конкатенации.

Языком в алфавите Σ называется произвольное множество слов этого алфавита. Язык, включающий все слова в алфавите Σ (в том числе и пустое слово ε), будем обозначать через Σ^*.

Конечные автоматы часто используются для определения тех или иных свойств слов, т.е. для распознавания языков: автомат, распознающий некоторый язык L должен по произвольному слову w ответить на вопрос " w L? ". Для решения такой задачи функция выходов может быть заменена на проверку того, в какое состояние переходит автомат после получения входного слова w - "принимающее" или "отвергающее".

Определение 33.1: Детерминированный конечный автомат (ДКА) - распознаватель - это система вида



включающая следующие компоненты:

• Σ ={a₁, … , a_m} (m 1) - конечное множество - входной алфавит;
  
• Q={q₀, … , q_n-1} (n 1) - конечное множество - алфавит внутренних состояний;
  
• q₀ Q - начальное состояние автомата;
  
• F Q - множество принимающих (допускающих, заключительных) состояний;
  
• Φ: Q × Σ Q - функция переходов,
  
• Φ(q, a) - это состояние, в которое переходит автомат из состояния q, когда получает на вход символ a.
  

Функцию Φ называют программой автомата A и задают как список из m n команд вида q_ia_j Φ(q_i,a_j) .

Удобно также задавать функцию Φ с помощью описанной выше таблицы размера n × m, строки которой соответствуют состояниям из Q, а столбцы - символам из входного алфавита Σ, и в которой на пересечении строки q_i и столбца a_j стоит состояние Φ(q_i,a_j).

Автоматы-распознаватели можно представлять с помощью размеченных ориентированных графов, называемых диаграммами.

Определение 33.2: Диаграмма ДКА A = <Σ, Q, q₀, Φ > - это ориентированный (мульти)граф D_A=(Q, E) с помеченными ребрами, в котором выделена вершина - начальное состояние q_0, из каждой вершины q Q выходит |Σ_X| ребер, помеченных символами a Σ так, что для каждой q Q и каждого символа a Σ имеется единственное ребро из q в вершину q' =Φ(q,a) с меткой a .

Скажем, что представленный последовательностью ребер путь p=e₁e₂ … e_t в диаграмме несет слово w=w₁w₂ … w_t, если w_i - это метка ребра e_i (1 i t). Если q - начальная вершина (состояние) этого пути, а q' - его заключительная вершина, то будем говорить, что слово w переводит q в q'.

Работа конечного автомата-распознавателя состоит в чтении входного слова и изменению состояний в зависимости от его символов.

Определение 33.3: Назовем конфигурацией ДКА A = <Σ, Q, q₀, F, Φ, > произвольную пару вида (q, w), в которой q Q и w Σ^*.

На множестве конфигураций введем отношение перехода за один шаг :



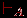Если w=ε, то положим для каждого q Q: (q, ε) 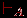(q, ε).

Через 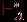обозначим рефлексивное и транзитивное замыкание .

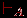Содержательно, 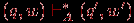означает, что автомат A, начав работу в состоянии q на слове w=w₁ … w_l, через некоторое конечное число шагов 0 k l прочтет первые k символов слова w и перейдет в состояние q', а w' =w_k+1 … w_l - это непрочтенный остаток слова w.

Определение 33.4: ДКА A распознает (допускает, принимает) слово w, если для некоторого q F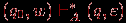

, т.е. после обработки слова w автомат переходит в принимающее состояние.

Язык L_A, распознаваемый (допускаемый, принимаемый) автоматом A, состоит из всех слов, распознаваемых этим автоматом:



Язык называется конечно автоматным, если он распознается некоторым ДКА.

Из этого определения, в частности, следует, что ε L_A q₀ F. Один и тот же язык может распознаваться разными автоматами.

Определение 33.5: Автоматы-распознаватели A и B называются эквивалентными, если совпадают распознаваемые ими языки, т.е. L_A = L_B.

Определение распознавания слова и языка можно легко перевести на язык диаграмм.

Лемма 33.1: Автомат A распознает (допускает, принимает) слово w, если для некоторого q F в диаграмме D_A имеется путь из q₀ в q, который несет слово w, т.е. w переводит q₀ в заключительное состояние q.


34. Автоматы с распределёнными состояниями. Матрица переходов.

Определение 34.1: Автоматы с распределенными состояниями каждой паре z_i-x_i имеют в соответствии состояние z_k и только одно, где Z={z₁, z₂, ……z_n} – состояния автомата и X={x₁,x₂,……x_n} – входной алфавит. При этом выходного алфавита у автомата может и не быть.

Таким образом, в зависимости от текущего состояния автомата и пришедшего входного возмущения последующее состояние автомата определяется однозначно, а выходных дуг из текущего состояние не может быть больше, чем символов входного алфавита.

Описанием такого автомата может явиться не только таблицы переходов и выходов, граф автомата, но и его матрица переходов. Заголовками столбцов и строк матрицы переходов служат состояния автоматов, а значениями элементов являются входные возмущения (символы входного алфавита), переводящие автомат в следующее состояние (следующее состояние не всегда бывает отлично от предыдущего, как, например, в случаях предельных состояний автомата).

Пример: Матрицу переходов рассмотрим на примере автомата, который ищет в строке, состоящей их символов А и В, первую подстроку типа ABBAA. Входной алфавит Х={А, В}. Из графа автомата имеем следующие состояния Z={S₀,……S₅}.

Граф автомата:

A


A


B

B


A





B


B



A

A


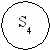
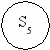
A+B

B









Матрица переходов:

В	А	х	х	х	х
х	А	В	х	х	х
х	А	х	В	х	х
В	х	х	х	А	х
х	х	В	х	х	А
х	х	х	х	х	В+А

35. Устойчивые предельные состояния распределенных автоматов.

Пусть дан распределённый автомат.

Определение 35.1: Если на вход распределённого автомата поступают сигналы из алфавита X={x₁, x₂,……,x_n}, то в этом автомате устойчивым предельным состоянием называется состояние z_k, в которое автомат переходит под действием сигналов отличных от x_k.Состояния z_k изображаются так:




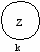
x_k




x_k

Если все состояния автомата устойчивы, то автомат называется устойчивым.


V W V


W

Триггер типа Т – неустойчивый автомат, т.е. если на входе присутствует сигнал W, то он будет менять своё состояние непредсказуемо.

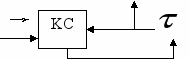Q(t+1)

q(t)



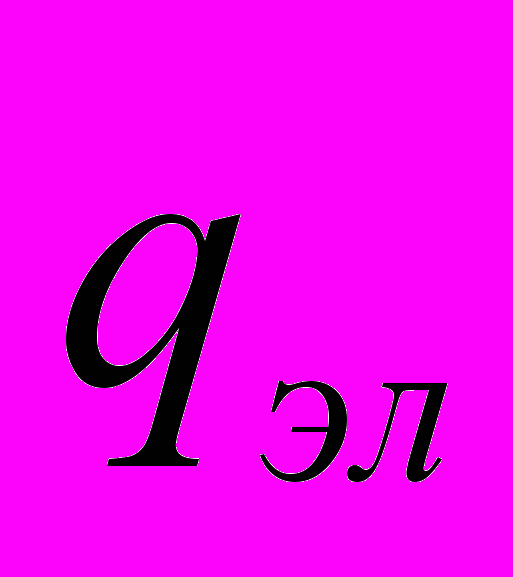
пусть
>t

Вывод: триггер T- очень чувствителен к задержкам.

RS-триггер является устойчивым триггером.


V Z V




U U

Z




Q(t+1)

q(t)




Так как RS триггер не зависит от длительности входного сигнала, то элемент задержки не нужен.


36. Эквивалентные автоматы. Минимизация автоматов.

Определение 36.1: Два автомата считаются эквивалентными, если они реализуют одну и ту же функцию, т.е. на одинаковое входное значение дают одинаковое выходное значение.

Минимизация автоматных форм состоит в построении эквивалентного автомата, имеющего наименьшее количество состояний.

Определение 36.2: Два состояния (одного автомата или разных автоматов) считаются k-эквивалентными, если любая допустимая входная последовательность длины k приводит к одинаковым выходным последовательностям при условии, что автоматный процесс начинается с этих состояний.

Определение 36.3: Состояния называются k+1 различимыми, если любая допустимая входная последовательность длины k приводит к одинаковым выходным последовательностям при условии, что автоматный процесс начинается с этих состояний, а входная последовательность длины k+1 приводит к различным выходным последовательностям при тех же условиях.

Алгоритм Мили.

Алгоритм Мили состоит в следующей последовательности.

1. Состояния автомата разбивают на классы эквивалентности π_i. В один класс попадают состояния, имеющие одинаковую реакцию на входные последовательности длины 1 (т.е. состояния, имеющие одинаковые строки в таблице выходов).
   
2. Для k от двух до предпоследнего состояния автомата из возможных производится дробление пока π_k<>π_k-1.
   
3. В новое разбиение π_k входит состояния, которые либо уже ранее входили в разные классы, либо входили в один класс, но показали разную реакцию на последовательности длины k.
   

По результирующим классам эквивалентности формируется новый (минимизированный) автомат, где число состояний равно мощности разбиения, а таблица переходов в соответствии с выходами формируется в терминах классов.

Алгоритм Мили может быть использован для анализа минимальности конструкций: конструкция минимальна, если в каждый класс результирующего разбиения входит не более одного состояния.

Алгоритм Мили может быть использован для анализа эквивалентности автоматов: множество состояний автоматов рассматриваются как единое целое (для «объединённого автомата решается задача минимизации»), в классах результирующего разбиения должны присутствовать представители от обоих автоматов.