Вучебниках информатики в общем виде информацион­ный процесс

Вид материала

Учебник

Содержание Копирование формул. Абсолютные и относительные ссылки. В Автоматическое заполнение. Экономика. Расчет месячной заработной платы Технология (кулинария). Продукты для похода Успеваемость. Итоги первого полугодия по школе Математическая обработка статистических данных, результатов эксперимента Статистический анализ Экологический пример. Медицинская статистика Экономический пример. Темпы прироста показателей банковского сектора Математический эксперимент

Подобный материал:

• 3. Процесс восприятия и управление впечатлением, 191.28kb.
• Понятие о программах и программировании, 592.28kb.
• Поволжская Государственная Академия Телекоммуникаций и Информатики задания и методические, 262.31kb.
• Общеобразовательный стандарт по информатике является нормативным документом, определяющим, 237.91kb.
• Финансы предприятий, 2102.05kb.
• Исходные технические данные, 34.3kb.
• Тема: Личность в системе современного, 42.1kb.
•     После то­го как я на­пи­сал «Счас­т­лив по соб­с­т­вен­но­му же­ла­нию», как-то, 1995.16kb.
• Компьютерная технология обучения и опережающая подготовка преподавателей, 49.99kb.
• Активизация познавательной деятельности школьников на уроках информатики, 32.08kb.

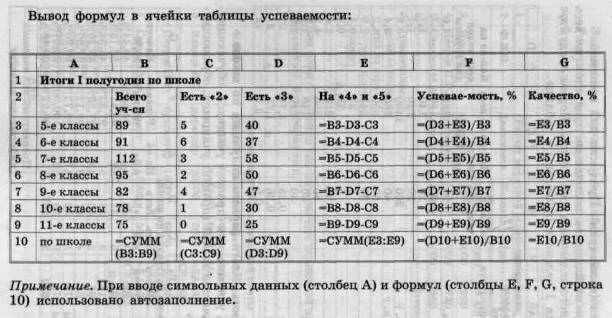
Копирование формул. Абсолютные и относительные ссылки. В формулах используются ссылки на адреса (содер­жимое) ячеек. Различие между ними проявляется при копи­ровании формул. ЭТ Excel по умолчанию интерпретирует ссылки в формулах как относительные. Это означает, что если вы копируете формулу в другие ячейки рабочего листа, то ссылки на ячейки в новой формуле автоматически изме­няются так, чтобы соответствовать новому расположению формулы. Изменение «координат» (номера строки и имени столбца) производится на столько единиц, на сколько строк и столбцов смещена ячейка, в которую помещают копию формулы. Например, копирование формулы =СУММ(СЗ:ЕЗ) из ячейки F3 в ячейку G4 приведет к появлению в ячейке G4 формулы =CyMM(D4:F4). Если необходимо, чтобы ссыл­ки не изменялись при копировании формулы в другую ячей­ку, воспользуйтесь абсолютными ссылками. Абсолютный адрес указывает на точное положение адресуемой ячейки в таблице и записывается со знаком $ перед именем столбца и номером строки, например $А$3. Возможна абсолютная ад­ресация только столбца или строки, такая адресация назы­вается смешанной, например $А4, А$4.

Автоматическое заполнение. Вы можете сэкономить вре­мя на ввод с клавиатуры последовательного ряда чисел (арифметической прогрессии), обозначений, названий меся­цев и дней недели, как в строках, так и в столбцах:

1. Для создания числового ряда введите в смежные ячей­ки два первых числа.

2. Выделите эти ячейки.
   
3. Установите указатель мыши на точку в правом ниж­нем углу выделения, он примет вид тонкого черного крестика +.
   
4. Нажмите левую кнопку мыши и, не отпуская ее, пере­тащите указатель + по строке или столбцу.
   
5. Отпустите кнопку, и ячейки будут заполнены.
   

Для автозаполнения названиями месяцев или дней неде­ли достаточно ввести название в одну ячейку и выполнить пункты 3-5.

Для автозаполнения формул достаточно выделить ячейку с формулой и выполнить пункты 3-5. При абсолютной адре­сации адреса ячеек копируются без изменения, а при отно­сительной изменяются.

В MS Excel имеется множество дополнительных возмож­ностей, ускоряющих и облегчающих работу с таблицами:

• автоматический подбор высоты строк и ширины столб­цов;
  

• объединение ячеек и перенос слов в ячейке;
  
• наложение защиты на лист и книгу;
  
• возможность сортировки данных таблицы;
  
• удобная справочная система;
  
• использование векторного редактора;
  
• использование буфера обмена;
  

• изменение вида информации в ячейках: формулы — значения;
  

• печать рабочих листов. Предварительный просмотр;
  

• работа с несколькими рабочими листами. Переключе­ние рабочих листов. Именование рабочих листов.
  

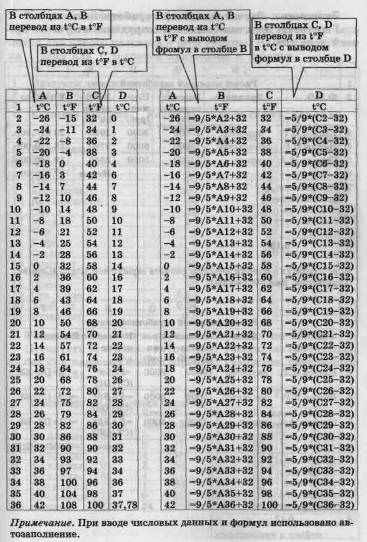
Примеры задач для обработки числовых данных [8, 22] Физика. Пересчет температуры из шкалы Цельсия в температуру по шкале Фаренгейта и обратно

Немецкий физик Г. Фаренгейт в 1724 году предложил температурную шкалу, названную его именем. Температура по шкале Фаренгейта t°F связана с температурой по шкале Цельсия t°C соотношением: t°C = —(t°F - 32). Составить таблицу, переводящую температуру, измеренную по шкале Фа­ренгейта, в температуру по шкале Цельсия и обратно.


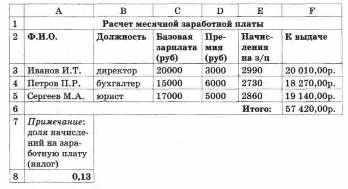
Экономика. Расчет месячной заработной платы

Рассчитать месячные выплаты сотрудникам с учетом пре­мий и налога.




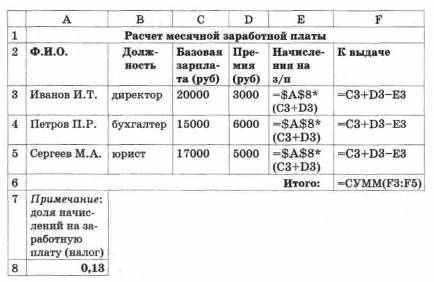
Вывод формул в ячейки таблицы расчета заработной платы (Сервис, Параметры, Вид, Формулы):






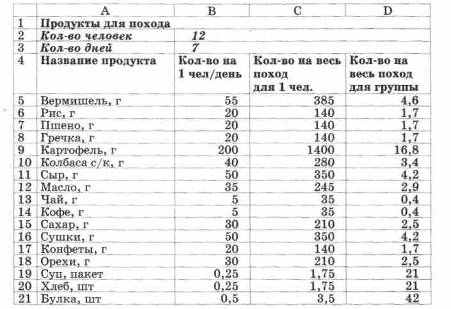
Технология (кулинария). Продукты для похода

Рассчитать необходимое количество продуктов на весь поход для одного человека и всей группы. Нормы продуктов на 1 день для 1 человека приведены в таблице.


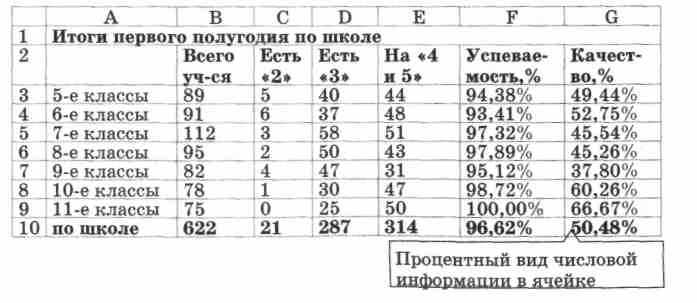
Успеваемость. Итоги первого полугодия по школе

Посчитать успеваемость (процент учащихся, обучающих­ся без 2) и качество знаний (процент учащихся, обучающих­ся на 4 и 5).







Билет № 23

Математическая обработка статистических данных, ре­зультатов эксперимента. Использование динамических (электронных) таблиц для обработки и представления результатов естественно-научного и математического эк­сперимента, экономических и экологических наблюде­ний, социальных опросов.

Математическая обработка статистических данных, результатов эксперимента

Зависимости между параметрами некоторого объекта, процесса, явления могут быть выражены с помощью мате­матических формул. Но в некоторых случаях коэффициен­ты в этих формулах могут быть получены в результате ста­тистической обработки экспериментальных данных. Стати­стика — это наука о сборе, измерении и анализе больших массивов количественных данных. Статистические данные носят приближенный, усредненный характер, получаются путем многократных измерений. Математический аппарат статистики разрабатывает раздел науки под названием «Ма­тематическая статистика». Статистические данные исполь­зуются, в частности, для получения упрощенного математи­ческого описания сложной или неизвестной зависимости между данными некоторой системы (регрессионные моде­ли). Статистические функции электронных таблиц позво­ляют обрабатывать статистические данные, например, вы­числять среднее арифметическое числовых данных (СРЗНАЧ), среднее геометрическое положительных число­вых данных, минимальное и максимальное значения из на­бора данных, выполнять подсчеты (СЧЁТ, СЧЁТЕСЛИ, СЧЁТЗ, СЧИТАТЫГУСТОТЫ и т. д.).

Статистический анализ данных широко используется:

• в народном хозяйстве при: анализе результатов дея­тельности предприятий и организаций; оценке состоя­ния финансового, сырьевого и других рынков; анализе прибыльности инвестиционной деятельности; составле­нии краткосрочных планов и долгосрочных прогнозов;
  
• в социологии и психологии для обработки и анализа ре­зультатов опросов, тестирования, анкетирования;
  

• в научной деятельности для обработки результатов экс­периментов, оценки их достоверности, проверки гипо­тез и пр.

Использование динамических (электронных) таблиц для обработки и представления результатов естественно-научного и математического эксперимента, экономических и экологических наблюдений, социальных опросов

Для определения статистической зависимости необходимо выпол­нить два шага:

1. На основании физического смысла статистических данных принять вид аналитических зависимостей. Это может быть, например, полином второй степени у = ах² + Ъх + с, линейная зависимость у = ах + Ъ и т. п. Во всех формулах х — аргумент, у — значение функции, а, Ъ, с — параметры функций.
   
2. С помощью метода наименьших квадратов (МНК) по имеющимся статистическим данным найти значения величин о, Ъ, с, определяющих конкретный вид приня­той зависимости.
   

Полученная аналитическая зависимость называется рег­рессионной моделью.

MS Excel позволяет построить регрессионную модель по статистическим данным и получить значение коэффициента детерминированности (достоверности) R² (КД). КД опреде­ляет, насколько удачной является полученная регрессион­ная модель. КД принимает значения от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели совсем неу­дачен. Чем R² ближе к 1, тем удачнее модель.

Алгоритм построения регрессионной модели:

1. Выделить обе колонки исходных данных (наборы X и Y).
   
2. Вызвать Мастер диаграмм.
   
3. Построить Точечную диаграмму.
   
4. Для полученной диаграммы выбрать команду Доба­вить линию тренда (из текстового меню Диаграмма или контекстного меню для любой точки диаграммы).
   

Тренд — это график регрессионной модели (от англ. trend — тенденция).

5. Выбрать, например, линейную линию тренда. Перейти к вкладке Параметры.
   
6. В открывшемся диалоговом окне параметров выбрать опции: показывать уравнение на диаграмме и помес­тить на диаграмму величину достоверности аппрок­симации (R/2).
   
7. На экране появится линия тренда, уравнение с число­выми параметрами и коэффициент R².
   
8. Проанализировать линию тренда (как часто ее точки совпадают с точками точечной диаграммы) и значение R² и повторить построение регрессионной модели для других видов аналитических зависимостей.
   
9. Выбрать из полученных регрессионных моделей ту, ко­торая имеет наибольшее значение R².
   

Примеры построения регрессионных моделей

Пример географических наблюдений. Зависимость тем­пературы воздуха от широты города [28]

Определить зависимость температуры воздуха от широты города.



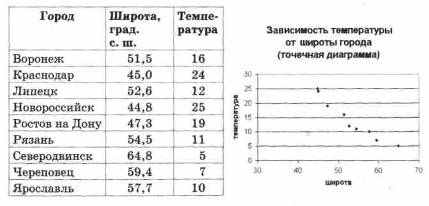
Статистические данные метеорологических наблюдений позволяют высказать гипотезу о том, что средняя темпера­тура зависит от широты города и может быть описана неко­торой математической формулой.



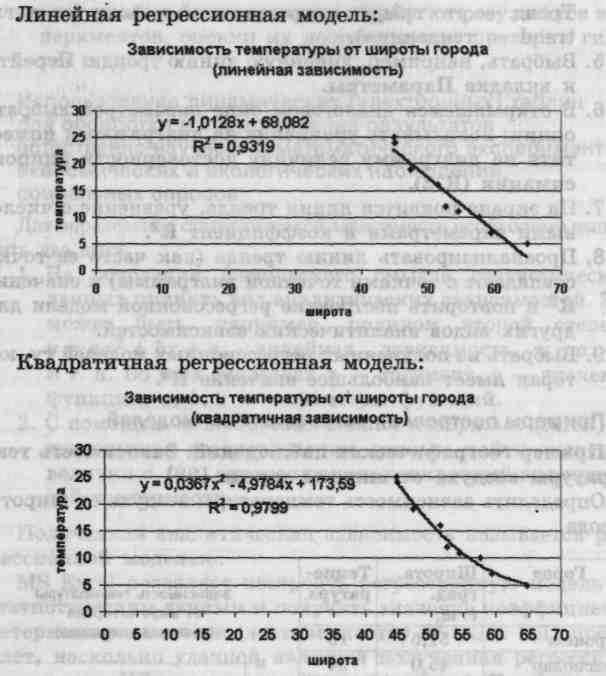
Регрессионный анализ показал, что зависимость средней температуры от широты города является квадратичной, так как R² = 0,98, что ближе к 1, чем R² для линейной за­висимости. Используя зависимость у = 0,0367je² - 4,9784л: + + 173,59 можно восстановить значение средней температу­ры для города, находящегося на 50-й широте (16,42 °С), и высказать прогноз средней температуры для города, находя­щегося на 70-й (4,9 °С) или 40-й (33,2 °С) широте. Если представится возможность получить данные о температуре на этих широтах, то можно проверить точность модели и убедиться в достоверности (или ошибочности) данных, кото­рые получены при ее использовании. Во втором случае новый набор статистических данных позволит уточнить мо­дель или ее коэффициенты и предоставит возможность для более точного прогноза температуры.

Экологический пример. Медицинская статистика

Определить зависимость частоты заболеваемости жителей города бронхиальной астмой от качества воздуха. Очевидно, чем хуже воздух, например, выше концентрация С угарного газа в атмосфере, тем больше хронических больных Р на 1000 жителей.

Статистические данные являются усредненными и при­ближенными, их собирают в разных городах в течение дли­тельного времени. Далее данные анализируют и обобщают.




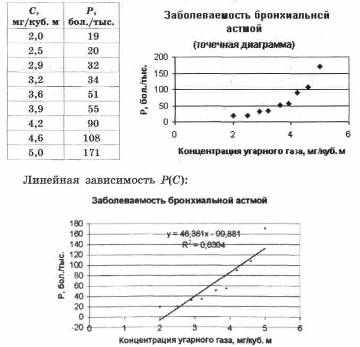
Квадратичная зависимость Р(С):



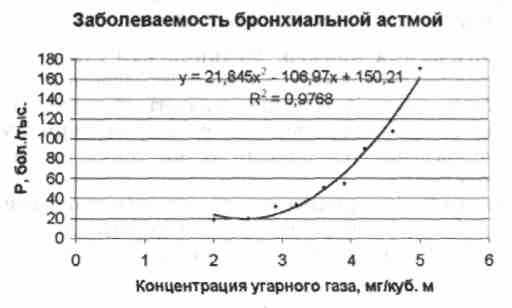
Далее регрессионная модель может быть использована для восстановления значений и для прогнозирования забо­леваний.

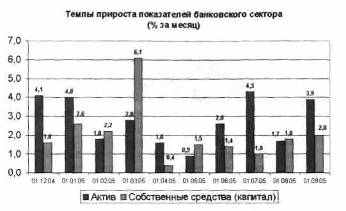
Экономический пример. Темпы прироста показателей банковского сектора

Представить экономические показатели в табличном виде и с помощью диаграмм (журнал «Итоги» 2005, № 47). Та­кую информацию анализируют специалисты банковского дела, финансисты и экономисты.

Месяц	Актив	Собственные средства (капитал)
01.12.04	4,1	1,6
01.01.05	4,0	2,6
01.02.05	1,8	2,2
01.03.05	2,8	6,1
01.04.05	1,6	0,4
01.05.05	0,9	1,5
01.06.05	2,6	1,4
01.07.05	4,3	1,0
01.08.05	1,7	1,8
01.09.05	3,9	2,0

Социальные опросы

Опросы разных категорий населения страны проводят для того, чтобы выявить, например, проблемы трудоустрой­ства, места размещения магазинов, школ и детских садов, мнения избирателей перед выборами и т. п. Анализ резуль­татов опросов позволяет принять правильные решения по тому или иному вопросу. Выбор будущей профессии являет­ся одним из важных решений, принимаемых человеком в своей жизни. Поэтому ответы на вопрос: «Какой фактор яв­ляется для вас наиболее значимым при выборе профессии, и, соответственно, вуза?» (Журнал «Обучение и карьера», 2006, № 4) представляют интерес для многих специалистов.

Фактор	Процент выбравших данный фактор
Интерес к определенной деятельности	54,63
Престиж и доходность выбираемой специальности	16,49
Возможность последущего трудоустройства	12,37
Другое	7,21
Предназначение	5,25
Возможности родителей	3,09
Советы родителей и друзей	1,06

Математический эксперимент

Для игрального кубика идеальной формы выпадение чи­сел от 1 до б будет равновероятным при числе опытов, стре­мящемся к бесконечности. То же справедливо для идеальной монеты, после подбрасывания она с одинаковой вероятно­стью Р = 1/2 будет падать на обе стороны (орел или решка). Чтобы убедиться в этом, можно провести эксперимент с боль­шим числом опытов. Результаты такого эксперимента приве­дены в следующей таблице. Ниже приведен фрагмент табли­цы одного из опытов. Всего было выполнено 14 серий опытов (с использованием случайной функции MS Excel).

№ опыта	Орел — 1 Решка — 0	№ опыта	Орел — 1 Решка — 0	№ опыта	Орел — 1 Решка — 0
1	0	13	0	25	0
2	0	14	0	26	0
3	1	15	1	27
4	1	16	1	28
5	0	17	0	29
6	1	18	1	30
7	1	19	0	31
8	1	20	0	32	0
9	0	21	1	33
10	0	22	0	34
11	0	23	1	35	0
12	1	24	0	36	1
37	0	177	0	189	0
38	0	178	0	190
39	1	179	1	191
40	1	180	0	192
41	1	181	0	193
42	1	182	1	194
43	0	183	1	195	0
44	0	184	1	196	0
45	0	185	1	197	1
46	1	186	0	198	0
47	1	187	0	199	0
48	0	188	0	200	0