Вучебниках информатики в общем виде информацион­ный процесс

Вид материала

Учебник

Содержание Логические выражения и их преобразования Законы логики и правила преобразования логических выражений Типовые логические устройства R = 0 и S = O.jro триг­гер находится в режиме хранения, на выходах Q Сумматоры [9, 31] Информационные (нематериальные) модели. Моделирование как метод познания Материальные модели Информационные модели Предметом изучения информатики являются общие принципы построения информационных моделей. Назначение и виды информационных моделей Для отражения состояния систем Для отражения систем с различными структурами В иерархических моделях Сетевые модели Основные этапы компьютерного моделирования 3. Анализ объекта моделирования для выделения су­щественных свойств с точки зрения цели моделирова­ния. 5. Разработка компьютерной модели для проведения эк­ сперимента 6. Компьютерный эксперимент Пример построения информационной модели

Подобный материал:

• 3. Процесс восприятия и управление впечатлением, 191.28kb.
• Понятие о программах и программировании, 592.28kb.
• Поволжская Государственная Академия Телекоммуникаций и Информатики задания и методические, 262.31kb.
• Общеобразовательный стандарт по информатике является нормативным документом, определяющим, 237.91kb.
• Финансы предприятий, 2102.05kb.
• Исходные технические данные, 34.3kb.
• Тема: Личность в системе современного, 42.1kb.
•     После то­го как я на­пи­сал «Счас­т­лив по соб­с­т­вен­но­му же­ла­нию», как-то, 1995.16kb.
• Компьютерная технология обучения и опережающая подготовка преподавателей, 49.99kb.
• Активизация познавательной деятельности школьников на уроках информатики, 32.08kb.

Логические выражения и их преобразования

Будем называть две функции F1 и F2 равносильными, или тождественными, если при любых значениях всех пере­менных, входящих вЛ и F2, эти функции принимают оди­наковые значения. Равносильность обозначается знаком ра­венства (=).



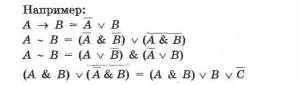
Посредством приведенных операций над высказывания­ми могут быть образованы другие, сколь угодно сложные высказывания.

Так можно получать из одной функции другую, равно­сильную ей.

Логические операции имеют следующий приоритет: дей­ствия в скобках, инверсия, &, v, —>, ~.

В алгебре логики имеется ряд законов, позволяющих осу­ществлять равносильные преобразования формул.

Законы логики и правила преобразования логических выражений

В алгебре, которую мы изучаем в школе, существуют пять основных законов: переместительные, сочетательные и распределительный. Среди законов алгебры логики есть по­добные законы.







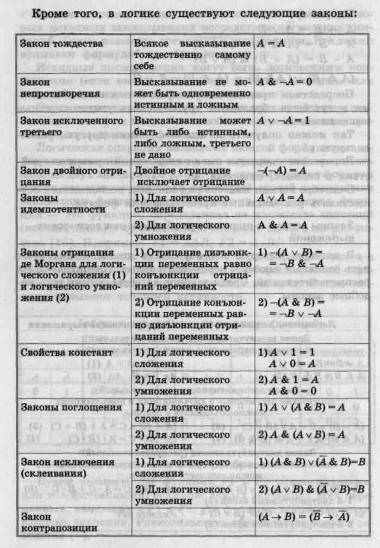
С использованием законов алгебры логики выполняются преобразования сложных логических функций.

Если логическая функция представлена с помощью дизъ­юнкций, конъюнкций и инверсий, то такая форма представ­ления называется нормальной.

Логическая функция называется тождественно ложной, если она принимает значение «ложь» на всех наборах вхо­дящих в нее простых высказываний. Например:



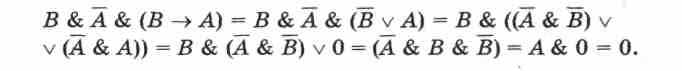
Логическая формула называется тождественно истин­ной, если она принимает значение «истина» на всех наборах входящих в нее простых высказываний (тождественно ис­тинные высказывания часто называют тавтологиями). На­пример:



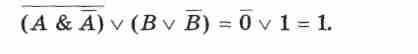
Построение таблиц истинности логических выражений

Таблица истинности логического выражения — это таб­лица, содержащая значения логического выражения, полу­ченные на всех значениях входящих в него логических пе­ременных.

Правило построения таблицы истинности:

1. Подсчитать количество N используемых переменных.
   
2. Определить число строк М в таблице по формуле М = 2*.
   
3. Подсчитать количество логических операций в логиче­ском выражении и определить количество столбцов в таблице, которое равно: количество переменных плюс количество логических операций.
   
4. Ввести названия столбцов таблицы в соответствии с по­следовательностью выполнения логических операций с учетом скобок и приоритетов.
   
5. Заполнить столбцы логических переменных наборами значений.
   

6. Провести заполнение таблицы истинности по столб­цам, выполняя логические операции в соответствии с установленной в п. 4 последовательностью.

Приведенные выше законы можно доказать построением таблиц истинности.

Построим таблицу истинности для доказательства равно-



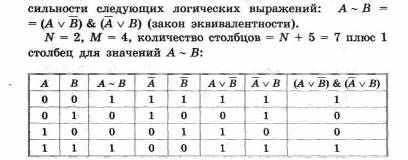
Столбцы, соответствующие искомым выражениям, совпа­ли. Следовательно, выражения равносильны.


Билет № 9

Логические элементы и схемы. Типовые логические устройства компьютера: полусумматор, сумматор, триг­геры, регистры.

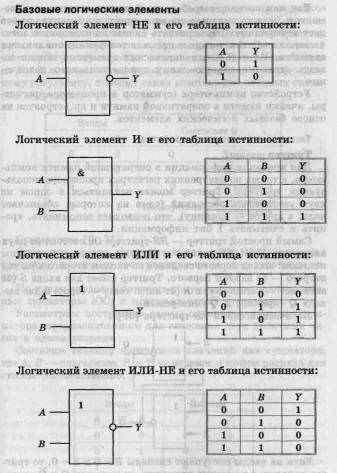
Работа компьютера состоит в операциях над двоичными кодами и пересылке этой информации по линиям связи. Средством обработки двоичных сигналов в компьютере яв­ляются логические элементы. Причем, для реализации лю­бых логических операций над двоичными сигналами доста­точно элементов трех типов, реализующих три основные ло­гические операции — И, ИЛИ, НЕ. Логический элемент — это электронная схема с одним или несколькими входами и одним выходом, через которые проходят электрические сиг­налы, представляющие цифры 1 и 0; на выходе логический элемент выдает значение логического произведения, логиче­ской суммы или отрицания.

Так как сигнал, выработанный одним логическим эле­ментом, можно подавать на вход другого элемента, то это дает возможность образовывать схемы из отдельных логи­ческих элементов, которые называются функциональными схемами. Из отдельных логических элементов можно со­здать функциональную схему арифметического назначе­ния.

Устройства компьютера (сумматор в процессоре, регист­ры, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.





Типовые логические устройства

Триггер

Для хранения информации в оперативной памяти компь­ютера, а также во внутренних регистрах процессора исполь­зуются триггеры. Триггер может находиться в одном из двух устойчивых состояний (одно из которых обозначает ноль, а другое — единицу), что позволяет запоминать, хра­нить и считывать 1 бит информации.

Самый простой триггер — iJS-трштер. Он состоит из двух элементов ИЛИ-НЕ, входы и выходы которых соединены кольцом: выход первого соединен со входом второго и выход второго — со входом первого. Триггер имеет два входа S (от англ. set — установка) и R (от англ. reset — сброс) и два вы­хода Q (прямой) и Q (инверсный).

Логическая схема .RS-триггера [39]:



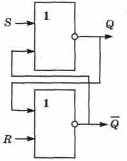
Е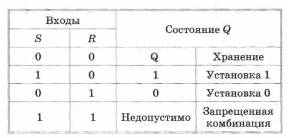сли на входы поступают сигналы R = 0 и S = O.jro триг­гер находится в режиме хранения, на выходах Q и Q сохра­няются установленные ранее значения.

Если на установочный вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет со­хранять это состояние, т. е. будет хранить 1. При подаче 1 на вход R триггер перейдет в состояние 0. Подача на оба вхо­да S и R логической единицы может привести к неоднознач­ному результату, поэтому такая комбинация входных сигна­лов запрещена.


Сумматоры [9, 31]

Сумматор — это вычислительная схема, выполняющая процедуру сложения поступающих на ее вход двоичных ко­дов.

По числу входов различают полусумматоры, одноразряд­ные сумматоры (ОС) и многоразрядные сумматоры.

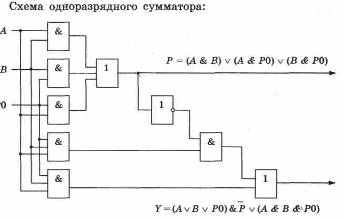
Рассмотрим построение схемы одноразрядного полусум­матора, предназначенного для сложения двух двоичных чи­сел в одном разряде.

С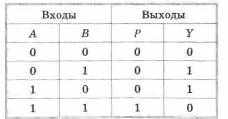оставим таблицу логических значений для сумматора, где А, В — слагаемые, Р и Y — перенос и цифра разряда для суммы соответственно:

Заметим, что Р — это функция, реализующая операцию конъюнкции двух переменных А и В, а У — отрицание опе­рации эквивалентности:

На основе полученных логических функций можно по­строить схему полусумматора. Схема требует два логиче­ских элемента И, один логический элемент ИЛИ, один логи­ческий элемент НЕ.



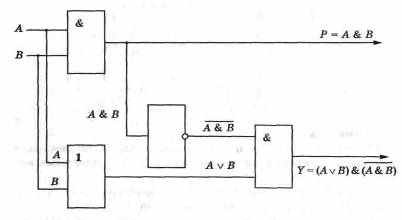
Эта схема называется полусумматором, так как в ней от­сутствует третий вход — перенос из предыдущего разряда.

С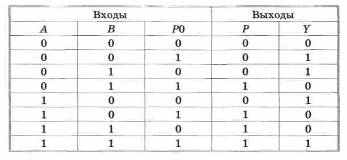хема полного одноразрядного сумматора должна содер­жать три входа: два слагаемых одного разряда и перенос из предыдущего разряда; и два выхода: сумму в данном разря­де и перенос в следующий разряд.

Составим таблицу логических значений для одноразряд­ного сумматора, где А, В — слагаемые, Pq — перенос из пре­дыдущего разряда, Р js.Y — перенос в следующий разряд и цифра разряда для суммы соответственно. В таблице будет 8 строк, так как имеется 3 входа.


Для сложения двух четырехразрядных чисел потребуется три одноразрядных сумматора и один полусумматор. Схема суммирования, на основе таких блоков, будет иметь вид:






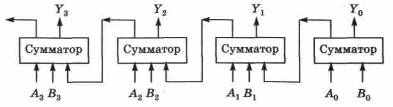
Здесь As, А₂, А\, Aq, В3, В%, 1» 0 — соответственно дво­ичные цифры слагаемых, У₃> 2» 1> о — двоичные цифры результата. Если единица переноса возникнет в старшем разряде, то она будет потеряна, говорят, что произойдет пе­реполнение разрядной сетки.

Чтобы избежать таких ситуаций, следует для перемен­ных в программах задавать соответствующий тип данных для целых чисел (например, LONGINT вместо INTEGER) или выбирать экспоненциальную форму записи (например, REAL).

Суммируемые коды поступают на входы сумматора одно­временно по всем разрядам. Для этого в каждом разряде ис­пользуется сумматор на три входа, на выходах которого об­разуются значения суммы Yi данного разряда и переноса Pj₊i в старший разряд. В процессе распространения сигнала переноса устанавливается окончательное значение суммы в каждом разряде. Очевидно, что в течение этого времени на входах сумматора присутствуют сигналы A_t, B_t, соответству­ющие суммируемым кодам. Максимальное по времени сум­мирование получается в том случае, когда перенос, возник­ший в первом разряде, распространяется по всем разрядам (например, при сложении кодов 11..11 и 00..01).

Регистр

Триггер запоминает один разряд двоичного числа. Для запоминания га-разрядного двоичного числа необходимо п соединенных между собой триггеров. Получаем n-разрядный регистр.


Билет № 10

Информационные (нематериальные) модели. Моделиро­вание как метод познания. Назначение и виды информа­ционных моделей. Основные этапы компьютерного моде­лирования.

Информационные (нематериальные) модели. Моделирование как метод познания

Прежде чем перейти к информационным и математиче­ским моделям, следует рассмотреть несколько примеров, по­ясняющих, что такое модель.

Прежде чем построить новый корабль, кораблестроитель сначала строит модель — маленький деревянный кораб­лик — и испытывает ее. Для того чтобы объяснить, как фун­кционирует система кровообращения, лектор демонстрирует плакат, на котором стрелочками изображены направления движения крови. Это модель системы кровообращения. Пе­ред тем как запустить в производство самолет, его помеща­ют в аэродинамическую трубу и с помощью соответствую­щих датчиков определяют величины напряжений, возника­ющих в различных местах конструкции. Это модель нагрузок, которые испытывает самолет .

Во всех перечисленных примерах имеет место сопоставле­ние некоторого объекта с другим, его заменяющим: реаль­ный корабль — деревянный кораблик; система кровообра­щения — схема на плакате; серийный самолет — единич­ный самолет в аэродинамической трубе. Причем во всех случаях предполагается, что какие-то свойства сохраняются при переходе от исходного объекта к его заменяющему. На­пример, хотя самолет, находящийся в аэродинамической трубе, и не летит, но напряжения, возникающие в его кор­пусе, соответствуют условиям полета.

Итак, можно сказать, что модель — это такой мате­риальный или мысленно представляемый объект, который замещает объект-оригинал с целью его исследования, сохра­няя некоторые важные для данного исследования типич­ные черты и свойства оригинала, т. е. его существенные стороны.

Хорошо построенная модель, как правило, доступнее для исследования, чем реальный объект (например, такой, как экономика страны, Солнечная система и т. п.). Другое, не ме­нее важное назначение модели состоит в том, что с ее помо­щью выявляются наиболее существенные факторы, формиру­ющие те или иные свойства объекта. Модель также позволяет учиться управлять объектом, что важно в тех случаях, когда экспериментировать с объектом бывает неудобно, трудно или невозможно (например, когда эксперимент имеет большую продолжительность или когда существует риск привести объ­ект в нежелательное или необратимое состояние).

Таким образом, мы можем сделать вывод, что модель не­обходима для того, чтобы:

• понять, как устроен конкретный объект — каковы его структура, основные свойства, законы развития и взаи­модействия с окружающим миром;
  
• научиться управлять объектом или процессом и опреде­лить наилучшие способы управления при заданных це­лях и критериях (оптимизация);
  
• прогнозировать прямые или косвенные последствия ре­ализации заданных способов и форм воздействия на объект.
  

Интересно, что хорошо построенная модель обладает уди­вительным свойством: ее изучение может дать некоторые новые знания об объекте-оригинале. Примером может слу­жить Периодическая система химических элементов Д. И. Менделеева. С ее помощью оказалось возможным как предсказание свойств существующих элементов, так и от­крытие новых элементов.

Процесс построения модели называется моделированием.

Модели могут быть материальными и информационны­ми. Материальные модели воспроизводят физические, гео­метрические и другие свойства объекта. Примеры: глобус, скелет, макеты зданий и мостов, модели самолетов, кораб­лей, автомобилей.

Предметом изучения информатики являются информаци­онные модели. Информационные модели представляют объекты в образной или знаковой форме. Объектом информа­ционного моделирования могут быть физические (падение тел), химические (реакции горения), биологические (фото­синтез в листьях растений) процессы, метеорологические яв­ления (гроза, торнадо), экономические (падение курса валю­ты), социальные (миграция, рост населения) процессы и т. д. Знаковая информационная модель может быть представлена в виде текста (программа на языке программирования), фор­мулы (второй закон Ньютона F = ma), таблицы (периодиче­ский закон Д. И. Менделеева), карты, схемы, чертежа (испо­льзуется язык графических элементов). Естественные языки используются для создания описательных информационных моделей (гелиоцентрическая модель мира Коперника). С по­мощью формальных языков строятся формальные информа­ционные модели (математические, логические). Модели, по­строенные с использованием математических понятий и формул, называются математическими моделями. В физике рассматривается много различных функциональных зависи­мостей, выраженных на языке алгебры, которые представля­ют собой математические модели изучаемых явлений или процессов.

Предметом изучения информатики являются общие принципы построения информационных моделей. Компьютер позволяет ученым работать с такими информационными мо­делями, которые требуют больших объемов вычислений, не­возможных в «докомпьютерную» эпоху. Лишь с помощью компьютера появилась возможность рассчитать прогноз пого­ды раньше, чем наступит завтрашний день.

Один и тот же объект может иметь множество различных моделей, и одна и та же модель может описывать разные объекты.

Назначение и виды информационных моделей

Назначение информационных моделей чаще всего состо­ит в получении данных, которые могут быть использованы для подготовки и принятия решений экономического, соци­ального, организационного или технического характера, для достижения наилучших показателей деятельности объ­екта моделирования. Объект моделирования можно рассмат­ривать как систему. Система — это сложный объект, состоя­щий из взаимосвязанных частей (элементов) и существую­щий как единое целое. Всякая система имеет определенное назначение (функцию, цель). Структура — это совокупность связей между элементами системы, т. е. внутренняя органи­зация системы.

Для отражения состояния систем используются статиче­ские и динамические модели.

Модели, описывающие состояние системы в определен­ный момент времени, называются статическими информа­ционными моделями (строение молекул, строение Солнеч­ной системы, «Система природы» К. Линнея).

Модели, описывающие процессы изменения и развития систем, называются динамическими информационными моделями (процесс протекания химической реакции, ядер­ной реакции, движения тел, развитие организмов и попу­ляций).

Для отражения систем с различными структурами ис­пользуются различные виды информационных моделей:

• Табличные модели применяются для описания объектов, обладающих одинаковыми наборами свойств. Могут быть динамическими и статическими. Свойства объекта пред­ставлены в виде списка, а их значения размещаются в ячейках прямоугольной таблицы (закон и Периодическая таблица химических элементов Д. И. Менделеева).
  
• В иерархических моделях объекты распределены по уровням. Каждый элемент более высокого уровня мо­жет состоять из элементов нижнего уровня, а элемент нижнего уровня может входить в состав только одного элемента более высокого уровня (генеалогическое дере­во, классификация объектов).
  
• Сетевые модели применяются для отражения таких си­стем, в которых связи между элементами имеют слож­ную структуру (сеть Интернет, телефонная сеть, про­цесс передачи мяча в коллективной игре, например, в футболе). Могут быть статическими и динамическими.
  

Основные этапы компьютерного моделирования

1. Постановка задачи характеризуется описанием объ­екта моделирования в общем виде, определением конечного результата моделирования и имеющихся условий (возможно
ограничений).

2. Определение цели моделирования. От выбранной цели зависит, какие характеристики объекта моделирова­ния считать существенными, какие методы лучше подходят для решения данной задачи.

3. Анализ объекта моделирования для выделения су­щественных свойств с точки зрения цели моделирова­ния. Нет единственно правильного способа выделения суще­ственных свойств объекта моделирования, поскольку объек­ты моделирования серьезно отличаются. Это может быть материальный объект, некая сложная информационная сис­тема, промышленный процесс и пр. Иногда необходимые
свойства объекта могут быть очевидны, а порой приходится перебрать множество вариантов, прежде чем будет достигну­ та цель моделирования. Поэтому к этапам п. 2 и п. 3 можно
возвращаться многократно. Адекватность модели объекту моделирования будет зависеть еще и от того, как выделен­ные существенные свойства мы сможем формализовать, т. е. в какой форме мы их отобразим.

4. Формализация (определение и приведение к выбран­ной форме). Важный этап моделирования, влияющий на ре­зультат. От выбранной формы представления данных зави­сит, насколько точен будет конечный результат, в какой степени построенная модель соответствует объекту. Форма­ми представления могут быть: словесное описание, чертеж, таблица, формула, схема, алгоритм, компьютерная програм­
ма и т. п.

Итак, форма представления модели определена, и данные формализованы для обработки. Конечной целью этого этапа является создание информационной модели.

5. Разработка компьютерной модели для проведения эк­ сперимента:

а) создание математической или имитационной модели
для исследования с помощью компьютера;

б) проверка данных и условий на непротиворечивость;

в) планирование эксперимента.

Существует множество программных комплексов, кото­рые позволяют строить и исследовать самые разные по на­значению модели. Разнообразное программное обеспечение позволяет преобразовать исходную информационную модель в компьютерную и провести компьютерный эксперимент.

В процессе разработки компьютерной модели исходная информационная модель будет претерпевать некоторые из­менения по форме представления, так как должна ориенти­роваться на определенную программную среду и инструмен­тарий. После внесения уточнений необходимо перепрове­рять данные и условия на непротиворечивость. В результате проверки может возникнуть необходимость возврата к п. 2 или п. 3.

План эксперимента должен четко отражать последова­тельность работы с моделью.

6. Компьютерный эксперимент:

а) исследованиме модели;

б) анализ полученных результатов на соответствие цели
моделирования;

в) уточнение модели.

Компьютерный эксперимент включает в себя исследова­ние модели в соответствии с поставленной целью.

Конечная цель моделирования — принятие решения, ко­торое должно быть выработано на основе всестороннего ана­лиза результатов моделирования. Анализ полученных ре­зультатов на соответствие цели моделирования — решаю­щий этап для дальнейшей работы. Если результаты не соответствуют целям поставленной задачи, значит, на пре­дыдущих этапах были допущены ошибки. Если такие ошиб­ки выявлены, то требуется уточнение (корректировка) моде­ли. Корректировка может быть незначительной в рамках проведения самого эксперимента или существенной, требую­щей возврата к предыдущим этапам.

Процесс повторяется до тех пор, пока результаты не бу­дут удовлетворять цели моделирования и их можно будет использовать для принятия решений.

Пример построения информационной модели

Задача Фибоначчи (из «Книги абака» итальянского ма­тематика Фибоначчи, 1228 г.) [27]:

«Некто поместил пару кроликов в некоем месте, огоро­женном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что каждый месяц пара кроликов произво­дит на свет другую пару, а рождают кролики через два меся­ца после своего рождения».

Задача Фибоначчи сводится к последовательности чисел:

1, 1, 1, 2, 3, 5, 8, 13, 21, ... ,

где каждый последующий член равен сумме двух предыду­щих, за исключением первых двух членов.

Математическая модель размножения кроликов:

fib(n) = fib(n - 1) + fib{n -2), п > 2,

где fib(n) — количество пар кроликов, рожденных за п меся­цев, fib(l) = 1 и fib(2) = 1.

Анализ модели

В таблице приведены результаты моделирования процес­са размножение кроликов, из которых видно, что кролики размножаются катастрофически быстро. Согласно модели у кроликов нет врагов и запас корма у них не ограничен, что, вероятно, и ведет к бесконтрольному размножению. С дру­гой стороны, в модели ограничено количество рождаемых пар кроликов — только одна пара, казалось бы, это должно сдерживать их рост. В модели не отражена возможность за­болеваний и эпидемий. Можно ли считать такую модель адекватной реальной ситуации?




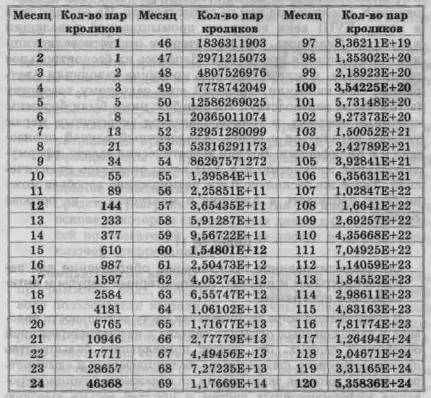
Модель строится, в частности, для того, чтобы получить дополнительную информацию об объекте моделирования. При этом подразумевается, что информация, полученная при исследовании модели, может быть с той или иной степенью достоверности перенесена на объект. Адекватность модели объекту предполагает воспроизведение моделью с необходи­мой полнотой всех характеристик объекта, существенных для целей моделирования. То есть, создав модель, надо отве­тить на вопрос, возможно ли такое в действительности.

В книге Я. И. Перельмана «Живая математика» приведе­ны несколько примеров необыкновенно быстрого размноже­ния животных, поставленных в благоприятные условия. О реальном размножении кроликов в Австралии мы знаем из учебника истории. Когда этот материк был открыт евро­пейцами, кроликов на нем не существовало. Их завезли туда в конце XVIII века во время промышленной революции в Англии. Оказалось, что на материке отсутствовали хищ­ники, питающиеся кроликами. Началось их бесконтрольное размножение, и вскоре полчища кроликов наводнили Авст­ралию. Они наносили огромный вред сельскому хозяйству (в том числе овцеводству). На борьбу с ними были брошены огромные средства, и только благодаря энергичным мерам удалось справиться с бедой. Аналогичный случай произо­шел и в Калифорнии. Вот так теоретическая задача, сформу­лированная математиком в XIII веке, оказалась практиче­ской. Такое же бесконтрольное размножение воробьев мож­но было наблюдать в Америке и мангустов — на острове Ямайка.