А. Б. Тазаян Учебно-методический комплекс дисциплины "Логика" Ростов-на-Дону 2010 Учебно-методический комплекс
| Вид материала | Учебно-методический комплекс |
- А. Б. Тазаян Учебно-методический комплекс дисциплины "Юридическая логика" (для студентов, 1003.39kb.
- А. Б. Тазаян Учебно-методический комплекс дисциплины "Философия права" (для студентов, 524.1kb.
- И. Д. Алекперов учебно-методический комплекс дисциплины "информатика" Ростов-на-Дону, 952.05kb.
- И. Л. Литвиненко учебно-методический комплекс по дисциплине международный туризм ростов-на-Дону, 398.8kb.
- О. А. Миронова Учебно-методический комплекс дисциплины «международная торговля» Ростов-на-Дону, 727.71kb.
- М. Л. Сирунян учебно-методический комплекс дисциплины «Долгосрочная финансовая политика», 366.75kb.
- Л. Л. Гришан Учебно-методический комплекс по дисциплине «Аудит» Ростов-на-Дону, 2010, 483.53kb.
- Н. В. Брюханова учебно-методический комплекс по дисциплине «История менеджмента», 307.48kb.
- О. А. Миронова Учебно-методический комплекс дисциплины «основы международного бизнеса», 782.97kb.
- Г. С. Яблоновская Учебно-методический комплекс дисциплины " Деньги, кредит, банки", 642.15kb.
2.2.2. Виды понятий.
Выделение видов понятий осуществляется по трем основаниям : 1) по некоторым характеристикам объектов понятия ; 2) по типам обобщаемых понятий ; 3) по характеру признаков, составляющих видовое отличие мыслимых предметов в понятии ( по характеру предмета, выражающих это видовое отличие ).
По объему понятия делятся на пустые и непустые. Непустые понятия в сою очередь делятся на единичные и общие.
Пустые понятия имеют в качестве объема пустой класс, т.е. понятие , в объеме которых нет ни одного элемента. Различают понятия логически и фактически пустые.
Например, «круглый квадрат», «космонавт, побывавший на Марсе», «частица, движущаяся со скоростью больше скорости света».
К единичным относятся понятия, в объеме которых содержится ровно один элемент.
Например, «первый космонавт», «альпинист, впервые покоривший Эверест», «автор романа «Война и мир»». и т.д.
(добавить отличие понятий от имен)
К общим относятся понятия, в объеме которых содержится более чем один элемент.
Например, «астронавт, побывавший на Луне», «человек, любящий игровые виды спорта», «прямоугольный треугольник» и т.д.
Среди общих понятий выделяют универсальные понятия. Универсальными являются понятия, объемы которых совпадают с родом этого понятия.
Например, «квадрат, у которого все стороны равны», «человек, умеющий мыслить и производить искусственные орудия труда» и т.д.
В этих понятиях видовые отличия – « равенство все сторон» и «умеющий мыслить и производить искусственные средства труда» - присущи всем квадратам и людям, поэтому эти признаки не позволяют из универсума (родового понятия) выделить видовое понятие.
По типу обобщаемых предметов понятия делятся на конкретные и абстрактные, собирательные и несобирательные.
Конкретными являются понятия, элементами объема которого
являются отдельные предметы, представленные в универсуме рассуждения.
Например, «белый костюм», «мужественный человек»,, «свидетель»
Абстрактными являются понятия, в которых обобщены отдельные стороны, свойства, отношения предметов, представленные в универсуме рассуждения.
Например, «белизна», «мужество», «справедливость» и т.д.
Собирательными являются понятия, элементами объема которых предстают некоторые совокупности, мыслимые как целое.
Например, «флот», «библиотека», «рота» и т.д.
Несобирательными являются понятия, элементами объема которых выступают предметы, мыслимые как нерасчлененное целое.
Например, «студент», «юрист», «адвокат».
По характеру видового отличия понятия делятся на положительные и отрицательные, относительные и безотносительные.
Понятие положительно, если оно выражает наличие у предмета какого-либо свойства или отношения.
Например, «Ростов-на-Дону – столица ЮФО».
Понятие отрицательно, если признак указывает на отсутствие какого-либо свойства или отношения.
Например, «Ростов-на-Дону – не является столицей РФ».
Относительными являются понятия , в которых признак представляет реляционное свойство ( реляция – от лат. relatio донесение ): содержание которого представляет собой наличие или отсутствие отношения мыслимого в нем предмета к некоему другому предмету, в котором мыслиться предмет, обусловливающий существование другого предмета.
Примеры относительных понятий : «брат», «студент ИУБиП» и т.д.
Безотносительными являются понятия, видовые отличия которых не являются реляционными свойствами , т.е. отображают признак предмета вне его связи с другими предметами.
Например, «рабочий», «устав» и т.д.
2.2.3. Отношения между понятиями.
Понятия находятся в различных отношениях друг к другу. Они, прежде всего, являются сравнимыми и несравнимыми. Понятия сравнимы, если они имеют общий род. Если у понятий нет общих родовых признаков, то они несравнимы. Несравнимые понятия не вступают в какие-либо логические отношения. Сравнимые понятия делятся на совместимые и несовместимые.
Совместимые понятия делятся на три вида отношений: равнозначности, подчинения, пересечения.
Отношение равнозначности между понятиями имеет место тогда и только тогда, когда объемы этих понятий полностью совпадают. Другими словами, равнозначные понятия отсылают к одному и тому жен классу предметов, но делают это по-разному.
Отношение подчинения между понятиями имеет место тогда и только тогда, когда объем одного полностью входит в объем другого, но обратное не верно.
Отношение перекрещивания (пересечения) между понятиями имеет место тогда и только тогда, когда их объемы частично совпадают.
По несовместимости понятия делятся на три вида отношений: противоречия (контрадикторности), противоположности ( контрарности), соподчинения (координации).
Отношение противоречия (контрадикторности) между понятиями имеет место тогда и только тогда, когда они являются видами одного и того рода, притом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, не заменяя их другими признаками.
Отношение противоположности ( контрарности) между понятиями имеет место тогда и только тогда, когда они являются видами одного и того рода, притом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, заменяя признаками их исключающими.
Отношение соподчинения (координации) между понятиями имеет место тогда и только тогда когда, когда, объемы двух и более понятий исключают друг друга, но принадлежат общему родовому понятию. Это виды одного и того рода.
Отношения между понятиям можно изобразить в виде круговых схем.
Отношение равнозначности. Понятия «студент» и «учащийся высшего учебного заведения» находятся в отношении равнозначности. Если понятие
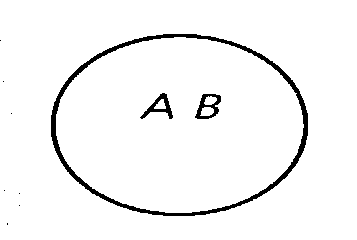
«студент» обозначим буквой А, а понятие «учащийся высшего учебного заведения» — буквой В, то отношение равнозначности между этими понятиями изобразится в виде двух совпадающих кругов (Рис. 1).
Рис. 1
Отношение подчинения. Понятия «студент» и «студент ИУБиП» находятся в отношении подчинения. Подчиняющим понятием будет «студент», подчиненным – «студент ИУБиП». Если понятие «студент» обозначим буквой А, а понятие «студент ИУБиП» - буквой В, то отношение подчинения между этими понятиями изобразиться в виде двух кругов, причем объем подчиненного понятия полностью входит в объем подчиняющего (Рис. 2).
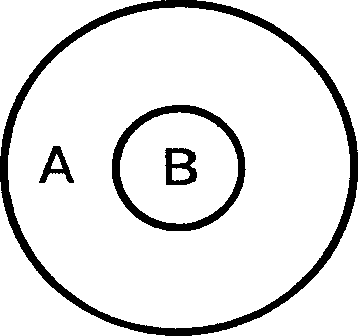
Рис.2.
Отношение перекрещивания ( пересечения). Понятия «студент» и «спортсмен» находятся в отношении перекрещивания. Если понятие «студент» обозначим буквой А , а понятие «спортсмен» - буквой В, то отношение перекрещивания между этими понятиями изобразится в виде пересекающихся двух кругов ( Рис. 3).

Рис. 3.
Отношение противоречия (контрадикторности). Понятия «студент» и «нестудент» находятся в отношении противоречия. Если понятие «студент» обозначим буквой А, а понятие «нестудент» - буквой не-А, то отношение противоречия между этими понятиями изобразится в виде разделенного круга (Рис.4).
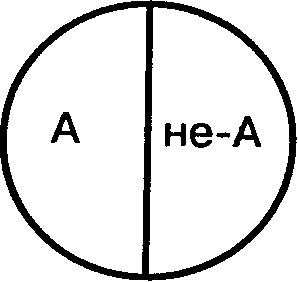
Рис.4
Отношение противоположности (контрарности). Понятия «белый» и «черный» находятся в отношении противоположности. Если понятие «белый» обозначим буквой А, а понятие «черный» - буквой В, то отношение противоположности между этими понятиями изобразится в виде следующего рисунка ( Рис. 5).
Рис. 5.
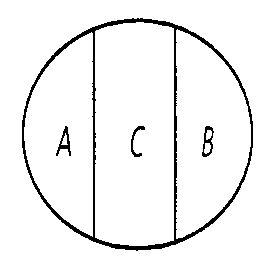
Отношение соподчинения (координации). Понятия «учащийся», «школьник» и «студент» находятся в отношении соподчинения. Если понятие «учащийся» обозначим буквой С, понятие «школьник» - буквой А, а понятие «студент» буквой В, то отношение соподчинения между этими понятиями изобразится в виде отдельных неперекрещивающихся кругов внутри третьего круга (Рис.6).
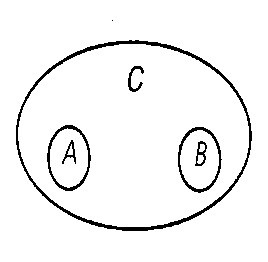
Рис. 6.
2.2.4. Определение.
В научной деятельности широко используется логическая операция, получившая название определения. Определение ( или дефиниция от лат. definition – определение) – это логическая операция, заключающая в придании точного смысла языковому выражению. Процедура определения решает две теоретические задачи: (1) уточняет содержание уже используемых понятий; (2) вводит в научный оборот новые понятия. Сама процедура определения наделяет предмет отличительными признаками, указывающими, с одной стороны, способ его бытия, с другой, - выделяющими и отличающими его от других предметов. Эти признаки предмета, следуя классической философской традиции, называют существенными.
Логика выделяет различные способы и правила определений, выявляет типичные ошибки, допускаемые в исследовательской деятельности, и их теоретические последствия.
В науке применяются определения различных видов. Это, прежде всего, реальные и номинальные определения. В реальных определениях на основе системы признаков осуществляется выделения предмета или класса однородных предметов в понятие. Посредством реальных определений в основном уточняется смысл используемых языковых выражений. Номинальные определения – это соглашение относительно способов употребления тех или иных языковых выражений ( понятий, терминов и т.д.).
Деление определений на реальные и номинальные – это деление по их выполняемым функциям в научном познании. По форме определения можно разделить на два вида: явные и неявные.
Явными называются определения, имеющими структуру: «Dfd ≡ Dfn» где Dfd - дефиниендум (определяемое выражение), Dfn – дефиниенс (определяющее). Знак «≡» - устанавливает логическое отношение между дефиниендумом и дефиниенсом. Это обычно отношение тождества или эквивалентности. Неявные определения такой формы не имеют.
Среди явных определений выделяют определение через род и видовое отличие, которое широко используется в социально-гуманитарных науках.
Определение через род и видовое отличие делится на:
1) атрибутивно-реляционные определения. В этих определениях видовыми отличиями выступают или свойства(атрибуты) предметов, или отношения (реляции) между ними.;
2) генетические определения. В качестве видового отличия выступает способ происхождения предмета;
3) операциональные определения, определения в которых указывается действие, с помощью которого становится возможным распознавание предмета.
К явным определениям предъявляются следующие требования:
1) правила взаимозаменяемости: при замене Dfd на Dfn (или же Dfn на Dfd) истинностное значение языкового выражения, в которую они входят, должно оставаться неизменным. Это правило соразмерности Dfd и Dfn, т.е. их объемы должны совпадать. При нарушении этого правила возникают следующие ошибки:
- «ошибка слишком широкого определения»: объем Dfn( определяющего) понятия шире Dfd (определяемого);
- «ошибка слишком узкого определения»: объем Dfn (определяющего) уже Dfd(определяемого);
- «перекрещивающееся определение»: объемы Dfd и Dfn частично совпадают;
2) в определении не должно быть «порочного круга». Нельзя определять понятие через само себя или понятие, которое, в свою очередь, определяется через определяемое понятие;
3) определение должно быть ясным ( в классической логике это требование приобретает строгою форму и предстает в качестве правила однозначности): каждому Dfd должен соответствовать
Среди неявных определений выделяют остенсивные и контекстуальные определения.
Остенсивные ( от лат. ostensio – показывание)- это разъяснение слов и словосочетаний путем непосредственного указывания на предмет.
Контекстуальные [ от лат. contextus ( тесная связь, соединение) – законченный в смысловом отношении отрывок текста.] определения – определения смысловое содержание которых следует из отрывка текста. Смысловая целостность контекста описания, установившаяся связь данного понятия с другими, уже известными, выражениями языка, позволяет выявить его содержание. Контекстуальные определения, конечно, далеки от идеала строгости, хотя имеют большое хождение в современном неклассическом дискурсе.
2.3. Лекция: Суждение
2.3.1. Общая характеристика суждения.
2.3.2 Простые суждения.
2.3.3 Отношение между суждениями по истинности.
2.3.4. Сложное суждение и его виды.
2.3.1. Общая характеристика суждения.
Структура языка в целом, в общих чертах совпадает со структурой мысли. Поэтому можно выявить соответствие между семантическими категориями языка логики с грамматическими составляющими естественного языка. В зависимости от грамматической структуры предложения, например, русского языка могут быть: а) повествовательными; б) вопросительными, повелительными, Эти грамматические формы позволяют адекватно выразить в языке различные стороны человеческой активности. Логика, являясь неотъемлемым компонентом познания, представлена в такой грамматической форме языковых выражений, в которой представлены утверждения, то есть форме повествовательных предложений. Только повествовательные предложения ( которые репрезентируют одну из форм мыслительной деятельности) могут утверждать нечто о положении дел в мире. А определяющая цель познания – постижение истины. Истинность и ложность утверждений, представленные в повествовательных предложениях, в значительной мере обусловлены их логической формой. В логике эта форма мысли называется суждением. Суждение - форма мысли, в которой утверждается или отрицается что-либо относительно вещей и явлений, их свойств, отношений, и которая обладает признаком выражать либо истину, либо ложь.
Суждения разделятся на простые и сложные.
2.3.2. Простые суждения.
Среди простых суждений различают атрибутивные суждения и суждения с отношениями. В основе этого разделения лежит отличие признаков: свойства от отношений.
В атрибутивных суждениях утверждается или отрицается принадлежность предмету определенных свойств (атрибутов). В состав (элементы структуры) простого атрибутивного суждения входят: субъект-термин, предикат-термин, связка. Та часть суждения, которая обозначает предмет мысли, о котором в суждении нечто утверждается (наличие или отсутствие некоего признака), называется субъектом и обозначается латинской буквой S ( от лат. subjectum- подлежащее). Часть суждения, которая обозначает то, что утверждается о предмете мысли ( субъекте) – называется предикатом и обозначается латинской буквой Р ( от лат.praedicatum- сказуемое). В нестрогом смысле, можно говорить о субъекте как о логическом подлежащем, а о предикате – логическом сказуемом. Отношение между субъектом и предикатом устанавливается посредством связки. Связка указывает на характер связи между предметом мысли и определенным свойством. Она всегда представлена в какой-либо форме глагола быть: «есть», «суть», «является», иногда она заменяется тире. Схема атрибутивного суждения может быть представлена “S есть Р” или “S не есть Р”.
Определив элементы структуры простого атрибутивного суждения, понятным становится его определение: суждение называется простым, если оно не содержит в себе частей, которые сами являются суждениями. То есть не являются суждениями выражения, имеющие схему: «S есть», «есть Р», «Р» и т.д.
Пример атрибутивного суждения: «Аристотель является основателем логики как науки». Субъектом данного суждения является «Аристотель», предикатом – « основателем логики как науки», а связкой – «является». Логическая структура данного простого суждения имеет вид: « S есть P».
Суждения отношениями устанавливают отношения причины и следствия, , пространственные, временные и т.д. В них говориться об отношении между предметами. Символически суждения отношения выражаются формулой "х Rу", где символы х и у – имена предметов, а R – имя, обозначающее отношение между этими предметами. Читается формула: "х и у находятся в отношении R", или "х находится в отношении R к у". Суждения с отношениями можно рассматривать субъектно-предикатной форме, где предметы ( х, у) – субъект суждения, а R их связывающий предикат.
Пример суждения с отношениями. « Краснодар (х) южнее (R) Ростова-на-Дону (у)».
Виды простых категорических суждений. Исторически сложилось так, что в традиционной логике особо выделяют вид простых атрибутивных суждений – категорические суждения. Первая теория логического вывода, силлогистика Аристотеля, устанавливает логические отношения между этим видом суждений. В категорическом суждении утверждается или отрицается о наличии у предмета мысли какого–либо свойства. То есть между субъектом и предикатом данного вида суждения устанавливается категорическая (утвердительная или отрицательная) связь.
Категорические суждения делятся на виды по качеству и количеству.
По качеству категорические суждения разделяются на утвердительные и отрицательные. В утвердительных суждениях указывается на наличие у предмета некоторого свойства ( «Некоторые студенты – отличники»). В отрицательных суждениях утверждается от отсутствии какого-либо свойства у предмета мысли. ( «Ни один космонавт не был на Марсе»). В отрицательных суждениях речь идет не об отрицательных признаках, а об отсутствии у предмета того или иного свойства. В отрицательных суждениях частица «не» модифицирует связку. Например, возьмем два суждения: « Некоторые отличники являются нестудентами» и «Некоторые отличники не являются студентами». По смыслу они совпадают, оба суждения утверждают, что определенная часть отличников исключена из класса студентов. Но если первое суждение является утвердительным, то второе - отрицательным. Суждения, имеющие структуру «S есть Р» - являются утвердительными, а « S не есть Р» - отрицательными.
По количеству категорические суждения делятся на единичные, общие и частные. Суждение является общим, частным или единичным в зависимости от того говорим ли мы обо всех элементах субъекта-термина, только некоторых из них, или же об одном предмете. Примеры суждений: «Все студенты имеют высшее образование»(общее), «Некоторые студенты являются отличниками» (частное), « А.С. Пушкин является гениальным поэтом» ( единичное).
Единичные суждения в традиционной логике трактуются как общие, так как они, как и общие суждения, наделяют определенным свойством все элементы объема субъекта-термина ( но объемом субъекта единичного суждения является одноэлементный класс). То есть по формальным основаниям единичные и общие суждения можно рассматривать в качестве тождественных. [Конечно, с точки зрения современной (математической) логики такое рассмотрение не имеет необходимых логических оснований и является в значительно мере произвольным]. Таким образом, простые категорические суждения по количеству делятся на общие и частные.
При анализе рассуждений на предмет их корректности (правильности или неправильности) используется объединенная классификация категорических суждений по качеству и количеству.
Объединенная классификация простых категорических суждений по качеству и количеству включает в себя следующие типы суждений:
а) общеутвердительные ( суждения , которые одновременно являются
общими утвердительными). Логическая структура общеутвердительного
суждения: « Все S суть Р»;
б) общеотрицательные (одновременно общие и отрицательные). Структура
общеотрицательных суждений: «Ни одно S не суть Р»;
в) частноутвердительные (одновременно частные и утвердительные).
Структура частноутвердительных суждений: «Некоторые S суть Р»;
г) частноотрицательные ( одновременно частные и отрицательные).
Структура частноотрицательного суждения: « Некоторые S не суть Р».
Выделенные объединенной классификацией типы категорических суждений получили буквенные обозначения. Общеутвердительные суждения называются суждения типа А , общеотрицательные – типа Е, частноутвердительное – типа I. а частноутвердительное – суждение типа О.
Таким образом, вышеуказанные субъектно-предикатную структуру категорических суждений можно выразить посредством буквенных обозначений:
«Все S суть Р» ─ «S a P»;
« Ни одно S не суть Р» ─ «S e P»;
« Некоторые S суть Р» ─ «S i P»;
« Некоторые S не суть Р» ─ « S o P».
2.3.3.Отношение между категорическими суждениями.
Категорические суждения находятся в различных логических отношениях, в отношениях их совместимости по истинности, ложности. Выделяют следующие отношения между категорическими суждениями: противоречия ( контрадикторности), противоположности (контрарности), субконтрарности и логического подчинения.
Отношение противоречия(контрадикторности) Два суждения находятся в отношении противоречия, если и только если они несовместимы не по истинности, ни по ложности.
Отношение противоположности( контрарности). Два суждения находятся в отношении противоположности, если и только если они не совместимы по истинности, но совместимы по ложности.
Отношение субконтрарности. Два суждения находятся в отношении субконтрарности, если и только если они совместимы по истинности, но не совместимы по ложности.
Отношение логического подчинения. Суждение В логически подчиняется суждению А, если и только если из А логически следует В, но из В не следует А.
Отношение между категорическими суждениями можно изобразить посредством логического квадрата:
Противоположность (контрарность)
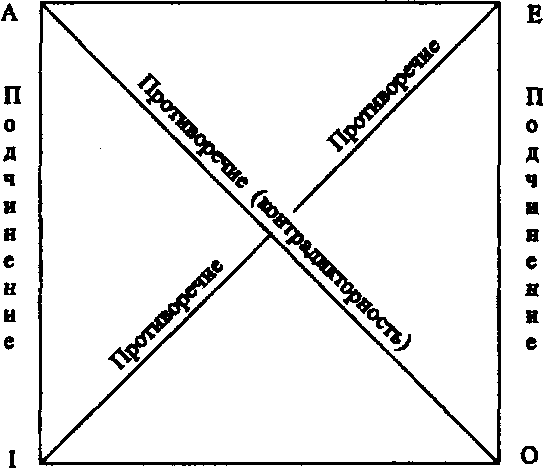
Субконтрарность
Распределенность терминов в категорических суждениях.
Установление отношения между объемами терминов в категорических суждениях является необходимым условием проверки корректности определенного типа рассуждений. Субъект(S) и предикат (Р) могут быть взяты в полном или не в полном объеме в их отношениях в суждениях. Если термин взят в полном объеме, то он распределен( распределенный термин обозначается знаком «+»), в противном случае он нераспределен (нераспределенный термин обозначается знаком «─»).То есть, если объемы терминов суждения находятся одно-однозначном отношении или их объемы не имеют общих элементов , то эти термины распределены, распределенным также считается термин объем которого является частью объема другого термина. Если термин частично включается или частично исключается из объема другого термина, он нераспределен. Объемные отношения между терминами в категорических суждениях могут быть изображены при помощи круговых схем Эйлера.
Рассмотрим некоторые отношения объемов терминов всех четырех типов категорических суждений.
Суждение А – общеутвердительное( “Все S+ суть Р ─”): «Все люди – смертны»(Рис.1)
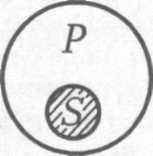
Рис.1.
Суждение Е – общеутвердительное ( Ни одно S+ не суть Р+): «Ни одно преступление не совершается в рамках закона» (Рис.2).
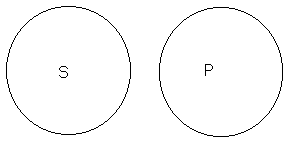
Рис.2.
Суждение I – частноутвердительное ( Некоторые S─ суть Р─): «Некоторые преступления совершаются непреднамеренно»(Рис.3).

Рис.3.
Суждение О – частноотрицательное ( Некоторые S─ не суть Р+): «Некоторые преступления не являются преднамеренными» (Рис.4).
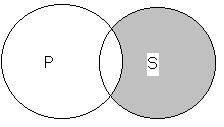
Рис.4.
Сводная таблица распределенности терминов в категорических суждениях:
.
| Термины | Виды суждений | |||
| А | Е | I | О | |
| S | + | + | – | – |
| Р | – | + | – | + |
