Математическая интеллектуальная игра

Вид материала

Подобный материал:

МОУ Россоловская ООШ

Математическая

интеллектуальная

игра

Разработала учитель математики

Груздева Галина Викторовна

2010 год

Величие человека - в его способности мыслить.

Б. Паскаль

Интеллектуальная игра «Морской бой»

Цель игры: повышение интереса к изучению математики, развитие логического мышления, развитие личностных качеств учащихся

«Морской бой» - излюбленная игра и младших, и старших школьников.

Главная цель – «потопить» корабли противника путём прямого попадания в корабль.

Игровое поле – квадрат, состоящий из 10 строк, обозначенных числами от 1 до 10, и 10 столбцов, обозначенных буквами от А до К. Координаты цели определяются именем столбца и строки.

Все участники делятся на 2 команды. Игровое поле – одно для обеих команд. На игровом поле размещены «корабли»: четырёхпалубный, трёхпалубные, двухпалубные и однопалубные.

Все клетки кораблей закрашены. Клетки, касающиеся бортов, обозначены буквами, соответствующими разделу математики (теме): «А» - алгебра, «С» - задачи на смекалку, «Ч» - всё о числах, «К» - комбинаторика, «Г» - геометрия, «Л» - логические задачи, «И» - из истории математики, «М» - о математиках. (Последние две темы связаны между собой).

О

стальные клетки пустые. Участникам необходимо «овладеть» всеми кораблями. По очереди команды делают выстрелы – указывают координаты на игровом поле. Ведущий называет указанный квадратик. Если под ним окажется одна из палуб корабля, то команде начисляется 1 очко и даётся право на следующий выстрел. Если произошло попадание в букву, то это значит, что рядом находится борт одного из кораблей. Команде задаётся соответствующий вопрос. Если ответ правильный, команда также получает 1 очко и право на следующий выстрел. Игра завершается после того, как участники «потопят» все корабли. Побеждает команда, набравшая наибольшее количество очков.

Вопросы на «А»:

Д 1. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Дедка, Бабка, Внучка, Жучка, Кошка и Мышка могут вытащить Репку, а без Мышки не могут. Сколько надо позвать Мышек, чтобы они сами смогли вытащить Репку?

(1237)

Е 1. Масса рыбы 8 кг плюс половина её собственной массы. Какова масса рыбы?

(16 кг)

Ж 1. Вычислите:

.

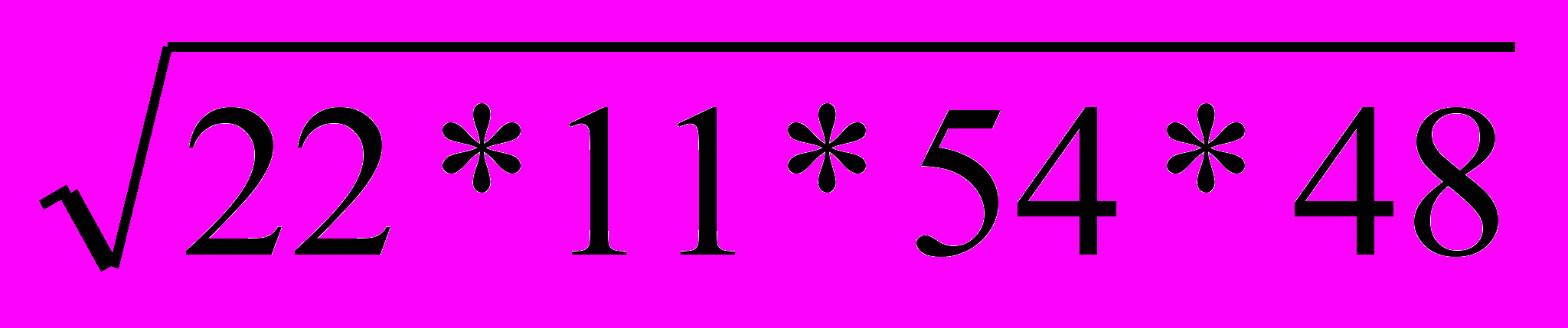(792)

З 2. Летели Галки,

Сели на палки.

Сели по одной –

Галка лишняя.

Сели по две –

Палка лишняя.

Сколько было Галок

И сколько было палок?

(4 Галки и 3 палки)

Ж 3. – Который теперь час? – спросил Миша у отца.

- А вот сосчитай: до конца суток осталось втрое меньше того времени, которое прошло от их начала. Миша сосчитал. Сосчитайте и вы.

(18 часов)

Е 3. Я задумал 3 числа. Какие это числа, если известно, что произведение всех трёх чисел равно 240, произведение первых двух равно 60, а произведение второго и третьего чисел равно 80?

(3; 20; 4)

Д 3. Кирпич имеет массу 1,5 кг и ещё полкирпича. Какова масса кирпича?

(3 кг)

Г 2. После того как пешеход прошёл 1 км и половину оставшегося пути, ему осталось пройти треть всего пути и 1 км. Как велик весь путь?

(9 км)

Вопросы на «С»:

Б 1. В комнате 4 угла. В каждом углу сидит кошка. Напротив каждой кошки сидит кошка. Сколько всего кошек в комнате?

(4)

В 2. Число 666 увеличить в полтора раза, не производя никаких арифметических действий.

(Перевернуть, будет 999)

В 3. Может ли дробь, в которой числитель меньше знаменателя, быть равной дроби, в которой числитель больше знаменателя?

(Может, например, -3/6 = 5/-10)

Б 4. Сколько ударов в сутки делают часы с боем?

(156)

А 3. К Айболиту пришли на приём животные: все, кроме двух, собаки; все, кроме двух, кошки; все, кроме двух, зайцы. Сколько всего животных пришли лечиться?

(3)

А 2. Президент кондитерской компании спрашивает: «Чьё предложение принять, если первый дилер предлагает за продукцию 2² 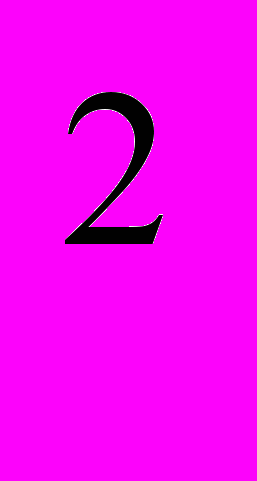тыс. руб., а второй – (2²)²)² тыс. руб.?»

(Предложение второго дилера выгоднее, т.к. 2²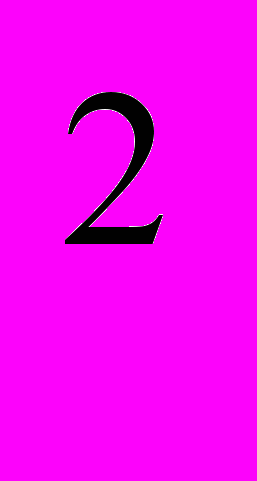= 16, (2²)²)² = 256.)

Вопросы на «Г»:

А 4. Можно ли вычислить длину дуги, если известно только число градусов, содержащихся в этой дуге?

(Нельзя, нужно знать ещё длину радиуса)

А 6. Если на угол 15 посмотреть в лупу с четырёхкратным увеличением, какой угол мы увидим?

(15)

Б 5. Из одной точки окружности проведены 3 хорды. Сколько получилось сегментов?

(6 сегментов)

Вопросы на «Ч»:

Г 4. Семь девяток выписали подряд: 9 9 9 9 9 9 9. Поставить между некоторыми из них знаки «+» или «-», чтобы получилось 1989.

(999 + 999 – 9 = 1989)

Д 4. Одна треть числа равна 100. Чему равно число?

(300)

Е 4. Какая цифра будет последней после возведения числа 29 в степень 29?

(9)

Ж 4. Расставьте в кружках числа от 1 до 11 так, чтобы суммы трёх чисел по всем прямым линиям были равны 18.

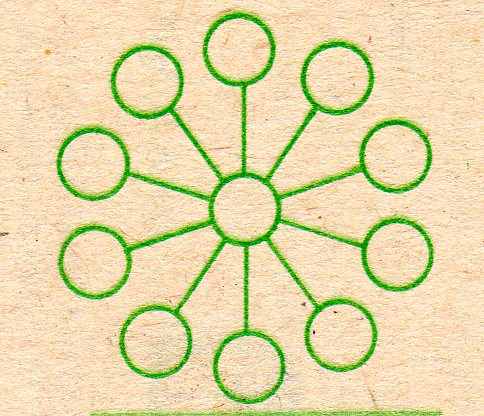
З 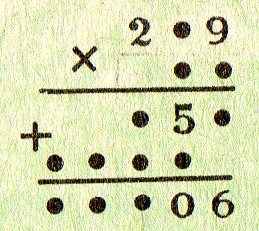5. Решить числовой ребус:

(239 * 54 = 12906)

Ж 6. Найти недостающее число в ряду: 1; 5; 6; 11; …; 28.

(17)

Е 6. Какими должны быть два следующие числа в последовательности:

10; 8; 11; 9; 12; 10; 13; …; …?

(11; 14)

Д 6. Как изменится дробь, если числитель её увеличить на знаменатель?

(Увеличится на 1)

Г 6. Какую последнюю цифру имеет произведение всех нечётных чисел от 1 до 99?

(5)

В 5. У скольких двузначных чисел сумма цифр равна 10?

(9 чисел: 19, 28, 37, 46, 55, 64, 73, 82, 91)

Вопросы на «Л»:

И 6. Разложить термины в логической последовательности: а) геометрический образ: б) квадрат; в) плоская фигура; г) выпуклый многоугольник.

(а, в, г, б)

К 7. Расшифровать ребус:

О

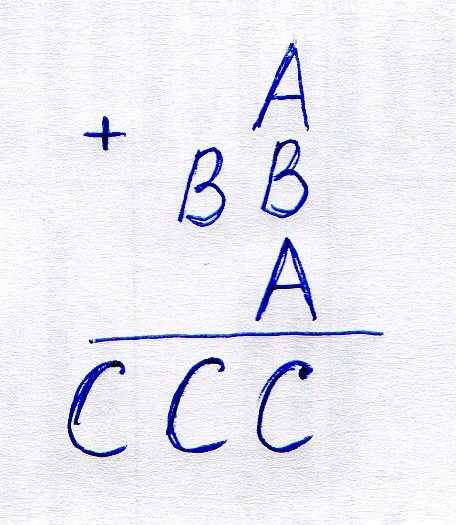динаковым буквам соответствуют одинаковые цифры, разным – разные.

К 8. Нужно вписать в квадрат буквы К, Л, Ю, Ч так, чтобы каждая буква встречалась только один раз по каждой горизонтали, по каждой вертикали, по каждой диагонали.

к	л	ю	ч

И 9. Какой знак нужно поставить между числами 5 и 6, чтобы получилось число больше 5, но меньше 6.

(Запятую, получится 5,6)

З 8. Встретились три мальчика: Белов, Чернов и Рыжов.

- Вы только посмотрите, - воскликнул Белов, - у нас у всех разные волосы, и их цвет не совпадает с фамилией.

- Ты прав, - ответил ему черноволосый мальчик.

Определите цвет волос каждого.

(Белов – рыжий, Чернов – белый, Рыжов – чёрный; или Белов – чёрный, Чернов – рыжий, Рыжов - белый)

З 7. На столе лежат в ряд квадрат, круг и треугольник (в таком порядке). Одна из фигур красного цвета, другая – жёлтого, третья – синего. Квадрат не красный, с одной стороны от синей фигуры лежит жёлтая, а с другой – красная. Определить цвет каждой фигуры.

(Квадрат – жёлтый, круг – синий, треугольник - красный)

Вопросы на «К»:

З 4. Пять друзей, встретившись, обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

(10)

И 3. На уроке физкультуры Андрей, Марат, Костя и Саша готовятся к прыжкам в высоту. Сколькими способами можно установить для них очерёдность прыжков?

(24)

И 5. Из города А в город В ведут две дороги, а из города В в город С – три дороги, из города С до пристани – две дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут?

(12)

К 4. Учащиеся 9 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 7 учащихся?

(42)

Вопросы на «И»:

А 8. Какие единицы измерения длины применялись в Древней Руси?

(Косая сажень, маховая сажень, локоть, аршин, пядь, верста)

Б 7. Какие меры массы применялись в старину в России?

(Золотник, фунт, пуд, берковец)

Б 9. Однажды в школе учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у десятилетнего мальчика был готов ответ. Кто этот мальчик?

(Карл Гаусс)

В 7. Какими часами пользовались в старину? Они известны более 3000 лет.

(Солнечными)

В 9. Монеты каких достоинств использовались в старину на Руси?

(Грош – ½ к., полушка – ¼ к., алтын – 3 к., пятак, пятиалтынный – 15 к., гривенник – 10 к., двугривенный – 20 к., четвертак – 25 к., полтинник – 50 к.)

Г 7. В первых учебниках математики (в 17 веке) некоторые числа назывались «ломаные числа». А сейчас как мы их называем?

(Дроби)

Г 9. Кто сказал: «Арифметика, сиречь наука числительная»?

(Леонтий Филиппович Магницкий, в 1703 году он создал первый учебник математики, который так и назывался «Арифметика, сиречь наука числительная»)

Д 8. Как в древности называлось первое «вычислительное устройство», которое просуществовало до 17 века?

(Абак)

Вопросы на «М»:

Д 9. Кто был создателем неевклидовой геометрии?

(Н. И. Лобачевский)

Е 8. Чья жизнь трагически прервалась в 21 год?

(Эварист Галуа)

Е 10. Чьё имя носит теорема о сумме и произведении корней приведённого квадратного уравнения?

(Француа Виет, 1540 – 1603 г.г.)

Ж 8. Чьё имя носит теорема о сумме квадратов катетов в прямоугольном треугольнике?

(Пифагор, древнегреческий учёный, 6 век до нашей эры)

Ж 10. Учёный-геометр, внёсший свой вклад в развитие математики ещё задолго до Евклида, уроженец города Милета, расположенного на берегу Эгейского моря.

(Фалес Милетский)

З 9. Французский учёный, который изобрёл метод координат.

(Рене Декарт)

Blog

Математическая интеллектуальная игра