Geum.ru

Моделирование экономической устойчивости систем энергетики

Вид материалаАвтореферат

Содержание


Структурная устойчивость
Третья глава
Подобный материал:
1   2   3   4
второй главе – «Системные свойства устойчивости, гибкости, адаптивности» - формулируется авторское понимание экономической устойчивости и связанных с ней характеристик, произведено количественное измерение и описание последних введением некоторых показателей и зависимостей, рассматриваются принципиальные возможности управления экономической устойчивостью в электроэнергетике.

В диссертации под системами энергетики понимаются такие объекты исследования как: современная вертикально интегрированная региональная энергокомпания - ОАО-энерго, энергетическое предприятие, будущие субъекты оптового электроэнергетического рынка – поставщики электрической энергии (генерирующие компании), покупатели (энергосбытовые организации), ассоциации предприятий топливно-энергетического комплекса (ТЭК), отрасли ТЭК в системе межотраслевых и межрегиональных связей.

Экономические, в том числе энергетические системы являются социотехническими, организационными системами, в которых реализовано целенаправленное управление действиями коллективов людей. Им в наибольшей степени присуща не только организация, но и самоорганизация. В силу наличия указанной специфики под экономической устойчивостью различных экономических систем понимается их способность (свойство) в условиях флуктуаций рыночной конъюнктуры, непредсказуемости поведения партнеров, производственно-технологических сбоев, ненадежности ресурсных поставок и других возможных возмущений обеспечивать реализацию, поддержание на определённых уровнях своих целевых установок. Такие затронутые в обзоре аспекты устойчивости, как ресурсный, технологический, ценовой, финансовый отражают проявления свойства устойчивости в отношении либо отдельных параметров, либо определенных функциональных областей объекта хозяйствования – производства, логистики, финансов. Экономическая устойчивость классифицируется на структурную и функционально-параметричекую.

Структурная устойчивость – это способность экономической системы как сообщества хозяйствующих субъектов к самосохранению и самовоспроизводству; к сохранению своей целостности, организационного единства при наличии разных (не вполне совпадающих) интересов субъектов, входящих в систему. Она предполагает сохранение структуры, как совокупности некоторых взаимосвязей самостоятельных составных частей целого, определяющего указанную систему. Структурная устойчивость является по сути необходимым условием обеспечения экономической устойчивости такой системы, воплощением структурного аспекта данной устойчивости. Действительно, если целевые установки системы реализуются, то можно говорить, что уж по крайней мере она сохраняет свою целостность. Если же система разрушается (распадается), то вопрос о достижении ее целевых установок снимается вообще. Более подробному рассмотрению структурной устойчивости посвящена пятая глава диссертации.

Функционально-параметрическая устойчивость подразделяется на устойчивость к малым возмущениям (устойчивость «в малом») и устойчивость к большим, глубоким возмущающим воздействиям, которая формируется за счёт управляемости и адаптивности. Устойчивость в малом означает, что малые изменения условий развития (функционирования) экономического объекта приводят и к малым отклонениям фактических значений его целевых показателей от плановых. Управляемость – свойство системы адекватно реагировать на управляющие воздействия. Адаптивность есть свойство приспосабливаться (пассивно или активно), адекватно реагировать на изменения внешней и внутренней среды. Сам процесс такого приспособления есть процесс адаптации, который в широком смысле предполагает как приспособление к изменениям условий, так и изменение их самих. В нём можно выделить два разреза. Первый – надёжностный - связан со способностью экономической системы при «отрицательных» возмущениях противодействовать снижению качества ее целевых установок (экономическая надёжность). Заметим, что категория экономической надёжности мыслится нами как взаимообратная известной в литературе категории риска. Второй – с освоением дополнительных возможностей в условиях «положительных» возмущений и повышением на этой основе своей эффективности. Оба разреза тесно связаны и определяются гибкостью и маневренностью. Гибкость экономической системы – способность адаптироваться без структурных изменений. Маневренность – способность системы к маневрированию, т.е. реализации целенаправленных мероприятий, внесению активных изменений, структурному перестраиванию в ответ на возмущения. Содержательно данные мероприятия могут выливаться в изменение состава объектов планируемой системы, их переразмещение, в изменение направлений НТП, организационно-экономических характеристик объектов, топологии связей между ними, направлений распределения возмущений и т.д.

В диссертации рассмотрен вопрос о предпосылках адаптации. Выделяется группа структурных факторов, определяющих различие в маневренных качествах развития / функционирования любой экономической системы - уровни стандартизации, унификации оборудования и материалов, специализации производства и комбинирования процессов, возможности взаимозамен; наличие разнообразия структуры и состава элементов системы; доля условно-постоянных издержек в себестоимости продукции; факторы целостности и другие. Анализируются значение и формы «избыточности».

Возможности повышения экономической надёжности, а следовательно и устойчивости в рамках электроэнергетики связываются прежде всего с сохранением и развитием единой национальной электрической сети и единой иерархической системы оперативно-диспетчерского управления. Широко применяемым средством формирования надежности функционирования электроэнергетических систем является резервирование генерирующих мощностей и пропускной способности электрических сетей. Помимо технологической составляющей для сохранения и укрепления экономической устойчивости необходимо поддержание баланса прав и обязанностей на всех уровнях управления электроэнергетикой. В условиях реструктуризации обеспечивать указанный баланс призваны рынки и срочные контракты. Последние позволяют управлять устойчивостью не только функционирования, но и развития систем энергетики. Проблема обеспечения их экономической устойчивости не может быть решена без опережающего развития генерирующих мощностей и электросетей, осуществляемого прежде всего на базе инноваций; без жесткого контроля собственника за старением основных средств и их обновлением. Направлениями повышения устойчивости, живучести электроэнергетических систем являются осуществление диверсификации сферы их деятельности, а также проведение политики активного воздействия на режим электропотребления – реализация функции управления спросом на энергию.

Внешним проявлением гибкости и маневренности выступает эластичность как способность экономической системы нейтрализовывать, демпфировать возмущения, испытывая при этом определённые «деформации» (потери) в достижении целевых установок, минуя, однако, полного их невыполнения. Величина потерь характеризует при прочих равных условиях и уровень эластичности – он тем выше, чем ниже потери и наоборот. Последние являются своеобразной «платой» за неопределенность используемой в управлении информации. Эластичность какого-либо объекта планирования при заданном плане его развития / функционирования может быть описана с помощью некоей платёжной вектор-функции или её специального вида – функции эластичности, аппроксимирующей связь между входными возмущениями и отклонениями от плановых (программных) ориентиров. Определение и измерение эластичности в данном контексте представляется зеркальным переносом (распространением) этого понятия из разреза формирования продуктивности экономической системы (производственная функция) на разрез адаптации. В диссертации приведены конкретные примеры функций эластичности, полученные соответствующим преобразованием из известных типовых производственных функций. Свойство эластичности непосредственно «примыкает» к надежности, ибо последняя определяется эластичностью и уровнем возможных возмущений, соответствующих оцениваемому варианту развития / функционирования экономической системы.

Ниже представлены некоторые из предлагаемых в диссертационной работе показателей экономической надёжности по выпуску продукции (услуг) и затратам:

Н1 = 1 - М () ,

H2 = 1 – ,

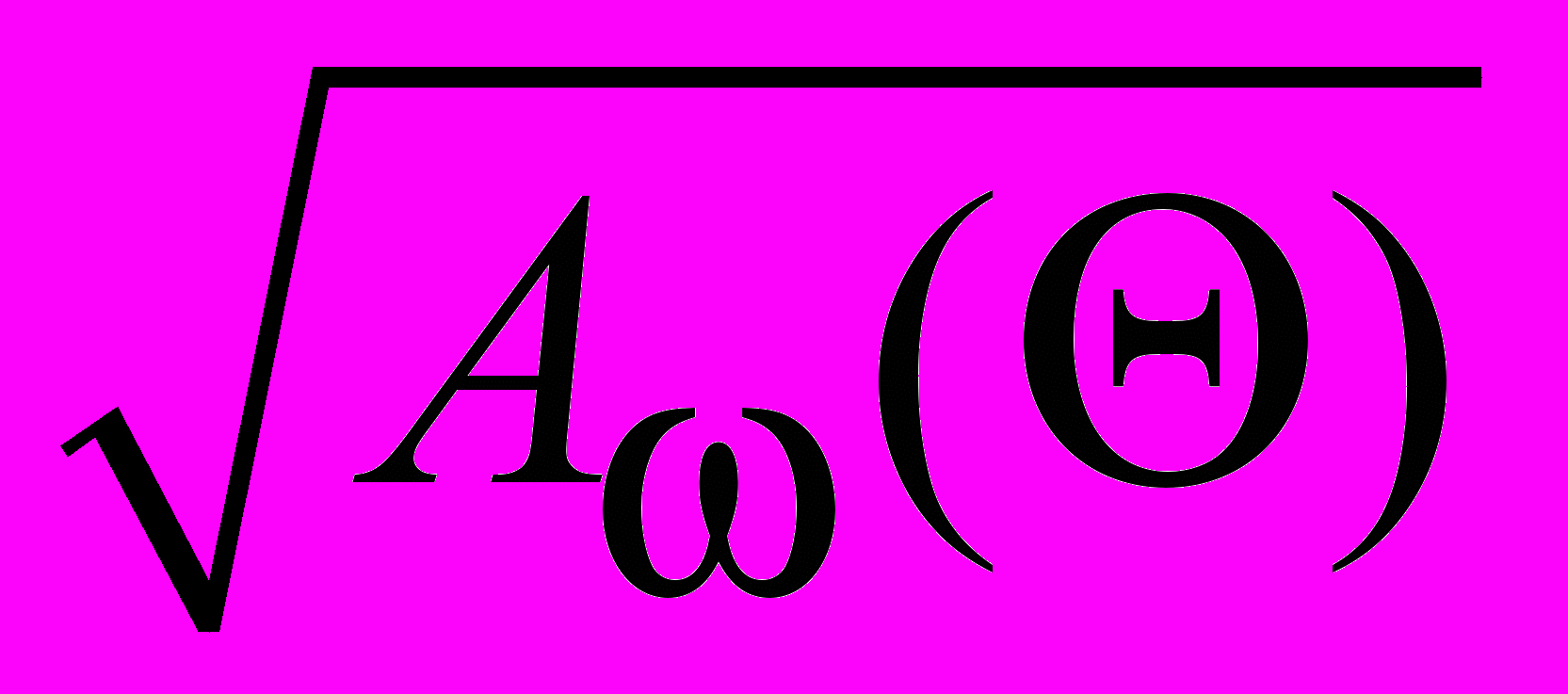Н3 = 1 – (М() + k·М/– М()/) ,

Нco = ,

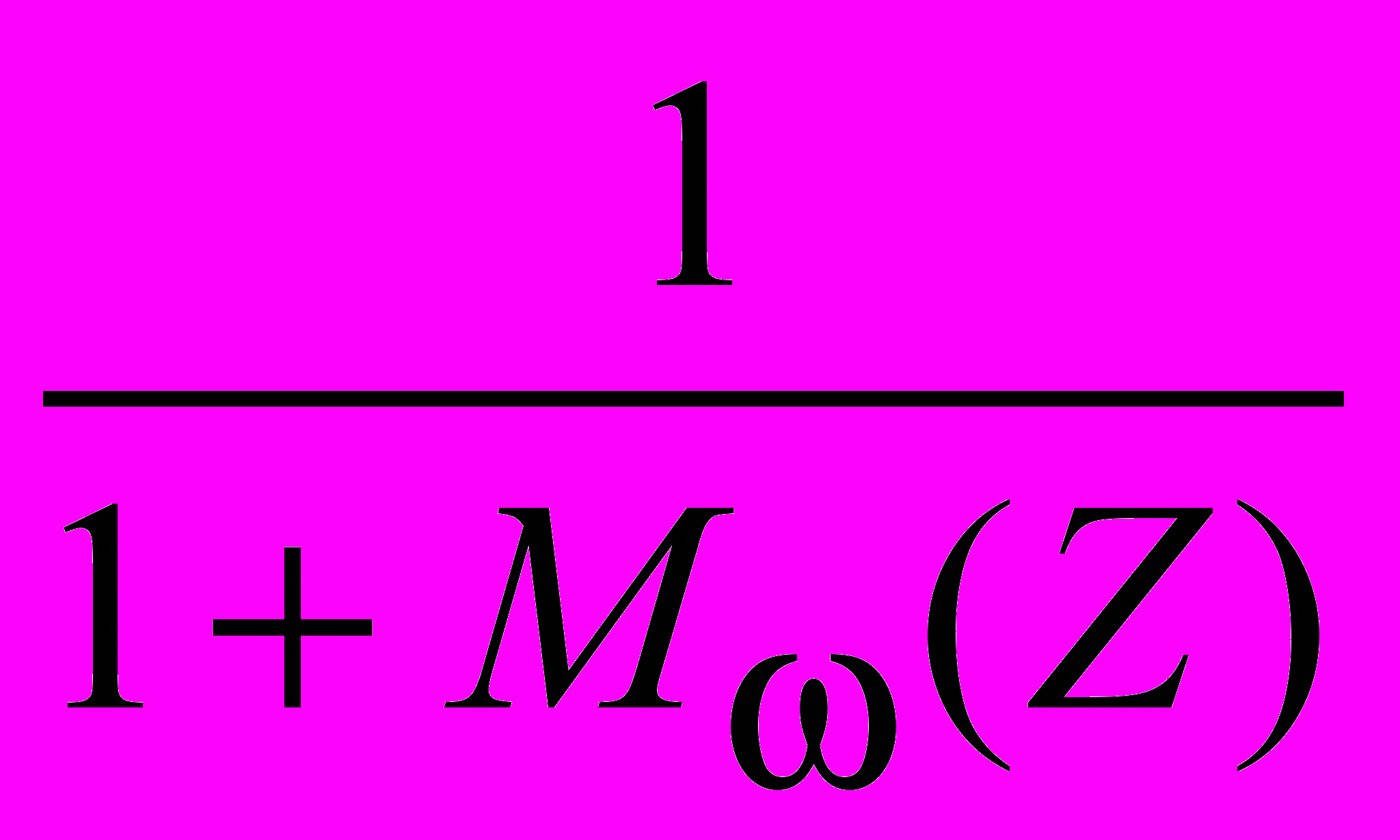где М и А – операторы 1-го и 2-го начальных моментов; 0 ≤ k ≤ 1; - нормированная случайная величина недовыполнения (потерь) в отношении некоторого планового ориентира; Z – с.в. относительного против плана превышения затрат.

Данные показатели подробно проанализированы и служат своего рода индикаторами в процедурах формирования адаптивных планов различных объектов управления.

Третья глава – «Постановки и анализ задач формирования адаптивных планов развития (функционирования) экономических систем» - посвящена моделированию составляющих адаптивности (маневренности, эластичности), являющейся важнейшим атрибутом, обеспечивающим экономическую устойчивость, а также исследованию её предпосылок – разнообразия и избыточности.

Для выбора и построения потенциально адаптивных планов экономических / энергетических систем разработаны два подхода.

Первый основан на использовании специальной адаптивной модели (или её разновидности – модели стабилизации) вариантов плана (программы) функционирования / развития сложной экономической системы из некоторого множества (зоны неопределённости), являющегося, вообще говоря, результатом выполнения предшествующих процедур в общей схеме формирования окончательного планового (программного) решения. Она относится к классу оптимизационных статистических моделей, включает в явном виде платёжные функции объектов планирования и строится как задача математического программирования на графе эластичности , отражающем структуру связей системы при известном варианте плана (программы): I – множество вершин (объектов планирования); дуги 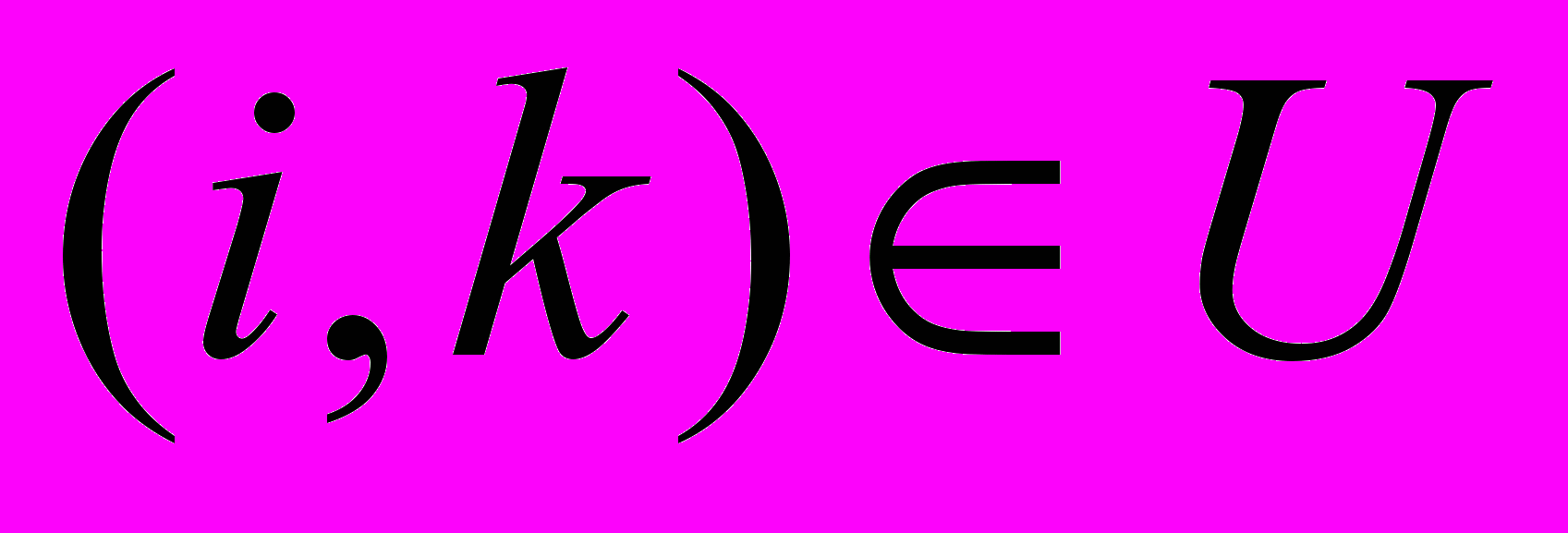характеризуют наличие связи в смысле эластичности недовыполнения k – го целевого показателя от относительных возмущений со стороны i – го ресурса-фактора; переменные , определяют поток возмущений в системе. Модель имитирует целенаправленное поведение – реакцию сложной экономической системы при заданном плане (программе, проекте) ее развития в ответ на некоторый набор возмущений с точки зрения необходимости наиболее полного выполнения (перевыполнения) с учетом заданного приоритета первоначальных плановых установок. Она исследована как в общем случае (включая возможности управления резервами), так и в частных – для некоторых конкретных функций эластичности. Показатели надежности, рассчитываемые на основе данной модели, рассматриваются как дополнительные критерии отбора вариантов из зоны их неопределенности. Самостоятельный интерес адаптивная модель представляет в связи с вопросами, касающимися изучения закономерностей распределения возмущений.

Отметим также, что с её помощью формально проанализировано влияние параметрического разнообразия объектов планирования на компенсирующую способность системы в целом.

Второй подход предполагает построение моделей формирования адаптивного или эластичного для всего диапазона предполагаемых условий развития системы плана, оперируя выбранными показателями надежности и непосредственно способами маневрирования, набор которых, в свою очередь, определяется в зависимости от общей постановки задачи планирования. Суть его состоит в следующем.

Процедура формирования эластичного плана должна опираться на объединение двух связанных между собой этапов: этапа выбора предварительного варианта плана с учетом его возможного в будущем изменения и этапа целенаправленного изменения (корректировки) ранее выбранного варианта в пределах заданных правил маневрирования по мере уточнения информации об условиях развития системы. При наличии неопределенности прогнозной и плановой информации наиболее полное объединение указанных этапов может быть достигнуто в рамках некоторых агрегативных стохастических моделей.

Пусть некоторая детерминированная задача оптимизации плана экономической системы имеет вид:

С(х) 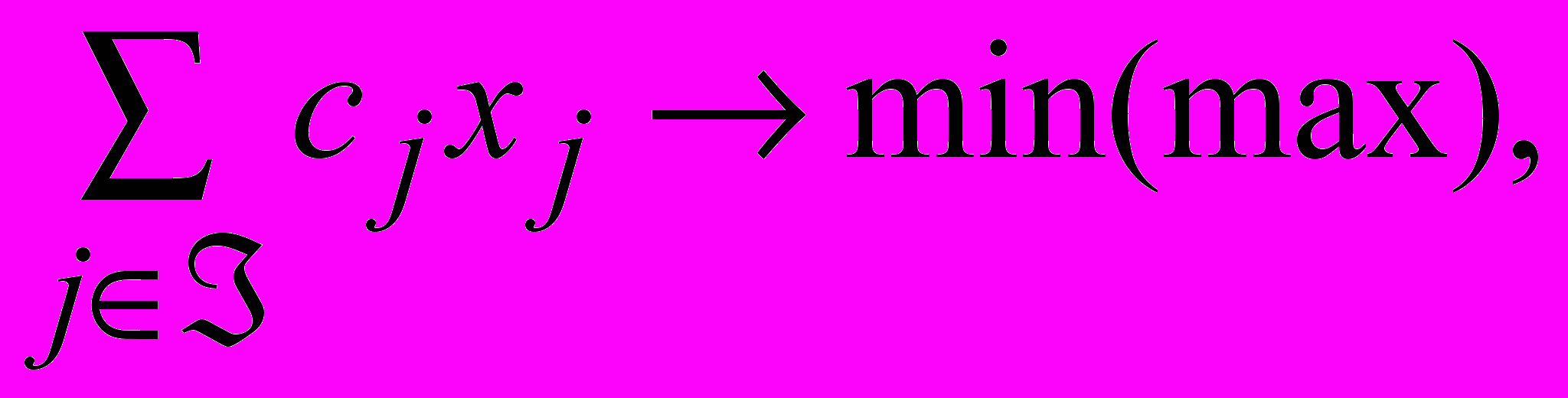 (3. 1)

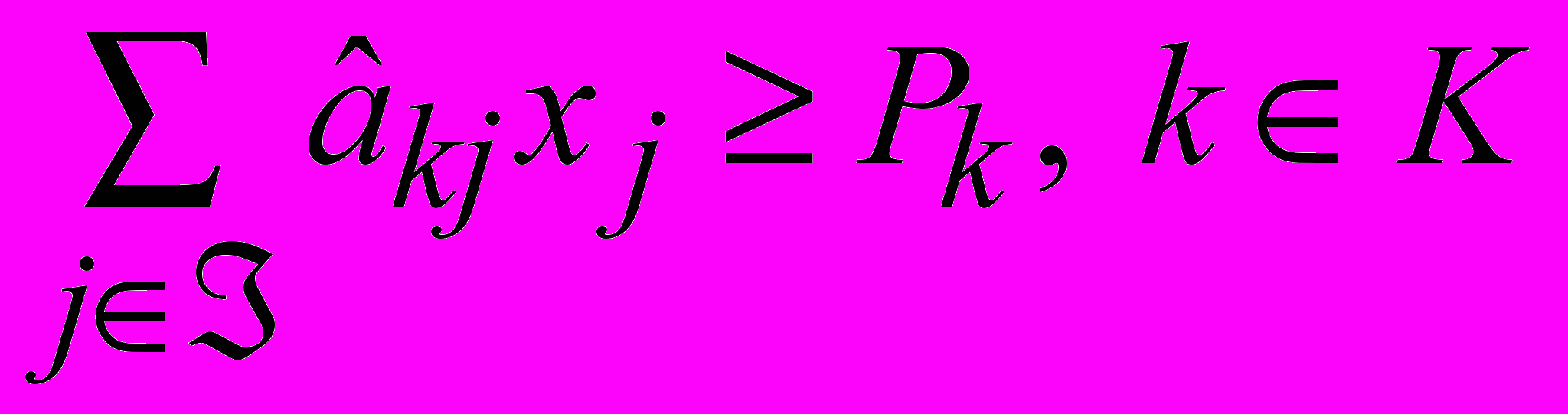, (3. 2)

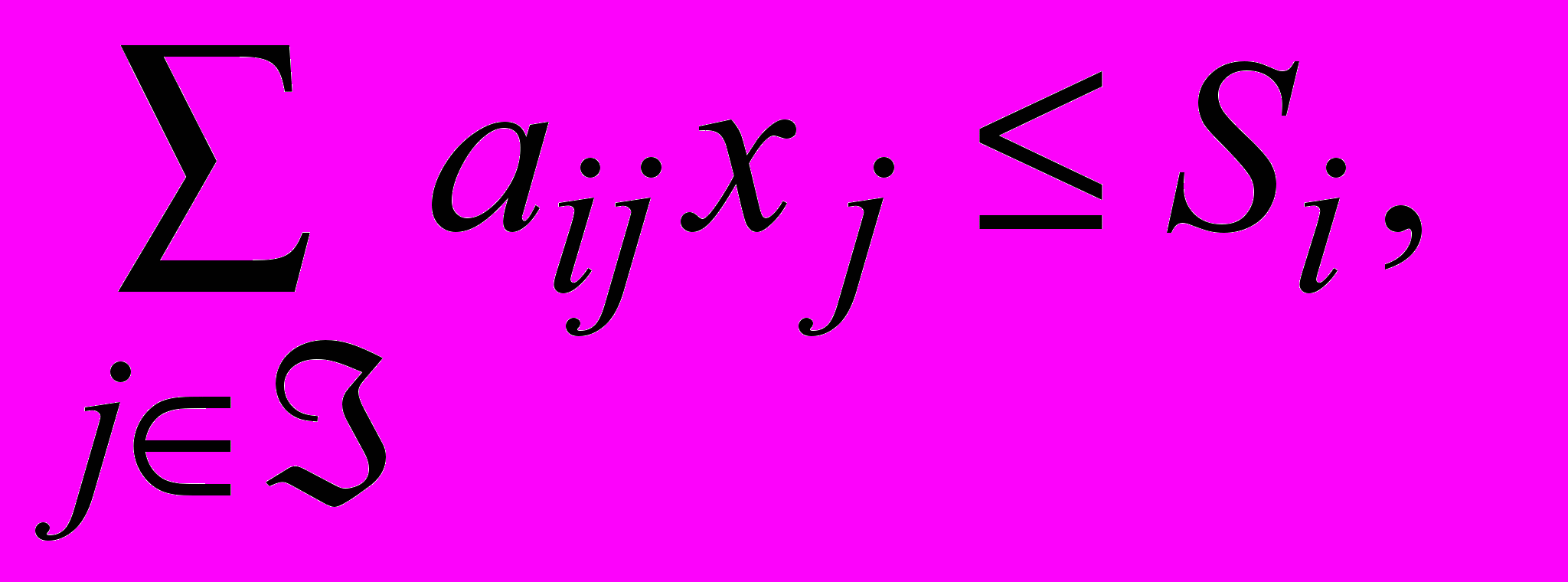i  Í, (3. 3)

0  x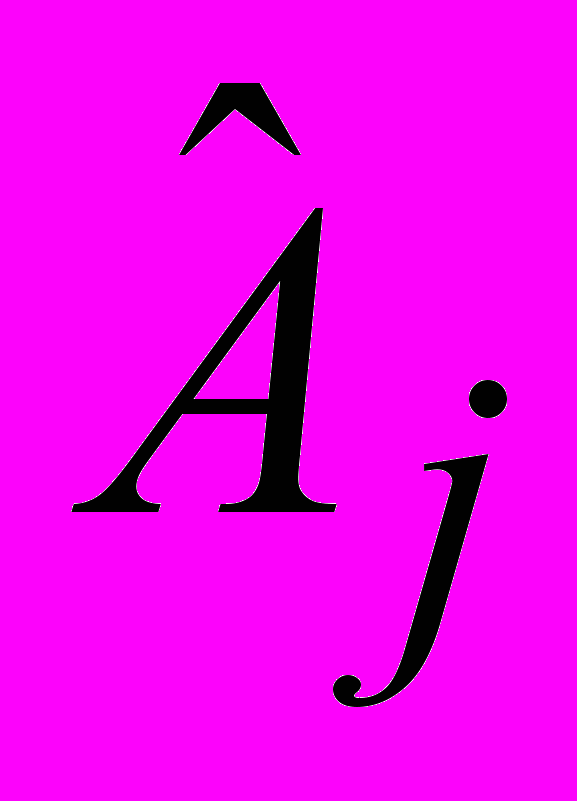j, j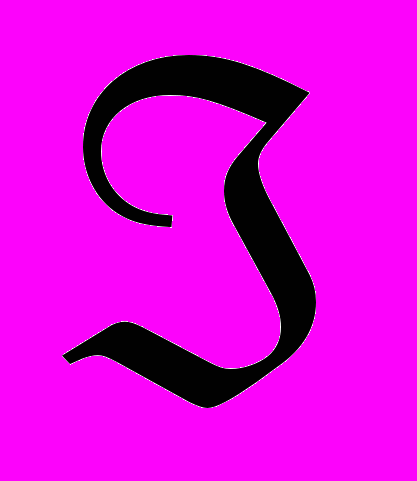. (3. 4)

Здесь С(х) – скалярная целевая функция интегральных или приведенных затрат (критерием оптимальности может являться минимизация или максимизация любых других результирующих экономических показателей системы, например, прибыли); xj – интенсивность использования j-го программного способа в сплошной независимо от объектов нумерации; ограничения (3. 2) устанавливают требования по плановым заданиям; (3. 3) – по ресурсам.

Линейность постановки не является с принципиальной точки зрения определяющим фактором. Результаты настоящего раздела распространяются и на регулярные задачи выпуклого программирования. С учётом сказанного в терминах (3.1) – (3.4) может быть описано, по-видимому, большинство задач текущего и стратегического планирования.

Будем рассматривать параметры Cj, , , 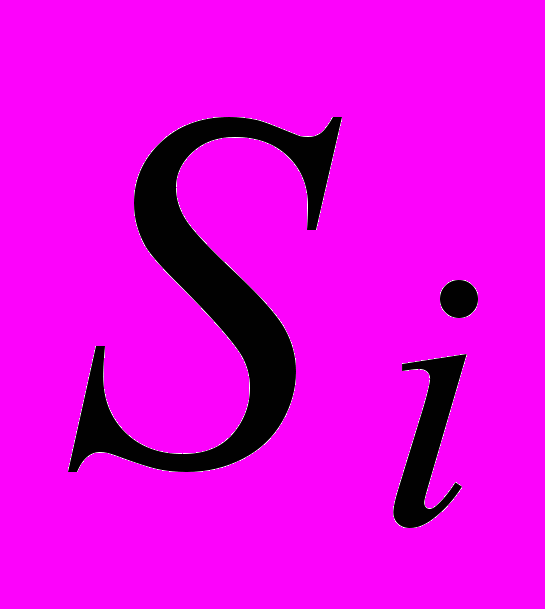и 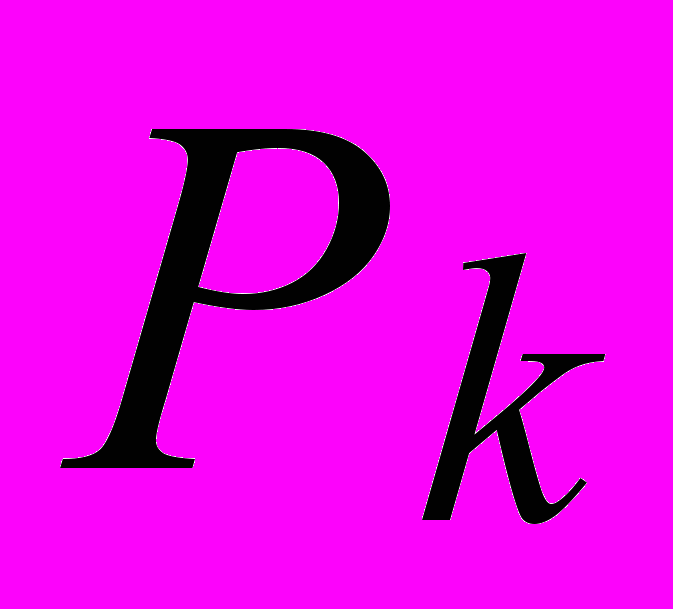как случайные величины. В общем случае удобно говорить, что эти параметры являются функциями элементарного события  некоторого вероятностного пространства: Cj = Cj (), = (), aij = aij (), Si = Si (), Pk = Pk (), j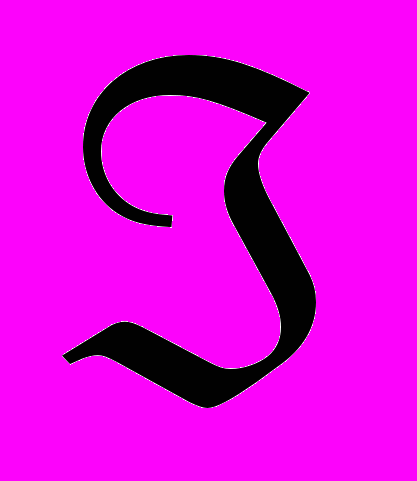, kK, iÍ. Последнее равенство, в частности, означает наличие неопределенности требований к величинам плановых заданий, проистекающей от случайного характера предполагаемого спроса на продукцию и услуги. Конкретная реализация s случайного события  определяет в целом и конкретные условия развития или функционирования управляемой системы.

Собственно под планом (вариантом плана) в терминах задачи математического программирования со случайными неконтролируемыми параметрами будем понимать детерминированный вектор 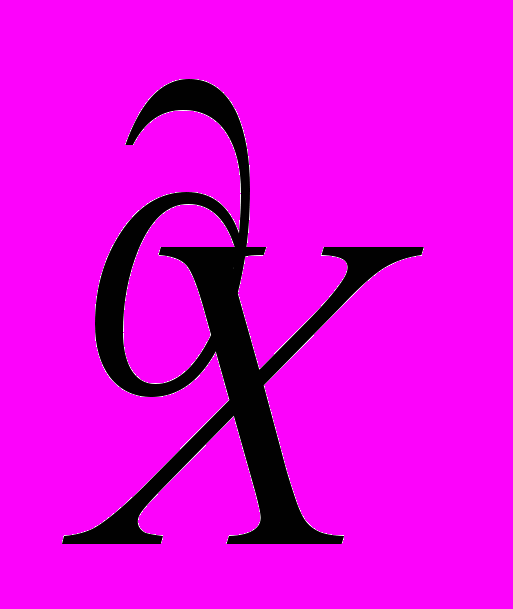интенсивностей использования программных способов, выбор которого необходимо произвести до наблюдения над состоянием природы – исчерпывающего выяснения будущих условий развития. Это понимание плана можно расширить включением в него вектора 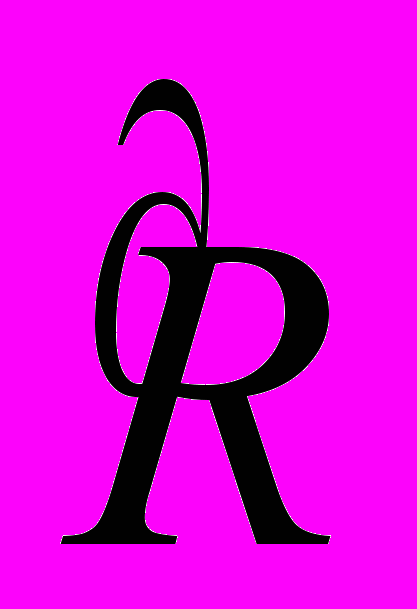резервов производственных мощностей, а также набора каких-либо других управляемых параметров, подлежащих априорному установлению. Вектор х = х() определим как результат корректировки плана после наблюдения реализации условий развития. Аналогично трактуется и R = R().

Запишем задачу:

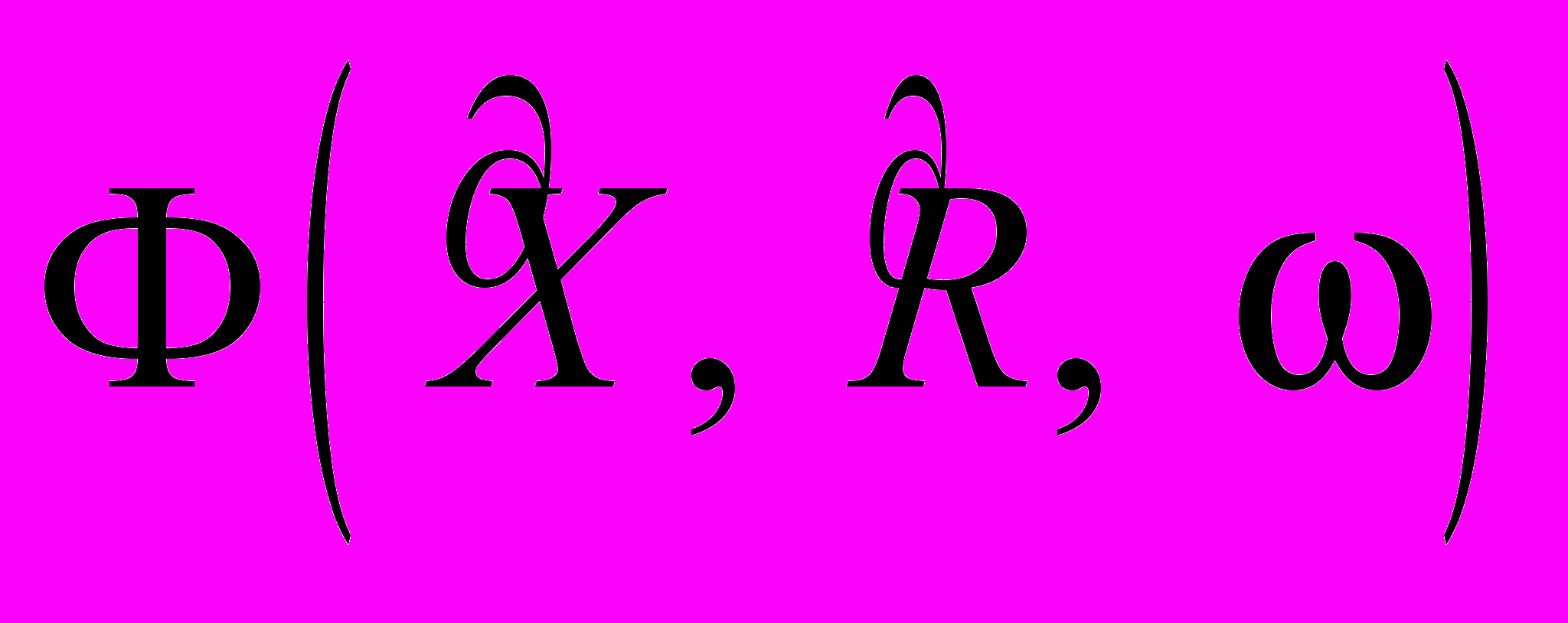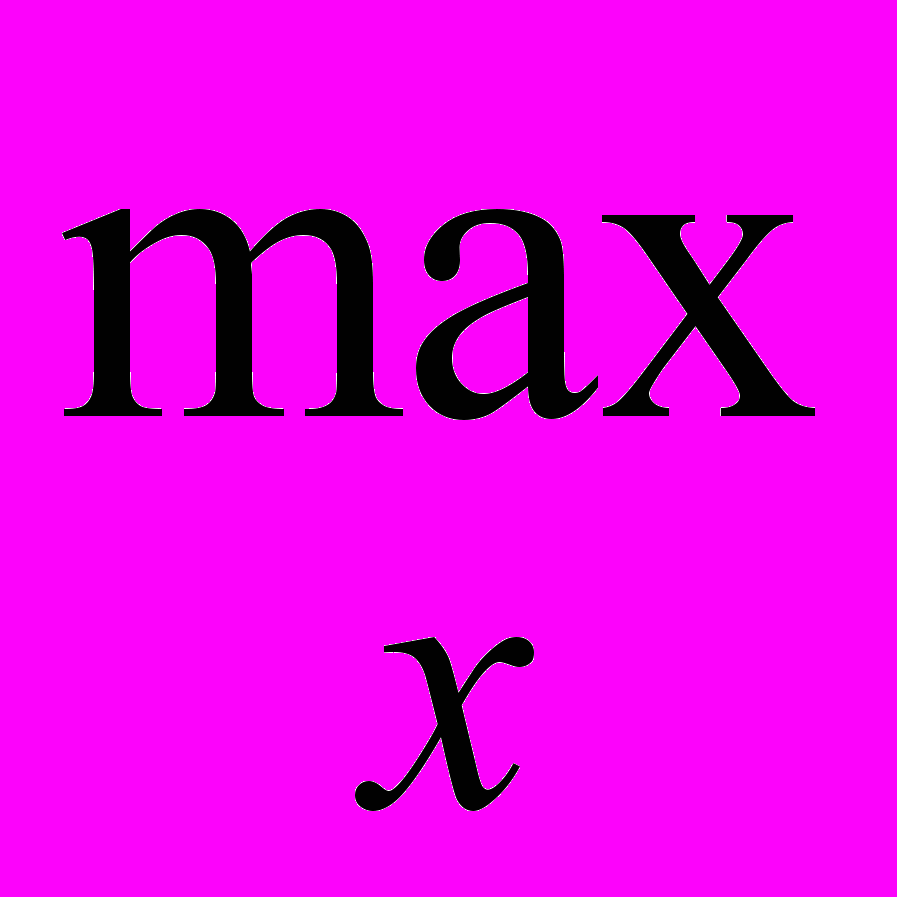= f n, ,..., ,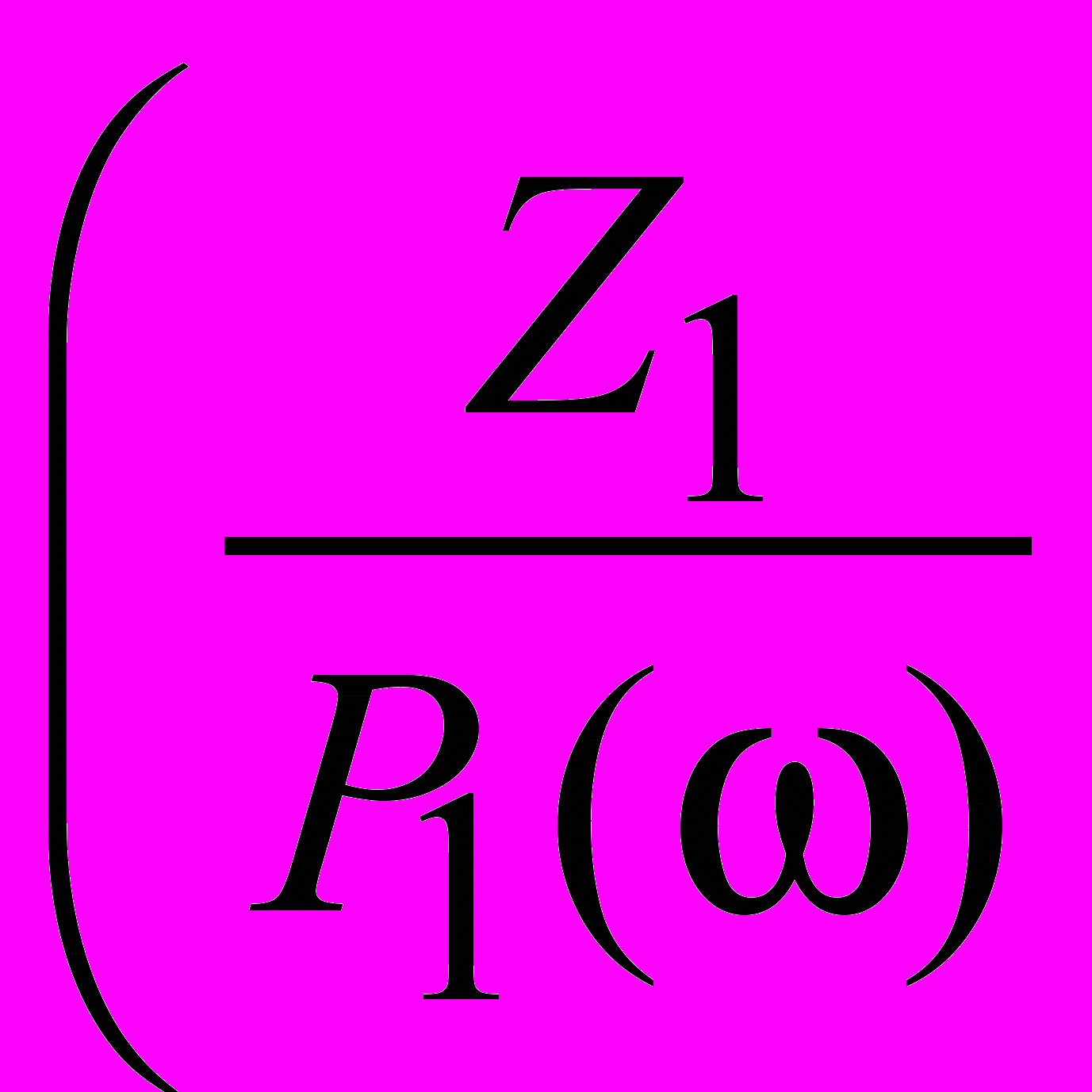


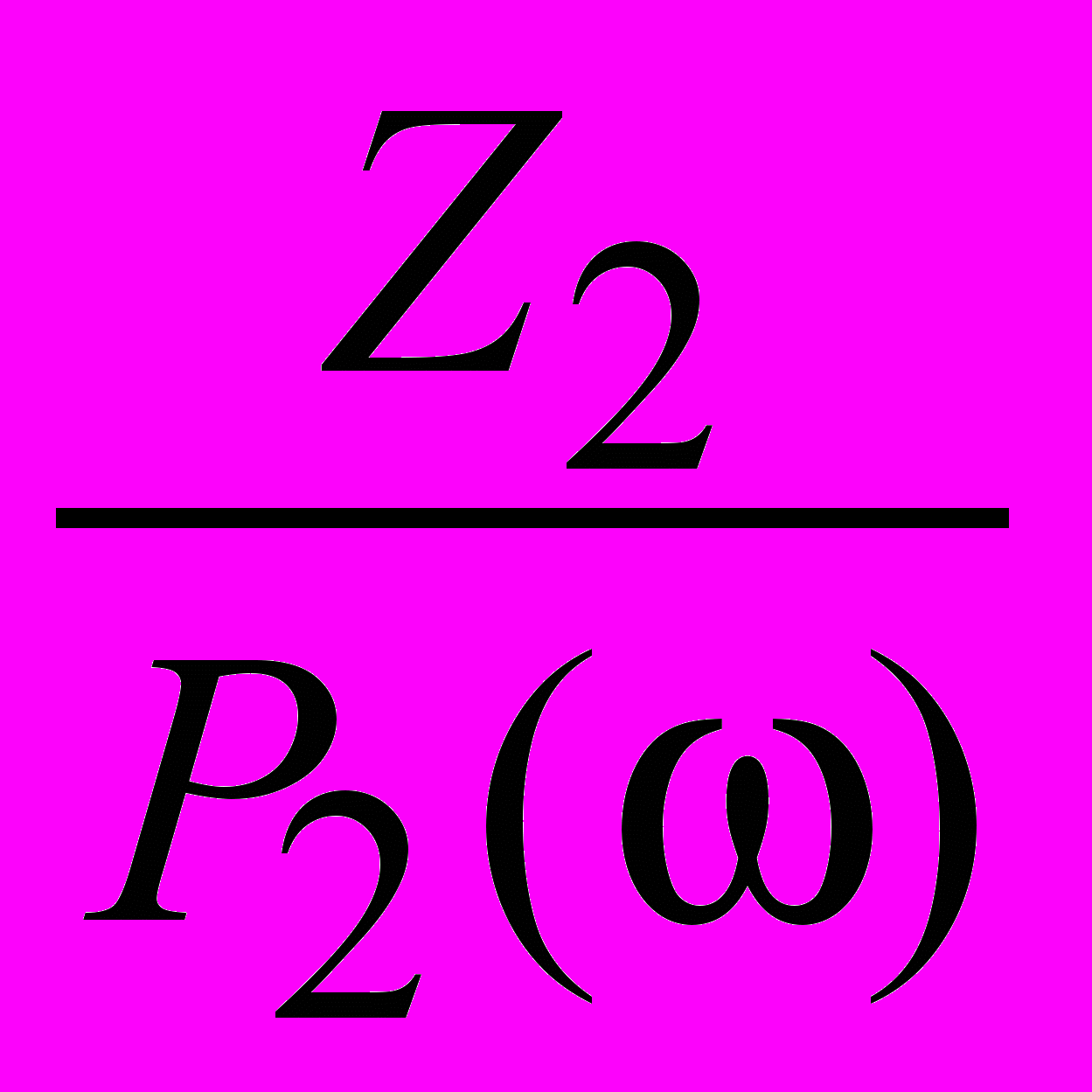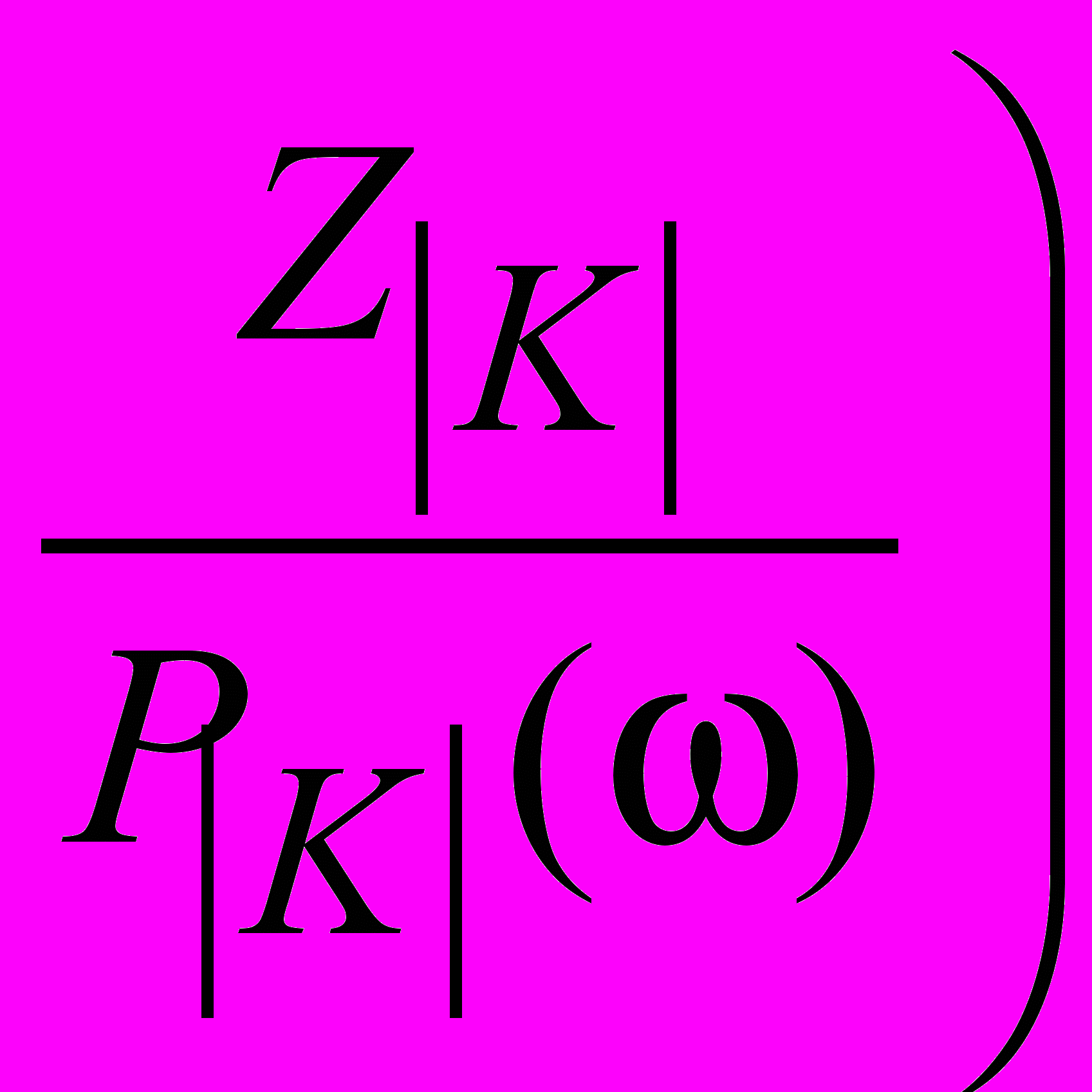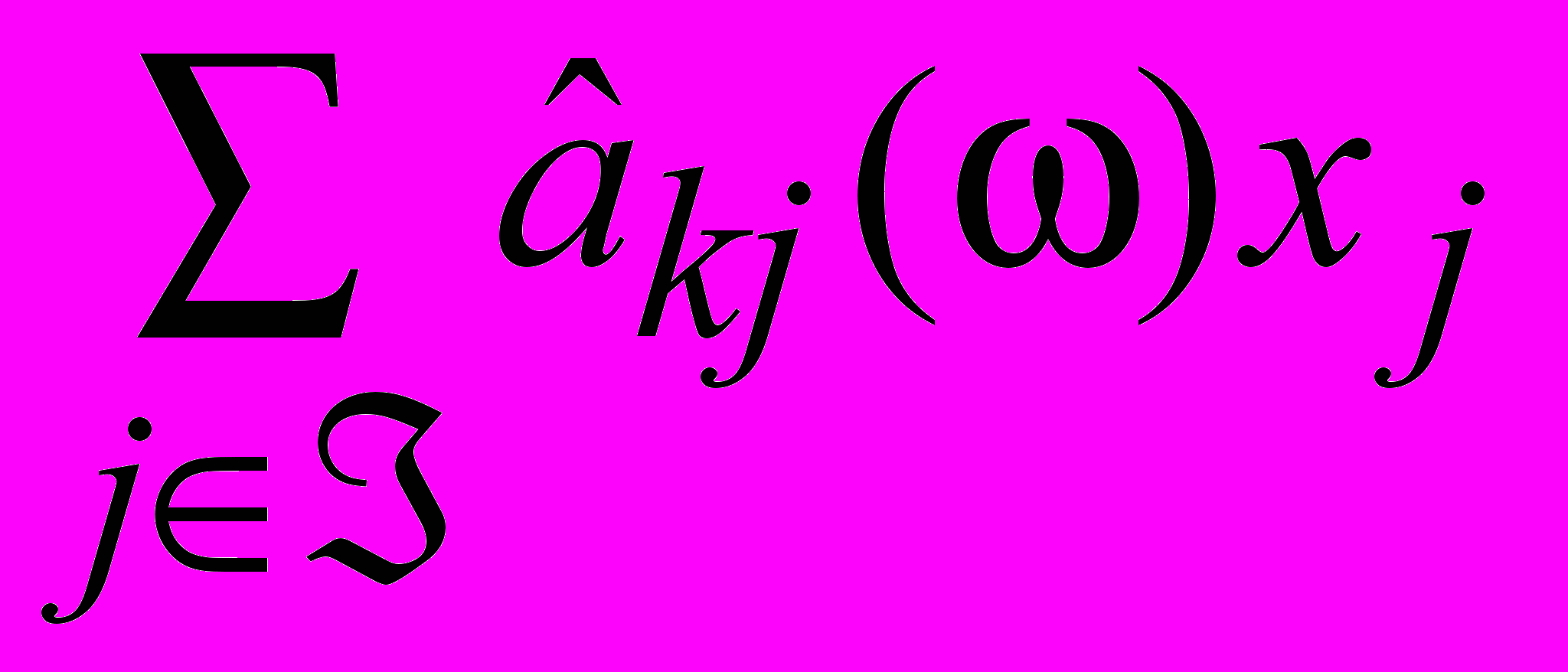– Zk  0, kK,

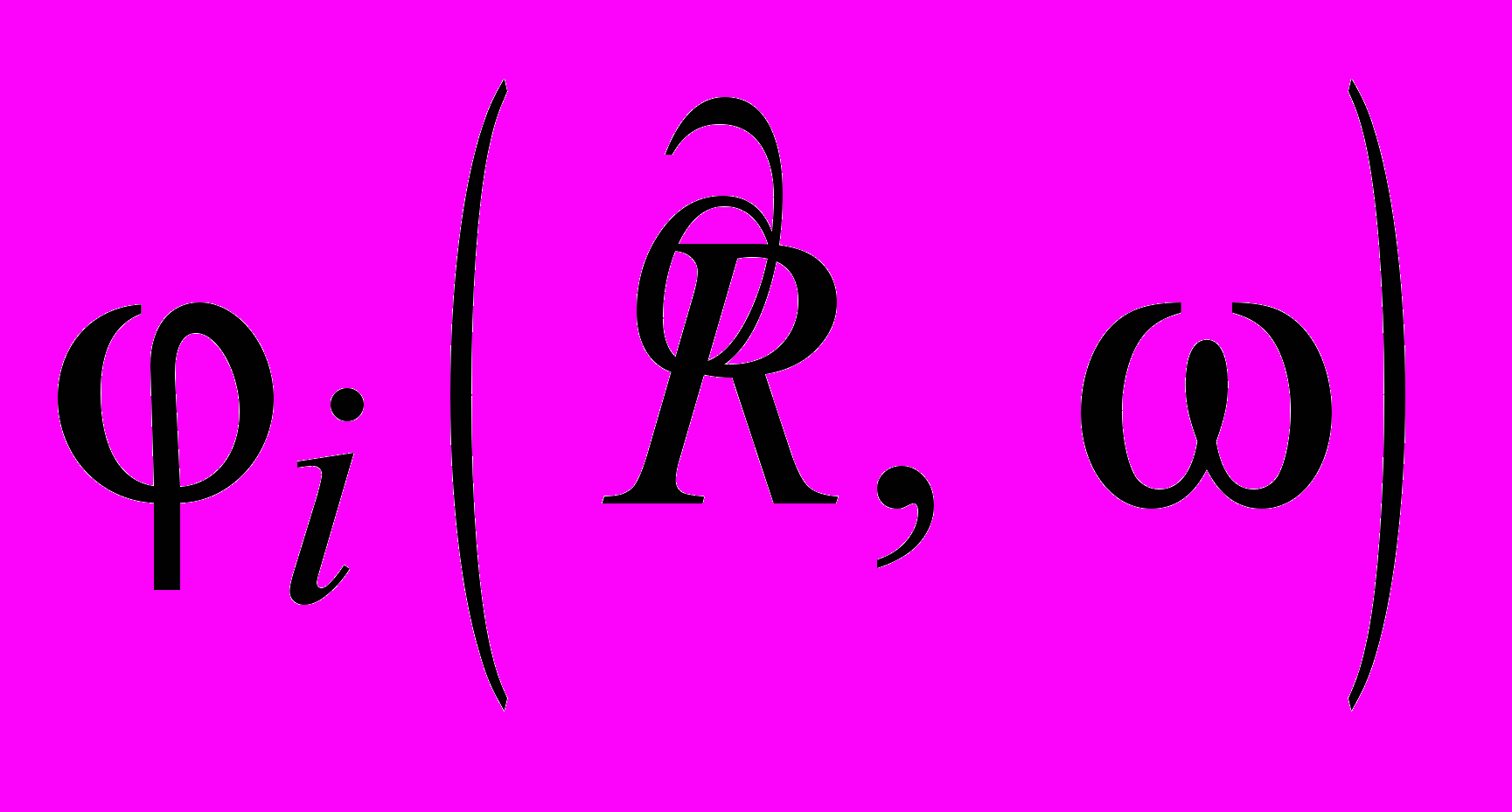, i Í , (3.5)

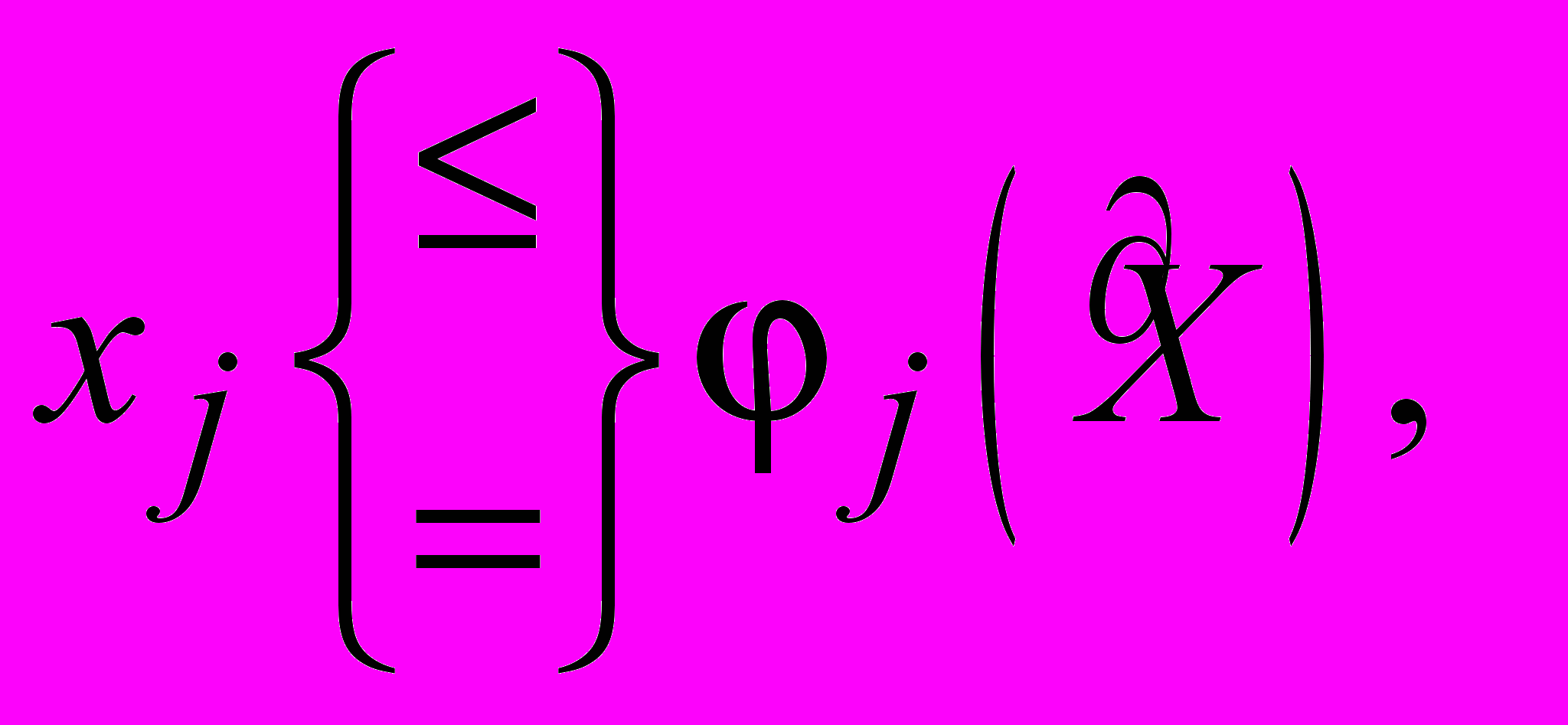j ,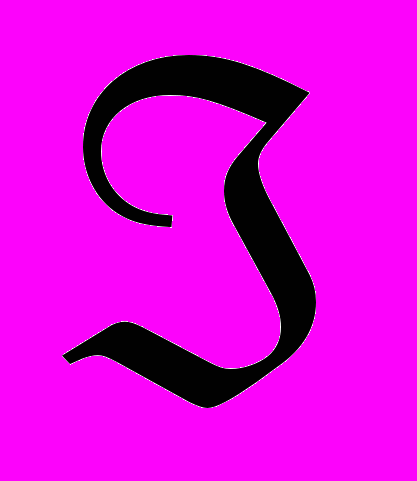

xj  0, j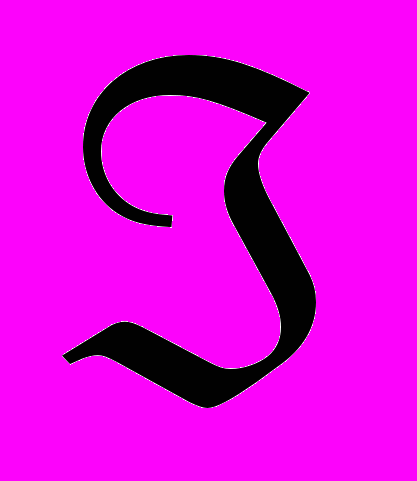, Zk  0, k K.

Pk () > 0 для всех ; f n(·) 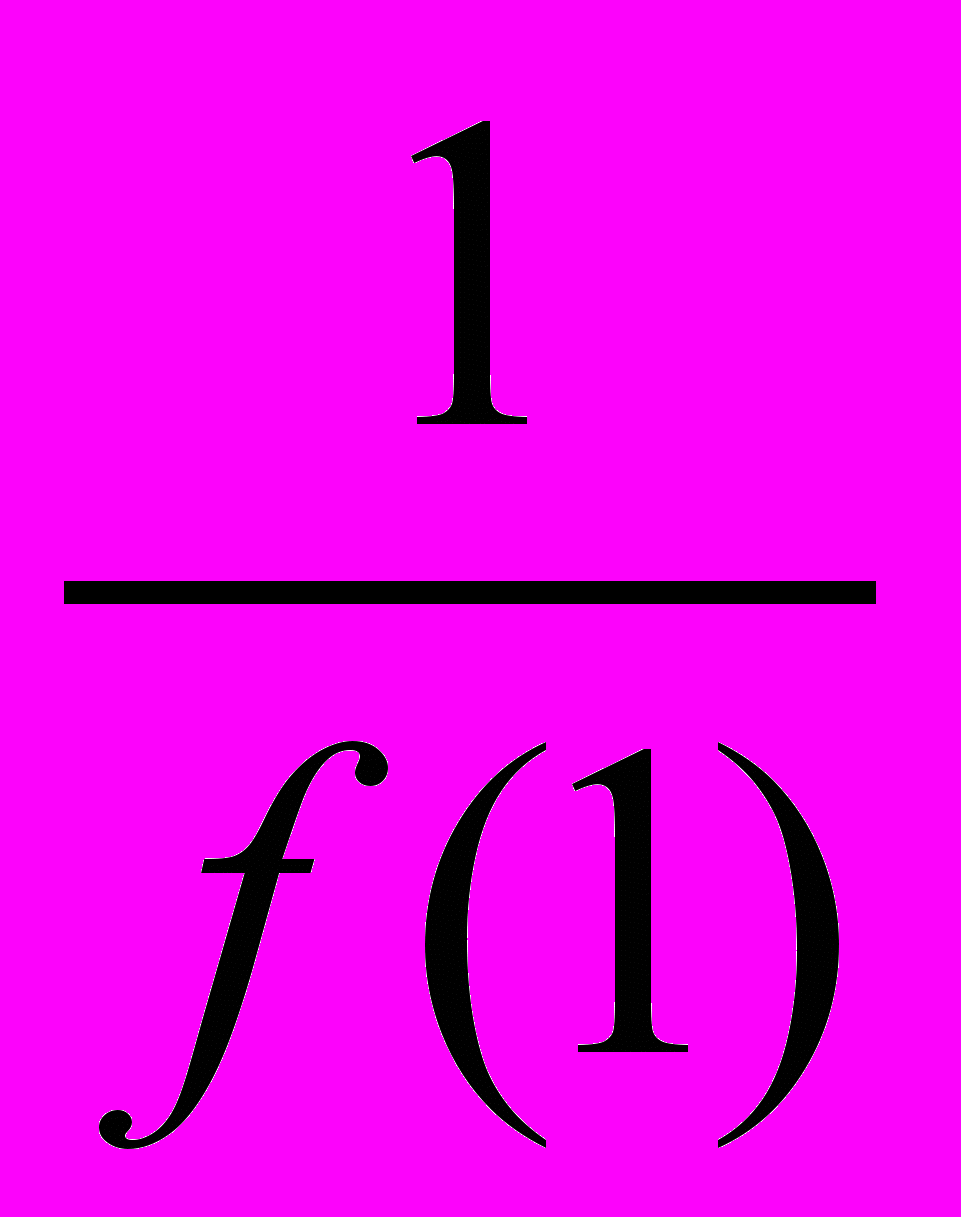f(·), где f(·) – скалярная функция-свертка; (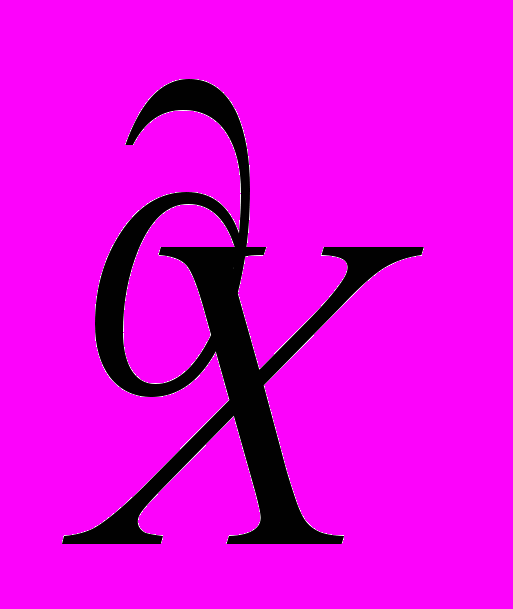) и (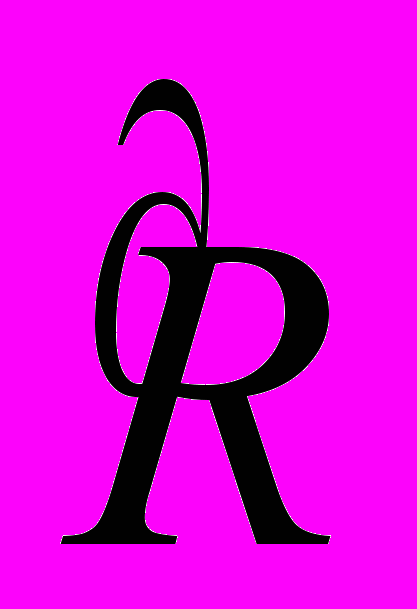, ) устанавливают пределы (возможности) маневрирования интенсивностями программных способов – компонентами вектора .

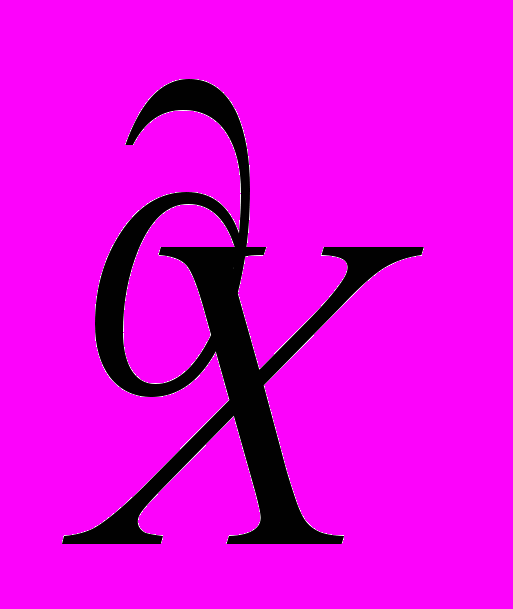Сформулированная выше задача при фиксированных 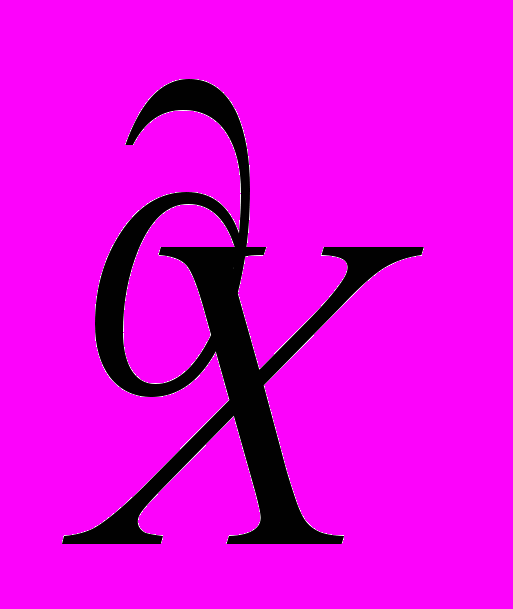, 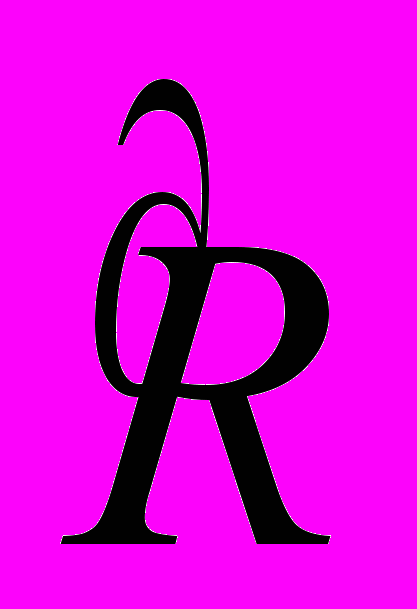и известном состоянии природы  моделирует целенаправленное поведение экономической системы в некоторых условиях развития с точки зрения необходимости наиболее полного выполнения и перевыполнения с учетом заданного приоритета плановых ориентиров. Ее решение х* зависит от , т.е. х* = х*(). В связи со сказанным постановку (3.5) по аналогии с первым подходом будем называть адаптивной моделью плана 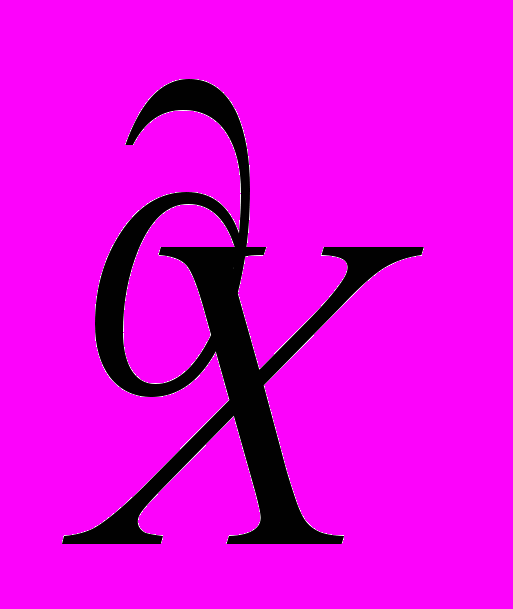при известном . Заметим, что Ф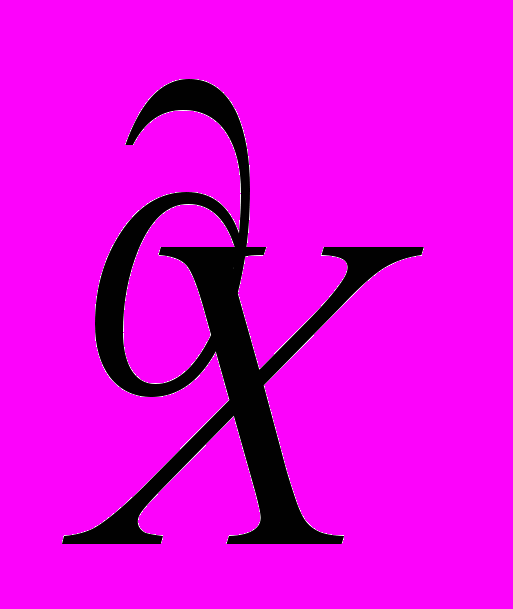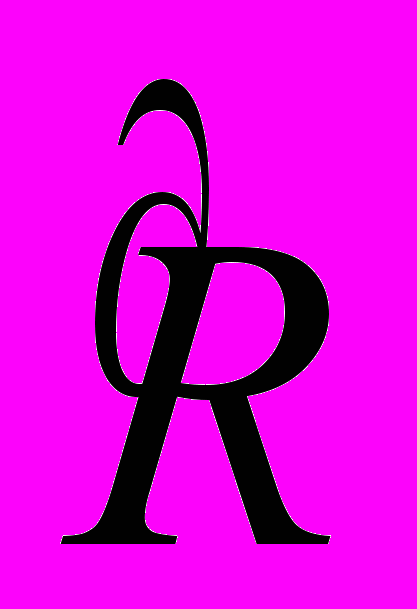(, ,) является функцией «минимума» модели стабилизации.

В диссертации приводятся примеры функци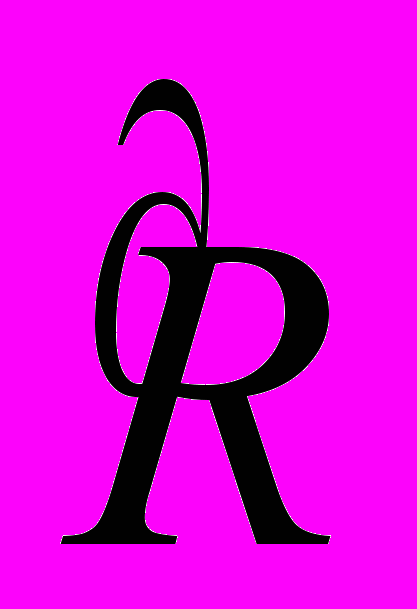й (, ) и (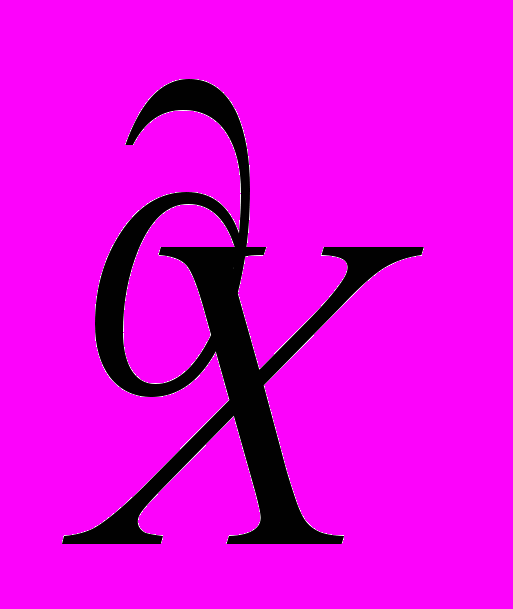),а также различные модификации и дополнения к (3.5). В частности, в неё могут быть включены аварийные (или подстроечные) способы с переменными, которые не «дублируются» соответствующими компонентами вектора 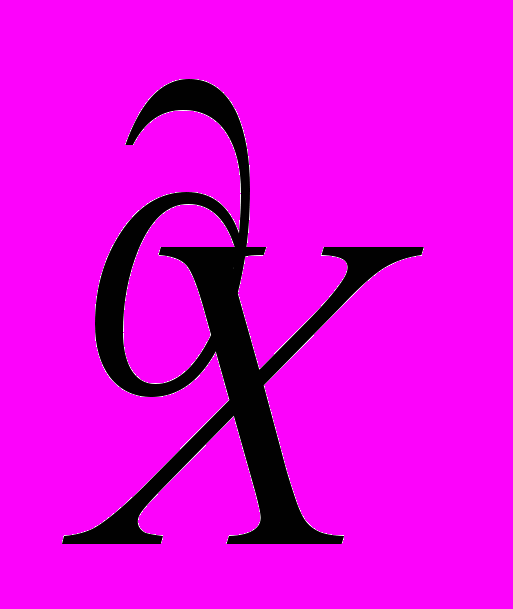и подчиняются своим особым условиям.

Модель (3.5) с наиболее распространенными вариантами скаляризации – ассортиментной и линейным взвешиванием – сводится (естественно, при заданных 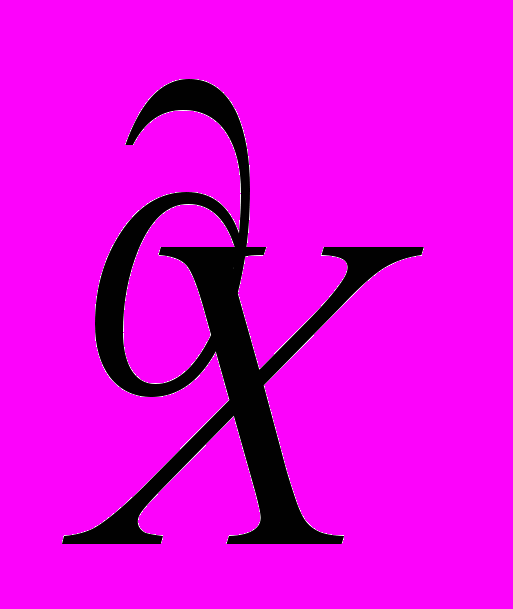, 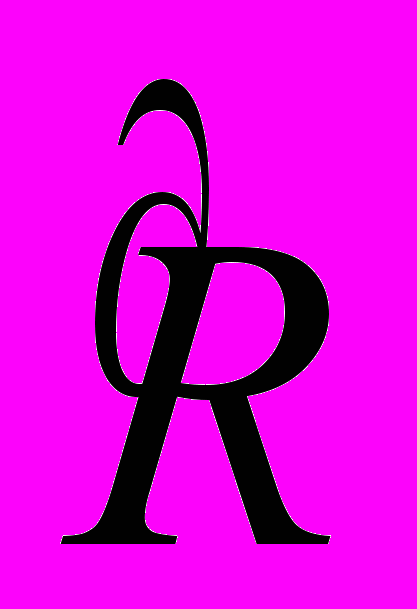и ) к обычной задаче математического программирования. Способы маневрирования выражаются в корректировке интенсивностей первоначально принятых программных способов (более кардинально – переходе от одного их набора к другому), в использовании резервов производственных мощностей и проведении некоторых подстроечных мероприятий. Правила маневрирования задаются функциями i и j , и вообще всей системой ограничений.

Может быть записано несколько постановок модели формирования эластичного плана, различающихся между собой, например, видом учитываемых затрат (средние плановые затраты или текущие затраты, сопровождающие скорректированный вариант X первоначального плана 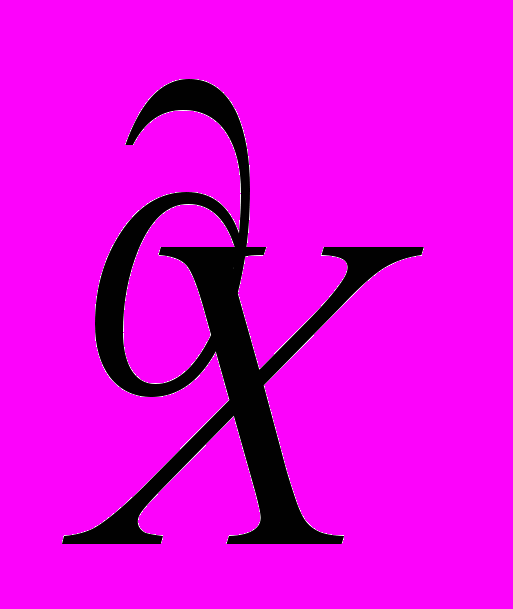после реализации некоторых условий функционирования / развития). Ниже приводятся две из них, причём взаимные друг другу ( 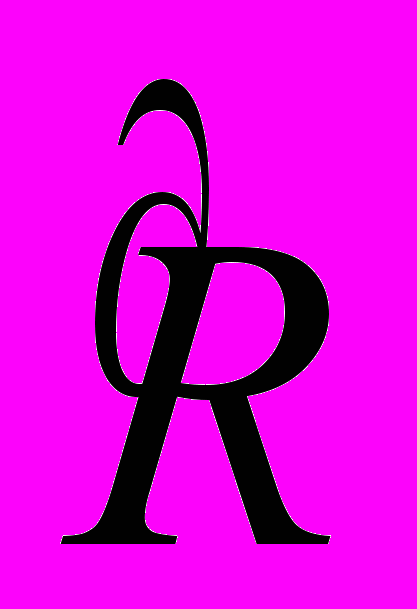для простоты считается заданным):

F () =

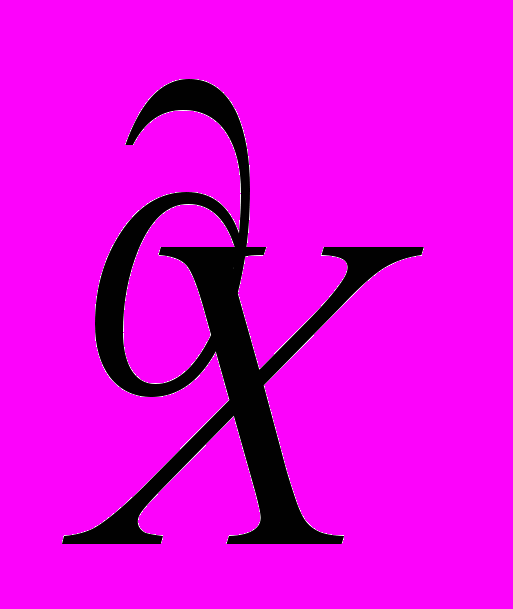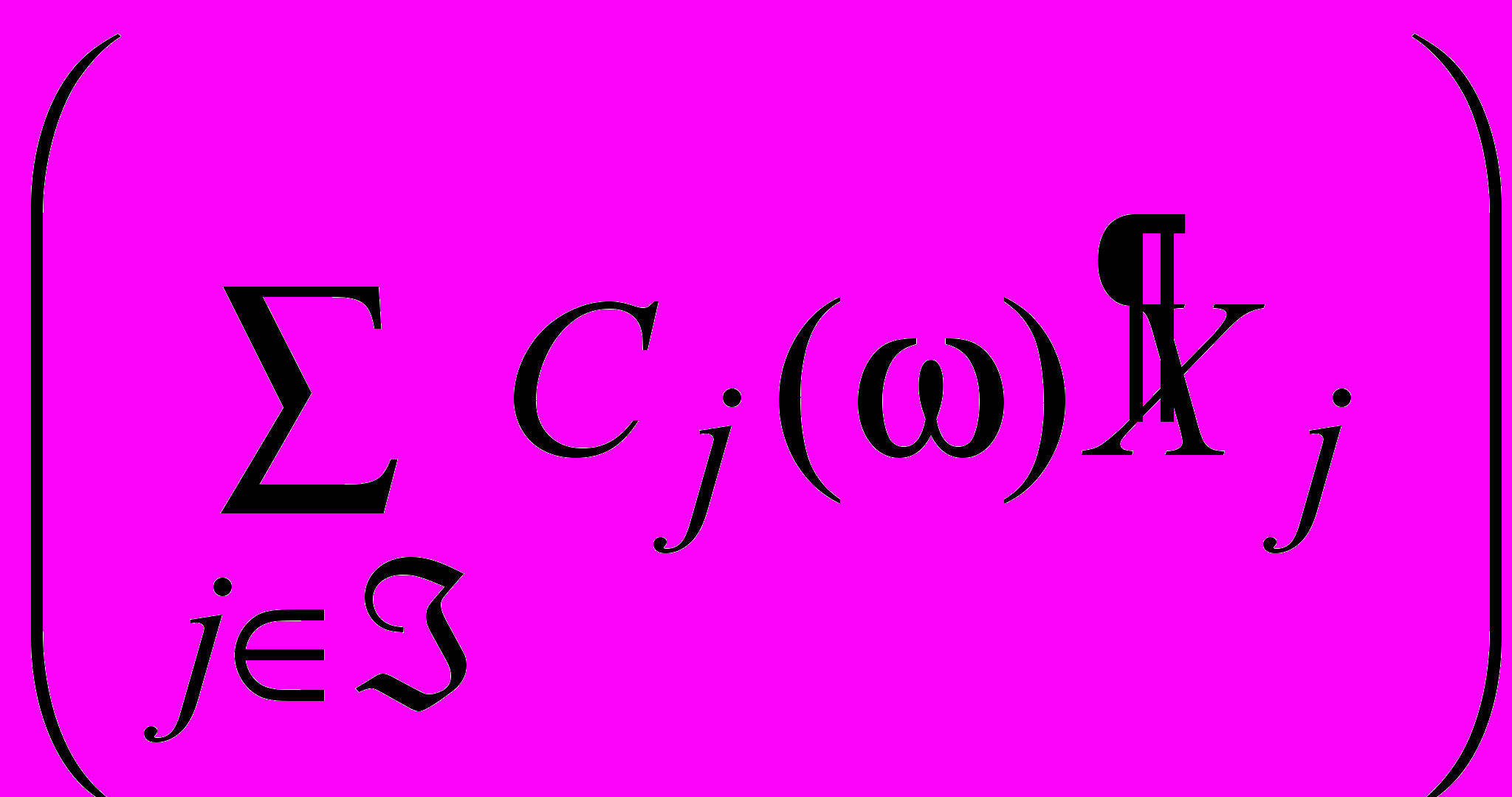
M 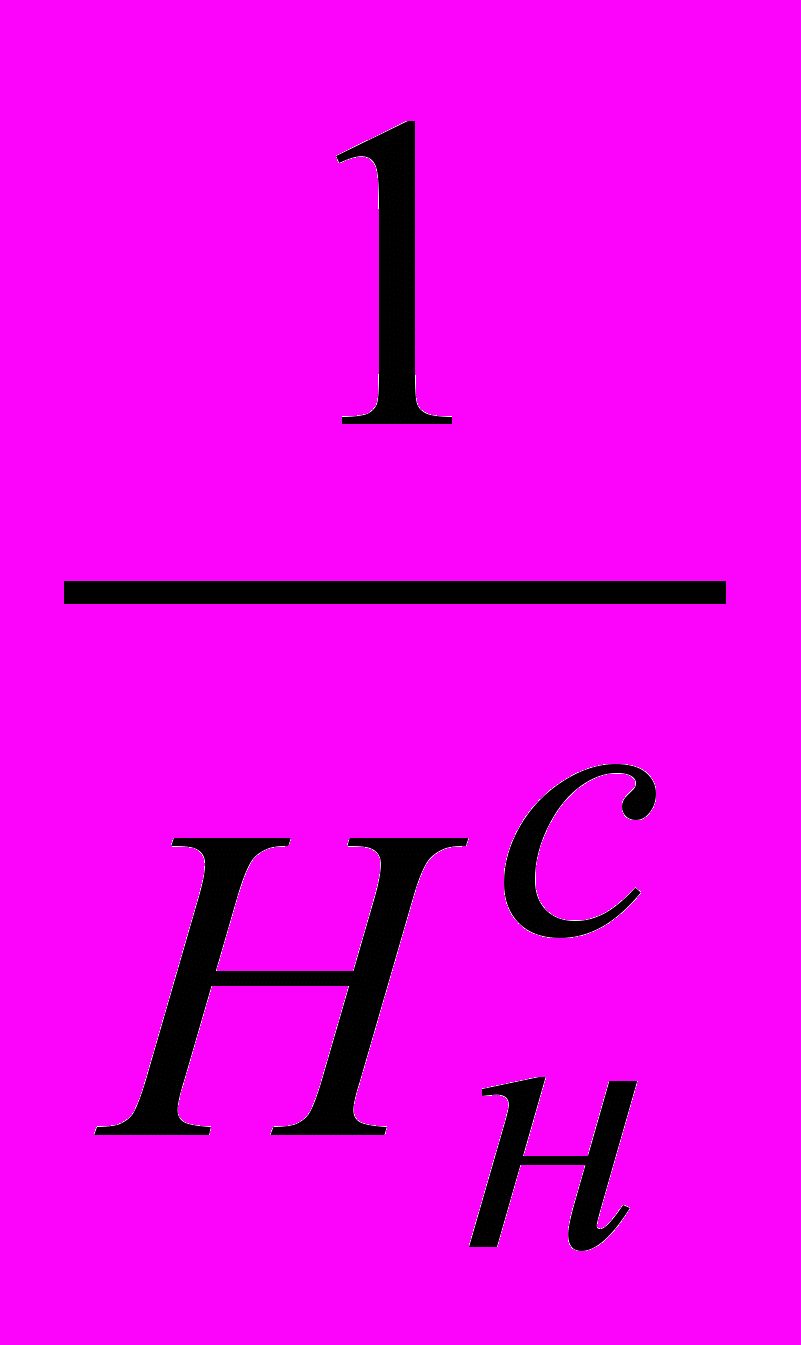C0 и 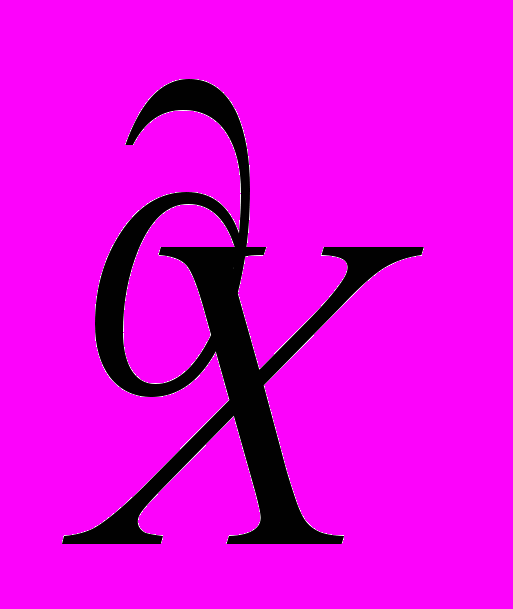Q (3.6)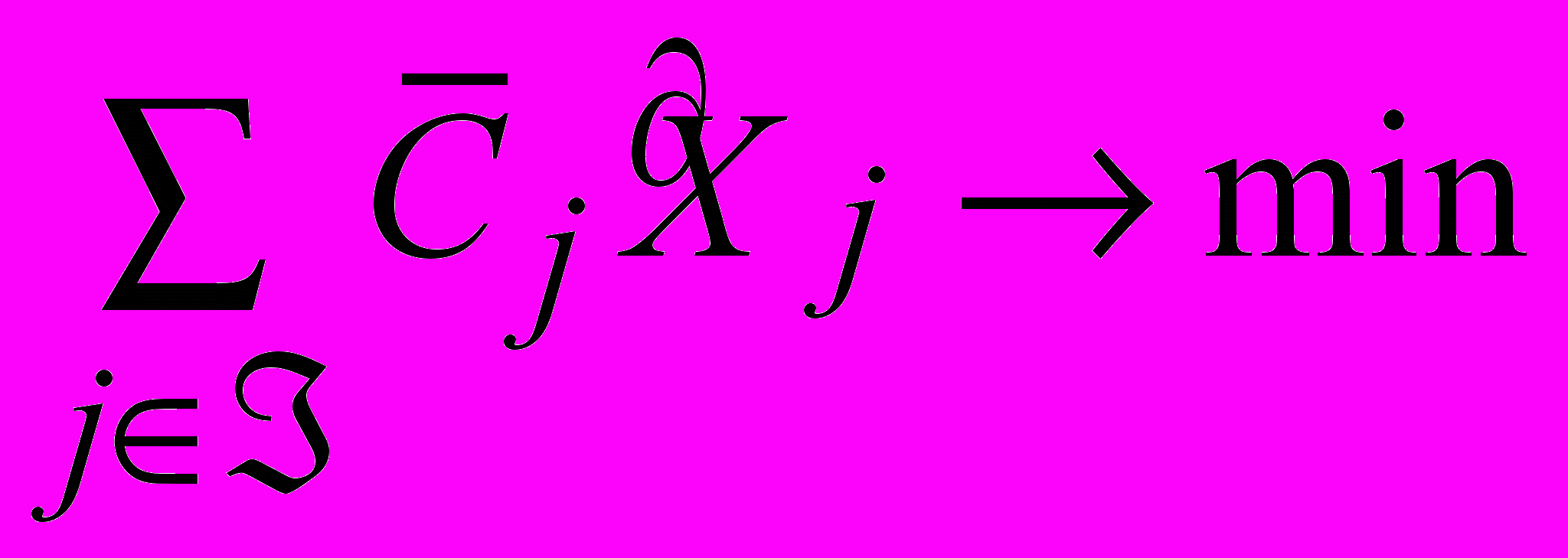




F(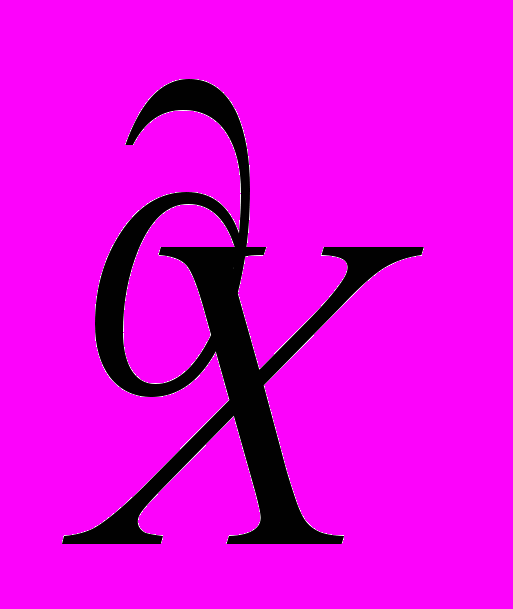) ≥ Нн и 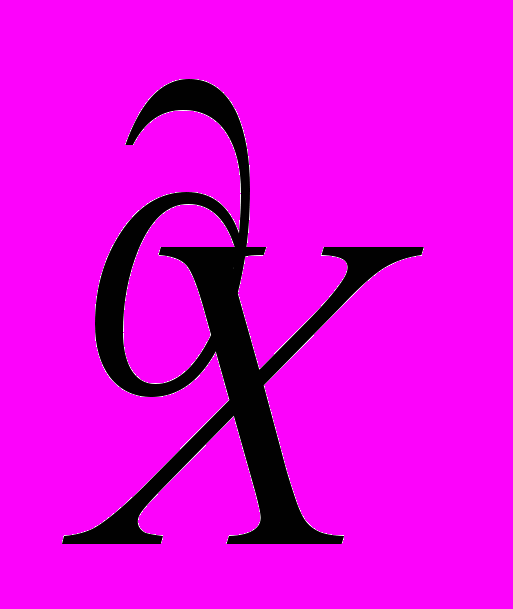Q . (3.7)

F(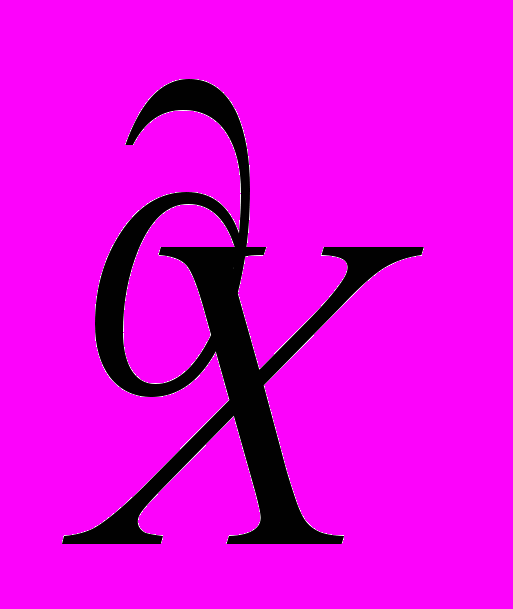) – в общем случае сложная функция регрессии; C0 – допустимый уровень затрат; Нн и Ннс - нормативы по надёжности; множество Q чаще всего может быть задано ограничениями типа двусторонних неравенств.

В моделях (3.6), (3.7) тот или иной вид функции регрессии соответствует измерению уровня надёжности плана 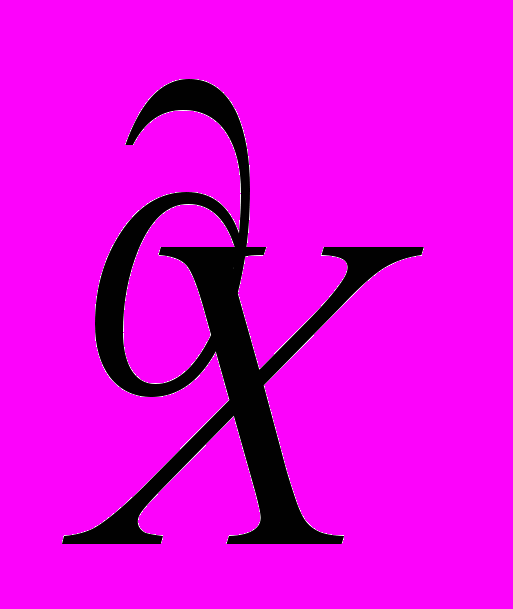с помощью того или иного показателя экономической надёжности.

В рамках настоящей главы указаны условия корректности всех описанных постановок модели формирования эластичного плана; доказано, что при весьма слабых требованиях к i и j для большинства показателей надёжности данные постановки являются задачами «перспективного» стохастического выпуклого программирования; исследованы вопросы эффективного применения для их решения прямых стохастических квазиградиентных методов; намечен путь практической реализации процедуры динамизации рассмотренных моделей.

Помимо вышесказанного в третьей главе предлагаются и анализируются модели оптимизации структуры инвестиционных вложений в финансовые активы, основанные на использовании некоторых функций от эффективности (доходности) различных направлений вложения финансовых ресурсов как случайной величины и «эксплуатирующие» разнообразие показателей доходности по данным направлениям.

В