Г. П. Щедровицкий «Избранные труды» в 4-х тт

Вид материала

Документы

Содержание Iii. формирование арифметико-геометрических задач и геометрических способов решения задач § 2. составные задачи

Подобный материал:

• И. И. Ш м альгаузен избранные труды организм как целое в и ндивидуальном и и сторическом, 7370.54kb.
• А. Н. Леонтьев Избранные психологические произведения, 6448.08kb.
• А. Н. Леонтьев Избранные психологические произведения, 6931kb.
• Д. Б. Эльконин Избранные психологические труды, 9094.25kb.
• Отечества избранные психологические труды в 70-ти томах, 4620.69kb.
• Эльконин Д. Б. К проблеме периодизации психического развития в детском возрасте, 217.77kb.
• В. В. Виноградов об основных типах фразеологических единиц в русском языке, 424.21kb.
• В. В. Виноградов вопрос об историческом словаре русского литературного языка XVIII-XX, 283.61kb.
• Избранные научные труды. М.: Наука, 1988, с. 722-734, 363.13kb.
• Становление: основные положения психологии личности, 1002.65kb.

III. ФОРМИРОВАНИЕ АРИФМЕТИКО-ГЕОМЕТРИЧЕСКИХ ЗАДАЧ И ГЕОМЕТРИЧЕСКИХ СПОСОБОВ РЕШЕНИЯ ЗАДАЧ

§ 1. ПРЯМЫЕ ЗАДАЧИ

1. Рассмотрим, например, как мог сформироваться арифметический способ решения следующей задачи, которую мы отнесли к классу прямых: величина одного поля а, а другого Ь; определить величину поля В, полученного в результате соединения этих полей (или величину поля, полученного при вычитании полей, когда от поля величиной а отрезали поле величиной Ь). На первом этапе, естественно, эта задача должна была решаться с помощью уже сложившихся способов. По ним решение нужно строить так: первое поле присоединить ко второму (или от первого поля отрезать второе) и полученное поле измерить. Этот процесс можно изобразить в следующей схеме:

 Конец страницы 249 

 Начало страницы 250 




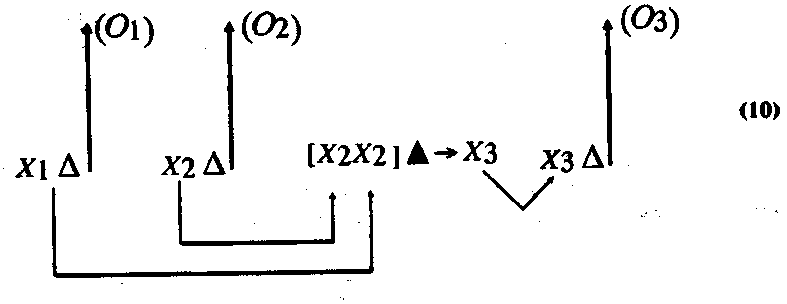
где x₁ — первое поле; x₂ — второе поле; (О₁) — число, выражающее величину первого поля; (О₂) — число, выражающее величину второго поля. Символом 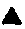обозначена операция соединения полей или операция отделения части поля (дальше мы будем говорить просто отделение), В результате операции А. из первого и второго полей получается поле хз, величина которого выражается в числе (О₃).

Новый способ вычисления, по которому нужно сложить числа а и Ь или из числа а вычесть о, может возникнуть, если данная задача в некоторых случаях не решается с помощью описанного здесь способа.

Такие случаи возникают, когда поле В нельзя измерить и в то же время необходимо вычислить его величину. В новом способе решения этих задач операции с полями (объединение и отделение) переносятся в знаковый план, а число с, фиксирующее величину поля В, получается непосредственно из данных чисел а и Ь. Необходимым условием для такого решения является знание о том, что «число с — результат измерения двух объединенных полей, имеющих величины а и Ь,— равно сумме чисел а и b».

Если обозначить это знание символом А, то строение сформировавшейся процедуры решения задачи можно изобразить следующим образом:




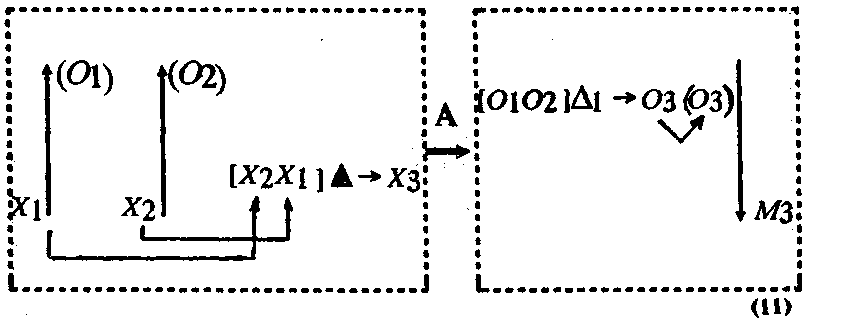
 Конец страницы 250 

 Начало страницы 251 

Здесь знание А обеспечивает переход от процедуры, изображенной в левом блоке схемы (11), к процедуре, изображенной в правом блоке; операция Δ_І — сложение или вычитание чисел (О\) и (О?) (для других типов прямых задач — это деление или умножение).

2. Для трансляции системы операций, изображенной в модели (11), также должны использоваться рисунки с числами. Например, для задач на соединение полей рисунки с числами должны быть такими:





где а, Ь, с — конкретные числа; для задач на разделение полей — такими:





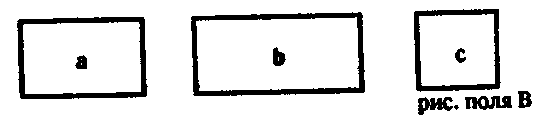
Здесь в первом случае рисунок поля В получается из рисунка первого поля, когда к нему пририсовывается рисунок второго поля, а во втором случае — когда от рисунка первого поля отчеркивается рисунок второго поля.

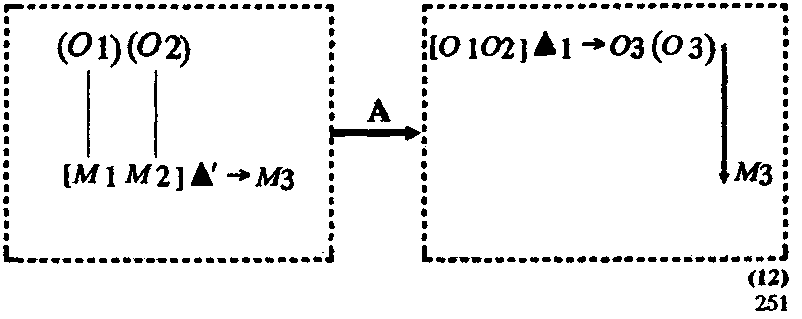
При трансляции сложившегося способа решения данные рисунки с числами начинают выступать в качестве моделей полей x₁ х₂, х₃; это возможно, так как рисунки с числами по отношению к объектам x₁ х₂, х₃ являются знаками-моделями. В результате действия с полями как бы переносятся в плоскость рисунков: действия с полями имитируются в действиях с рисунками (например, действию пририсовывания ставится в соответствие действие объединения полей, действию отчеркивания — действие отделения). Все это позволяет применять знание А уже непосредственно к рисункам полей:




 Конец страницы 251 

 Начало страницы 252 

где М₁—.рисунок первого поля; М₂ — второго; М₃—.-третьего; Δ'_: — операции с рисунками (пририсрвывание и отчеркивание); токой линией, обозначена связь сосуществования между рисунками М\Мг и знаками (O_t), (О₂) — в эмпирической интерпретации числами а и b (эта связь «обеспечивается» модельной функцией рисунков полей).

Непосредственная связь между знанием А и рисунками и числами может быть изображена так:





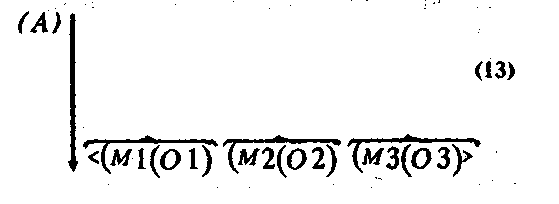
где стрелкой обозначена связь отнесения знания А к рисункам с числами, угловыми скобками — связи между рисунками и числами (эти связи образуются за счет операций Δ' и Δ₁, см. схему (12).

Схемы (12) и (13) позволяют построить описание процедуры решения прямой задачи. В условии этой задачи даны одни элементы — рисунки полей М₁, М₂, М₃ и числа (О₁), (О₂) — и требуется определить другие — число (О₃). Это можно изобразить так:





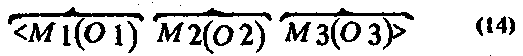
где угловыми штриховыми скобками обозначены связи между рисунками с числами, заданные в условии задачи. Условимся структуру, изображенную на схеме (14), называть обобщенным объектом задачи. Тогда построение решения прямой задачи можно представить как отнесение знания А к обобщенному объекту прямой задачи — см. схемы (13) и (14),— которое дает возможность построить процедуру.

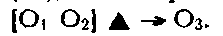
Следовательно, главную роль в построении процедуры решения прямой задачи выполняет знание А, которое позволяет установить связи между известными и неизвестными элементами условия задачи, т. е. между элементами, задан-

 Конец страницы 252 

 Начало страницы 253 

ными в условии задачи, и теми элементами, которые необходимо определить. Именно эти связи указывают на те операции и процедуры, которые нужно осуществить для решения задачи.

§ 2. СОСТАВНЫЕ ЗАДАЧИ

І. Рассмотрим, как мог сформироваться способ решения следующего типа задач: «Два поля сложены: 60; поле над полем на 20 выдается; каковы мои поля?» (х+у=60, х—у=20, х=?, у=?). В текстах приводится следующий алгоритм вычислений: 1) 60:2=30, 2) 20:2=10, 3) 30+10=40, 30—10=20.

Обобщенный объект этой задачи выражается с помощью текста-условия задачи, включающего рисунки и числа (см. рисунок слева и соответствующую модель справа):





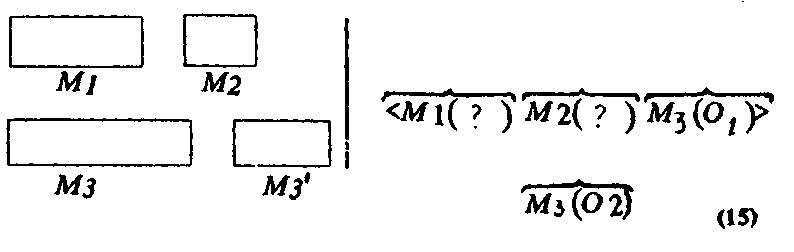
где (О₁) — число 60, а (О₂) — число 20.

Чтобы построить решение этой задачи, нужно определить, во-первых, арифметические операции с числами 60 и 20 и их последовательность и, во-вторых, последующие операции с полученными числами. Для этого, следуя сформировавшемуся способу решения, нужно рассмотреть обобщенный объект данной задачи и установить связи между теми элементами, которые даны, и теми, которые нужно определить.

Анализ условия задачи показывает, что известны сумма двух полей 60 и их разность 20, а также операции, которые осуществлялись с полями (поля складывались и вычитались). Следовательно, известно отношение между полями, выраженное с помощью знаний, которые мы будем обозначать как А₁ и А₂. («число 60 получено в результате сложения величины исходных полей», а «число 20 — в результате вычитания их»). Если опираться на способ решения прямых задач,

 Конец страницы 253 

 Начало страницы 254 

то решение данной задачи должно строиться в результате отнесения к обобщенному объекту задачи — схемы (13) и (15) — знаний А, А1, А₂. Такое отнесение позволяет установить связи между числами, выражающими величины исходных и преобразованных полей, а связи определяют соответствующие операции с числами.

Однако, как мы видим, знание этих связей в данном случае не дает возможности определить числа, фиксирующие величину исходных полей: по типу операции и ее результату (продукту) еще нельзя определить объекты операций¹. Это затруднение может быть снято, если между элементами М₁, М₂ и М₃, а также М₁, М₂ и М'₃ и элементами (О₁) (О₂) установить также и другие связи, которые позволяют числа 60 и 20 сделать объектами операций, а числа, фиксирующие величину исходных полей, получить как продукты этих операций. Дальше мы рассмотрим один из возможных способов установления таких связей.

2. Предположим, что решению анализируемого нами типа задач предшествовало решение нескольких связанных между собой прямых задач.

Задача Ї. Величина (площадь) поля 40. Разделить его пополам. Решение: 40:2=20. Для восстановления все три поля изображались в чертежах с числами:





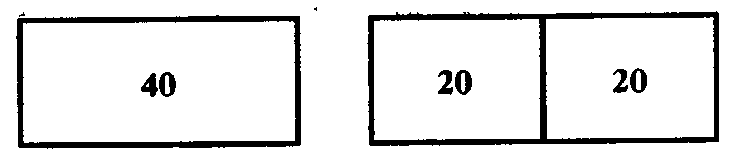
¹ Можно, правда, подобрать эти объекты, ориентируясь на вид операции и ее продукт Для этого достаточно найти два числа, сумма которых равна 60, а разность 20 Можно даже выделить способ подборки таких чисел Например, одно число должно быть больше 30 (половины суммы), а другое настолько же меньше, иначе не получится разность чисел или их сумма Тогда встает вопрос- какое число надо добавить к 30 и отнять от 30, чтобы получить нужные числа? Предположим, что к 30 добавили и отняли число 20, выражающее разность полей, и получили числа 50 и 10 Сумма этих чисел действительно равна 60, а разность (50—10=40) в два раза больше необходимой Следовательно, к числу 30 надо добавить (отнять) не число 20, а число в два раза меньше, т е. 10 Отсюда и способ решения 1) раздели сумму чисел пополам (60 2=30), 2) раздели разность чисел пополам (20 2=10), 3) к половине суммы прибавь половину разности (30+10 = 40), от половины суммы отними половину разности (30—10=20) Тем не менее указанный путь решения маловероятен в силу его крайней формальности

 Конец страницы 254 

 Начало страницы 255 

Задача 2. Поле 20 и другое поле 20. От одного поля отрезали участок, равный 5 и прибавили его к другому полю. Узнай величину получившихся полей. Решение: 20—5=15, 20+5=25. При восстановлении эта ситуация также изображалась в рисунках с числами:





Задача 3. Одно поле 25, а другое 15. Узнай, на сколько одно поле выступает (больше) над другим. Решение: 25—15=10.

Задача 4. Одно поле 25, другое 15. Оба поля соединили. Как велико получившееся поле? Решение: 25+15=40.

При сопоставлении решений этих задач можно получить несколько знаний. Во-первых, знание Аз о том, что разность 10 между двумя полями, заданными в задаче 3, равна удвоенной величине участка 5, о котором говорится в задаче 2. Во-вторых, знание А₄ — величина полей, данных в задаче 3 (15 и 25), равна величине полей, полученных в результате решения задачи 2. В-третьих, знание А₅ — сумма полей, равных 15 и 25 (о них также говорится в задаче 4), дает поле, равное 40, т. е. величину поля, заданного в задаче 1. В-четвертых, знание А₆ — величина полей, данных в условии задачи 2 (20 и 20), равна величине полей, полученных в результате решения задачи 1*. Таким образом, знания А₃—А₆ позволяют установить связи между известными и неизвестными элементами всех четырех задач. Это можно изобразить так (для облегчения чтения схемы мы опустили рисунки полей, соответствующие термины, входящие в условия задачи, и описания):

________________

* Отождествить задачи и их элементы можно по рисункам полей и геомегричоским терминам, но не по одинаковым числам, поскольку в задачах одного типа сохраняются рисунки полей и геометрические термины, а числа, выражающие величину полей, меняются

 Конец страницы 255 

 Начало страницы 256 




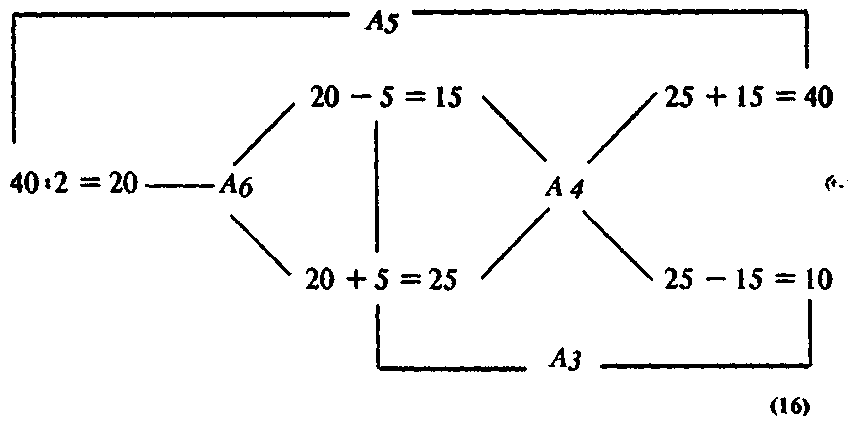
Если теперь учесть рисунки полей, понятийные описания и термины, то связи между известными и неизвестными элементами могут быть изображены так:





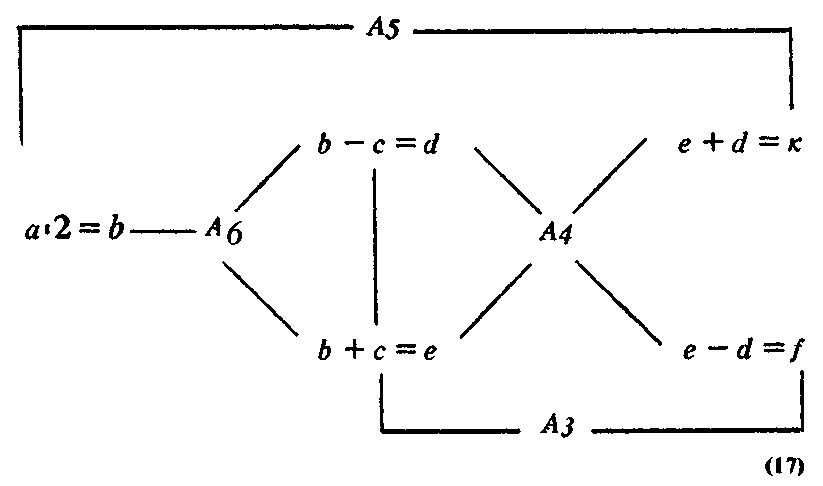
Здесь маленькими латинскими буквами обозначены уже не числа, а величины. Каждая величина задается рисунком и числом, проставленным в рисунке поля и выражающим величину поля. Например, буквой а обозначена величина суммы двух полей, а буквой с — величина участка, который отрезается от одного поля и добавляется к другому.

Предположим далее, что решения задач 1—4 и знания

 Конец страницы 256 

 Начало страницы 257 

A₅—А₆ используются в качестве средств для решения анализируемой выше составной задачи. Это использование предполагает прежде всего процедуру сопоставления условия составной задачи с условиями задач 1—4. В результате сопоставления можно получить знание А₇ о том, что задача, которую нужно решить, как бы обратная по отношению к задачам 3 и 4. Действительно, в подготовительных задачах 3 и 4 известна величина двух полей и необходимо найти их сумму и разность, а в составной задаче, которую нужно решить, наоборот, известна разность и сумма двух полей и необходимо найти величину исходных полей.

Следовательно, обобщенные объекты этих задач практически тождественны; только те элементы, которые в подготовительных задачах известны, в анализируемой задаче нужно определить, а те, которые неизвестны, в анализируемой задаче даны. Изобразим это:





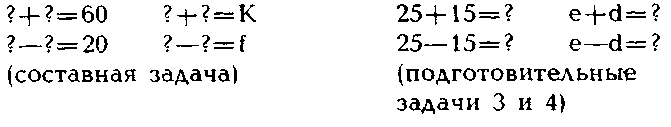
Именно знание А₇ позволяет свести решение анализируемой составной задачи к решению задач I—4, поскольку отнесение этого знания к обобщенному объекту анализируемой задачи включает решение этой задачи в цепь решений задач 3—4.




 Конец страницы 257 

 Начало страницы 258 

Двигаясь по этой цепи, уже можно установить связи между известными и неизвестными элементами анализируемой задачи (связи между этими элементами устанавливаются за счет знаний А₃—А₄ и соответствующих вычислений).

Таким образом, между суммой величин двух полей, величиной каждого поля и величиной участка, который нужно отрезать от одного поля и присоединить к другому, чтобы их уравнять, существуют определенные связи. С их помощью можно определить величину исходных полей, если заданы величина этого участка и сумма исходных полей. Кроме того, существует связь между величиной участка, отрезаемого от одного исходного поля и присоединяемого к другому, и размером того участка, на который одно поле превышает другое. Эта связь позволяет найти величину этого участка, если задана разность (и наоборот)

На основе этих связей задачу, в которой известны сумма двух полей и их разность, можно решить так: поле, равное сумме двух неизвестных полей (60), сначала нужно представить как сложенное из двух равных полей (30 и 30), разность между полями (20) рассмотреть как удвоенную величину участка, отрезанного от одного поля и присоединенного к другому. Это рассуждение задает последовательность арифметических действий: сначала нужно определить величину равных полей: 60:2=30, затем величину передаваемого участка: 20:2=10, затем величину исходных полей: 30—10=20 и 30+10=40.

3. Итак, решение составной задачи состоит в том, чтобы установить между известными и неизвестными элементами задачи связи, и благодаря этому известные элементы сделать объектами операций, а неизвестные получить как продукты операций'. Связи между известными и неизвестными элементами решаемой задачи устанавливаются за счет дополнительной цепочки связанных между собой элементов, взятой из решений специально подобранной серии связанных между

____________

¹ Факты эмпирического материала хорошо подтверждают эту гипотезу А А Вайман в частности, показал, что многие задачи вавилонские математики решали путем подбора арифметических операций, обеспечивающих связь известных и неизвестных элементов (величин), входивших в условия задач Иногда, подбирая такие арифметические операции, они допускали ошибки например, забывали использовать тог или иной элемент условия задачи или использовали в качестве известных такие элементы, которые в условии задачи не были даны (см , А А Вайман. Шумеро-вавилонская математика, стр 210, п 5)

 Конец страницы 258 

 Начало страницы 259 

собой задач. Чтобы использовать указанную цепочку для решения задачи, нужно осуществить полное или частичное отождествление величин, данных в условии решаемой задачи, и величин, данных в условиях подобранной серии задач. Именно за счет этого связи, принадлежащие обобщенным объектам подобранной серии задач, могут быть приписаны обобщенным объектам решаемой задачи. Описанные здесь отношения между задачами на схеме можно изобразить так:





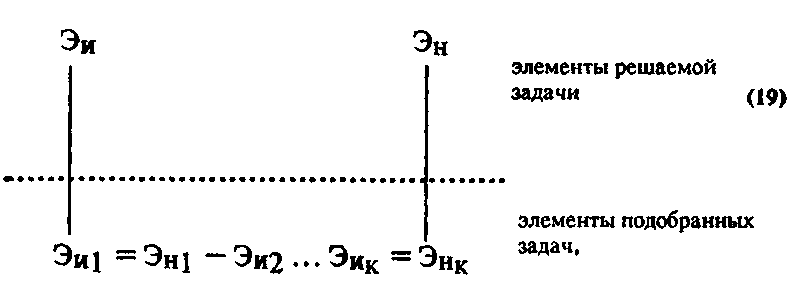
где Эи — известные элементы задач, Эн — неизвестные элементы, двойные черточки « = » — связи между известными и неизвестными элементами разных задач, одинарные «—» — связи между элементами разных задач.

Употребление рисунков полей в качестве средств при построении решений задач приводит к изменению их природы. В прежнем употреблении рисунки полей выступали знаками-моделями (см. текст выше). Теперь же, сохраняя свои прежние знаковые функции, они превращаются в особые объекты (объекты оперирования. Действительно, при решении арифметика-геометрических задач необходимо, как мы показали, отождествлять рисунки полей и одновременно сопоставлять числа, проставленные на этих рисунках. Такие операции требуют, чтобы рисункам полей наряду с другими свойствами были приписаны еще два свойства: проницаемость, которая дает возможность в одном рисунке поля выделять рисунки других полей — см. схемы (13)—(18),— и относительная величина, по которой, например, один рисунок, изображающий поле величиной а, должен быть частью другого рисунка, изображающего поле величиной 2а.

4. Однажды полученное решение задачи в дальнейшем может использоваться в функции образца решения. С помощью образца полученный способ решения переносится

 Конец страницы 259 

 Начало страницы 260 

на решение задач того же типа, но с другими числовыми значениями. Рассуждение, которое мы провели при анализе трансляции способов .вычисления полей (см. §3, раздел II), можно перенести и на случай трансляции способов решения задач. Из этого анализа, в частности, следует, что трансляция описанного способа решения может осуществляться за счет рисунков полей с числами, арифметических и геометрических терминов и арифметических выкладок. В дальнейшем рисунки полей заменяются арифметическими и геометрическими выражениями, например такими: «добавили поле 5», «поле 20», «отрезали поле 15», «сумма двух полей 40», «разность двух полей 20» и т. д.¹.

Это означает, что если решение задачи построено, то дальше оно может передаваться с помощью арифметических и геометрических терминов. При этом способ, с помощью которого впервые было получено решение задачи, дальше при решении задач подобного же типа не используется. Факты эмпирического материала позволяют утверждать, что именно так и произошло в вавилонской математике многочисленные образцы решений задач, собранные в специальных учебных сборниках, позволили забыть, как были получены сами способы решения задач, и решать все другие подобные задачи по имеющимся образцам.

Можно показать, что решения всех остальных типов арифметико-геометрических и геометрических задач, имеющихся в вавилонской и египетской математике, складываются точно таким же образом. Способ решения этих задач не является ни алгебраическим, ни геометрическим, как это утверждают историки-математики; решение достигается за счет движения в рисунках с числами, изображающих поля, и в алгоритмах вычисления площадей. Одно из важнейших условий получения нового решения — подбор связанных между собой задач и сопоставление этих задач между собой для выявления отношений между величинами и числами, полученными в разных вычислениях Однажды построенное решение начинает выступать в особой функции метода решения других задач, отличающихся от решенной задачи числовыми значениями. Это достигается за счет особого использования «скелета» решения, образуемого рисунками полей,

_______________

¹Б Л Ван-дер-Варден Пробуждающаяся наука, стр 85—105, А А Ваиман Шумеро-вавилонская математика стр fil—84, 232— 259, 171 — 180

 Конец страницы 260 

 Начало страницы 261 

а также геометрическими и арифметическими терминами операций («отрезали», «добавили», «удвоили», «сложили» и т. д.). После того, как решение задачи одного типа получено, сам способ построения решения теряется, поскольку им перестают пользоваться¹.