Руководство по выполнению курсовой работы по дисциплине «Имитационное моделирование экономических процессов» составлено в соответствии с требованиями государственного стандарта России и предусмотрено учебным планом специальности.
| Вид материала | Руководство |
- Руководство к выполнению курсовой работы по дисциплине «Финансы предприятий», 244.13kb.
- Рабочая программа по курсу «Имитационное моделирование экономических процессов» для, 150.96kb.
- Методические указания к выполнению контрольных, курсовых работ По дисциплине Имитационное, 222.24kb.
- Методические указания к выполнению курсовой работы Владивосток, 732.88kb.
- Пособие предназначено для студентов, выполняющих курсовые работы по дисциплине «Направления, 589.33kb.
- Методические указания по выполнению курсовой работы по дисциплине "Стратегический менеджмент", 33.46kb.
- Методические указания по выполнению курсовой работы для студентов по специальности, 161.11kb.
- Тематика курсовых работ. Всоответствии с учебным планом предусмотрено написание курсовой, 39.43kb.
- Методические указания к выполнению курсовой работы учебным планом дисциплины «Макроэкономика», 94.82kb.
- Учреждения, 299.24kb.
Задание 6
На участке термической обработки выполняют цементирование и закалку шестерен, поступающих через каждые Т1 минут. Цементирование занимает Т2 минут, а закалка — Т3 минут. Качество шестерни определяется суммарным временем ее обработки без учета времени ожидания. Шестерни со временем обработки более Т4 минут (первый сорт) покидают участок, со временем обработки от Т5 до Т4 минут (второй сорт) передаются на повторную закалку, а со временем обработки менее Т5 минут (третий сорт) повторно проходят полную обработку и остаются того же сорта. Стоимость шестерен первого, второго и третьего сортов равна S3, S4 и S5 единиц стоимости, соответственно.
Увеличение на k процентов (0 < k < 50) среднего времени цементирования требует k*S1 единиц стоимости для каждой шестерни. Увеличение на q процентов (0 <= q <= 50) среднего времени закаливания требует q*S2 единиц стоимости для каждой шестерни. Эти изменения могут производиться независимо друг от друга.
Определить характеристики операций цементирования и закалки, при которых достигается максимум суммарной стоимости шестерен, выпускающихся за единицу времени.
Варианты заданий приведены в табл. 6.
Таблица 6- Варианты к заданию 6
| Вариант | Параметры | |||||||||
| T1 | T2 | T3 | T4 | T5 | S1 | S2 | S3 | S4 | S5 | |
| 1 | 15±5 | 10±5 | 10±5 | 25 | 18 | 0,01 | 0,03 | 2 | 8 | 5 |
| 2 | 20±8 | 15±7 | 20±10 | 35 | 25 | 0,02 | 0,03 | 3 | 12 | 7 |
| 3 | 40±9 | 30±10 | 30±12 | 70 | 55 | 0,03 | 0,01 | 4 | 16 | 10 |
| 4 | 35±9 | 25±8 | 30±10 | 65 | 58 | 0,02 | 0,02 | 3 | 18 | 11 |
Задание 7
В механическом цеху есть М станков. Каждый из них может выйти из строя. Неисправности станков делятся на три типа. Неисправности i-го типа представляют собой пуассоновский поток с параметром λi минут-1.
В цеху есть две категории мастеров-ремонтников. Функции распределения времени их работы по устранению неисправностей равномерные (табл. 7).
Час работы станка дает прибыль S1 единиц стоимости; заработная плата ремонтника - S2 единиц стоимости в час для первой категории и S3 единиц стоимости для второй.
Определить состав бригады ремонтников, при котором суммарная прибыль достигает максимума.
Варианты заданий приведены в табл. 7 и 7.1.
Таблица 7- Варианты к заданию 7
| Категория мастера | Время работы на устранение неисправности j | |||||
| Варианты 1 и 2 | Варианты 3 и 4 | |||||
| j=1 | j=2 | j=3 | j=1 | j=2 | j=3 | |
| 1 | 16±4 | 18±4 | | 26±4 | 22±5 | 15±5 |
| 2 | 10±3 | 15±6 | 19±5 | 17±4 | 14±2 | |
Таблица 7.1- Варианты к заданию 7
| Вариант | Параметры | ||||||
| M | λ1 | λ2 | λ3 | S1 | S2 | S3 | |
| 1 | 50 | 1⁄100 | 1⁄200 | 1⁄300 | 7000 | 30 | 80 |
| 2 | 30 | 1⁄200 | 1⁄150 | 1⁄200 | 8000 | 50 | 35 |
| 3 | 40 | 1⁄300 | 1⁄200 | 1⁄300 | 6000 | 45 | 65 |
| 4 | 45 | 1⁄250 | 1⁄180 | 1⁄250 | 7000 | 60 | 40 |
Задание 8
В сборочном цеху на изделия монтируются агрегаты двух типов. Предполагается, что на входе цеха имеется такое количество агрегатов, которое является достаточным для бесперебойной работы цеха.
Агрегаты первого типа поступают на операцию ОП1 проверки параметров агрегатов с длительностью T1 минут. Агрегаты второго типа поступают на операцию ОП2 проверки параметров с длительностью Т2 минут. Монтирование агрегатов на изделия может начаться только при наличии двух агрегатов первого типа и одного агрегата второго типа и после монтирования предыдущего изделия. Монтирование двух агрегатов первого типа занимает Т3 и Т4 минут, соответственно, монтирование агрегата второго типа занимает Т5 минут. Операции монтирования производятся параллельно. Длительность каждой из операций зависит от числа задействованных на ней рабочих.
Прибыль от реализации каждого смонтированного изделия составляет S1 единиц стоимости. На участке может быть задействовано не более N работников. Заработная плата одного работника составляет S2 единиц стоимости в час.
Определить необходимое количество работников и их распределение между операциями, при которых достигается максимальная экономическая эффективность работы цеха (прибыль за единицу времени).
Варианты заданий приведены в табл. 8.
Таблица 8- Варианты к заданию 8
| Параметры | Количество работников | Варианты | |||
| 1 | 2 | 3 | 4 | ||
| Т1 | 1 | 30±11 | 88±20 | 70±20 | 90±15 |
| 2 | 22±8 | 60±18 | 55±10 | 70±11 | |
| 3 | 18±5 | 50±15 | 45±11 | 55±10 | |
| Т2 | 1 | 20±10 | 50±12 | 45±10 | 60±10 |
| 2 | 18±8 | 40±11 | 40±8 | 45±6 | |
| 3 | 15±5 | 35±9 | 30±7 | 40±8 | |
| Т3 | 1 | 20±8 | 50±15 | 40±14 | 45±10 |
| 2 | 13±6 | 35±8 | 30±5 | 38±5 | |
| 3 | 8±3 | 25±7 | 20±7 | 22±7 | |
| Т4 | 1 | 25±9 | 45±13 | 40±12 | 50±12 |
| 2 | 17±6 | 30±10 | 25±7 | 33±6 | |
| 3 | 12±4 | 20±7 | 18±6 | 19±6 | |
| Т5 | 1 | 27±10 | 42±15 | 40±10 | 45±10 |
| 2 | 18±7 | 20±10 | 18±9 | 25±9 | |
| 3 | 10±3 | 15±6 | 15±4 | 20±4 | |
| N | 11 | 14 | 13 | 15 | |
| S1 | 500 | 1000 | 800 | 1100 | |
| S2 | 50 | 80 | 40 | 90 | |
Задание 9
Служба заказа такси имеет N1 каналов дня одновременного приема заказов по телефону. Интервалы времени между попытками вызова такси распределены по закону Эрланга второго порядка со средним T1 секунд. Абонент затрачивает T2 секунд на набор номера. Если он застает все каналы заказа занятыми или после соединения выясняет, что очередь на обслуживание превышает N заказов (в таком случае заказы не принимаются), то через T3 секунд он повторяет набор. После K попыток абонент прекращает набор. Служба заказа имеет в своем распоряжении N2 машин для обслуживания пассажиров. Время, затраченное для проезда к клиенту, зависит от расстояния. Распределение расстояния приведено в табл. 9. Стоимость проезда к клиенту недоплачивается. Скорость движения машины равномерно распределена в интервале V1±V2 километров в час (табл. 9.1). Время обслуживания клиента равномерно распределено в интервале T4 ± T5 минут. Стоимость предварительно заказа составляет S1 рублей, стоимость проезда 1 км равна S2 копеек табл. 9.1
Найти оценку интервала времени выполнения заказа (время от момента заказа такси до момента доставки клиента на место). Считая, что операторы-телефонисты и водители такси взаимозаменяемы, перераспределить их между участками работы так, чтобы минимизировать время выполнения заказов (штат службы не должен превышать N1 + N2 человек).
Определить такое количество операторов на телефонах и водителей такси, при которых прибыль службы за сутки работы (суточная заработная плата каждого из работников составляет S3 рублей) будет максимальной.
Таблица 9- Варианты к заданию 9
| Расстояние, км | 5 | 8 | 9 | 11 | 12 | 20 |
| Вероятность | 0,10 | 0,20 | 0,25 | 0,17 | 0,23 | 0,05 |
Таблица 9.1 - Варианты к заданию 9
| Параметр | Варианты | |||
| 1 | 2 | 3 | 4 | |
| N1 | 5 | 4 | 3 | 4 |
| N2 | 10 | 8 | 9 | 10 |
| T1 | 180 | 150 | 190 | 170 |
| T2 | 30 | 25 | 35 | 20 |
| T3 | 60 | 50 | 70 | 40 |
| t4±t5 | 40±10 | 45±15 | 40±20 | 35±15 |
| K | 10 | 12 | 8 | 9 |
| V1±V2 | 40±5 | 43±7 | 45±5 | 50±8 |
| S1 | 2 | 3 | 2,5 | 4 |
| S2 | 50 | 60 | 70 | 70 |
| S3 | 10 | 14 | 16 | 15 |
| N | 2 | 1 | 3 | 2 |
Задание 10
В сборочном цеху из агрегатов двух типов монтируются готовые изделия. Агрегаты первого (второго) типа поступают в цех через интервалы времени, распределенные нормально с математическим ожидание m1 (m2) минут и среднеквадратическим отклонением σ1 (σ2) минут (табл. 10).
Агрегаты первого типа поступают на операцию настройки ОН1 с длительностью операции Т1 минут. Агрегаты второго типа поступают на операцию настройки ОН2 с длительностью Т2 минут. Монтирование агрегатов для получения готового изделия может начаться только при наличии одного агрегата первого типа и двух агрегатов второго типа и только после монтирования предыдущего изделия. Монтирование агрегата первого типа занимает Т3 минут, двух агрегатов второго типа – Т4 и Т5 минут, соответственно. Операции монтирования производятся параллельно. Длительность каждой операции зависит от количества задействованных на ней рабочих.
На участке может быть задействовано не более N рабочих. Заработная плата одного рабочего составляет Z единиц стоимости за 1 час. Стоимость хранения одного агрегата каждого типа в цеху на протяжении 1 часа составляет S единиц стоимости.
Определить наилучшее с экономической точки зрения распределение рабочих между операциями.
Варианты заданий приведены в табл. 10.
Таблица 10 - Варианты к заданию 10
| Вариант | Параметры | ||||||||||
| m1, σ1 | m2, σ2 | N | Z | S | Кол-во рабочих | T1 | T2 | T3 | T4 | T5 | |
| 1 | 30, 5 | 18, 3 | 15 | 10 | 0,5 | 1 | 50±15 | 35±12 | 20±8 | 25±9 | 27±10 |
| 2 | 29±10 | 17±8 | 13±6 | 17±6 | 18±7 | ||||||
| 3 | 20±8 | 12±5 | 8±5 | 12±4 | 10±3 | ||||||
| 2 | 75, 10 | 51, 6 | 14 | 30 | 0,6 | 1 | 95±20 | 80±15 | 50±15 | 45±13 | 42±15 |
| 2 | 70±18 | 50±11 | 35±8 | 30±10 | 20±10 | ||||||
| 3 | 45±15 | 35±9 | 25±7 | 20±7 | 15±6 | ||||||
| 3 | 80, 12 | 56, 7 | 13 | 40 | 0,8 | 1 | 90±18 | 70±15 | 55±12 | 40±11 | 35±10 |
| 2 | 75±15 | 55±10 | 30±7 | 25±9 | 22±8 | ||||||
| 3 | 50±12 | 30±6 | 20±6 | 18±5 | 16±5 | ||||||
| 4 | 60, 10 | 50, 8 | 15 | 50 | 0,7 | 1 | 95±18 | 75±15 | 60±15 | 40±11 | 40±10 |
| 2 | 65±15 | 50±10 | 38±10 | 27±9 | 30±7 | ||||||
| 3 | 45±12 | 35±6 | 25±7 | 18±6 | 22±5 | ||||||
Задание 11
На участок поступают пуассоновские потоки узлов двух типов с параметрами λ1 мин-1 и λ2 мин-1 для первого и второго, соответственно (табл. 11).
Первая операция - операция предварительной подгонки - начинается в том случае, если в наличии есть по одному узлу каждого типа и завершена подгонка предыдущих узлов. Длительность этой операции Т1 минут. Дальше с вероятностью p1 над узлом первого типа и р2 над узлом второго типа производится операция доводки, которая длится Т2 и Т3 минут, соответственно. После этого узлы поступают на операцию сборки, которая начинается после поступления узлов обоих типов, которые ранее были взаимно подогнаны. Сборка длится Т4 минут.
Длительность каждой операции зависит от количества задействованных на ней рабочих. Всего на участке может быть задействовано не более N рабочих.
Прибыль от реализации одного готового изделия составляет S1 единиц стоимости, но, если после завершения подгонки узлов до момента их сборки проходит более T минут, прибыль от реализации изделия уменьшается вдвое. Заработная плата каждого рабочего - S2 единиц стоимости в час.
Определить такое количество занятых в производстве рабочих и их распределение между операциями, которое бы обеспечило максимальную экономическую эффективность производства.
Варианты заданий приведены в табл. 11.
Таблица 11 - Варианты к заданию 11
| Параметры | Количество рабочих | Вариант | |||
| 1 | 2 | 3 | 4 | ||
| λ 1 | 1/20 | 1/40 | 1/30 | 1/25 | |
| λ 2 | 1/20 | 1/40 | 1/30 | 1/25 | |
| T1 | 1 | 20±10 | 55±12 | 40±15 | 50±10 |
| 2 | 15±5 | 37±10 | 29±11 | 30±8 | |
| 3 | 12±4 | 30±8 | 22±8 | 20±6 | |
| T2 | 2 | 18±5 | 40±10 | 40±10 | 30±11 |
| 3 | 10±3 | 18±5 | 25±7 | 20±6 | |
| T3 | 1 | 20±8 | 25±6 | 28±9 | 30±5 |
| 2 | 12±6 | 20±6 | 20±8 | 18±4 | |
| T4 | 1 | 20±7 | 48±12 | 40±10 | 45±10 |
| 2 | 18±6 | 35±8 | 30±7 | 35±7 | |
| 3 | 15±5 | 29±6 | 20±5 | 25±5 | |
| 4 | 10±4 | 18±5 | 16±4 | 15±3 | |
| ρ1 | 0,75 | 0,70 | 0,65 | 0,55 | |
| ρ2 | 0,90 | 0,55 | 0,85 | 0,65 | |
Продолжение табл. 11
| Параметры | Количество рабочих | Вариант | |||
| 1 | 2 | 3 | 4 | ||
| S1 | 400 | 600 | 560 | 650 | |
| S2 | 75 | 90 | 50 | 60 | |
| N | 9 | 11 | 10 | 12 | |
| T | 20 | 35 | 30 | 35 | |
Задание 12
Детали, необходимые для работы цеха, находятся на цеховом и центральном складах. На цеховом складе может хранится до n комплектов деталей, потребность в которых возникает через А
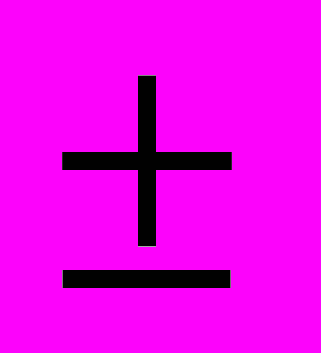В минут и составляет один комплект. В случае понижения уровня до k комплектов на протяжении С минут формируется запрос на пополнение запасов цехового склада до полного объёма в n комплектов. Запрос посылают на центральный склад, где на протяжении D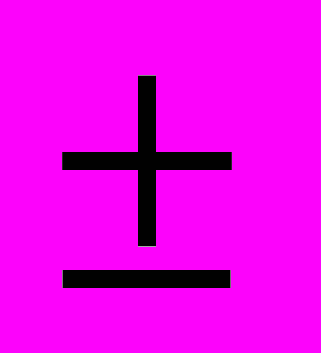E минут комплектуются детали и через F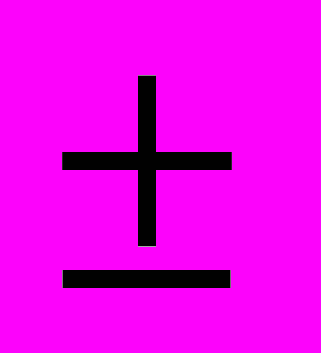G минут доставляются в цех.Следующий запрос на пополнение запасов может подаваться только после выполнения предыдущего.
Хранение одного комплекта на цеховом складе требует S1 единиц стоимости за единицу времени. Штраф за задержку поставки комплекта составляет S2 единиц стоимости за единицу времени.
Определить, при каких значениях n и k достигается максимальная экономическая эффективность работы склада.
Варианты заданий приведены в табл. 12.
Таблица 12 - Варианты к заданию 12
| Вариант | Параметры | ||||||||||
| n | A | B | k | C | D | E | F | G | S1 | S2 | |
| 1 | 20 | 60 | 10 | 3 | 60 | 80 | 20 | 70 | 10 | 10 | 150 |
| 2 | 35 | 100 | 20 | 4 | 90 | 110 | 50 | 120 | 30 | 15 | 300 |
| 3 | 25 | 50 | 10 | 2 | 40 | 30 | 20 | 80 | 35 | 20 | 200 |
| 4 | 30 | 70 | 15 | 3 | 40 | 30 | 20 | 80 | 35 | 20 | 200 |
Задание 13
Частный магазин покупает партию из N единиц товара по оптовой цене S единиц стоимости. Деньги на приобретение товара владелец магазина берет в кредит. Процентная ставка за кредит составляет k процентов от суммы непогашенного кредита в день (табл. 13).
Поток покупателей, приходящих в магазин, - пуассоновский с параметром λ мин-1.
Вероятность того, что покупатель не будет покупать товар и сразу уйдет из магазина, зависит от длины очереди и розничной цены товара:
Руход=1 - р1*р2, (1)
где
р1 - вероятность того, что длина очереди «устраивает» покупателя,
р2 - вероятность того, что он купит товар по установленной розничной цене.
Время обслуживания покупателя в магазине - равномерно распределенная случайная величина в интервале А ± В мин.
Определить наиболее выгодную розничную цену продажи товара в магазине с учетом платы за кредит.
Примечание. Считать, что после продажи единицы товара величина кредита уменьшается на отпускную цену проданного товара (если долг еще существует). Это приводит к тому, что величина кредита и выплата процентов по нему уменьшаются.
Варианты заданий приведены в табл. 13.
Таблица 13 - Варианты к заданию 13
| Параметры | Варианты | |||
| 1 | 2 | 3 | 4 | |
| N | 600 | 1000 | 2000 | 1500 |
| S | 1000 | 500 | 1500 | 800 |
| k, % | 1 | 2 | 3 | 2 |
| λ | 0,05 | 0,033 | 0,04 | 0,08 |
| p1 - очередь до 3 человек | 0,55 | 0,67 | 0,62 | 0,6 |
| 4 - 6 человек | 0,2 | 0,15 | 0,2 | 0,2 |
| 7 - 10 человек | 0,15 | 0,1 | 0,13 | 0,12 |
| Свыше 11 человек | 0,1 | 0,08 | 0,05 | 0,08 |
| p2 - цена до 1,5 S | 0,67 | 0,65 | 0,6 | 0,68 |
| 1,5S - 2S | 0,14 | 0,2 | 0,2 | 0,15 |
| 2S - 3S | 0,11 | 0,1 | 0,1 | 0,1 |
| 3S - 4S | 0,08 | 0,05 | 0,1 | 0,07 |
| A | 20 | 30 | 25 | 12 |
| B | 4 | 5 | 4 | 3 |
Задание 14
Поток требований на получение книг в библиотеке - пуассоновский с интенсивностью n требований в час. Требования принимает один библиотекарь. Прием требований занимает интервал времени, распределенный по экспоненциальному закону со средним временем t1 минут. С вероятностью p1, приходят требования на научную литературу, с вероятностью р2 - на художественную литературу, с вероятностью р3 - на периодические издания. Соответственно типу запросы направляются в отделы научной, художественной литературы и периодических изданий. В этих отделах работают, соответственно, k1, k2 и k3 человек. Время поиска книги составляет t2 ± t3, минут в научном и художественном отделах, а время поиска литературы в отделе периодических изданий – t4 ± t5 минут. Потом заказанная литература приходит в отдел выдачи литературы, где работает k4 библиотекарей. Заказы на периодические издания имеют больший приоритет, нежели на научную и художественную литературу, а заказы на художественную и научную одинаковый приоритет. Время выдачи литературы распределено равномерно в интервале t6 - t7 минут.