Статистический анализ сейсмической активности прибайкалья the statistical analysis of seismic activity of pribaikalye

Вид материала

Документы

Содержание Графическое представление и описание поведения временного ряда, фрактальный и мультифрактальный анализ. Совместный спектральный анализ. Фильтр Калмана. Фрактальный анализ. X(t)-наблюдения в момент времени t Список литературы

Подобный материал:

• Использование свободного программного обеспечения (спо) в образовательном и научно-исследовательском, 29.06kb.
• Arry out the activity in territory of Russia, the legislator at the same time has provided, 301.49kb.
• Бакалаврская программа № 521200 Кафедра: Социологии Направление : Социология Дисциплина, 188.47kb.
• Институт, 132.47kb.
• «Бухгалтерский учет, анализ и аудит», 1051.73kb.
• «Экономико – статистический анализ внешней торговли страны ( по выбору) за 2000 – 2007, 140.36kb.
• Разработка технологии многопараметрового мониторинга сейсмической активности азово-черноморского, 353.57kb.
• Экономико-статистический анализ динамики и прогнозирования урожайности сельскохозяйственных, 560.04kb.
• Анализ и интерпретация информации, 212.2kb.
• «Статистический анализ эффективности экономической конъюнктуры», 779.99kb.

СТАТИСТИЧЕСКИЙ АНАЛИЗ СЕЙСМИЧЕСКОЙ АКТИВНОСТИ ПРИБАЙКАЛЬЯ


THE STATISTICAL ANALYSIS OF SEISMIC ACTIVITY OF PRIBAIKALYE

Фасхутдинова В.А.


Введение. Прогнозирование землетрясений - одно из важнейших направлений геофизики. Существует множество методик и подходов для решения данной проблемы. Несколько лет назад российскими учеными во главе с академиком В. Бабешко была разработана концепция предсказания землетрясений, основанная на предположении, что литосферная плита - это механический объект, а поведение такого объекта в отличие от геологического можно рассчитать («метод активного вибросейсмического мониторинга»).

На аппаратуре, разработанной Геологической службой США, было выполнено уникальное моделирование очага подземного удара. Разработанные алгоритмы позволяют обнаружить периоды сейсмического затишья, активизации и кластеры на фоне разнообразных шумов. В этих случаях анализируются сигналы, поступающие от многочисленных слабых толчков.

Достаточно апробированная количественная методика долгосрочного прогноза предложена С. Нишенко. Опасность сильного землетрясения описывается в терминах условной вероятности возникновения землетрясения заданной магнитуды в определенный интервал времени. На основе многомерного анализа разработана вероятностная модель, позволяющая создавать приближенный сценарий сейсмической активности, что важно для развития теории и практики глобального мониторинга и долгосрочного прогнозирования геодинамической активности Земли.

В данном докладе для построения прецизионных комплексных моделей характеристик сейсмической активности Прибайкалья, представленных в виде временных рядов (ВР), используется метод динамического регрессионного моделирования (ДРМ-подход)[1], реализованный в виде программной автоматизированной системы АС ДРМ[2].

Динамическое регрессионное моделирование в приложении к обработке временных рядов сейсмической активности. При анализе временных рядов последовательно реализуются этапы [3,6]:

1.^ Графическое представление и описание поведения временного ряда, фрактальный и мультифрактальный анализ.

2.Проверка ряда на стационарность. При исследовании ряда на стационарность проверяется выполнение условий: постоянство среднего значения, определяемое непараметрическим критерием сдвига и критерием инверсий; постоянство дисперсии, определяемое критерием Коxрена и критерием рассеяния, и проверка на стационарность по критерию согласия Пирсона.

3.Выделение неслучайных составляющих временного ряда на основе подхода [1]:

3.1.Выделение трендов методом наименьших квадратов;

3.2.Идентификация и выделение значимых гармоник с помощью спектрального анализа, вейвлет-анализа, метода пошаговой регрессии или метода случайного поиска с адаптацией;

4. Моделирование стационарных случайных процессов

4.1.Модели авторегрессии и скользящего среднего. На практике для достижения большей гибкости в подгонке моделей к наблюдаемым временным рядам иногда бывает целесообразным объединить в одной модели авторегрессию и скользящее среднее. При этом модель должна состоять из наиболее «экономных» структур, дающих хорошую аппроксимацию с помощью небольшого числа параметров: параметры авторегрессии (p), порядок разности (d), параметры скользящего среднего (q).

4.2.Фильтр Калмана. Фильтр представляет собой рекуррентный алгоритм взвешенного сглаживания и прогнозирования временных рядов [7]. Для его применения модель записывается в виде уравнений процесса и наблюдения. Алгоритм позволяет по ряду данных наблюдений за различные моменты времени получить оптимальные оценки в смысле минимума среднеквадратической ошибки оценивания. Измерения обрабатываются последовательно с использованием ранее полученных данных; тем самым обеспечивается эффективная фильтрация данных от шума. Условиями применимости метода является наблюдаемость динамики ВР, некоррелированность сигнала и шумов, марковость.

4.3.Мартингальная аппроксимация.

Программное обеспечение динамического регрессионного моделирования. Программный комплекс имеет широкий набор процедур и функций, необходимых для детального анализа свойств временных рядов, моделирования, прогнозирования и диагностики нарушений условий применения метода наименьших квадратов и оценки качества моделей по различным критериям.

При воплощении алгоритмического кода использовались методы объектно-ориентированного программирования, что позволило упростить структуру пакета. Его модульная структура позволяет добавлять новые методы расчета без изменения основной части программного обеспечения. Дополнительно к базовому программному обеспечению [2] разработаны три новых модуля пакета, описываемые ниже.

^ Совместный спектральный анализ. Модуль «Совместный спектральный анализ» [4] осуществляет: - проведение спектрального анализа выбранных факторов; - отображение графиков зависимости кросс-спектральных характеристик (кросс-перидограммы, коспектра, квадратурного спектра, кросс-амплитуды, фазового сдвига, квадрата когерентности и значений усиления) от частоты и периода; - формирование данных по составляющим спектрального анализа от частоты и периода. Интерфейс модуля представлен на рис.1:



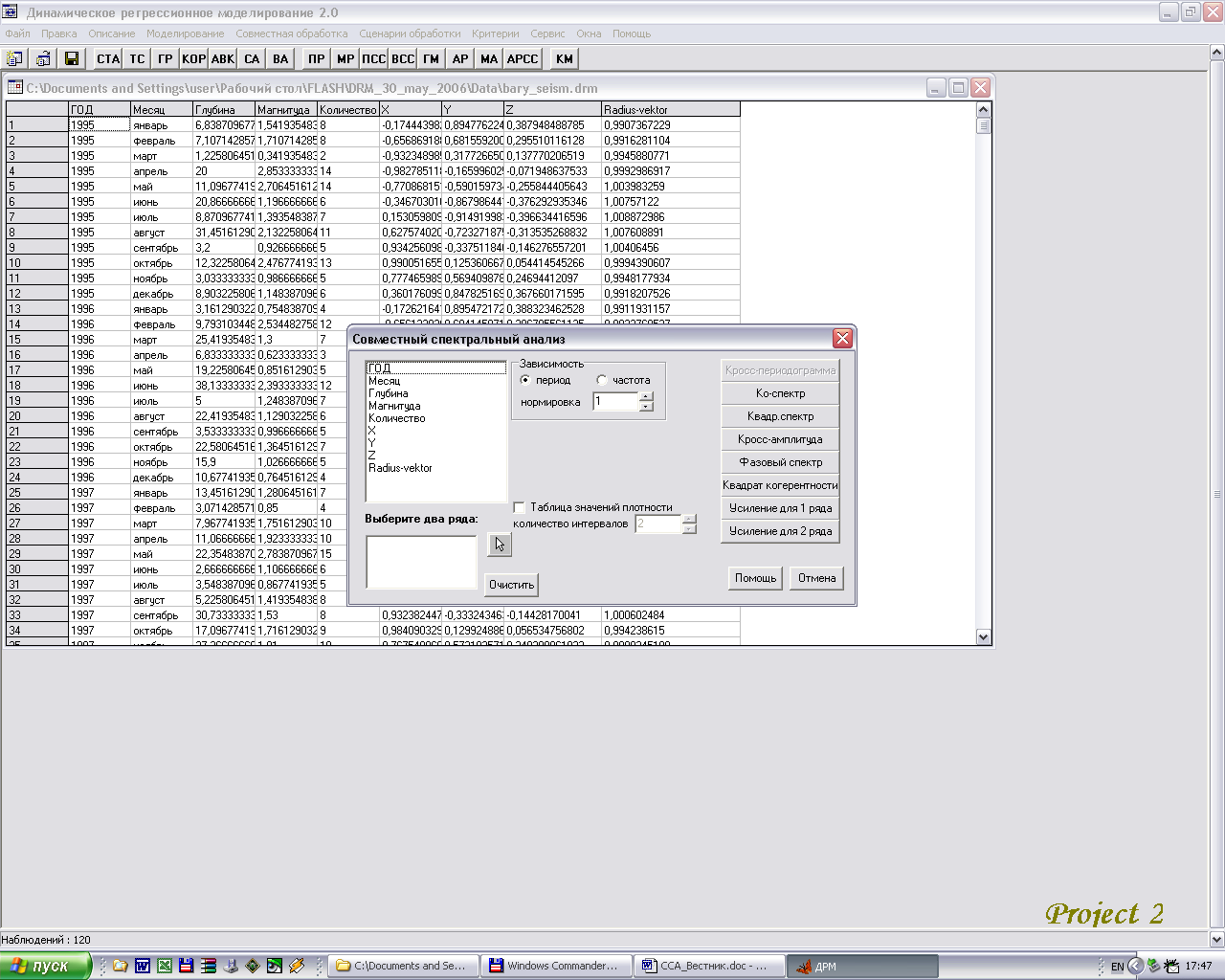
Рис.1. Интерфейс модуля «Совместный спектральный анализ»


^ Фильтр Калмана. Программная реализация алгоритма фильтрации осуществлена в виде отдельного модуля «Фильтр Калмана» (Рис.2) автоматизированной системы АС ДРМ. Модуль позволяет строить модели геосейсмической активности с высокой точностью предсказания.



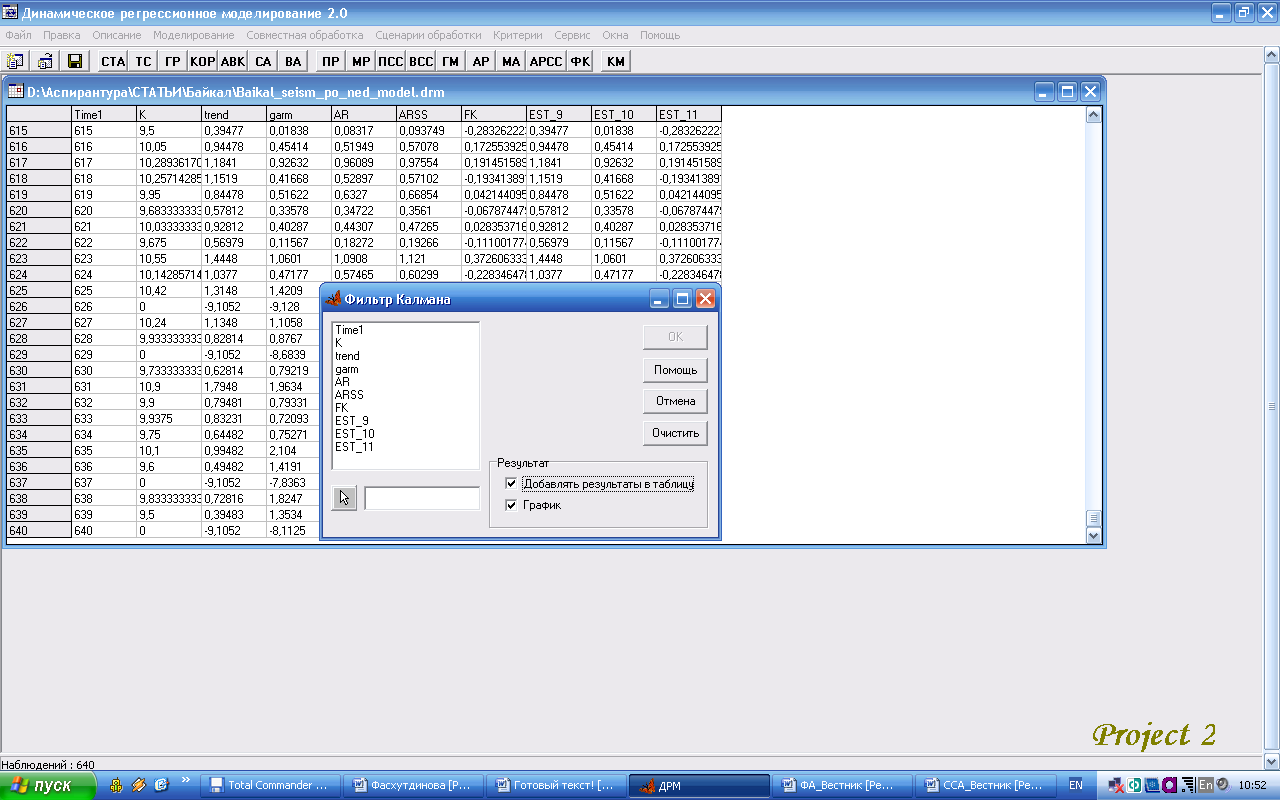
Рис.2. Интерфейс модуля «Фильтр Калмана»


^ Фрактальный анализ. Модуль фрактального анализа (Рис.3) выполняет следующие функции: - R/S анализ исходного ВР, с помощью которого можно классифицировать временные ряды (он позволяет отличить случайный ряд от неслучайного, даже если случайный ряд не гауссовский); - построение R\S и H траекторий, позволяющих определить наличие долговременной памяти ВР; - формирование нечетких множеств; - построение фазовой траектории для ВР, которая дает не только геометрическое изображение отдельных движений, состояний равновесия, периодических, хаотических движений, но и определяет «логику» поведения системы, его зависимость от параметров; - выполнение процедуры агрегирования.



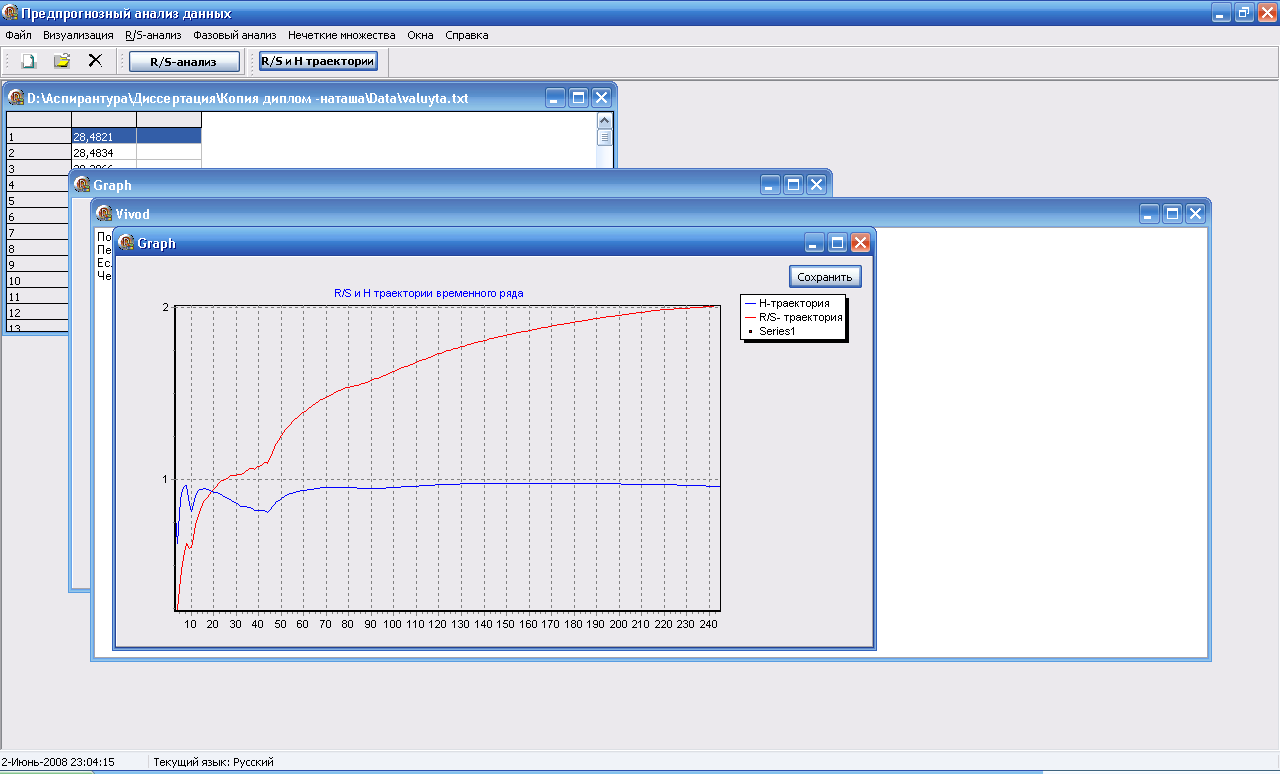
Рис.3. Интерфейс модуля «Фрактальный анализ»


Модели динамики сейсмической активности в Прибайкалье. В качестве исходных были взяты данные сейсмической активности Прибайкалья (ряд энергетического класса землетрясения (К)), зарегистрированные Байкальским Филиалом Геофизической Службы СО РАН за 1994-2007 годы (640 наблюдений) (ссылка скрыта?name =Data&da=1), усредненные по неделям.

Энергетический класс для землетрясений Прибайкалья определяется по методике Т.Г.Раутиан:

К=4+1,8М при К<= 14 и К=8,1+1,16M, если К>14, где M – магнитуда, измеряемая в баллах по шкале Рихтера.

На первом этапе анализа данных в рамках ДРМ-подхода проверяемая гипотеза о стационарности ряда была отвергнута с вероятностью 0,95. Построена модель тренда, являющаяся оптимальной из 17 построенных зависимостей по «внутреннему» среднему квадратичному отклонению (СКО)  = 1.749 и по «внешнему» СКО _Δ= 1,273 (Рис.4):



После диагностики остатков от тренда получены результаты: – предположение о равенстве нулю математического ожидания выполняется, – модель недоопределена, – остатки не распределены по нормальному закону, –авторегрессия отсутствует.



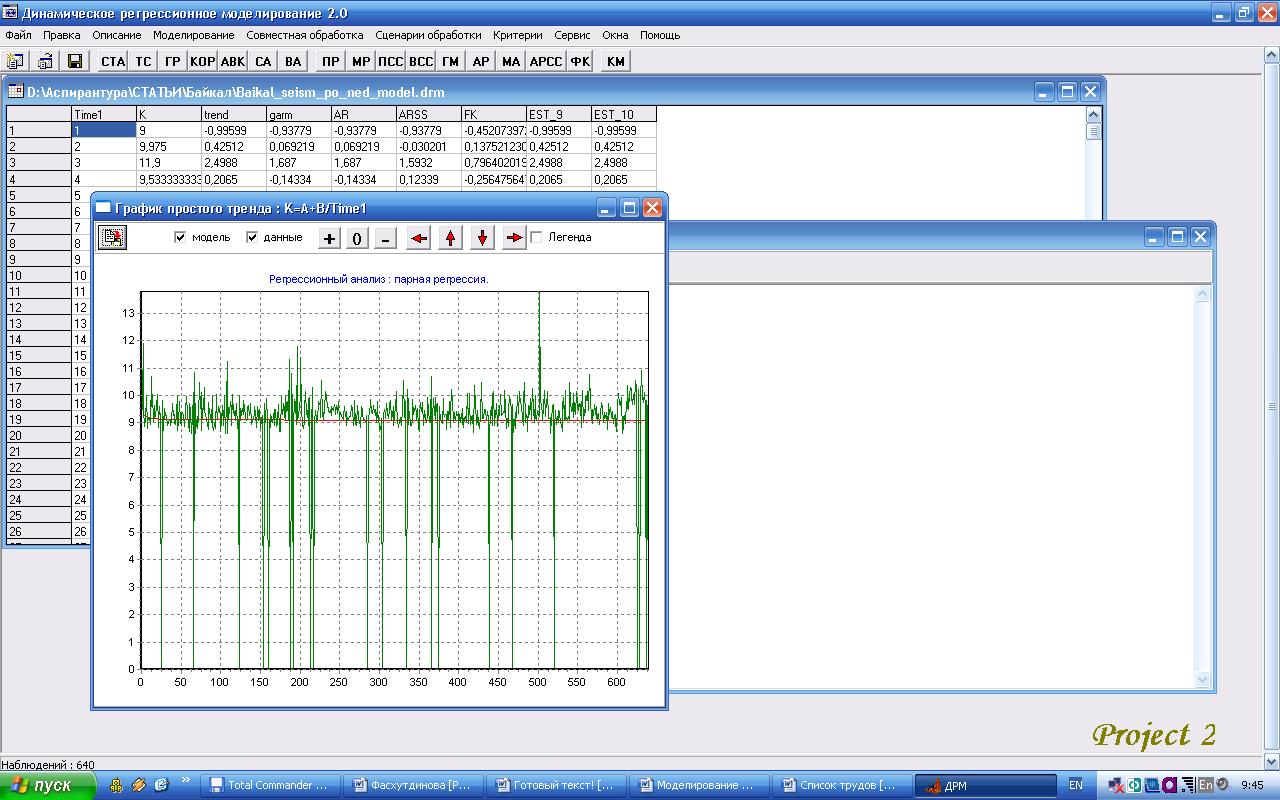
Рис. 4. График тренда ряда сейсмической активности Прибайкалья


Используемые для оценки точности прогноза среднеквадратические отклонения  и _Δ вычислялись по формулам:





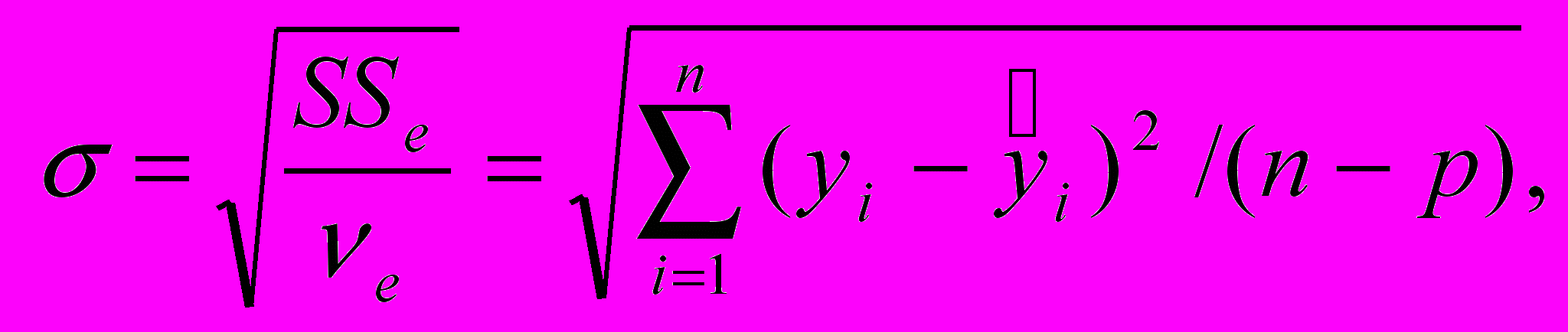
где n – количество наблюдений, k-объем контрольной выборки, p- число слагаемых в модели, 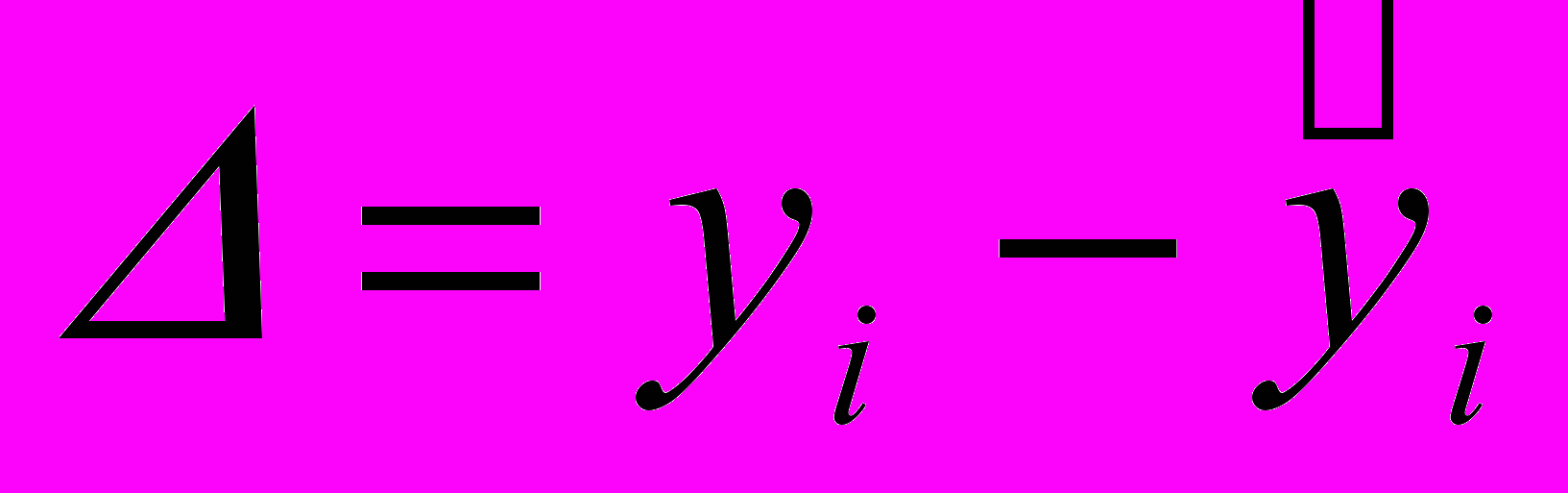; для 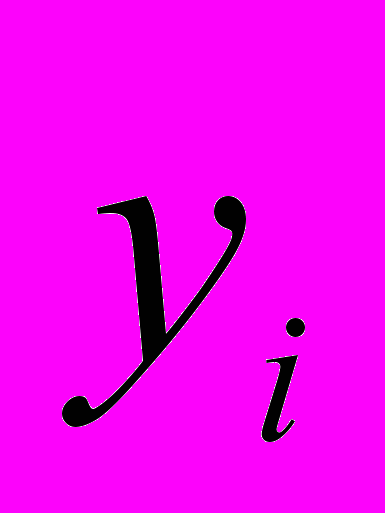 - наблюдения, 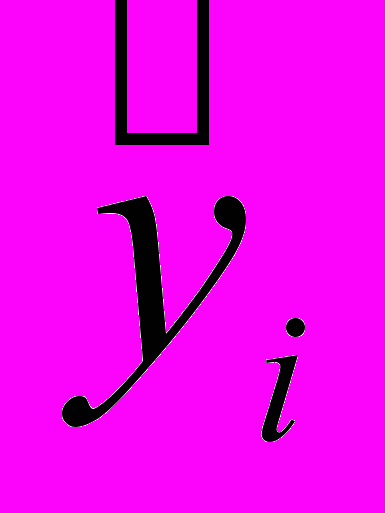- значения, вычисляемые после определения МНК-оценок; для _Δ 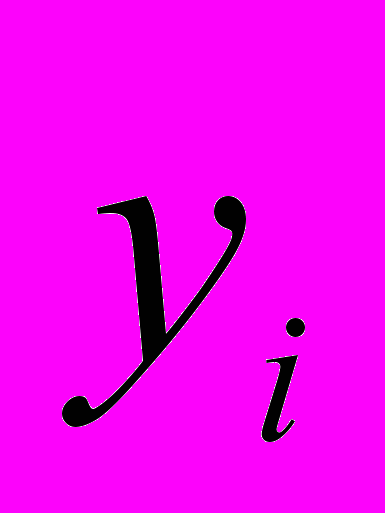- наблюдаемое значение отклика на исследуемом интервале (20% от исходного), 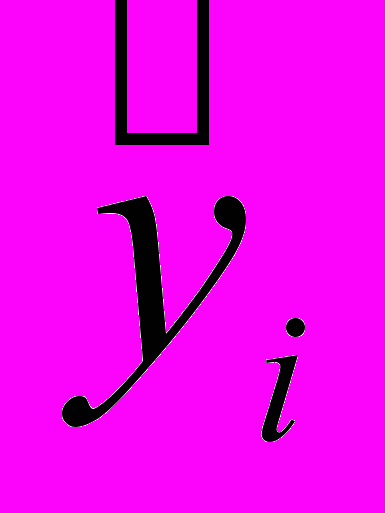- его прогноз – значения, вычисляемые по комплексной модели.

По результатам спектрального и вейвлет анализов (Рис.5,6) остатков выделены 14 гармоник. Полученная модель, график для которой представлен на рис.7, имеет вид:



СКО модели  равно 1,698; СКО по внешней точности _Δ=1,187.



Рис. 5. Спектральный анализ ряда сейсмической активности Прибайкалья



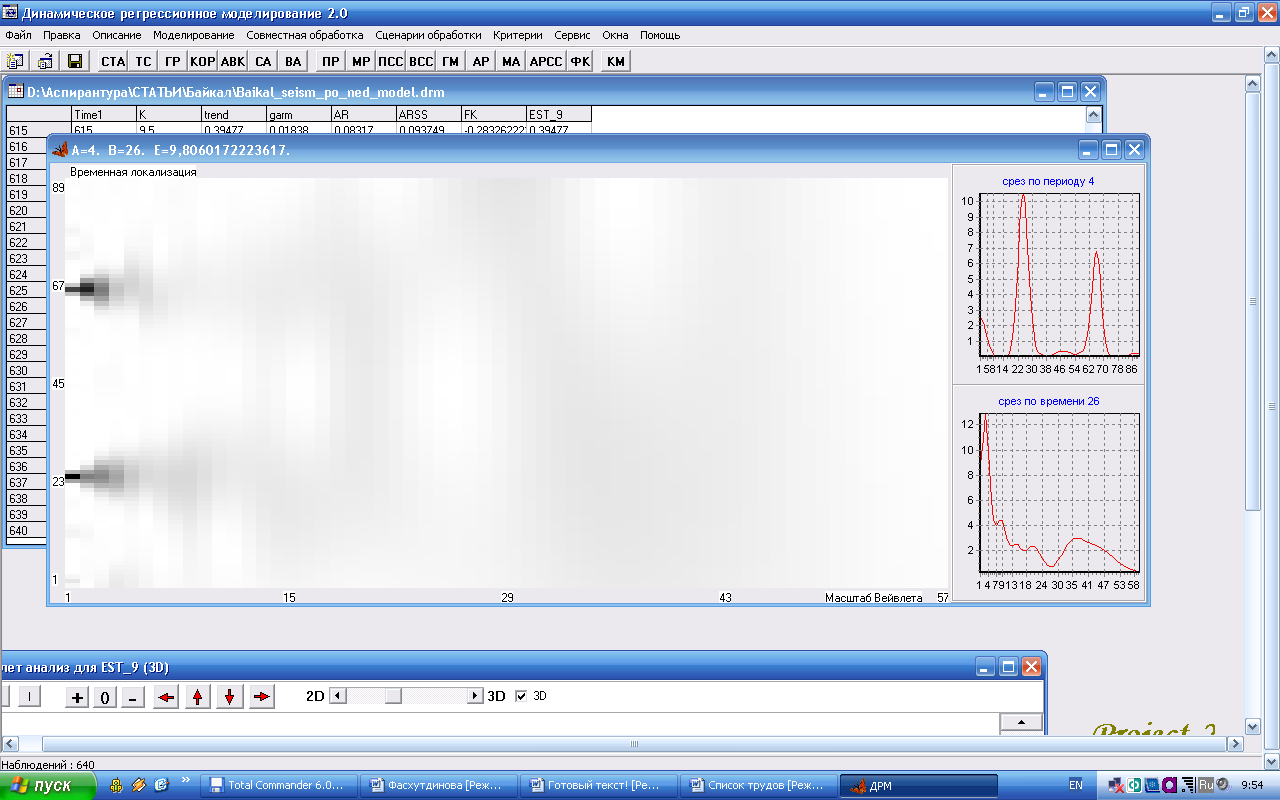
Рис. 6. Вейвлет анализ ряда сейсмической активности Прибайкалья



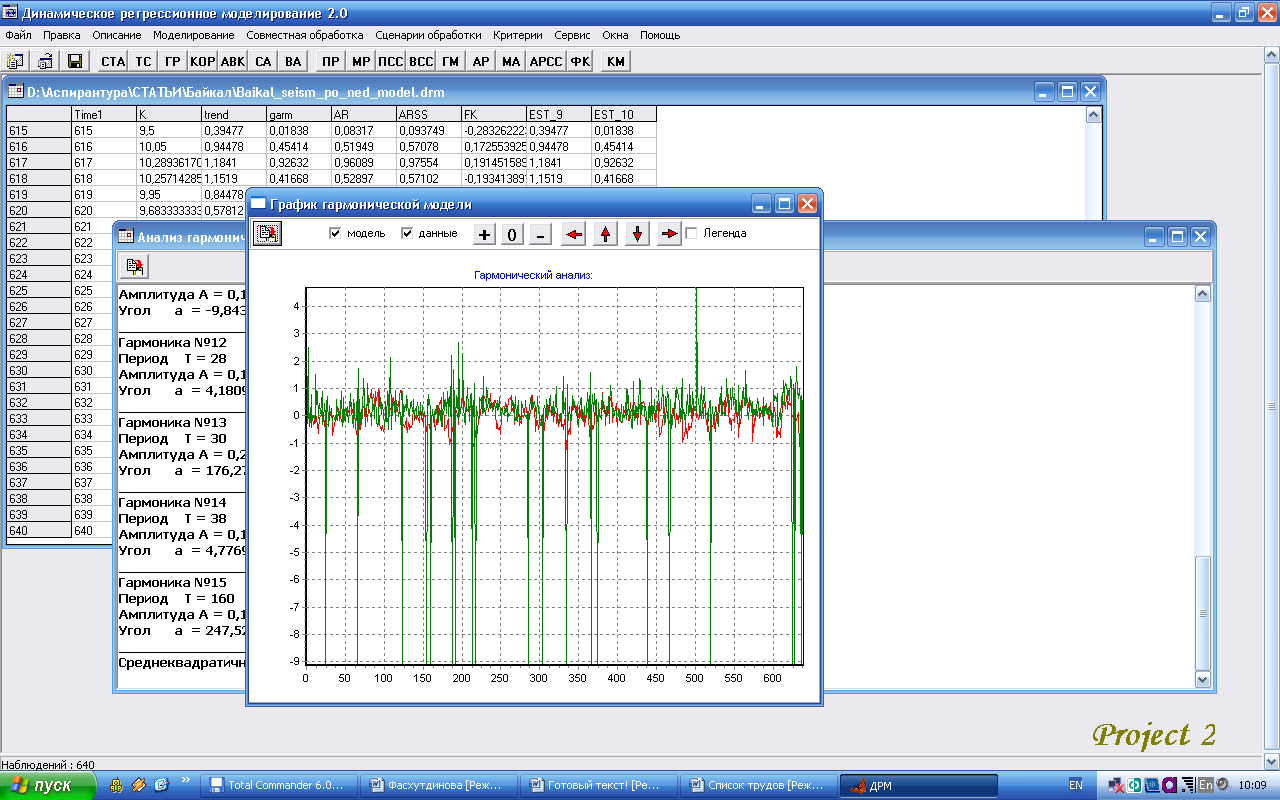
Рис. 7. График для полигармонической модели ряда сейсмической активности Прибайкалья


Результаты экспресс-диагностики остатков после полигармонической компоненты: – предположение о равенстве нулю математического ожидания выполняется, – модель недоопределена, – остатки распределены по нормальному закону.

При применении фильтра Калмана к остаткам после гармонического анализа выделена модель с параметром p = -0,404 при значении  = 0,985, _Δ=0,592. График для модели представлен на рис.8.



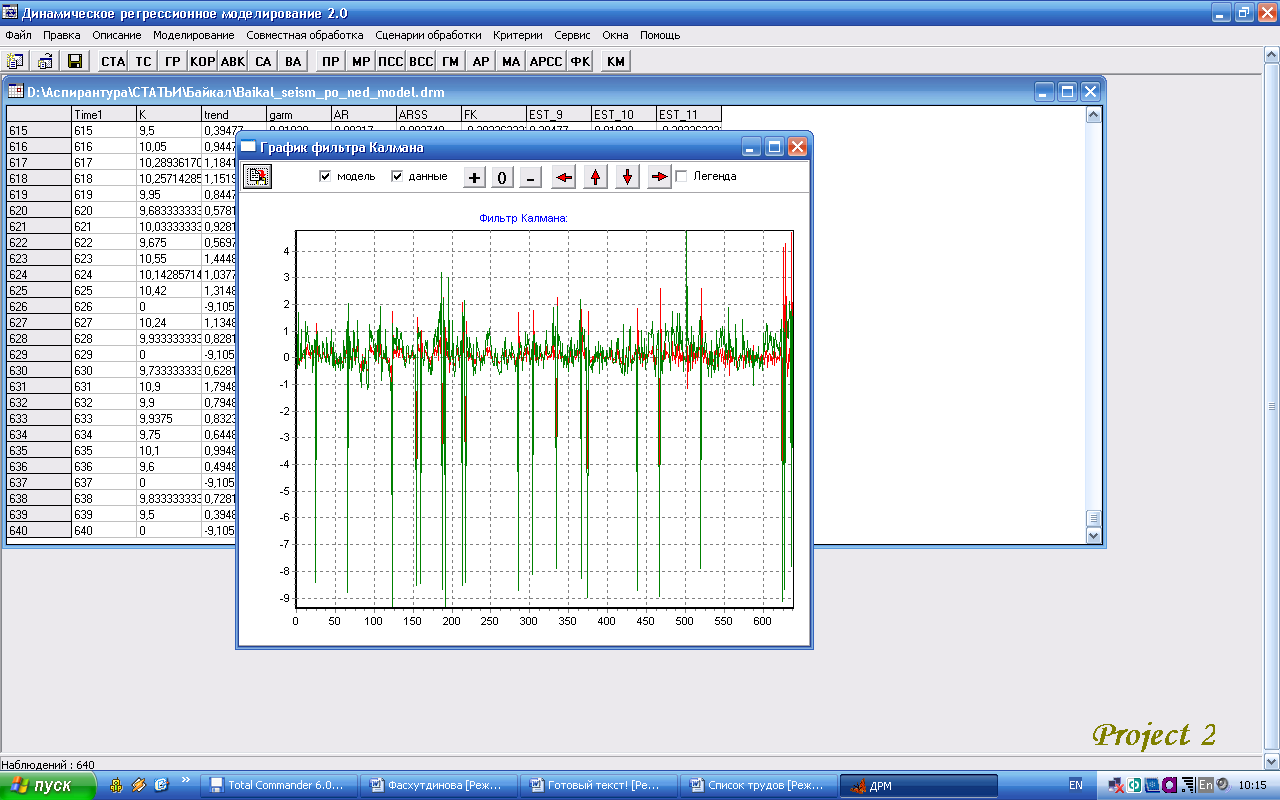
Рис. 8. График для комплексной модели ряда сейсмической активности Прибайкалья


Конечная модель для ряда представлена суммой квадратичного и периодического трендов и фильтра Калмана:



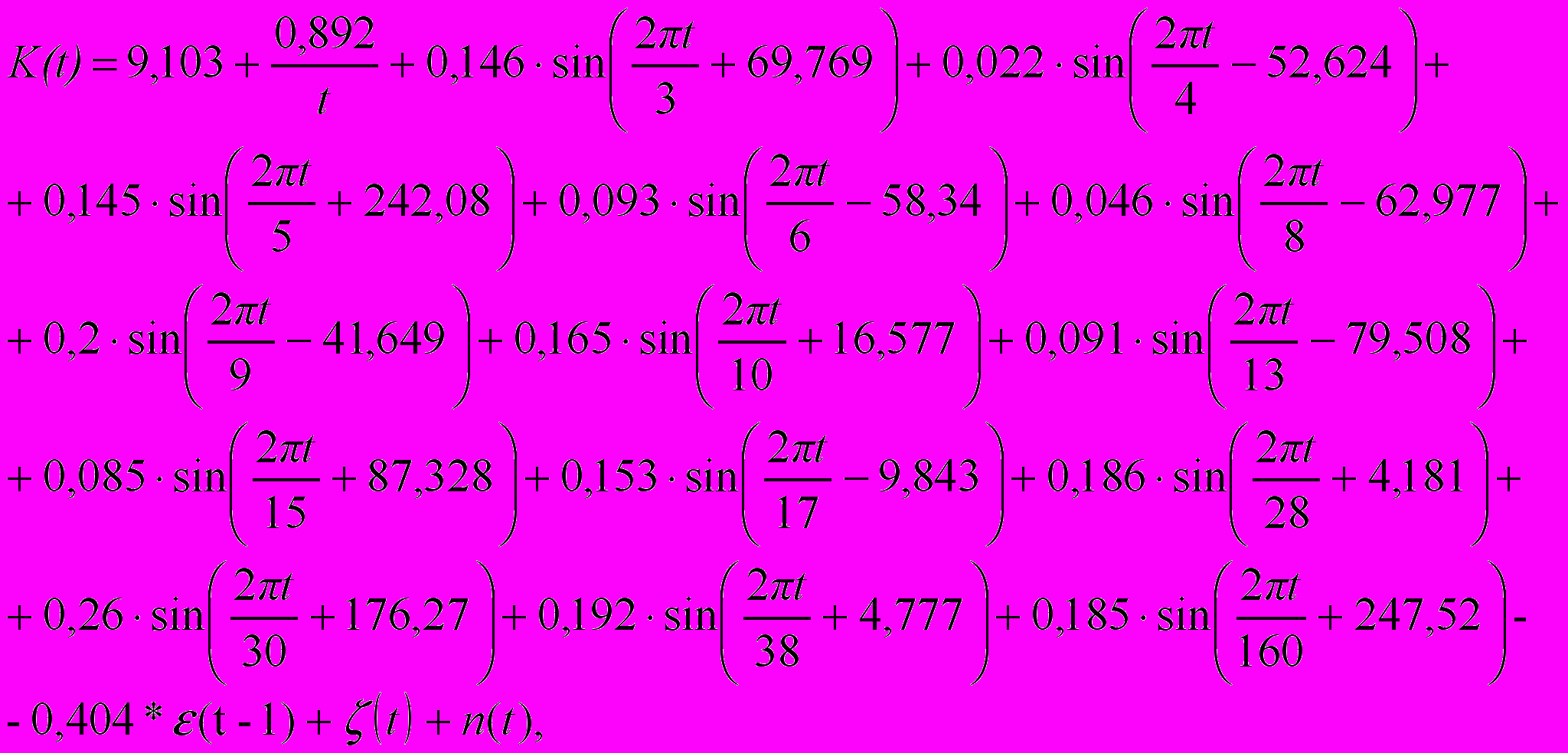
где ^ X(t)-наблюдения в момент времени t, 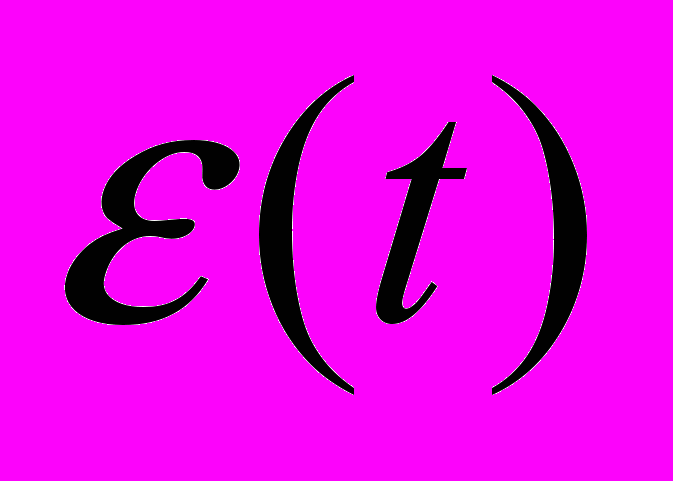- остаток, 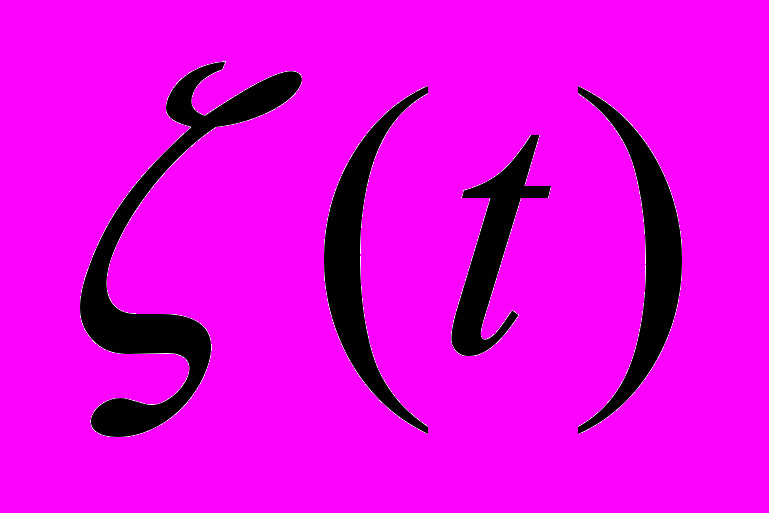- независимые случайные величины, 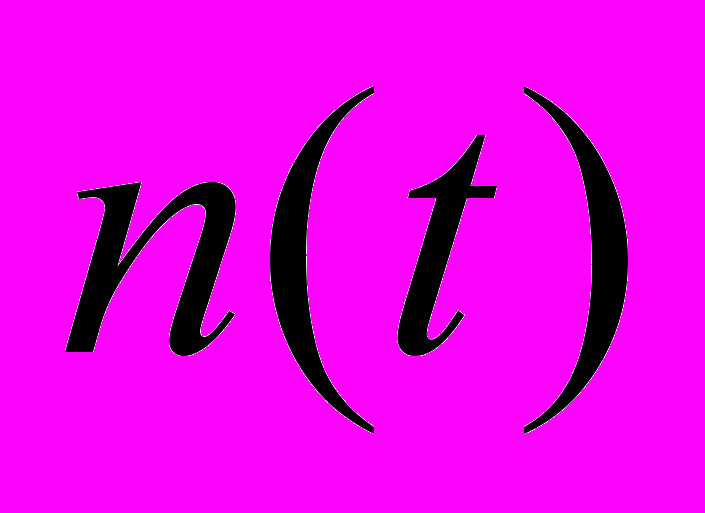- гауссовский белый шум;  = 0,985, _Δ = 0,592.

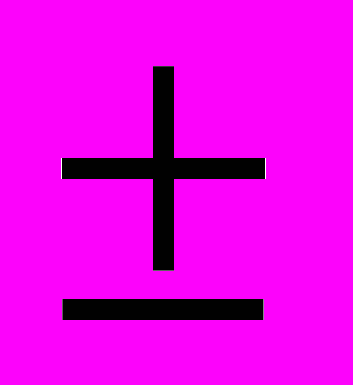При построении прогноза вычисляются значения энергетического класса на выбранные недели. Можно утверждать, что на каждой из этих недель прогнозируемые землетрясения имеют либо точечные оценки значений ряда, либо интервальные оценки при _Δ=0,592 в интервале 0,974, в который истинные значения попадают с доверительной вероятностью 0,95.

Заключение. В результате обработки ряда получена оптимальная по критерию минимума _Δ модель, описывающая динамику сейсмической активности Прибайкалья и позволяющая получать точечные и интервальные оценки прогноза К в среднем на неделю. Анализируются результаты и точность прогнозирования на октябрь 2008 года; рассматривается возможность моделирования ВР по суточным регистрациям, в том числе и по неравномерным ВР.

Программное обеспечение автоматизированной системы с интегрированными модулями может быть использовано для обработки достаточно широкого круга временных рядов в гео- и гелиофизике, астрометрии, планетодезии и др., обеспечивая заметное повышение точности по сравнению со стандартными пакетами.

Автор выражает признательность проф. С.Г. Валееву за консультации и помощь в работе.


^ СПИСОК ЛИТЕРАТУРЫ:

1. 
   Валеев С.Г. Регрессионное моделирование при обработке наблюдений. – М.: Наука, 1991. 272 с. (второе издание, дополненное и переработанное: Валеев С.Г. Регрессионное моделирование при обработке данных. Казань: ФЭН, 2001. 296 с.)
   
2. Валеев С.Г., Куркина С.В. Программная реализация ДРМ-подхода для обработки и анализа временных рядов // Изв. вузов. Геодезия и аэрофотосъемка, 2006. № 5. С. 10-21.
   
3. Валеев С.Г., Куркина С.В., Фасхутдинова В.А., Замалтдинова Р.Э. Моделирование временных рядов сейсмической активности с использованием фильтра Калмана// Труды международной «Конференции по логике, информатике, науковедению»: Математические методы и модели в науке, технике, естествознании и экономике. Ульяновск: изд. УлГТУ, 2007. С. 55-57.
   
4. Валеев С.Г., Фасхутдинова В.А. Кросс-спектральный анализ временных рядов// Вестник. – Ульяновск: изд. УлГТУ, 2006. №4. С. 30-32.
   
5. Валеев С.Г., Фасхутдинова В.А. Модификация программного комплекса АС ДРМ применительно к обработке гео- и гелиофизических данных//Вопросы современной науки и практики. Университет им. В.И. Вернадского. 2008. №2(12). С.64-68.
   
6. Валеев С.Г., Фасхутдинова В.А. Статистические модели динамики сейсмической активности// Сб. докладов IV междун. конф. «Солнечно-земные связи и предвестники землетрясений». Петропавловск-Камчатский: изд. ИКИР ДВО РАН, 2007. С. 269-274.
   
7. Сейдж Э.П., Мелс Дж. Теория оценивания и ее применение в связи и управлении. / Пер. с англ.; Под ред. Б.Р. Левина. – М.: Связь, 1976. – 495с.