Лекция 4 модулированные сигналы

Вид материала

Лекция

Содержание 4.3. Модуляция на импульсном переносчике 4.4. Цифровые виды модуляции Импульсно-кодовой модуляцией 4.5. Модуляция на шумоподобном переносчике

Подобный материал:

• Тема 15. Модулированные сигналы мир создан ради богов и людей, 406.06kb.
• Программа экзамена по курсу «Радиотехнические цепи и сигналы,, 67.29kb.
• Сигналы личности, 2891.95kb.
• Сигналы личности, 2905.23kb.
• Урок лекция, урок-практикум, опорные сигналы, семинар, игровая форма, 11.4kb.
• 1 Электрические сигналы, их классификация и параметры, 101.06kb.
• 1 Аналого-цифровое и цифро-аналоговое преобразование. Параметры типичных ацп и цап, 512.11kb.
• Конспект лекций по курсу «психология» Челябинск 2011, 2151.7kb.
• Курс лекций «Основы радиоэлектроники» Часть Сигнал и его свойства. Линии передачи, 33.21kb.
• Метод шичко геннадия Андреевича, 196.91kb.

ЛЕКЦИЯ 4

МОДУЛИРОВАННЫЕ СИГНАЛЫ


4.1. Модуляция

Передаваемая информация обычно имеет вид первичного электрического низкочастотного сигнала. Это может быть телефонный сигнал в полосе частот 0,3÷3,4 кГц, сигнал видеоизображения в полосе
50 Гц – 6 МГц, дискретный (цифровой) сигнал в форме видеоимпульсов в полосе от 0 до F_в и т.д. Все первичные сигналы имеют одну общую особенность – они низкочастотны, т.е. их спектральный состав начинается от частот, близких к постоянному току. Линии связи, как уже отмечалось в первой лекции, определяются физической средой передачи. Главные задачи системы передачи информации – передать информацию без потерь и искажений по выбранной линии связи. И в организации такой системы основная проблема – согласование линии связи с первичным электрическим сигналом. Для этого согласования используется канал, как комплекс аппаратных средств, преобразующих сигнал к виду, возможному для передачи по физической линии связи. Низкочастотные проводные (кабельные, воздушные), рельсовые и др. линии связи требуют для согласования сигнала с линией усиления, обеспечения необходимой полосы пропускания, предотвращения искажений, согласование сопротивлений и т.д. без коренного изменения формы сигнала (например, телефонные сети, громкоговорящая связь). При использовании широкополосных линий связи (например, при частотном или временном уплотнении линии радиосвязи) исходные первичные сигналы нуждаются в преобразовании к виду, удобному для передачи по реальной физической линии. Это может быть перенос спектра сигнала в другую область частот, применение дискретного представления сигналов и т.д. Очень часто эти преобразования (не изменяя передаваемую информацию) приводят к новому виду преобразованного первичного сигнала. Для реализации процесса преобразования первичного сигнала обычно привлекается дополнительный стационарный сигнал – переносчик (несущий сигнал) – как "работящая лошадка", на которую "насаживают" информационный сигнал, Этот процесс "посадки" сигнала на переносчик называют модуляцией, а процесс "ссаживания" информационного сигнала с несущего колебаний называют демодуляцией или детектированием. Вид переносчика (несущего колебания) определяется физической природой лини связи и выбранного метода передачи информации.

В качестве переносчика применяют гармонические колебания, различные виды импульсного представления сигнала, сложные многоуровневые сигналы или специальные функции. Рассмотрим некоторые наиболее часто применяемые методы модуляции.


Литература:

[1] стр. 61. [2] стр. 82. [3] стр. 16.


Контрольные вопросы:

1. Дайте определение термину "модуляция".
   
2. Дайте определение термину "демодуляция".
   
3. Какие сигналы могут быть переносчиками информационного сообщения?
   
4. Зачем нужна модуляция?
   

4.2. Модуляция на гармоническом переносчике

В качестве несущего колебания частот используют гармонические колебания вида:

u(t) = A(t) cos[ω(t)t + φ(t)]. (4.1)

В этом колебании переменной, как правило, может быть только одна величина – амплитуда A(t), частота ω(t) или фазы φ(t), две других величины (в простейших видах модуляции) должны оставаться неизменными. В зависимости от переменного параметра, выбранного для передачи информационного сигнала различают: амплитудную модуляцию (АМ) u(t) = A(t)cos(ω₀t + l₀), частотную (ЧМ) u(t) = A₀ cos[ω(t)t + φ₀] и фазовую (ФМ) u(t) = A₀ cos[ω₀t + φ(t)]. Следует отметить, что частотный и фазовый параметры гармонического колебания входят в состав более общего представления несущего колебания – u(t) = A₀ cos Ψ(t) – в состав углового параметра гармонического сигнала, что привело к принятию более общего термина для ЧМ и ФМ – угловая модуляция. Рассмотрим виды модуляции на гармоническом несущем колебании. АМ –амплитудная модуляция непрерывным (аналоговым) сигналом, представляющим передаваемую информацию (например, телефонный сигнал в полосе 0,3÷3,4 кГц).

S(t) = A(t) cos (ω₀t + φ₀)

примем φ₀ = 0,

S(t) = A₀ + ∆Ax(t) = A₀(1 + 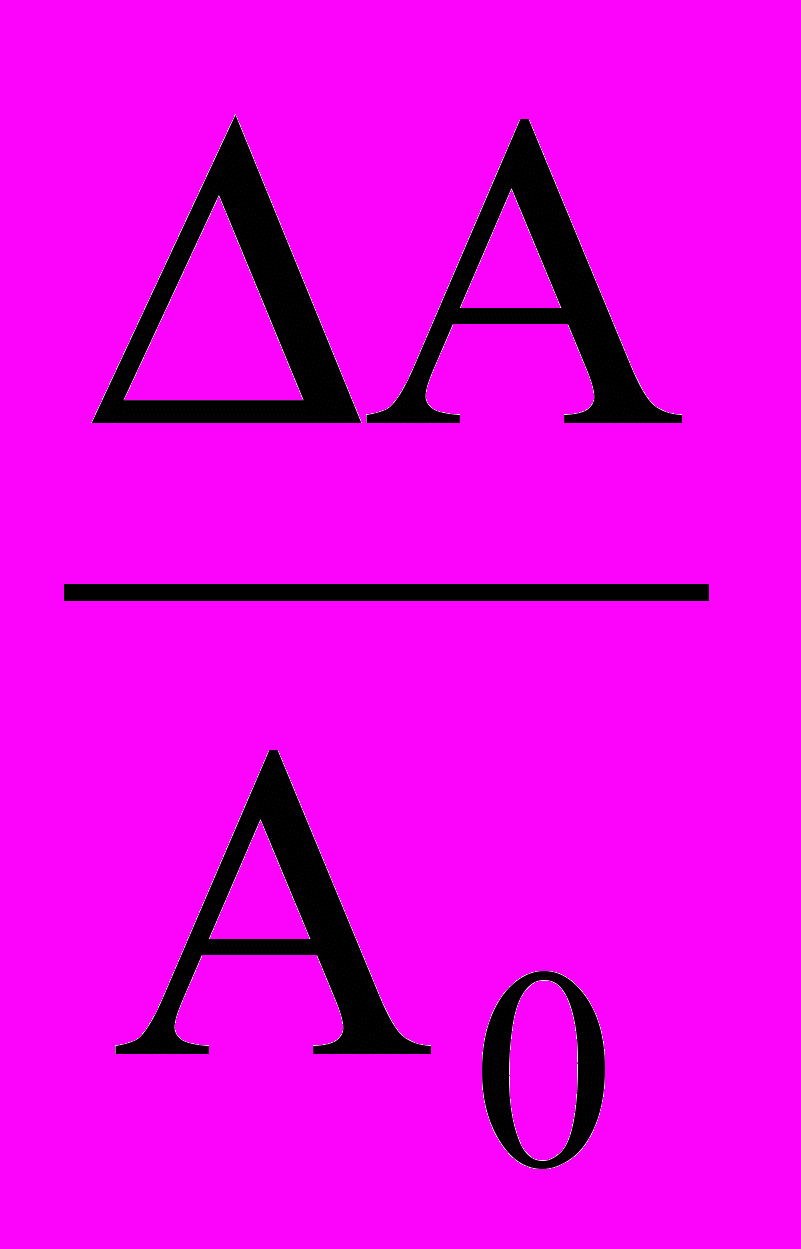x(t)),

где А₀ – начальное (среднее) значение амплитуды несущего колебания
cos ω₀t;

∆А – возможное отклонение амплитуды несущего колебания.

Величину ΔА/А₀ = m определим как параметр модуляции - глубина модуляции: 0 ≤ m ≤ 1. Обычно m измеряют в пределах 0% ≤ m ≤ 100%.

Модулированное по амплитуде колебание:

S(t) = A₀[1 + m x(t)]cos ω₀t. (4.2)

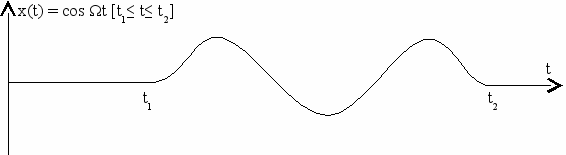
В качестве простейшего полезного информационного сигнала примем низкочастотный гармонический сигнал x(t) = cos Ω(t); Ω << ω₀.

Теперь амплитуда модулированного колебания будет изменяться по закону передаваемого информационного сигнала x(t). Временное изображение АМ сигнала представлено на рис. 4.1.

а)


б)


Рис. 4.1.


Глубину модуляции можно измерить по максимальному и минимальному отклонениям амплитуды: .

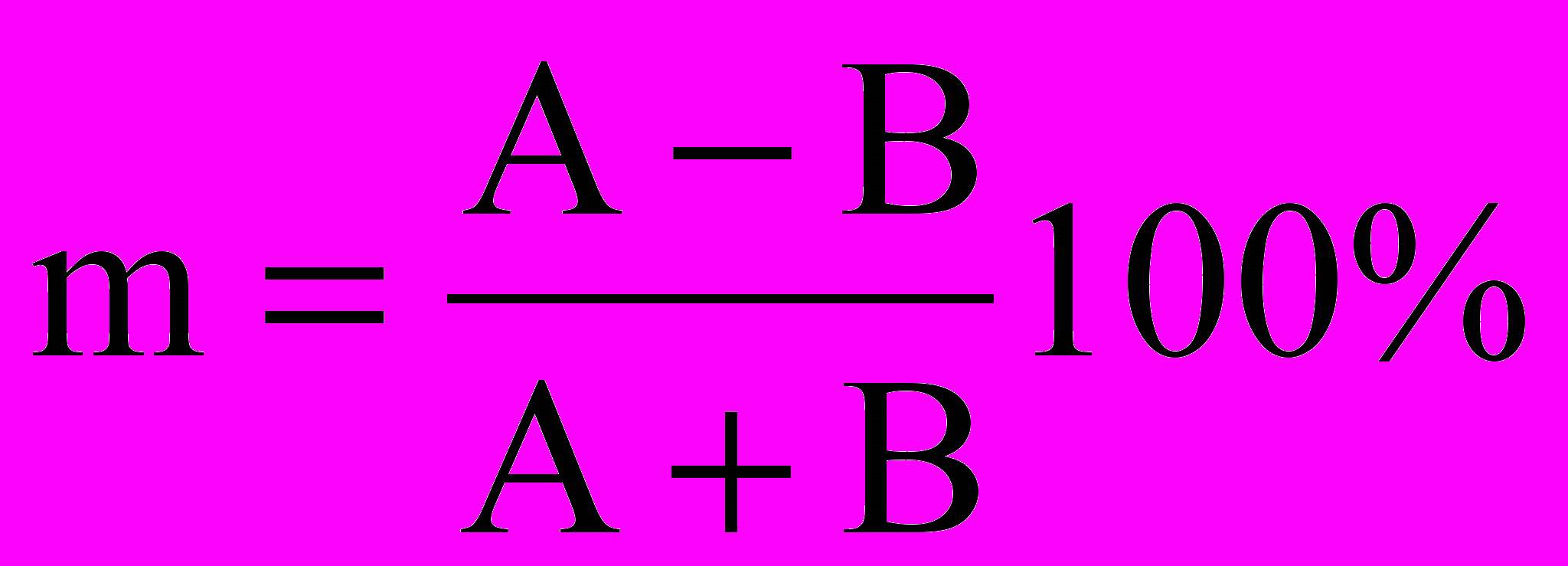Преобразуем выражение для s(t) (4.2), раскрыв скобки:

S(t) = A₀[1 + m cos Ωt]cos ω₀t = A₀ cos ω₀t + A₀ m cos Ωt cos ω₀t =

= A₀ cos ω₀t + A₀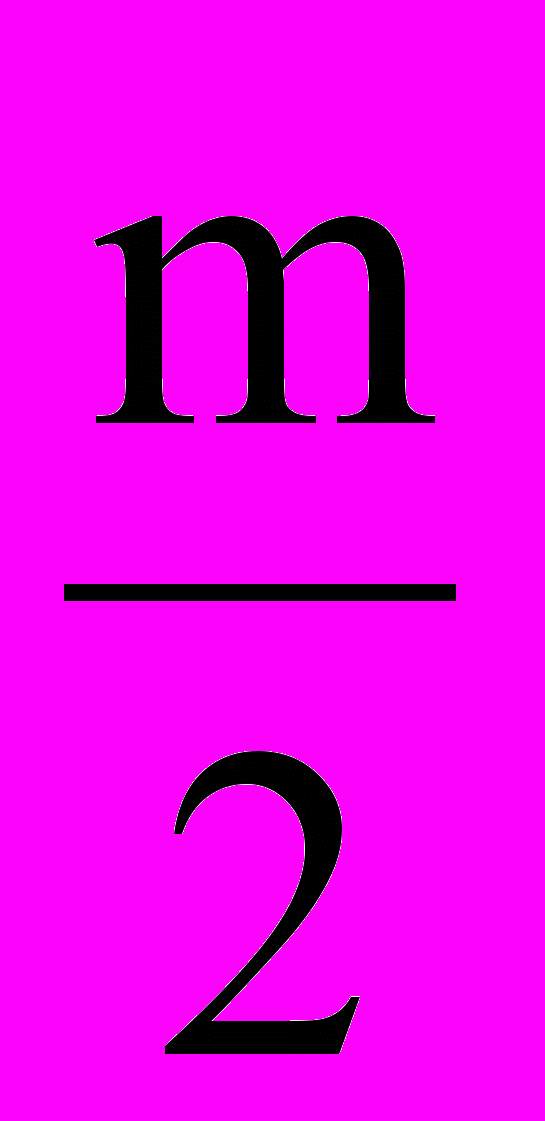[cos(ω₀ + Ω)t + cos (ω₀ - Ω)t] = (4.3)

= A₀ cos ω₀t + 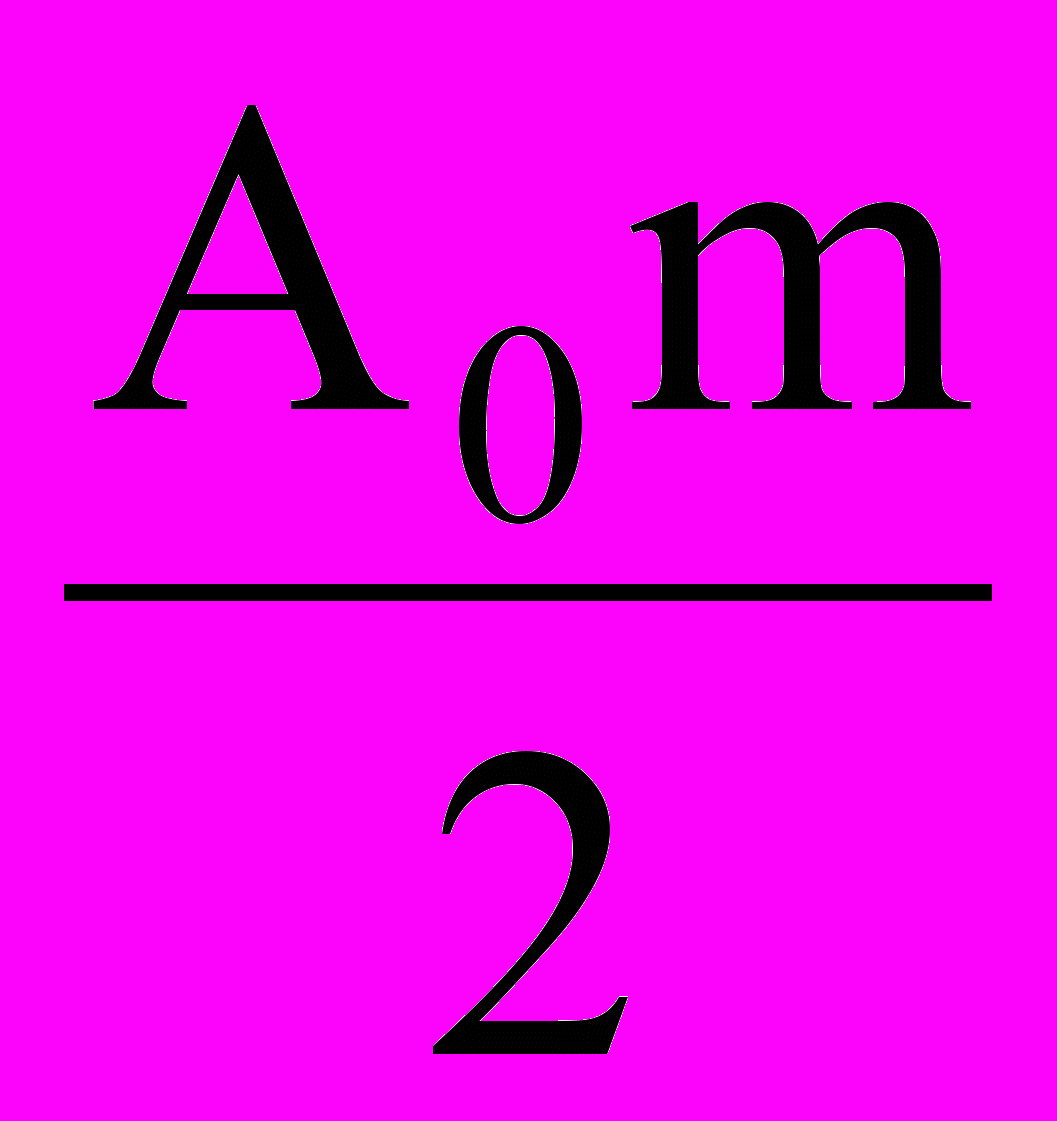cos(ω₀ + Ω)t + 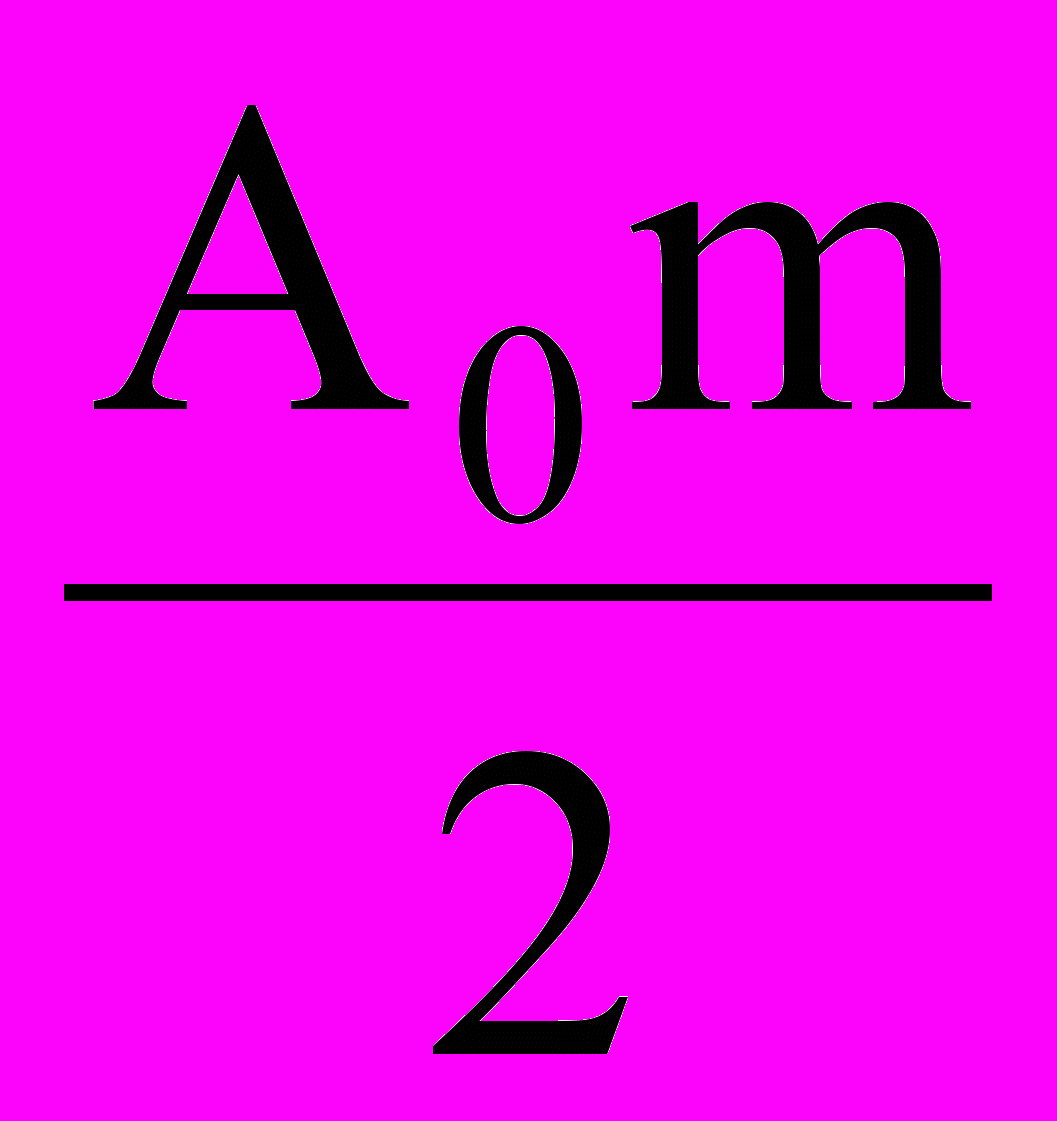cos (ω₀ - Ω)t.

Исследуя полученное выражение, замечаем, что оно состоит из трех гармонических составляющих и каждая на своей частоте ω₀, ω₀+Ω, ω₀-Ω. Построим графически полученное спектральное распределение составляющих (рис. 4.2).




Рис. 4.2.


В случае модуляции несущей не гармоническим (тональным) сигналом, а белее сложным сигналом x(t) в полосе частот (например, телефонный сигнал в полосе 0,3÷3,4 кГц) получается более сложный спектр, состоящий из несущей и двух боковых полос: НБП - нижней боковой полосы и ВБП - верхней боковой полосы (нанесены пунктиром на рис. 4.2). На рис. 4.3. приведены временные графики произвольного телефонного сигнала (рис. 4.3а) и его модулированный вид (рис. 4.3б).

Несущее колебание на частоте ω₀ имеет амплитуды А₀, боковые составляющие равны А₀m/2 и при m = 1 (100%), составляют А₀/2. Несущее колебание имеет максимальную амплитуду, однако, не несет никакой полезной информации, поэтому в некоторых системах связи (при априори точном известном положении по оси частот сигнала несущей, что позволяет ее всегда восстановить на приемном конце) для экономии излучаемой энергии несущую можно не передавать - это системы с балансной модуляцией - БМ (несущая необходима только при детектировании в качестве опорного колебания, относительно которого отсчитывают частоты боковых составляющих, поэтому в БМ несущую восстанавливают в приемнике по небольшому пилот-сигналу или известному кварцевому значению несущей). Обе боковые полосы несут информацию о модулирующем информационном сигнале x(t), располагаясь зеркально по частоте относительно несущего колебания. Для экономии энергии излучения и снижения занимаемой полосы частот можно передавать только одну боковую полосу - такая модуляция называется амплитудной модуляцией с одной боковой полосой АМ с ОБП.




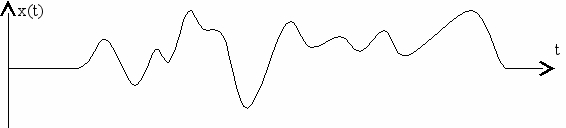
а)





б)


Рис. 4.3


Амплитудная модуляция осуществляется в пределах схемы с нелинейными элементами (диоды, транзисторы с рабочей точкой на нелинейном участке характеристики), так как только с помощью нелинейного преобразования можно получить сигналы новых частот (или осуществить функцию перемножения двух сигналов, в результате чего образуются сигналы новых частот). Демодуляция должна проводиться тоже только на нелинейном элементе для получения (выделения) низкочастотной (модулирующей) составляющей АМ сигнала. Фильтрация низкочастной части спектра демодулированного сигнала фильтром низкой частоты выделяет информационный сигнал от высокочастотных компонент АМ сигнала.

Пока мы рассмотрели амплитудную модуляцию при воздействии модулирующего сигнала x(t) - непрерывного (аналогового). Однако, подобные преобразования возможны и при импульсных последовательностях. Чаще всего встречается необходимость передачи бинарных сигналов, т.е. сигналов, имеющих два значения амплитуды
(0 и 1) (например, цифровые сигналы или сигналы в системе АЛС - автоматической локомотивной сигнализации). Модуляция несущего колебания бинарными информационными сигналами называется манипуляцией Мн или, иногда, применительно к амплитудной манипуляции - АТ - амплитудной телеграфией (АМн, АТ).

При воздействии на несущую информационным сигналом в виде последовательности прямоугольных импульсов (бинарных сигналов)
(рис. 4.4а) образуется промодулированная последовательность прямоугольных по огибающей радиоимпульсов, представленных на
рис. 4.4б.

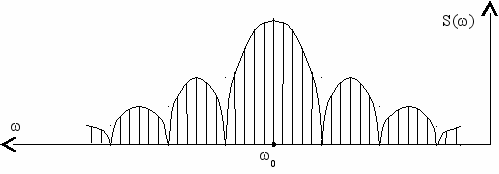
Спектральный состав одного радиоимпульса рассмотрен в первой лекции и представлен на рис. 1.20. Здесь уместно повторить его на
рис. 4.5а.





а)





б)


Рис. 4.4




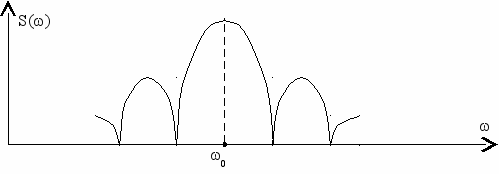
а)





б)


Рис. 4.5


Если последовательность радиоимпульсов регулярная, т.е. имеет постоянную скважность, то спектральный состав будет дискретным
(см. рис. 4.5б). При случайной последовательности ("телеграфный" сигнал) спектр последовательности будет содержать как сплошную, так и дискретную составляющие.

Понятие глубины модуляции при АМн отсутствует для бинарных символов, однако, его можно применить, если исходные импульсы имеют разную амплитуду.


Литература:

[1] стр. 61-73, 103-104. [2] стр. 88-96. [3] стр. 19-20.


Контрольные вопросы:

1. Какой параметр несущего колебания используется при АМ модуляции? Как ведут себя другие параметры несущего колебания при АМ?
   
2. Чем отличается манипуляция от модуляции?
   
3. Дайте определение видам модуляции БМ, ОБП.
   
4. Чем определяется ширина спектра АМ сигнала?
   
5. Что такое "глубина" модуляции АМ и как ее измерить?
   

Рассмотрим особенности угловой модуляции. Несущее колебание может передавать информационный сигнал изменением частоты или фазы несущего колебания:

S(t) = A₀ cos Ψ(t) = A₀ cos [ω(t)t + φ(t)]. (4.4)

Изменение фазы связано с изменением частоты через зависимость:

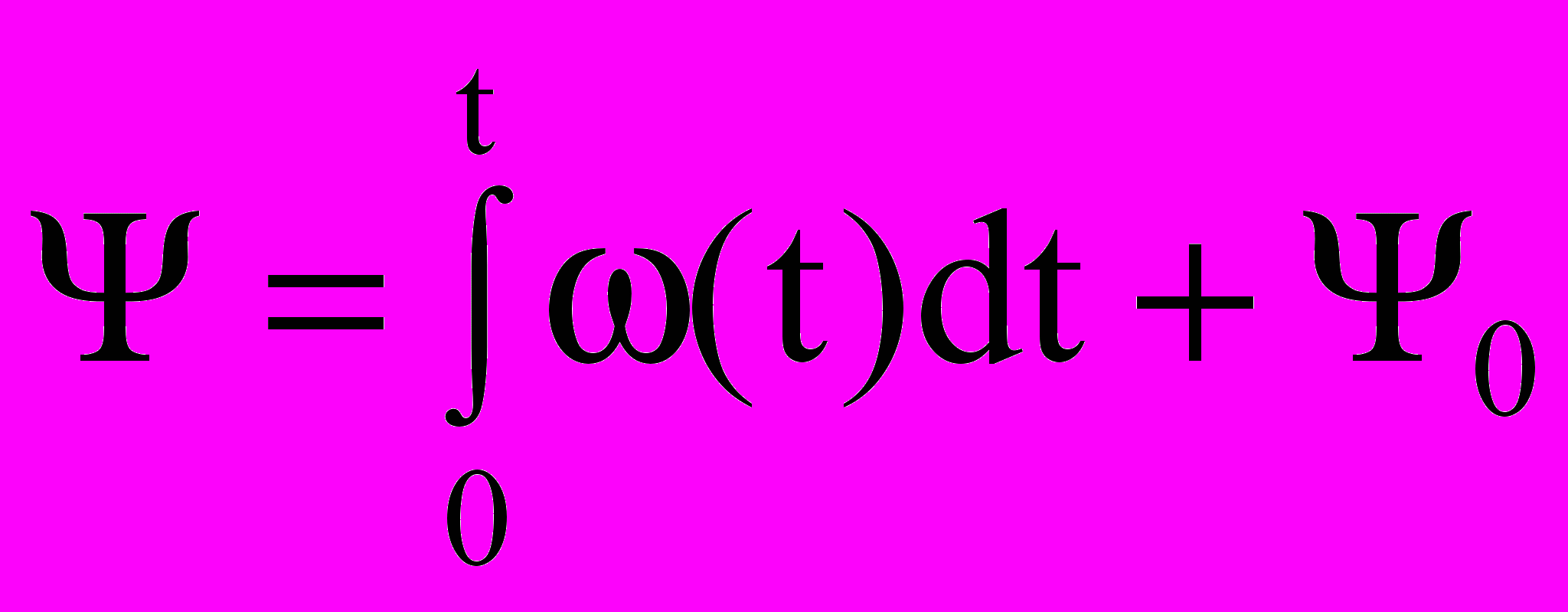(4.5)

и соответственно

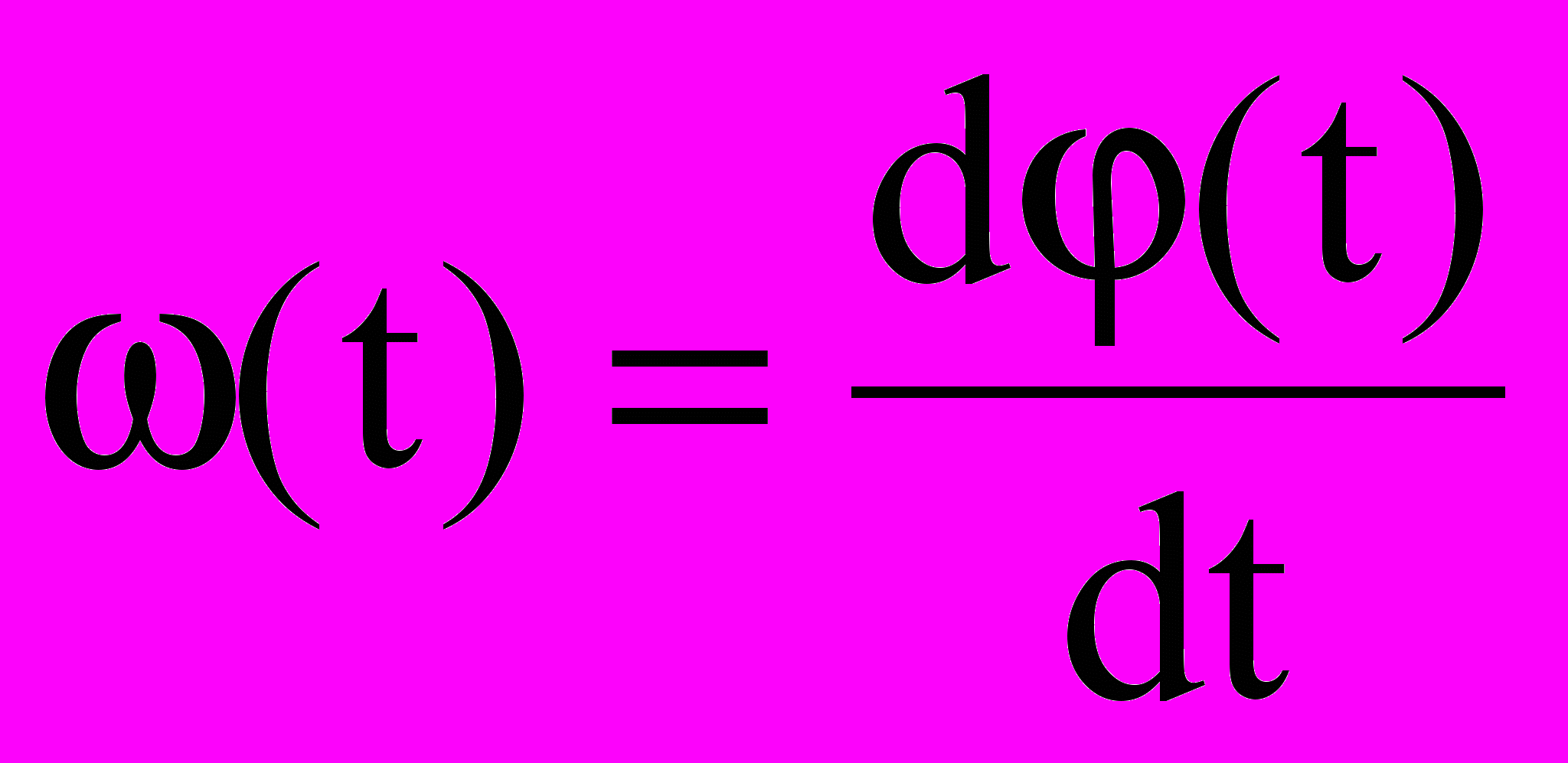. (4.6)

При исследовании частотной модуляции ω(t) для упрощения записи положи фазу φ(t) = 0. По аналогии с АМ изменение частоты:

ω(t) = ω₀[1 + m_ωx(t)], (4.7)

здесь ω₀ – основное (исходное значение частоты несущего колебания;

m_ω = ∆ω₀/ω₀;

∆ω – отклонение частоты (девиация частоты).

С учетом (4.5) и при Ψ₀ = 0, а также (4.7) выражение (4.4) приводится к виду:



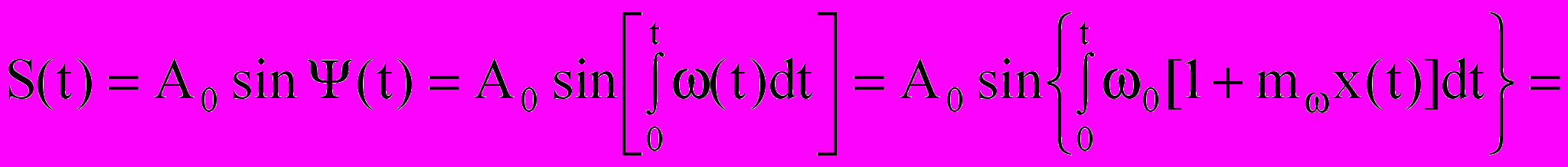
(4.8)

Как и ранее для АМ, в качестве простейшего сигнала, представляющего полезную информацию, примем низкочастотный гармонический (тональный) сигнал

x(t) = cos Ωt, Ω << ω₀

Тогда выражение для частотной модуляции



,

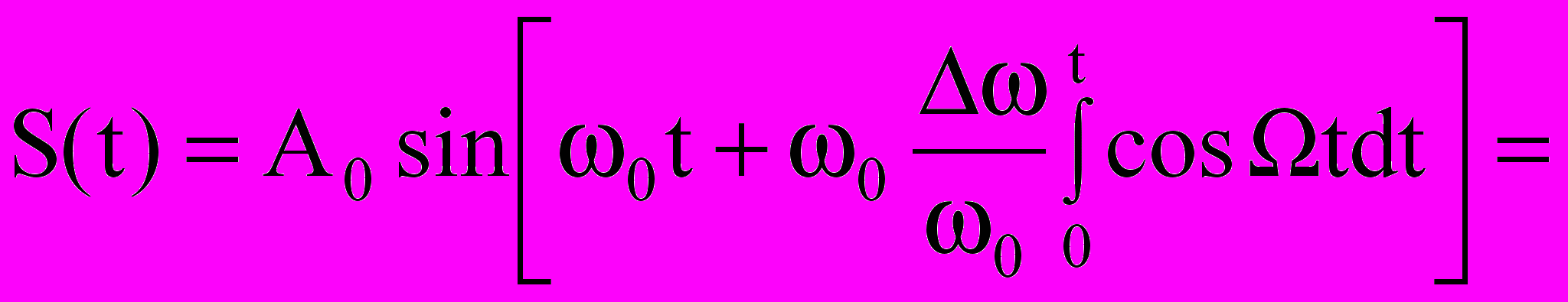
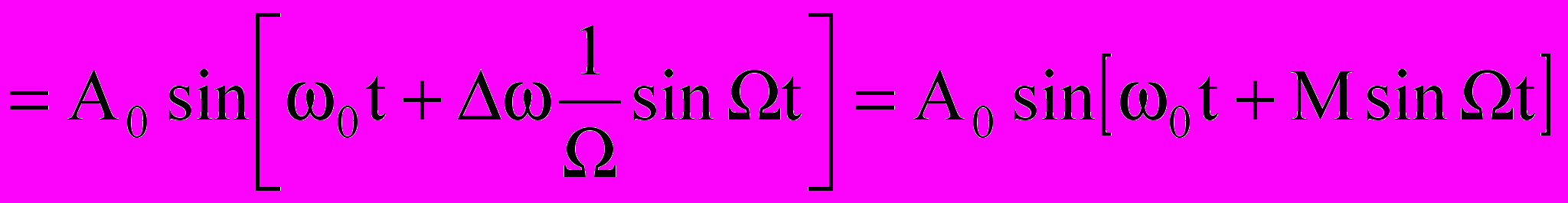здесь М = ∆ω/Ω – индекс модуляции, показывающий максимальное отклонение частоты (девиацию) несущего колебания при заданном (обычно 1000 Гц) значении частоты модулирующего колебания. Заметим, что индекс модуляции совершенно не зависит от средней (немодулированной) частоты ω₀, а определяется исключительно девиацией ∆ω и модулирующей частотой Ω.

Временные графики ЧМ при модуляции гармоническим сигналом (4.6а) представлены на рис. 4.6б.




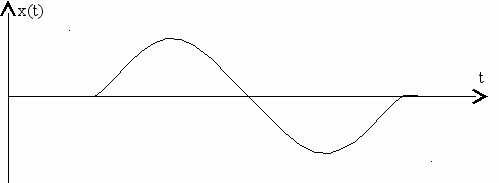
а)





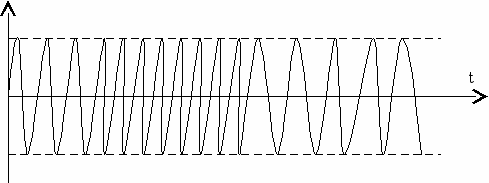
б)


Рис. 4.6


Преобразуем выражения для частотной модуляции (для синуса сумма двух углов):

S(t) = A₀ sin ω₀t  cos [M sin Ωt] + A₀ cos ω₀t  sin [M sin Ωt] (4.9)

В теореме Бесселевых функций известны соотношения:

sin(M sin Ωt) = 2I₁(M) sin 2Ωt + 2I₃(M) sin 3Ωt + ...

cos(M sin Ωt) = I₀(M) + 2I₂(M) cos 2Ωt + 2I₄(M) cos 4Ωt + ...

sin(M cos Ωt) = 2I₁(M) cos 2Ωt - 2I₃(M) cos 3Ωt + 2I₅(M) cos 5Ωt - ...

cos(M cos Ωt) = 2I₀(M) - 2I₂(M) cos 2Ωt + 2I4₅(M) cos 4Ωt - ...

I_k(M) – функция Бесселя k-го порядка от аргумента М. График нормированных (приведенных по I_0max = 1) приведен на рис. 4.7, а значения функций для разных М в табл. 4.1.


Таблица 4.1

M	I0	I1	I2	I3	I4
0,0	+1,00	0,00	0,00	0,00	0,00
0,5	+0,94	+0,24	+0,01	0,00	0,00
1,0	+0,76	+0,44	+0,11	+0,02	+0,002
2,0	+0,22	+0,58	+0,35	+0,13	+0,003
3,0	-0,26	+0,34	+0,48	+0,31	+0,13
4,0	-0,39	-0,06	+0,36	+0,43	+0,18
5,0	-0,18	-0,33	+0,04	+0,36	+0,39
10,0	-0,25	+0,04

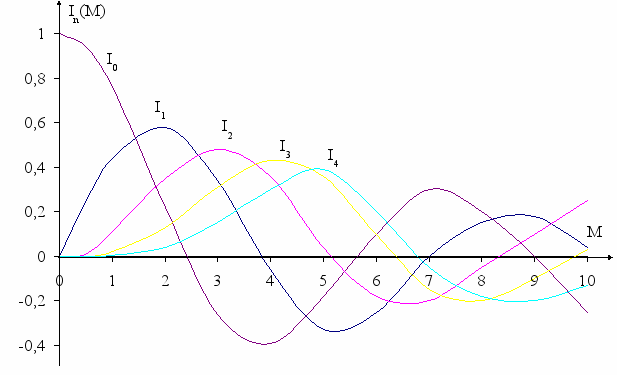
Рис. 4.7


Выберем из набора Бесселевых соотношений нужные для уравнения (4.9):

cos [M sin Ωt] = I₀(M) + 2 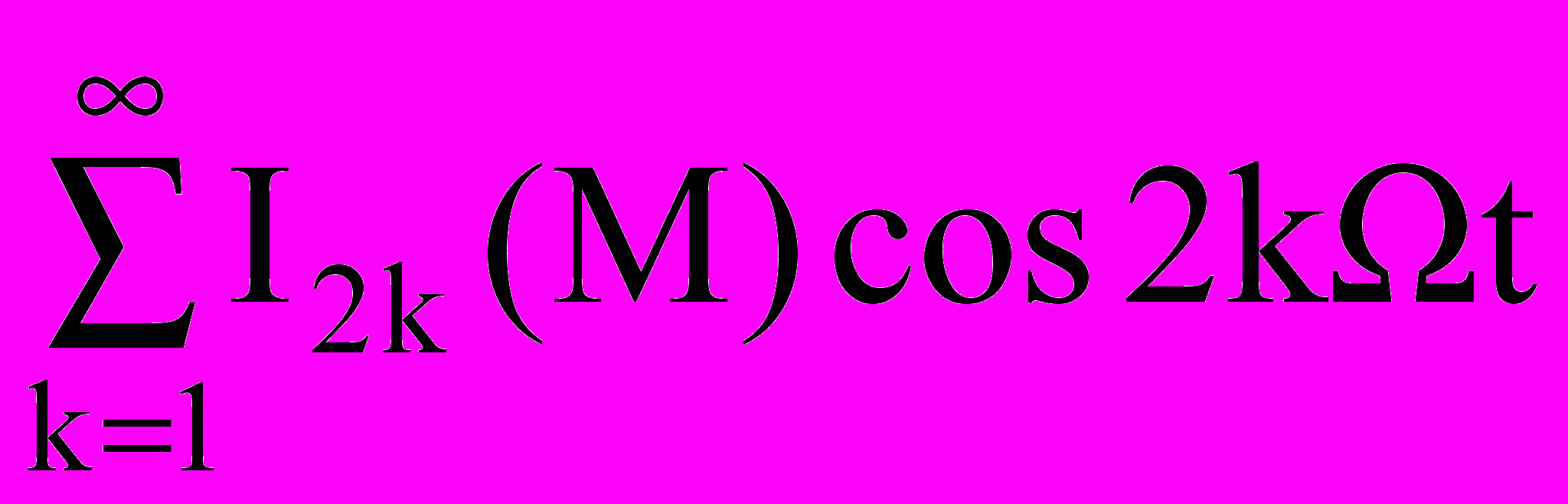(4.10)

sin[M sin Ωt] = 2 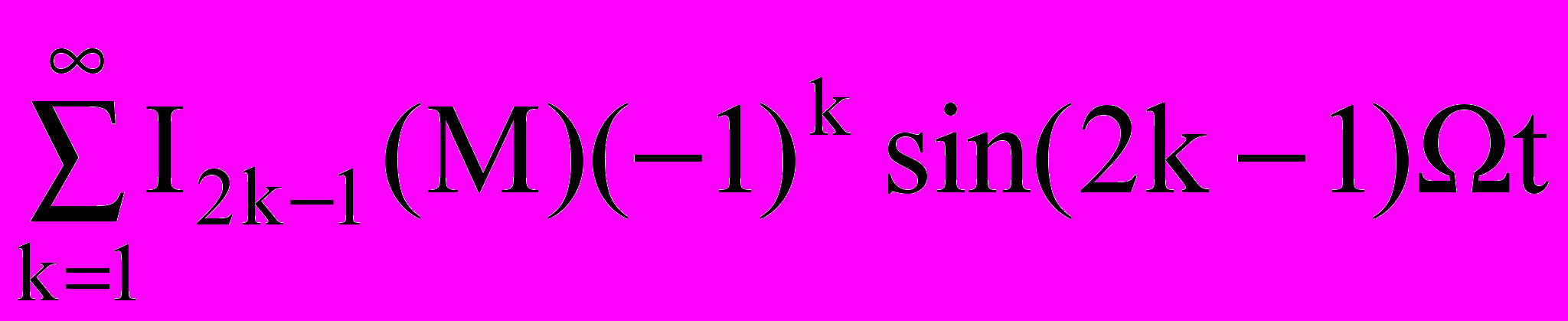(4.11)

Тогда сигнал частотной модуляции представляется рядом:

(4.12)

Спектральный состав ЧМ колебания оказывается достаточно сложным, состоящим из несущей и нескольких боковых составляющих выше и ниже по частоте относительно несущей и раздвинутых на Ω частоту модулирующего сигнала (см. рис. 4.8).




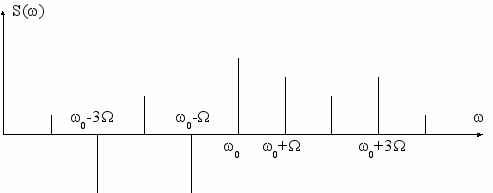
Рис. 4.8


Ширина спектра принципиально бесконечна, однако, если пренебречь составляющими с уравнением менее 1% от несущей, то ширина спектра сигнала определяется из выражения:

∆F = 2F_мод(1 + М +)

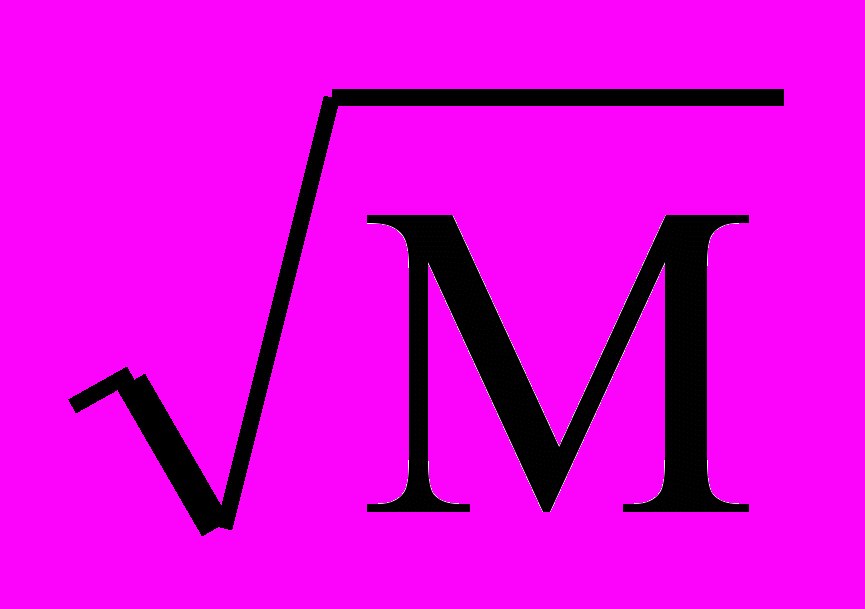при М >> 1 можно пренебречь составляющей 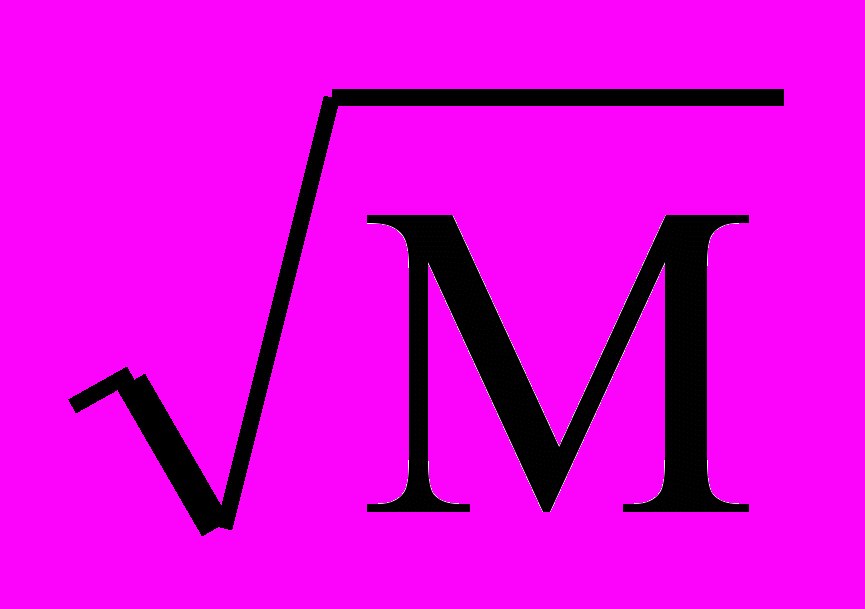, и тогда

∆F = 2F_мод(1 + М),

при M < 1 в спектре остается только несущая и две боковых составляющих (рис. 4.9а).

Фаза спектральных составляющих, расположенных в нижней боковой полосе имеет для нечетных составляющих отрицательный знак (сдвинута по фазе на 180°) вследствие (4.11).

Если оценить спектр только по модулю, то спектр (рис. 4.9б) полностью совпадает со спектром АМ колебания (см. рис. 4.2).




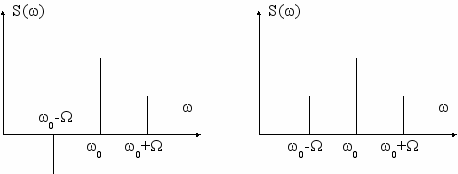
а) б)

Рис. 4.9


Литература:

[1] стр. 73-84. [2] стр. 96-102. [3] стр. 20.


Контрольные вопросы:

1. Дайте определение частотной модуляции.
   
2. Что такое "девиация"?
   
3. Что такое "индекс модуляции"? От чего он зависит и от чего не зависит?
   
4. Чем определяется ширина спектра ЧМ сигнала?
   
5. В чем отличие спектра ЧМ от АМ при малых (m < 1) индексах модуляции?
   

Фазомодулированный сигнал (ФМ)

S(t) = A₀ sin [ω₀t + φ(t)], (4.13)

у которого сдвиг фазы (по отношению с cos ω₀t) изменяется от начального значения φ₀ пропорционально модулирующему колебанию x(t):

φ(t) = φ₀ + ax(t).

Теперь модулированный ФМ сигнал:

S(t) = A₀ cos [ω₀t + φ₀ + ax(t)].

Так как мгновенное значение частоты является производной от фазы по времени (4.6), то при фазовой модуляции частота может быть определена в виде:

ω(t) = 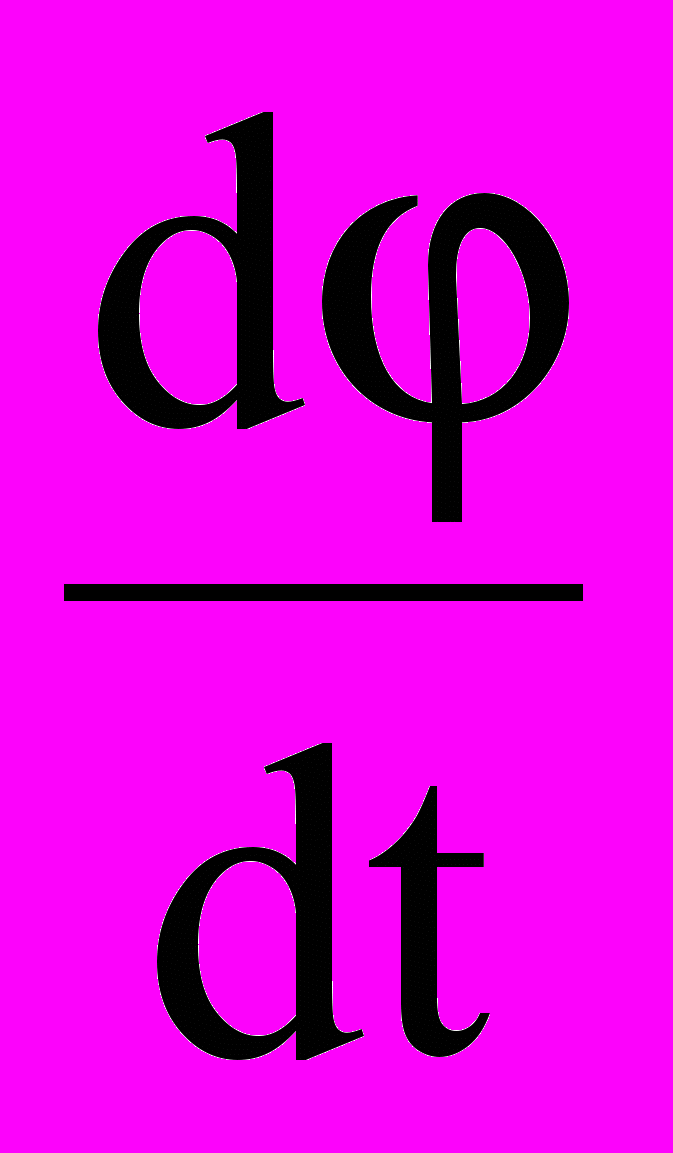= ω₀ + φ₀ + a,

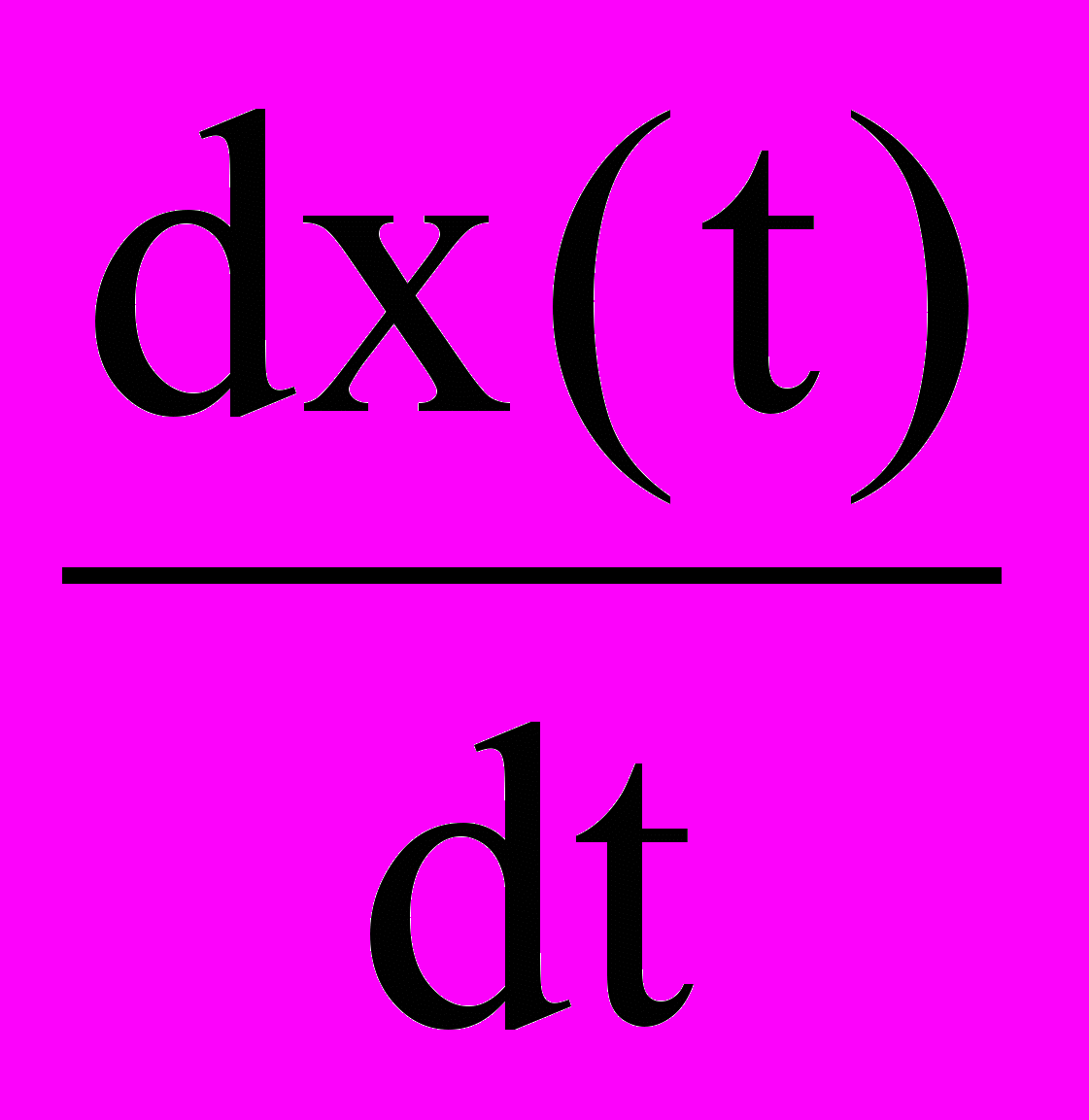т.е. фазомодулированный сигнал эквивалентен сигналу с частотной модуляцией с модулирующим сигналом .

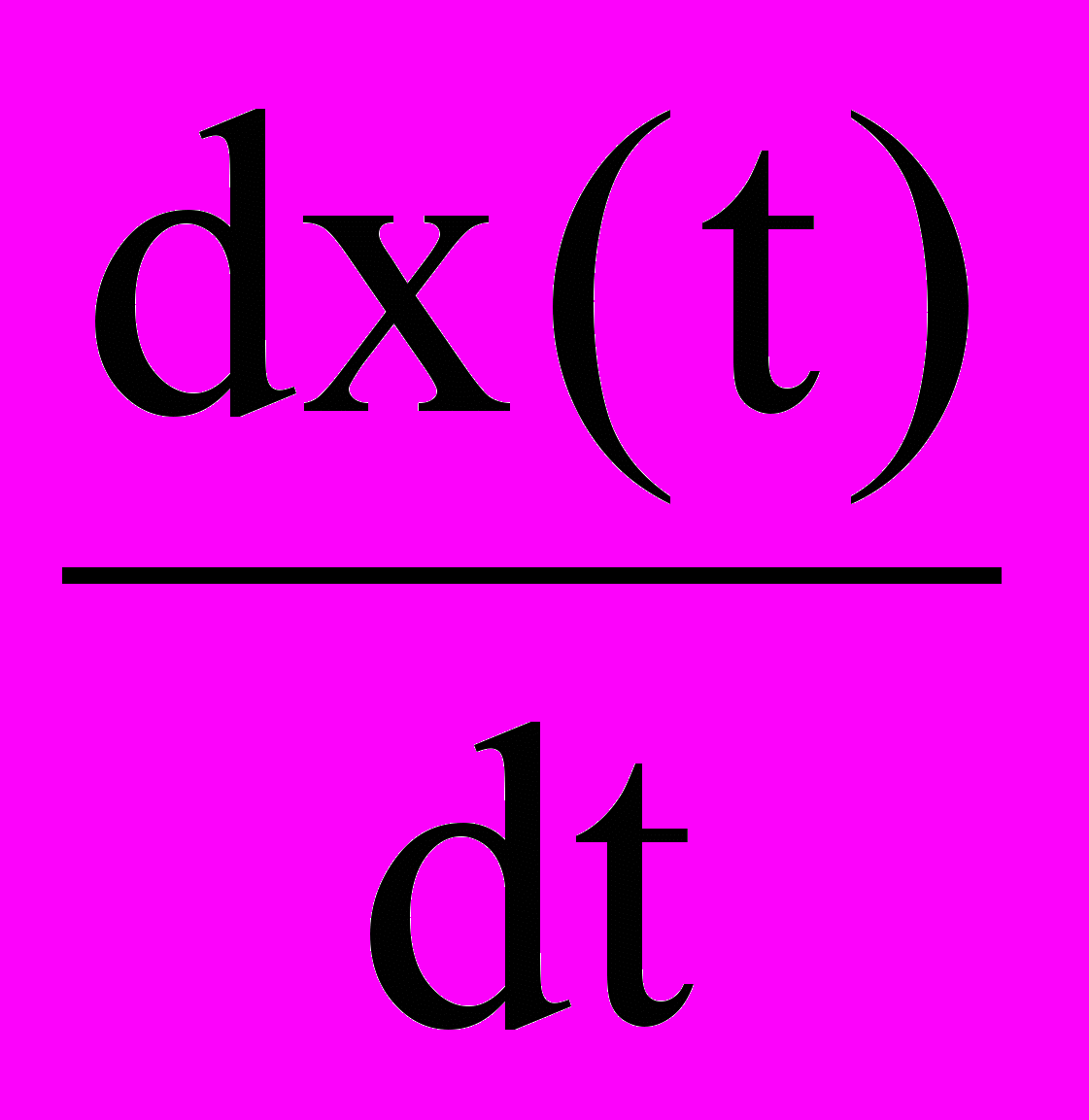В случае, когда модулирующий информационный сигнал является, как и ранее, гармоническим (тональным), x(t) = U₀ cos Ωt (Ω << ω₀), полная фаза ФМ сигнала определяется равенством:

φ(t) = ω₀t + φ₀ + aU₀ cos Ωt

а сам фазомодулированный сигнал:

S(t) = A₀ sin[ω₀t + φ₀ + aU₀ cos Ωt]. (4.14)

Величину aU₀ = М_φ называют индексом фазовой модуляции. Так как наибольшее значение cos(Ωt + φ₀) равно 1, то М_φ численно равно максимальному отклонению начального значения фазы колебания от среднего значения φ₀.

Временные характеристики ФМ колебания представлены на рис. 4.10 (а – модулирующий сигнал, б – модулированный).

Мгновенное значение частоты ФМ сигнала:

ω(t) = 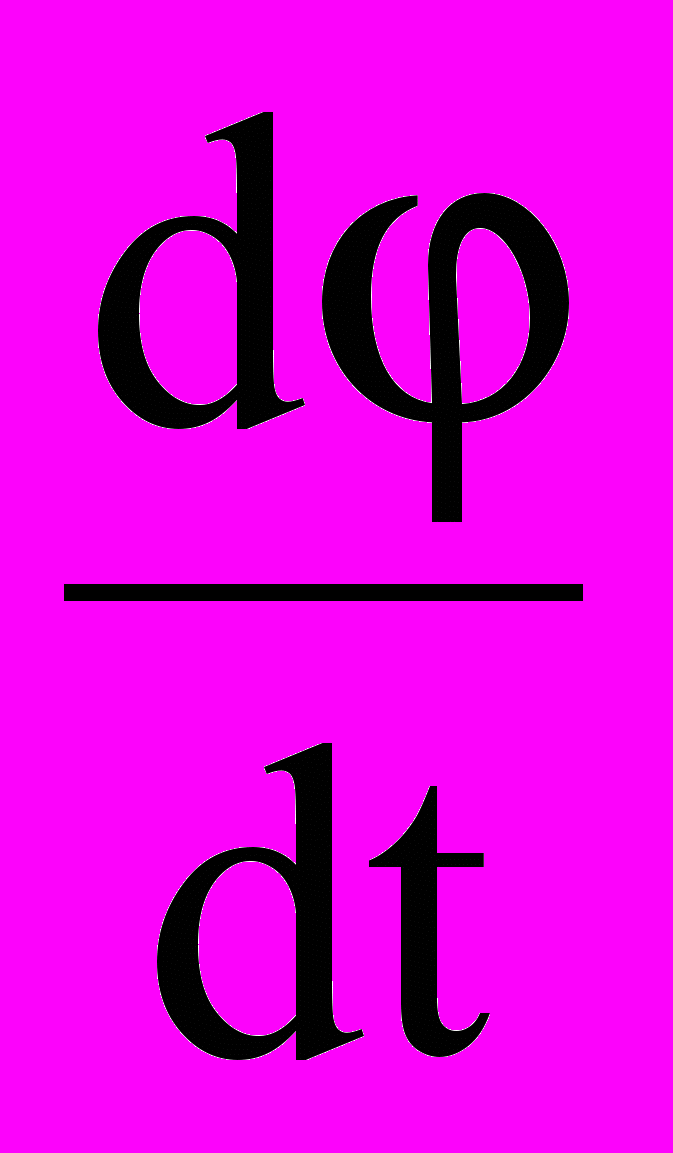= ω₀ -∆φΩ sin Ωt = ω₀ -∆ω sin Ωt,

здесь ∆ω = ∆φΩ – девиация частоты ФМ колебания.

Спектральный состав ФМ колебания при гармонической модулирующей функции полностью совпадает со спектром ЧМ колебания при гармонической x(t); различить, где модуляция ЧМ, где ФМ невозможно.




а)





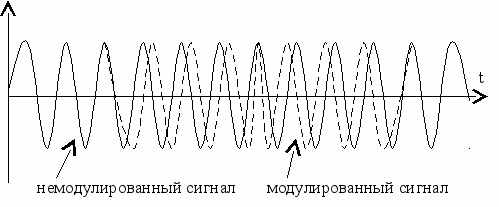
б)


Рис. 4.10


Иное положение при негармоническом модулирующем сигнале x(t). В этом случае вид модуляции можно установить по характеру изменения частоты и фазы во времени.

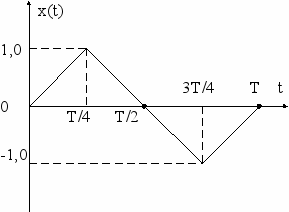
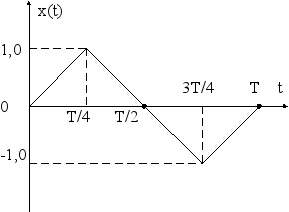
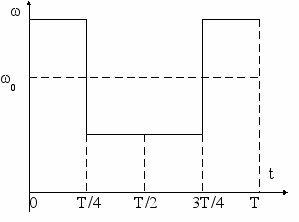
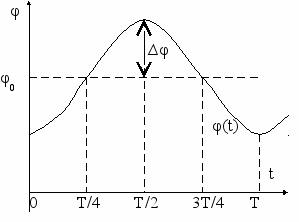
Покажем это на примере пилообразного модулирующего сигнала x(t).

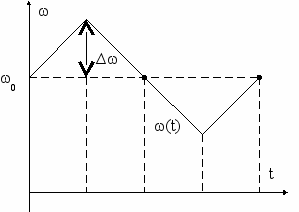
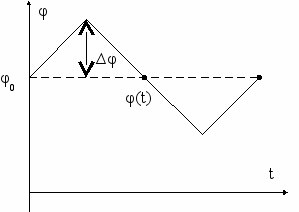
Очевидно, что пилообразные изменения частоты ω(t) (рис. 4.11б), по форме совпадающие с x(t), свидетельствуют о наличии ЧМ, а такое же изменение φ(t) (рис. 4.11д) о наличии ФМ. Из рис. 4.11е – скачкообразные изменения частоты соответствует производной от пилообразного изменения фазы.





а) г)




б) д)




в) е)

Рис. 4.11


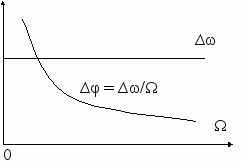
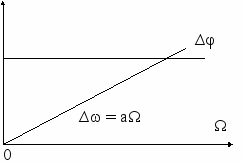
При ЧМ девиация ∆ω пропорциональна амплитуде модулирующего сигнала x(t) и не зависит от частоты модуляции Ω.

При ФМ величина ∆φ пропорциональна амплитуде x(t) и не зависит от частоты модуляции Ω.

На рис. 4.12 показаны зависимости индекса модуляции ∆ω т ∆φ от модулирующей частоты при ЧМ (см. рис. 4.12а) и ФМ (рис. 4.12б).




а) б)


Рис. 4.12


ЧМ модуляция осуществляется изменением частоты автогенератора с помощью электронного конденсатора-варикапа (variable capacitor - переменная емкость) полупроводникового прибора с управляемой внешним напряжением емкостью p-n перехода.

ФМ модуляция осуществляется применением варикапа в контуре, расстроенном относительно частоты внешнего генератора, при этом изменение фазовой характеристики обусловлено установлением рабочей частоты на скате частотной характеристики колебательного контура.

Демодуляция ЧМ и ФМ сигналов производится в схемах, сравнивающих частоты и фазы приходящих сигналов с опорными колебаниями, вырабатываемыми в схемах демодуляторов.

Рассмотрим воздействия бинарных информационных сигналов при ЧМн и ФМн.

При частотной манипуляции изменяется скачкообразно частота в зависимости от значения бинарного сигнала (рис. 4.13).

В сигналах ЧМн или Чт (частотная телеграфия) стремятся к сохранению фазы колебания при переходе от одной частоты к другой. При этом помехоустойчивость системы ЧТ оказывается выше. Спектральный состав ЧМн сигнала оказывается композицией двух спектров со средними частотами ω₁ и ω₂. Составляющие спектра в общем случае подобны спектрам радиосигналов. Полоса частот спектра имеет расширение примерно на величину разности несущих частот двух бинарных радиосигналов.




Рис. 4.13


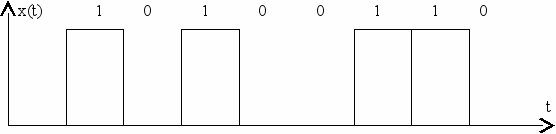
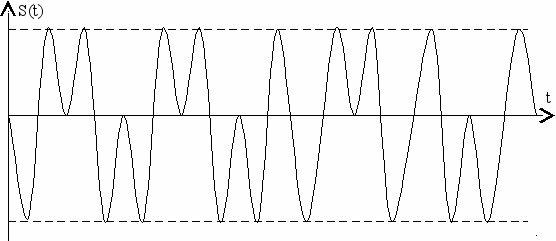
Особый интерес для систем связи представляют сигналы ФМн с фазовой манипуляцией (или ФТ – фазовая телеграфия). Применение в простейших системах двух сигналов, различающихся по фазе на 180° (противоположных) обеспечивает максимальную помехоустойчивость системы связи по сравнению с АМн и ЧМн ввиду использования наиболее различающихся сигналов (противоположных). Временная диаграмма ФМн приведена на рис. 4.14.





а)





б)


Рис. 4.14


На рис. 4.14. фаза несущего колебания при передаче сигнала "1" равна 0° и для сигнала "0" равна 180°. В моменты перехода от "0" к "1" и наоборот наблюдаются перескоки фазы на 180°.

К сожалению, системы связи с ФМн обладают существенным недостатком, связанным с демодуляцией. Демодуляция должна осуществляться на основе сравнения фазы приходящего сигнала с фазой некоего опорного колебания. Его нужно либо передавать по отдельному каналу связи, что ведет к удвоению аппаратуры связи и использованию двух каналов связи, что крайне не экономично, потому и не используется, либо восстанавливать опорное напряжение в приемнике из принимаемой последовательности ФМн сигналов. Устройство формирования опорного напряжения (УФОН) строится по двум основным принципам: пассивные и активные. В пассивных УФОН (в частности схема Пистолькорса, рис. 4.15) для формирования опорного колебания с постоянной фазой используют метод удвоения частоты входящей последовательности (при этом вследствие применения процедуры двухполупериодного выпрямления для удвоения частоты значение фазы в 0° и в 180° теряется), последующее деление частоты на два приводит опорный сигнал к частоте, совпадающей с частотой входящего сигнала, но теперь уже без скачков фазы, с постоянной фазой.

На рис. 4.15 УРФ – узкочастотный (а значит, инерционный) резонансный фильтр, ФВ – фазовращатель (для компенсации возможных фазовых сдвигов в схеме УФОНа).

На рис. 4.16 приведена схема Сифорова – активного УФОН, в котором вспомогательный управляемый генератор УГ вырабатывает опорное напряжение, зависящее от сравнения в фазовом детекторе ФД фаз приходящего сигнала и УГ (сравнение производится на удвоенной частоте, на которой отсутствуют скачки фаз входного сигнала).




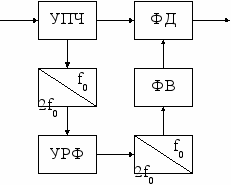
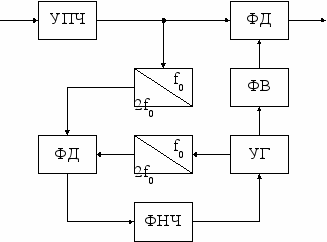
Рис. 4.15 Рис. 4.16


Кроме приведенных методов для восстановления опорного колебания в УФОН применяются активные схемы Костаса, также основанные на применении вспомогательного управляемого генератора совместно со схемами ФАПЧ – фазовой автоматической подстройки частоты, и некоторые другие.

Для всех приведенных методов создания УФОН присущ один серьезный недостаток – отсутствие начальной установки фазы, что может привести к приему сигналов "негативом". Такое явление, к сожалению, возможно и во время работы (перескок фазы) особенно при кратковременных пропаданиях сигнала.

Для устранения отмеченного недостатка русским ученым Петровичем Н.Т. был предложен метод передачи с использованием относительной фазовой манипуляции ОФМн (или ОФТ – относительная фазовая телеграфия). Метод ОФМн основан на сравнении фаз двух соседних посылок. Если передавалась "1", то фаза между посылками меняется на π, если "0", то фаза не меняется.

Такой принцип передачи цифровой информации позволяет демодулировать ОФМн сигнал без высоких требований к УФОНу. При этом возможны три способа демодуляции:

1. когерентный, при котором детектирование производится так же, как и для ФМн и в дальнейшем сравнение фаз производится по постоянному току;
   
2. некогерентный корреляционный, где также сравнение фаз двух посылок производится на постоянном токе после детектирования в квадратурных каналах;
   
3. автокорреляционный, в котором сравнение фаз двух соседних посылок производится на промежуточной частоте.
   

Дальнейшее развитие фазовых методов модуляции привело к созданию систем связи с многократными фазовыми сдвигами. Если в рассмотренной выше системе сдвиг фазы между двумя посылками принимался в 80°, то в двукратной ФМн возможна передача одновременно двух бит информации одной посылкой.

На рис. 4.17а изображена векторная диаграмма однократной ФМн (один из двух возможных положений вектора – посылки соответствуют передаче "0" или "1"), на рис. 4.17б изображена диаграмма двукратной ФМн (передается одна посылка–вектор, имеющая возможность принять одно положение из четырех возможных точек), при этом одной посылкой передается информация о двух битах информации. При применении ОФМн такая модуляция называется ДОФМн – двукратной относительной фазовой манипуляцией. По этому принципу возможно создание трехкратной ТОФМн, однако, с увеличением кратности фазовой манипуляции возрастают требования к точности фазового детектора, поэтому выше трехкратной модуляции не используют.







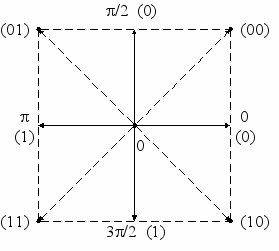
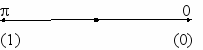
а) б)

Рис. 4.17


Фазовые методы манипуляции оказались весьма привлекательными ввиду их повышенной помехоустойчивости и относительной простоты модуляции и демодуляции. Развитие технической мысли привело к созданию конструкций сигналов с применением разных видов модуляций, позволяющих повысить скорость передачи информации за счет расширения информационных признаков у передаваемой посылки. Так, появился вид модуляции – КАМ – квадратно-амплитудная модуляция, которая объединила АМн и ОФМн, что значительно расширило число возможных изображающих точек в векторной диаграмме рис. 4.17 и позволило передавать одной посылкой (одним импульсом) 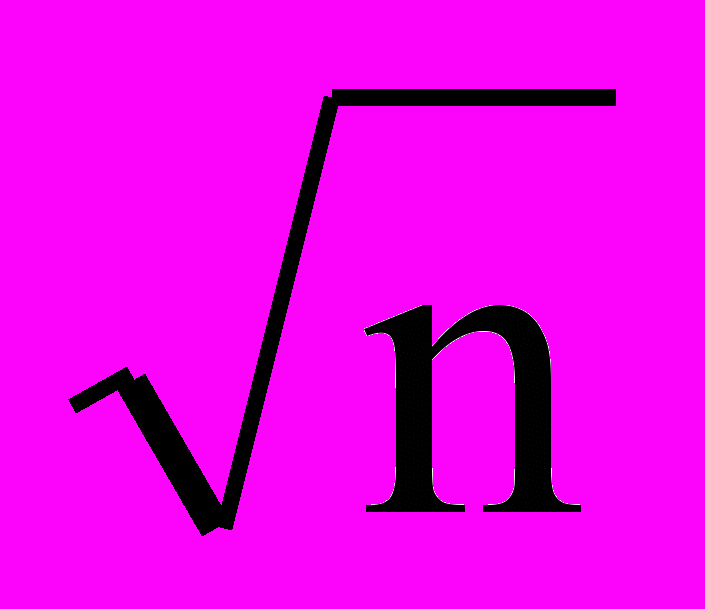бит информации, где n – количество изображающих точек (и, соответственно, векторов) в векторной диаграмме сигнала. На рис. 4.18а приведено примерное временное изображение сигнала, а на рис. 4.18б – векторная диаграмма для модуляции КАМ-8.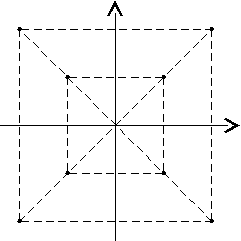




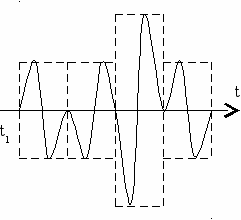
а) б)

Рис. 4.18


Ни рис. 4.18б – 8 изображающих точек (4 отличия по фазе и 2 отличия по амплитуде). Такая модуляция позволяет одним импульсом передать информацию о трех разрядах двоичного числа (или 3 бит) информационного цифрового сигнала. Максимально возможные конструкции на сегодня (по данным литературы) до КАМ-256, в котором одним импульсом передается информация о восьми разрядах двоичного информационного числа.


Литература:

[1] стр. 73-82, 103-114. [2] стр. 96-102. [3] стр. 20.


Контрольные вопросы:

1. Как связаны между собой ЧМ и ФМ модуляции?
   
2. Как определить отличие ЧМ и ФМ модуляции?
   
3. В чем отличие ОФМн от ФМн?
   
4. Дайте определение двукратной ОФМн.
   
5. Дайте определение КАМ модуляции.
   

^ 4.3. Модуляция на импульсном переносчике

В качестве несущего переносчика возможно использование импульсной периодической последовательности. При передаче аналоговой (непрерывной) информации необходимо только соблюсти условия целостного отображения (без потери информации). Это, прежде всего, условия теоремы Котельникова по временной дискретизации и условия требуемой точности в отображаемом импульсном преобразовании. Периодическая последовательность видеоимпульсов характеризуется амплитудой, длительностью импульсов, частотой их следования, фазой (временным положением) импульсов. Использование этих параметров для переноса информационного сигнала (мгновенных значений его) позволяет создать несколько видов модуляции, так же как и для гармонического переносчика. Это амплитудно-импульсная модуляция АИМ, широтно-импульсная модуляция ШИМ, частотно-импульсная модуляция ЧИМ и фазо-импульсная модуляция ФИМ или ВИМ – время-импульсная модуляция.

Простейшим видом импульсной модуляции является АИМ – амплитудно-импульсная модуляция (см. рис. 4.19).

Несущая импульсная последовательность представлена на рис. 4.19а. Рис. 4.19б отображает информационный сигнал, на рис. 4.19в представлена промодулированная последовательность видеоимпульсов, несущих полезный информационный сигнал. Во время действия импульса переноса передаются и мгновенные значения информационного сигнала. Такую модуляцию называют АИМ-I – амплитудно-импульсной модуляцией первого рода. На рис. 4.19г импульсная промодулированная последовательность, в которой каждый импульс имеет постоянную амплитуду. Такая модуляция называется АИМ-II. При снижении длительности импульсов несущей последовательности параметры АИМ-I и АИМ-II сближаются.




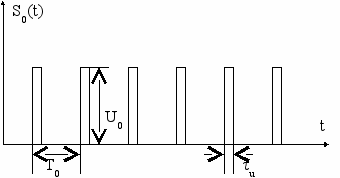
а)





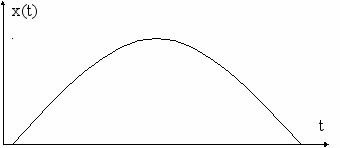
б)





в)





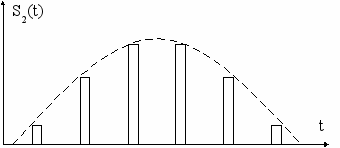
г)


Рис. 4.19

Немодулированная периодическая последовательность (рис. 4.19а) раскладывается в ряд Фурье (спектр):

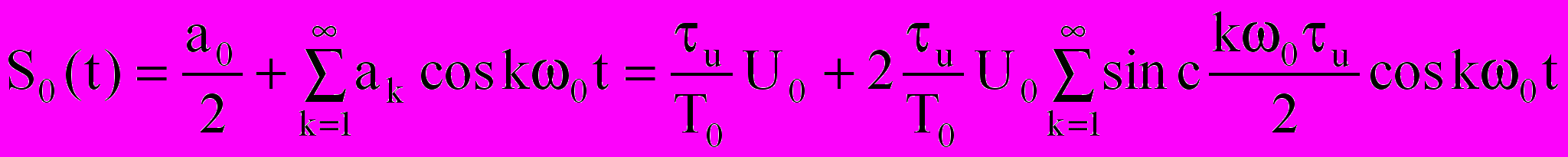. (4.15)

Для нахождения спектра АИМ нужно в спектр последовательности вместо U₀ внести амплитудную модуляцию:

U₀[1 + mX(t)],

где m – глубина АМ модуляции

X(t) – нормированная по максимуму информационная функция [x(t)]≤1.

Если X(T) = cos Ωt (гармонический сигнал, как и ранее), то

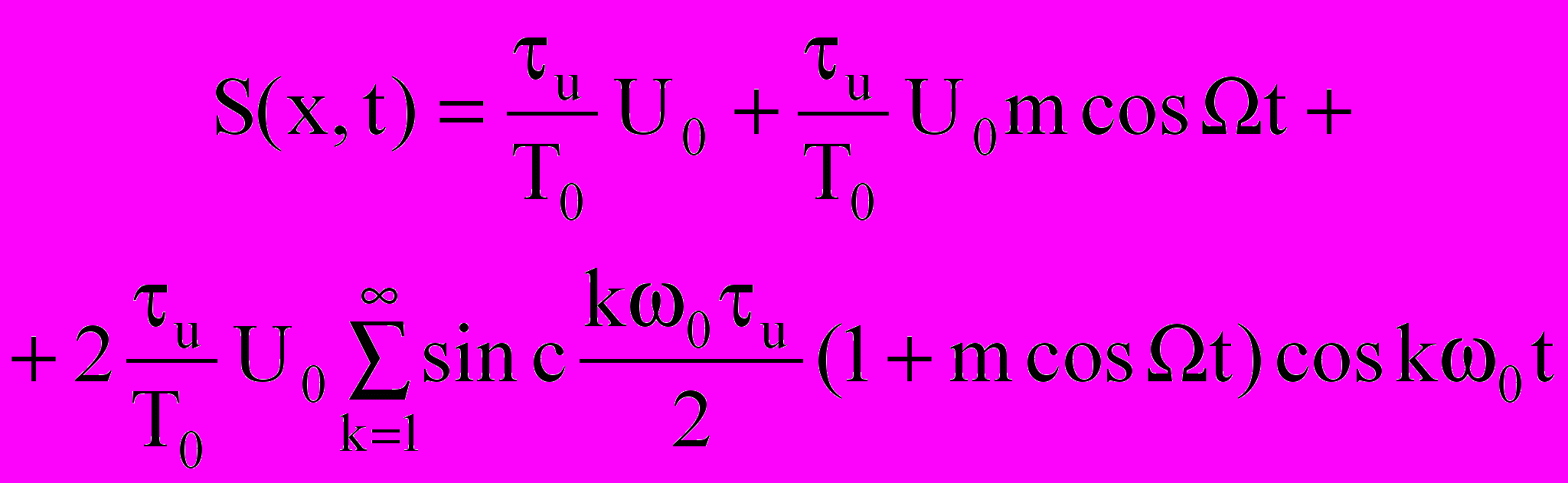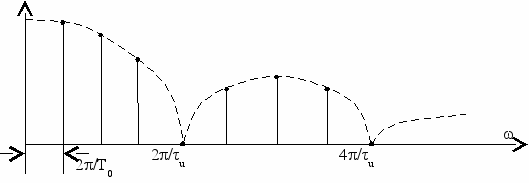
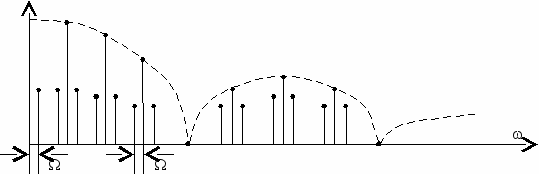
. (4.16)

Раскрытие скобок в (4.16) приводит к определению последовательности АМ спектров (рис. 4.20б). Спектр немодулированной последовательности представлен на рис. 4.20а. Если x(t) – представляет сложный непериодический сигнал, например, телефонный сигнал в полосе 0,3÷3,4 кГц, то спектр также будет содержать гармоники с боковыми полосами, определяемыми исходным телефонным спектром (рис. 4.20в). На рис. 4.20 приведены амплитудные частотные спектры, т.е. спектр, взятый по модулю.

Модуляция АИМ осуществляется ключевой схемой (для АИМ-II с фиксацией), демодуляция, как следует из рассмотрения спектра полностью совпадает с методом Котельникова восстановления непрерывного сигнала использованием фильтра низких частот, выделяющего первый участок спектра, примыкающий к началу координат.





а)





б)





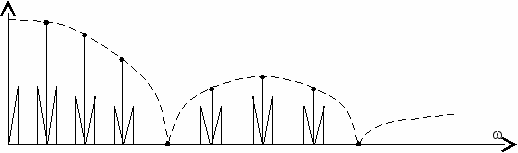
в)


Рис. 4.20


В ШИМ – широтно-импульсной модуляции информация о мгновенном значении (в точке отсчета по Котельникову) передается шириной (длительностью) импульсов. Различают ШИМ-I и ШИМ-II в зависимости от расположения импульса-переносчика относительно значащего момента отсчета (по Котельникову). На рис. 4.21а приведена несущая немодулированная последовательность, рис. 4.21б представляет передаваемый информационный сигнал. На рис. 4.21в отображается ШИМ-I, а на рис. 4.21г – ШИМ-II.





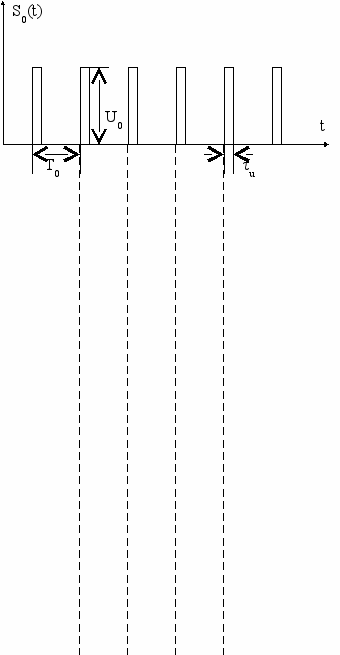
а)





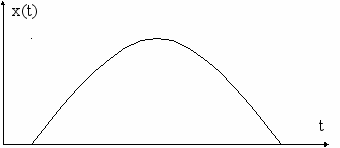
б)





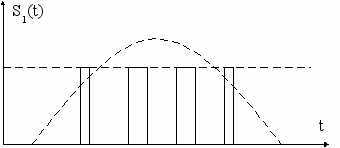
в)





г)


Рис. 4.21


Спектр ШИМ сигнала имеет много общего со спектром АИМ, но отличается более сложной структурой. В нем имеются неискаженные составляющие полезного сигнала и составляющие вида kω₀ + nΩ. Участок спектра, занимаемый полезным сигналом может быть "засорен" комбинационными составляющими на частотах ω₀ - nΩ, что может дополнительно исказить полезный информационный сигнал.

При фазо-импульсной модуляции (ФИМ, ВИМ) используется модуляционный параметр измерения временного положения несущих импульсов. Аналитическое выражение ФИМ сигнала имеет вид:

,

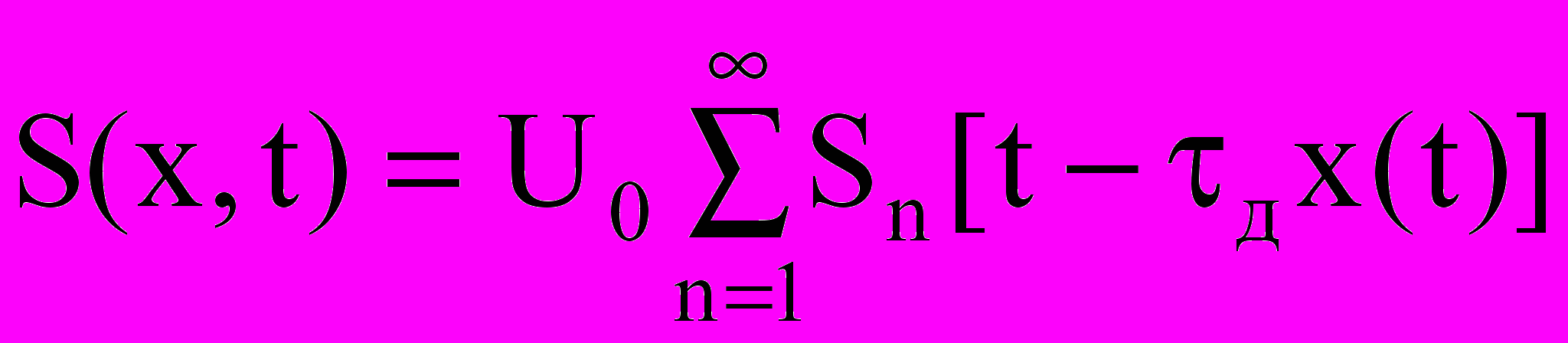здесь U₀ – амплитуда импульса;

S_n(t) – функция, описывающая огибающую импульса;

τ_д – девиация временного положения импульса;

x(t) – передаваемый информационный сигнал.

На рис. 4.22а приведена немодулированная несущая импульсная последовательность. Рис. 4.22б отображает полезный информационный сигнал. На рис. 4.22в приведена промодулированная импульсная последовательность. Время задержки τ_з передает сведения о мгновенном значении сигнала (в смысле Котельникова) и зависит от амплитуды дискретного отсчета.

Модуляция и демодуляция ФИМ сигналов непосредственно невозможна, поэтому ФИМ сигналы сначала преобразуют в сигналы АИМ или ШИМ (аналогично при модуляции сначала получают сигналы АИМ или ШИМ, затем преобразуют их в ФИМ) и в дальнейшем детектируют уже в другой системе модуляции.

Спектральный состав ФИМ сигналов достаточно сложен, хотя занимаемая полоса частот определяется, в основном, исходной несущей импульсной последовательностью.





а)





б)





в)


Рис. 4.22


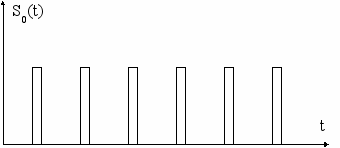
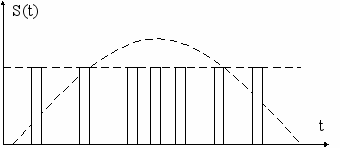
При ЧИМ – частотно-импульсной модуляции в качестве модулирующего параметра принимается частота следования несущих импульсов. Временные графики приведены на рис. 4.23.

На рис. 4.23а приведена немодулированная несущая импульсная последовательность. Рис. 4.23б отображает полезный информационный сигнал. На рис. 4.23в приведена промодулированная импульсная последовательность. Изменение частоты следования передает мгновенные значения (в смысле Котельникова) передаваемого информационного сигнала. По многим свойствам ЧИМ сигнал близок к ЧМ сигналу на гармонической несущей, что предопределяет близкие по причинам модуляцию и демодуляцию ЧИМ сигналов.




а)





б)





в)


Рис. 4.23


Литература:

[1] стр. 85-91. [2] стр. 112-115.


Контрольные вопросы:

1. Повторите условия теоремы Котельникова для дискретизации сигналов.
   
2. Дайте определение модуляции АИМ-I, АИМ-II.
   
3. Какова ширина спектра АИМ?
   
4. Дайте определение ШИМ-I, ШИМ-II модуляции.
   
5. Чем модуляция ФИМ отличается от АИМ?
   
6. Чем модуляция ЧИМ отличается от ФИМ?
   

^ 4.4. Цифровые виды модуляции

Хотя цифровые виды модуляции также являются модуляцией на импульсном переносчике, принципы их образования коренным образом отличаются от предыдущих импульсных видов модуляции, что позволяет выделить их в отдельный вид модуляции. Кроме того, следует отметить, что информацию о полезном сигнале передают не сами импульсы, а их сочетания в отдельных группах и особых последовательностях. В настоящее время различают три основных класса цифровых сигналов: импульсно-кодовую модуляцию (ИКМ), дифференциальную ИКМ (ДИКМ), дельта-модуляцию (ДМ).

^ Импульсно-кодовой модуляцией (ИКМ) называется представление информационного сигнала дискретными отсчетами, взятыми по условиям Котельникова и представленными, в свою очередь, в квантовом виде. Таким образом, процесс импульсно-кодовой модуляции содержит два этапа: сначала сигнал дискретизируется и затем полученный дискретный отсчет квантуется, т.е. делится на части. На рис. 4.24 представлены процедуры дискретизации и квантования.

На рис. 4.24а представлена исходная немодулированная импульсная последовательность (в соответствии с теоремой Котельникова T≤1/2F_в, что для телефонного сигнала с полосой 0,3÷3,4 кГц составляет Т=1/6,8 кГц) Для повышения точности частота дискретизации выбрана по рекомендации МККТТ – 8 кГц, тогда Т = 1/8 кГц = 125 мкс. На рис. 4.24б представлен информационный сигнал, а на рис. 4.24в этот сигнал дискретизирован и представлен своими отсчетами. На рис. 4.24г эти дискретные отсчеты проквантованы (разделены на отрезки) и на рис. 4.24д представлен численными значениями в двоичном коде с помощью бинарного сигнала (0;1). Неточное совпадение величины отсчета с цифровой сеткой образует "остатки" ε(t) (рис. 4.24е), которые в силу случайности создают шум квантования.




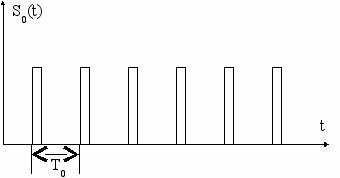
а)





б)





в)





г)





д)





е)


Рис. 4.24

Шаг квантования ∆ определяет точность числового представления отсчета. Обычно шкалу квантования применяют нелинейную, для малых сигналов она мекая, для больших – крупная. Этому способствует применение, так называемого, компандирования, которое включает в себя два этапа: сжатие (компрессию) динамического диапазона при передаче и расширение (экспандирование) его при приеме. По рекомендациям МККТТ количество разрядов двоичного числа для квантования уровня отсчетов принято равным 8. Первый разряд несет информацию о знаке отсчета (+ или -), три последующих оценивают отсчет по грубой шкале
2³ = 8 уровней в положительной и 8 уровней в отрицательной областях нахождения отсчета (причем уровни эти, называемые сегментами, неравномерны, для малых сигналов малы, для больших сигналов постепенно увеличиваются). Четыре оставшихся разряда представляют более подробный анализ уровней отсчетов, своеобразную "лупу" – 2⁴ = 16 равномерных уровней квантования в том сегменте, который определился первыми тремя разрядами. Естественно, что шкала этой "лупы" в зависимости от номера сегмента разная. Шум квантования (см. рис. 4.24е) ограничивает снизу динамический диапазон преобразования сигнала (максимальная величина "остатка" несовпадения отсчета не превышает ∆/2 – половины шага квантования).

Спектральный состав ИКМ сигнала определяется элементарными импульсами, представляющими восьмиразрядное двоичное число. Обычно период дискретизации Т₀ = 125 мкс делится на восемь участков, и в каждом участке располагается один возможный импульс, составляющий "1", занимающий 0,5 этого участка, т.к. вторая половина отведена под защитный интервал. Из этого следует, что полоса частот ИКМ сигнала значительно шире, чем для АМ сигнала при прочих равных условиях. Итак, для телефонного сигнала полоса ИКМ больше соответствующей полосы АМ сигнала не менее чем в 16 раз (а при дополнительных условиях еще больше). Это один из существенных недостатков системы ИКМ. Если принять полосу частот для АМ-ОБП в 4 кГц, то для ИКМ будет 64 кГц, что соответствует скорости передачи цифрового канала в 64 кбит/с.

Для снижения занимаемой полосы и уменьшения количества разрядов (т.е. импульсов) можно применять дифференциальную импульсно-кодовую модуляцию ДИКМ, которая передает не абсолютное значение отсчета, а только разницу между предыдущим и настоящим отсчетами (так, например, на рис. 4.24д разница между вторым и третьим отсчетами составляет один разряд двоичного числа, а между третьим и четвертым вообще разница равна нулю). Такой подход позволяет существенно уменьшить разрядность передаваемого числа. Можно проанализировать систему ДИКМ на основе принципа предсказания, т.е. по предыдущим отсчетам можно с некоторой долей вероятности "предсказать" следующий отсчет (таких предыдущих отсчетов по рекомендации МККТТ-6-721 нужно 6).

Существует значительное число схем, реализующих систему ДИКМ. Проблемой может быть начальный отсчет, но по истечению некоторого срока передачи эта проблема снимается. Кроме того, при передаче случайного сигнала, каковым является телефонный сигнал, предсказатель позволяет иногда реже снимать отсчеты, что эквивалентно снижению скорости передачи (т.е. эффективной ширины спектра сигнала).

Системы с изменяющимся шагом опроса являются адаптивными (т.е. приспосабливающимися к реальным условиям) и образуют адаптивную дифференциальную импульсно-кодовую модуляцию АДИКМ. За счет снижения числа разрядов и адаптивного алгоритма модуляции удается снизить скорость передачи телефонного сигнала в 2 раза с 64 кбит/с до
32 кбит/с (т.е. полосу частот, занимаемую АДИКМ сигналом снизить до
32 кГц, что только в 8 раз больше полосы, отводимой для АМ-ОБП).

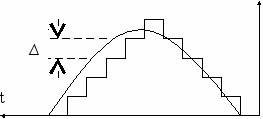
Дальнейшее развитие методов ИКМ привело к созданию метода дельта-модуляции (ДМ). При увеличении частоты дискретизации различие между соседними отсчетами уменьшается и может дойти до значения, передаваемого одним разрядом двоичного числа. При этом непрерывная исходная информационная функция аппроксимируется ступенчатой одношаговой функцией, как приведено на рис. 4.25.

а)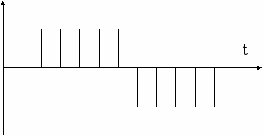





б)


Рис. 4.25


На рис. 4.25а приведен передаваемый информационный сигнал со ступенчатой функцией, а на рис. 4.25б передаваемая импульсная последовательность, которую можно отразить в двоичной системе (0,1) одним разрядом. Как видно из рис. 4.25а, при передаче полезного сигнала возможны ошибки, связанные с недостаточной скоростью дискретизации (ступенчатая функция отстает от передаваемого сигнала). Для устранения этого явления необходимо на отдельных временных участках увеличивать частоту дискретизации. Таким образом, мы приходим к понятию адаптивной дельта-модуляции АДМ.

По сравнению с ИКМ сигнал ДМ имеет повышенную частоту дискретизации, но меньшее число разрядов (в 8 раз). При этом частота следования импульсов, отражающих разряды двоичного числа дискретных отсчетов, примерно одинакова, техническая реализация ДМ модуляции значительно проще, а шум ложных импульсов реже.


Литература:

[1] стр. 91-103. [2] стр. 335-348. [3] стр. 242-256.


Контрольные вопросы:

1. Повторите условия теоремы Котельникова для дискретизации непрерывных сигналов. Какая принята частота дискретизации телефонного сигнала согласно рекомендациям МККТТ?
   
2. Дайте определение "квантованию" сигнала.
   
3. Что такое "шум квантования"?
   
4. Как отличается по занимаемой полосе частот спектр ИКМ сигнала от спектра АМ-ОБП?
   
5. Дайте определение ДИКМ модуляции.
   
6. Дайте определение АДМ модуляции.
   

^ 4.5. Модуляция на шумоподобном переносчике

Шумоподобные сигналы (ШПС) или, иначе говоря, широкополосные сигналы или, иначе, псевдослучайные или сложные сигналы имеют ряд существенных преимуществ перед простыми сигналами. Понятие простого и сложного сигналов определяется величиной, называемой базой сигнала
B = ∆FT, которая находится произведением занимаемой полосы частот на длительность. У простых сигналов база примерно равна или близка к единице В ≈ 1. Например, если считать, что основной спектр прямоугольного видеоимпульса заключен в первом "лепестке" спектра, т.е. до частоты f = 1/τ_u (кстати, эффективная полоса частот прямоугольного видеоимпульса определяется как ∆f_эф = 1,37/τ_u), то произведение ∆Fτ_u = 1. У сложных сигналов В>>1. Для финитных сигналов с ограниченной длительностью полоса частот крайне велика, что дало возможность называть их широкополосными. Корреляционная функция у них имеет острый пик, что дало возможность называть их шумоподобными, т.к. для шумового сигнала имеет острый пик корреляционной функции, но т.к. эти сигналы все же не случайные, а вполне детерминированные, определился термин псевдослучайные. ШП сигналы обладают повышенной помехоустойчивостью, позволяющей принимать и обрабатывать сигналы, имеющие мощность ниже уровня шума. Коэффициент усиления ШП сигнала определяется способом его формирования и находится из выражения К_ус = q²/ρ², где q² – отношение сигнал/шум на выходе схемы обработки, а ρ² – отношение на входе системы (например, у системы GPS - Global Position System – системы спутникового самоопределения, использующей сложный ФМ сигнал при ширине спектра в 25 мГц, коэффициент усиления составляет 47).

Существует большое разнообразие сложных сигналов. Применяются они для импульсной модуляции (манипуляции) и заключаются, в основном, во внутриимпульсной дополнительной модуляции. Это:

• частотно-модулированные сигналы ЧМ (наиболее распространенный ЛЧМ – линейный ЧМ сигнал);
  
• многочастотные сигналы МЧ;
  
• дискретные составные частотные сигналы ДСЧ;
  
• с кодовой частотной модуляцией КЧМ;
  
• фазоманипулированные сигналы ФМ;
  
• фазоманипулированные кодовые сигналы КФМ.
  

Здесь кратко рассмотрим сигналы КФМ. Это, прежде всего, создание внутренней кодовой манипуляции, создание специальной импульсной последовательности бинарных сигналов. Рассмотрим принцип кодового уплотнения на примере кода Баркера-5. Передаваемый импульс в системе связи разделим на пять временных участков, каждый из которых в дальнейшем будет заполнен гармонической несущей, но в каждом участке со своей фазой (0;π).




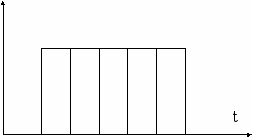
Рис. 4.26


Код Баркера представляет собой особую числовую (двоичную) последовательность, обладающую специфическим свойством, а именно корреляционной функцией с максимальным пиком (корреляционная функция, определяющая связь между мгновенными значениями сигнала, совпадает с выходным напряжением оптимального согласованного фильтра (см. лекцию 5)).

Коды Баркера для разной длины кода имеют значения:

N = 3	код	1,1,-1; 1,-1,1	(110, 101)
N = 4	код	1,1,-1,1; 1,1,1,-1	(1101, 1110)
N = 5	код	1,1,1,-1,1	(11101)
N = 7	код	1,1,1,-1,-1,1,-1	(1110010)
N = 11	код	1,1,1,-1,-1,-1,1,-1,-1,1,-1	(11100010010)
N = 13	код	1,1,1,1,1,-1,-1,1,1,-1,1,-1,1	(1111100110101)

Код Баркера существует только для перечисленных последовательностей. Построим корреляционную функцию для пятиэлементного кода Баркера, взятого нами для примера. Строим таким образом: запишем пятиэлементный код знаками + и – в строку, слева в столбец также запишем этот код. Строка и столбец образуют обрамление матрицы, которую начинаем заполнять по строкам выбранного кода, каждый раз сдвигая строку на один шаг (один элементарный импульс) и инвертируя код, если в столбце оказывается "-".

+	+	+	+	-	+
-		-	-	-	+	-
+			+	+	+	-	+
+				+	+	+	-	+
+					+	+	+	-	+
Σ	+	0	+	0	5+	0	+	0	+

Нанесем полученные значения на график и соединим точки отсчета:




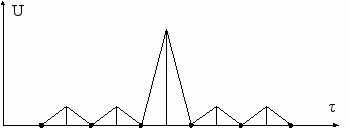
Рис. 4.27


График корреляционной функции на рис. 4.27 показывает уровень огибающей сигнала на выходе согласованного фильтра, наличие острого пика в этой функции определяется сложением по фазе всех составляющих сложного сигнала и позволяет уверенно выделить этот сигнал из всех других.

Реальный временной сигнал с уплотненным кодом Баркера и применением фазоманипулированных сигналов представлен на рис. 4.28.

На рис. 4.28а приведен передаваемый импульс, а на рис. 4.28б в системе АМ-КФМ_н, на рис. 4.28в сигнал на выходе согласованного фильтра.





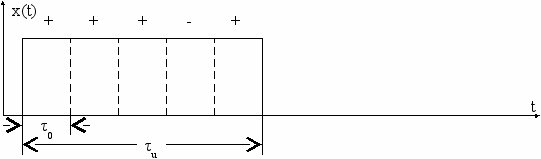
а)





б)





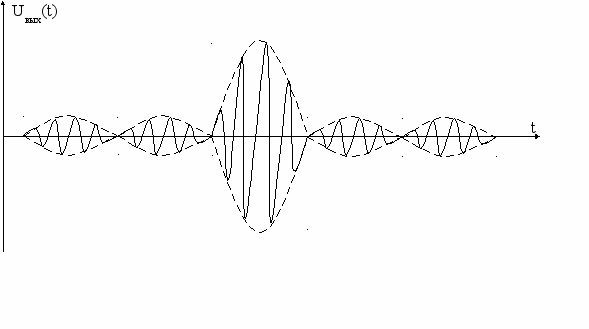
в)


Рис. 4.28


Кроме кодов Баркера существует значительное число других кодов, обладающих подобными свойствами: это, прежде всего, m-последовательности (квазислучайные), коды, построенные на полиномах Лежандра, Холла, Якоби и др., сигналы Фрэнка и т.д. Некоторые кодовые последовательности рассмотрим в лекции 6 при исследовании многоканальных систем.

Сейчас только отметим преимущества сложных сигналов:

• помехоустойчивость;
  
• скрытность;
  
• хорошее использование каналов связи;
  
• возможности создания параллельных каналов связи, работающих в одной полосе частот в одно и то же время и различающихся только кодовым набором (асинхронно-адресные системы связи).
  

Литература:

[1] стр. 117-123.


Контрольные вопросы:

1. Какие сигналы называются сложными?
   
2. Дайте определение базы сигнала.
   
3. Как строится внутренняя структура видеоимпульса?
   
4. Что такое код Баркера?
   
5. Почему сигнал с кодом Баркера имеет лучшие показания по помехоустойчивости?